Abstract
Dynamic coefficients of a bearing are basic elements of rotor dynamics analysis. At present, there are still some issues in the calculation of the dynamic coefficient of air foil bearing. In this paper, the dynamic coefficients of the air foil bearing are calculated by time-domain identification. This method does not need to linearize the system equations, so it is generally applicable to different models for air foil bearings. Using the established method, this paper verified the calculation results using the foil model with axial uniform deformation for the first time, and the influence of the foil model on the dynamic coefficients was studied. The calculation results of the foil models with axial uniform deformation and axial independent deformation have significant differences. Furthermore, the accuracy of the dynamic coefficient method for different disturbance amplitudes was compared. The results indicate that the dynamic coefficient method has good accuracy over a large disturbance range.
1. Introduction
The air foil bearing is a self-acting hydrodynamic bearing that uses ambient air as the lubricant and has a flexible surface. It has the advantages of low power consumption, no need for an additional lubrication system, good temperature resistance, and high-speed performance [1,2,3,4]. Therefore, it is environmentally friendly and widely used in green technology such as air cycle machines in aircraft, turboexpanders for cryogenic applications, turbochargers, and micro gas turbine engines [3]. As the dynamic viscosity coefficient of air is low, the air foil bearing provides limited damping under high-speed conditions and may suffer from hydrodynamic instability; thus, dynamic design and analysis are necessary for the safe operation of a rotor. Obtaining the dynamic characteristics of a bearing is a prerequisite for rotor dynamic design [5,6]. The dynamic coefficient of a bearing is typically used to describe the dynamic characteristics.
Lund [7] first proposed a numerical calculation method to determine the four stiffness coefficients and four damping coefficients of the tilting pad bearings. The stiffness and damping coefficients are collectively referred to as the dynamic coefficients of the bearing. Then, Lund proposed a small perturbation method for calculating the dynamic coefficient of gas bearings with rigid surfaces [8]. Based on the bearing dynamic coefficients, analysis of rotor dynamic properties, such as unbalanced response, Campbell diagrams of modes, and stability can be performed. In 1993, Peng and Carpino [9] applied Lund’s small disturbance method to calculate the dynamic coefficient of air foil bearings. They simplified the foil structure as a simple elastic foundation model (SEFM), and the foil deformation equation can be directly combined with the Reynolds equation, and they derived the small disturbance equation and then calculated the dynamic coefficient of the bearing. Subsequently, many researchers [10,11,12,13,14] have studied the influence of the dynamic pressure gas-bearing design parameters on the stability of the rotor system based on the calculation method of Peng and Carpino. The studies show that the geometric parameters of the bearing and the design parameters of the foil (such as stiffness, distribution, and dissipation damping) have a great influence on the stability of the system.
The bearing dynamic coefficients have a clear physical meaning, so they are widely used in engineering practice [15,16]. However, there are still problems in the calculation of dynamic coefficients of air foil bearings. Hoffmann et al. [17] compared the linear stability prediction based on dynamic coefficients with the simulation results of time-domain nonlinear dynamics and found that the differences between the two were 0.5% and 7.2% under load and static load of 5 N and 30 N, respectively. Furthermore, Larsen et al. [18] found that there is a significant difference between the rotor instability speed predicted based on the dynamic coefficient of the bearing and the onset instability speed obtained by time-domain nonlinear dynamics, and the difference increases with a decrease in foil stiffness. Osmanski et al. [19] pointed out that the cause of divergence is that the SEFM model with axially independent deformation is used in solving the disturbance equation of the dynamic coefficient, while the axial uniform deformation SEFM model is used in the time-domain simulation. Therefore, it is necessary to develop a bearing dynamic coefficient calculation method that can be applied to different foil models. Gu et al. [20] recently proposed a novel dynamic coefficient calculation method that can adopt different linear foil structure models. This method enables the dynamic coefficient method to obtain the onset instability speed results consistent with the time-domain method. Bonello and Pourashraf [21] showed that the modal analysis of a rotor supported by an air foil bearing using the bearing dynamic coefficient method has good accuracy in comparison with the direct linearization method proposed in [22].
Accurate calculation of bearing dynamic coefficients is crucial for rotor dynamic analysis [23]. However, at present, the calculation of the dynamic coefficient is mainly obtained using the frequency-domain perturbation method, in which the system governing the equation needs to be linearized. Linearization requires very complicated derivation work, and even direct linearization cannot be performed for discontinuous behaviors such as Coulomb friction.
Recently, the time-domain calculation method has been greatly developed. A fully coupled method was proposed by Bonello and Pham [24]. In this method, all the variables of the system are solved simultaneously, which significantly improves the calculation efficiency. One important advantage of the time-domain simulation is that it can be applied to air foil bearings with different foil models. Therefore, the time-domain simulation using the fully coupled method is general for different air foil bearing models. The efficient fully coupled integration method enables a fast time-domain calculation of the dynamic coefficients.
This paper presents a time-domain identification method to calculate the dynamic coefficient of the air foil bearing. This method can also be used to identify the dynamic coefficient based on experimental data [25]. The calculation method is directly based on the nonlinear simulation of the bearing, so it is generally applicable to different models for air foil bearings. Using the established method, the influence of the foil model and the disturbance amplitude on the dynamic coefficients are studied.
2. Modeling of the Bearing
This section presents the dynamic modeling of the air foil bearing, which is the basis for the calculation of the bearing capacity coefficients. As the governing equations of the bearing are partial differential equations, the finite difference method is used to obtain the numerical solutions. The bump-type air foil bearing given in Figure 1 is used in this work as it is widely used and studied.
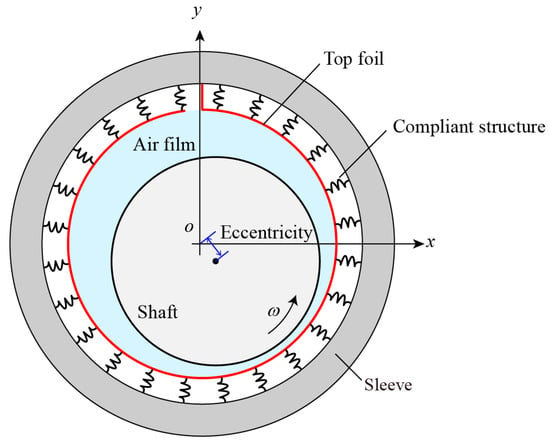
Figure 1.
Configuration of an air bump foil bearing.
2.1. Governing Equation
2.1.1. Air Film
It is assumed that the air flow in the bearing is laminar, Newtonian, and has a compressible thin film flow under isothermal conditions. Therefore, the variation in the hydrodynamic pressure across the film thickness is negligible, and the pressure is considered the only function of in the spatial domain, where and , with being the angular coordinate along the direction of rotation of the journal, being the axial coordinate, and being the bearing length. The film pressure is governed by the Reynolds equation for a compressible perfect fluid [26]:
where is the viscosity of air, is the radius of the journal, is the surface velocity of the shaft, is the rotational speed of the journal, and is the film thickness.
For a uniform cylinder bearing shown in Figure 1, the height film thickness is calculated using the following equation:
where is the radial clearance, and are the displacements of the shaft with respect to the bearing center, and is the radial deflection of the top foil.
The boundary conditions for the Reynolds Equation (1) are as follows:
where is the ambient pressure.
The Reynolds Equation (1) can be formulated in terms of the state variable as follows [26]:
The reaction forces from the dynamic pressure air film acting on the rotor surface are calculated as follows:
The contribution of the sub-ambient in the above integration is ignored to impose the Gümbel condition, which is necessary when separations between the top foil and bump foil are ignored.
2.1.2. Foil Structure
The foil structure is modeled as the commonly used SEFM [27]. It is a Winkler foundation model that assumes that the foil deflections are only dependent on the local air pressure. Furthermore, according to the authors of [28,29], the foil is assumed to deform uniformly in the axial direction, which has been shown to be a reasonable assumption. The governing equation of the SEFM with uniform deformation in the axial direction is written as follows:
where and are the damping coefficient and stiffness coefficient per unit length of the bump foil structure, respectively. is the mean net film pressure applied on the foil along the axial direction, and is calculated by
The structural damping of the foil is assumed to be viscous, quantified by the hysteretic loss factor as follows:
2.2. Discretization and Solution
The finite difference method is adopted for the discretization of the system equation. The air film is meshed using a two-dimensional (2D) grid with points, as shown in Figure 2. The foil structure is correspondingly meshed with a one-dimensional (1D) grid with points.
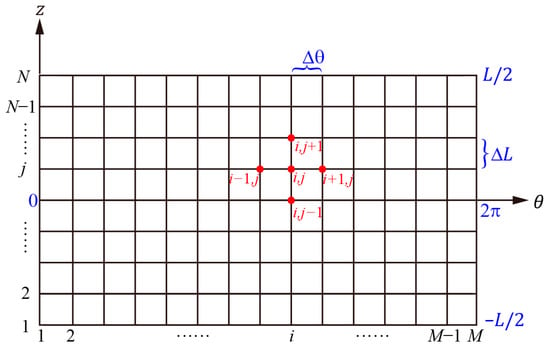
Figure 2.
The finite difference mesh of the air film.
By applying a central difference scheme in the spatial domain [30], the partial derivatives of the pressure are expressed as
Similarly, the partial derivatives of the foil deformation can be expressed as
where and refer to the step sizes in the and directions, respectively. Note that these numerical difference calculations are only applied to the inner points (i.e., and ). For the boundary points, the boundary conditions are implemented by applying and .
Then, the governing equation of nodal can be discretized as a nonlinear ODE as follows:
The governing equation for nodal is discretized as follows:
where the axial average gauge pressure is calculated as follows:
After the discretization, the governing equations of the system can be written as
where and are the generalized coordinate vectors of the air film and the foil structure, respectively, and is the generalized coordinate vector of the rotor.
The system in Equation (11) is a system of nonlinear ordinary differential equations (ODEs). By providing a motion for the journal, this system of ODEs can be integrated into the time domain numerically. As this is a stiff system of ODEs, the ode23s function in MATLAB [31], which is an implicit solution integrator, is used to obtain the response of the bearing. It is worth noting that the analytical Jacobian matrix of the system can greatly improve the solution efficiency. A detailed derivation of the analytical Jacobian can be found in [32].
3. Dynamic Coefficients
3.1. Definition
Rotor dynamics studies the dynamic behavior of the rotor around the equilibrium position. The bearing reaction force can be decomposed into static and dynamic parts:
where and are the static components, and and are the dynamic components.
For small journal motions, the changes in the film force components around the equilibrium can be linearized for the displacement perturbations (denoted as and ) and velocity perturbations (denoted as and ). Using the Taylor series expression and ignoring higher-order terms, the dynamic film force can be approximated as follows [24]:
is defined as the dynamic stiffness coefficient, and is the damping coefficient, as shown in Figure 3.
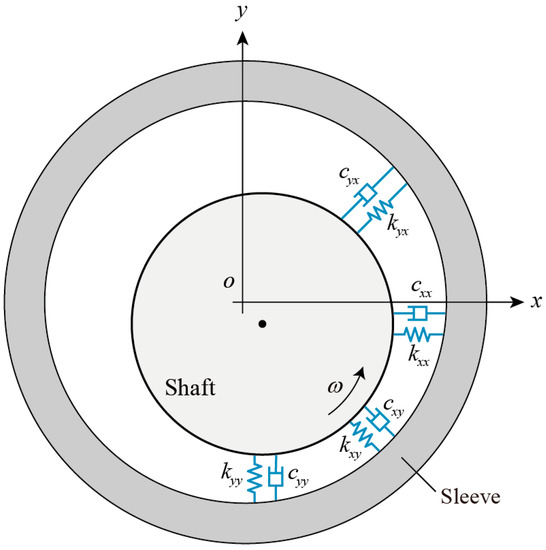
Figure 3.
Dynamic coefficients model of an air foil bearing.
3.2. Calculation
This subsection presents the calculation method of the bearing dynamic coefficients. First, the equilibrium of the bearing is solved for a given external load . The solution starts with a guess value of the rotor eccentricity, . At iteration step , the following system of equations is solved using Newton’s method:
Then, the bearing reaction forces and are calculated, and then the rotor eccentricity is updated using the secant method as follows:
When the bearing reaction force and the external load reach equilibrium, i.e., and , the iterative solution ends.
Second, the dynamic reaction forces are calculated using the time-domain integration. A simple harmonic motion around the equilibrium of the journal with a perturbation frequency is applied to the journal:
where and are the amplitudes of the disturbance motion in the x- and y-directions, respectively.
Then, the responses of the air foil bearing can be solved. By extracting the steady-state responses (typically after ten excitation cycles), the total bearing reaction forces and can be obtained, as shown in Figure 4. The perturbed bearing force is calculated by removing the static components as follows:
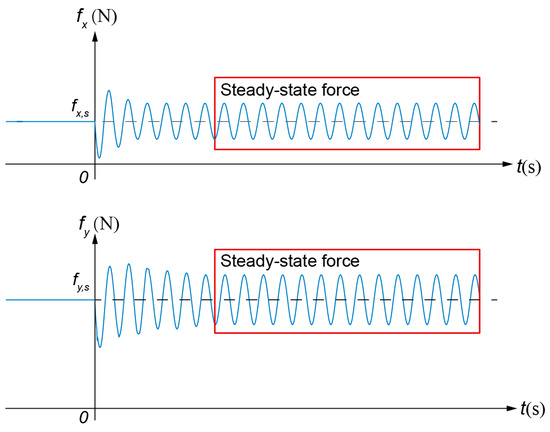
Figure 4.
Extraction of the steady-state bearing reaction forces.
Finally, the dynamic coefficients can be obtained by fitting the model in a least-squares manner. The error of the dynamic forces obtained by the nonlinear model and the dynamic coefficient model at are defined as:
The total least-square error for all data points of the steady-state bearing reaction forces is written as
where is the number of data points used for the coefficient identification. Using the least-squares method to minimize the error, the dynamic stiffness and damping coefficients can be identified. This nonlinear fitting problem is solved using the lsqcurvefit function in MATLAB.
4. Results and Discussion
A widely studied bearing configuration is used in this section [20,32]. The parameters of the air foil bearings are listed in Table 1. The finite difference grid of the gas film is 80 × 20 for all the numerical examples. The number of the grids chosen is based on a mesh convergence analysis. For the ode23 function, both the relative tolerance and absolute tolerance are set as 1 × 10−6.

Table 1.
Parameters of the air foil bearing.
4.1. Verification
In this subsection, the proposed method is verified by comparing it with the results in the literature [17]. The normalized least root mean square error (NRMSE) is used to evaluate the accuracy of the dynamic coefficient model. The NRMSE is calculated as
where is the duration of the steady-state bearing reaction force used for the fitting.
Figure 5a,b shows a comparison of the nonlinear simulation and the fitting curve of the dynamic coefficient model of the two cases with a rotational speed of 20,000 rpm and a perturbation frequency ratio of 1.0. The figures show that the force–time curve of the dynamic coefficient model coincides with the nonlinear simulation result. For and , the NRMSEs of and are 1.54 × 10−4 and 2.25 × 10−4, respectively. For and , the NRMSEs are 1.96 × 10−4 and 2.21 × 10−4, respectively. To sum up, the dynamic coefficient model can describe the air film force well when the amplitude of the disturbance motion is very small.
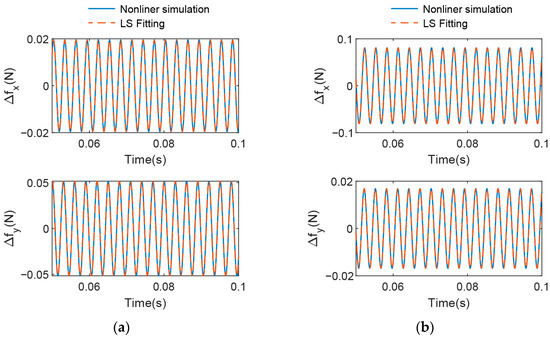
Figure 5.
Comparison of the nonlinear simulation and the fitting curve of the dynamic coefficient model. (a) ; (b) .
With a given perturbation frequency, the corresponding eight dynamic coefficients of the bearing can be obtained using the fitting calculation shown in Figure 5. Figure 6 shows a comparison between the calculation results of the dynamic coefficient curve in this study and the results in the literature [20] at a rotational speed of 20,000 rpm. As can be seen, the dynamic coefficients obtained using the present time-domain identification method are in good agreement with the results proposed in the literature, which proves the effectiveness of the proposed method. In fact, this is the first time that the dynamic coefficient of an air foil bearing model with an axially averaged SEFM has been independently verified.
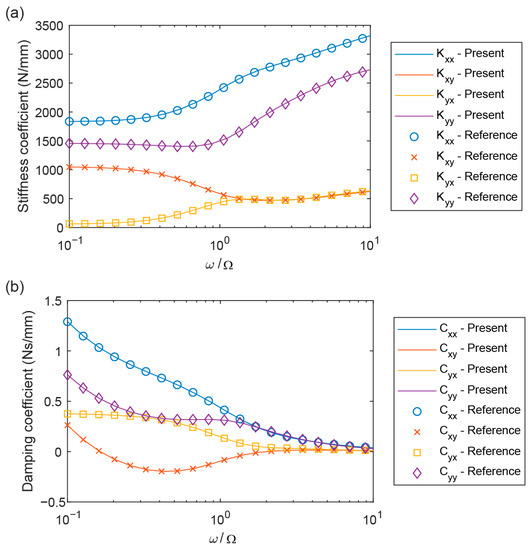
Figure 6.
Verification of the present method to calculate the dynamic coefficients. (a) The stiffness coefficients, and (b) the damping coefficients at 20,000 rpm.
4.2. Comparison of the Results by Two Foil Models
As mentioned in the introduction, the traditional calculation method [8] of the dynamic coefficient assumes that the deformation of the foil is independent in the width direction (called the 2D foil model). The differences between the dynamic coefficients of the bearings in 1D and 2D foil models have not been compared in previous studies. Therefore, this section analyzes the influence of these two deformation assumptions on the dynamic coefficients. The calculation results are shown in Figure 7 and Figure 8.
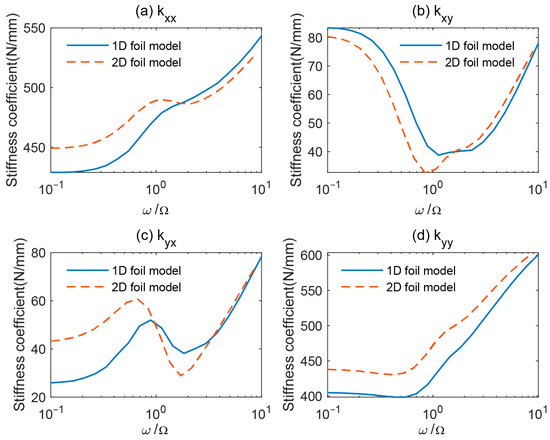
Figure 7.
The stiffness coefficients calculated by two foil models at 20,000 rpm. (a) kxx; (b) kxy; (c) kyx; (d) kyy.
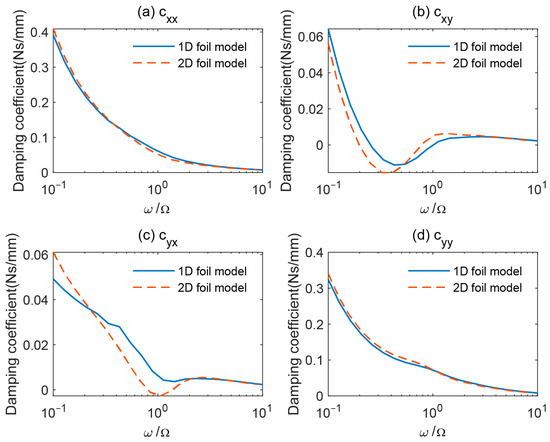
Figure 8.
The damping coefficients calculated by two foil models at 20,000 rpm. (a) cxx; (b) cxy; (c) cyx; (d) cyy.
It can be seen that the calculation results of the two models are different. For the 1D foil model, the stiffness coefficients are smaller, and the damping coefficients are larger at a small perturbation frequency ratio. Because the leading unstable mode of a rotor bearing system has a frequency ratio of less than one, the onset instability speed of a bearing with the 1D foil model is higher than that with the 2D foil model, as reported in the literature [16]. The proposed results provide an intuitive explanation for this phenomenon.
4.3. Influence of the Disturbance Amplitude
In this section, the influence of the disturbance amplitude on the accuracy of the dynamic coefficient model is investigated. The calculation results are plotted in Figure 9. It can be seen that the NRMSE increases with an increase in the disturbance amplitude. The disturbance dynamic force in the same direction as the disturbance displacement has a smaller error. When the disturbance amplitude is lower than 0.1 times the radius clearance, the maximum error is about 5%. This indicates that the dynamic coefficient model has good accuracy in characterizing the dynamic disturbance forces.
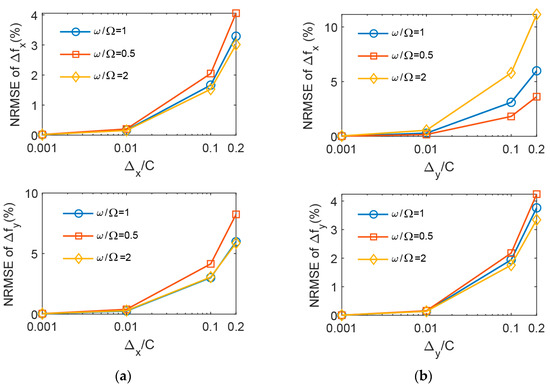
Figure 9.
The NRMSEs of dynamic coefficient model for different amplitudes. (a) ; (b) .
The maximum NRMSE is 11.39%, corresponding to with , and . Figure 10 shows a comparison of the nonlinear simulation and the fitting curve of the dynamic coefficient model.
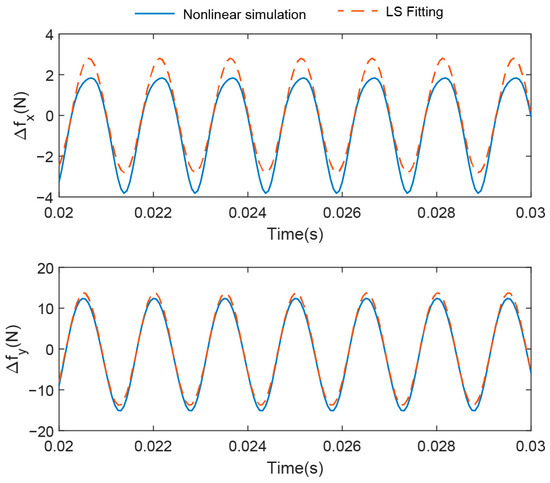
Figure 10.
Comparison of the nonlinear simulation and the fitting curve of the dynamic coefficient model with , and .
5. Conclusions
In this paper, the calculation of the dynamic coefficient of an air foil bearing is presented using a time-domain identification method. The proposed method avoids the complicated linearization of the system equations and can be applied to different bearing models. The proposed method has been verified by comparing it with the calculation results reported in the literature. This is the first time the calculation results of the dynamic coefficients using a foil model with axial uniform deformation have been verified.
The relevant influences on the calculation of the dynamic coefficients were studied. The differences between the foil models with axial uniform deformation and those with axial independent deformation were compared. The stiffness coefficients of the model with uniform axial deformation were smaller than those of the model with independent axial deformation, and the damping coefficients were larger. Furthermore, the influence of the disturbance amplitude on the accuracy of the dynamic coefficient model was investigated. When the disturbance amplitude was lower than 0.1 times the radius clearance, the maximum error was about 5%. This shows that the dynamic coefficient method has good accuracy over a large disturbance range.
Author Contributions
Methodology, formal analysis, and writing—original draft preparation: G.F. and Y.Z.; writing—review and editing, and funding acquisition: B.L. and L.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the National Key Research and Development Program of China (No. 2022YFB2503504), the Fundamental Research Funds for the Central Universities (No. FRF-TP-19-044A1), and the EDD Research Program (No. 24588DD6).
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- DellaCorte, C. Oil-Free shaft support system rotordynamics: Past, present and future challenges and opportunities. Mech. Syst. Signal Process. 2012, 29, 67–76. [Google Scholar] [CrossRef]
- Hou, Y.; Zhao, Q.; Guo, Y.; Ren, X.; Lai, T.; Chen, S. Application of Gas Foil Bearings in China. Appl. Sci. 2021, 11, 6210. [Google Scholar] [CrossRef]
- Samanta, P.; Murmu, N.C.; Khonsari, M.M. The evolution of foil bearing technology. Tribol. Int. 2019, 135, 305–323. [Google Scholar] [CrossRef]
- Bou-Saïd, B.; Lahmar, M.; Mouassa, A.; Bouchehit, B. Dynamic Performances of Foil Bearing Supporting a Jeffcot Flexible Rotor System Using FEM. Lubricants 2020, 8, 14. [Google Scholar] [CrossRef]
- Zhou, R.; Gu, Y.; Ren, G.; Yu, S. Modeling and stability characteristics of bump-type gas foil bearing rotor systems considering stick–slip friction. Int. J. Mech. Sci. 2022, 219, 107091. [Google Scholar] [CrossRef]
- Sarrazin, M.; Liebich, R. A Numerical Analysis of the Nonlinear Dynamics of Shimmed Conical Gas Foil Bearings. Appl. Sci. 2023, 13, 5859. [Google Scholar] [CrossRef]
- Lund, J. Spring and damping coefficients for the tilting pad journal bearing. ASLE Trans. 1964, 7, 342–352. [Google Scholar] [CrossRef]
- Lund, J. Calculation of stiffness and damping properties of gas bearings. J. Lubr. Technol. 1968, 90, 793–803. [Google Scholar] [CrossRef]
- Peng, J.; Carpino, M. Calculation of stiffness and damping coefficients for elastically supported gas foil bearings. J. Tribol. 1993, 115, 20–27. [Google Scholar] [CrossRef]
- Lee, Y.B.; Kim, T.H.; Kim, C.H.; Lee, N.S.; Choi, D.H. Unbalance response of a super-critical rotor supported by foil bearings—Comparison with test results. Tribol. Trans. 2004, 47, 54–60. [Google Scholar] [CrossRef]
- Kim, D. Parametric studies on static and dynamic performance of air foil bearings with different top foil geometries and bump stiffness distributions. J. Tribol. 2006, 129, 354–364. [Google Scholar] [CrossRef]
- Vleugels, P.; Waumans, T.; Peirs, J.; Al-Bender, F.; Reynaerts, D. High-speed bearings for micro gas turbines: Stability analysis of foil bearings. J. Micromech. Microeng. 2006, 16, S282. [Google Scholar] [CrossRef]
- Larsen, J.S.; Hansen, A.J.; Santos, I.F. Experimental and theoretical analysis of a rigid rotor supported by air foil bearings. Mech. Ind. 2015, 16, 106. [Google Scholar] [CrossRef]
- Sim, K.; Yong-Bok, L.; Ho Kim, T.; Lee, J. Rotordynamic performance of shimmed gas foil bearings for oil-free turbochargers. J. Tribol. 2012, 134, 031102. [Google Scholar] [CrossRef]
- Han, D.; Bi, C. The Partial Derivative Method for Dynamic Stiffness and Damping Coefficients of Supercritical CO2 Foil Bearings. Lubricants 2022, 10, 307. [Google Scholar] [CrossRef]
- Hoffmann, R.; Munz, O.; Pronobis, T.; Barth, E.; Liebich, R. A valid method of gas foil bearing parameter estimation: A model anchored on experimental data. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 2018, 232, 4510–4527. [Google Scholar] [CrossRef]
- Hoffmann, R.; Pronobis, T.; Liebich, R. Non-linear Stability Analysis of a Modified Gas Foil Bearing Structure. In Proceedings of the 9th IFToMM International Conference on Rotor Dynamics, Milan, Italy, 22 September 2014; Pennacchi, P., Ed.; Springer: Berlin/Heidelberg, Germany, 2015; Volume 21. [Google Scholar] [CrossRef]
- Larsen, J.S.; Santos, I.F.; von Osmanski, S. Stability of rigid rotors supported by air foil bearings: Comparison of two fundamental approaches. J. Sound Vib. 2016, 381, 179–191. [Google Scholar] [CrossRef]
- von Osmanski, S.; Larsen, J.S.; Santos, I.F. Multi-domain stability and modal analysis applied to Gas Foil Bearings: Three approaches. J. Sound Vib. 2021, 472, 115174. [Google Scholar] [CrossRef]
- Gu, Y.; Ren, G.; Zhou, M. A novel method for calculating the dynamic force coefficients of Gas Foil Bearings and its application in the rotordynamic analysis. J. Sound Vib. 2021, 515, 116466. [Google Scholar] [CrossRef]
- Bonello, P.; Pourashraf, T. A comparison of modal analyses of foil-air bearing rotor systems using two alternative linearisation methods. Mech. Syst. Signal Process. 2022, 170, 108714. [Google Scholar] [CrossRef]
- Bonello, P. The extraction of Campbell diagrams from the dynamical system representation of a foil-air bearing rotor model. Mech. Syst. Signal Process. 2019, 129, 502–530. [Google Scholar] [CrossRef]
- Brenkacz, L. Bearing Dynamic Coefficients in Rotordynamics: Computation Methods and Practical Applications; John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar]
- Bonello, P.; Pham, H.M. The efficient computation of the nonlinear dynamic response of a foil–air bearing rotor system. J. Sound Vib. 2014, 333, 3459–3478. [Google Scholar] [CrossRef]
- Zywica, G.; Baginski, P.; Bogulicz, M.; Martowicz, A.; Roemer, J.; Kantor, S. Numerical identification of the dynamic characteristics of a nonlinear foil bearing structure: Effect of the excitation force amplitude and the assembly preload. J. Sound Vib. 2022, 520, 116663. [Google Scholar] [CrossRef]
- Bonello, P.; Pham, H.M. Nonlinear dynamic analysis of high speed oil-free turbomachinery with focus on stability and self-excited vibration. J. Tribol. 2014, 136, 041705. [Google Scholar] [CrossRef]
- Heshmat, H.; Walowit, J.A.; Pinkus, O. Analysis of gas-lubricated foil journal bearings. J. Lubr. Technol. 1983, 105, 647–655. [Google Scholar] [CrossRef]
- San Andrés, L.; Kim, T.H. Analysis of gas foil bearings integrating FE top foil models. Tribol. Int. 2009, 42, 111–120. [Google Scholar] [CrossRef]
- Gu, Y.; Lan, X.; Ren, G.; Zhou, M. An efficient three-dimensional foil structure model for bump-type gas foil bearings considering friction. Friction 2021, 9, 1450–1463. [Google Scholar] [CrossRef]
- Zhou, R.; Gu, Y.; Cui, J.; Ren, G.; Yu, S. Nonlinear dynamic analysis of supercritical and subcritical Hopf bifurcations in gas foil bearing-rotor systems. Nonlinear Dyn. 2021, 103, 2241–2256. [Google Scholar] [CrossRef]
- Shampine, L.F.; Reichelt, M.W. The MATLAB ODE Suite. SIAM J. Sci. Comput. 1997, 18, 1–35. [Google Scholar] [CrossRef]
- Nielsen, B.; Santos, I.F. Transient and steady state behaviour of elasto–aerodynamic air foil bearings, considering bump foil compliance and top foil inertia and flexibility: A numerical investigation. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2017, 231, 1235–1253. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).