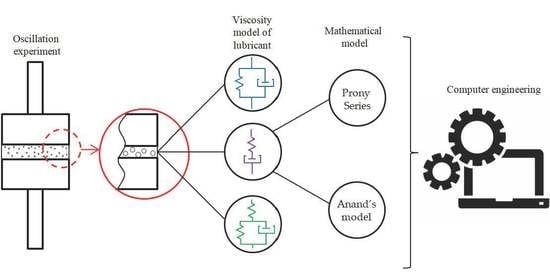
Experimental Study of the Rheology of Grease by the Example of CIATIM-221 and Identification of Its Behavior Model
Abstract
1. Introduction
1.1. Research Objectives
- Conducting a series of full-scale experiments to determine the viscoelastic lubricants properties over a wide range of temperatures;
- Identifying a mathematical model of the viscoelastic lubricant behavior in the form of the Maxwell body based on two viscoelasticity models: the Prony series and the Anand’s model;
- Creating a unified numerical procedure to determine approaches to the parameters from item two based on the application of the multi-parameter Nelder–Mead optimization.
1.2. Problem Context and Description
- Study of tribological, electromechanical, and thermal characteristics of lubricants, including those with various additives and solutions;
- Experimental research on a wide range of temperatures to identify dynamic and static characteristics;
- Identification of mathematical models of material behavior and their implementation in numerical analogues of friction nodes.
2. Materials and Methods
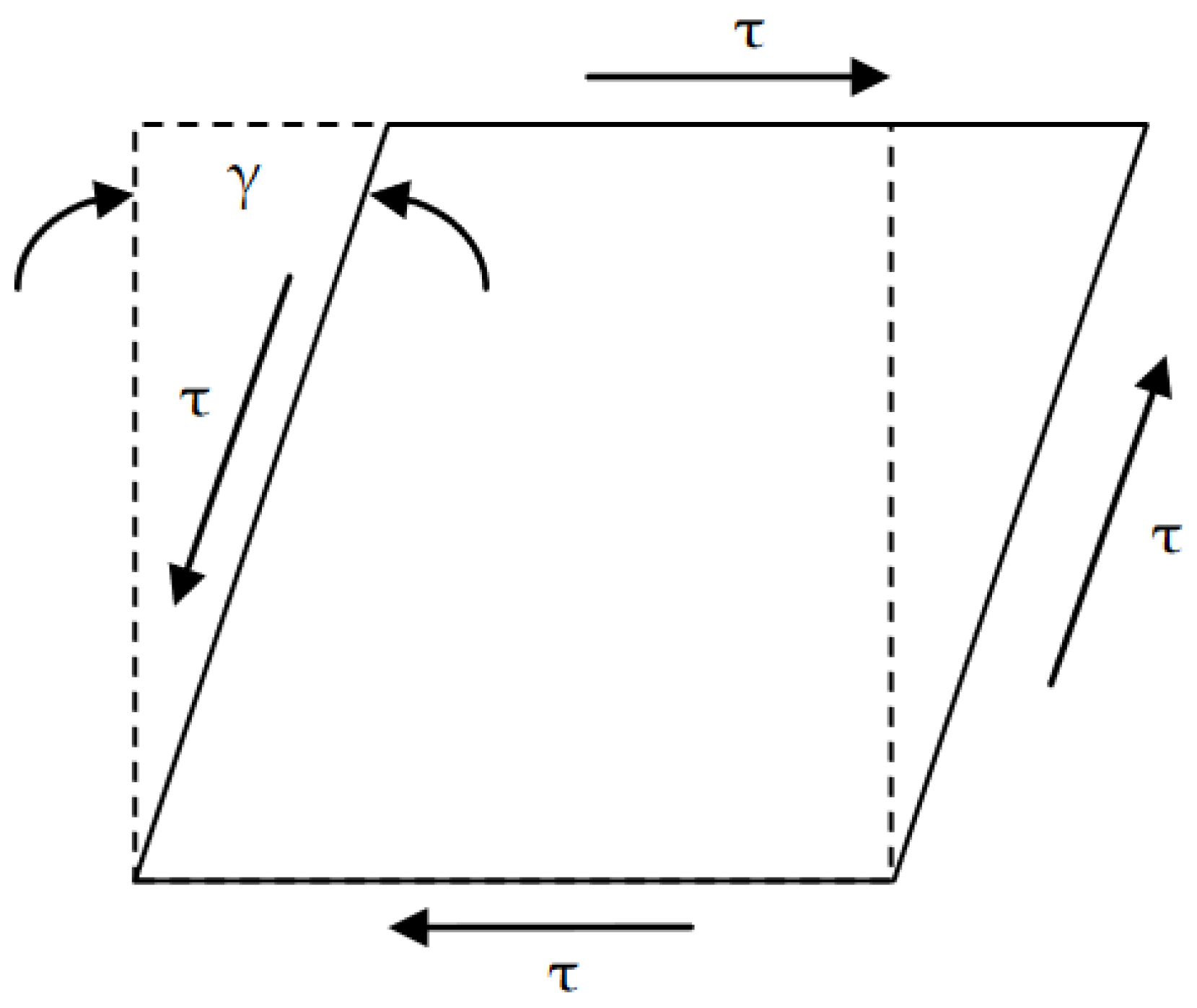
2.1. Experimental Research
- -
- minimum oscillation torque 2;
- -
- minimum sustained shear torque 10;
- -
- maximum torque 200;
- -
- torque resolution 0.1;
- -
- minimum frequency;
- -
- maximum frequency 100;
- -
- minimum angular frequency 0;
- -
- maximum angular frequency 300;
- -
- displacement resolution 10, etc.
2.2. Identification of a Mathematical Model of Lubricant Behavior
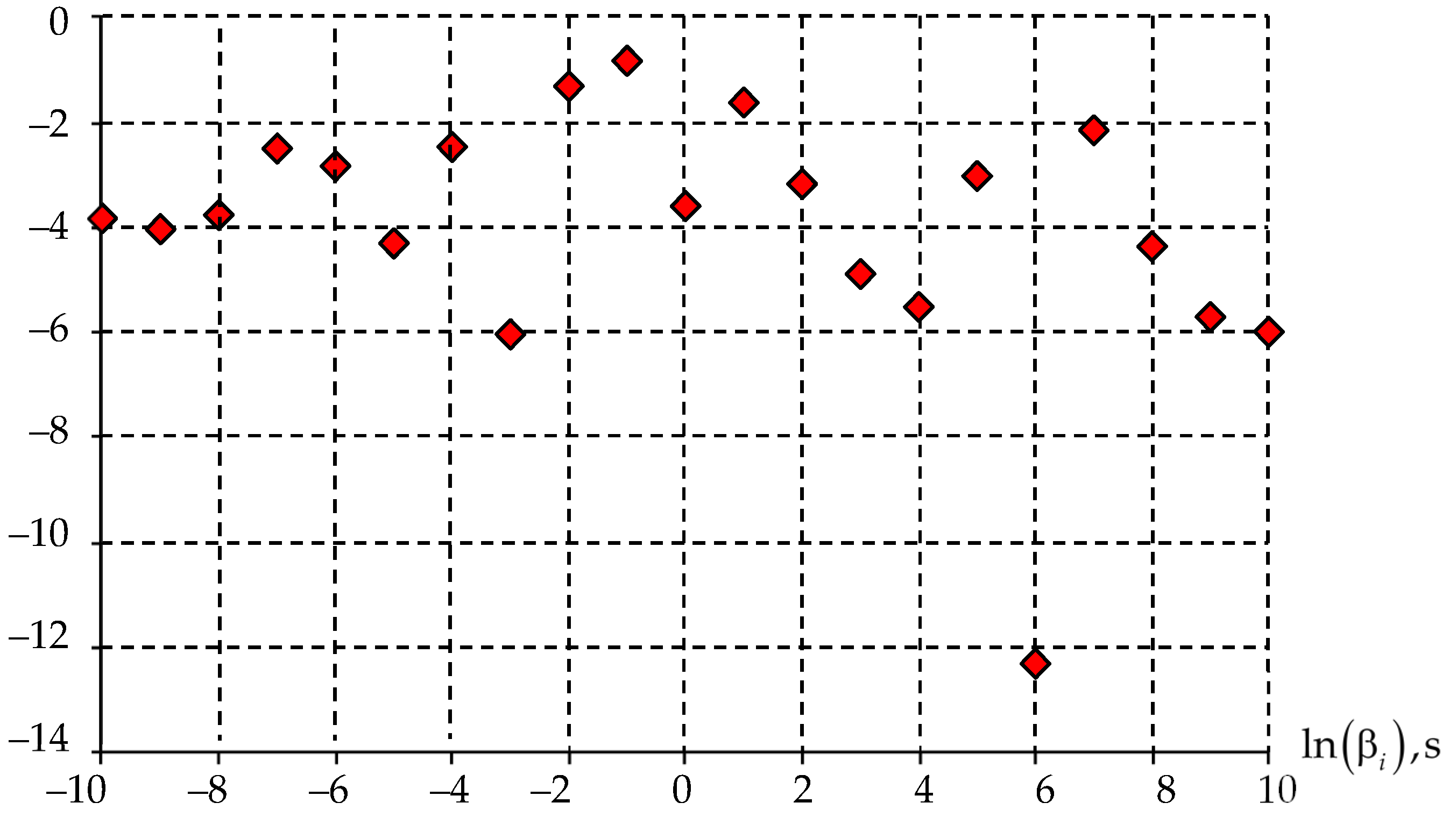
2.2.1. Prony Series
2.2.2. Anand’s Model
2.3. Mathematical Model Identification Procedure
- -
- Preliminary step. It consists in the form of experimental data into the procedure, the choice of a mathematical model, and the setting of initial values of the unknowns vector ;
- -
- Nelder–Mead multi-parameter optimization operations. An ANSYS file is generated with a sequence of commands to build the numerical model. The pure shift problem is solved with the generation of a results file. The function is calculated and comparing to the required error. If the condition is not met, a new vector of unknowns is generated. Then, the optimization procedure is repeated;
- -
- Obtaining a result file. If the error condition is met, the final value of the unknowns vector is written down and the procedure is exited.
3. Results
3.1. Results of Full-Scale Experiments
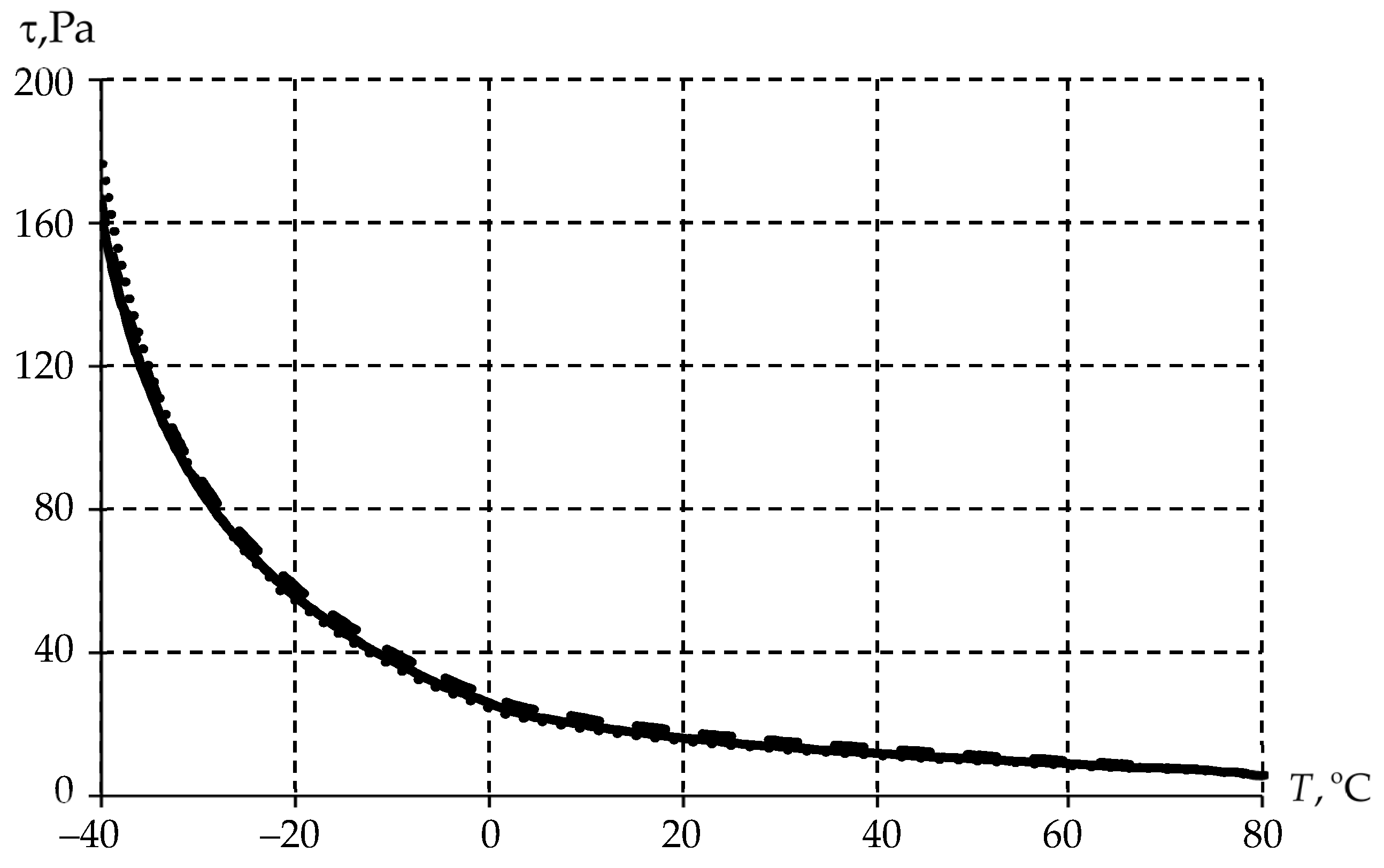
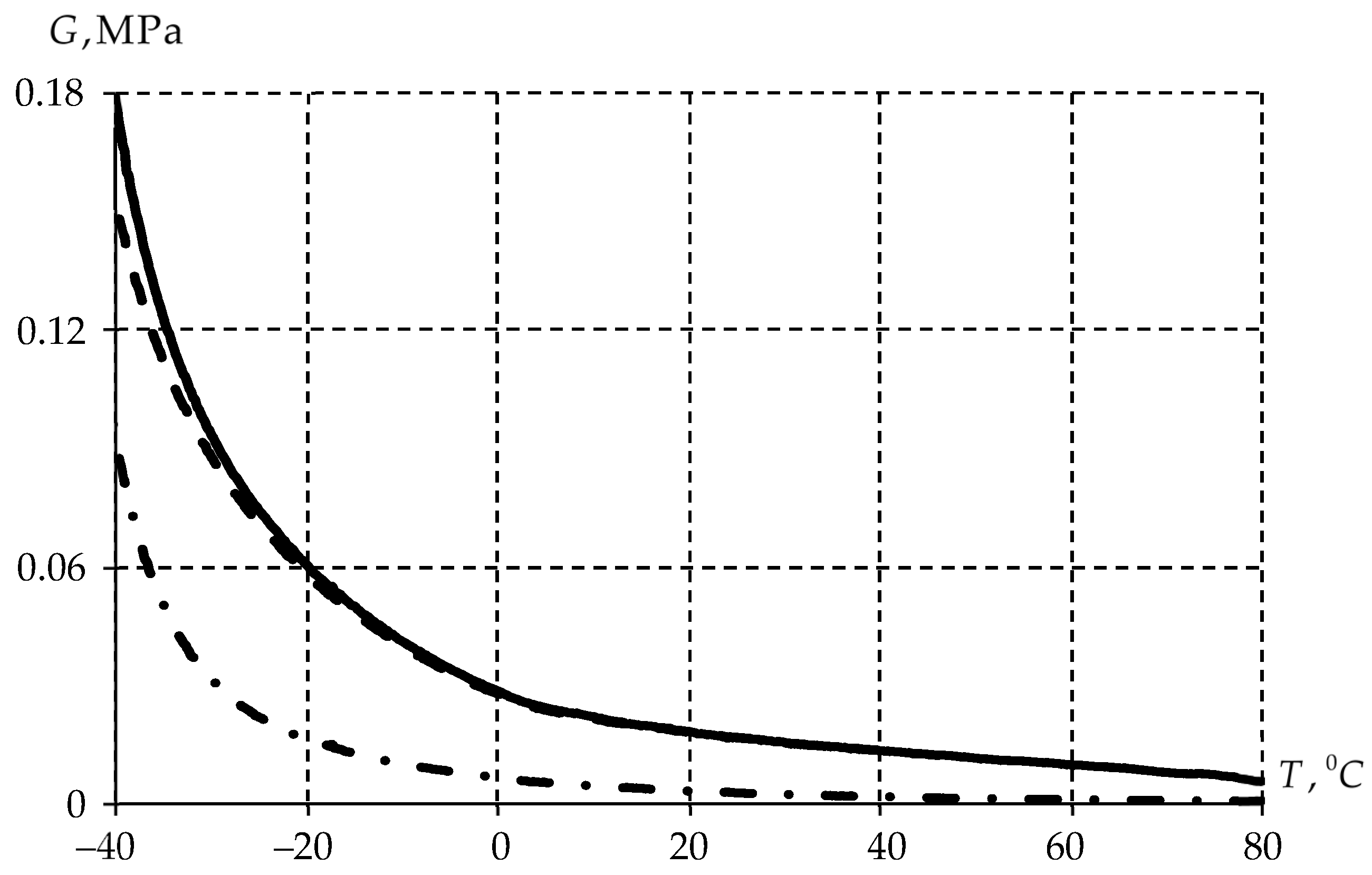
3.2. Identification of a Mathematical Model of the Lubricant as a Function of Temperature
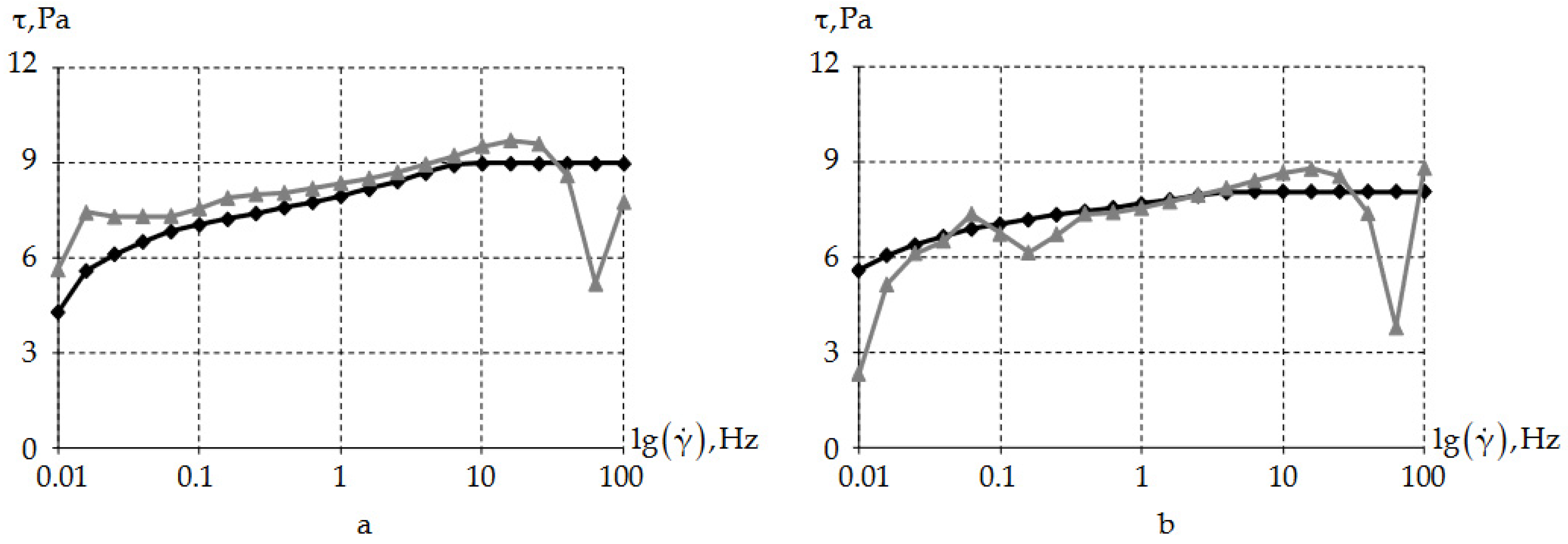
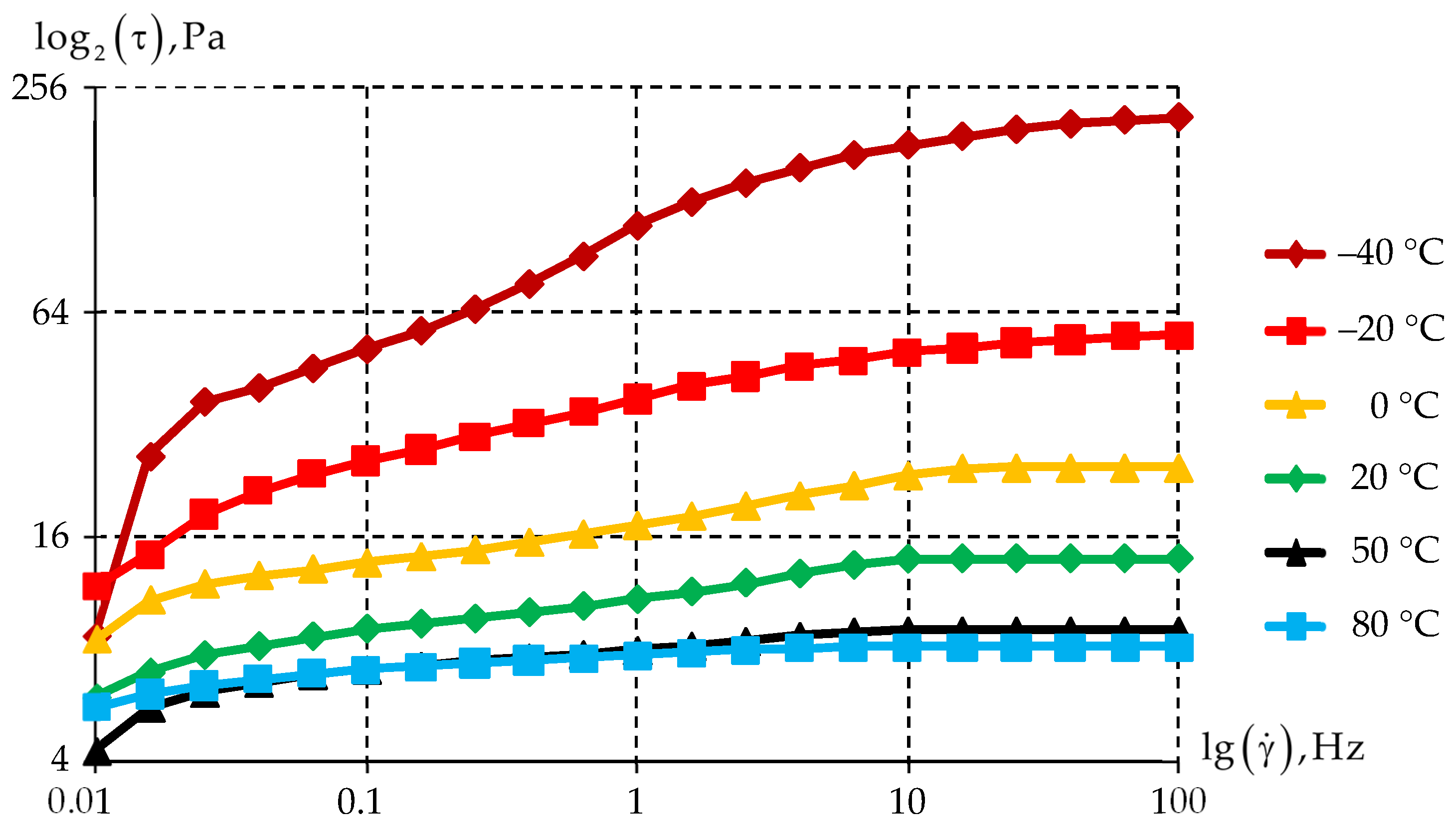
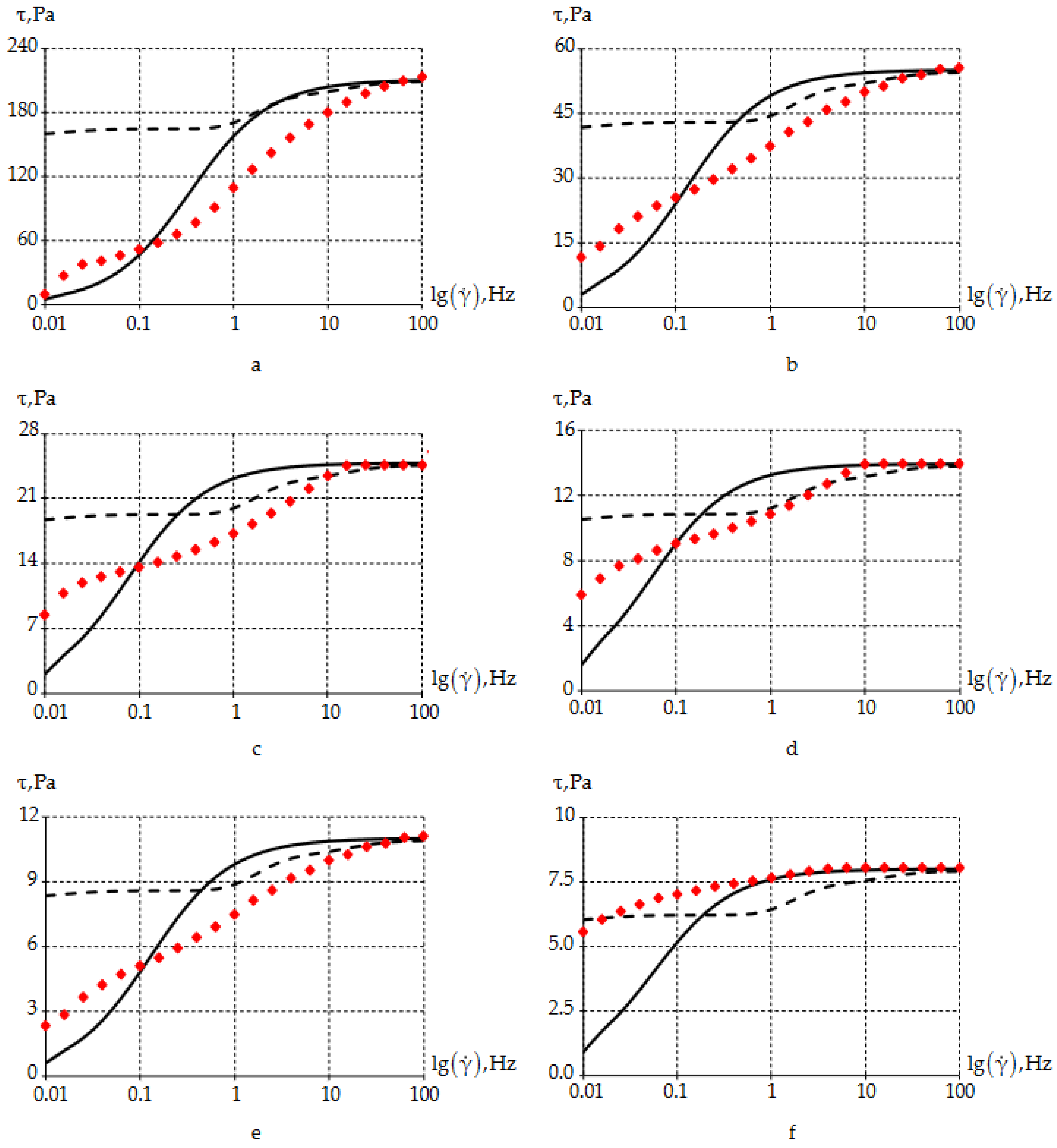
3.3. Dependence of Rheological Properties of the Lubricant on the Shear Rate
4. Discussion
4.1. Limitation Statement
- -
- The full-scale experiment is conducted in a small range of shear rates, from 0.01 to 100 Hz, which does not give a complete picture of the viscous and elastic components at small and large share rates, respectively;
- -
- The behavior of the lubricant was investigated using the Discovery HR2 rotational viscometer with a limited range of temperatures and share rates;
- -
- The lubricant is capable of operating in the temperature range of −60 to +150 °C, but the equipment allows evaluation of behavior at temperatures of −40 to +80 °C;
- -
- Lubricant is treated as a Maxwell body, in fact, the object of study has a more complex pattern of behavior;
- -
- Lubricant is considered within the problem of deformable solid mechanics; the problem of fluid and gas mechanics is not set.
- -
- Consideration of other linear viscoelastic models (Kelvin model, Voigt model, etc.);
- -
- Using a temperature–time superposition to be able to describe and analyze decreased and increased shear rates and temperatures;
- -
- Numerical simulation of the structure as a whole with the use of a lubricant, using the example of a spherical sliding bearing of a bridge span;
- -
- The lubricant will be examining using the DWS technology.
4.2. Prediction of Structure Behavior Based on Computer Engineering
4.3. On the Choice of a Mathematical Model
4.4. Scope of Application Results
- -
- Numerical experiments to be conducted on the operation of structural elements during the life cycle;
- -
- Extension of the presented study to determine the rheological properties of polymeric materials [74];
- -
- -
- The reduction of material and time costs for field research, etc.
5. Conclusions
- -
- At higher frequencies, the error is minimal;
- -
- At low frequencies, there is a significant error.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| angular displacement of the rheometer; | |
| complex shear modulus; | |
| shear strain; | |
| tangential stress of an elastic element; | |
| shear strain of an elastic element; | |
| tangential stress of a viscous element; | |
| viscosity; | |
| the rate of viscous shear strain; | |
| functional; | |
| experimental tangential stress; | |
| numerical tangential stress; | |
| vector of unknowns; | |
| long shear modulus; | |
| initial shear modulus; | |
| weight coefficients; | |
| reduced time; | |
| number of relaxation times; | |
| temperature-time analogy shift function; | |
| absolute temperature; | |
| empirical material constants; | |
| base temperature; | |
| pre-exponential multiplier; | |
| activation energy; | |
| universal gas constant; | |
| stress multiplier; | |
| shear strain resistance; | |
| material hardening constant; | |
| saturation value of the hardening function; | |
| sample saturation as a function of shear rate. |
References
- Wen, C.; Meng, X.; Gu, J.; Xiao, L.; Jiang, S.; Bi, H. Starved lubrication analysis of angular contact ball bearing based on a multi-degree-of-freedom tribo-dynamic model. Friction 2023, 11, 1395–1418. [Google Scholar] [CrossRef]
- Stahl, L.; Müller, M.; Ostermeyer, G.P. On the experimental characterization of the fluid volume influence on the friction between rough surfaces. Friction 2023, 11, 1334–1348. [Google Scholar] [CrossRef]
- Jiang, S.; Liu, J.; Yang, Y.; Lin, Y.; Zhao, M. Experimental research and dynamics analysis of multi-link rigid–flexible coupling mechanism with multiple lubrication clearances. Arch. Appl. Mech. 2023, 93, 2749–2780. [Google Scholar] [CrossRef]
- Sokolov, N.V.; Khadiev, M.B.; Fedotov, P.E.; Fedotov, E.M. Influence of the Lubricant’s Supply Temperature on the Operation of a Fluid Film Thrust Bearing. Russ. Eng. Res. 2023, 43, 264–271. [Google Scholar] [CrossRef]
- Li, Y.; Shi, L.; Liu, Z.; Wang, X.; Qiao, X.; Zhang, Z.; Yan, S. Study on the lubrication state and pitting damage of spur gear using a 3D mixed EHL model with fractal surface roughness. J. Mech. Sci. Technol. 2022, 36, 5947–5957. [Google Scholar] [CrossRef]
- Cao, W.; He, T.; Pu, W.; Xiao, K. Dynamics of lubricated spiral bevel gears under different contact paths. Friction 2022, 10, 247–267. [Google Scholar] [CrossRef]
- Zhang, Y.; Shakil, A.; Humood, M.; Polycarpou, A.A. Finite element simulations of sliding contact of the head-disk interface in magnetic storage with lubricant effects. Appl. Surf. Sci. Adv. 2021, 6, 100155. [Google Scholar] [CrossRef]
- Smith, E.H. On the Design and Lubrication of Water-Lubricated, Rubber, Cutlass Bearings Operating in the Soft EHL Regime. Lubricants 2020, 8, 75. [Google Scholar] [CrossRef]
- Wang, P.; Qiu, J.; Gao, P.; Dong, R.; Han, Y.; Fan, M. The tribological behaviors and anti-corrosion performances of 5-phenyltetrazole ionic liquid additives for water lubricants. Wear 2023, 516–517, 204621. [Google Scholar] [CrossRef]
- Sharma, S.C.; Singh, A. A study of double layer conical porous hybrid journal bearing operated with non-Newtonian lubricant. Tribol. Int. 2023, 179, 108183. [Google Scholar] [CrossRef]
- Qiu, Y.L.; Zhou, C.G.; Ou, Y.; Feng, F.T. Theoretical and experimental analysis of the temperature rise of a ball screw. Int. J. Adv. Manuf. Technol. 2023, 127, 703–715. [Google Scholar] [CrossRef]
- Li, Z.; Shen, H.; Liang, K.; Chen, X.; Zhu, Z. A numerical study on the effect of oil lubricant on the heat transfer and efficiency of a vapour compression refrigeration system. Int. Commun. Heat Mass Transf. 2022, 134, 106016. [Google Scholar] [CrossRef]
- Torabi, A.; Alidousti, M.H. Numerical and experimental study of elastohydrodynamic grease lubrication of dimple textured surfaces. Acta Mech. 2023, 234, 2919–2931. [Google Scholar] [CrossRef]
- Dang, R.K.; Goyal, D.; Chauhan, A.; Dhami, S.S. Numerical and Experimental Studies on Performance Enhancement of Journal Bearings Using Nanoparticles Based Lubricants. Arch. Comput. Methods Eng. 2021, 28, 3887–3915. [Google Scholar] [CrossRef]
- Jadhav, S.; Thakre, G.D.; Sharma, S.C. Numerical modeling of elastohydrodynamic lubrication of line contact lubricated with micropolar fluid. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 326. [Google Scholar] [CrossRef]
- Summer, F.; Bergmann, P.; Grün, F. On the Wear Behaviour of Bush Drive Chains: Part II—Performance Screening of Pin Materials and Lubricant Effects. Lubricants 2023, 11, 157. [Google Scholar] [CrossRef]
- Bouchehit, B.; Bou-Saïd, B.; Tichy, J. Towards Ecological Alternatives in Bearing Lubrication. Lubricants 2021, 9, 62. [Google Scholar] [CrossRef]
- Nosov, Y.O.; Kamenskikh, A.A. Influence Analysis of Lubricant Recesses on the Working Capacity of the Bridge Span Spherical Bearing. Lubricants 2022, 10, 283. [Google Scholar] [CrossRef]
- Wu, P.; Chen, J.; Sojka, P.E.; Li, Y.; Cao, H. Experimental study of the lubricant-refrigerant flow in a rotary compressor. Int. J. Refrig. 2023. [Google Scholar] [CrossRef]
- Singh, N.; Sinha, S.K. Tribological and mechanical analysis of hybrid epoxy based polymer composites with different in situ liquid lubricants (silicone oil, PAO and SN150 base oil). Wear 2022, 504–505, 204404. [Google Scholar] [CrossRef]
- Katsaros, K.P.; Nikolakopoulos, P.G. Performance Prediction Model for Hydrodynamically Lubricated Tilting Pad Thrust Bearings Operating under Incomplete Oil Film with the Combination of Numerical and Machine-Learning Techniques. Lubricants 2023, 11, 113. [Google Scholar] [CrossRef]
- Tomanik, E.; Aubanel, L.; Bussas, M.; Delloro, F.; Lampke, T. Tribological Performance of a Composite Cold Spray for Coated Bores. Lubricants 2023, 11, 127. [Google Scholar] [CrossRef]
- Qiang, H.; Gao, G.; Ye, S.; Cheng, L.; Wang, Q. Effect of Characteristic Parameters and Distribution of Friction Pair Surface Texture on Lubrication Properties. Lubricants 2023, 11, 139. [Google Scholar] [CrossRef]
- Kodnyanko, V.; Shatokhin, S.; Kurzakov, A.; Pikalov, Y. Mathematical Modeling on Statics and Dynamics of Aerostatic Thrust Bearing with External Combined Throttling and Elastic Orifice Fluid Flow Regulation. Lubricants 2020, 8, 57. [Google Scholar] [CrossRef]
- Orozco Lozano, W.; Fonseca-Vigoya, M.D.S.; Pabón-León, J. Study of the Kinematics and Dynamics of the Ring Pack of a Diesel Engine by Means of the Construction of CFD Model in Conjunction with Mathematical Models. Lubricants 2021, 9, 116. [Google Scholar] [CrossRef]
- Yang, H.; Majeed, A.; Al-Khaled, K.; Abbas, T.; Naeem, M.; Khan, S.U.; Saeed, M. Significance of Melting Heat Transfer and Brownian Motion on Flow of Powell–Eyring Fluid Conveying Nano-Sized Particles with Improved Energy Systems. Lubricants 2023, 11, 32. [Google Scholar] [CrossRef]
- Valigi, M.C.; Malvezzi, M.; Logozzo, S. A Numerical Procedure Based on Orowan’s Theory for Predicting the Behavior of the Cold Rolling Mill Process in Full Film Lubrication. Lubricants 2020, 8, 2. [Google Scholar] [CrossRef]
- Poliakov, A.M.; Pakhaliuk, V.I. Predictive Estimates of Short-Term and Long-Term Results for Regenerative Rehabilitation of Local Articular Cartilage Defects in Synovial Joints. Lubricants 2023, 11, 116. [Google Scholar] [CrossRef]
- Slabka, I.; Henniger, S.; Kücükkaya, D.; Dawoud, M.; Schwarze, H. Influence of Rheological Properties of Lithium Greases on Operating Behavior in Oscillating Rolling Bearings at a Small Swivel Angle. Lubricants 2022, 10, 163. [Google Scholar] [CrossRef]
- Farré-Lladós, J.; Westerberg, L.G.; Casals-Terré, J.; Leckner, J.; Westbroek, R. On the Flow Dynamics of Polymer Greases. Lubricants 2022, 10, 66. [Google Scholar] [CrossRef]
- Conrad, A.; Hodapp, A.; Hochstein, B.; Willenbacher, N.; Jacob, K.-H. Low-Temperature Rheology and Thermoanalytical Investigation of Lubricating Greases: Influence of Thickener Type and Concentration on Melting, Crystallization and Glass Transition. Lubricants 2022, 10, 1. [Google Scholar] [CrossRef]
- Li, X.K.; Luo, Y.; Qi, Y.; Zhang, R. On non-Newtonian lubrication with the upper convected Maxwell model. Appl. Math. Model. 2011, 35, 2309–2323. [Google Scholar] [CrossRef]
- Madsen, E.; Rosenlund, O.S.; Brandt, D.; Zhang, X. Adaptive feedforward control of a collaborative industrial robot manipulator using a novel extension of the Generalized Maxwell-Slip friction model. Mech. Mach. Theory 2021, 155, 104109. [Google Scholar] [CrossRef]
- Suarez-Afanador, C.A.; Cornaggia, R.; Lahellec, N.; Maurel-Pantel, A.; Boussaa, D.; Moulinec, H.; Bordas, S.P.A. Effective thermo-viscoelastic behavior of short fiber reinforced thermo-rheologically simple polymers: An application to high temperature fiber reinforced additive manufacturing. Eur. J. Mech. A/Solids 2022, 96, 104701. [Google Scholar] [CrossRef]
- Sun, Y.; Huang, B.; Chen, J.; Jia, X.; Ding, Y. Characterizing rheological behavior of asphalt binder over a complete range of pavement service loading frequency and temperature. Constr. Build. Mater. 2016, 123, 661–672. [Google Scholar] [CrossRef]
- Zhang, X.; Gu, X.; Lv, J.; Zou, X. 3D numerical model to investigate the rheological properties of basalt fiber reinforced asphalt-like materials. Constr. Build. Mater. 2017, 138, 185–194. [Google Scholar] [CrossRef]
- Lesnikova, Y.I.; Trufanov, A.N.; Kamenskikh, A.A. Analysis of the Polymer Two-Layer Protective Coating Impact on Panda-Type Optical Fiber under Bending. Polymers 2022, 14, 3840. [Google Scholar] [CrossRef]
- Sakhabutdinova, L.R.; Smetannikov, O.Y.; Il’inykh, G.V. Numerical Simulation of the Process Manufacture of Large-Scale Composite Shell Taking Into Account Thermo Viscoelastic. Tomsk. State Univ. J. Math. Mech. 2022, 76, 165–181. [Google Scholar] [CrossRef]
- Nuwayer, H.M.; Newaz, G.M. Flexural Creep Behavior of Adhesively Bonded Metal and Composite Laminates. Int. J. Adhes. Adhes. 2018, 84, 220–226. [Google Scholar] [CrossRef]
- Anand, L. Constitutive Equations for Hot-Working of Metals. Int. J. Plast. 1985, 3, 213–231. [Google Scholar] [CrossRef]
- Puchi-Cabrera, E.S.; Guérin, J.D.; Barbera-Sosa, J.G.; Dubar, M.; Dubar, L. Plausible Extension of Anand’s Model to Metals Exhibiting Dynamic Recrystallization and its Experimental Validation. Int. J. Plast. 2018, 108, 70–87. [Google Scholar] [CrossRef]
- Liu, E.; Bhogaraju, S.K.; Wunderle, B.; Elger, G. Investigation of stress relaxation in SAC305 with micro-Raman spectroscopy. Microelectron. Reliab. 2022, 138, 114664. [Google Scholar] [CrossRef]
- Liang, Z.; Yonghuan, G.; Lei, S.; Chengwen, H. Reliability of SnAgCuFe Solder Joints in WLCSP30 Device. Rare Met. Mater. Eng. 2016, 45, 2823–2826. [Google Scholar] [CrossRef]
- Larson, R.G.; Wei, Y. A Review of Thixotropy and its Rheological Modeling. J. Rheol. 2019, 63, 477–501. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, X.; Gao, Y.; Xu, J.; Ding, Y. Numerical Simulation of Effect of Glass Lubricant on Hot Extrusion of Inconel 625 Alloy Tubes. Procedia Manuf. 2019, 37, 119–126. [Google Scholar] [CrossRef]
- Wolak, A.; Zając, G.; Słowik, T. Measuring Kinematic Viscosity of Engine Oils: A Comparison of Data Obtained from Four Different Devices. Sensors 2021, 21, 2530. [Google Scholar] [CrossRef]
- Cerpa-Naranjo, A.; Pérez-Piñeiro, J.; Navajas-Chocarro, P.; Arce, M.P.; Lado-Touriño, I.; Barrios-Bermúdez, N.; Moreno, R.; Rojas-Cervantes, M.L. Rheological Properties of Different Graphene Nanomaterials in Biological Media. Materials 2022, 15, 3593. [Google Scholar] [CrossRef]
- Kaushik, S.; Sonebi, M.; Amato, G.; Das, U.K.; Perrot, A. Optimisation of Mix Proportion of 3D Printable Mortar Based on Rheological Properties and Material Strength Using Factorial Design of Experiment. Materials 2023, 16, 1748. [Google Scholar] [CrossRef]
- Xue, X.; Gao, J.; Wang, J.; Chen, Y. Evaluation of High-Temperature and Low-Temperature Performances of Lignin–Waste Engine Oil Modified Asphalt Binder and Its Mixture. Materials 2022, 15, 52. [Google Scholar] [CrossRef]
- Peng, Y.; Via, B. The Effect of Cellulose Nanocrystal Suspension Treatment on Suspension Viscosity and Casted Film Property. Polymers 2021, 13, 2168. [Google Scholar] [CrossRef]
- Quan, L.; Kalyon, D.M. Parallel-Disk Viscometry of a Viscoplastic Hydrogel: Yield Stress and Other Parameters of Shear Viscosity and Wall Slip. Gels 2022, 8, 230. [Google Scholar] [CrossRef]
- Kozdrach, R. The Innovative Research Methodology of Tribological and Rheological Properties of Lubricating Grease. Tribol. Ind. 2021, 43, 117–130. [Google Scholar] [CrossRef]
- Trufanova, N.M.; Ershov, S.V. Comparative Analysis of Heat and Mass Transfer Processes in the Extruder Dosing Zone with the Use Different Spatial Mathematical Model and Rheological Law. J. Appl. Mech. Tech. Phys. 2017, 2, 153–163. [Google Scholar] [CrossRef]
- Davydova, V.A.; Shcherbinin, A.G.; Naumiv, M.D.; Ershov, S.V. A Numerical Study on Induction-Resistive Electric-Heating Processes of Pipelines. Russ. Electr. Eng. 2021, 11, 668–671. [Google Scholar] [CrossRef]
- Schramm, G. A Practical Approach to Rheology and Rheometry; Gebrueder HAAKE GmbH: Karlsruhe, Germany, 1994; 290p. [Google Scholar]
- Barnes, A.H. A Handbook of Elementary Rheology; University of Wales, Institute of Non-Newtonian Fluid Mechanics: Cardiff, Wales, 2000; 200p. [Google Scholar]
- Zhai, M.; Zhou, K.; Sun, Z.; Xiong, Z.; Du, Q.; Zhang, Y.; Shi, L.; Hou, J. Rheological Characterization and Shear Viscosity Prediction of Heavy Oil-in-Water Emulsions. J. Mol. Liq. 2023, 381, 121782. [Google Scholar] [CrossRef]
- Song, Y.; Won, C.; Kang, S.; Lee, H.; Park, S.; Park, S.H.; Yoon, J. Characterization of Gglass Viscosity with Parallel Plate and Rotational Viscometry. J. Non-Cryst. Solids 2018, 486, 27–35. [Google Scholar] [CrossRef]
- Cherecheş, E.I.; Ibanescu, C.; Danu, M.; Minea, A.A. Studies on Rheological Properties and Isobaric Heat Capacity of ZnO-[C4mim][BF4] Nanoparticle Enhanced Ionic Liquid. J. Mol. Liq. 2023, 380, 121759. [Google Scholar] [CrossRef]
- Romanova, Y.N.; Koroleva, M.Y.; Musina, N.S.; Maryutina, T.A. Rheology of Gel-Containing Water-in-Crude Oil Emulsions. Geoenergy Sci. Eng. 2023, 226, 211757. [Google Scholar] [CrossRef]
- Adamov, A.A.; Kamenskikh, A.A.; Pankova, A.P.; Strukova, V.I. Comparative Analysis of the Work of Bridge Spherical Bearing at Different Antifriction Layer Locations. Lubricants 2022, 10, 207. [Google Scholar] [CrossRef]
- Kim, J.-H.; Kim, W.S.; Yoo, Y. Friction Properties of Solid Lubricants with Different Multiwalled Carbon Nanotube Contents. Materials 2022, 15, 4054. [Google Scholar] [CrossRef]
- Adamov, A.A.; Kamenskikh, A.A.; Pankova, A.P. Influence Analysis of the Antifriction Layer Materials and Thickness on the Contact Interaction of Spherical Bearings Elements. Lubricants 2022, 10, 30. [Google Scholar] [CrossRef]
- Chong, W.W.F.; Hamdan, S.H.; Wong, K.J.; Yusup, S. Modelling Transitions in Regimes of Lubrication for Rough Surface Contact. Lubricants 2019, 7, 77. [Google Scholar] [CrossRef]
- Mukutadze, M.A.; Lagunova, E.O. Mathematical Model of Flow of Lubricant and Molten Coating with Micropolar Rheological Properties in Running Clearance of Journal Bearing with Non-circular Bearing Surface Profile, Considering Pressure Dependence of Viscosity. In Proceedings of the 8th International Conference on Industrial Engineering, Belgrade, Serbia, 29–30 September 2022; ICIE, Lecture Notes in Mechanical Engineering; Springer: Cham, Switzerland, 2022; pp. 587–597. [Google Scholar] [CrossRef]
- Jadhao, V.; Robbins, M.O. Rheological Properties of Liquids Under Conditions of Elastohydrodynamic Lubrication. Tribol. Lett. 2019, 67, 66. [Google Scholar] [CrossRef]
- Gamaniel, S.S.; Dini, D.; Biancofiore, L. The Effect of Fluid Viscoelasticity in Lubricated Contacts in the Presence of Cavitation. Tribol. Int. 2021, 160, 107011. [Google Scholar] [CrossRef]
- Ivins, E.R.; Caron, L.; Adhikari, S.; Larour, E. Notes on a Compressible Extended Burgers Model of Rheology. Geophys. J. Int. 2022, 228, 1975–1991. [Google Scholar] [CrossRef]
- Kvarda, D.; Skurka, S.; Galas, R.; Omasta, M.; Shi, L.; Ding, H.; Wang, W.; Krupka, I.; Hartl, M. The Effect of Top of Rail Lubricant Composition on Adhesion and Rheological Behaviour. Eng. Sci. Technol. Int. J. 2022, 35, 101100. [Google Scholar] [CrossRef]
- Mujumdar, A.; Beris, A.N.; Metzner, A.B. Transient Phenomena in Thixotropic Systems. J. Non-Newton. Fluid Mech. 2002, 102, 157–178. [Google Scholar] [CrossRef]
- Mendes, P.R.; Thompson, R.L. A Critical Overview of Elasto-Viscoplastic Thixotropic Modeling. J. Non-Newton. Fluid Mech. 2012, 187–188, 8–15. [Google Scholar] [CrossRef]
- Radhakrishnan, R.; Divous, T.; Manneville, S.; Fielding, S.M. Understanding Rheological Hysteresis in Soft Glassy Materials. Soft Matter 2017, 9, 1834–1852. [Google Scholar] [CrossRef]
- Niemierko, A. Modern Bridge Bearings and Expansion Joints for Road Bridges. Trans. Res. Procedia 2016, 14, 4040–4049. [Google Scholar] [CrossRef]
- Yi, X.; Du, S.; Zhang, L. Composite Materials Engineering, Volume 1: Fundamentals of Composite Materials; Springer: Singapore, 2018. [Google Scholar] [CrossRef]
- Adamov, A.A.; Kamenskih, A.A.; Pankova, A.P. Numerical analysis of the spherical bearing geometric configuration with antifriction layer made of different materials. PNRPU Mech. Bull. 2020, 4, 15–26. [Google Scholar] [CrossRef]
- Ono, K. Structural materials: Metallurgy of bridges. In Metallurgical Design and Industry; Springer: Cham, Switzerland, 2018; pp. 193–269. [Google Scholar] [CrossRef]





| Values | , MPa | , K | , MPa | |||
|---|---|---|---|---|---|---|
| Initial | 1 | 1000 | 1 | 1 | 1 | |
| Final | 15.6218 | 3.518 × 109 | 985.0634 | 7.023 × 10−7 | 4.498 × 10−4 | 2.8112 |
| Matehematical Model | Scheme of the Model | Equation |
|---|---|---|
| Kelvin–Voigt model | 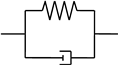 | |
| Burgers Material (Maxwell representation) |  | |
| Burgers Material (Kelvin representation) | 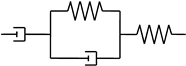 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nosov, Y.O.; Kamenskikh, A.A. Experimental Study of the Rheology of Grease by the Example of CIATIM-221 and Identification of Its Behavior Model. Lubricants 2023, 11, 295. https://doi.org/10.3390/lubricants11070295
Nosov YO, Kamenskikh AA. Experimental Study of the Rheology of Grease by the Example of CIATIM-221 and Identification of Its Behavior Model. Lubricants. 2023; 11(7):295. https://doi.org/10.3390/lubricants11070295
Chicago/Turabian StyleNosov, Yuriy O., and Anna A. Kamenskikh. 2023. "Experimental Study of the Rheology of Grease by the Example of CIATIM-221 and Identification of Its Behavior Model" Lubricants 11, no. 7: 295. https://doi.org/10.3390/lubricants11070295
APA StyleNosov, Y. O., & Kamenskikh, A. A. (2023). Experimental Study of the Rheology of Grease by the Example of CIATIM-221 and Identification of Its Behavior Model. Lubricants, 11(7), 295. https://doi.org/10.3390/lubricants11070295