A Contribution to Experimental Identification of Frequency-Dependent Dynamic Coefficients of Tilting-Pad Journal Bearings with Centered and Off-Centered Pivot
Abstract
:1. Introduction
2. Method and Test Equipment
2.1. Test Rig
2.2. Experimental Procedure
2.2.1. Error Estimation
2.2.2. Evaluating the Frequency Response Using the KC-Model
2.3. Test bearing
3. Results
3.1. Predicted Frequency-Dependent Characteristics of KC-Coefficients
3.2. Experimental Results
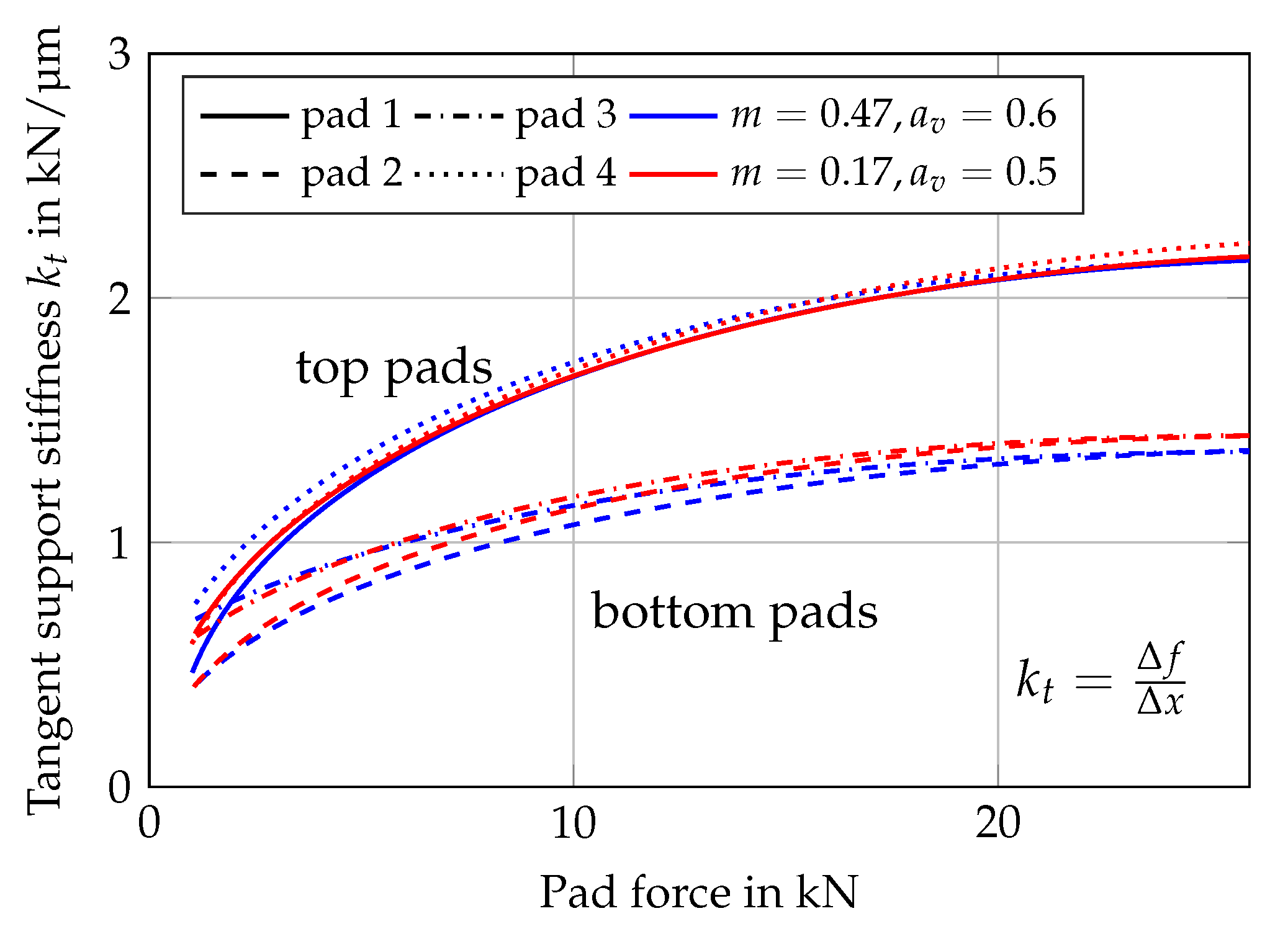
3.2.1. Support Stiffness
3.2.2. Influence of the Support Stiffness on the Dynamic Coefficients
3.2.3. Impact of Pad Preload and Pivot Offset on Dynamic Bearing Coefficients
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Roman letters | Q | Volume flow () | |
| a | Acceleration (m/s) | Modified Reynolds number | |
| Pivot offset position | s | Empirical standard deviation | |
| c | Damping (N s/m) | t | Student t distribution |
| d | Displacement (m) | T | Tot. measurement time (s) |
| f | Force (N) | Lube oil supply temperature (°C) | |
| Excitation frequency (Hz) | Lube oil supply temperature (°C) | ||
| Synchronous frequency (Hz) | u | Uncertainty | |
| Spectral density, auto correlated signal | Output signal, 2D | ||
| Spectral density, cross correlated signal | Input signal, 2D | ||
| H | Transfer function, 1D | Greek letters | |
| Frequency response function | Frequency ratio | ||
| I | Clean signal, 1D | Rotation frequency (rad) | |
| J | Noisy signal, 1D | Load direction () | |
| k | Stiffness (N/m) | Direction of coordinate system () | |
| Tangent support stiffness (N/m) | Superscripts and subscripts | ||
| m | Preload | * | Conjugate complex numbers |
| Excited mass (kg) | T | Test | |
| n | No. of measurements | 0 | Baseline |
| N | Tot. no. of frequencies | x,y | x,y-direction |
| Unit Load (MPa) | |||
References
- Reinhardt, E.; Lund, J.W. The Influence of Fluid Inertia on the Dynamic Properties of Journal Bearings. J. Lubr. Technol. 1975, 97, 159–165. [Google Scholar] [CrossRef]
- Parsell, J.K.; Allaire, P.E.; Barrett, L.E. Frequency Effects in Tilting-Pad Journal Bearing Dynamic Coefficients. ASLE Trans. 1983, 26, 222–227. [Google Scholar] [CrossRef]
- Dimond, T.W.; Younan, A.A.; Allaire, P.E.; Nicholas, J.C. Modal Frequency Response of a Four-Pad Tilting Pad Bearing With Spherical Pivots, Finite Pivot Stiffness, and Different Pad Preloads. J. Vib. Acoust. 2013, 135, 041101. [Google Scholar] [CrossRef]
- Cloud, C.H.; Maslen, E.H.; Barrett, L.E. Influence of tilting pad journal bearing model on rotor stability estimation. In Proceedings of the 8th IFToMM International Conference on Rotordynamic, Seoul, Republic of Korea, 12–15 September 2010; Korean Society of Mechanical Engineers: Red Hook, NY, USA, 2010. [Google Scholar]
- Schmied, J.; Fedorov, A.; Grigoriev, B.S. Non-synchronous tilting pad bearing characteristics. In Proceedings of the 8th IFToMM International Conference on Rotor Dynamics, Seoul, Republic of Korea, 12–15 September 2010; Curran: Red Hook, NY, USA, 2010; pp. 143–148. [Google Scholar]
- Yang, J.; Palazzolo, A. Three-Dimensional Thermo-Elasto-Hydrodynamic Computational Fluid Dynamics Model of a Tilting Pad Journal Bearing—Part II: Dynamic Response. J. Tribol. 2019, 141, 061703. [Google Scholar] [CrossRef]
- Glienicke, J. Paper 13: Experimental Investigation of the Stiffness and Damping Coefficients of Turbine Bearings and Their Application to Instability Prediction. Proc. Inst. Mech. Eng. Conf. Proc. 1966, 181, 116–129. [Google Scholar] [CrossRef]
- Rouvas, C.; Childs, D.W. A Parameter Identification Method for the Rotordynamic Coefficients of a High Reynolds Number Hydrostatic Bearing. J. Vib. Acoust. 1993, 115, 264–270. [Google Scholar] [CrossRef]
- Childs, D.W.; Hale, K. A Test Apparatus and Facility to Identify the Rotordynamic Coefficients of High-Speed Hydrostatic Bearings. ASME J. Eng. Gas Turbines Power 1994, 116, 337–343. [Google Scholar] [CrossRef]
- Al-Ghasem, A.; Childs, D.W. Rotordynamic Coefficients Measurements Versus Predictions for a High-Speed Flexure-Pivot Tilting-Pad Bearing (Load-Between-Pad Configuration). J. Eng. Gas Turbines Power 2006, 128, 896–906. [Google Scholar] [CrossRef]
- Kulhanek, C.; Childs, D.W.; Wade, J. Measured Static and Rotordynamic Coefficient Results for a Rocker-Pivot, Tilting-Pad Bearing With 50 and 60% Offsets. J. Eng. Gas Turbines Power 2012, 134, 052505. [Google Scholar] [CrossRef]
- Coghlan, D.; Childs, D.W. Characteristics of a Spherical Seat TPJB With Four Methods of Directed Lubrication—Part II: Rotordynamic Performance. J. Eng. Gas Turbines Power 2017, 139, 122503. [Google Scholar] [CrossRef]
- Suh, J.; Palazzolo, A.B. Three-Dimensional Dynamic Model of TEHD Tilting-Pad Journal Bearing—Part I: Theoretical Modeling. J. Tribol. 2015, 137, 041703. [Google Scholar] [CrossRef]
- Wilkes, J.C.; Childs, D.W. Improving Tilting Pad Journal Bearing Predictions—Part I: Model Development and Impact of Rotor Excited Versus Bearing Excited Impedance Coefficients. J. Eng. Gas Turbines Power 2013, 135, 012502. [Google Scholar] [CrossRef]
- Wilkes, J.C.; Childs, D.W. Improving Tilting-Pad Journal Bearing Predictions—Part II: Comparison of Measured and Predicted Rotor-Pad Transfer Functions for a Rocker-Pivot Tilting-Pad Journal Bearing. J. Eng. Gas Turbines Power 2013, 135, 012503. [Google Scholar] [CrossRef]
- Childs, D.W.; Harris, J. Static Performance Characteristics and Rotordynamic Coefficients for a Four-Pad Ball-in-Socket Tilting Pad Journal Bearing. J. Eng. Gas Turbines Power 2009, 131, 062502. [Google Scholar] [CrossRef]
- Wagner, L.F.; Allaire, P.E. Tilting-pad journal bearings—frequency-dependent dynamic coefficients and pivot flexibility effects. Lubricants 2022, 10, 20. [Google Scholar] [CrossRef]
- Wagner, L.F. Tilting-Pad Bearings—The Contact Flexibility of the Pivot. Lubricants 2023, 11, 189. [Google Scholar] [CrossRef]
- Dang, P.V.; Chatterton, S.; Pennacchi, P. The effect of the pivot stiffness on the performances of five-pad tilting pad bearings. Lubricants 2019, 7, 61. [Google Scholar] [CrossRef]
- Hagemann, T.; Schwarze, H. A Theoretical Study on Frequency Effects on Tilting-Pad Journal Bearing Dynamic Coefficients. In Proceedings of the 9th IFToMM International Conference on Rotor Dynamics, Milan, Italy, 22–25 September 2014; Pennacchi, P., Ed.; Springer: Cham, Switzerland, 2015; Volume 21, pp. 1069–1080. [Google Scholar] [CrossRef]
- Rodriguez, L.E.; Childs, D.W. Frequency Dependency of Measured and Predicted Rotordynamic Coefficients for a Load-On-Pad Flexible-Pivot Tilting-Pad Bearing. J. Tribol. 2006, 128, 388–395. [Google Scholar] [CrossRef]
- Tschoepe, D.P.; Childs, D.W. Measurements Versus Predictions for the Static and Dynamic Characteristics of a Four-Pad, Rocker-Pivot, Tilting-Pad Journal Bearing. J. Eng. Gas Turbines Power 2014, 136, 052501. [Google Scholar] [CrossRef]
- Hensley, J.; Childs, D.W.; Wade, J. Measurements Versus Predictions for Rotordynamic Characteristics of a Flexure Pivot-Pad Tilting Pad Bearing in an LBP Condition at Higher Unit Loads; American Society of Mechanical Engineers Digital Collection: New York, NY, USA, 2008; Volume 5, pp. 873–881. [Google Scholar] [CrossRef]
- Dmochowski, W. Dynamic Properties of Tilting-Pad Journal Bearings: Experimental and Theoretical Investigation of Frequency Effects due to Pivot Flexibility. J. Eng. Gas Turbines Power 2007, 129, 865–869. [Google Scholar] [CrossRef]
- Warner, R.E.; Soler, A.I. Stability of Rotor-Bearing Systems with Generalized Support Flexibility and Damping and Aerodynamic Cross-Coupling. J. Lubr. Technol. 1975, 97, 461–469. [Google Scholar] [CrossRef]
- Barrett, L.E.; Allaire, P.E.; Wilson, B. The Eigenvalue Dependence of Reduced Tilting Pad Bearing Stiffness and Damping Coefficients. Tribol. Trans. 1988, 31, 411–419. [Google Scholar] [CrossRef]
- Kirk, R.G.; Reedy, S.W. Evaluation of Pivot Stiffness for Typical Tilting-Pad Journal Bearing Designs. J. Vib. Acoust. 1988, 110, 165–171. [Google Scholar] [CrossRef]
- Lund, J.W.; Pedersen, L. The Influence of Pad Flexibility on the Dynamic Coefficients of a Tilting Pad Journal Bearing. J. Tribol. 1987, 109, 65–70. [Google Scholar] [CrossRef]
- Brockwell, K.; Kleinbub, D.; Dmochowski, W. Measurement and Calculation of the Dynamic Operating Characteristics of the Five Shoe, Tilting Pad Journal Bearing. Tribol. Trans. 1990, 33, 481–492. [Google Scholar] [CrossRef]
- Rouch, K.E. Dynamics of Pivoted-Pad Journal Bearings, Including Pad Translation and Rotation Effects. ASLE Trans. 1983, 26, 102–109. [Google Scholar] [CrossRef]
- Ha, H.; Yang, S. Excitation Frequency Effects on the Stiffness and Damping Coefficients of a Five-Pad Tilting Pad Journal Bearing. J. Tribol. 1999, 121, 517–522. [Google Scholar] [CrossRef]
- Dmochowski, W.; Brockwell, K. Dynamic Testing of the Tilting Pad Journal Bearing. Tribol. Trans. 1995, 38, 261–268. [Google Scholar] [CrossRef]
- Wygant, K.D.; Flack, R.D.; Barrett, L.E. Measured Dynamic Performance of a Tilting Pad Journal Bearing Over a Range of Forcing Frequencies—Part II: Dynamic Operating Conditions. Tribol. Trans. 2006, 47, 585–593. [Google Scholar] [CrossRef]
- Carter, C.; Childs, D.W. Measurements Versus Predictions for the Rotordynamic Characteristics of a Five-Pad Rocker-Pivot Tilting-Pad Bearing in Load-Between-Pad Configuration. J. Eng. Gas Turbines Power 2009, 131, 012507. [Google Scholar] [CrossRef]
- Delgado, A.; Vannini, G.; Ertas, B.; Drexel, M.; Naldi, L. Identification and Prediction of Force Coefficients in a Five-Pad and Four-Pad Tilting Pad Bearing for Load-on-Pad and Load-Between-Pad Configurations. J. Eng. Gas Turbines Power 2011, 133, 092503. [Google Scholar] [CrossRef]
- Childs, D.W.; Delgado, A.; Vannini, G. Tilting-Pad Bearings: Measured Frequency Characteristics of Their Rotordynamic Coefficients; Texas A&M University, Turbomachinery Laboratories: College Station, TX, USA, 2011. [Google Scholar] [CrossRef]
- Zemella, P.; Hagemann, T.; Pfau, B.; Schwarze, H. Identification of Dynamic Coefficients of a Five-Pad Tilting Pad Journal Bearing Up to Highest Surface Speeds. J. Eng. Gas Turbines Power 2021, 143, 081013. [Google Scholar] [CrossRef]
- Hagemann, T.; Blumenthal, H.; Kraft, C.; Schwarze, H. A study on energetic and hydraulic interaction of combined journal and thrust bearings. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air. American Society of Mechanical Engineers, Montreal, QC, Canada, 15–19 June 2015; Volume 56765, p. V07AT31A019. [Google Scholar]
- Bendat, J.E.; Piersol, A. Random Data; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2010. [Google Scholar] [CrossRef]
- Schroeder, M. Synthesis of low-peak-factor signals and binary sequences with low autocorrelation (Corresp.). IEEE Trans. Inf. Theory 1970, 16, 85–89. [Google Scholar] [CrossRef]
- JCGM 100:2008; Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement. Joint Committee for Guides in Metrology: Geneva, Switzerland, 1993.
- Gerdes, R.; Fuchs, A. Nachgiebigkeit in der Segmentabstützung von Radial-Kippsegmentlagern und deren Einfluss auf die Lagerkennwerte und das Schwingungsverhalten schnelllaufender Rotor-Lager-Systeme. FVA-Forschungsheft Nr. 511, FVV/ FVA Frankfurt am Main. 1997. [Google Scholar]
- Allaire, P.E.; Parsell, J.K.; Barrett, L.E. A pad perturbation method for the dynamic coefficients of tilting-pad journal bearings. Wear 1981, 72, 29–44. [Google Scholar] [CrossRef]
- White, M.F.; Chan, S.H. The Subsynchronous Dynamic Behavior of Tilting-Pad Journal Bearings. J. Tribol. 1992, 114, 167–173. [Google Scholar] [CrossRef]
- Wilkes, J.C. Measured and Predicted Rotor-Pad Transfer Functions for a Rocker-Pivot Tilting-Pad Journal Bearing. Ph.D. Thesis, Texas A&M University, College Station, TX, USA, 2011. [Google Scholar]
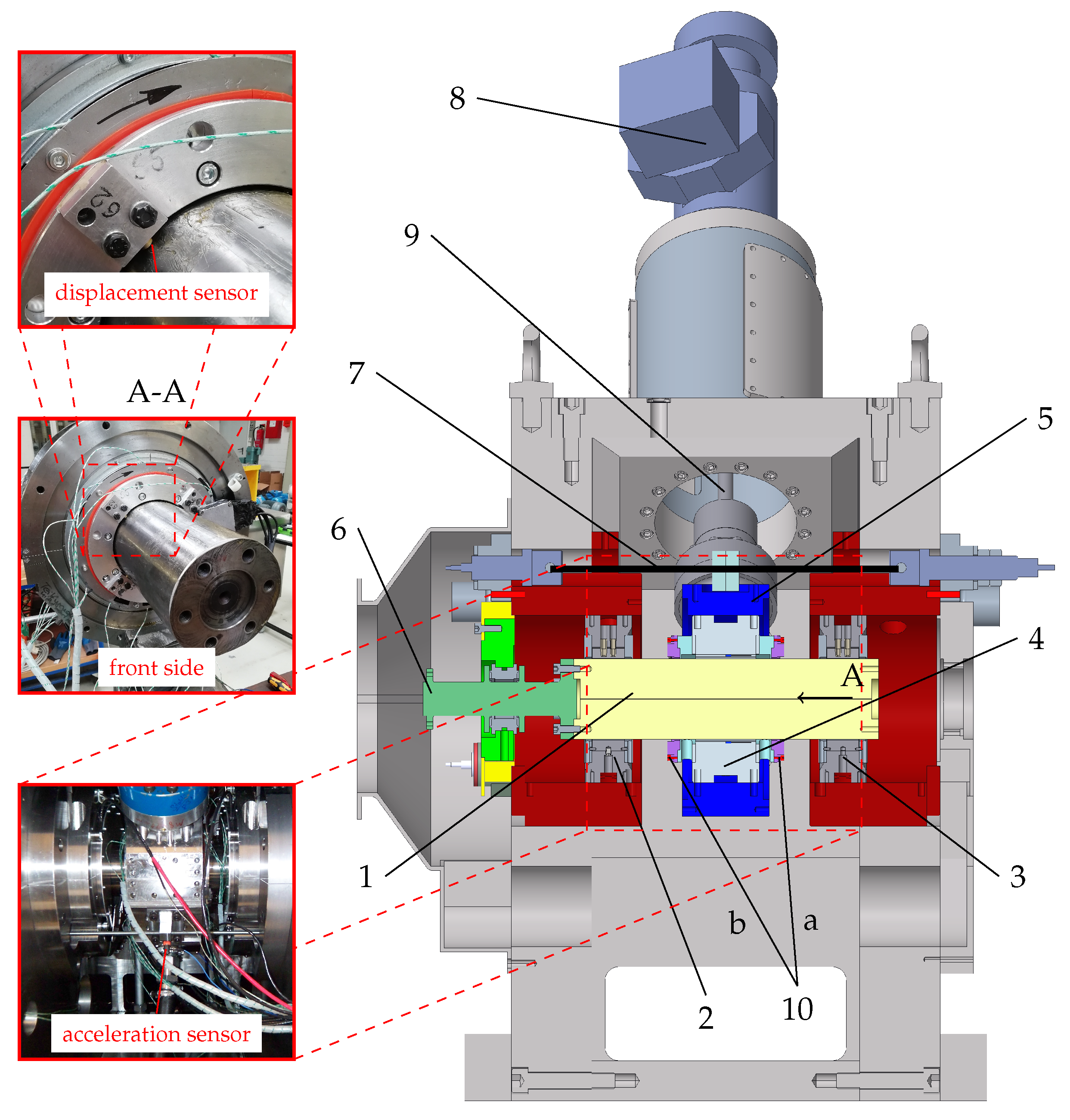








| Sensor | Function Principle | Non-Repeatability |
|---|---|---|
| Force | Strain gauge | ±10 N |
| Proximity probe | Eddy current | ±2 µm |
| Oil flow rate | Ovalmeter | ±0.3 l/min |
| Pad and lubricant temperature | Thermocouple | ±1.5 K |
| Acceleration | Piezoelectric | ±5.0 m/s |
| Parameter | Value | |
|---|---|---|
| Geometrical Properties | Set 1 | Set 2 |
| Number of tilting pads | 4 | |
| Nominal diameter, mm | 120 | |
| Tilting-pad thickness, mm | 15 | |
| Bearing width, mm | 72 | |
| Pad arc length, | 70 | |
| Pivot offset | 0.5 | 0.6 |
| Radial clearance, mm | (manufactured 0.102) assembled 0.107 | |
| Geometrical preload | 0.17 | 0.47 |
| Static analysis parameters | ||
| Bearing load, kN | 0.0–27.0 | |
| Rotational speed, rpm | 4000–22,000 | |
| Lubricant supply temperature, C | 50 | |
| Lubricant flow rate, l/min | 90 | |
| Dynamic analysis parameters | ||
| Excitation frequency, Hz | 8–496 | |
| Spectral force amplitude, kN | 0.2 | |
| Lubricant properties | ||
| Lubricant/kinematic viscosity mm/s | ISO VG 32/32 @ 40 C, 5.7 @ 100 C | |
| Lubricant density, kg/m | 865 @ 40 C | |
| Lubricant specific heat capacity, kJ/(kg K) | 2.0 @ 20 C | |
| Lubricant thermal conductivity, W/(m K) | 0.13 | |
| Material properties; sliding material (Babbitt)/pad and journal material (steel) | ||
| Modulus of elasticity, GPa | 57/210 | |
| Poisson’s ratio | 0.3 | |
| Heat expansion coefficient, 1/K | 21/11 | |
| Thermal conductivity, W/(m K) | 45 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zemella, P.; Vetter, D.; Hagemann, T.; Schwarze, H. A Contribution to Experimental Identification of Frequency-Dependent Dynamic Coefficients of Tilting-Pad Journal Bearings with Centered and Off-Centered Pivot. Lubricants 2023, 11, 428. https://doi.org/10.3390/lubricants11100428
Zemella P, Vetter D, Hagemann T, Schwarze H. A Contribution to Experimental Identification of Frequency-Dependent Dynamic Coefficients of Tilting-Pad Journal Bearings with Centered and Off-Centered Pivot. Lubricants. 2023; 11(10):428. https://doi.org/10.3390/lubricants11100428
Chicago/Turabian StyleZemella, Philipp, Daniel Vetter, Thomas Hagemann, and Hubert Schwarze. 2023. "A Contribution to Experimental Identification of Frequency-Dependent Dynamic Coefficients of Tilting-Pad Journal Bearings with Centered and Off-Centered Pivot" Lubricants 11, no. 10: 428. https://doi.org/10.3390/lubricants11100428
APA StyleZemella, P., Vetter, D., Hagemann, T., & Schwarze, H. (2023). A Contribution to Experimental Identification of Frequency-Dependent Dynamic Coefficients of Tilting-Pad Journal Bearings with Centered and Off-Centered Pivot. Lubricants, 11(10), 428. https://doi.org/10.3390/lubricants11100428







