Abstract
The nonconstant concrete flow due to the alternating pumping of the twin cylinder of the hydraulic pump will cause vibration of concrete pump trucks. Furthermore, the discontinuous pumping of concrete caused by inadequate suction and air doping will exacerbate the vibration. In order to study the effect of nonconstant and discontinuous pumping of concrete on the dynamic response and vibrational stability of the whole vehicle, multi-fluid pumping models with concrete-lubrication gas for straight and elbow pipes are established, respectively, and the boundary conditions of periodic pumping speed are taken into account to compare the rheological characteristics of concrete and the exciting force on the pipe wall under nonconstant pumping, discontinuous pumping and nonconstant discontinuous pumping conditions. Results show that the pipe pressure and the exciting force vary periodically with the pumping speed under nonconstant pumping conditions, and the peak-to-peak value of the pipe pressure and excitation for discontinuous pumping depend on the volume fraction and distribution state of the gas in the pipe.
1. Introduction
Concrete pump trucks play an important role in long-distance and high-rise transportation [1,2], due to their high efficiency and convenience, as shown in Figure 1. However, alternating pumping of concrete will cause nonconstant flow and inadequate suction during the working process of concrete pump trucks will induce discontinuous flow. Under the comprehensive influence of these two factors, the pipe pressure and the fluid exciting force on the pipe wall will increase the vibration amplitude of the pump truck, which may endanger the safety of people and vehicles. Therefore, the research on the concrete pumping process is an indispensable part for the design of concrete pump trucks.

Figure 1.
Panoramic view of a concrete pump truck.
Pipe pressure fluctuation during the working process of the concrete pump truck can be measured by the instrument and sensors, but it is difficult to measure the exciting force of the concrete flow on the pipe. Numerical simulation methods provide a possibility to overcome this difficulty.
For concrete pumping simulations, the flow process of concrete in the pipe is complex since it involves the interaction of sand, stone, cement slurry and gas. it is difficult to simulate this process and predict the rheological properties. Therefore, concrete is often simplified into one and more different materials with coupling treatment. So far, there are three methods commonly used to simulate concrete pumping: The first is the continuous fluid model method [3,4,5,6,7,8], which simplifies concrete into Bingham fluid that is a non-Newtonian fluid, achieving the same rheological properties as concrete on a macro level. However, in the actual simulation, the pressure loss of the pipe is much larger than the actual pumped pressure loss, and its velocity model is inconsistent with the plunger flow. After improvement, a two-fluid model (Euler–Euler) is proposed that divided the concrete pipe flow model into the lubrication layer at the boundary of the pipe wall and the center of the concrete layer. In this case, the pipe pressure loss and velocity distribution of the model are in good agreement with the actual pumping, and the main influence of the pipe pressure loss is the material properties of the lubricating layer. The second method is discrete element method (Lagrange) [9,10,11,12], in which concrete is dispersed into a large number of mortar units. The flow of concrete is equivalent to the flow of dense particles, and its flow properties are controlled by the normal and tangential forces between particles. The third method is the fluid–solid interaction (Euler–Lagrange) [13,14], which divides concrete into mortar in the liquid phase and coarse aggregate in the solid phase. The liquid phase mortar is simulated by computational fluid dynamics method based on Euler grid, and the movement of coarse aggregate particles is tracked in Lagrange coordinate system.
The two-fluid model method can clearly reveal the physical phenomenon of concrete flow, and there is mature commercial software for it [15,16], but it cannot simulate the particle blockage and segregation in the pipe. The discrete element method can simulate the accumulation of particles, but cannot accurately observe the influence of gas and predict the flow model of fluid. The fluid–solid interaction can clearly reflect the physical model of fluid and particle flow, so the solution of the fluid–solid two-phase pipe flow with fluid–DEM (discrete element method) coupling can well reflect the problem of concrete, but the calculation time is too long and the efficiency is very low, especially for the calculation of free flow in pipe involving the gas–liquid–solid multi-phase.
With the development of time, many studies have been carried out with experimental and numerical simulations on pipe pressure loss during concrete pumping [17,18,19,20,21], pipe wall erosion [22,23,24], and concrete pumping suction process [25,26]. Jang [18] conducted full scale pumping tests with four different length pipes, and the results showed that the pressure loss per unit length of the pipeline remained unchanged when the pipeline length was determined. Chio [21] proposed a method for estimating the pipe pumping pressure loss, which is in good agreement with the pipe pressure loss obtained from horizontal coiled pipe experiments, and also obtained the pressure loss per unit length in the pumping line by comparing simulation with experiment. Tan [22] proposed a new impact-based time-averaged collision strength model to study the wear mechanism of bends using the fluid–solid interaction, and accurately predicted the wear behavior of the bends. periodically changing law, and predicted the flow dead zone of the hopper and optimized the hopper structure.
However, these studies all focus on the pressure loss in the pipe during steady pumping of concrete, or the flow properties of concrete. There are few reports on the nonconstant flow caused by alternating hydraulic pumping of the concrete pump truck, the discontinuous pumping caused by insufficient suction of material, and the changes in the pipe pressure and the pipe wall exciting force caused by these two factors.
Therefore, to solve the above problems, this paper adopts numerical simulation method to study the nonconstant and discontinuous pumping characteristics of concrete. Dual-fluid concrete pumping model based on Bingham fluid model is proposed. Accounting for the periodic pumping velocity boundary conditions, the nonconstant flow model of concrete is established. By coupling the gas phase with the two-fluid model, the discontinuous pumping model is established. A comprehensive analysis of the pipe pressure and the excitation force during nonconstant and discontinuous pumping of concrete is carried out. Finally, the change trend of the simulated pipe pressure is compared with the measured hydraulic cylinder pumping pressure.
2. Concrete Pumping Model
2.1. Concrete Pipeline Flow Model
The Herschell–Bulkley model is a three-parameter rheological model with static shear stress, which can represent the properties of Newtonian fluid, Bingham fluid, and exponential rheological modes. The model is commonly used for slurries and cement slurries. The fluid constitutive model can be represented as follow [3,27]:
where is the yield stress, is the critical shear rate, is the plastic viscosity, is the shear rate, is the power law index, and this model is suitable for Bingham fluid when .
The concrete flow model mainly includes the lubrication layer, the shear layer and the plunger layer [28], as shown in Figure 2. The lubrication layer and the slip layer at the boundary are the main influences on the pumping pressure of concrete; followed by the shear layer, where the shear rate decreases gradually; and the center is the plunger layer, where the concrete shear rate tends to be close to zero. The velocity gradient along with the radius is shown by the red line in Figure 2. According to the research of Ingber [29], the lubrication and shear layers during pumping of fresh concrete are caused by shear-induced particle migration. When the concrete flows steadily in the pipe, the shear stress from the pipe wall to the center is gradually reduced, and near the pipe wall, this reduction is more pronounced due to the wall effect, and the shear stress gradient formed by this distribution of shear stress causes the coarse aggregate in the concrete to migrate toward the center of the pipe.

Figure 2.
Concrete flow model and velocity distribution in pipeline.
According to the above model, if the concrete inlet flow rate is certain, it is a common concrete constant flow model, while for the concrete nonconstant pumping model, the ideal concrete pumping speed can be approximated according to the stroke of the piston rod of the concrete pump. The time-varying pumping speed can be yielded from Equation (2), and a sketch diagram is shown in Figure 3.
where is the flow rate of concrete at constant velocity of the piston rod, i.e., the maximum flow rate, is the initial pumping interval, is the stabilize the pumping interval, and is the commutation interval, as shown in Figure 3.

Figure 3.
The velocity model.
For the discontinuous pumping model, on the basis of the constant pumping model, the volume fraction between the phases in the velocity inlet boundary condition can be controlled to achieve the discontinuous pumping state with intermittent gas–liquid flow. If the gas is columnar and periodically distributed in the pipe, the distribution function of the volume fraction of the gas phase as a function of time is:
where is the volume fraction proportion of gas under the boundary condition of velocity inlet, is the distribution period of the gas column, is the number of cycles, is the time point at which a section of the gas column begins to flow into the pipeline, is the end time point, and is the total time at which the gas column completely flows into the pipeline. The time-varying gas phase volume fraction through the inlet section is shown in Figure 4.

Figure 4.
Volume fraction of the gas phase through the velocity inlet cross-section.
2.2. Volume of Fluid (VOF) Model Control Equations
The Fluent software is adopted to simulate the rheological characteristics of concrete. Calculation models in the software include the VOF model, Mixture model and Eulerian model [30]. The VOF model is usually used to simulate two or more incompatible fluids, such as tank shaking and bubble breaking. The mixed model can be used for two or more kinds of fluids or particles, in which the different phase can permeate each other. Euler model, which can be used to solve any polyphase, is only limited by the performance of the computer and the convergence of the solution, and is the most widely used model.
The steady and unsteady flow models of concrete include the lubrication layer material, the core concrete material and gas. The three phases do not interpenetrate each other and have obvious interface. So, the VOF model is adopted in this paper.
The VOF method is an interface tracking method based on Euler grid. In this method, the incompatible fluid components share a set of momentum equations, and the volume fraction of each phase is introduced to realize the tracking of the interphase interface in the computing domain. For a micro space, if there is a phase fluid and its volume fraction is , then there are three cases in this micro space: when , the phase fluid in the micro space is empty. When , the phase fluid in the micro space is fully filled. When , the mixing of the phase fluid exists in the micro space, and there is an interface.
In the mathematical model of VOF, for the phase, its volume fraction equation is:
where is the volume fraction of the phase and , is the density of the phase, is the velocity of the phase fluid, is the source phase, which is zero at default, is transport from the phase to the phase, and is mass transport from the phase to the phase. Instead of solving the initial phase, the volume fraction equation gives a constraint on the volume fraction of each phase, namely .
The volume fraction equation can be solved by explicit or implicit method. The explicit solution equation adopted in this paper is:
where indicates the new time step pointer, is the pointer to the previous time step, is the value of the phase volume fraction in the first-order upwind, second-order upwind, QUICK algorithm, is the unit volume, is the volume flow through the surface at the normal phase velocity.
The momentum equation yields:
where is the mixture density and , is the mixture velocity, is the static pressure, is the molecular viscosity, is the gravitational force, and is all external forces except for the effects of gravity and pressure.
The gas is simplified to an incompressible fluid and all fluids are ignored for temperature variation and the solution of the energy equation is neglected.
3. Rheological Characteristics of Nonconstant Concrete Pumping
3.1. Concrete Material Properties and Lubrication Layer Parameters
The main factors affecting the properties of concrete materials are yield stress and plastic viscosity, which can be measured by concrete rheometer. C30 concrete is used, which material property can be found in [21] and are shown in Table 1.

Table 1.
Concrete material properties.
As the most important factor affecting pumping pressure loss, the lubrication layer has been studied by many researchers. According to the cement slurry volume, water-cement ratio, high efficiency water reducing agent content and fine sand content of concrete, the thickness of the lubrication layer is generally between 1 mm and 9 mm [31]. In this paper, the research data of Choi [21] are adopted, and the lubrication layer is set as 2 mm.
3.2. Force Analysis and Nonconstant Fluid Characteristic Simulation of Straight Pipe Pumping
In the pumping pipe of concrete pump trucks, the straight pipe is the main component of the pipe, so the analysis of the force characteristics of the pipe is of great significance to the analysis of the vibration characteristics of the vehicle boom.
During steady pumping, according to the research of Choi [21], the formula of pressure loss is:
where is the pressure loss caused by friction, is the pipe length, is the concrete velocity, is the lubrication layer viscosity, is the core concrete viscosity, is the pipe radius, and is the lubrication layer thickness.
For the nonconstant flow, the stress in the process of straight pipe flow is analyzed, as shown in Figure 5.
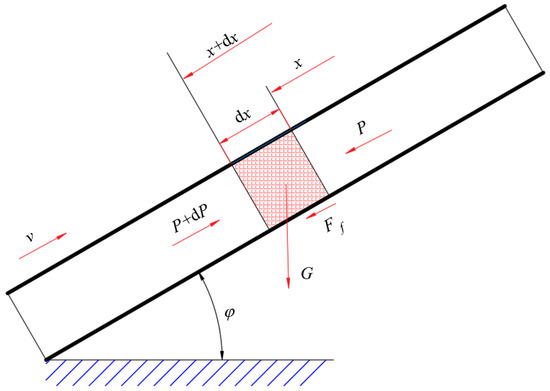
Figure 5.
Force analysis of straight pipe pumping.
The tube wall friction is . According to the conservation of momentum the following equation can be obtained:
Combining Equation (7) with Equation (8), the pipeline pressure loss can be yielded:
where is the pipe pressure, is the density, is the is the acceleration of gravity, and is the straight pipe tilt angle.
Additionally, the wall excitation force (axial force) of the straight pipe is the sum of the wall friction force and gravity, i.e.,
The geometric model of the pipe structure is established in Solidworks software, the ICEM meshing tool is used to divide the fluid domain into structured grids of the boundary layer and the central layer, the grid model is imported into Fluent software, and the pressure-based transient solution method is selected, the VOF model is used to define the material properties of the boundary lubrication layer and the central concrete in the laminar flow mode, and the concrete two-fluid flow model is established, the boundary conditions are set to the velocity inlet, the pressure outlet and the non-slip wall surface.
A horizontal placed straight pipe with a diameter of 125 mm and a length of 1.1 m was selected to reduce the simulation time. The element number in the pipeline model is 49,256. A commonly used pumping condition with a pumping frequency of 0.267 Hz (16 times/min) was adopted. The corresponding flow rate is 85 . The velocity of concrete at the inlet of the pipeline can be obtained from Equation (2), where t1 = 0 s, t2 = 0.69 s, t3 = 2.71 s, t4 = 3.75, v = 2.53 m/s. The velocity diagram of concrete inlet is shown in Figure 6. The inlet velocity is defined by using the user defined function (UDF) file. After simulation calculations, post process was done. The pipeline pressure 0.1 m away from the inlet was monitored, and the excitation force was calculated by considering all the results of the last 1 m pipeline. Comparison between the simulated pipeline pressure and the exciting force and the theoretical results is shown in Figure 7 and Figure 8.
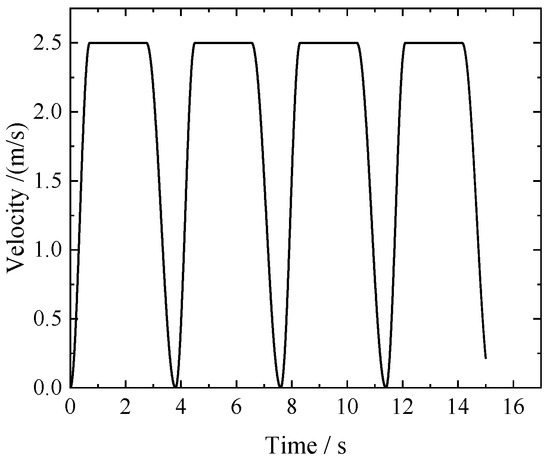
Figure 6.
Concrete pumping velocity.

Figure 7.
Pipeline pressure comparison between simulation and theoretical values.

Figure 8.
Excitation forces comparison between simulation and theoretical values.
According to the simulation results in Figure 7, it can be seen that in the initial acceleration interval, affected by the transient changes in concrete mass and concrete velocity, namely momentum , the pipeline pressure has an obvious abrupt peak. Followed by the constant velocity motion interval in the middle range, at which time the pipeline pressure is almost constant. Finally, the velocity decay, the pipeline pressure also decreases accordingly. Pipeline pressure fluctuates periodically during the whole pumping process. In Figure 8, the variation trend of the exciting force is roughly the same as that of the pressure, but there is no peak change in the initial acceleration stage, because the exciting force of the straight pipe is mainly provided by the friction force of the pipe wall. In addition, the theoretical calculation results are the same as the simulation results, but the values are slightly different, which is because the thickness of the lubrication layer of the concrete in the pipe is not completely accurate to the theoretical value during the simulation.
3.3. Force Analysis and Nonconstant Fluid Characteristic Simulation of Elbow Pipe Pumping
In the pumping pipeline, an elbow pipe is mainly used to connect the pipes between two booms to change the direction of the fluid. This may cause particle blockage in an elbow pipe, erosion wear on pipe wall [22,23,24] and other conditions that seriously affect the pressure loss of the pipe and the pipe structure. When the fluid flows through the elbow, the change in flow direction and the exciting force generated under the nonconstant pumping condition will seriously affect the stability of the boom.
Regardless of gravity, the force analysis for an elbow pipe is shown in Figure 9.
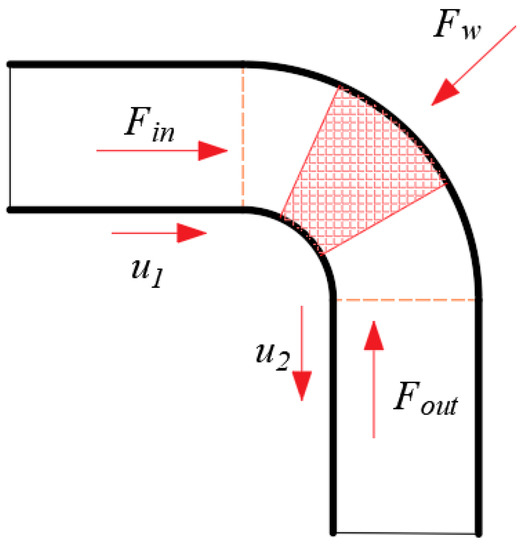
Figure 9.
Force analysis for elbow pipe pumping.
According to the conservation of momentum, the following equation is obtained:
where is the inlet velocity, is the outlet velocity, is the concrete flow rate in the pipe, , , is the inlet pressure, is the pipe cross-sectional area, is the outlet pressure, is the excitation force, and its direction is towards the normal of the outer arc.
A similar pumping model used in Section 3.2 is adopted, and UDF files related to speed and time is loaded. Other boundary conditions remained unchanged. The pipe model is a curved pipe with a curvature radius of 140 mm and a bending angle of 90°, as shown in Figure 10. Figure 11 shows the comparison of the excitation force between the theoretical calculation value and the simulated one.

Figure 10.
Geometry model of the elbow pipe.

Figure 11.
Comparison of the elbow pipe excitation force between simulation and theoretical value.
In Figure 11, the simulated excitation force of elbow pipes remains the same as the theoretical result, which means Equation (11) can well represents the elbow pipe exciting. Different from the straight pipe, the elbow pipe excitation force is also affected by the radius of curvature and bending angle of the pipe.
4. Rheological Characteristics of Discontinuous Concrete Pumping
4.1. Discontinuous Flow Model
During the pumping process, the gas will inevitably be sucked into the concrete. There are two states for the gas in the pipe: irregular air bubbles and air columns. The influence of bubbles on the pipeline pressure and the wall excitation force is relatively small, and during the concrete flow process, bubbles gradually gather together to form air columns, as shown in Figure 12. So, only air columns are considered in this model.

Figure 12.
Schematic diagram of concrete flow under the influence of gas in a pipeline.
To simplify the analysis, the gas is modeled as incompressible fluid. A large amount of air is directly imported in the inlet to form air columns, and Equation (3) is used to define the time of air flowing into the pipeline and the volume fraction of air. In the actual pumping situation, the volume fraction of the gas column and the distribution of the gas column are all randomly changing. In order to facilitate research, two kinds of simulation are performed in this paper. The first one contains only one gas column, while the gas volume fraction changes. The second one contains a multi-stage gas column distributed more frequently.
4.2. Pumping Characteristics of Concrete in the Straight Pipe
- (a)
- Pumping characteristics in the straight pipe under the influence of a single gas column
By editing the function of volume fraction with time and loading it into the velocity inlet boundary conditions, the gas phase and the liquid phase are controlled to enter alternately from the velocity inlet boundary to form a discontinuous flow with a constant velocity of 2.53 m/s. The flow diagram is shown in Figure 13.

Figure 13.
Discontinuous flow diagram of concrete.
Keeping other conditions unchanged, numerical simulation is carried out on four cases where the volume fraction of the gas column is 10%, 20%, 30% and 40% (the percentage of the gas column in the total volume of 1 m pipe). The relationship between the pipe pressure P and the wall exciting force with the volume fraction of the gas is shown in Figure 14, Figure 15, Figure 16 and Figure 17.

Figure 14.
Concrete pressure in a single period.

Figure 15.
Gas volume fraction and peak pressure value.

Figure 16.
Wall excitation force in a single period.

Figure 17.
Influence of gas volume fraction on the peak-to-peak value of the excitation force.
There is a significant pressure drop when gas is sucked in Figure 14. The higher the gas volume fraction, the more significant the pressure reduction and the more intense the pressure fluctuations. Additionally, compared with the continue pumping, the pressure fluctuation curve is non-smooth for the discontinuous case. This is because the pipeline pressure is derived from the pressure of a special section, and influenced by the gas phase, the pressure gradient inside the pipeline exhibits a complex and nonlinear distribution.
There is also a significant drop for the wall excitation force when gas is considered in Figure 16. The higher the gas volume fraction, the more significant the force reduction and the more intense the force fluctuations. Unlike the curves in Figure 14, the excitation force curves in Figure 16 are smooth. This is because the excitation force comprehensively considered all the results of the last 1 m pipeline.
As shown in Figure 15 and Figure 17, with the increase in gas volume fraction, the peak-to-peak values of the pipe pressure and the exciting force gradually increase, and these values are only related to the total gas content in the pipe. The peak-to-peak value of the exciting force on the pipe wall is , where is the percentage of gas in the total volume in the pipe.
- (b)
- Pumping characteristics in the straight pipe under the influence of air column groups
The concrete flow velocity is 2.53 m/s, and the volume fraction of a single gas column is limited to 10%. The time distribution frequency of the gas column flowing into the pipe is 0.1 s, 0.2 s, 0.3 s, 0.4 s and 0.5 s, respectively (the volume fraction of gas in the whole cycle is 40%, 20%, 13%, 10% and 8%). The flow diagram is shown in Figure 18. The results of the pipe pressure and the pipe wall exciting force obtained are shown in Figure 19.
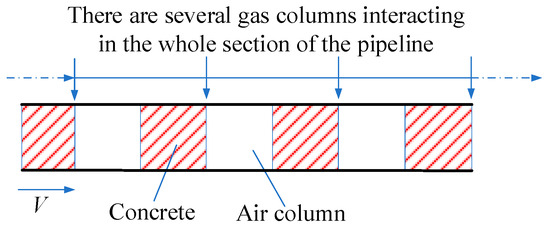
Figure 18.
Schematic diagram of the high-frequency distribution flow of air columns.

Figure 19.
Variation trend of the pipe pressure with different volume fraction.
As shown in Figure 19, different distribution frequencies of the air column result in different pipeline pressure fluctuation. With the increase in air column distribution frequency, pressure fluctuation trends to be more and more chaotic. When the time distribution frequency of the gas column flowing into the pipe is 0.1 s, pipe pressure fluctuation has no obvious rule. This is because the space between gas columns is very small, resulting in fusion and separation among the gas columns in the pipe. Therefore, the gas in the pipe has an atmospheric bubble or gas column shape with random distribution.
The time-variation excitation force curves with different air column distribution frequencies are shown in Figure 20, and the peak-to-peak value of the excitation forces are shown in Figure 21.

Figure 20.
Excitation with different distribution frequencies.

Figure 21.
Peak-to-peak value of excitation with different distribution frequencies.
As can be seen from Figure 21, the wall excitation force changes periodically with the air column distribution frequency when the period is between 0.2 s and 0.4 s. As the distribution period increases, the mean value of the excitation force gradually increases. Due to the influence of multiple air columns in the pipeline on the excitation force, the fluctuation of the excitation has no obvious change pattern, but its peak-to-peak value does not exceed the product of the proportion of the total volume fraction of gas and the excitation force of steady pumping state. In addition, when the distribution period decreases to a critical value, with the flow of concrete, air columns break or aggregate with each other, resulting in the irregular changes in the excitation force.
As can be seen from Figure 21, affected by the superposition of multiple gas columns in the pipe, the peak-to-peak value of the excitation force on the pipe wall fluctuates irregularly, but its peak-to-peak value does not exceed the product of the proportion of the total integral number of gas in the pipe and the excitation force in the pipe during steady-state pumping.
The relation between the effective excitation force and the comprehensive volume fraction proportion is shown in Figure 22. Under the influence of the high-frequency distribution of the gas column, multiple gas columns in the pipe interact with each other causing their peak-to-peak value to vary irregularly, but their effective values are linearly related to the volume fraction of the of the air column occupying the whole cycle, that is, .

Figure 22.
Relation between effective value of the excitation force and the proportion of comprehensive volume fraction.
4.3. Rheological Characteristics of Discontinuous Concrete Pumping in Elbow Pipes
In order to study the excitation force on the pipe wall in the discontinuous flow process of concrete, a same pipe model with a constant velocity of 2.53 m/s mentioned in Section 3.3 is used to simulate the influence of different volume fractions of the air column on the excitation force on the pipe wall.
The time interval of air columns flowing into the pipe is 3.75 s, and the volume fraction of the air column is 10%, 20%, 30% and 40% (the volume fraction is the percentage of the total integral number of the 1 m pipe). The concrete flow diagram in the elbow pipe is shown in Figure 23.

Figure 23.
Flow diagram of an elbow pipe with different gas volume fractions.
As can be seen from Figure 23, with the presence of gas, when the gas passes through the elbow pipe, the gas will be significantly close to the inner wall and the concrete close to the outer wall due to the centrifugal force. The elbow pipe excitation force is shown in Figure 24.
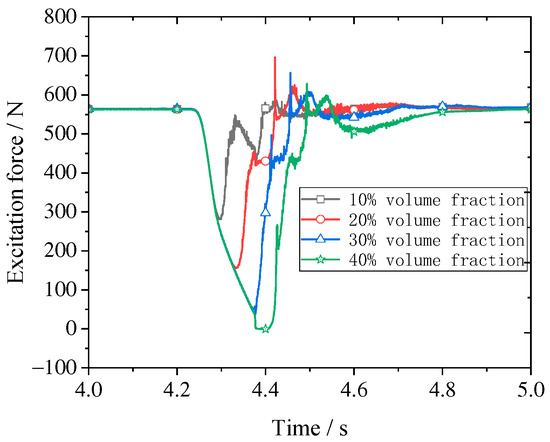
Figure 24.
Excitation force of an elbow pipe.
It can be seen from Figure 24 that when the gas flows into the pipe, the excitation force of the elbow begins to decrease until the whole gas column flows into the pipe. The exciting force of the elbow reaches the minimum, then the concrete begins to flow into the pipe, and the exciting force of the elbow begins to rise. When the concrete flows through the elbow, it will have an impact on the pipe wall of the elbow. At this time, the excitation force of the elbow will have an obvious mutation peak, then as the concrete continues to flow, the excitation force of the elbow continues to increase until the flow is stable.
Figure 25 shows the relationship between the peak-to-peak values of the exciting force in the elbow pipe and the volume fraction of gas under different conditions. The peak-to-peak value of the bend exciting force increases with the increase in gas volume fraction. Additionally, with the increase in gas volume fraction, the slope of the curve decreases.

Figure 25.
Peak-to-peak value of the elbow pipe excitation force.
5. Nonconstant and Discontinuous Concrete Pumping Characteristics
During the working process of the pump truck, the force of concrete on the pipe wall can be divided into: nonconstant flow generated by alternating pumping of hydraulic pumps and discontinuous flow caused by inadequate suction material of concrete pump. In order to explore its comprehensive influence on the wall pressure and the excitation force, this paper designed the simulation of gas in the pipe under two conditions: low-frequency distribution and high-frequency distribution.
A two-fluid concrete pumping model is used, with a lubrication layer thickness of 2 mm, a pipe length of 1.1 m, and an inlet velocity of 2.53 m/s, a pumping frequency of 0.267 Hz, and a maximum velocity of 2.5 m/s.
For low-frequency gas column distribution, for the case that there is only one gas segment in a pumping cycle, and the volume fraction of a single gas column is 20% of the total pipe volume, the pipe pressure and the exciting force obtained by simulation are shown in Figure 26 and Figure 27.

Figure 26.
Pipeline pressure for a single gas column.

Figure 27.
Excitation force for a single gas column.
From Figure 26 and Figure 27, it can be seen that the trend of the pipe pressure and the excitation force fluctuates periodically with the change in pumping speed. When there is only one gas column, the pipeline pressure and the excitation force will have a sudden peak value during the gas column passing through the pipeline, and the value is related to the volume fraction of the gas column.
In the high-frequency gas columns distribution case, take the gas column interval period 0.2 s as example, the volume fraction of the single section of the gas column is 10% of the total volume of the pipe, the simulated pipe pressure and the exciting force at this time are shown in Figure 28 and Figure 29.

Figure 28.
Pipeline pressure for multi-air columns.

Figure 29.
Excitation force for multi-air columns.
It can be seen from Figure 28 and Figure 29 that in the case of the high-frequency distribution of the air column, the pipe pressure and the excitation force are also affected by pumping speed and air column distribution frequency. However, the pipe pressure and the exciting force fluctuate more frequently compared with the low-frequency air column distribution case.
In order to explore the characteristics of the pipe pressure and the excitation force during actual pumping, the pumping pressure of the hydraulic cylinder of a certain type of pump trucks is collected, as shown in Figure 30. The sensor is installed on the hydraulic cylinder by the manufacturer before delivery, so the detailed arrangement, model and parameters are not available. This curve can only serve as a reference for research to a certain extent. So, only the changing trend of the collected pressure is compared with the simulation concrete pressure.

Figure 30.
Real car pumping pressure.
From Figure 30, one of the dual-cylinders of concrete hydraulic drive pumping pushes the piston to accelerate from zero, compresses the concrete into the feeding tube, at which time, the pressure has obvious sudden peak. After reaching a certain speed, the piston moves at a constant speed, and the pressure is relatively stable at this time. Finally, the piston is near the end of the stroke and starts to decelerate. The pressure drops until the piston collides with the bottom of the cylinder, the pressure rises suddenly, and the other concrete hydraulic cylinder push the piston to work, so the cycle repeated. The results are similar to the simulation in Figure 28 for the high-frequency distribution of the gas column case. Since bottom collision is not considered in the simulation model, there is no sudden change in pressure at the end of the cycle. After subtracting this difference, the change trend is basically the same for simulation model and experimental results. Thisindicates that the pipe pressure is mainly affected by two factors: nonconstant pumping generated by alternate working of dual-pump and discontinuous pumping influenced by gas.
6. Conclusions
A multi-fluid pumping simulation model for concrete pump trucks is proposed. The rheological properties of concrete and its excitation force on the pipe wall during nonconstant pumping, discontinuous pumping, and nonconstant discontinuous pumping are studied for straight and elbow pipes, respectively. Corresponding research can provide guidance for the pumping mechanism, vibration response, and working stability analysis of the concrete pump truck. The conclusions are as follows:
- 1.
- For the nonconstant pumping of the concrete pump truck with two alternating cylinders, the pipeline pressure and the excitation force vary periodically with the pumping speed of concrete. With the change in pumping speed, the pipe pressure will have an obvious sudden peak in the initial stage of pumping; followed by the stable conveying stage, the pipe pressure is almost constant; and finally the reversing stage, the pressure will also decrease. The simulated pipeline pressure and the excitation force are basically consistent with the theoretical results.
- 2.
- For discontinuous concrete pumping caused by inadequate suction, the mean value of the pipe pressure and the wall excitation force is negatively correlated with the volume fraction of gas in the pipe under the condition that the volume fraction of gas does not exceed 40% of the total integral number of the pipe. The peak-to-peak value is positively correlated with the volume fraction when the gas column is distributed at low frequency. While the peak-to-peak value changes irregularly when the air columns are distributed at high frequency.
- 3.
- The air column will significantly increase the pipeline excitation force. The impact on the excitation of an elbow pipe is greater than the that of the straight pipe, and the impact law is more complex.
- 4.
- The pipe pressure of the nonconstant discontinuous concrete pumping model has a good consistency with the variation trend of pumping pressure of a real truck hydraulic cylinder, and the model can better reflect the nonconstant flow caused by the alternating pumping and the discontinuous flow caused by insufficient suction material. However, due to the limitations of experimental conditions, it is not yet possible to compare the specific simulation results with the experimental values.
Author Contributions
Conceptualization, Y.R. and J.Z.; methodology, Y.R.; software, C.B.; validation, J.L.; data curation, W.L. and H.W.; writing—original draft preparation, C.B.; writing—review and editing, W.L. and W.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Shanxi Basic Research Project (Grant No. 20210302124445, 201901D111245), Shanxi Provincial Science and Technology Platform (201805D121006), Shanxi Excellent Doctor’s Work Award Fund (Grant No. 20202061), and Shanxi Excellent Postgraduate Innovation Project (Grant No. 2022Y677).
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wu, Y.Z.; Li, W.J.; Liu, Y.H. Fatigue life prediction for boom structure of concrete pump truck. Eng. Fail. Anal. 2016, 60, 176–187. [Google Scholar] [CrossRef]
- Tang, H.B.; Ren, W. Research on rigid-flexible coupling dynamic characteristics of boom system in concrete pump truck. Adv. Mech. Eng. 2015, 7, 1–7. [Google Scholar] [CrossRef]
- Zhaidarbek, B.; Tleubek, A.; Berdibek, G.; Wang, Y. Analytical predictions of concrete pumping, Extending the Khatib–Khayat model to Herschel–Bulkley and modified Bingham fluids. Cem. Concr. Res. 2023, 163, 107035. [Google Scholar] [CrossRef]
- Roussel, N.; Geiker, M.R.; Dufour, F.; Thrane, L.N.; Szabo, P. Computational modeling of concrete flow, General overview. Cem. Concr. Res. 2007, 37, 1298–1307. [Google Scholar] [CrossRef]
- Dufour, F.; Pijaudier-Cabot, G. Numerical modelling of concrete flow, homogeneous approach. Int. J. Numer. Anal. Methods Geomech. 2005, 29, 395–416. [Google Scholar] [CrossRef]
- Li, H.; Sun, D.; Wang, Z.; Huang, F.; Yi, Z.; Yang, Z.; Zhang, Y. A Review on the Pumping Behavior of Modern Concrete. J. Adv. Concr. Technol. 2020, 18, 352–363. [Google Scholar] [CrossRef]
- Kim, J.S.; Kwon, S.H.; Jang, K.P.; Choi, M.S. Concrete pumping prediction considering different measurement of the rheological properties. Constr. Build. Mater. 2018, 171, 493–503. [Google Scholar] [CrossRef]
- Jang, K.P.; Kwon, S.H.; Choi, M.S.; Kim, Y.J.; Park, C.K.; Shah, S.P. Experimental Observation on Variation of Rheological Properties during Concrete Pumping. Int. J. Concr. Struct. Mater. 2018, 12, 79. [Google Scholar] [CrossRef]
- Remond, S.; Pizette, P. A DEM hard-core soft-shell model for the simulation of concrete flow. Cem. Concr. Res. 2014, 58, 169–178. [Google Scholar] [CrossRef]
- Shyshko, S.; Mechtcherine, V. Developing a Discrete Element Model for simulating fresh concrete, Experimental investigation and modelling of interactions between discrete aggregate particles with fine mortar between them. Constr. Build. Mater. 2013, 47, 601–615. [Google Scholar] [CrossRef]
- Mechtcherine, V.; Shyshko, S. Simulating the behaviour of fresh concrete with the Distinct Element Meth—Deriving model parameters related to the yield stress. Cem. Concr. Compos. 2015, 55, 81–90. [Google Scholar] [CrossRef]
- Hao, J.; Jin, C.; Li, Y.; Wang, Z.; Liu, J.; Li, H. Simulation of Motion Behavior of Concrete in Pump Pipe by DEM. Adv. Civ. Eng. 2021, 2021, 3750589. [Google Scholar] [CrossRef]
- Jiang, S.; Chen, X.; Cao, G.; Tan, Y.; Xiao, X.; Zhou, Y.; Liu, S.; Tong, Z.; Wu, Y. Optimization of fresh concrete pumping pressure loss with CFD-DEM approach. Constr. Build. Mater. 2021, 276, 122204. [Google Scholar] [CrossRef]
- Jiang, S.; Zhang, W.; Chen, X.; Cao, G.; Tan, Y.; Xiao, X.; Liu, S.; Yu, Q.; Tong, Z. CFD-DEM simulation research on optimization of spatial attitude of concrete pumping boom based on evaluation of minimum pressure loss. Powder Technol. 2022, 403, 117365. [Google Scholar] [CrossRef]
- Wang, Z.G.; Hao, J.; Li, Y.; Tian, X. Simulation of Concrete Pumped in Horizontal Coil and Super High-Rise Building Based on CFD. J. Adv. Concr. Technol. 2022, 20, 328–341. [Google Scholar] [CrossRef]
- Le, H.D.; Kadri, E.H.; Aggoun, S.; Vierendeels, J.; Troch, P.; De Schutter, G. Effect of lubrication layer on velocity profile of concrete in a pumping pipe. Mater. Struct. 2015, 48, 3991–4003. [Google Scholar] [CrossRef]
- Secrieru, E.; Cotardo, D.; Mechtcherine, V.; Lohaus, L.; Schröfl, C.; Begemann, C. Changes in concrete properties during pumping and formation of lubricating material under pressure. Cem. Concr. Res. 2018, 108, 129–139. [Google Scholar] [CrossRef]
- Jang, K.P.; Choi, M.S. How affect the pipe length of pumping circuit on concrete pumping. Constr. Build. Mater. 2019, 208, 758–766. [Google Scholar] [CrossRef]
- Feys, D.; Khayat, K.H.; Khatib, R. How do concrete rheology, tribology, flow rate and pipe radius influence pumping pressure? Cem. Concr. Compos. 2016, 66, 38–46. [Google Scholar] [CrossRef]
- Chen, J.; Xie, H.; Guo, J.; Chen, B.; Liu, F. Preliminarily experimental research on local pressure loss of fresh concrete during pumping. Measurement 2019, 147, 106897. [Google Scholar] [CrossRef]
- Choi, M.S.; Roussel, N.; Kim, Y.; Kim, J. Lubrication layer properties during concrete pumping. Cem. Concr. Res. 2013, 45, 69–78. [Google Scholar] [CrossRef]
- Tan, Y.; Zhang, H.; Yang, D.; Jiang, S.; Song, J.; Sheng, Y. Numerical simulation of concrete pumping process and investigation of wear mechanism of the piping wall. Tribol. Int. 2012, 46, 137–144. [Google Scholar] [CrossRef]
- Bozzini, B.; Ricotti, M.E.; Boniardi, M.; Mele, C. Evaluation of erosion–corrosion in multiphase flow via CFD and experimental analysis. Wear 2003, 255, 237–245. [Google Scholar] [CrossRef]
- Zhang, R.; Xu, K.; Liu, Y.; Liu, H. A general numerical method for solid particle erosion in gas–liquid two-phase flow pipelines. Ocean Eng. 2023, 267, 113305. [Google Scholar] [CrossRef]
- Jiang, S.; He, Z.; Zhou, Y.; Xiao, X.; Cao, G.; Tong, Z. Numerical simulation research on suction process of concrete pumping system based on CFD method. Powder Technol. 2022, 409, 117787. [Google Scholar] [CrossRef]
- Cazzulani, G.; Ghielmetti, C.; Giberti, H.; Resta, F.; Ripamonti, F. A test rig and numerical model for investigating truck mounted concrete pumps. Autom. Constr. 2011, 20, 1133–1142. [Google Scholar] [CrossRef]
- Güneyisi, E.; Gesoglu, M.; Naji, N.; Ipek, S. Evaluation of the rheological behavior of fresh self-compacting rubberized concrete by using the Herschel–Bulkley and modified Bingham models. Arch. Civ. Mech. Eng. 2016, 16, 9–19. [Google Scholar] [CrossRef]
- Nerella, V.N.; Mechtcherine, V. Virtual Sliding Pipe Rheometer for estimating pumpability of concrete. Constr. Build. Mater. 2018, 170, 366–377. [Google Scholar] [CrossRef]
- Ingber, M.S.; Graham, A.L.; Mondy, L.A.; Fang, Z. An improved constitutive model for concentrated suspensions accounting for shear-induced particle migration rate dependence on particle radius. Int. J. Multiph. Flow 2009, 35, 270–276. [Google Scholar] [CrossRef]
- Ansys Inc. Ansys Fluent Theory Guide; ANSYS Inc.: Canonsburg, PA, USA, 2023. [Google Scholar]
- Ngo, T.T.; Kadri, E.H.; Bennacer, R.; Cussigh, F. Use of tribometer to estimate interface friction and concrete boundary layer composition during the fluid concrete pumping. Constr. Build. Mater. 2010, 24, 1253–1261. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).