Rollover Stability of Heavy-Duty AGVs in Turns Considering Variation in Friction Coefficient
Abstract
1. Introduction
2. The Mechanism of Steering Rollover of AGV
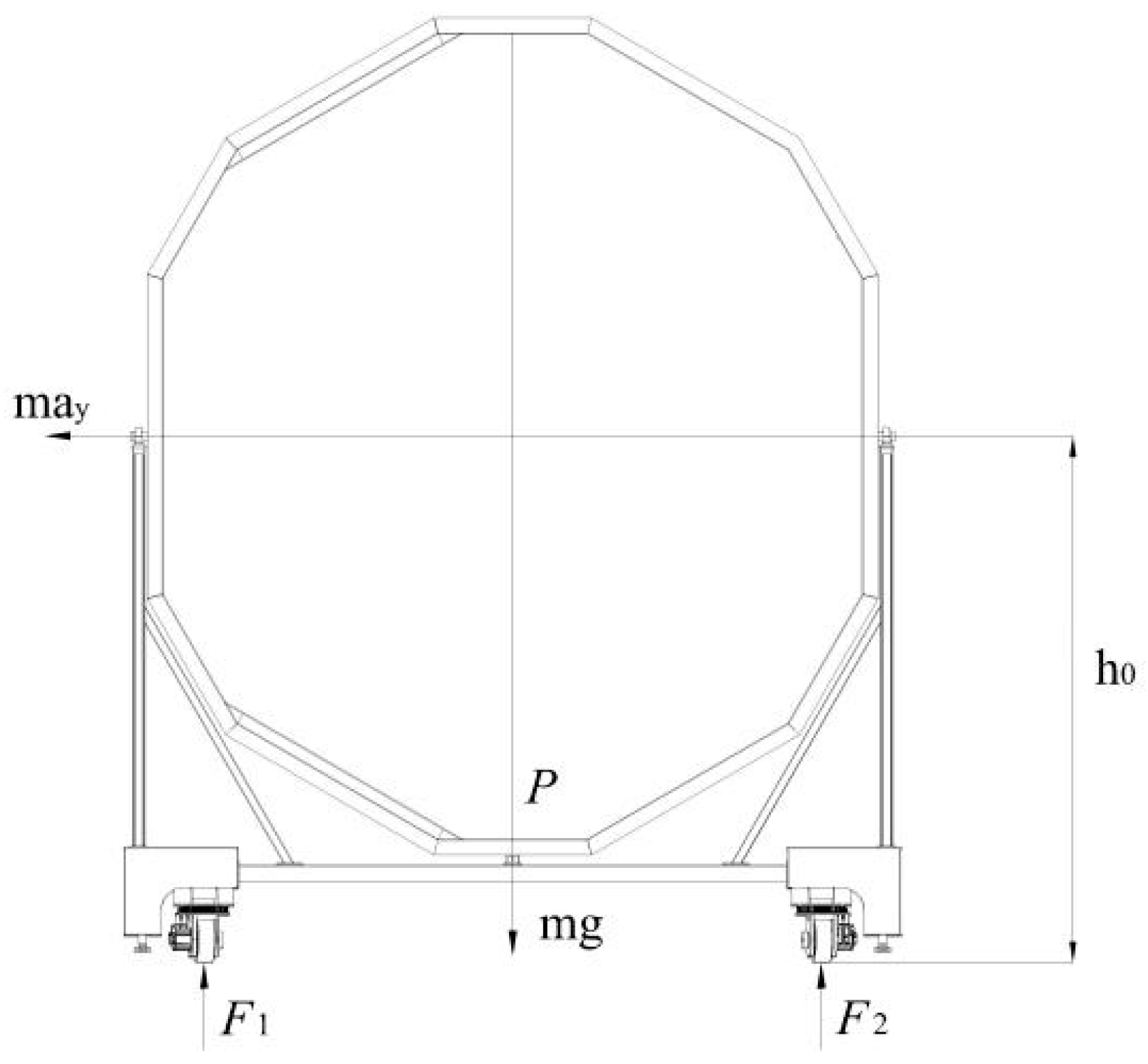
2.1. Model of AGV Rollover
2.2. Dynamic Rollover Model for Heavy-Duty AGV
2.3. The Omnidirectional Kinematics Model of Heavy-Duty AGV
2.3.1. Mathematical Model of a Heavy-Duty AGV with Four Helm Wheels
2.3.2. Mathematical Model for Positive Kinematics Analysis of Heavy-Duty AGV
- (1)
- The heavy-duty AGV is a rigid body.
- (2)
- The running ground of the heavy-duty AGV is horizontal and of suitable smoothness.
- (3)
- The motion speed of heavy-duty AGV is low and there is no air resistance.
- (4)
- The driving wheel of heavy-duty AGV has good contact with the ground, and the driving wheel does pure rolling.
2.3.3. Inverse Kinematics Analysis of the Model
3. Heavy-Loaded AGV Rollover Simulation Analysis
3.1. Simplification of AGV Model
- (1)
- Simplify the AGV into a mass point, so that the AGV mass is concentrated in one point;
- (2)
- Ignoring the influence of suspension characteristics when considering the AGV model as a rigid object to perform force analysis;
- (3)
- Ignoring the asymmetry of the left and right tires and the front and rear axles;
- (4)
- Ignoring the effect of longitudinal motion of the AGV on rollover during steady-state steering and driving;
- (5)
- The influence of the dynamic characteristics of the AGV in the pitch direction on rollover is not considered.
3.2. Simulation Modelling
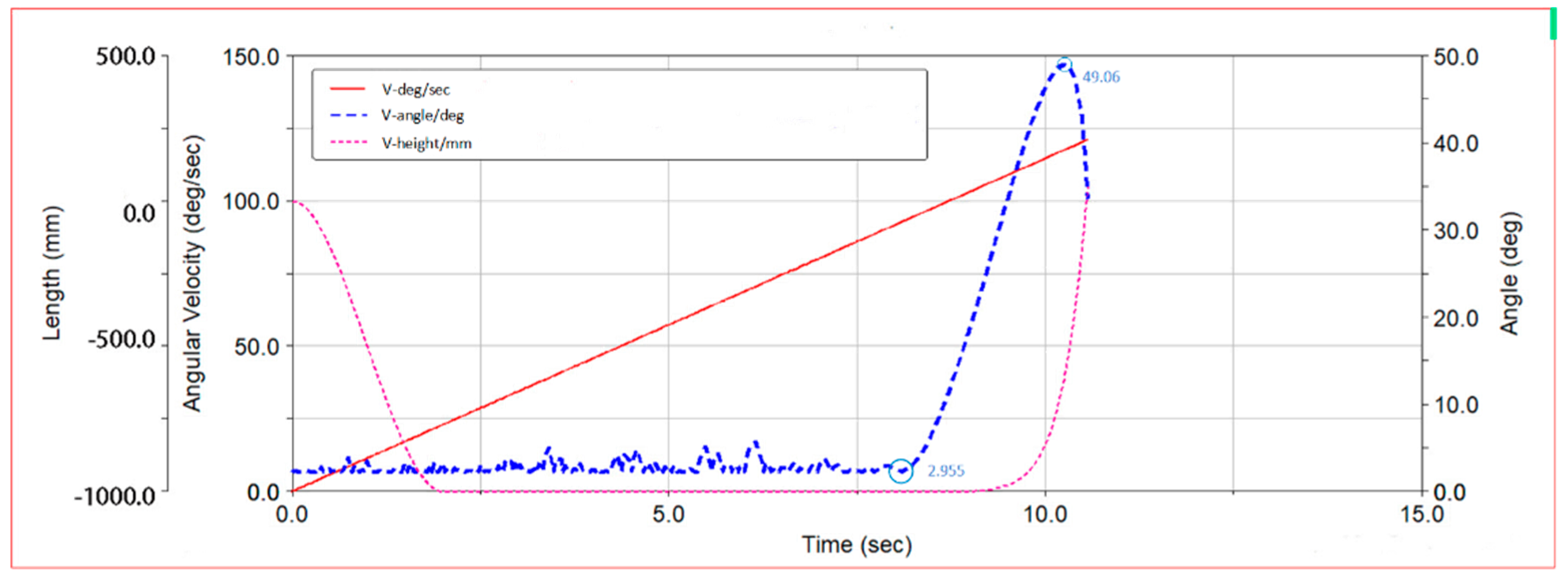
3.3. Simulation Process of Heavy-Duty AGV
3.4. Analysis of Factors Affecting the Rollover Stability of AGV
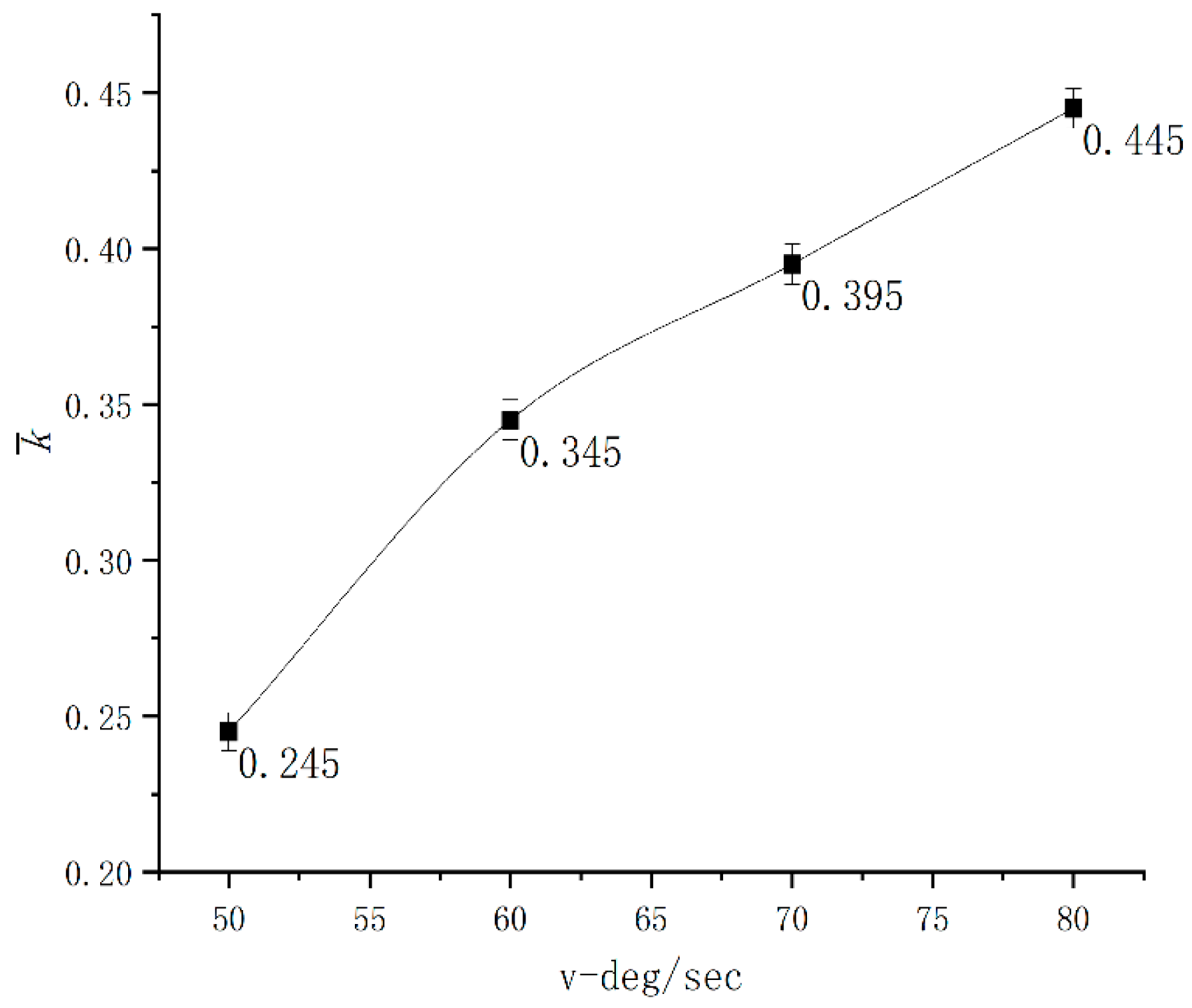
3.4.1. Impact of Turning Speed on the Stability of Rollover in AGV
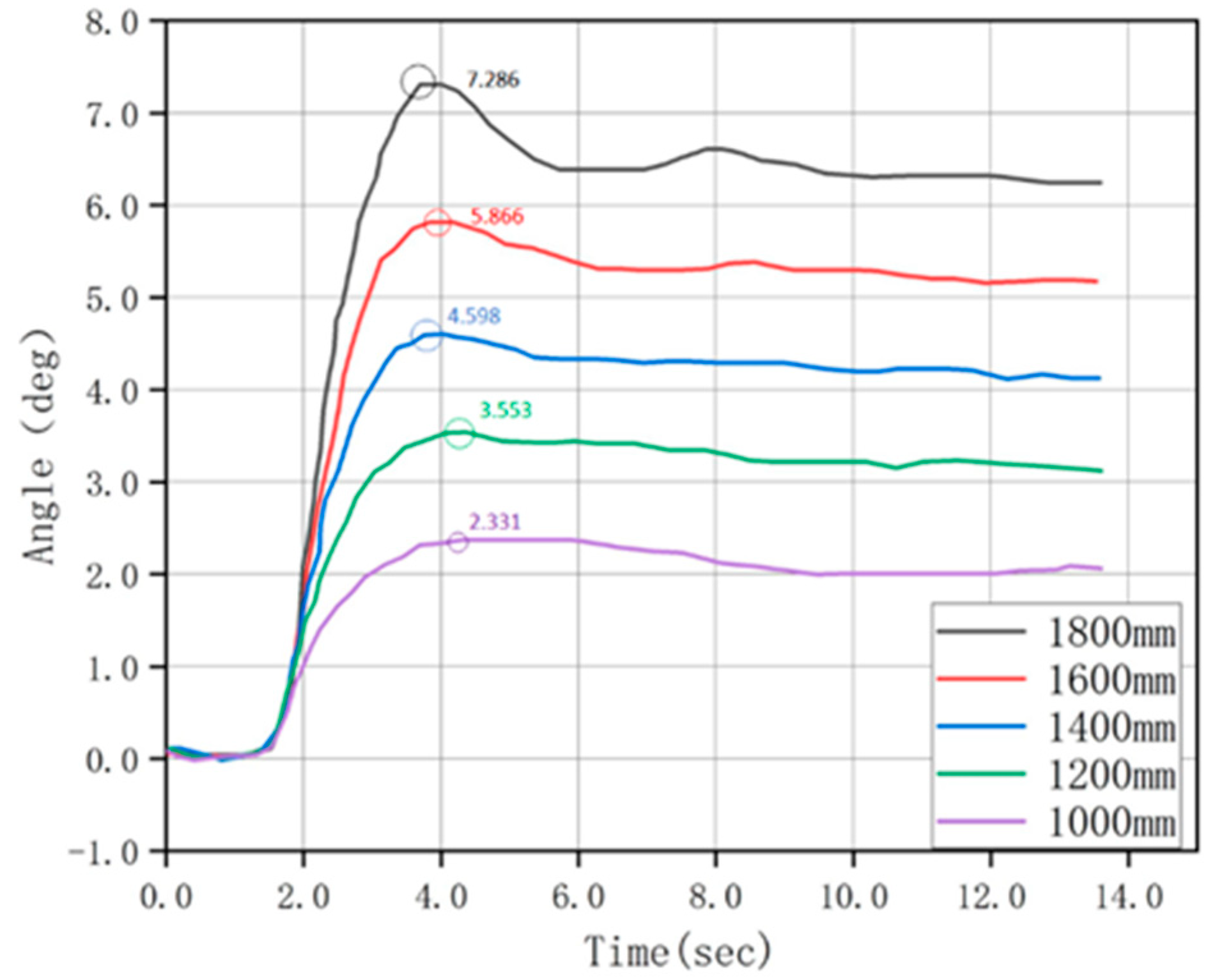
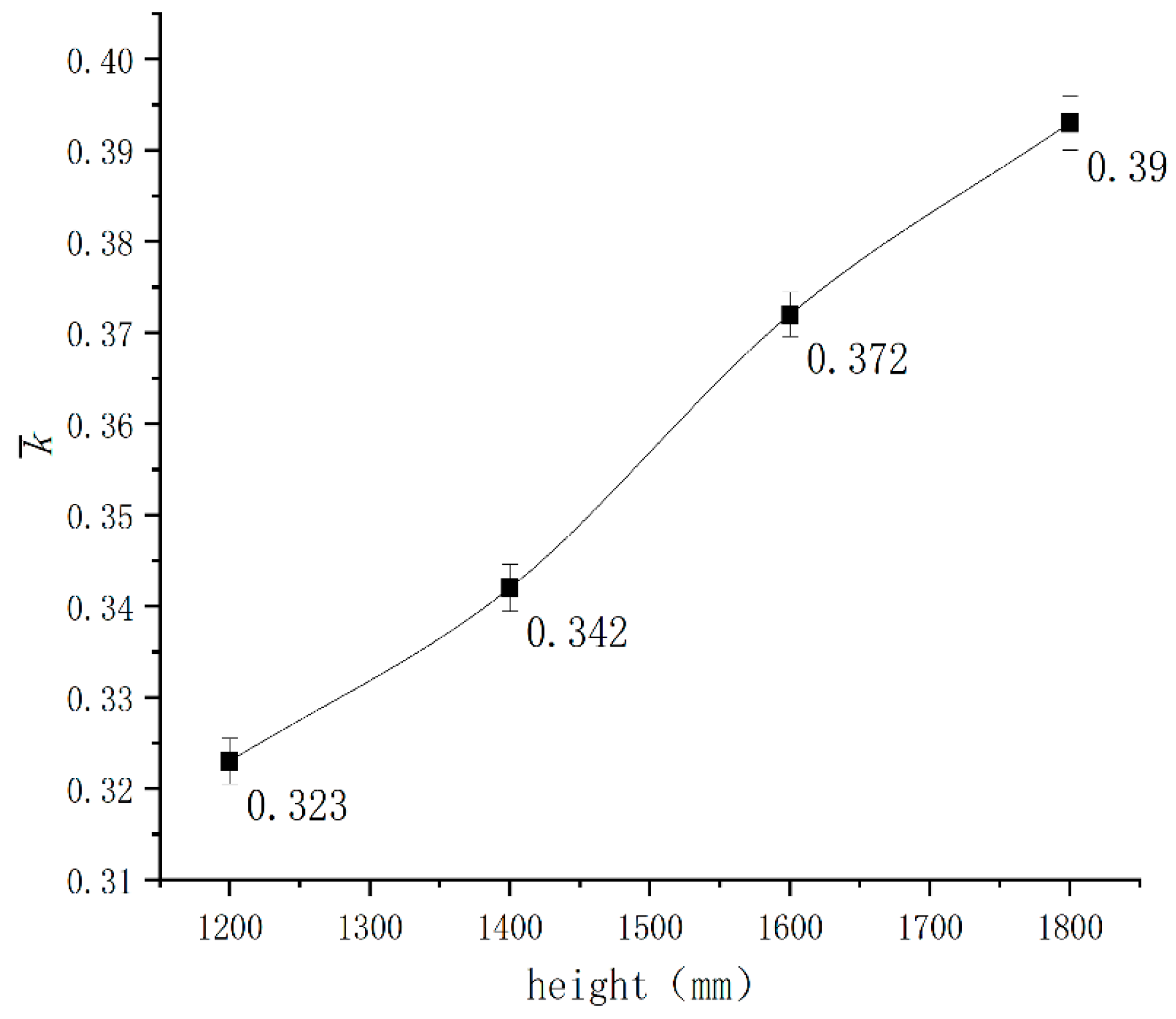
3.4.2. The Impact of Centre of Gravity Position on the Stability of AGV Rollover
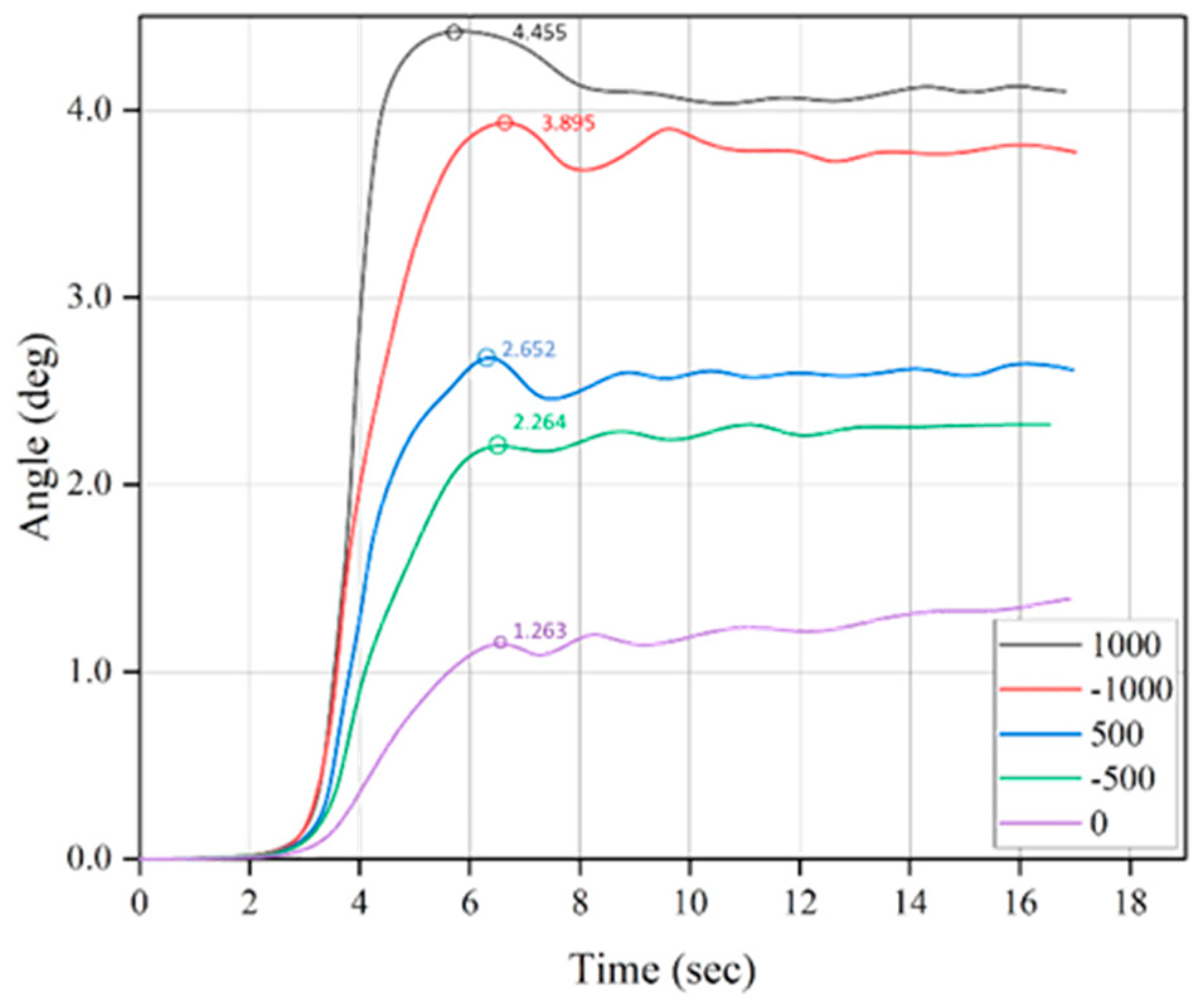
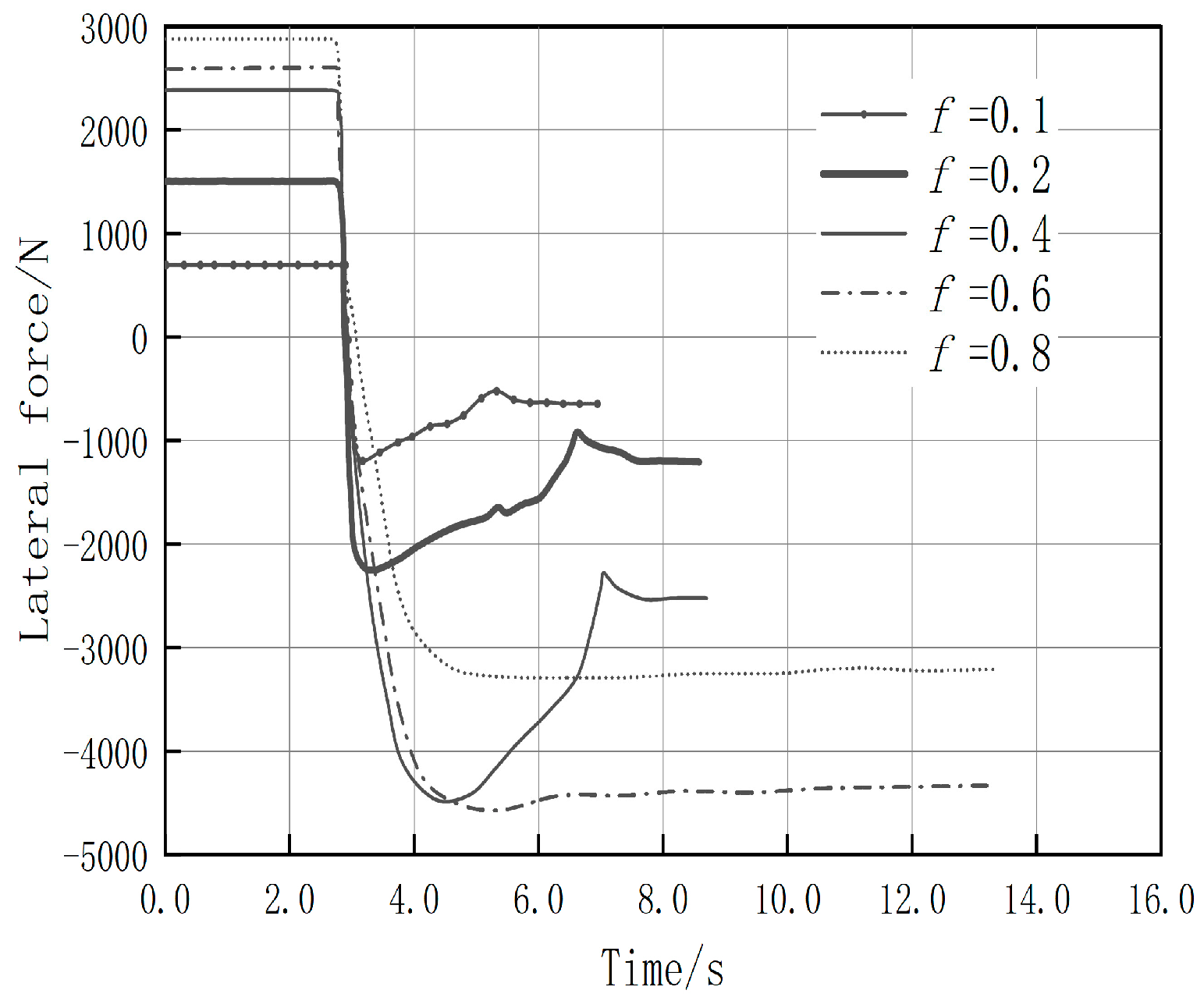
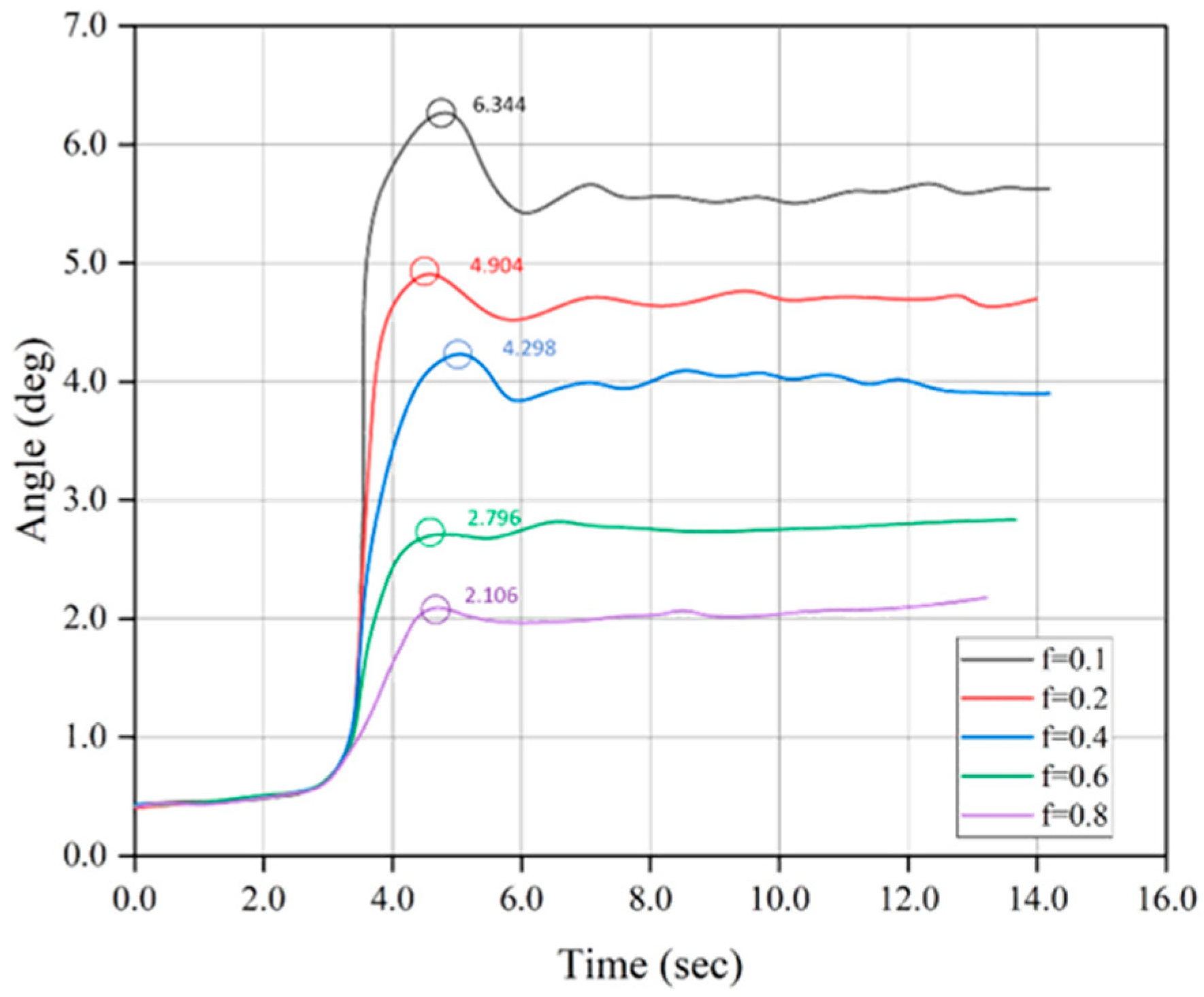
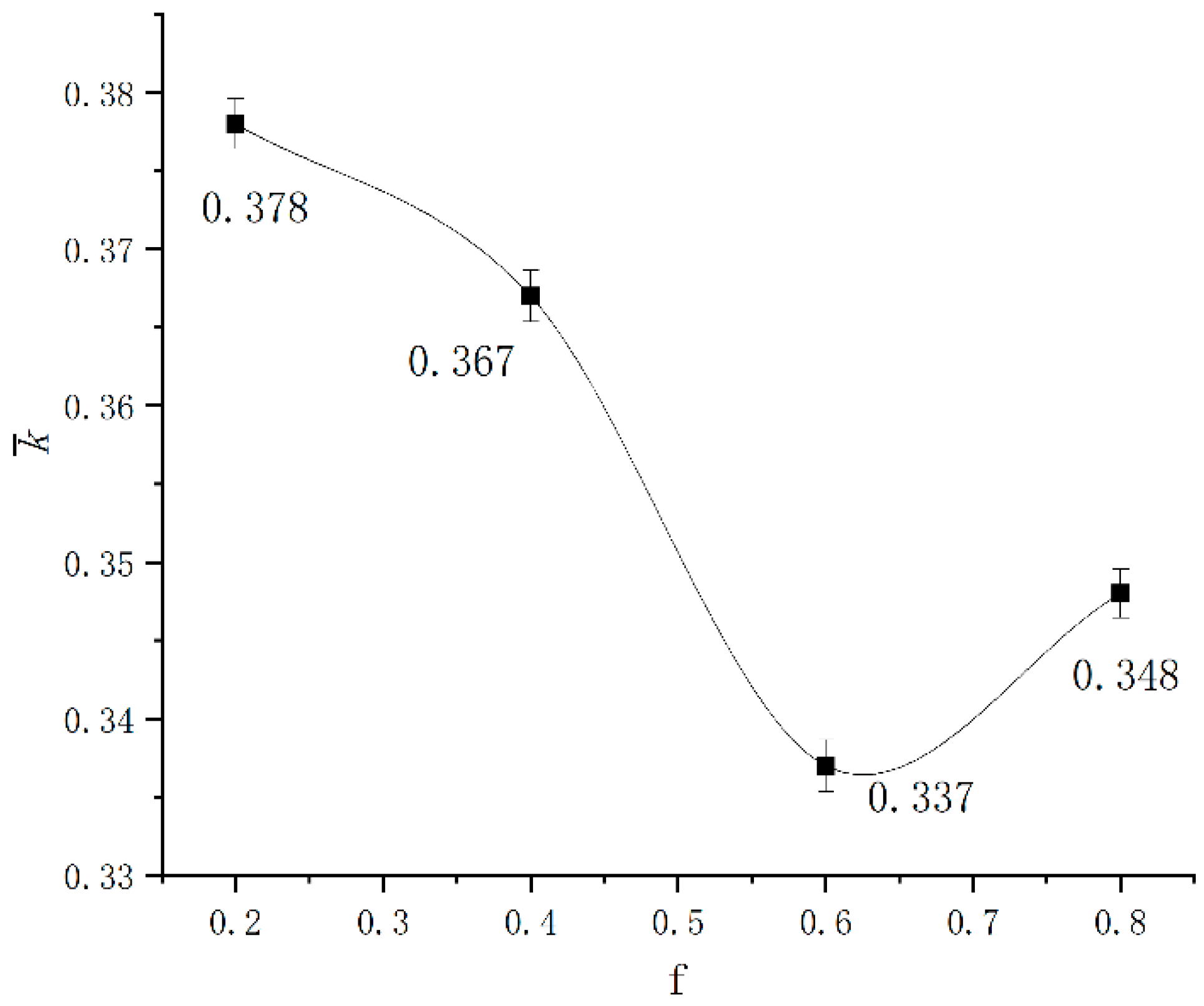
3.4.3. The Influence of Road Friction Coefficient on the Stability of AGV Rollover
4. Comprehensive Evaluation of Factors Affecting Rollover
4.1. Rollover Risk Metrics
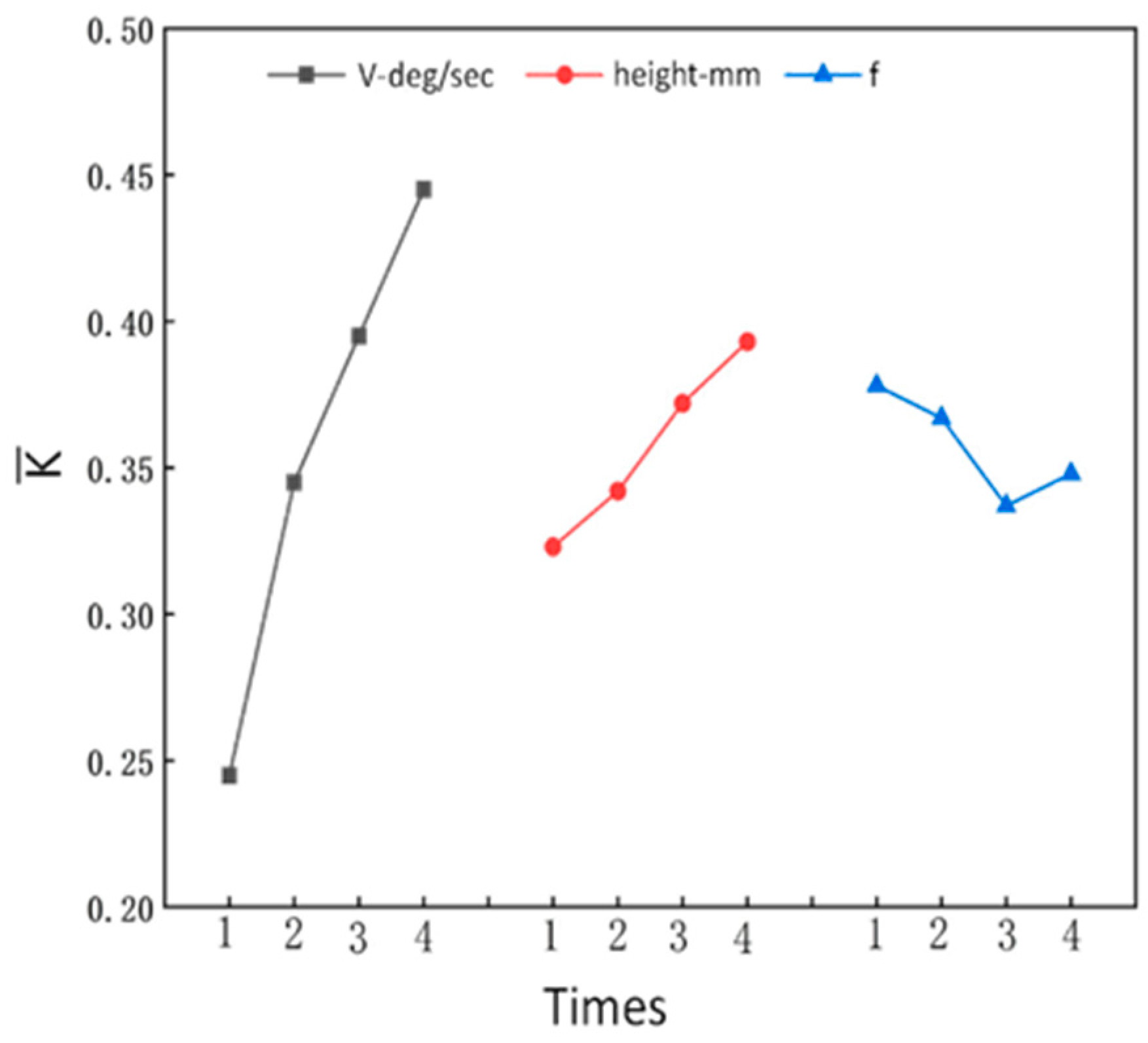
4.2. Orthogonal Test Analysis of Rollover Influencing Factors
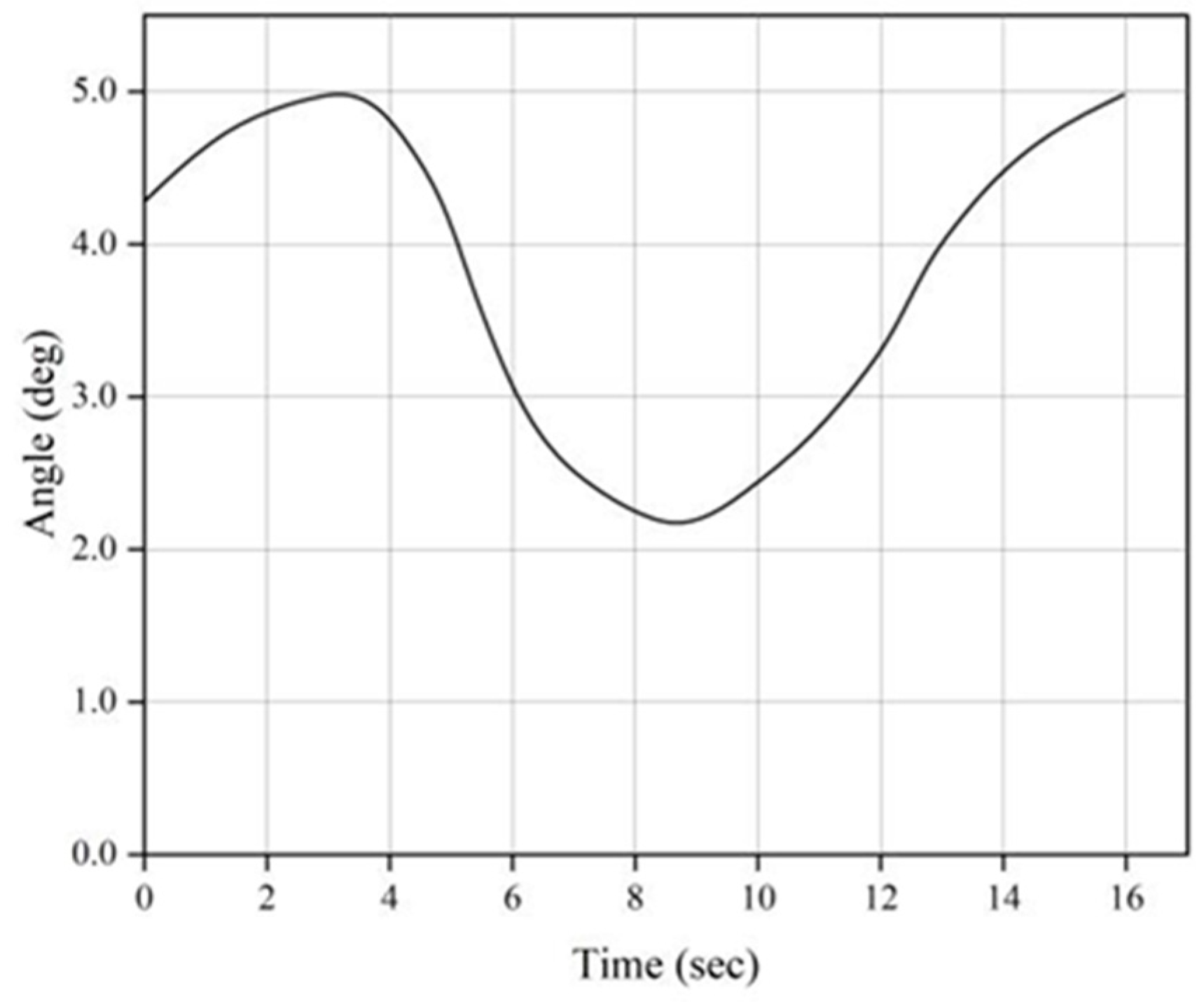
4.3. Influence of Rollover Factors on the Load Transfer Rate
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dahlberg, E. A Method Determining the Dynamic Rollover Threshold of Commercial Vehicles International Truck & Bus Meeting & Exposition. SAE Trans. 2000, 109, 789–801. [Google Scholar]
- Thomas, P.J.; Woodrooffe, J. Feasibility Study of a Rollover Warning Device for Heavy Trucks; The National Academies of Sciences, Engineering, and Medicine: Washington, DC, USA, 1990. [Google Scholar]
- Zheng, M.; Han, L.; Wang, C.; Xu, Z.; Li, H.; Ma, Q. Simulation of permanent deformation in high-modulus asphalt pavement with sloped and horizontally curved alignment. Appl. Sci. 2017, 7, 331. [Google Scholar] [CrossRef]
- Sampson, D.J.M.; Cebon, D. Active roll control of single unit heavy road vehicles. Veh. Syst. Dyn. 2003, 40, 229–270. [Google Scholar] [CrossRef]
- Hac, A. Rollover stability index including effects of suspension design. SAE Trans. 2002, 111, 1403–1413. [Google Scholar]
- Dunwoody, A.B.; Froese, S. Active roll control of a semi-trailer. SAE Trans. 1993, 102, 999–1004. [Google Scholar]
- Sampson, D.J.M.; Cebon, D. Achievable roll stability of heavy road vehicles. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2003, 217, 269–287. [Google Scholar] [CrossRef]
- Constantine, C.J.; Law, E.H. The Effects of Roll Control for Passenger Cars during Emergency Maneuvers [R]. SAE Technical Paper. 1994. Available online: https://www.sae.org/publications/technical-papers/content/940224/ (accessed on 5 February 2023).
- Sampson, D.J.M.; Cebon, D. An investigation of roll control system design for articulated heavy vehicles. In Proceedings of the 4th International Symposium on Advanced Vehicle Control, Nagoya, Japan, 14–18 September 1998; pp. 311–316. [Google Scholar]
- Torbic, D.J.; Donnell, E.T.; Brennan, S.N.; Brown, A.; O’Laughlin, M.K.; Bauer, K.M. Superelevation design for sharp horizontal curves on steep grades. J. Transp. Res. Board 2015, 2436, 81–91. [Google Scholar] [CrossRef]
- Kallebasti, T.; Abdi Kordani, A.; Mavromatis, S.; Boroomandrad, S.M. Lateral friction demand on roads with coincident horizontal and vertical sag curves. Proc. Inst. Civ. Eng.-Transp. 2021, 174, 159–169. [Google Scholar]
- Kordani, A.A.; Sabbaghian, M.H.; Kallebasti, B.T. Analyzing the influence of coinciding horizontal curves and vertical sag curves on side friction factor and lateral acceleration using simulation modeling. In Proceedings of the International Symposium on Highway Geometric Design 2015, Vancouver, BC, Canada, 2 April 2015. [Google Scholar]
- Easa, S.M. Superelevation side friction and roadway consistency. J. Transp. Eng. 1999, 125, 569–570. [Google Scholar] [CrossRef]
- Mavromatis, S.; Psarianos, B.; Tsekos, P.; Kleioutis, G.; Katsanos, E. Investigation of vehicle motion on sharp horizontal curves combined with steep longitudinal grades. Transp. Lett. 2016, 8, 220–228. [Google Scholar] [CrossRef]
- Qu, G.; He, Y.; Sun, X.; Tian, J. Modeling of lateral stability of tractor-semitrailer on combined alignments of freeway. Discret. Dyn. Nat. Soc. 2018, 2018, 1–17. [Google Scholar] [CrossRef]
- Cong, S.; Shangbin, S.; Zan, L. Vehicle roll stability analysis considering lateral-load transfer rate. In Proceedings of the International Conference on Transportation Information and Safety (ICTIS) 2015, Wuhan, China, 25–28 June 2015; pp. 398–402. [Google Scholar]
- Muir, P.F.; Neuman, C.P. Kinematic modeling for feedback control of an omnidirectional wheeled mobile robot. In Autonomous Robot Vehicles; Springer: New York, NY, USA, 1990; pp. 25–31. [Google Scholar]
- Spentzas, K.N.; Alkhazali, I.; Demic, M. Kinematics of four-wheel-steering vehicles. Forsch. Ing. 2001, 66, 211–216. [Google Scholar] [CrossRef]
- Bai, H.Y.; Fu, C.Y.; Zhang, X.Z. Kinematics analysis of heavy dump truck lifting mechanism. Adv. Mater. Res. 2012, 472, 2245–2250. [Google Scholar] [CrossRef]
- Koskinen, S. Sensor Data Fusion Based Estimation of Tyre-Road Friction to Enhance Collision Avoidance. Ph.D. Thesis, Tampere University of Technology (TUT), Tampere, Finland, 2010. [Google Scholar]
- Miege, A.J.P.; Cebon, D. Optimal roll control of an articulated vehicle: Theory and model validation. Int. J. Veh. Mech. Mobil. 2005, 43, 867–893. [Google Scholar] [CrossRef]
- Blow, P.W.; Woodrooffe, J.H.; Sweatman, P.F. Vehicle stability and control research for US comprehensive truck size and weight study. SAE Trans. 1998, 107, 617–623. [Google Scholar]
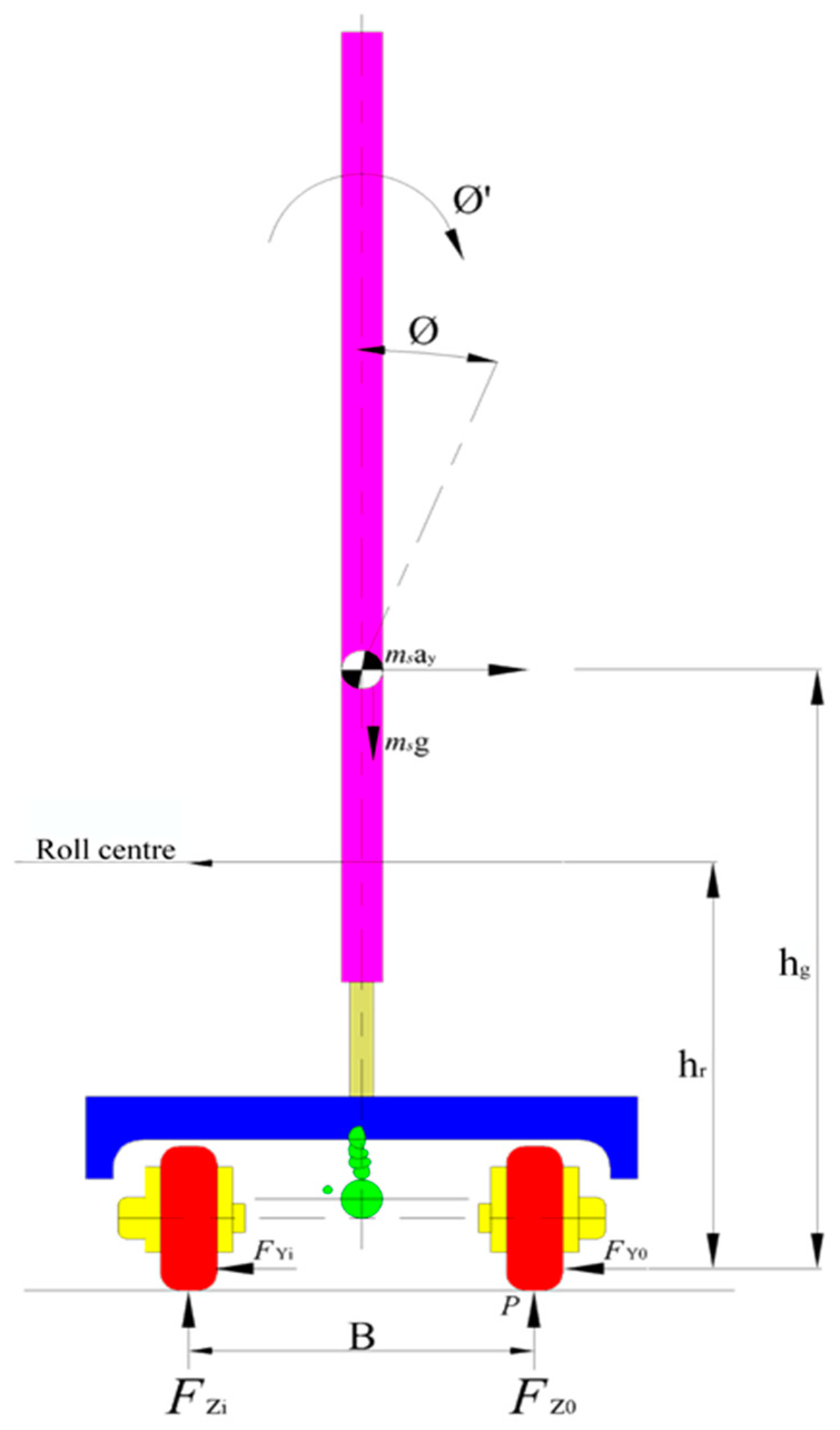
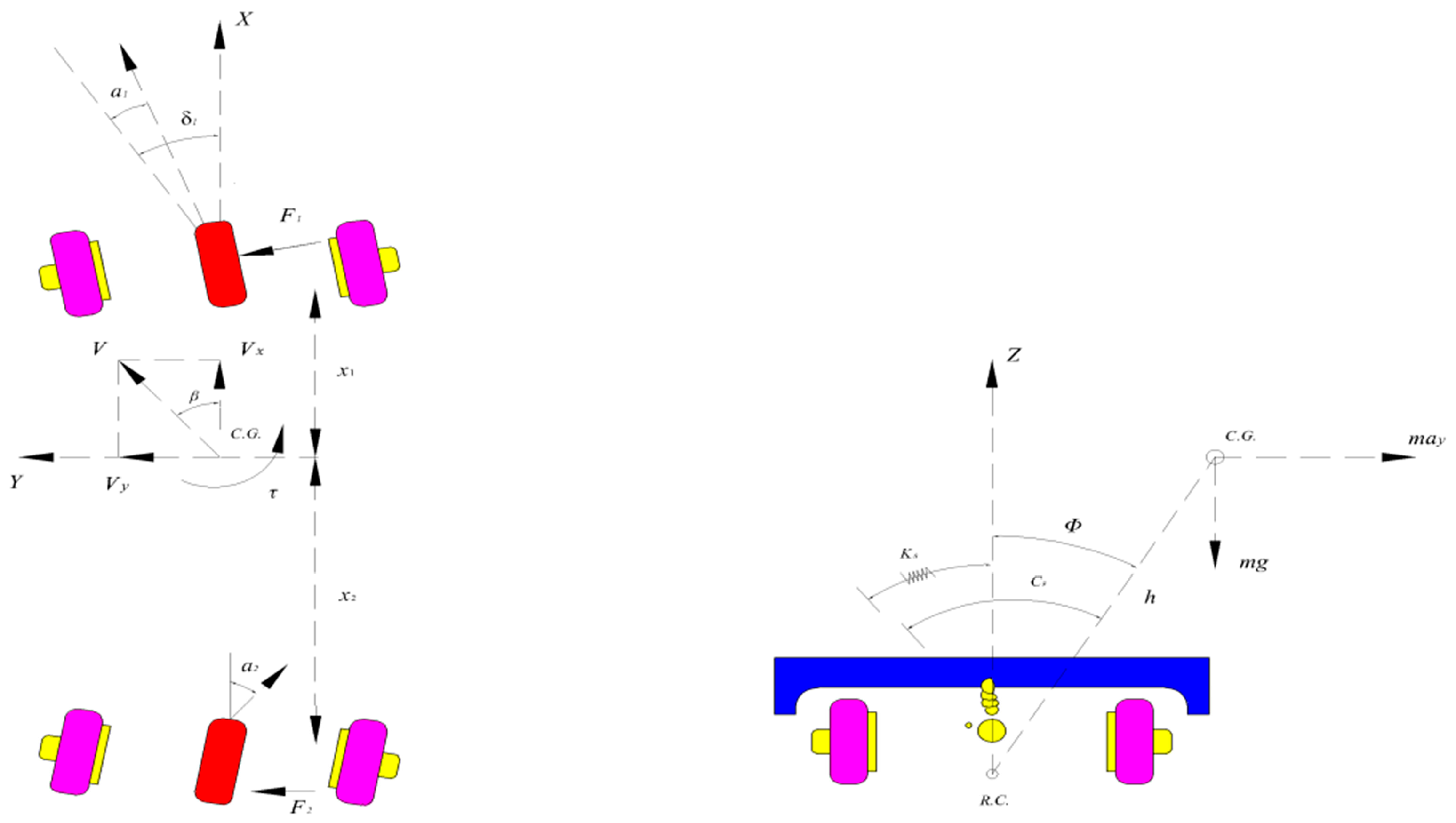

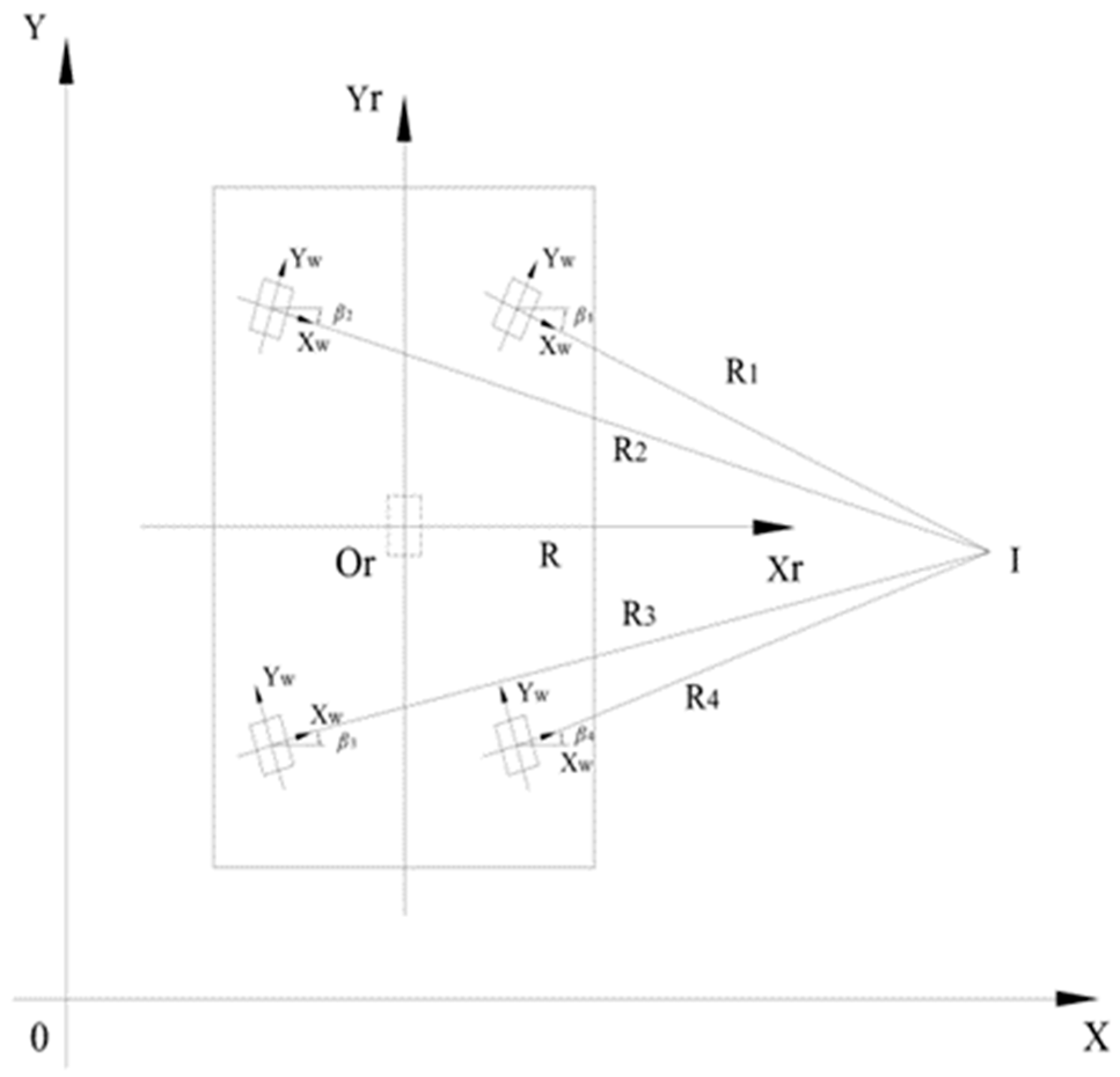

| Symbols | Implication | Symbols | Implication |
|---|---|---|---|
| V1 | Right front helm wheel speed | V2 | Left front helm wheel speed |
| V3 | Left rear helm wheel speed | V4 | Right rear helm wheel speed |
| β1 | Angle between right front helm wheel and AGV coordinate system | β2 | Angle between left front helm wheel and AGV coordinate system |
| β3 | Angle between left rear helm wheel and AGV coordinate system | β4 | Angle between right rear helm wheel and AGV coordinate system |
| W1 | Right front helm wheel angular velocity | W2 | Left front helm wheel angular velocity |
| W3 | Left rear helm wheel angular velocity | W4 | Right rear helm wheel angular velocity |
| r1 | Right front helm wheel rotation radius | r2 | Left front helm wheel rotation radius |
| r3 | Left rear helm wheel rotation radius | r4 | Right rear helm wheel rotation radius |
| V | Heavy-duty AGV speed | R | Heavy-duty AGV rotation radius |
| Heavy-duty AGV angular velocity | I | Heavy-duty AGV rotary centre | |
| Xi | The lateral distance of the helm wheel from the centre position | Yi | The longitudinal distance between the helm wheel and the centre position |
| α | Heavy load AGV rotary centre abscissa | b | Heavy load AGV rotary centre ordinate |
| Variable Names | Symbols | Numerical Values | Units |
|---|---|---|---|
| AGV quality | M | 5 | t |
| Duty | MS | 10 | t |
| Total height | h | 5 | m |
| Rotational inertia around the x-axis | IX | 21,300 | kg×m2 |
| Distance from the centre of mass to the front axle | a | 3.5 | m |
| Distance from the centre of mass to the rear axis | b | 3.5 | m |
| Sway stiffness | 90,672 | N/rad | |
| Sway damping | 5677 | N/rad | |
| Rotational inertia around the z-axis | 58,893 | kg×m2 | |
| Turning radius | r | 6 | m |
| Wheelbase | l | 3.590 | m |
| Sum of lateral deflection stiffness of two front wheels | k1 | −60 | kN/rad |
| Sum of lateral deflection stiffness of both rear wheels | k2 | −60 | KN/rad |
| The inertia of rotation around the centre of the lateral roll | Ixeq | 64,952 | kg×m2 |
| Level | Turning Speed V°/s | Centroid Height h/mm | Road Friction Coefficient f |
|---|---|---|---|
| 1 | 50 | 1200 | 0.2 |
| 2 | 60 | 1400 | 0.4 |
| 3 | 70 | 1600 | 0.6 |
| 4 | 80 | 1800 | 0.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, W.; Wang, X.; Zhang, X. Rollover Stability of Heavy-Duty AGVs in Turns Considering Variation in Friction Coefficient. Lubricants 2023, 11, 119. https://doi.org/10.3390/lubricants11030119
Fu W, Wang X, Zhang X. Rollover Stability of Heavy-Duty AGVs in Turns Considering Variation in Friction Coefficient. Lubricants. 2023; 11(3):119. https://doi.org/10.3390/lubricants11030119
Chicago/Turabian StyleFu, Weijie, Xinyu Wang, and Xinming Zhang. 2023. "Rollover Stability of Heavy-Duty AGVs in Turns Considering Variation in Friction Coefficient" Lubricants 11, no. 3: 119. https://doi.org/10.3390/lubricants11030119
APA StyleFu, W., Wang, X., & Zhang, X. (2023). Rollover Stability of Heavy-Duty AGVs in Turns Considering Variation in Friction Coefficient. Lubricants, 11(3), 119. https://doi.org/10.3390/lubricants11030119





