Dynamic Instability of Rigid Shoe Modes in a Drum Brake System

Abstract

This study examined the dynamic instability of a drum brake induced by the rigid modes of the brake shoe. The brake shoe was modeled as a rigid curved plate subject to frictional contact with a rotating drum. In the presence of a negatively sloped friction curve, dynamic instability was numerically analyzed with respect to variation in the system parameters. The results showed that mode-coupling instability did not occur, but dynamic instability was induced by negative damping in a specific rigid mode, and its propensity varied with the operating conditions and geometric changes.

1. Introduction

Brake squeal has been a challenging vibration and noise problem within the automotive industry for several decades. This problem has been mainly handled using squeal testing with brake dynamometers and linearized complex eigenvalue analysis based on the finite element method. Analytical investigation has also proven to be a suitable approach for the detailed analysis of squeal mechanisms [1,2]. However, it is generally more difficult to derive experimental correlations for brake squeal than for other vibration issues because brake squeal is a friction-based problem, and friction is extremely nonlinear. Thus, chaotic behavior is often observed in squeal tests, which results in a discrepancy between experimental and numerical analyses [3].

Several major mechanisms responsible for friction-induced noise can be explained analytically [4,5]. In linearized equations, the motion of a brake system can be written as

$$M\ddot{x}+\left(G+D\right)\dot{x}+\left(K_s+K_{ns}\right)x=0$$

where $M$, $G$, and $D$ are the symmetric mass, skew-symmetric gyroscopic, and symmetric damping matrices, respectively, while $K_s$ and $K_{ns}$ are the symmetric stiffness and nonsymmetric friction-engaged matrices, respectively. In this relation, $K_{ns}$ is the essential component responsible for the generation of squeal associated with mode-coupling instability.

Mode-coupling instability is caused by the merging of two adjacent vibration modes, and this has been investigated in a number of previous studies. For example, the analytical derivation of disc brake systems in association with mode-coupling mechanisms has been reported, and the mode-coupling instability of flexible modes in disc brake systems has also been investigated [6,7,8]. The mode-coupling instability among the rigid vibration modes of a brake pad has also been theoretically described, and they were identified as some of the major low-frequency squeal modes [9,10]. Mode-coupling instability in a drum brake system has also been theoretically formulated [11], while the mode-coupling propensity of flexible vibration modes in a drum brake system has been studied using eigenvalue perturbation [12,13].

Another major mechanism is the dynamic instability induced by a negative friction–velocity slope, which is a form of negative damping. This negative friction–velocity curve has often been observed in the Stribeck friction curve when contact occurs under mixed lubrication. In brake applications, the negative friction–velocity curve has been measured [14], and the negative slope effect on brake squeal has also been analytically investigated in an analytical disc brake squeal model [15,16]. In reference [16], disc torsion modes were found to be the squeal mode using the negative friction–velocity curve, and one of the brake pad rigid modes was identified as a negative damping-susceptible mode in the squealing disc brake. The authors also suggested that negative damping-susceptible modes may produce squeal at low speeds. This conclusion is in agreement with the physical observation of drum brake squeal noise occurring at low speeds, thus it is worth studying negative-damping-susceptible modes in more detail.

The mode-coupling effect may destabilize the brake system in both rotating and nonrotating system models. In the absence of rotation (or neglecting the rotational effect), the gyroscopic matrix $G$ is zero and the only factor causing linear instability in this equation is $K_{ns}$. These nonconservative friction-engaged mechanisms stem from the frictional follower force [17,18,19] and the friction couple [20,21,22]. The friction model has occasionally been assumed to be point contact [23] but, in order to accurately assess squeal onset and its mechanisms, a distributed contact model is required. The effect of the distributed contact area has been well explained in past analytical research [24]. When rotating matrix $G$ is accounted for, the gyroscopic effect has been found to generate dynamic instability [25,26,27]. In particular, the gyroscopic effect has been coupled with nonconservative friction stiffness, and this coupling increased the real parts of the potential squeal modes [27].

It should be noted that there are an infinite number of vibration modes that are potential squeal mode candidates. In order to simplify the process and focus on brake design that prevents the specific squeal modes of interest, minimal models capturing specific squeal modes have often been developed [28,29,30]. For example, as mentioned in [9,10], dynamic instability due to the rigid pad modes of a disc brake has already been investigated by neglecting the flexible modes of the disc and pad, and they were found to contribute to low-frequency squeal. However, the squeal onset of the rigid modes of a brake shoe in a drum brake system has not yet been investigated in detail in previous research.

Experimental testing using a brake dynamometer is an important tool for determining brake squeal propensity and the robustness of a brake design [31,32,33,34,35,36]. It is also used to validate numerical brake squeal simulations and compensate for any uncertainty in these simulations. Because computational complex eigenvalue analysis can only account for squeal behaviors near the steady sliding equilibrium, nonlinear responses far from this equilibrium need to be obtained from experiments. Moreover, uncertainty in numerical simulations and friction materials often generates discrepancies in the squeal frequencies between simulation and experimental results.

Nevertheless, complex eigenvalue analysis of linearized brake systems is useful for assessing potential mechanisms associated with brake squeal and devising solutions in the design stage for a brake system. Squeal propensity has been estimated by solving linearized equations of motion in a friction-engaged brake system. The real parts of the system eigenvalues are used as indicators of squeal onset, which means that squeal onset can be controlled and even reduced if the brake design is well defined. After squealing, the frequency pattern completely follows nonlinear behavior, which cannot be predicted using a linearized model. In turn, squeal onset analysis is limited only to brake system design, regardless of whether it starts to produce squeal and which vibration modes become unstable.

The motivation for this study arises from the fact that drum brake squeal generally occurs at relatively low frequencies and speeds, and our previous study [9,10] also showed that squeal modes due to rigid pad modes in disc brakes appeared at low frequencies and low speeds. Therefore, it is worth investigating squeal onset characteristics and the mechanisms causing squeal onset due to the rigid modes of a drum brake system that may affect low-frequency and low-speed drum brake squeal.

This paper focuses on the dynamic instability of the rigid modes of a drum brake system using a minimal model that ignores the flexible modes of the drum brake components. Therefore, the rotation-dependent squeal propensity of the drum brake due to rigid modes is investigated. The mode-coupling instability of the flexible modes in a drum brake system has been addressed in previous studies [11,12,13]. In the present study, the brake shoe is assumed to be rigid and in contact with a rotating rigid drum. The squealing mechanisms due to the rigid modes of the shoe are identified and associated parametric analysis is conducted.

2. Materials and Methods

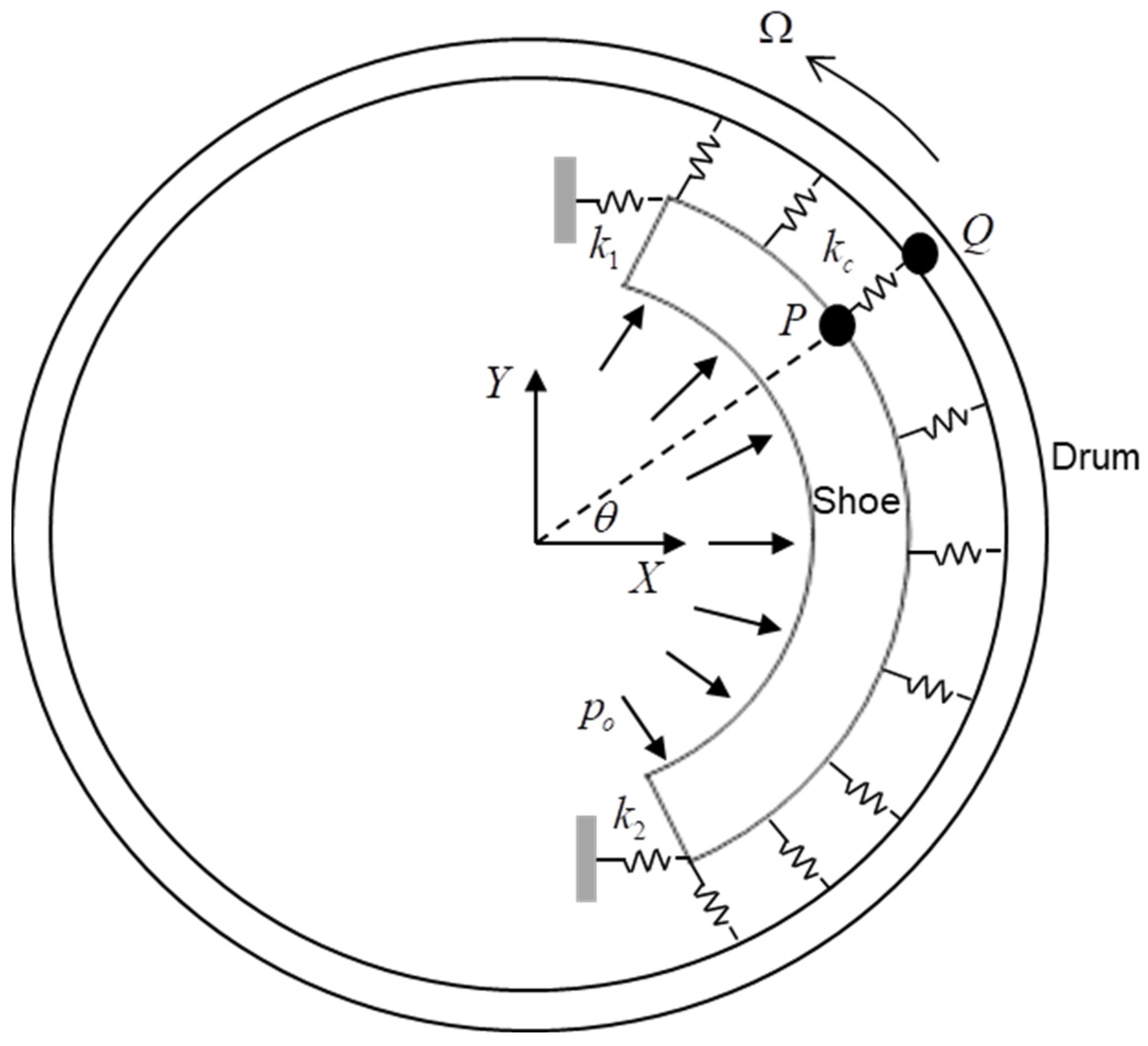
This study focuses on the dynamic instability of the rigid modes in a brake shoe. The rigid shoe is modeled as a curved plate (Figure 1). The brake shoe is subject to uniformly distributed and normal pre-stress ($p_o$) along the inner radius and friction contact along the outer radius. The friction lining material is modeled with a uniformly distributed contact stiffness ($k_c$) on the contact surface along the outer radius. Drum rotation at a constant speed ($\mathsf{\Omega }$) generates friction stresses over the friction lining of the brake shoe. The brake shoe is supported on the edge, with supporting stiffness ($k_1$ and $k_2$) for the shoe firmly placed in the brake assembly.

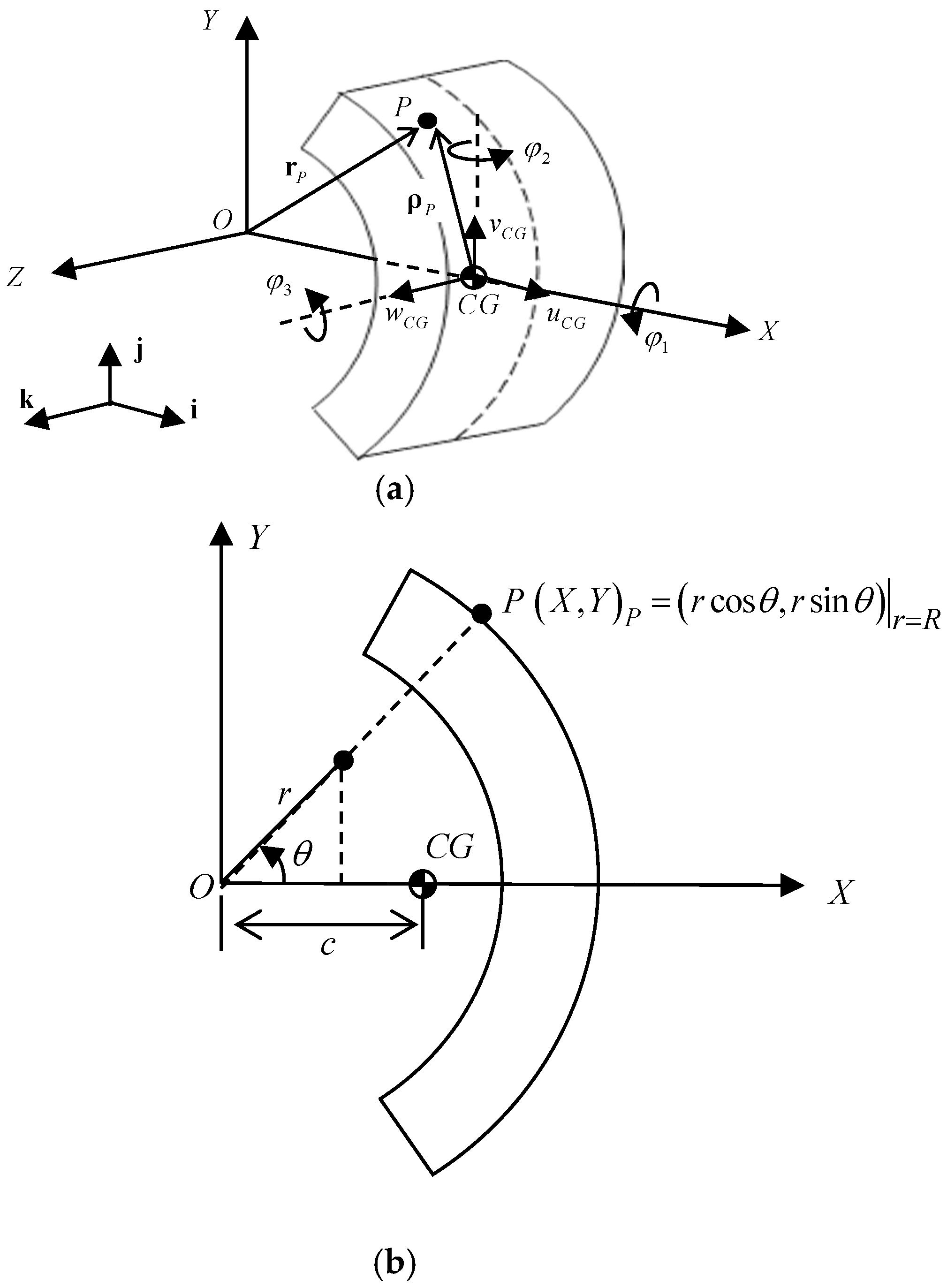
In order to describe the contact displacement of the discrete rigid modes of the brake shoe under a distributed contact load, the contact position vector for the shoe at P in Figure 2a is given by

$${\rho }_P=\left(R\cos \theta -c\right)i+R\sin \theta j+zk,$$

(1)

where $\mathit{i},\mathit{j},\mathrm{a}\mathrm{n}\mathrm{d}\mathit{k}$ are the unit direction vector in the X-, Y-, and Z-directions, respectively, h is the shoe thickness, $R$ is the outer radius of the shoe, and $c$ is the distance of the center of gravity (CG) from the origin (Figure 2b), which is calculated as

$$c=\frac{4\left(h^2-3hR+3R^2\right)}{3\beta \left(2R-h\right)}\sin \left(\frac{\beta }{2}\right),$$

(2)

where $\beta$ is the arc angle limit of the brake shoe (${\theta }_{\max }=\beta$ and ${\theta }_{\min }=-\beta$).

The corresponding contact displacement vector at $P$ can be expressed by the translation vector at CG and the rotational vector such that

$$u_P=u_{CG}+\phi \times {\rho }_P,$$

(3)

where $u$ is the translational displacement vector and $\phi$ is the rotational vector, which is given by

$$u_{CG}=u_{CG}i+v_{CG}j+w_{CG}k,$$

(4)

$$\phi ={\phi }_{1}i+{\phi }_{2}j+{\phi }_{3}k,$$

(5)

where the subscript c denotes the CG. In turn, the modal coordinates $q_i$ can be defined as the physical coordinates of rigid motion in the combination of three translation and three rotation variables in the six degrees of freedom of the three-dimensional rigid motion:

$$\left\{\begin{array}{cccccc}{q}_1& q_2& q_3& q_4& q_5& q_6\end{array}\right\}\equiv \left\{\begin{array}{cccccc}{u}_{CG}& v_{CG}& w_{CG}& {\phi }_1& {\phi }_2& {\phi }_3\end{array}\right\}.$$

(6)

Therefore, the contact displacement vector at $P$ can be expressed using the modal expansion form of the six rigid modes where the system modes are composed of the six component rigid modes of the brake shoe as follows:

$$\begin{array}{l}{u}_P=\left(q_1+z\cdot q_5-R\sin \theta \cdot q_6\right)i+\left\{q_2-z\cdot q_4+\left(R\cos \theta -c\right)\cdot q_6\right\}j\\ +\left\{q_3+R\sin \theta \cdot q_4-\left(R\cos \theta -c\right)\cdot q_5\right\}k\end{array}$$

(7)

Here the components of $u_P$ are described in the cylindrical coordinates for the contact kinematics such that

$$u_{\theta }=u_P\cdot e_{\theta }\equiv {\displaystyle \sum _{i=1}^6\left({\varphi }_i^{\theta }(\theta ,z)\cdot q_i(t)\right),}$$

(8)

$$u_r=u_P\cdot e_r\equiv {\displaystyle \sum _{i=1}^6\left({\varphi }_i^r(\theta ,z)\cdot q_i(t)\right),}$$

(9)

$$u_z=u_P\cdot k\equiv {\displaystyle \sum _{i=1}^6\left({\varphi }_i^z(\theta ,z)\cdot q_i(t)\right),}$$

(10)

where ($\cdot$) denotes the inner product of two vectors, ${\varphi }_i^{\theta }$, ${\varphi }_i^r$, and ${\varphi }_i^z$ are the $i$th mode shape functions for the rigid modes in the $\theta$-, $r$-, and $z$-directions of the cylindrical coordinates, respectively, while their direction vectors are

$$e_r=\cos \theta i+\sin \theta j,$$

(11)

$$e_{\theta }=-\sin \theta i+\cos \theta j.$$

(12)

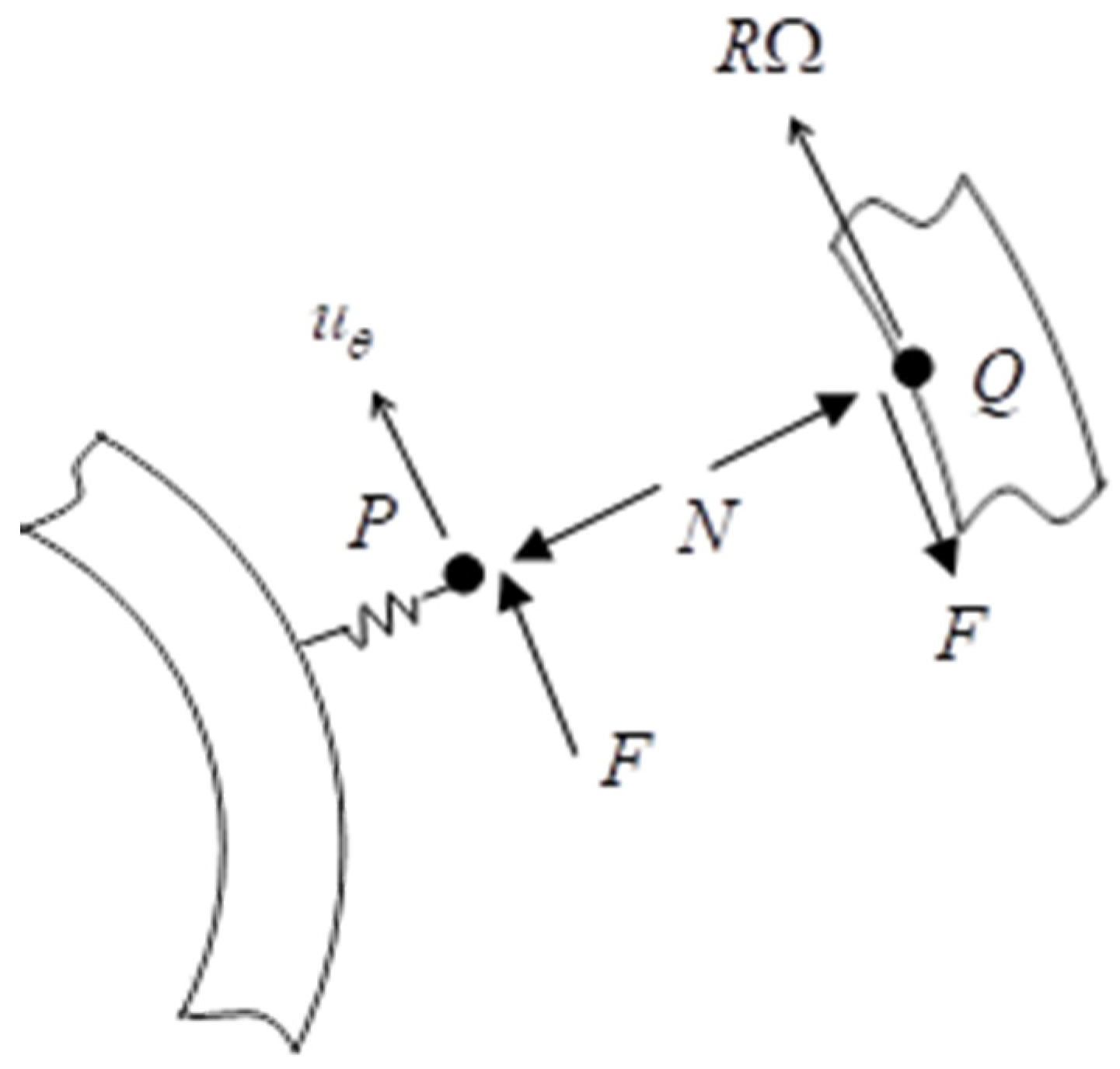
In turn, the relative velocity between the stationary rigid shoe and the rotating rigid drum at contact point P and its mating point Q is given in the cylindrical coordinates as

$$V_{PQ}=\frac{d{r}_P}{dt}-\frac{d{r}_Q}{dt}=\left({\dot{u}}_{\theta }-R\mathsf{\Omega }\right)e_{\theta }+{\dot{u}}_{z}k.$$

(13)

Therefore, the contact friction force in Figure 3 can be obtained from the direction vector of the relative velocity such that

$$F=-\mu N\frac{V_{PQ}}{\left|V_{PQ}\right|},$$

(14)

where normal stress is defined as a combination of pre-stress and normal load variation in the radial direction ($N=p_o+k_c\cdot u_r$).

Using Taylor expansion on each component of Equation (14) in a steady-sliding state, the linearized term takes the form of

$$F=-\mu N\left[-e_{\theta }+\frac{{\dot{u}}_z}{R\mathsf{\Omega }}k+h.o.t\right],$$

(15)

where $h.o.t$ stands for higher-order terms. Here, the friction coefficient is a function of relative velocity such that

$$\mu ={\mu }_k+\left({\mu }_s-{\mu }_k\right)e^{-\alpha \left|V_{PQ}\right|},$$

(16)

and where ${\mu }_s$, ${\mu }_k$, and $\alpha$ are the parameters determined by the friction curve. This friction curve can also be linearized using Taylor expansion in a steady-sliding state such that

$$\mu ={\mu }_o+{\mu }_t\cdot {\dot{u}}_{\theta }+h.o.t,$$

(17)

where

$${\mu }_o={\mu }_k+\left({\mu }_s-{\mu }_k\right)e^{-\alpha R\mathsf{\Omega }},$$

(18)

$${\mu }_t=\alpha \left({\mu }_s-{\mu }_k\right)e^{-\alpha R\mathsf{\Omega }}.$$

(19)

The higher-order terms are ignored in the linearized equations. Particularly, $1/\mathsf{\Omega }$ appears in the Z-direction of Equation (15), which is perpendicular to the tangential friction stress. This term represents friction damping, which suppresses the squeal propensity dependent on the rotation speed.

Friction damping in the disc brake squeal model occurs in the radial direction perpendicular to the friction stress [24]. In contrast, the direction perpendicular to the friction stress of a drum brake system is the Z-direction, thus friction damping in the drum brake acts in the Z-direction. This difference in the direction of friction damping between disc and drum brakes suggests that different design strategies for squeal suppression are required.

The virtual work due to friction and normal contact forces can determined as follows:

$$\delta W={\displaystyle {\int }_{-b/2}^{b/2}{\displaystyle {\int }_{-\beta /2}^{\beta /2}\left[-N\delta u_r+F\cdot \left(\delta u_{\theta }\cdot e_{\theta }+\delta u_{z}k\right)\right]}}\cdot Rd\theta dz,$$

(20)

where $b$ is the contact width limit of the brake shoe ($z_{\max }=b$ and $z_{\min }=-b$) in the contact area. The generalized force Q is then formulated by expressing Equation (20) using generalized modal coordinate $q_i$:

$$\delta W\equiv {\displaystyle \sum _{i=1}^6{\displaystyle \sum _{j=1}^6{Q}_{ij}(q_j)\cdot \delta q_i}}.$$

(21)

The linearized equations of motion for the friction-coupled rigid shoe are thus obtained using Lagrange equations:

$$\frac{d}{dt}\left[\frac{\partial T}{\partial {\dot{q}}_i}\right]-\frac{\partial U}{\partial q_i}={\displaystyle \sum _{j=1}^6{Q}_{ij}(q_j)},i=1,\cdots ,6,$$

(22)

where the kinetic and strain energy T and U, respectively, are given by

$$T=\frac{1}{2}m\cdot V_{CG}^2+\frac{1}{2}\left(I_1{\dot{\phi }}_1^2+I_2{\dot{\phi }}_2^2+I_3{\dot{\phi }}_3^2\right),$$

(23)

$$U=\frac{1}{2}\left(k_1+k_2\right)\cdot u_c^2+\frac{1}{2}\left(k_1+k_2\right)R^2{\sin }^2{\phi }_3,$$

(24)

$$V_{CG}^2=u_c^2+v_c^2+w_c^2.$$

(25)

The moment of inertia in T is derived from geometric calculations:

$$I_1=\rho {\displaystyle {\int }_V\left\{{\left(r\sin \theta \right)}^2+z^2\right\}dV},$$

(26)

$$I_1=\rho {\displaystyle {\int }_V\left\{{\left(r\cos \theta -c\right)}^2+z^2\right\}dV},$$

(27)

$$I_1=\rho {\displaystyle {\int }_V\left\{{\left(r\cos \theta -c\right)}^2+{\left(r\sin \theta \right)}^2\right\}dV},$$

(28)

where ${\displaystyle {\int }_V(·)}dV={\displaystyle {\int }_V(·)rdrd\theta dz}$.

As a result, the linearized equations of motion can be expressed as a matrix of modal coordinates:

$$\begin{gathered} \left[M\right]\left\{\ddot{q}\right\}+\left[{\displaystyle {\int }_{-b/2}^{b/2}{\displaystyle {\int }_{-\beta /2}^{\beta /2}\left\{\frac{{\mu }_o{p}_o}{R\mathsf{\Omega }}\left[{\varphi }_i^z\cdot {\varphi }_j^z\right]-{\mu }_t{p}_o\left[{\varphi }_i^{\theta }\cdot {\varphi }_j^{\theta }\right]\right\}}}\cdot Rd\theta dz\right]\left\{\dot{q}\right\} \\ +\left[k_c{\displaystyle {\int }_{-b/2}^{b/2}{\displaystyle {\int }_{-\beta /2}^{\beta /2}\left\{\left[{\varphi }_i^r\cdot {\varphi }_j^r\right]-{\mu }_o\left[{\varphi }_i^{\theta }\cdot {\varphi }_j^r\right]\right\}}}\cdot Rd\theta dz\right]\left\{q\right\}=\left\{0\right\}, \end{gathered}$$

(29)

where  and $j=1,2,\cdots ,6$, and $\left[M\right]=diag(M,M,M,I_1,I_2,I_3)$.

$k_c\left[{\varphi }_i^r\cdot {\varphi }_j^r\right]$ is the symmetric contact stiffness matrix determining the stiffness-coupled system frequencies, while $k_c{\mu }_o\left[{\varphi }_i^{\theta }\cdot {\varphi }_j^r\right]$ is the nonsymmetric nonconservative work matrix. $\frac{{\mu }_o{p}_o}{R\mathsf{\Omega }}\left[{\varphi }_i^z\cdot {\varphi }_j^z\right]$ is velocity-dependent dissipative matrix proportional to $1/\mathsf{\Omega }$, which is friction damping (Equation (15)). An important system matrix in the present study is ${\mu }_t{p}_o\left[{\varphi }_i^{\theta }\cdot {\varphi }_j^{\theta }\right]$, which is the negative slope matrix stemming from the linearization of the friction–velocity curve that is also dependent on the rotation speed because ${\mu }_t$ for the friction curve in Equation (17) is a function of the relative speed between the mating contact materials. Therefore, Equation (29) can provide the squeal propensity of the drum brake shoe dependent on rotation speed due to friction damping and negative friction-slope effects.

By setting $\left\{q_i\right\}\equiv q(t)=\tilde{q}{e}^{\lambda t}$ in Equation (29), the system eigenvalues $\lambda$ can be numerically calculated using complex numbers, namely, $\lambda =\mathrm{Re}(\lambda )+i\mathrm{Im}(\lambda )$. The solution can then be rewritten as

$$q(t)=\tilde{q}{e}^{\mathrm{Re}(\lambda )t}\left(\cos \mathrm{Im}(\lambda )t+i\sin \mathrm{Im}(\lambda )t\right),$$

(30)

where the solution oscillates with an exponential increase if $\mathrm{Re}(\lambda )$ becomes a positive number. Thus, $\mathrm{Re}(\lambda )>0$ indicates the onset condition for brake squeal, and corresponding $\mathrm{Im}(\lambda )$ is the frequency of the squeal onset near the equilibrium state. However, the squealing frequency may not match the frequency of the squeal onset obtained from a linearized system. Nevertheless, it is important to identify the unstable modes for a linearized system and its mechanisms because they cause nonlinear squealing. Indeed, if the dynamic instability of a linearized system is eliminated, the brake system does not generate nonlinear squealing.

3. Results

In the present study, only the six rigid modes of the drum brake shoe are applied to the brake squeal model in the linear stability analysis; flexible modes are ignored to allow a focus on the influence of the rigid modes on brake squeal. The nominal values used in this analysis (

Table 1. System parameters for the modeled drum brake shoe.

Parameter	Symbol	Value
Outer radius of the shoe	$R$	100 mm
Thickness of the shoe	h	20 mm
Width of the shoe	$b$	36.5 mm
Contact angle	$\beta$	$130°$
Density of the shoe	$\rho$	$7820{\mathrm{kg}/\mathrm{m}}^3$
Pre-normal load	$-$	2000 N
Rotating speed	$\mathsf{\Omega }$	5 $\mathrm{rad}/\mathrm{s}$
Nominal contact stiffness	$k_{\mathrm{c}}$	$0.35\times {10}^{11}{\mathrm{N}/\mathrm{m}}^3$
Upper spring constant	$k_1$	$1\times {10}^8\mathrm{N}/\mathrm{m}$
Lower spring constant	$k_2$	$6\times {10}^8\mathrm{N}/\mathrm{m}$

) are derived from the actual drum brake in reference [11], with some treated as variable parameters in the parametric stability analysis. The cross-section of the shoe is simplified to be rectangular, and structural damping is not considered. However, velocity-dependent system damping occurs during braking due to friction damping perpendicular to the tangential friction stress.

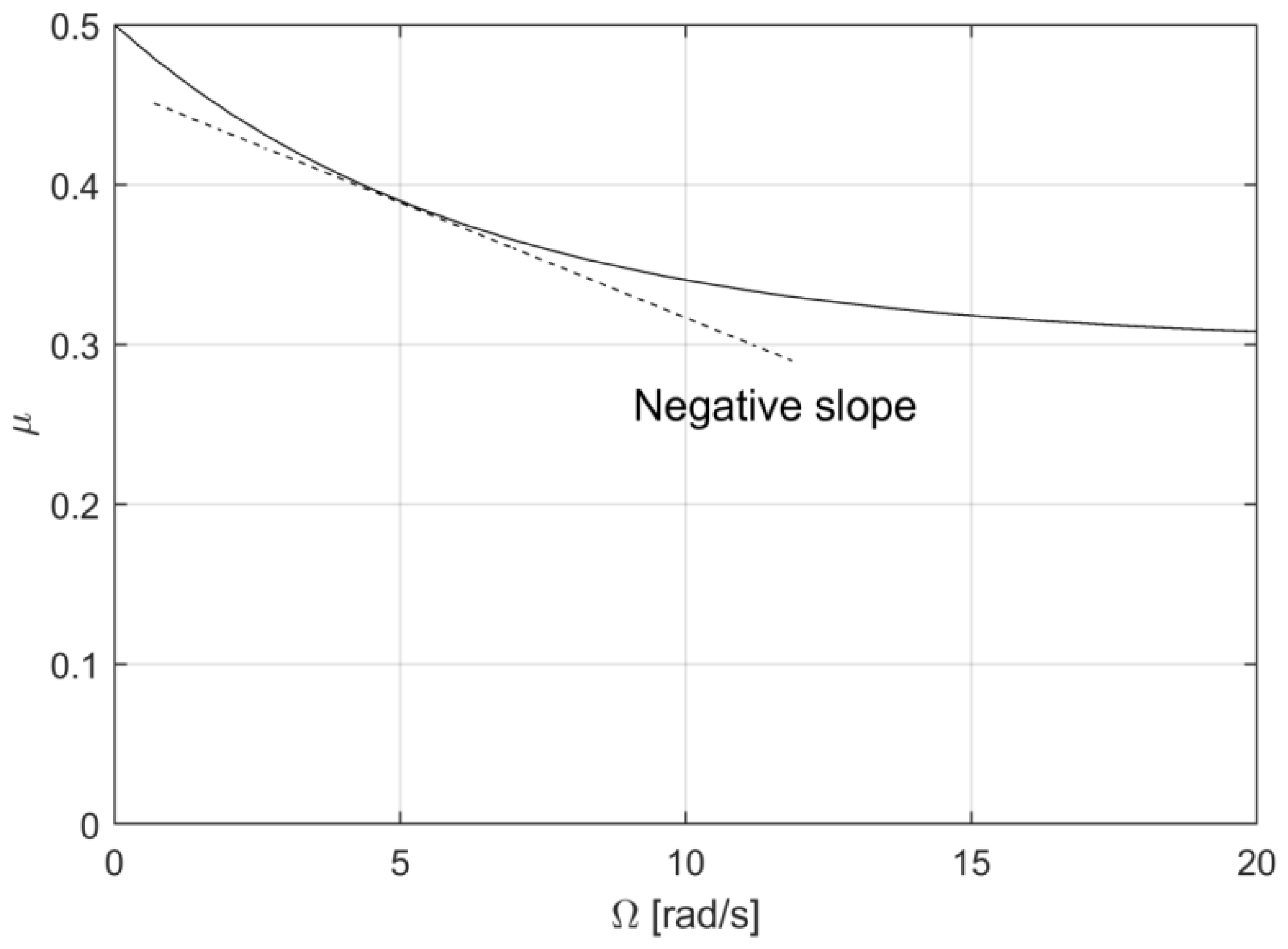
The velocity-dependent effects are reproduced as a friction–velocity curve in Figure 4, showing the magnitude and slope of the friction coefficient with respect to the relative speed between the mating friction materials. The values for the parameters in Equation (16) are ${\mu }_s=0.5$, ${\mu }_k=0.3$, and $\alpha =1.0$.

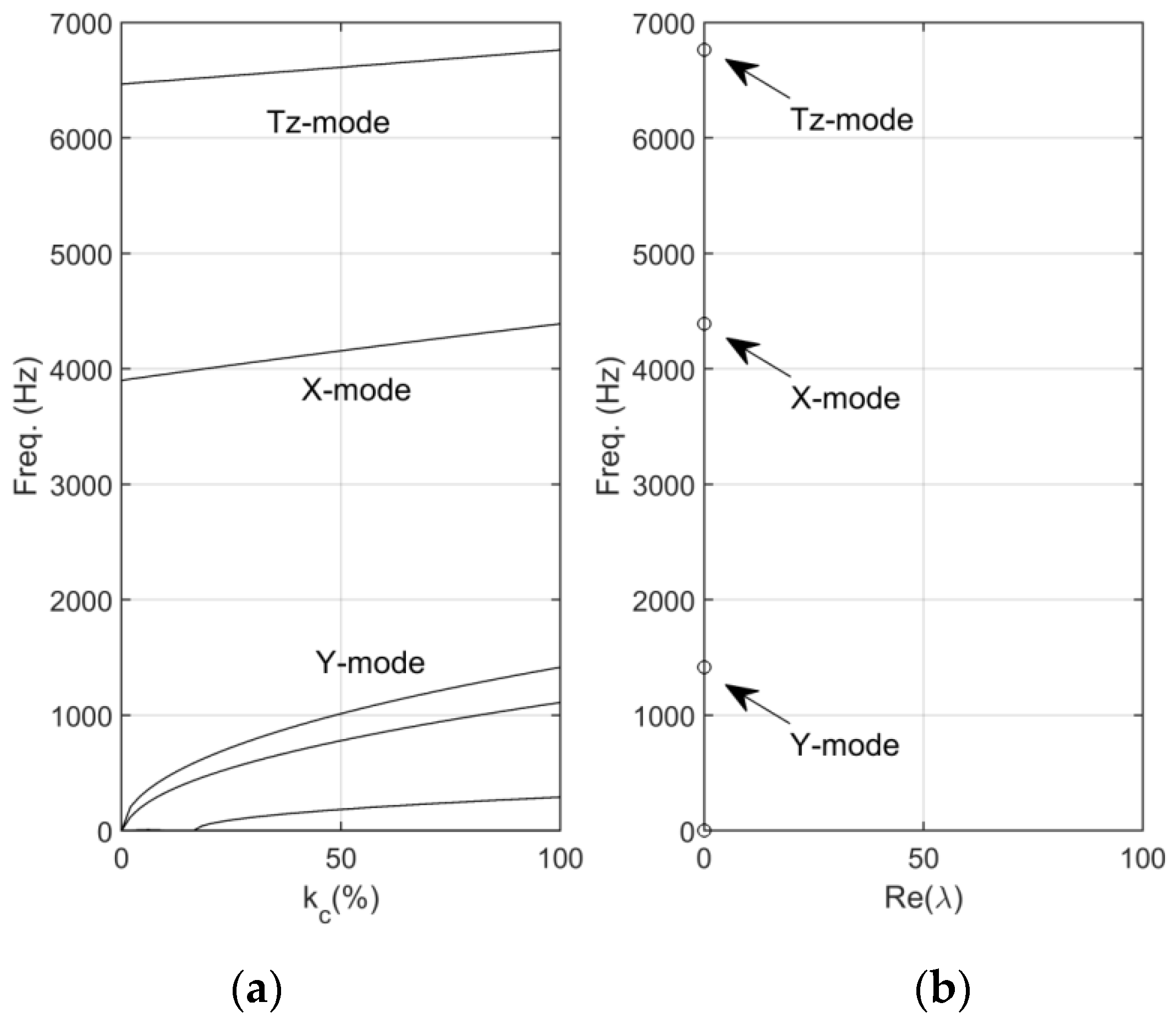
Figure 5a shows that the frequency loci increase with the contact stiffness. At $k_{\mathrm{c}}=0$, two modes have nonzero frequencies that correspond to one translation mode in the x-direction (X-mode) and one rotation mode in the z-direction (Tz-mode). These nonzero frequencies at $k_{\mathrm{c}}=0$ originate from the supporting stiffness of the upper and lower support spring holding the brake shoe in the assembly. The other modes are the purely rigid modes that have zero frequency at $k_{\mathrm{c}}=0$. As the contact stiffness $k_{\mathrm{c}}$ increases from zero, the zero-frequency rigid modes become nonzero-frequency vibration modes that represent potential squeal candidate modes. The positive real parts are marked in Figure 5a on their corresponding frequency loci if they are present, while the absolute values of the positive real parts at $k_{\mathrm{c}}=100\%$ are plotted in Figure 5b. The two figures show that two translation modes (X-mode and Y-mode) and one rotation mode (Tz-mode) become dynamically unstable in the presence of contact stiffness and a negative slope in the friction–velocity curve.

In order to validate the negative friction slope mechanism leading to squeal onset, the eigenvalue analysis with respect to the contact stiffness is repeated in the case of the constant friction coefficient ($\mu =0.4=\mathit{const}$) which does not have a negative-slope effect. Figure 6a presents similar features for the frequency loci with variation in the contact stiffness as depicted in Figure 5a. In contrast, positive real parts are not generated (Figure 6b), which indicates that the onset of squeal due to the rigid modes of the drum brake shoe does not occur without a negative slope in the friction–velocity curve.

Figure 5 and Figure 6 show that the negative-slope mechanism does not require the mode-coupling effects of the other modes for squeal generation. Therefore, a squeal model with a limited number of modes is useful when we want to modify the squeal propensity of specific vibration modes. In particular, it can be used to investigate the squeal propensity induced by a negative friction slope and suggest design modifications.

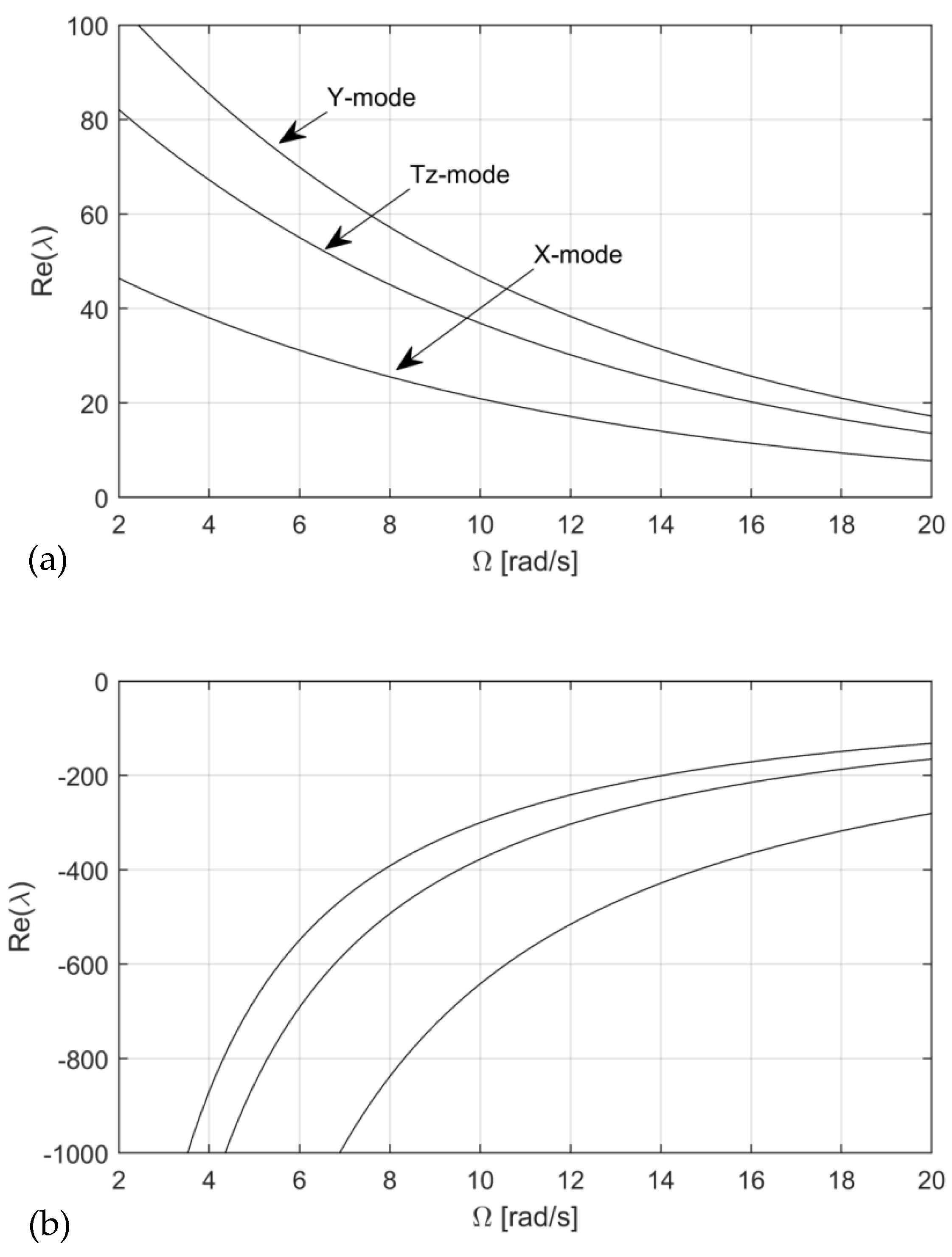
Parametric stability analysis is conducted by varying several system parameters when a negative friction–velocity slope causes squeal onset. In this analysis, only the real part loci of the unstable modes are traced. Figure 7 shows that the real parts of the unstable rigid shoe modes vary with the rotation speed of the drum. Figure 7a reveals that the squeal propensity of the unstable rigid modes increases with a decrease in the drum rotation speed. The negative slope mechanism arises from the negative slope matrix ${\mu }_t{p}_o\left[{\varphi }_i^{\theta }\cdot {\varphi }_j^{\theta }\right]$, whose elements require tangential displacement ${\varphi }_i^{\theta }$. This result corresponds with the fact that the two translation modes in the X- and Y-directions and the one rotation mode in the Z-direction generate tangential displacement, and ${\mu }_t$ is proportional to the decrease in the rotation speed. These three modes are not affected by friction-damping matrix $\frac{{\mu }_o{p}_o}{R\mathsf{\Omega }}\left[{\varphi }_i^z\cdot {\varphi }_j^z\right]$ because they do not have the z-component of their modal displacement vectors. That is why the squeal propensity is not suppressed when the rotation speed decreases.

In contrast, Figure 7b shows that the other three rigid modes are susceptible to friction damping because they contain the z-component in their modal vectors. For example, the rigid rotation mode along the X-axis (Tx-mode) produces slip in the Z-direction, so modal friction damping from the Tx-mode results in the negative real part of the eigenvalue (Figure 7b). This suggests that modal displacements in tangential and perpendicular directions are essential in the rotation effects on drum brake squeal. In addition, friction-damping-susceptible modes are strongly influenced by rotation speeds via $1/\mathsf{\Omega }$.

The rotation-dependent squeal propensity of the rigid modes in a drum brake system can be summarized as follows:

-

The rotation effects stem from the negative friction–velocity slope and friction damping.

-

Negative-slope-susceptible modes have the major component ${\varphi }_i^{\theta }$ tangential to the sliding direction in their modal vectors.

-

The friction-damping-susceptible modes have the major z-component ${\varphi }_i^z$ perpendicular to the sliding direction in their modal vectors.

-

The squeal propensity of the friction-damping-susceptible modes is suppressed at low speeds.

-

The Z-mode, Tx-mode, and Ty-mode are susceptible to friction damping, meaning their squeal propensity is suppressed at low speeds.

-

The X-mode, Y-mode, and Tz-mode are susceptible to a negative slope, but they are rarely influenced by friction damping. The squeal propensity of these modes increases at low speeds. It is suggested that these three rigid modes be investigated and modified because the squeal of a drum brake system often occurs only at low speeds.

Figure 8 shows that the positive real parts of the unstable three rigid modes increase with an increase in the normal load. This is a typical characteristic of the negative-slope-type instability. The negative damping matrix ${\mu }_t{p}_o\left[{\varphi }_i^{\theta }\cdot {\varphi }_j^{\theta }\right]$ is dominated by tangential displacement and is proportional to pre-normal contact stress $p_o$. Therefore, the positive real parts linearly increase with a normal load.

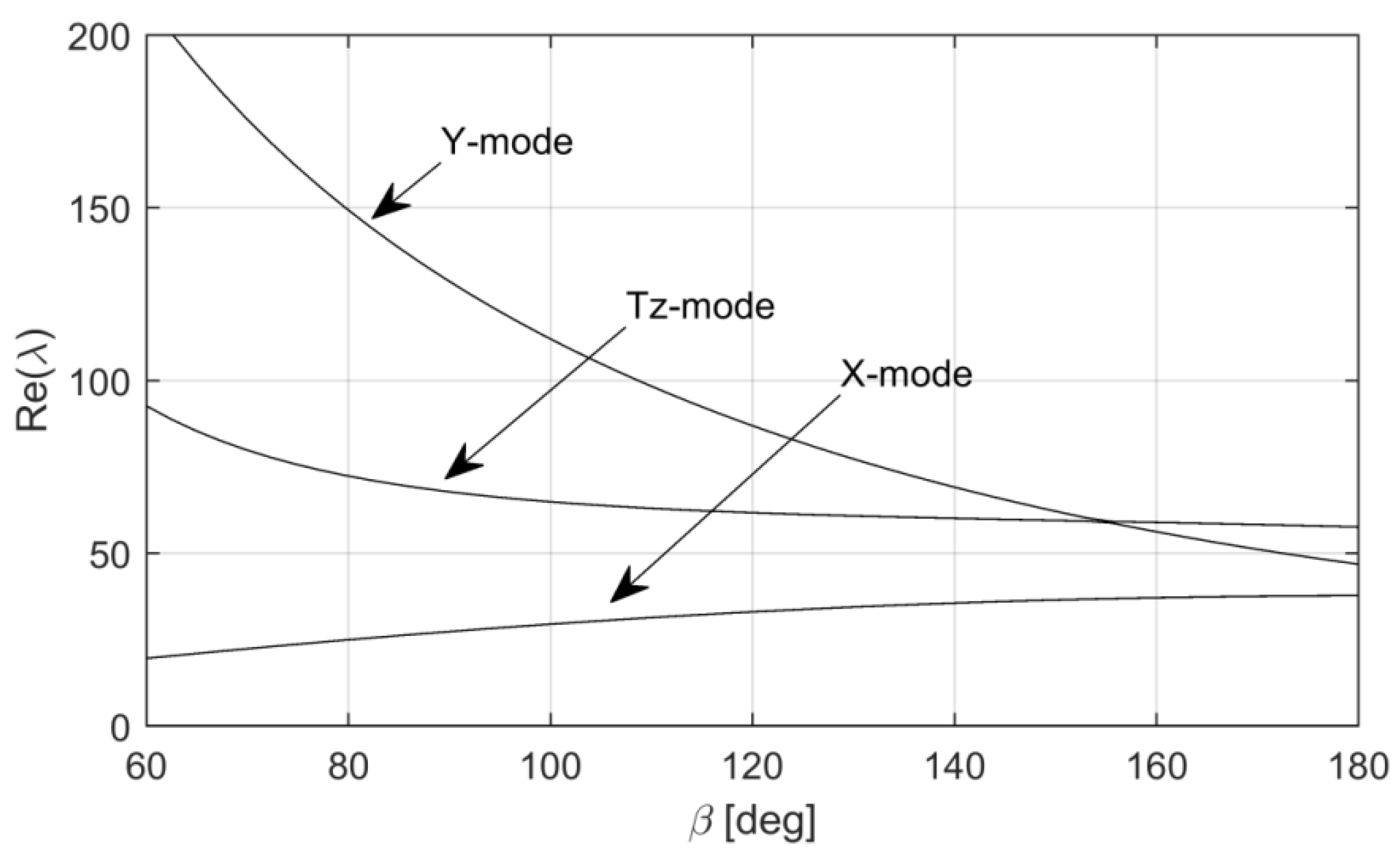
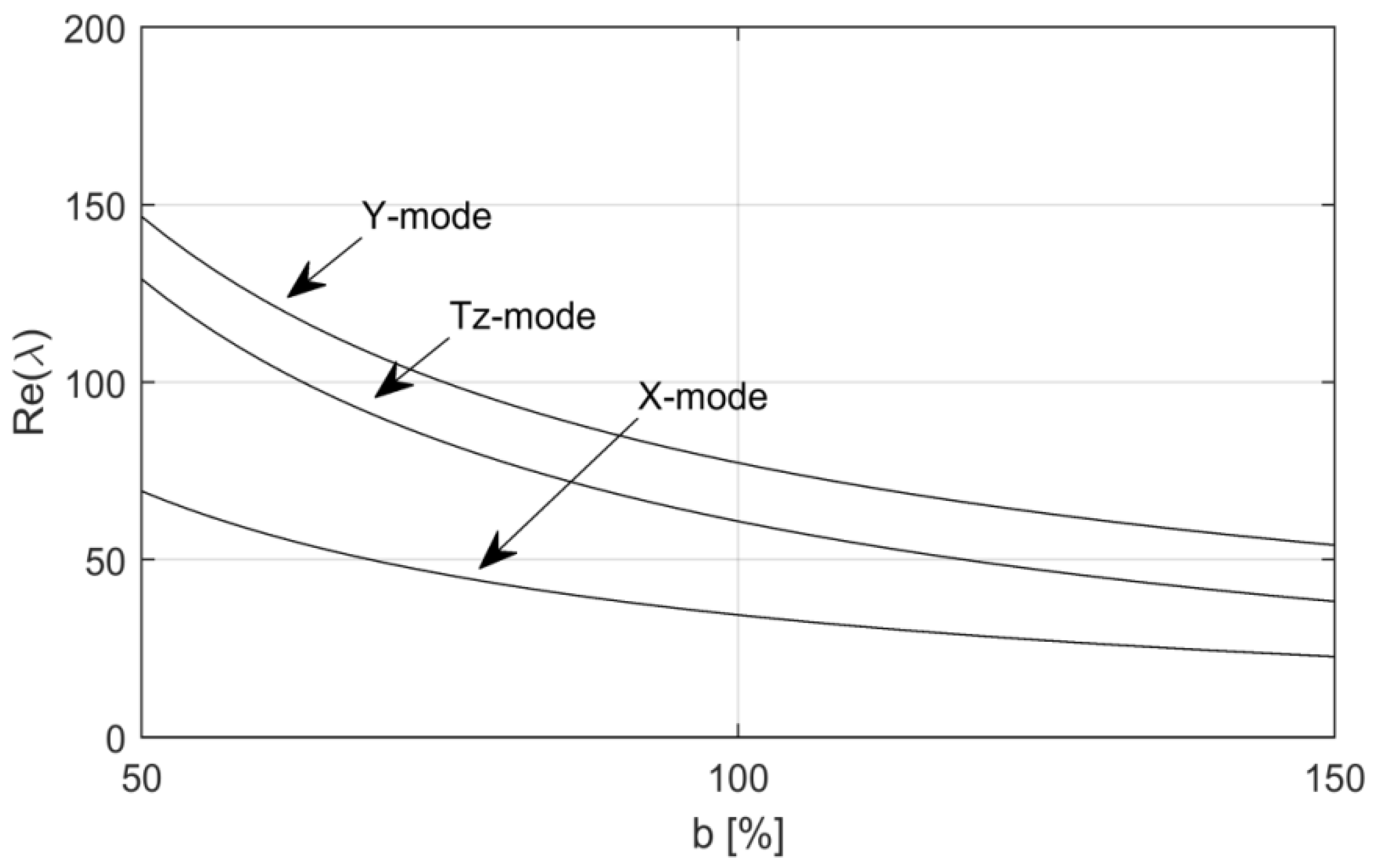
It is also important to investigate squeal propensity in relation to the geometry of the design parameters. In particular, the size of the brake shoe can be a focus of design modification. Figure 9 shows that the real parts of the unstable rigid modes change with variation in the contact arc angle. It is interesting that the real part of the Y-mode drastically decreases with an increase in the contact arc angle. In contrast, the change in the real parts of the X-mode and Tz-mode is relatively minor.

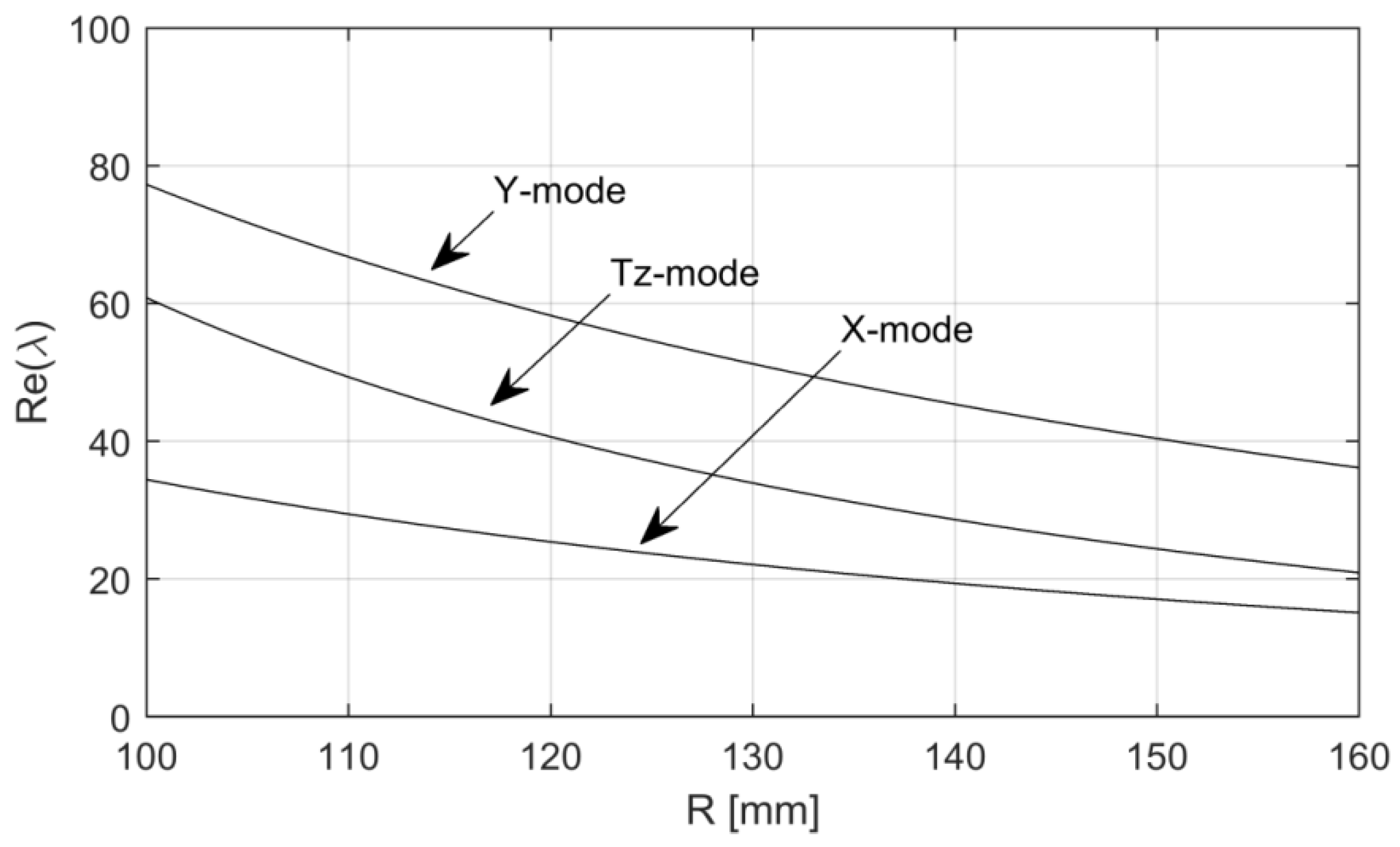
Figure 10 and Figure 11 show that the squeal propensity of the rigid shoe decreases with an increase in the shoe radius and width. This indicates that an increase in the radius, width, and contact arc angle of the shoe reduces the squeal propensity due to the rigid shoe modes.

4. Conclusions

In this paper, the dynamic instability of rigid brake shoe modes was analytically investigated. The squeal propensity of these modes was numerically analyzed, with mathematical derivations used to identify the cause of drum brake squeal. The squeal mechanism was found to be a negative slope mechanism that strongly influences the rotation dependency of drum brake squeal.

The numerical simulation revealed that two translation modes (X- and Y-modes) and one rotation mode (Tz-mode) become dynamically unstable in the presence of a negative slope in the friction–velocity curve. This indicates that the three rigid modes of the drum shoe are negative-damping-susceptible modes. The squeal propensity of these modes increases as the rotation speed of the brake drum decreases and the brake pressure increases. In terms of brake shoe design, the size of the drum brake shoe was found to affect the squeal propensity. Generally, a brake shoe with a larger radius, width, and contact arc angle reduces the squeal propensity. Without a negative slope in the friction–velocity curve, mode-coupling-type instability among the rigid modes of the brake shoe is not generated. This represents a significant difference from the characteristics of a brake pad in a disc brake system, where the mode-coupling instability of rigid modes in the brake pad is normally observed as shown in [9,10].

It was found that the X-, Y-, and Tz-modes are susceptible to negative slope, but they are rarely influenced by friction damping. Therefore, the squeal propensity of these modes increases at low speeds. It is strongly suggested that these three rigid modes be modified when the squeal of the drum brake system occurs only at low speeds. In future research, the squeal propensity of the rigid modes of a drum brake will be correlated with the experimental results from a brake dynamometer.