The Influence of Scratches on the Tribological Performance of Friction Pairs Made of Different Materials under Water-Lubrication Conditions

Abstract

Water-lubricated bearings are widely used in marine equipment, and the lubricating water often contains hard particles. Once these particles enter the gap between the bearing and the shaft, they can scratch the smooth surfaces of the shaft and bearing, influencing the working performance of the bearing system. To investigate the effect of scratch parameters on tribological performance, this paper conducts multiple block-on-ring experiments and constructs a mixed-lubrication model under water-lubrication conditions. The results show that among the three commonly used bearing materials, the tribological performance of graphite block is the most sensitive to scratches on the test ring surface. Under the condition of one scratch (N = 1), the loading area of water film pressure is divided into two separate zones (a trapezoidal pressure zone and an extremely low-pressure zone). In addition, the variation of maximum water film pressure is determined by the positive effect (hydrodynamic pressure effect of fluid) and negative effect (“piercing effect” of the asperities). Compared with the scratch depth and scratch location, the scratch width has the most significant effect on the tribological performance of the block-on-ring system. The maximum contact pressure is located at both edges of the scratch due to the formation of a water sac structure. The scratch has a great influence on the transition of the lubrication state of the block-on-ring system. The existence of scratches increases the critical speed at which the lubrication state transits from mixed-lubrication to elastohydrodynamic lubrication, and the critical speed is directly proportional to the scratch width.

1. Introduction

Due to the advantages of a simple structure, no pollution, and a good cooling effect, water-lubricated bearings are used as a key transmission component [1,2,3] in ship propulsion systems. However, because the lubricating water has low viscosity and poor load capacity, the bearing and shaft often operate in a mixed-lubrication state, resulting in rapid wear [4,5,6] of the bearing. The friction behavior under water-lubrication conditions has attracted great interest [7,8,9,10] from many scholars. Jia et al. [11] investigated the friction properties between PI-based composites and stainless steel using a block-on-ring test rig. The results showed that the plastic deformation and micro-cracking phenomena of the composite material were reduced under water-lubrication conditions, and the anti-wear performance of the composite material was enhanced. Chen et al. [12] studied the tribological properties of carbon fiber-reinforced polyetheretherketone composites under different lubricant conditions. The friction coefficient under the seawater lubrication condition was lower than that under the pure water-lubrication condition. This was because seawater helps to form compounds and deposit them on friction surfaces. Zhao et al. [13] discovered that increasing the content of potassium titanate whiskers helped reduce the wear rate of polyurethane composites under water-lubrication conditions. Xiao et al. [14] conducted block-on-ring friction experiments under different loads and speeds. Among the four lubrication conditions (dry friction, pure water lubrication, seawater lubrication, and sand water lubrication), the friction coefficient and wear rate under seawater lubrication were the lowest. Huang et al. [15] investigated the frictional characteristics of stainless-steel blocks and alloy steel rings under water-lubrication conditions. They found that the friction pairs entered a stable friction state (friction coefficient μ ≥ 0.5) after a running-in distance of 3 m. Wang et al. [16] studied the friction behavior between a rubber block and a coated ring whose surface had Cr/CrN/GLC coatings. Compared with the uncoated ring, the coated ring exhibited a markedly lower friction coefficient and wear rate under water-lubrication conditions. Xiong [17] pointed out that carbon fiber could improve the friction performance of a test block made of ultra-high molecular weight polyethylene under water-lubrication conditions. Nobili et al. [18] deposited DLC coatings on different substrate surfaces to obtain multiple groups of test blocks, and experimental results showed that DLC coatings deposited on high-hardness substrate surfaces had better wear resistance. Xu et al. [19] discovered that the friction coefficient (0.12) of a test block coated with carbon fiber-reinforced polyphenylene sulfide (PPS) under water lubrication was much lower than that (0.40) under dry friction. All the above studies focus on using the block-on-ring test rig to evaluate the friction performance under water-lubrication conditions, but there is currently a lack of research on using the block-on-ring theoretical model to explain the experimental phenomenon. Therefore, it is necessary to construct a finite-width mixed-lubrication model and research the friction behavior and the lubrication performance of the block-on-ring system.

If the lubricant contains hard particles, once particles enter the gap between the bearing and the shaft, the surfaces of the friction pairs may be scratched, and the scratched surfaces will affect the lubrication performance of the bearings. Currently, scholars have gradually started to pay attention to the relationship between surface scratches and the working performance of the bearing systems [20,21]. Dobrica et al. [22,23] used the numerical simulation method to study the influence of surface scratches on the performance of journal bearings. Shallow scratches had almost no effect on bearing performance, while deep scratches had a destructive effect. There was almost no fluid hydrodynamic pressure effect in the deep scratches, resulting in zero local pressure. Chatterton et al. [24] found that the dynamic performance of tilting pad bearings decreased with an increase in scratch depth and scratch number. Vo [25] discovered that scratches had a strong influence on bearings, with a significant decrease in film pressure in the scratched area and a reduction in the load capacity of the bearing. Deeper scratches increased the shaft center eccentricity and decreased the minimum film thickness. Chasalevris et al. [26] studied the influence of bearing scratch on system response and found subharmonics and superharmonics in the response signals of the worn bearing through continuous wavelet transform. Nicodemus et al. [27] researched the working performance of the scratched bearings under micro-polar lubricant conditions. The micro-polar effect made polar lubricant more sensitive to bearing scratches than Newtonian lubricant. Cai et al. [28] discussed the influence of the scratch of water-lubricated bearing on system dynamics response. The interesting thing is that the dynamic performance of water-lubricated bearings is improved under certain reasonable wear parameters. The above studies are all about the effects of bearing scratches on the static and dynamic performance of the system.

In fact, scratches may also appear on shaft surfaces, which is similar to the phenomenon whereby wear may occur both on the tool surface and the workpiece surface when the tool cuts the workpiece [29]. The scratches on the shaft surfaces will also significantly affect the bearing system, so scholars have started studying the influence of shaft scratches on bearing lubrication performance [30]. Jean et al. [31,32] found that different scratch locations could change the fluid pressure distribution. Branagan [33,34] simplified the long-bearing model into a short-bearing model to study the effects of scratch locations on the performance of oil-lubricated bearings. When the shaft scratch was located at the bearing center, it had a much greater effect on the bearing lubrication performance compared with the condition that the scratch was located at the bearing edge. Giraudeau et al. [35] studied the influence of the shaft scratch on the performance of double-leaf oil-lubricated bearings with experiments. When the order of magnitude of scratch depth and the minimum film thickness were the same, the existence of scratch dramatically affected the distribution of film pressure. To sum up, the above studies focus on the oil-lubricated bearings, and the structure parameters and location parameters of shaft scratches can markedly influence the pressure and thickness of the lubricating oil film.

Compared to oil-lubricated bearings, water-lubricated bearings often work in harsh environments where the lubricating water may contain hard particles (such as sand). When these hard particles enter the bearing clearance, although most of them will flow out from the bearing groove accompanying the flowing water, a small number of large particles may remain in the clearance between the shaft and the bearing. These large particles will scratch the smooth surfaces [36] of the shaft and the bearing when the shaft rotates, which is proved by the literature [37]. Regardless of whether scratches appear on the surface of the shaft or bearing, scratches will affect the lubrication performance and working quality of the bearing system. Because all the previous studies focus on the effects of shaft scratches on the oil-lubricated bearings, research on the influences of shaft scratches on the water-lubricated bearings is still in a blank state. In our previous work [38,39], we have already investigated the influence of shaft scratches on the lubrication performance of water-lubricated bearings using a theoretical model. However, further research is needed to study the effect of scratches on friction and wear performance of friction pairs by experiment. This paper experimentally studies the tribological performance under different scratch parameters and friction pair materials. We also established a theoretical model for a block-on-ring system to explain the change law of performance parameters observed in the experiments.

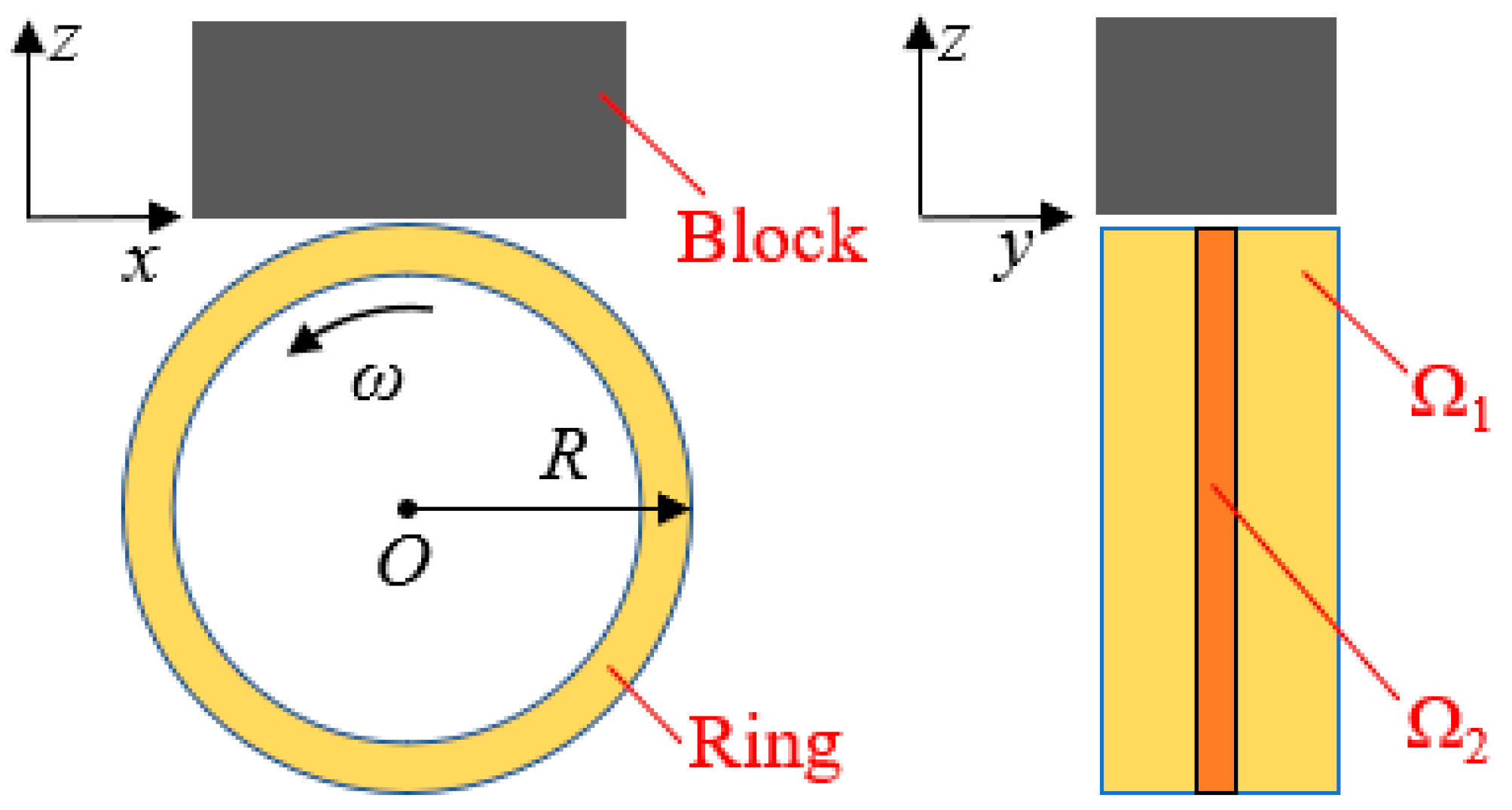
2. Theoretical Model

The model of the block-on-ring system is shown in Figure 1. The variable R represents the outer radius of the test ring, O represents the center of the test ring, ω represents the angular velocity of the test ring, Ω₁ represents the unscratched area, and Ω₂ represents the scratched area.

2.1. Average Flow Reynolds Equation

The average flow Reynolds equation [40,41] considering surface roughness and fluid flow state is used to calculate the fluid pressure, i.e.,

$$\left\{\begin{array}{ll}\frac{\partial }{\partial x}\left({\varphi }_x\frac{h^3}{\eta }\frac{\partial p}{\partial x}\right)+\frac{\partial }{\partial y}\left({\varphi }_y\frac{h^3}{\eta }\frac{\partial p}{\partial y}\right)=6u_s{\varphi }_c\frac{\partial h}{\partial x}+6u_s\sigma \frac{\partial {\varphi }_s}{\partial x}\hfill & ,Re<{Re}_c\hfill \\ \frac{\partial }{\partial x}\left({\varphi }_x\frac{h^3}{k_x\eta }\frac{\partial p}{\partial x}\right)+\frac{\partial }{\partial y}\left({\varphi }_y\frac{h^3}{k_y\eta }\frac{\partial p}{\partial y}\right)=6u_s{\varphi }_c\frac{\partial h}{\partial x}+6u_s\sigma \frac{\partial {\varphi }_s}{\partial x}\hfill & ,Re\ge {Re}_c\hfill \end{array}\right.$$

(1)

where ƞ is the dynamic viscosity of water, p is the water film pressure, h is the water film thickness, u_s is the linear velocity of the outer surface of the test ring, and (x, y) are the coordinates of points along block length and width directions. $\sigma =\sqrt{{\sigma }_b^2+{\sigma }_r^2}$ is the combined surface roughness of test ring and test block, σ_b is the roughness of test block, and σ_r is the roughness of the test ring. Re = ρu_sh₀₀/η is the Reynolds number [42], ρ is the density of water, and h₀₀ is the rigid central film thickness [43]. Re_c is the critical Reynolds number. k_x = 1 + (0.0136/12)Re^0.9 and k_y = 1 + (0.0136/12)Re^0.98 are both turbulence factors [44]. In this paper, the Reynolds number Re is 216.3, and the Reynolds number is significantly smaller than the critical Reynolds number [45] Re_c (2000), and the flow state of the lubricant is laminar [46]. $\left({\varphi }_x,{\varphi }_y\right)$ are the pressure flow factors [40] along x and y directions, ${\varphi }_s$ is the shear flow factor [41], and ${\varphi }_c$ is the contact factor [47]. The calculation formulas of pressure flow factors are

$$\left\{\begin{array}{ll}{\varphi }_x=1-C{e}^{-r\left(\frac{h}{\sigma }\right)}\hfill & ,\gamma \le 1\hfill \\ {\varphi }_x=1+C{\left(\frac{h}{\sigma }\right)}^{-r}\hfill & ,\gamma >1\hfill \end{array}\right.$$

(2)

$${\varphi }_y\left(\frac{h}{\sigma },\gamma \right)={\varphi }_x\left(\frac{h}{\sigma },\frac{1}{\gamma }\right)$$

(3)

where the values of three variables (γ, C, r) in the pressure flow factor formulas can be selected according to reference [40].

The shear flow factor can be gained as

$${\varphi }_s={\left(\frac{{\sigma }_r}{\sigma }\right)}^2{\Phi }_s\left(\frac{h}{\sigma },{\gamma }_1\right)-{\left(\frac{{\sigma }_b}{\sigma }\right)}^2{\Phi }_s\left(\frac{h}{\sigma },{\gamma }_2\right)$$

(4)

$$\left\{\begin{array}{ll}{\Phi }_s=A_1{\left(\frac{h}{\sigma }\right)}^{{\alpha }_1}{e}^{-{\alpha }_2\left(\frac{h}{\sigma }\right)+{\sigma }_3{\left(\frac{h}{\sigma }\right)}^2}\hfill & ,\frac{h}{\sigma }\le 5\hfill \\ {\Phi }_s=A_2{e}^{-0.25\left(\frac{h}{\sigma }\right)}\hfill & ,\frac{h}{\sigma }>5\hfill \end{array}\right.$$

(5)

where the value selection of five variables (A₁, A₂, α₁, α₂, α₃) in Equations (4) and (5) can be found in reference [41].

The equation of contact factor is

$$\left\{\begin{array}{ll}{\varphi }_c=e^{-0.6912+0.782\frac{h}{\sigma }-0.304{\left(\frac{h}{\sigma }\right)}^2+0.0401{\left(\frac{h}{\sigma }\right)}^3}\hfill & ,0\le \frac{h}{\sigma }<3\hfill \\ {\varphi }_c=1\hfill & ,\frac{h}{\sigma }\ge 3\hfill \end{array}\right.$$

(6)

where h/σ is the film thickness ratio.

2.2. Film Thickness Equation

According to the geometric relationship and elastic mechanics theory of the block-on-ring system, the calculation formula of the film thickness is

$$\left\{\begin{array}{ll}h\left(x,y\right)=h_{00}+\frac{x^2}{2R}+\frac{2}{\pi E^{\prime }}{\displaystyle \iint \frac{p\left(x^{\prime },y^{\prime }\right)}{\sqrt{{\left(x-x^{\prime }\right)}^2+{\left(y-y^{\prime }\right)}^2}}d{x}^{\prime }d{y}^{\prime }}\hfill & ,\Omega \in {\Omega }_1\hfill \\ h\left(x,y\right)=h_{00}+\frac{x^2}{2R}+h_c+\frac{2}{\pi E^{\prime }}{\displaystyle \iint \frac{p\left(x^{\prime },y^{\prime }\right)}{\sqrt{{\left(x-x^{\prime }\right)}^2+{\left(y-y^{\prime }\right)}^2}}d{x}^{\prime }d{y}^{\prime }}\hfill & ,\Omega \in {\Omega }_2\hfill \end{array}\right.$$

(7)

where h_c is the scratch depth, and Ω is the computational domain. $E^{\prime }={\left[\frac{\left(1-{\nu }_r^2\right)}{E_r}+\frac{\left(1-{\nu }_b^2\right)}{E_b}\right]}^{-1}$ is the composite elastic modulus, (ν_r, ν_b) are the Poisson ratio of ring and block, respectively, and (E_r, E_b) are the elastic modulus of ring and block, respectively.

2.3. Asperity Contact Model

To calculate the solid contact pressure and contact area between the ring surface and block surface, this paper adopts the GW model, i.e.,

$$\left\{\begin{array}{ll}{p}_{asp}=\frac{16\sqrt{2}\pi }{15}{\left(\sigma \beta D\right)}^2\sqrt{\frac{\sigma }{\beta }}{E}^{\prime }{F}_{2.5}\left(\frac{h}{\sigma }\right)\hfill & \hfill \\ A_c={\pi }^2{\left(\sigma \beta D\right)}^2{A}_0{F}_{2.0}\left(\frac{h}{\sigma }\right)\hfill & \hfill \end{array}\right.$$

(8)

where p_asp is the contact pressure, β is the curvature radius of asperities on either surface, and D is the number of asperities per unit contact area. In this paper, the value of β is 2.0 × 10⁻⁶ m, and that of D is 5.0 × 10¹¹/m². A_c and A₀ are the real contact area and nominal contact area, respectively. F_2.5 and F_2.0 are both Gaussian probability density functions, and the calculation formulas are [48,49]

$$F_{2.5}\left(\frac{h}{\sigma }\right)=\left\{\begin{array}{ll}2.134\cdot {10}^{-4}{e}^{3.804ln\left(4-\frac{h}{\sigma }\right)+1.34{\left[ln\left(4-\frac{h}{\sigma }\right)\right]}^2}\hfill & ,\frac{h}{\sigma }\le 3.5\hfill \\ 1.12\cdot {10}^{-4}{\left(4-\frac{h}{\sigma }\right)}^{1.9474}\hfill & ,3.5<\frac{h}{\sigma }\le 4.0\hfill \\ 0\hfill & ,\frac{h}{\sigma }>4.0\hfill \end{array}\right.$$

(9)

$$F_{2.0}\left(\frac{h}{\sigma }\right)=\left\{\begin{array}{ll}1.705\cdot {10}^{-5}{e}^{4.504ln\left(4-\frac{h}{\sigma }\right)+1.37{\left[ln\left(4-\frac{h}{\sigma }\right)\right]}^2}\hfill & ,\frac{h}{\sigma }\le 3.5\hfill \\ 8.8123\cdot {10}^{-5}{\left(4-\frac{h}{\sigma }\right)}^{2.15}\hfill & ,3.5<\frac{h}{\sigma }\le 4.0\hfill \\ 0\hfill & ,\frac{h}{\sigma }>4.0\hfill \end{array}\right.$$

(10)

2.4. Load Capacity Equation

The synthetic load capacity can be obtained as

$$W=F_h+F_c={\displaystyle \underset{{\Omega }_1+{\Omega }_2}{\iint }p\left(x,y\right)dxdy}+{\displaystyle \underset{{\Omega }_1+{\Omega }_2}{\iint }{p}_{asp}\left(x,y\right)dxdy}$$

(11)

where W is the synthetic load capacity, F_h is the component of load capacity generated by water film, F_c is the component of load capacity generated by asperity contact, Ω₁ represents the unscratched area, and Ω₂ represents the scratched area.

2.5. Friction Coefficient Equation

Friction is generated by fluid shear force and asperity shear force, so the calculation formulas [50] of friction f and friction coefficient μ are given as

$$f={\displaystyle \underset{{\Omega }_1+{\Omega }_2}{\iint }\left(\frac{\eta \omega R^2}{h}+\frac{h}{2}\frac{\partial p}{\partial x}\right)dxdy}+{\displaystyle \sum _{i=1}^N{\displaystyle \underset{{\Omega }_1+{\Omega }_2}{\iint }{\mu }_c{p}_{asp}}dxdy}$$

(12)

$$\mu =\frac{f}{W}$$

(13)

where μ_c is the dry friction coefficient between the ring surface and block surface, and N is the mesh number of the computational domain. The value of the dry friction coefficient μ_c is 0.15.

2.6. Boundary Conditions

The boundary conditions used in this paper are

$$\left\{\begin{array}{l}p\left(x_{in},y\right)=p\left(x_{out},y\right)=p\left(x,y_{in}\right)=p\left(x,y_{out}\right)=0\hfill \\ p\left(x,y\right)\ge 0,\left(x_{in}<x<x_{out},y_{in}<y<y_{out}\right)\hfill \end{array}\right.$$

(14)

where (x_in, y_in) are the entry boundary coordinates of the computational domain in the x and y directions, respectively. (x_out, y_out) are the exit boundary coordinates of the computational domain in the x and y directions, respectively.

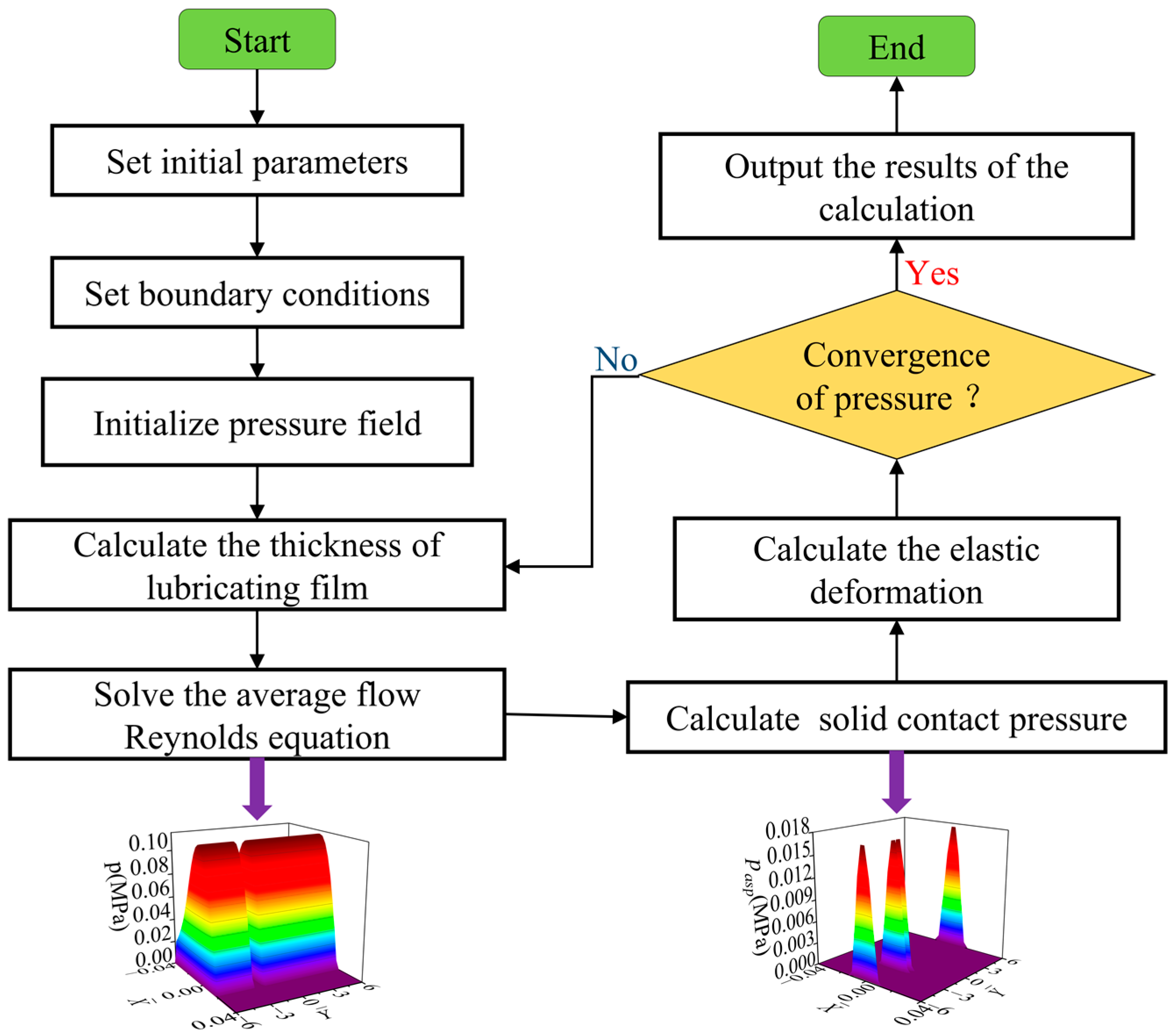
2.7. Numeric Calculation Scheme

In this paper, the finite difference method is used to solve the block-on-ring mixed-lubrication model, which includes the iterative processes of water film pressure and asperity contact pressure. The specific numerical calculation steps of the lubrication model are presented in Figure 2.

3. Experimental Equipment and Model Validation

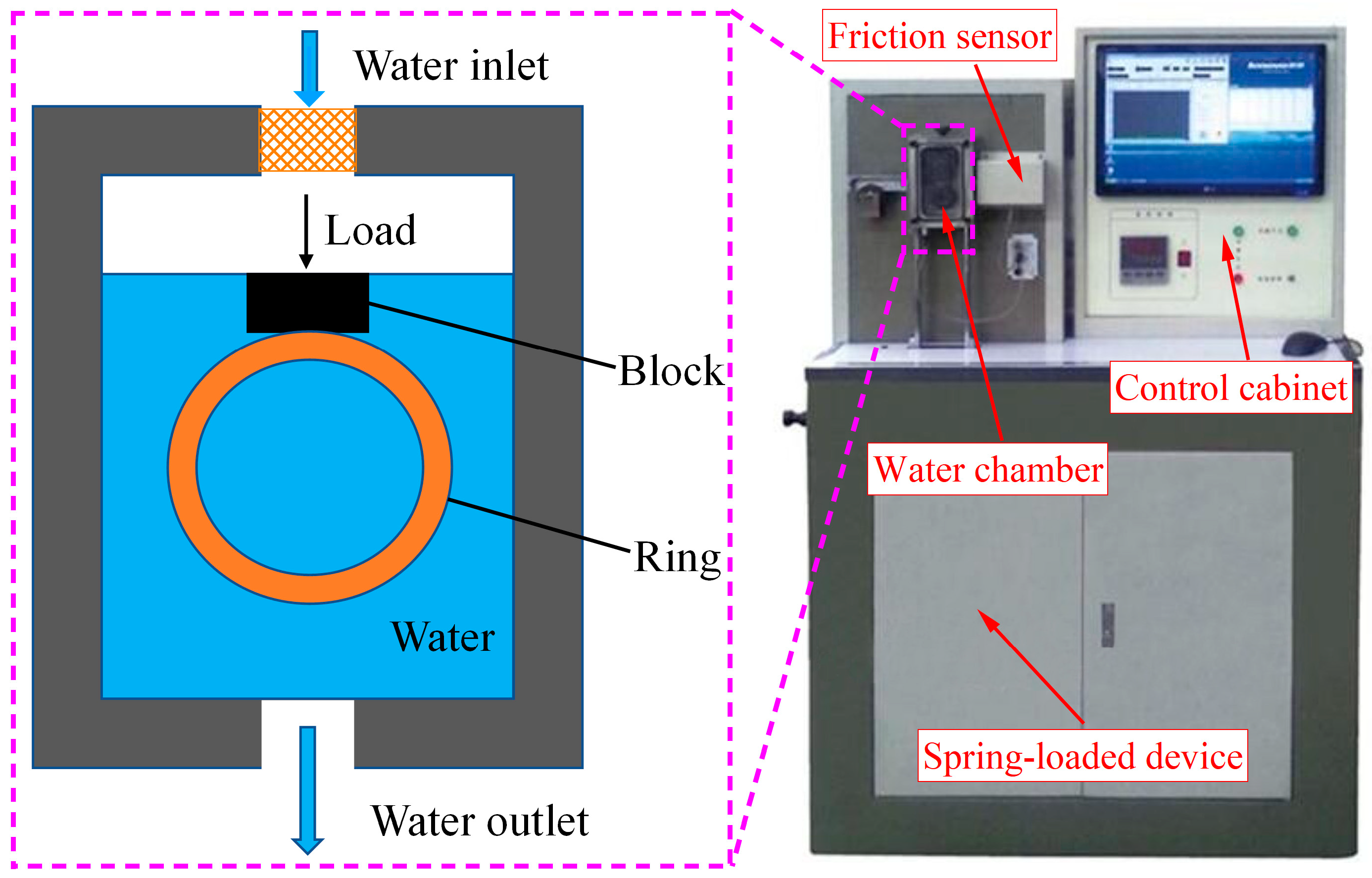
3.1. Experimental Equipment

With the use of block-on-ring friction and wear tester (model number is MRH-3) shown in Figure 3, the friction coefficient between the test ring and the test block can be measured [51].

Table 1. Parameters of tester.

Parameters	Value
Maximum load (N)	3000
Speed range (r/min)	10~3000
Accuracy of pressure sensor	0.03%FS
Accuracy of friction torque sensor	0.2%FS
Sampling frequency of data acquisition card (KS/s)	500

gives the acquisition system and sensor parameters of the tester. The tester mainly includes a spring-loaded device, a control cabinet, a water chamber, and a friction sensor. The control cabinet makes the output shaft of the variable frequency motor rotate, therefore driving the test ring in the water chamber to rotate. The sensor records friction force and friction coefficient in real time. Figure 3 also provides an enlarged image of the water chamber; water is supplied from the inlet, and there is also a water outlet to achieve the circulation flow of lubricating water. Because the impurities in the water may affect the experimental results, a filter is installed at the water inlet to remove all contaminants.

Figure 4 gives three types of test blocks made of different materials (i.e., rubber, thordon, and graphite), which are commonly used in water-lubricated bearings [52,53,54]. The test ring is made of stainless steel [55], Figure 5a provides a test ring without scratches, and Figure 5b presents another test ring whose surface has one scratch. The structure of this scratch is described in Figure 5c, W_c is the scratch width, h_c is the scratch depth, L_c is the scratch location, L is the width of the stainless-steel ring, and the scratch is located in the middle of the test ring. The structure and material parameters of the friction pairs are shown in

Table 2. Parameters of friction pairs.

	Test Ring	Test Block
Material	316 Stainless steel	Nitrile rubber	Thordon	Graphite
Size (mm)	Outside diameterΦ49.00 Width 13.65	Length 19.05, width 12.32, thickness 12.32
Roughness (μm)	Ra0.4	Ra0.6	Ra0.6	Ra0.6
Elastic modulus	210 GPa	6.1 MPa	490 MPa	7800 MPa
Poisson ratio	0.30	0.49	0.36	0.19

.

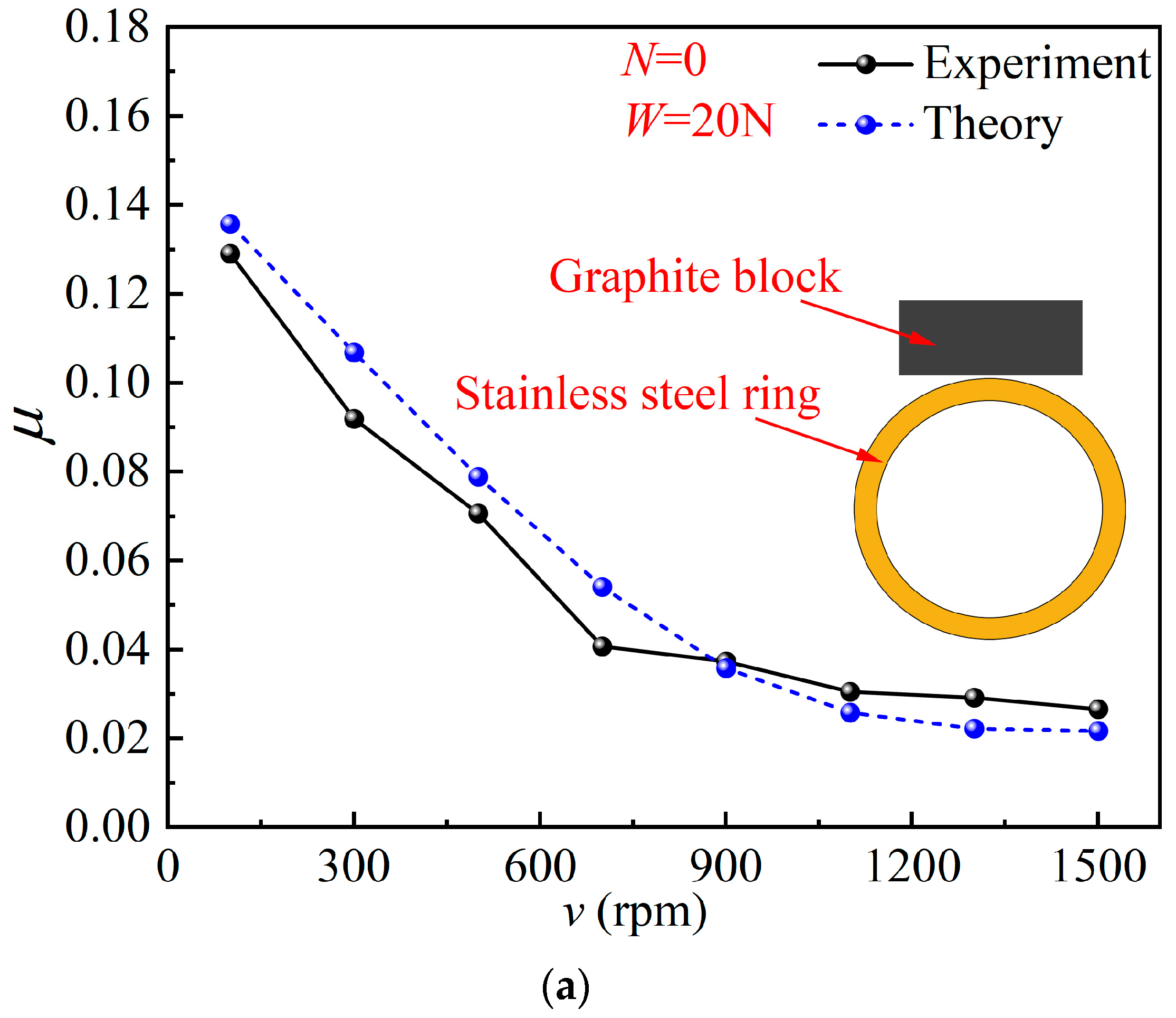
3.2. Model Validation

When the load is 20 N, the friction coefficients between the stainless-steel ring and the graphite block are measured, and the black curve in Figure 6a represents the experimental results of friction coefficients. The theoretical friction coefficients are also calculated by the block-on-ring model, and the blue curve in Figure 6a represents the theoretical friction coefficients. In addition, Figure 6b shows the simulation results (purple curve) and experimental results (orange curve) of the friction coefficients between the graphite block and scratched ring under a load of 30 N. As described in Figure 6, the theoretical simulation results are in good agreement with the experimental results, which validates the accuracy of the theoretical model proposed in this paper. It can also be seen from Figure 6 that (1) At low speeds, the experimental results are lower than the theoretical results. This is due to the surface wear of the test block during the experimental process, and the graphite powder enters the lubrication area and plays a lubricating role. Therefore, the friction coefficients under experimental conditions are lower than those under simulation conditions. (2) At high speeds, the experimental values of the friction coefficient are higher than the simulation values. This is because the high speeds cause vibration of the stainless-steel ring, enhancing the asperity contact between the stainless-steel ring and the graphite block. Therefore, the friction coefficient results under experimental conditions are greater.

4. Results and Discussion

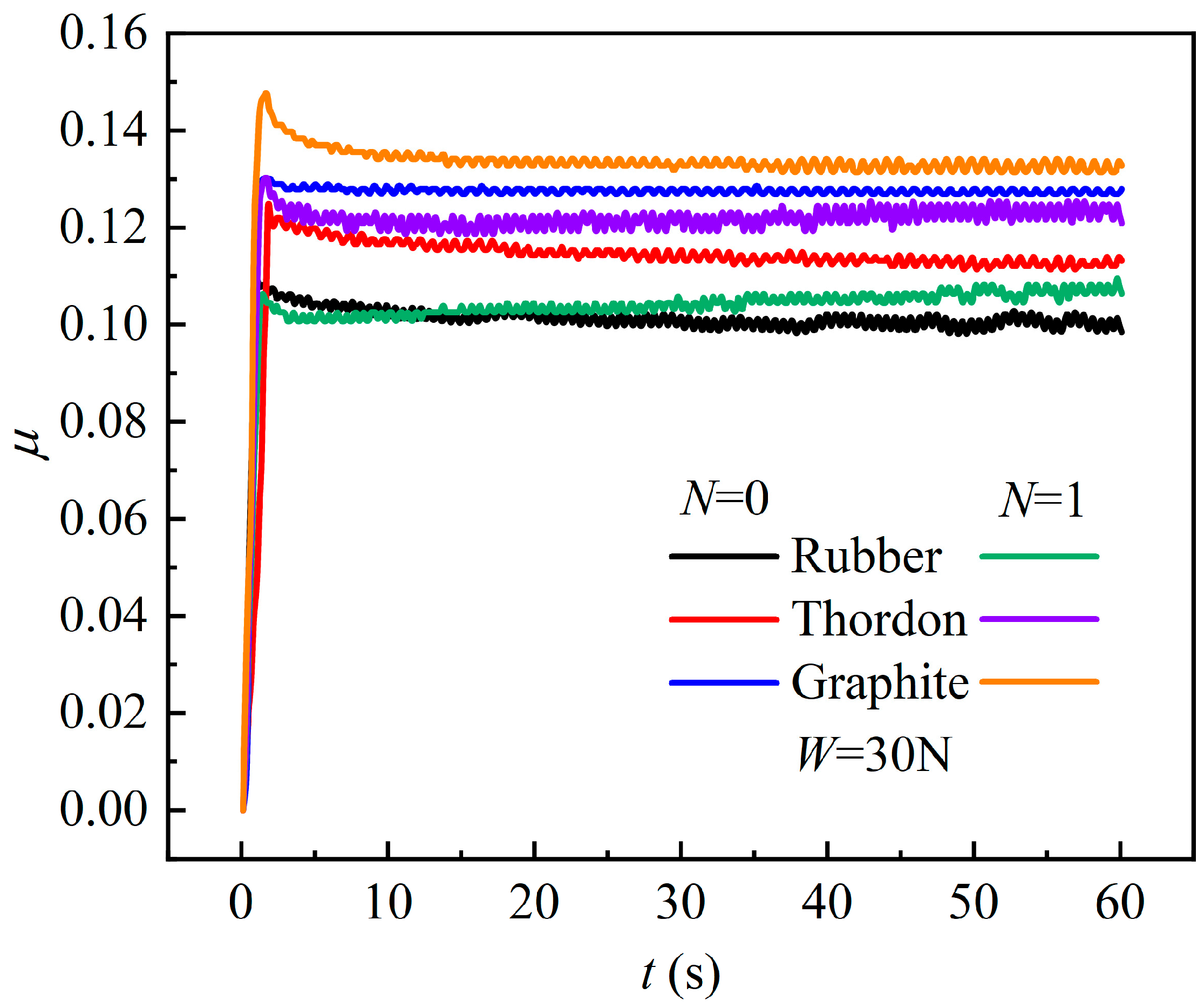
4.1. Sensitivity of Tribological Performance of Test Blocks Made of Different Materials to Scratches

Figure 7 plots the variations of the friction coefficients with time under water-lubrication conditions. During the experiment process, the load is 30 N, and the rotation speed of the test ring is 100 r/min. In the figure, “N = 0” indicates that there are no scratches on the surface of the test ring, while “N = 1” indicates that the test ring surface has one scratch. After the test ring starts rotating, the friction coefficient instantly rises to a peak value and then slightly decreases to a stable value. The material of the test block has a significant influence on the friction coefficient. When there are no scratches (N = 0) on the test ring surface, the stable friction coefficient of the rubber block and stainless-steel ring is approximately 0.101, that of the thordon block and stainless-steel ring is approximately 0.114, that of the graphite block and stainless-steel ring is approximately 0.127, and the friction coefficients of three types of test blocks have the following relationship: μ_graphite > μ_thordon > μ_rubber. This indicates that the bigger the elastic modulus of the test block is, the higher the friction coefficient of frictional pairs becomes. The friction coefficient of the scratched ring (N = 1) is greater than that of the unscratched ring (N = 0). In addition, the differences in friction coefficient between the two cases vary with test block materials. The above results indicate that the existence of scratches can affect the friction performance of the block-on-ring system, and the degree of influence is related to the material of the test block.

The rotation speed of the test ring in Figure 7 is only 100 r/min, so the sensitivity of the friction coefficient of the block-on-ring system to scratches at other speeds is unclear. Figure 8 indicates the variation curves of the friction coefficients within the speed range of 100–1000 r/min, and the experiment load is still 30 N. It can be seen from the figures that the variation trend of the friction coefficient is similar to the Stribeck curve [56]. In the initial stage of the friction coefficient curve, the block-on-ring system is in the mixed-lubrication state, and the friction coefficients under different test blocks differ significantly. The relationship between friction coefficients of the three types of blocks is μ_graphite > μ_thordon > μ_rubber. As the rotation speed goes up, the friction pairs gradually transit from the mixed-lubrication (ML) state to the elastohydrodynamic lubrication (EHL) state, and the differences in friction coefficient among the three test blocks become smaller. The critical speed is defined as the speed threshold at which the friction pairs transit from the ML state to the EHL state and is directly proportional to the elastic modulus of the test block. The comparison in friction coefficient between a scratched ring and an unscratched ring shows that the existence of scratches greatly increases the friction coefficient in the mixed-lubrication state but has very little effect on the friction coefficient in the elastohydrodynamic lubrication state. An increase in scratch number (from 0 to 1) raises the critical speed at which the block-on-ring system enters the EHL state, and there is no critical turning point (i.e., critical speed) in the friction coefficient curve of the graphite block–scratched ring. Figure 8 also presents the difference |Δμ| in friction coefficient between the scratched ring and unscratched ring and gives the average value |Δμ|_av of difference |Δμ| within the speed range of 100–1000 r/min. The difference |Δμ| is big when the rotation speed is slower than 600 r/min. However, when the rotation speed exceeds 600 r/min, the rubber block (or thordon block) and stainless-steel ring enter the elastohydrodynamic lubrication state, and the difference |Δμ| of friction coefficient becomes small. The graphite block and scratched ring are always in the mixed-lubrication state, so the friction coefficient of the scratched ring is markedly higher than that of the unscratched ring throughout the entire speed range. The average value |Δμ|_av for the rubber block is 0.0056, for the thordon block is 0.0047, and for the graphite block is 0.0112. In other words, the average values |Δμ|_av under different test blocks have the following relationship ${\left|\Delta {\mu }_{\mathrm{graphite}}\right|}_{av}>{\left|\Delta {\mu }_{\mathrm{rubber}}\right|}_{av}>{\left|\Delta {\mu }_{\mathrm{thordon}}\right|}_{av}$.

To analyze the relationship between the solid contact state and the friction coefficient, Figure 9a provides the simulation results of the contact pressure at a speed of 400 r/min and a load of 30 N. As the elastic modulus of the test block rises, the block-on-ring contact area (i.e., the area between two pink dashed lines in Figure 9a) reduces along the x direction, but the maximum contact pressure becomes bigger and bigger. For example, for the unscratched test ring (N = 0), the maximum contact pressure of the rubber block is only 0.075 MPa, while that of the graphite block grows to 0.187 MPa. Due to the small elastic modulus of the rubber block, a large deformation occurs in the middle area (black curve in Figure 10a) of the rubber block along the x direction, forming a water sac structure. This deformation makes the test ring only come into contact with the edge of the rubber block (see the upper left corner image in Figure 9a), avoiding large-scale solid contact. Because the graphite block hardly deforms, the test ring almost comes into contact with the entire graphite block along the y direction (see the bottom left corner image in Figure 9a). The maximum contact pressure of the rubber block–test ring and rubber block–scratched test ring is 0.075 MPa and 0.081 MPa, respectively. The maximum contact pressure of the thordon block–test ring and thordon block–scratched test ring is 0.107 MPa and 0.133 MPa, respectively. The maximum contact pressure of the graphite block–test ring and graphite block–scratched test ring is 0.187 MPa and 0.222 MPa, respectively. From the above results, it can be seen that (1) When there are scratches on the test ring surface, the maximum contact pressure of the test block is raised. (2) The larger the elastic modulus of block is, the greater the increment of the maximum contact pressure becomes. The above two aspects are the reasons why the friction coefficient of the graphite block–scratched ring is the highest in Figure 8.

Figure 9b presents the simulation results of water film pressure at a speed of 400 r/min. As the elastic modulus increases, the loading area (the area between two black dashed lines in Figure 9b) of water film pressure decreases along the x direction. When there are no scratches (N = 0) on the test ring surface, the maximum water film pressure of the thordon block is the highest (0.1635 MPa), while the maximum water film pressure (0.1255 MPa) of the graphite block is almost equal to that (0.1205 MPa) of the rubber block. There are different effects scratches exert on the maximum water film pressure of three test blocks when the test ring surface has scratches: (1) The scratches increase the maximum water film pressure of the rubber block. This is because the load on the rubber block is mainly supported by the water film (see the pressure distribution in Figure 9). If the test ring surface has scratches, then the water film thickness will be reduced, therefore increasing the maximum water film pressure of the rubber block. (2) Surface scratches decrease the maximum water film pressure of the graphite block (or thordon block). This is because the elastic modulus of the graphite block (or thordon block) is large, the block hardly deforms, and the water film is thin. Therefore, the load is mainly supported by asperity contact for the graphite block. When there are scratches on the test ring surface, although the decrease in film thickness tends to increase the water film pressure, this will also increase the number of asperities in contact state. The thin water film will be pierced by the microasperities, destroying the water film continuity and reducing the water film pressure. Therefore, the existence of scratches will decrease the maximum water film pressure of the graphite block due to the “piercing effect” of the asperities. To sum up, the variation of maximum water film pressure is determined by the positive effect (hydrodynamic pressure effect of fluid) and negative effect (“piercing effect” of the asperities).

Figure 10 shows the simulation results of lubrication parameters at the middle section of the test block. The rotation speed of the test ring is 400 r/min, and the experiment load is 30 N. As can be seen from Figure 10a, the deformation of the test block increases as the material elastic modulus decreases. In other words, the rubber block has the largest deformation, which causes the phenomenon that there is no asperity contact in the central area of the rubber block along the y direction (the contact pressure in this area is zero in the upper left corner image in Figure 9a). From Figure 9a and Figure 10a, it can be seen that the asperity contact of the graphite block is the most severe. As shown in Figure 10a, when the test ring surface has a scratch, the deformation of the test block grows slightly. In addition, the smaller the elastic modulus of the test block is, the greater the increment of deformation becomes. Because the deformation of the rubber block is the largest, the formed wedge gap is also the biggest (see Figure 10b), and the loading area of the rubber block is wider than that of the other two blocks along the x direction (see Figure 9b). Figure 10c shows the pressure distribution of the water film at the middle section ($\stackrel{—}{X}$ = 0) along the y direction. When there are no scratches on the test ring surface, the water film pressure exhibits a trapezoidal variation law. However, under the condition of one scratch (N = 1), the loading area of water film pressure is divided into two separate zones, i.e., trapezoidal pressure zone and extremely low-pressure zone. The water film pressure of the graphite block is much lower than that of the other two types of blocks.

Based on the analysis of Figure 9 and Figure 10, it can be concluded that the existence of scratch can reduce the loading area of asperity contact and water film, so the water film thickness should decrease, which results in a stronger contact pressure and a larger water film pressure to support the load. This is why the friction coefficient of a scratched ring is larger than that of an unscratched ring (see Figure 8).

4.2. The Effect of Scratch Parameters on the Tribological Performance of Block-on-Ring System

Because the friction pairs often operate in the mixed-lubrication state under water-lubrication conditions, the asperity contact has a great effect on the friction and wear of the friction pairs [57,58]. Among the three types of test blocks, graphite block has the most severe asperity contact. It can be seen from Figure 7 and Figure 8 that the friction parameters (|Δμ| and |Δμ|_av) of the graphite block are the largest, i.e., the tribological performance of the graphite block is the most sensitive to the scratches on the test ring surface. Therefore, the friction pairs composed of graphite block and stainless-steel ring are chosen as the object of further study. In the experiment, the scratch depth, scratch width, and scratch location are selected as the influencing factors on the tribological performance of the block-on-ring system. As shown in

Table 3. Factors and levels of experiment.

Influence Factor	Level Value
	1	2	3
Scratch depth hc (mm)	0.1	0.2	0.3
Scratch width Wc (mm)	0.2	0.4	0.6
Scratch location Lc	1/6L	1/3L	1/2L

, each factor has three level values. According to the knowledge of permutation and combination, the total number of experimental groups can be calculated as

$$M={\left(C_n^1\right)}^m={\left(C_3^1\right)}^3=27$$

(15)

where M is the number of experimental groups, n is the number of levels, m is the number of influence factors, and C is the combinatorial number. According to Equation (15), there are a total of 27 groups of experiments.

To improve experimental efficiency, this paper adopts the orthogonal method to design the experiment scheme. Based on the L9 orthogonal design table [59], only 9 groups of experiments (instead of 27 groups) need to be carried out, and these 9 groups of experimental friction coefficients can be seen in

Table 4. Orthogonal experiment scheme and results.

Group Number	hc (mm)	Wc (mm)	Lc	Friction Coefficient
1	0.3	0.6	1/6L	0.078
2	0.2	0.2	1/2L	0.059
3	0.1	0.6	1/2L	0.076
4	0.3	0.2	1/3L	0.057
5	0.3	0.4	1/2L	0.070
6	0.2	0.6	1/3L	0.074
7	0.2	0.4	1/6L	0.065
8	0.1	0.4	1/3L	0.069
9	0.1	0.2	1/6L	0.052
Adjoint probability (P)	0.596	0.030	0.528
Importance of influence	Wc > Lc > hc

. This table also gives the adjoint probabilities P of the three influence factors. For example, the adjoint probability P of scratch width W_c is 0.030, which is less than the significance level (0.050). The adjoint probabilities of scratch depth h_c and scratch location L_c are both greater than 0.050. The above results indicate that scratch width W_c has the most significant effect on the friction coefficient of the block-on-ring system, followed by the scratch location L_c, and lastly, the scratch depth h_c.

Figure 11a shows the friction coefficients of 9 groups of experiments. The rotation speed range of the experiments is between 100 r/min and 1500 r/min. As the rotation speed increases, the friction coefficient shows a trend of first decreasing and then increasing. The friction coefficient varies significantly with different scratch parameters at low speeds, but the differences in friction coefficient among the 9 groups of experiments are small when the speed is higher than 1100 r/min. As can be seen from Figure 8, the graphite block and scratched ring have not yet entered the elastohydrodynamic lubrication (EHL) state at a speed of 1000 r/min, but they will enter the EHL state (see Figure 11a) when v = 1100 r/min.

Figure 11b gives the simulation results of the film thickness ratio λ, and the increase in rotation speed will lead to an increase in the film thickness ratio. The film thickness ratio curves can be easily divided into three major groups according to scratch width, which indicates that the scratch width has the largest influence on the lubrication performance of the block-on-ring system among the three scratch parameters. This is because the scratch width affects the loading area. In other words, widening scratch can reduce the loading area of water film and asperity contact. A thinner water film and a stronger solid contact are needed to support the load, and thus, the friction coefficient will significantly go up (see Figure 11a). The difference in film thickness curves among the three major groups is not significant in the mixed-lubrication (ML) stage [60], but it becomes more pronounced in the elastohydrodynamic lubrication (EHL) stage when the rotation speed increases. This is because the asperity contact pressure is the main support body of the load in the mixed-lubrication stage, then the test block and the test ring gradually separate as the speed increases, and the fluid film pressure becomes the main body to support the load in the elastohydrodynamic lubrication stage. On the one hand, low rotation speed has little effect on asperity contact, and high speed has a big effect on the hydrodynamic pressure effect of water film. On the other hand, wide scratches will strongly damage the continuity and hydrodynamic pressure effect of the water film in the EHL state, significantly reducing the lubricating film thickness h and film thickness ratio λ. The scratch width also influences the critical speed at which the friction pairs transit from the ML state to the EHL state. For example, when the scratch width is 0.2 mm, the critical speed is 700 r/min, but the critical speed is 1100 r/min under the scratch width of 0.6 mm. This indicates that an increase in scratch width will raise the speed threshold for the block-on-ring system to enter the EHL state.

Figure 12 gives the simulation results of water film pressure and asperity contact pressure. As can be seen from Figure 12a, the water film pressure in the scratched area is almost zero [61], regardless of the value of scratch width. Additionally, the maximum water film pressure is determined by the scratch width, while the scratch depth and scratch location have little effect on the maximum water film pressure. For example, the 2nd, 4th, and 9th groups have the same scratch width (W_c = 0.2 mm) and different scratch depths (h_c = 0.1 mm, 0.2 mm, 0.3 mm), and the maximum water film pressure of these three groups is equal (0.150 MPa). From Figure 12b, it can be noticed that the maximum contact pressure of the 1st group is the highest, and the scratch width is 0.6 mm, which indicates that increasing the scratch width leads to more severe asperity contact between the test ring and test block. Under the same scratch width, the influence of scratch depth and scratch location on the maximum contact pressure is very weak. The scratch widths of the 4th, 5th, and 6th groups in Figure 12 are 0.2 mm, 0.4 mm, and 0.6 mm, respectively. As can be seen from the simulation results of these three groups, the maximum water film pressure is inversely proportional to the scratch width, while the maximum contact pressure is directly proportional to the scratch width. The maximum contact pressure is located at both edges of the scratch. This is because there is no pressure or deformation in the scratched area, while deformation occurs in the other areas of the test block. This nonuniform deformation results in a water sac structure between the scratch and the end face of the test block. Figure 13 illustrates the water sac structure in the water-lubricated bearing. If the water film pressure at a certain point is high, the elastic deformation at the point will be large. In addition, the elastic deformation at surrounding points is relatively small because of low water film pressure. Then, the water sac structure [62,63] forms, and it is full of water.

Figure 14 shows the simulation results of the minimum film thickness h_min and maximum deformation δ_max of the graphite block. From the figure, it can be seen that the scratch depth h_c and the scratch location L_c have little influence on the minimum film thickness and the maximum deformation. For example, the scratch depths of 1st group, 3rd group, and 6th group are 0.3 mm, 0.1 mm, and 0.2 mm, respectively, but the minimum film thickness h_min of these three groups is almost equal to 1.927 μm, and the maximum deformation δ_max is around 0.184 μm. Among the three scratch parameters, the scratch width determines the minimum film thickness and maximum deformation, i.e., under the same scratch width, the maximum deformation (or minimum film thickness) is almost equal. As can be seen from Figure 14, the maximum deformation is clearly divided into three major groups according to the scratch width. Therefore, although the scratch depths of 1st group, 3rd group, and 6th group are different, the minimum film thickness (or maximum deformation) of these groups is almost the same because the scratch widths are all 0.6 mm. As the scratch width increases, the minimum film thickness decreases while the maximum deformation increases. For example, when the scratch width W_c is 0.2 mm, the maximum deformation of the test block is 0.166 μm, while the maximum deformation rises to 0.184 μm under the condition of W_c = 0.6 mm.

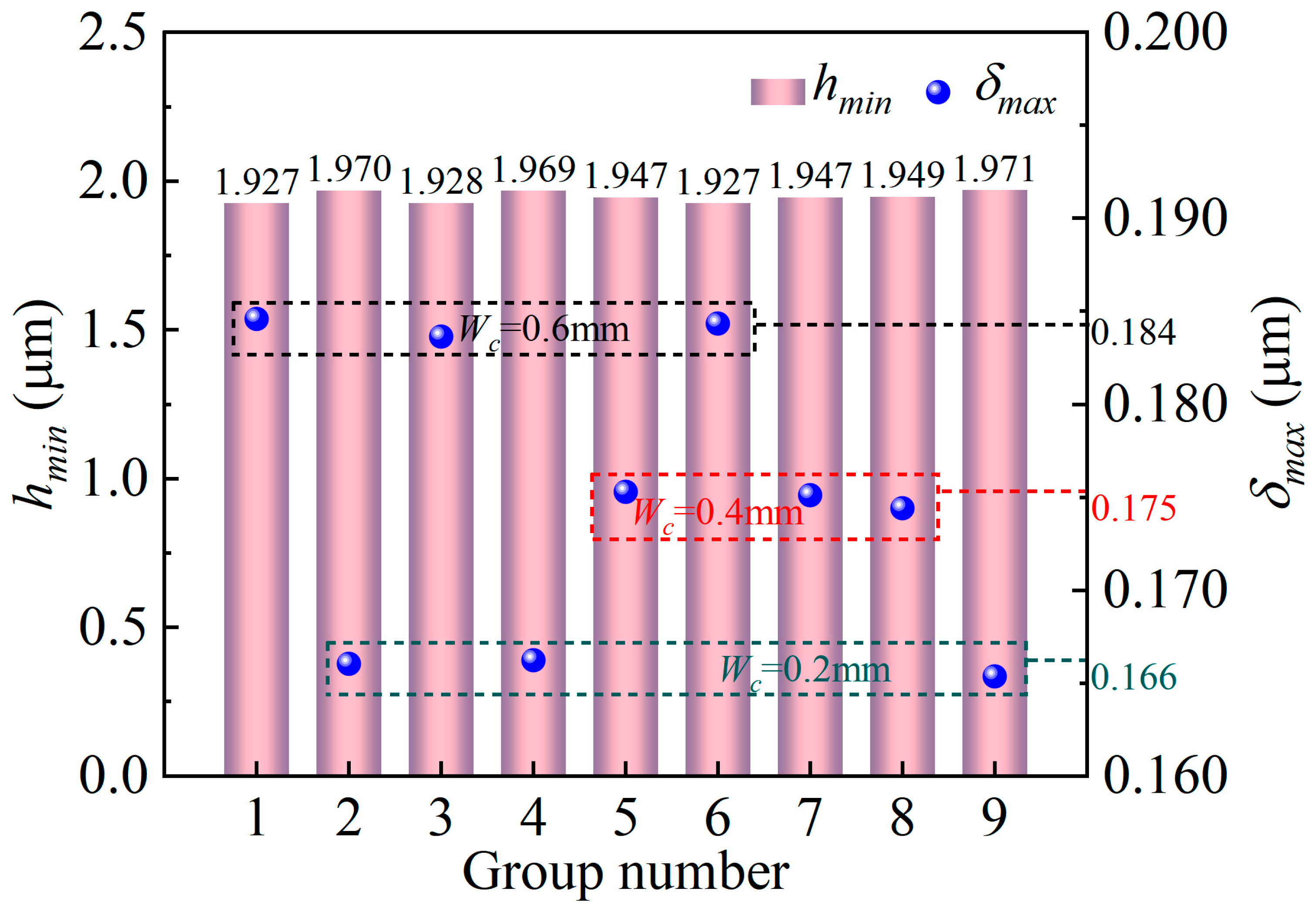
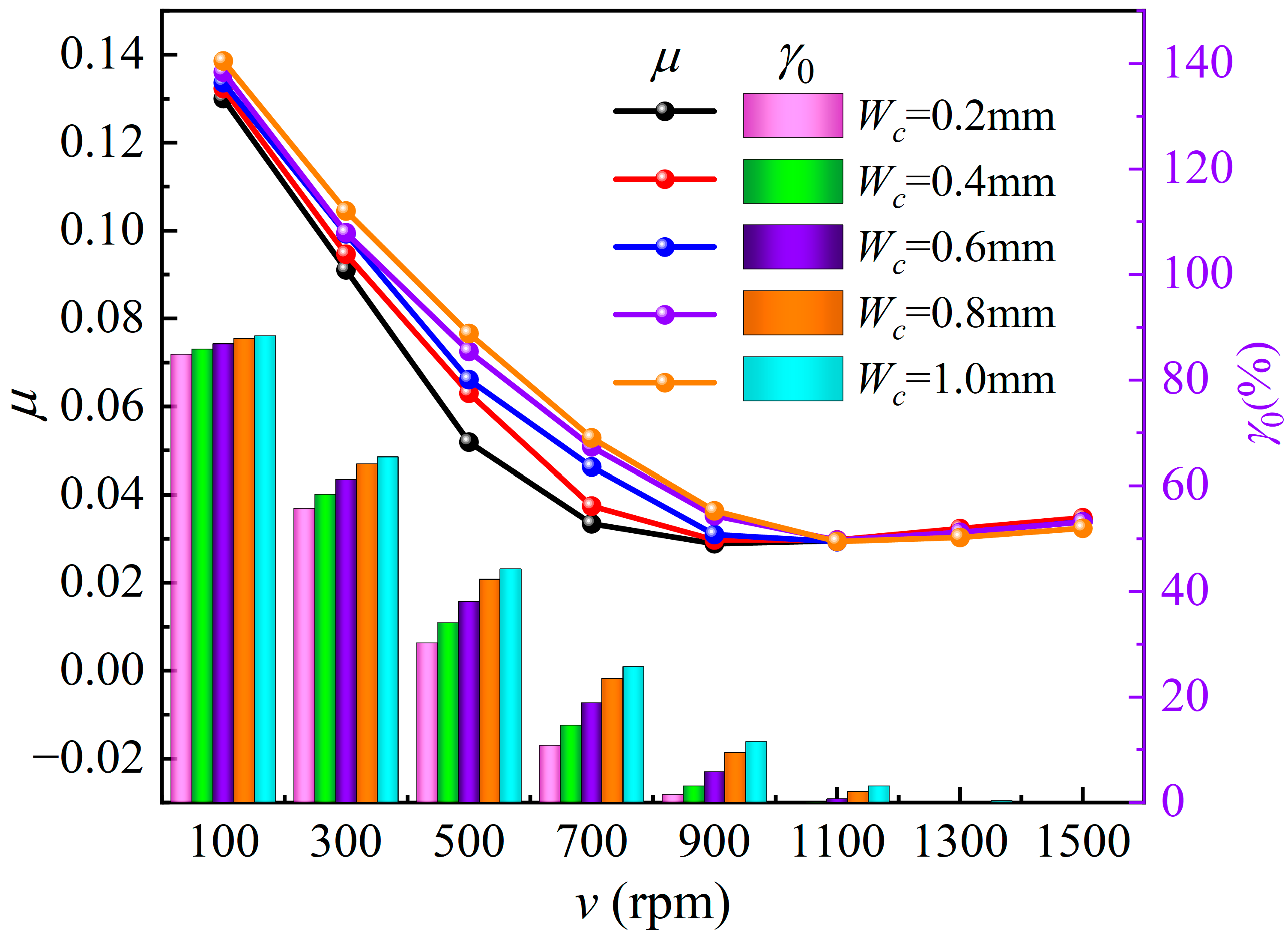
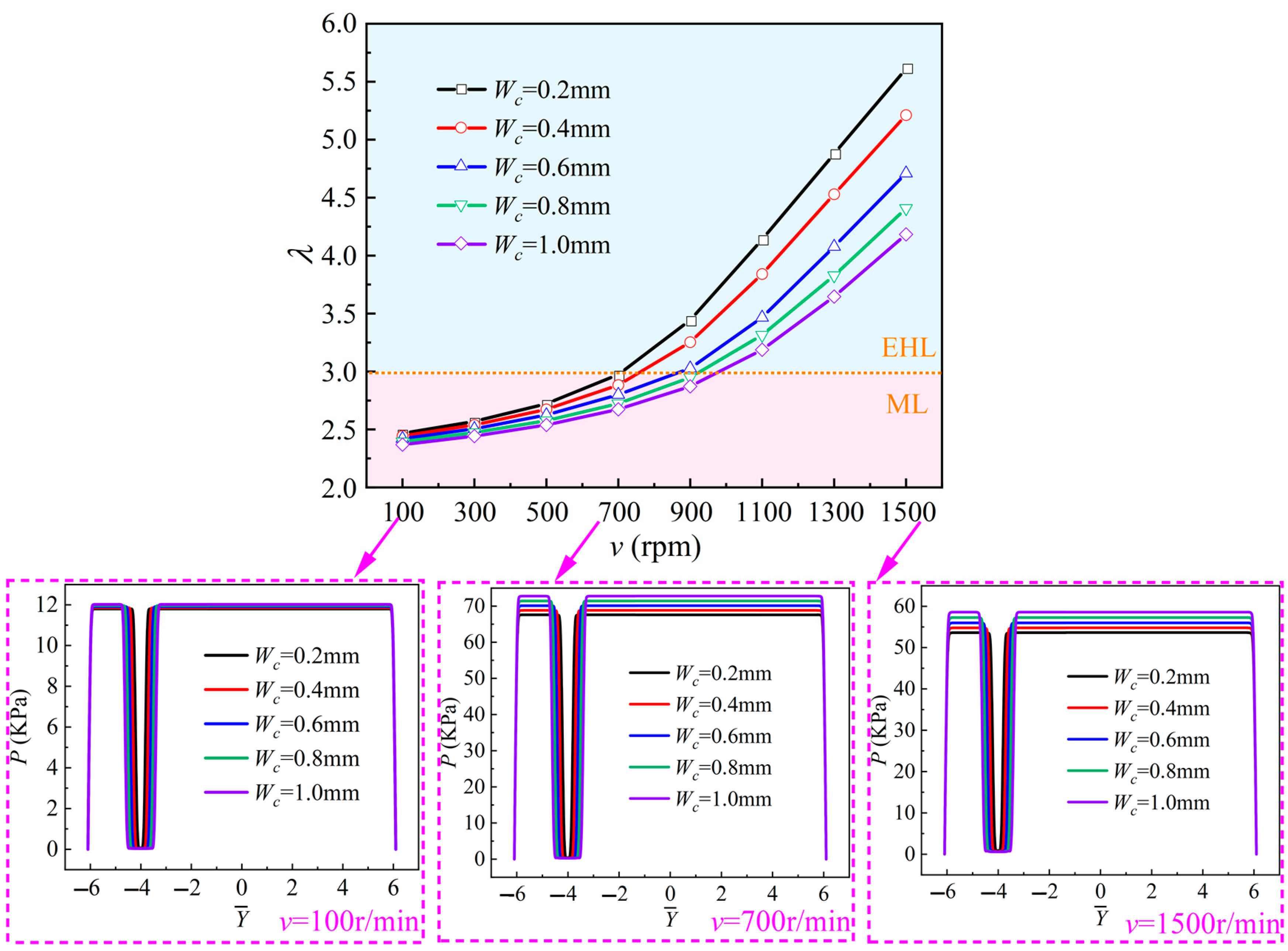
4.3. The Effect of Scratch Width on the Tribological Performance and Wear Performance of Block-on-Ring System

As described in Section 4.2, the scratch width has the greatest effect on the tribological performance (especially on friction coefficient and critical speed) of the block-on-ring system among the three scratch parameters. Therefore, to further study the influence of scratch width on the above two parameters, this part conducts block-on-ring friction experiments under different scratch widths (0.2~1.0 mm). In the experiment, the scratch depth h_c is 0.1 mm, and the scratch location L_c is 1/6L. Figure 15 presents the experimental results of the friction coefficient μ and the simulation results of the proportion γ₀ of contact load capacity. When the rotation speed is 100 r/min, friction coefficients among different scratch widths are slightly different, which is due to the weak hydrodynamic pressure effect at a low shear rate. The scratch width has little influence on the friction coefficient at this low speed, but when the speed range is (300~900 r/min), the friction coefficient varies greatly with different scratch widths. The total load capacity consists of two parts, i.e., contact load capacity and water film load capacity. The variable γ₀ is defined as the proportion of contact load capacity in the total load capacity. From the column chart of the proportion of contact load capacity, it can be found that the proportion γ₀ is greater than 80% when v = 100 r/min, which indicates that the main support body is asperity contact rather than water film. The proportion γ₀ is inversely proportional to the rotation speed. However, it is directly proportional to the scratch width, i.e., widening scratch results in more severe asperity contact and higher friction coefficient of the block-on-ring system. When the rotation speed is raised further to 1300 r/min or 1500 r/min, the proportion of contact load capacity is all 0, illustrating that all five groups of block-on-ring systems completely rely on water film to support the load.

The film thickness ratio λ is provided in Figure 16. It can be seen that the increase in film thickness ratio shows up with an increase in rotation speed, and the differences between neighboring film thickness ratio curves also increase with a rise in rotation speed. However, the film thickness ratio is inversely proportional to the scratch width. When the scratch width is 0.2 mm, the block-on-ring system enters the elastohydrodynamic lubrication state at a rotation speed of 700 r/min. When the scratch width grows to 1.0 mm, it is not until the rotation speed reaches 1000 r/min that the system can enter the EHL state. The pressure distribution at the middle section of the test ring under different rotation speeds is also provided in Figure 16. When the rotation speed is 100 r/min, the block-on-ring system mainly relies on the asperity contact to support the load, and the scratch width has little influence on the film thickness and film pressure. Therefore, the distribution of water film pressure is almost the same under different scratch widths (see pressure distribution image in the lower left corner). However, with the increased speed and enhanced hydrodynamic pressure effect, the frictional pairs enter the elastohydrodynamic lubrication state, and the scratch width gradually has a significant effect on the continuous distribution and thickness of the water film. Therefore, there are significant differences (see pressure distribution image in the lower right corner) in the pressure distribution curves of the water film under different scratch widths when v = 1500 rpm.

Figure 17 shows the variation of the maximum contact pressure $p_{asp}^{max}$ of the test block with rotation speed. The following conclusions can be gained from the figure: (1) When the rotation speed is less than 1100 r/min, the maximum contact pressure falls with the growth of speed. This is because the block-on-ring system operates in the mixed-lubrication state at low speeds, and increasing speed enhances the fluid hydrodynamic pressure effect and water film load capacity, which reduces the contact load capacity and the maximum contact pressure. Under the same rotation speed, the maximum contact pressure rises with increasing scratch width. For example, at a speed of 500 r/min, the maximum contact pressure (169.8 KPa) under W_c = 0.4 mm is 1.33 times larger than that (127.2 KPa) under W_c = 0.2 mm. This is because widening the scratch significantly destroys the continuity of the fluid film, which reduces the proportion of water film load capacity and increases the proportion of contact load capacity. Accordingly, the maximum contact pressure also has a great increase. (2) When the rotation speed exceeds 1100 r/min, the maximum contact pressure of all groups drops to zero. All block-on-ring friction pairs enter the Elastohydrodynamic lubrication state, and the load is entirely supported by the water film rather than asperity contact. This is consistent with the variation trend of the film thickness ratio curve in Figure 16.

To analyze the influence of scratch width on the wear of friction pairs, confocal microscopy is used to research the surface topography [64] of graphite block after 600 s of friction experiment under water-lubrication conditions (see Figure 18). The load applied in the experiment is 30 N, and the rotation speed is 100 r/min. The pink box in the figure represents the scratched area, and the dimensions of the surface wear of the graphite block are given below the topography image. As can be seen from the figure, both the wear width and the wear depth of the graphite block increase with an increase in the scratch width on the test ring. When the scratch width increases from 0.2 mm to 1.0 mm, there is an increase of 15.23% in wear width (from 5290.9 µm to 6096.6 µm) of the graphite block and an increase of 54.28% in wear depth (from 108.7 µm to 167.7 µm). This is consistent with the previous theoretical analysis conclusion that the wider the scratch on the test ring surface, the more severe the surface wear on the graphite block.

5. Conclusions

To study the effect of scratches on the tribological performance of friction pairs, this paper conducts several experiments and constructs a mixed-lubrication model of the block-on-ring system. Based on experimental results and theoretical models, the sensitivity of test blocks made of different materials to scratch parameters is studied. This paper also studies the relationship between the tribological performance of friction pairs and the structure parameters of scratches. The specific conclusions are as follows:

(1)

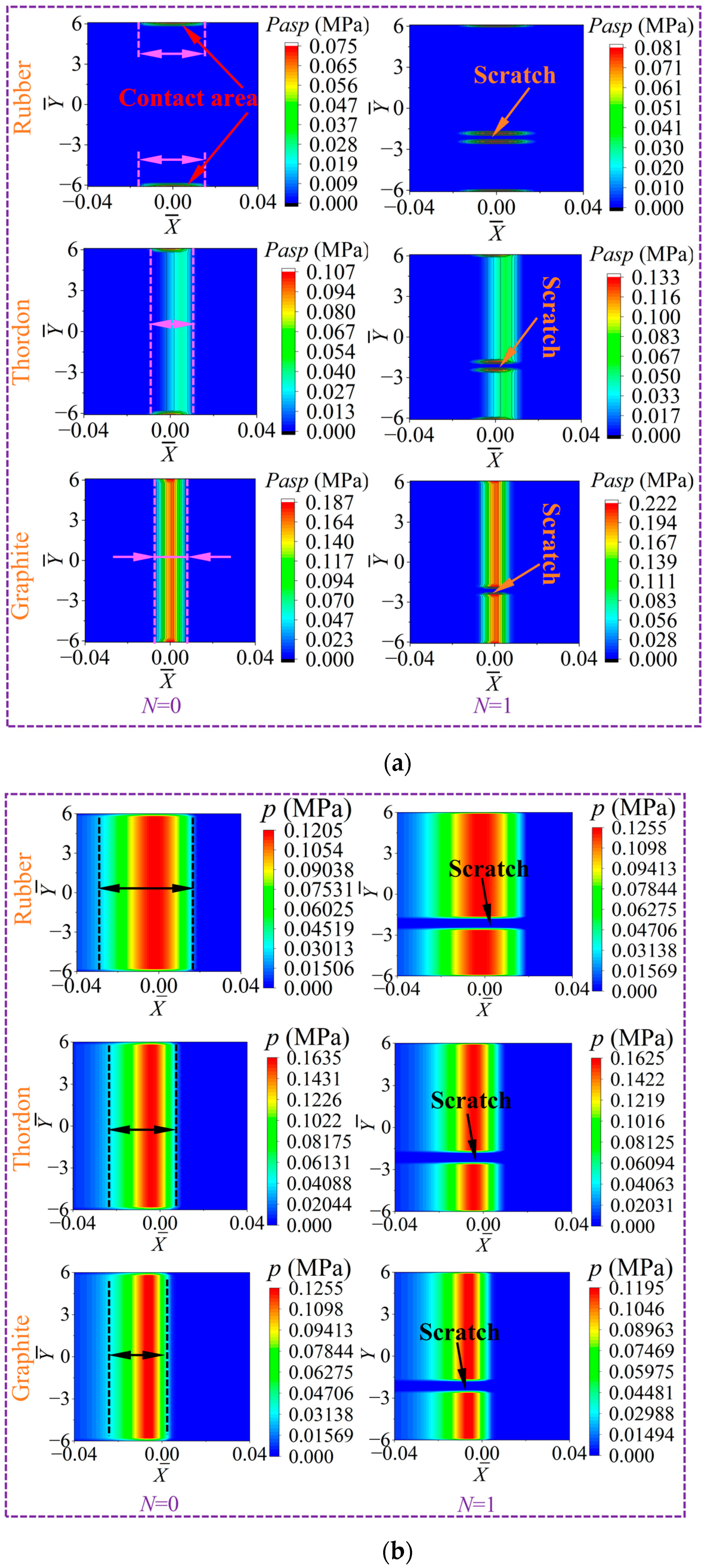
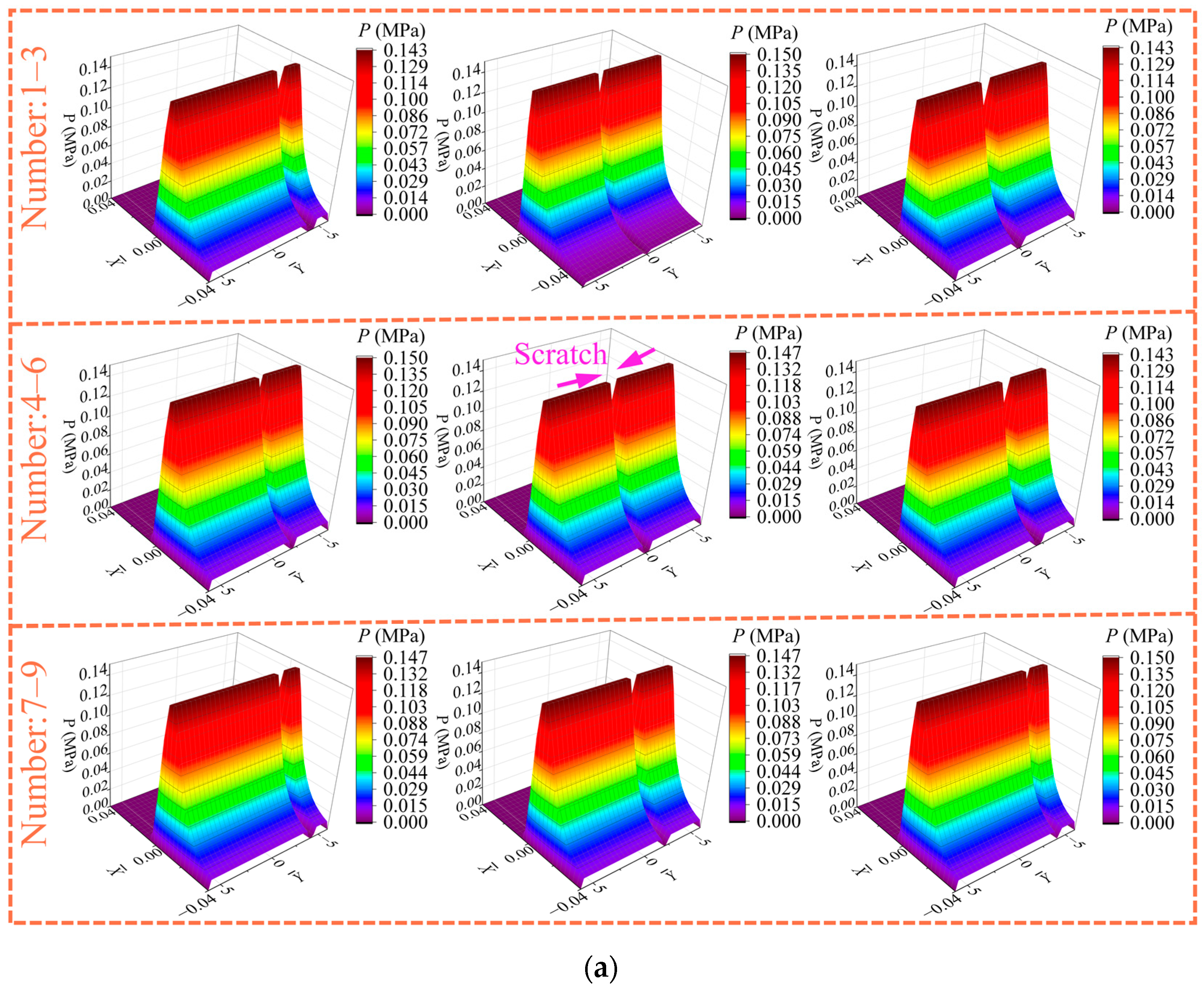
Among the three types of test blocks, the tribological performance of the graphite block is the most sensitive to scratches. Scratches have a great effect on the friction coefficient of the graphite block, and the existence of scratches aggravates the microconvex contact and wear, which can severely reduce the service life of the friction pairs. Under the condition of one scratch (N = 1), the loading area of water film pressure is divided into two separate zones, i.e., a trapezoidal pressure zone and an extremely low-pressure zone. In addition, the variation of maximum water film pressure is determined by the positive effect (hydrodynamic pressure effect of fluid) and negative effect (“piercing effect” of the asperities).

(2)

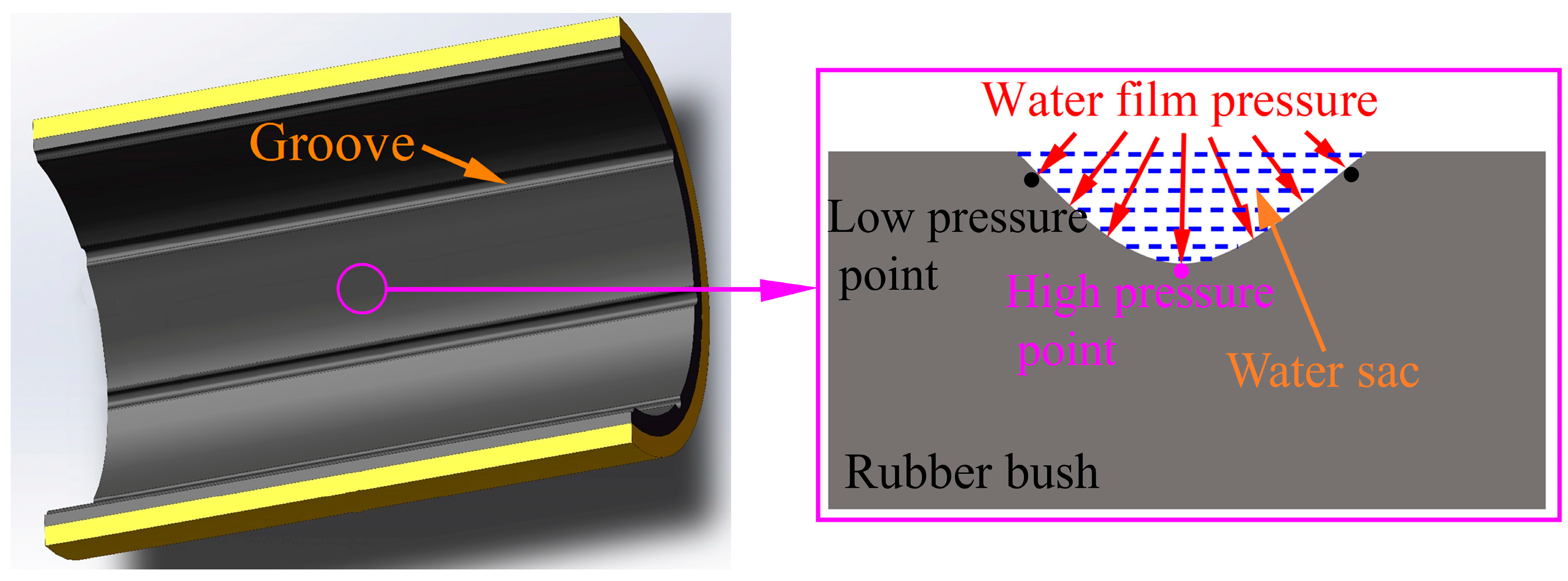
Compared with scratch depth and scratch location, the scratch width has the greatest influence on the tribological performance of the graphite block, especially on the friction coefficient. This is because a widening scratch can reduce the loading area of water film and solid contact. Supporting the load needs a smaller film thickness and a stronger asperity contact, and thus, the friction coefficient will significantly go up. The scratch depth and the scratch location have little influence on tribological performance (minimum film thickness, maximum deformation, maximum water film pressure, maximum contact pressure). The maximum contact pressure is located at both edges of the scratch due to the formation of a water sac structure.

(3)

The scratch has a great influence on the transition of the lubrication state of the block-on-ring system. The existence of scratches increases the critical speed at which the block-on-ring system transits from the mixed-lubrication state to the elastohydrodynamic lubrication (EHL) state. For the stainless-steel ring-graphite block frictional pairs, the system enters the EHL state at the speed of 700 r/min when there are no scratches on the ring surface. However, when there is one scratch on the ring surface, the system does not enter the EHL state until the speed reaches 1100 r/min. The critical speed is directly proportional to the scratch width. A widening scratch will markedly weaken the hydrodynamic pressure effect.