Abstract
In the presented work, a methodical approach was developed for determining rational operation modes of tribosystems, taking into account their design. This approach makes it possible in the designing stage, according to the predicted operating modes, to calculate the limits and margins of stable work in operation. The definition of the robustness of the tribosystem and the criteria for assessing the robustness are formulated based on the theory of stability of technical systems. It is shown that such a methodical approach allows for determining the modes of the rational operation of the designed structures without damaging the friction surfaces. Experimental studies have proven that not all designs of tribosystems lose stability due to the appearance of friction surface burrs. There are designs where the loss of stability occurs upon the appearance of accelerated wear. The developed criteria take into account two options for the loss of stability. An experimental verification of the modes of loss of stability of tribosystems was performed by the appearance of a burr or the beginning of accelerated wear with the calculated values of the robustness criteria. The obtained results allow us to conclude that the modeling error is within 8.3–18.7%, which is a satisfactory result in the study of friction and wear processes. Robustness criteria is based on the coefficient of friction RRf and wear rate RRI, and must be used when designing new constructions of tribosystems. Theoretical calculations of such criteria and the dependence of their change on changing the predicted operating modes will allow for justifying rational operating modes within their stability.
1. Introduction
The stable operation of tribosystems in the entire load–speed range of operation is the most important characteristic that the reliability indicators of machines and mechanisms depend on. The range of the stable operation of tribosystems is predicted at the stage of the construction development of new machines and is based on the experimental data of previous designs or experimental data of laboratory bench tests.
The most promising direction is mathematical modelling of the limits of the stable operation (robustness) of tribosystems, which will allow for significantly reducing material resources during the construction of new equipment. The development of such models is based on the theoretical foundations of the stability of technical systems, developed by O.M. Lyapunov, who created the modern theory of the stability of motion of mechanical systems determined by a finite number of parameters.
The concept of the stability of tribosystems is the most important qualitative assessment of their dynamic properties and depends on constructive, technological, and operational factors. Through the stability of the operation of tribosystem, it is possible to restore the original mode of operation after the removal of an external influence. In addition, an important parameter is the limit of the loss of the stable operation of the tribosystem, i.e., the amount of load and the sliding speed when burr or accelerated wear occurs [1,2]. According to this, three types of tribosystems were formulated in [1].
- Stable tribosystems, which, after being brought out of equilibrium by any external disturbance (change in load or sliding speed, or the short-term cessation of lubricant supply), after the removal of this disturbance, return to the original stable state, i.e., the established operating mode.
- Neutral tribosystems, which, after removing the disturbance, switch to a state of stable operation in a new mode, which is different from the original one.
- Unstable tribosystems, which, as they are brought out of equilibrium by any external disturbance, do not return to the original stable state after the removal of this disturbance, but switch to the mode of accelerated wear or to burr, i.e., cease operation.
It should be noted that majority of studies are devoted to the failure of tribosystems due to the burring (seizing) of friction surfaces. However, there are options for terminating the operation of tribosystems due to the appearance of accelerated wear.
The task of determining the limits of the stable operation (robustness) of tribosystems, considering the design, manufacturing technology, and the load–speed range of operation, is an urgent task. This task is solved in the stage of designing new structures of tribocouplers, which allows for increasing their resource and reliability in operation. This article deals only with sliding friction processes.
An analysis of recent publications on the use of mathematical models for predicting the reliability and service life of tribosystems at the stage of development and design allows us to conclude that entropy analysis is promising in the study of energy dissipation during friction [3,4,5,6]. For example, in [4], a mathematical model for predicting the reliability of rolling bearings is developed on the basis of the hierarchical Bayesian method of maximum entropy. Theoretical developments that show the relationship of wear with the thermodynamic concept of entropy are presented in [5,6,7]. This approach allowed the authors of the work to study the effect of consistent grease on the resources of tribosystems.
On the basis of the provisions of the thermodynamics of open systems in [8,9,10], equations for the conservation of mass and energy are proposed, which allow for simulating various modes of energy dissipation in a tribosystem, considering the friction surface. These equations can be considered as a tool for modelling various modes of energy dissipation in the dynamic contact of friction surfaces with the development of practical recommendations for the design of new structures.
For simulating the work of tribosystems and predicting the resource, the authors of [11,12,13] used the achievements of artificial intelligence, particularly artificial neural networks. The authors showed that the use of this approach allowed for modelling and forecasting the wear and reliability of tribosystems during exploitation.
The authors of [10,11,12,13,14] paid attention to the importance of considering the friction surface in mathematical models. For example, the importance of considering the roughness of the friction surface in the models is noted in [14], the values of the actual contact area are noted in [15,16], the change in the roughness of friction surfaces during running-in or running-out in is noted [17], and the distribution of actual pressures and stresses over the contact surface is noted in [18,19]. According to the results of the authors, consideration of the listed factors will increase the accuracy of modelling and predicting the resources during the operation of tribosystems.
The authors of [20,21] note that mathematical models of the functioning of tribosystems are tools for designing new friction units. The work presents a methodical approach and models that consider the design of the friction unit, which increases the accuracy of forecasting.
The authors of [22,23] aimed their work at considering the stability and efficiency of tribosystems. The models created by the authors were built on the basis of stochastic models of surface roughness. It was shown that the tribological behavior in contact depended on the properties of the friction surfaces and the spectrum of loads. Moreover, edge effects at the boundaries of the contact area affected the pressure distribution and membrane thickness, which should be taken into account while modelling.
The authors of [24,25,26] noted that when developing mathematical models for the functioning of tribosystems, it is necessary to consider wear during the running-in period. Because of the intense deformation of microprotrusions, the running-in mode allows for the formation of an equilibrium roughness of friction surfaces and a change in the structure of thin surface layers, which are analyzed in [24]. Optimal running-in conditions will help increase the service life and reliability of tribosystems.
The analyses of publications determining the boundaries of the stable operation of tribosystems shows that these are the operating modes when the scuffing or seizing of friction surfaces occurs with the transfer of material from one triboelement to another.
The difficulty in predicting the failure of tribosystems is a fundamental problem of tribology, which is noted in [27]. The article presents an analysis of various factors (residual stresses, surface free energy, and surface topography) that lead to the initial phase of the process of burr. The studies presented in [28] are aimed at a better understanding of the occurrence of burr. The authors affirm that the parametric assessment of the state of the friction surface is of crucial importance in the technology of preventing burrs.
The durability limits of the tribosystem and the transition from stable to unstable operating conditions, namely seizing, were studied in [29]. The purpose of the research was to determine the boundaries of the stable operation of tribosystems and to use the obtained results while designing tribosystems.
The authors of [30] studied the influence of random overloads on the occurrence of burrs in tribosystems. The results of the research were the determination of the boundary of the exit of the tribosystem to the burr. The mechanism of occurrence of burrs, based on adiabatic shear instability, was experimentally evaluated in [31]. The authors of the work related the mechanism of burr formation to the density of dislocations in the surface layer.
The equations for modeling the burr of friction surfaces, which were obtained on the basis of adiabatic shear instability, are presented in [32]. With the help of equations, it is proposed to model the mechanism of loss of strength from the surface layer of the material during adiabatic shear. The main factor in the loss of strength is the work of friction. On the basis of this mechanism, a quantitative criterion for predicting reliability has been developed, where burr formation is the result of competition between thermal strength loss and strain hardening during adiabatic shear.
The mechanism of burr formation in friction nodes was the subject of tribological studies in [33]. According to the authors, the approach to this problem requires taking into account a large number of working parameters for predicting burr. This work proposes using the parameter (pressure × velocity × time) instead of the frequently used parameter (pressure × velocity). According to the authors, such an approach will allow for taking into account the duration or frequency of loads during the operation of friction nodes. These parameters can significantly affect the stability of the properties of the lubricating membrane, especially in the context of the formation of an elastohydrodynamic membrane or boundary layer.
The results of the gear tests on a test bench with changes in the torque, sliding speed, oil bath temperature, gear geometry, and viscosity of the base lubricant are presented in [34]. The developed model takes into account normal pressure and tangential stresses at several points along the line of the clutch of the gear. Gear seizure results are analyzed using two different approaches: one takes into account the general parameters of the gear, including the clutch line, and the other, based on the local parameters of the roughness of the friction surfaces, is determined using the mixed lubrication model. An analysis of the roughness level was used to explain the causes of burr formation.
A method for predicting the appearance of burr on friction surfaces, using the analysis of the dynamics of the transient process, is proposed in [35]. Quasi-static and nonlinear dynamic models take into account the increase in temperature during the transition process when the load changes during operation. The model allows for determining the thickness of the lubricating membrane on the friction surface and for determining the limit of the burr when the load changes.
The processes of the stability of tribosystems when oscillations occur in frictional contact were studied in [36,37]. For example, strict criteria for the stable operation of tribosystems in various modes of frictional sliding and the occurrence of vibrations were presented in [36]. The stability of the tribosystem, with the help of a complex analysis of the oscillating elements of the tribosystem and their influence on the process was investigated in [37].
Studies on the burrs of the gear were presented in [38,39]. The flash point on the actual contact patches was explored in [38]. The optimization of the design of the gearbox according to the criterion of power loss due to friction in the gears was described in [39].
The analysis of works devoted to the determination of the limits of the stable operation of tribosystems allowed us to conclude that when developing and justifying such criteria, it is necessary to take into account the constructive, technological, and operational factors of tribosystems. In the works listed above, the geometric dimensions of tribocouplers, physical and mechanical properties of combined materials of triboelements, the tribological properties of the lubricating medium, and theroughness of friction surfaces are not sufficiently taken into account. Accounting for the mentioned factors will allow us to extend the obtained criteria to a wide class of tribosystems and make such an analysis systematic.
2. Materials and Methods
The purpose of this study is to develop a methodical approach for determining the robustness of tribosystems in conditions of extreme lubrication, modelling changes in the robustness of tribosystems at the stage of constructive development, and experimental verification of the modelling error.
To substantiate the methodical approach in the research, we will use the equation of the dynamics of tribosystem functioning, which is given in [1].
The friction unit is modeled as a series and parallel connection of dynamic links from which the equivalent transfer function of the friction unit is obtained. On the basis of the equivalent transfer function, a differential equation for the process of operation of the friction unit is written.
The differential equation of the third order is written in operator form, as follows:
where p is the differentiation operator, which is equivalent to writing d/dt;
T1, T2, T3 are the time constants in the dimension of seconds (s);
K1, K2, K3 are the gain coefficients, which are dimensionless quantities.
In [1], it was proven that time constant T1 characterizes the change in the structure of the materials of the surface layers during run-in. It is defined by the following expression:
where trun ia the tribosystem run-in time in the dimension of seconds.
Time constant T2 has a physical sense of the time, during which the temperature is equalized by the volumes of triboelement materials when the load and sliding speed change. It is defined by the following expression:
where Vrun is the stated volume of materials of the moving and stationary triboelements of the tribosystem, in the dimension of m3, and is determined by Expressions (2) and (3), which are given in [40], taking into account the total volume of the material of the friction node;
arun is the given coefficient of the thermal conductivity of the materials of the moving ar and stationary as triboelements, in the dimension of m2/s, and is calculated according to Expression (6), which is given in [40];
dacs is the diameter of the actual contact spot, in the dimension of m, and it is calculated according to the expression given in [41];
nacs is the number of contact spots on the friction surface, and is calculated according to the expression given in [41].
Time constant T3 characterizes the time until the friction and wear parameters stabilize in the new operating mode of the tribosystem. Time constant T3 has different expressions to the model wear rates T3(I) and friction coefficient T3(f):
where Vdef is the given volume of deformable surface layers, measured in m3, and is determined by the expression given in [40], using Formulas (15) and (16);
is the indicated value of the rate of deformation of the surface layers of the materials of the movable and immovable triboelements, in the dimension of c−1, which is calculated according to the formulas given in [30], using Formulas (8)–(10).
The coefficient K1 includes the degree of external influence on the tribosystem, considering the design features, which was proven in [40]:
where Q0 and Qmax are the initial value of the Q-factor of the tribosystem and the value of the Q-factor that was formed during the run-in. They are determined by the formulas given in [41].
Coefficient K2 characterizes the sensitivity of the tribosystem to changes in the external conditions:
where WTR is the speed of dissipation in the tribosystem, measured in J/s, which is calculated according to the equations given in [1], using Formula (8);
Kf is the shape coefficient of the tribosystem, in the dimension of m−1, and includes the friction areas and the volumes located under the friction areas of the moving and stationary triboelements. It is calculated according to the equation given in [41].
Coefficient K3 characterizes the ability of the tribosystem to change the structure of the surface layers of the triboelement materials during transient processes:
where RSTS(max) is the maximum value of the rheological properties of the combined materials in the tribosystem after running-in, measured in dimension m−1, and is calculated according to the equations given in [42].
Formulas (7) and (8) are obtained for the specific design of the friction unit. The design is taken into account by using the shape factor, Kf. The shape factor takes into account the magnitude of the friction areas and the volumes of material that are placed under the working areas of friction. Values of 5500 and 170 were introduced to improve the accuracy of the simulation. When changing the structure of the friction unit, it is necessary to adjust the values of these coefficients.
To analyze the stability of the technical systems, several special methods have been developed, which are called stability criteria in the theory of automatic regulation. Stability criteria are divided into two varieties—algebraic and frequency.
Algebraic criteria are analytical and frequency criteria are grapho analytical [43,44,45]. At the same time, all criteria are based on the theory of the stability of technical systems developed by Lyapunov [46,47,48,49].
The algebraic criterion, Hurwitz’s criterion [50,51,52], is the most common criterion and is used to determine the stability of technical systems when the characteristic equation is known. As the characteristic equation acts the left part of the differential equation in operator form (1).
Let us write down the characteristic equation, making a substitution and equating it to zero:
where
According to Hurwitz’s algebraic stability criterion, a technical system is stable when all coefficients Ai of the characteristic Equation (9) are more than zero. This is a necessary condition for stability:
A sufficient condition for stability is that all determinants from the coefficients Ai of the characteristics in Equation (9) are more than zero.
If at least one of the determinants is equal to zero, then the system is on the verge of loss of stability. If at least one of the determinants is negative, then the system is unstable. In the tribosystem, burr or accelerated wear occur.
According to the rules, let us write down all of the determinants for the characteristic Equation (9):
Let us write down the value of the determinant∆3 in the following form:
Expression (18) is a necessary and sufficient condition for the stable functioning of the tribosystem according to the Hurwitz criterion. Using this expression, you can determine the range of stable operation for the tribosystem, namely the range of robustness. The more the value of Δ3, measured in dimension s3, the more the margin of robustness for the tribosystem. When the value Δ3 = 0, the tribosystem works on the verge of loss of stability, with negative values for Δ3, and there is burr or accelerated wear and the tribosystem has “lost stability”.
To compare tribosystems and build a rating on the margin of stable operation, it is necessary to obtain a dimensionless parameter—a criterion that depends on constructive, technological, and operational factors. The most acceptable, in our opinion, is the analysis of the expression of the stability of technical systems based on the Hurwitz algebraic criterion, using formula (18).
Based on the formulated approach, let us write down, in a general form, the evaluation criterion for the margin of stable operation of the tribosystem—the robustness criterion:
where RR is criterion of tribosystem robustness, with a dimensionless value.
The physical meaning for determining the robustness of the technical systems is given in [53].
An analysis of Equation (1) shows that processes of friction and wear in the tribosystem, especially the running-in processes, depend on the first derivative of the input effect on the tribosystem, i.e., on the load speed. The load speed of the tribosystem can be considered by the coefficient of the change in the load speed, which is proportional to the right-hand side of the differential Equation (1):
where the amount of load (external influence during experimental studies) on the tribosystem is determined by the following expression:
where N is the load on the tribosystem, N;
vsl is the sliding speed, m/s;
tl is the load change time, s.
With the help of laboratory experimental studies carried out on various designs of tribosystems with different amounts of load on the tribosystem and different rates of load change, an expression for calculating the coefficient of change of the load speed was obtained.
Determining the robustness of the tribosystem using the friction coefficient parameter is completed as follows:
Evaluating the operation of the tribosystem by the wear rate parameter is completed as follows:
Including the expressions of the coefficient of change in the load speed (22) and (23), which were obtained according to the results of experimental studies, equations for determining the robustness of tribosystems (19), including expressions (10)–(13), will be presented in the following form.
To determine the robustness of the tribosystem by the friction coefficient:
To determine the robustness of the tribosystem by the rate of wear:
It is necessary to calculate criteria for the robustness of the tribosystem RRf and RRI for each load of the operating range of tribosystems, including the analysis of the obtained values. If the value of the criterion is more than one, then the tribosystem works in a stable range. The more the value of the robustness criterion, the more the margin of sustainable work.
If the value of the criterion is equal to one, the tribosystem works on the verge of loss of stability. If the value of the criterion is less than one, the tribosystem has lost stability, and burr or accelerated wear has occurred.
To answer the question of which the parameter loss of stability occurred in, it is necessary to calculate two criteria: according to the coefficient of friction, formula (24) and according to the rate of wear, formula (25). The value of the criterion, which first becomes less than one, answers the question on which parameter the loss of stability occurred.
Figure 1 presents the theoretical dependence of the change in the robustness criterion of various structures of tribosystems according to the friction coefficient on the value of the input influence, using formula (24). Input influence on the tribosystem, W, W, is represented as the product of load, N, and sliding speed, m/s, using formula (21). Different designs of tribosystems are included by the value of the Q-factor, Qo, J/m3, [41,42].
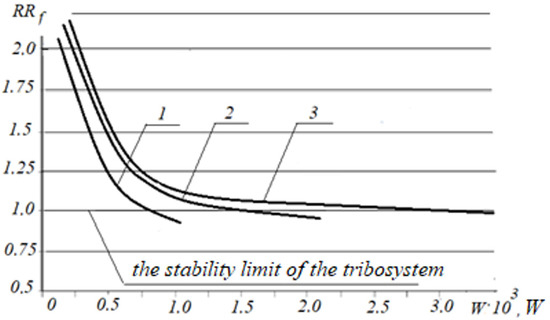
Figure 1.
Dependencies of changes in the robustness criterion of various designs of tribosystems according to the coefficient of friction on the value of the input impact: 1—steel 5140 + steel 5140, Kf = 6.25 m−1, hydraulic oil HH, ISO-L-HL, Q0 = 1.12·1010 J/m3; 2—steel 5140 + bronze C61900, Kf = 12.5 m−1, motor oil SAE 40, APICC, Q0 = 5.5·1010 J/m3; 3—steel 5140 + brass CW723R, Kf = 14.5 m−1; transmission oil SAE120, APIGL-4, Q0 = 7.69·1010 J/m3.
Experimental studies were carried out on a universal friction machine according to the «ring-ring» kinematic scheme. The design of the friction machine is presented in [41].
The friction unit is represented by movable sample 1 and fixed sample 2. The friction between the samples occurs over the area of the ends. During the tests, fixed sample 2 is pressed against movable sample 1 by load N. Friction occurs over the area of the ends. The movable sample performs a rotational movement around its axis. An acoustic emission sensor GT300 is mounted on fixed sample 2. The acoustic emission signal from the GT300 transducer with a frequency of 100–800 kHz is transmitted to a preamplifier and then to a USB oscilloscope, which acts as an A/D converter. Then, the signal in a digital code is entered into the computer to calculate the diagnostic parameters.
The AE signal from the friction zone is recorded by a broadband sensor GT300 (100–800 kHz), Figure 2, which is installed on a fixed triboelement, transmitted to an amplifier, then, in analog form, to a PV6501 USB oscilloscope, which performs the functions of an analog-to-digital converter and spectrum frequency analyzer at the same time. After processing in a USB oscilloscope, the digital signal enters the computer, where it is processed by special software.
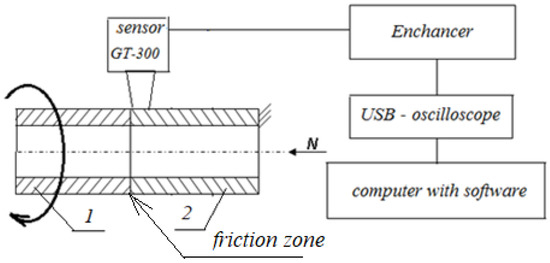
Figure 2.
Block diagram of experimental equipment for recording and processing AE signals: 1—movable triboelement; 2—fixed triboelement; N—load.
Samples for testing are presented in Figure 3, where movable sample 1 is made of steel5140, and fixed sample 2 is made of various materials: steel 5140, bronze C61900, and brass CW723R. Thus, during the tests, it was possible to obtain various constructions of tribosystems, for example, a movable sample of steel 5140 + fixed sample of steel 5140; movable sample steel 5140 + fixed sample bronze C61900; movable sample steel 5140 + fixed sample brass CW723R. At the same time, the friction area of fixed samples 2 was changed, which made it possible to obtain different coefficients for the shape of the tested tribosystems.

Figure 3.
Samples for testing: 1—movable sample steel 5140; 2—fixed samples: steel 5140, bronze C61900, brass CW723R with different friction areas on the end surfaces; 3—friction surfaces of the moving sample; 4—friction surfaces of a fixed sample.
During the tests, the load on the tribosystem increased at different load speeds: 1 s, 10 s, and 20 s.
The loss of stability of tribosystems, according to the coefficient of friction was determined by using the value of the moment of friction, which was registered by the recorder of machine 2070 SMT-1. According to the parameter of the start of accelerated wear, the loss of stability was determined by using of the acoustic emission method. The measuring complex and the method for recording the acoustic emission signals are given in [54]. To record acoustic eradiation from the friction zone, the acoustic emission sensor is installed on a stationary triboelement.
According to the results of three repetitions, the average burr load or the onset of accelerated wear, the root mean square deviation of values of registered values during experimental studies, formula (26); coefficient of variation of measurements of external influence, when the occasion of loss of stability of the tribosystem occurs, formula (27); modelling error according to the formula (28), were determined.
The root-mean-square deviation of the values of the external influence during experimental research is represented by the formula:
where Wb(i), Wb(aw) are the values of external influence on the tribosystem, formula (21), at which there is a loss of stability (burr or accelerated wear), which is measured during the experiment and is averaged over the number of repetitions n.
The coefficient of variation of measurements of external influence, when the occasion of loss of stability of the tribosystem occurs, is determined by the expression:
The relative error of modelling the robustness of tribosystems is determined by the expression:
where Wb(exp), Wb(s) is the value of the magnitude of the external influence on the tribosystem at which a loss of stability (burr or accelerated wear) occurs, which is measured during the experiment and according to the results of the simulation.
3. The Results of the Experimental Research
The results of modelling the robustness of tribosystems and the results of the experimental testing are presented in Table 1. The purpose of the experimental research is to compare the calculated values of the magnitude of the external influence on the tribosystem Wb(s), at which a loss of stability occurs (burr or accelerated wear), according to formulas (24) and (25), when RRf and RRI are equal to the unit, with the results of the experiment Wb(exp).

Table 1.
The results of testing the error of modelling the range of robustness of various designs of tribosystems.
The nature of the change in the value of the external influence on the tribosystem in which the loss of stability Wb(exp) for various designs of tribosystems occurs, which are evaluated by the shape factor Kf, m−1, is presented in the first block of Table 1. Experimental studies of the limits of the stable operation of tribosystems are performed for the tribosystem steel 5140 + bronze C61900, and lubricating medium Ey= 3.6·1014 J/m3, (motor oil SAE 40, API CC). The parameter Ey takes into account the tribological properties of the lubricating medium. The technique for determining Ey is described in [41]. The sliding speed is not changed and is equal υsl = 0.5 m/s. During the experiment, the values of the shape factor of the tribosystem vary, Kf = 6.25–22.6 m−1. This value is obtained by changing the friction area of the stationary triboelement. The load is increased from the initial value of 400 N, to the value when the tribosystem loses stability, i.e., burr or accelerated wear occur. The initial roughness of the friction surfaces for all experimental conditions was Ra = 0.2 μm.
With Kf = 6.25 m−1 the loss of stability for the tribosystem occurs after the appearance of a burr. When increasing the form factor to Kf = 22.6 m−1, the loss of stability of the tribosystem occurs after the appearance of accelerated wear.
The calculation of the error for determining the limit of the stable operation of tribosystems according to formula (28) when the shape factor of tribosystems changes allows us to confirm that the value of the error is equal to eW = 8.3–15.0%, at the coefficient of variation vW = 16.6–20.0%. As it follows from the obtained results, an increase in the shape factor leads to an increase in the modelling error.
The results of experimental studies on the change in the value of the external influence on the tribosystem in which the loss of stability occurs when the tribological properties of the lubricating medium are changed Ey is presented in the second block of Table 1.
The results are presented for the tribosystem: steel 5140 + bronze C61900; form factor Kf = 12.5 m−1. As a factor, the following changes have been selected: hydraulic oil HH, ISO-L-HL, (Ey = 2.43·1014 J/m3); motor oil SAE 40, API CC, (Ey = 3.6·1014 J/m3); transmission oil SAE 120, API GL-4, (Ey = 4.18·1014 J/m3). The sliding speed did not change and was equal υsl = 0.5 m/s.
The calculation of the error for determining the limit of the stable operation of tribosystems, when the tribological properties of the lubricating medium change, allows us to assert that the value of the modelling error is within eW = 10.6–15.0%, at the coefficient of variation vW = 14.8–20.0%. A greater error is inherent in the use of lubricants with low values of tribological properties.
The results of experimental studies on the change in the value of the external influence on the tribosystem in which the loss of stability occurs when the rheological properties of the structure of the combined materials in the tribosystem are changed RSTS(max) are presented in the third block of the Table 1.
The results are presented for the tribosystem: form factor Kf = 12.5 m−1. Lubricating medium—motor oil SAE 40, API CC, (Ey = 3.6·1014 J/m3). As a factor that changes, have been selected: steel 5140 + steel 5140, (RSTS(max) = 326.7 m−1); steel 5140 + bronze C61900, (RSTS(max) = 436.0 m−1); steel 5140 + brass CW723R, (RSTS(max) = 460.9 m−1).
Comparing the experimental results with the results of modelling when changing the rheological properties of the combined materials in the tribosystem allows us to affirm that the error value is within eW = 8.3–13.0%, at a coefficient of variation vW = 16.6–21.7%. A greater error is inherent in the use of composite materials with low values of rheological properties.
The results of experimental studies regarding the change in the value of the external influence on the tribosystem in which a loss of stability occurs when all of the above factors are changed, which can be considered by the Q-factor of the tribosystem Q0, are presented in the fourth block of Table 1. The determination of the Q-factor of the tribosystem is given in [41].
The results are presented for three tribosystems.
- Tribosystem №1: «steel 5140 + steel 5140», (RSTS(max) = 326.7 m−1); Kf = 6.25 m−1; lubricating medium Ey = 2.43·1014 J/m3, (HH, ISO-L-HL). The value of the Q–factor of the tribosystem Q0 = 1.12·1010 J/m3.
- Tribosystem №2: «steel 5140 + bronze C61900», (RSTS(max) = 436.0 m−1); Kf = 12.5 m−1; lubricating medium Ey = 3.6·1014 J/m3, (SAE 40, API CC). The value of the Q–factor of the tribosystem Q0 = 5.5·1010 J/m3.
- Tribosystem №3: «steel 5140 + brass CW723R», (RSTS(max) = 460.9 m−1); Kf = 14.5 m−1; lubricating medium Ey = 4.18·1014 J/m3, (SAE 120, API GL-4). The value of the Q–factor of the tribosystem Q0 = 7.69·1010 J/m3.
An increase in the Q-factor value of the tribosystem, which is subject to change at the same time, impacts: the shape factor, tribological properties of the lubricating medium, rheological properties of the combined materials in the tribosystem, the thermal conductivity of the materials of the moving and stationary triboelements, the load, and the sliding speed. The efficiency of tribosystems varies from values Q0 = 1.12·1010 J/m3, (tribosystem №1), to values Q0 = 7.69·1010 J/m3, (tribosystem №3). An increase in the Q-factor contributes to an increase in the robustness of tribosystems.
Comparing the experimental results with the simulation results when all of the above factors are changed, makes it possible to assert that the value of the simulation error is within eW = 14.8–18.7%, at the coefficient of variation vW = 12.9–18.7%. A bigger error is inherent in the application of tribosystems with low Q-values.
The results of the experimental studies allow us to state that not all tribosystems lose stability due to the appearance of burrs on the friction surfaces (according to the friction coefficient parameter), the mark in the table (f) *. There are a few possible options, when the loss of stability occurs due to accelerated wear of materials, a mark in the table (I) *. Or the appearance of a burr and accelerated wear have equal value, a mark in the table (I, f) *.
The experimental data, shown in Table 1, were obtained with a load time for the tribosystem equal to 20 s. At this value for the load time, the coefficient of change for the load speed corresponds to the minimum values: kd(f) = 3.42; kd(I) = 4.37, formulas (22) and (23). When the load time is reduced, to 1 s, the coefficients increase significantly, for example: kd(f) = 6.4; kd(I) = 7.38. The introduction of the coefficient for the change in the load speed (22) and (23) into the calculation expressions for determining the robustness of tribosystems (24) and (25) allows for reducing the modelling error.
4. Discussion
According to the obtained research results, it is possible to formulate a definition of the term that characterizes the limits for the stable operation of the tribosystem—the robustness of the tribosystem. This is a dimensionless value that corresponds to the modes of operation of the tribosystem without damaging the friction surfaces.
Calculation of tribosystem robustness criteria RRf, formula (24), and RRI, formula (25), makes it possible to determine the rational modes of operation of tribosystems at the stage of design and engineering development. The operation of tribosystems in a certain range will increase their resource and reliability.
The robustness criteria are obtained on the basis of the theory of stability of technical systems, the foundations of which were developed by Lyapunov and can be applied to a diverse class of tribosystem designs. Experimental studies have proven that not all designs of tribosystems lose their stability due to the appearance of burrs on the friction surfaces. There are structures where the loss of stability occurs after the appearance of accelerated wear. Developed criteria RRf and RRI consider two options for the loss of stability.
The obtained results for modelling the stable operation of tribosystems and the values of the reserve of stable operation should be used in the design of new structures. By solving constructive, technological, and operational tasks, it is possible to obtain a rational design of the tribosystem, which will satisfy the design tasks and will be operated in a range of speeds and loads with a margin of robustness.
5. Conclusions
A methodical approach has been developed to determine the rational modes of operation of tribosystems, considering their design. This approach makes it possible to calculate the limits and margin of stable operation in exploitation at the design stage, according to the predicted operating modes.
The definition of the robustness of the tribosystem and the criteria for assessing the robustness are formulated on the basis of the theory of stability of technical systems. It is shown that such a methodical approach allows for determining the modes of rational operation of the designed structures without damaging the friction surfaces. Experimental studies have proven that not all designs of tribosystems lose their stability due to the appearance of burrs on the friction surfaces. There are structures where loss of stability occurs after the appearance of accelerated wear. The developed criteria consider two variants of stability loss.
An experimental verification of the modes of loss of stability of tribosystems by the appearance of a burr or the beginning of accelerated wear with the calculated values of the robustness criteria was performed. The obtained results allow us to conclude that the modelling error was within the limits of 8.3–18.7%, which is a satisfactory result in the study of friction and wear processes.
Robustness criteria based on the coefficient of friction RRf and wear rate RRI, must be used when projecting new designs of tribosystems. Theoretical calculations of such criteria and the dependence of their change on changing the predicted operating modes will allow to justify rational operating modes within the limits of their stability.
Author Contributions
Conceptualization, T.M.A.A.-Q., F.A., I.F.S.A. and V.V.; methodology, T.A., O.M., A.V., A.K. (Andrey Kravtsov), F.A. and I.F.S.A.; software, V.V., O.M., A.K. (Andrii Kondratiev), and A.V.; validation, A.K. (Andrey Kravtsov), O.M., F.A., P.K. and V.P.; formal analysis, T.M.A.A.-Q., I.F.S.A. and V.V.; investigation, F.A., O.M. and A.K. (Andrey Kravtsov); resources, T.A, O.M., A.V. and A.K. (Andrey Kravtsov); data curation, I.F.S.A., O.M., A.K. (Andrii Kondratiev), and A.V.; writing—original draft preparation, T.M.A.A.-Q., F.A., I.F.S.A. and V.V.; writing—review and editing, T.M.A.A.-Q., F.A., I.F.S.A., A.V., P.K. and V.P.; visualization, F.A., I.F.S.A., O.M. and A.K. (Andrey Kravtsov); supervision, V.V., O.M. and A.V.; funding acquisition, F.A., O.M. and A.K. (Andrey Kravtsov). All authors have read and agreed to the published version of the manuscript.
Funding
The authors gratefully acknowledge the funding from the specific research on BUT FSI-S-20-6267.
Data Availability Statement
Not applicable.
Acknowledgments
The authors thank Brno University of Technology for support.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| T1, T2, T3 | time constants, dimension s. |
| K1, K2, K3 | amplification factors, dimensionless values. |
| trun | tribosystem run-in time, dimension s. |
| Vrun | the given volume of materials of the moving and stationary triboelements of the tribosystem, dimension m3 |
| arun | given coefficient of thermal conductivity of materials of movable ap and fixed an triboelements, dimension m2/s. |
| dacs | diameter of the actual spot of contact, dimension m. |
| nacs | the number of contact spots on the friction surface |
| Vdef | given volume of deformable surface layers, dimension m3. |
| the magnitude of the rate of deformation of the surface layers of the materials of the movable and fixed triboelements, dimension s−1. | |
| Q0 and Qmax | the initial Q-factor value of the tribosystem and the Q-factor value after run-in, dimension J/m3. |
| WTR | speed of dissipation in the tribosystem, dimension J/s. |
| Kf | tribosystem form factor, dimension m−1. |
| RSTC(max) | the maximum value of the rheological properties of the combined materials in the tribosystem after the completion of running-in, dimension m−1. |
| N | load on the tribosystem, dimension N. |
| vsl | sliding speed, dimension m/s. |
| tl | load change time, dimension s. |
| kd(f) | coefficient of change of load speed according to the friction coefficient parameter, dimensionless value. |
| kd(I) | coefficient of change of the load speed according to the parameter of the wear rate, dimensionless value. |
| RRf | robustness of the tribosystem according to the friction coefficient, dimensionless value. |
| RRI | robustness of the tribosystem according to the rate of wear, dimensionless value. |
| Wb(i), Wb(aw) | the value of the magnitude of the external influence on the tribosystem at which occurs the loss of stability (burr or accelerated wear), according to the results of the experiment and according to the results of simulation, dimension J/s. |
| Ey | tribological properties of the lubricating medium, dimension J/m3. |
| SWb | root mean square deviation of values of external influence during experimental studies, dimension J/s. |
| vWb | coefficient of variation of measurements of external influence, at which the event of loss of stability of the tribosystem occurs, %. |
| eWb | relative error of modeling the robustness of tribosystems, %. |
| Ra | initial roughness of friction surfaces, dimension µm. |
References
- Voitov, A. Structural identification of the mathematical model of the functioning of tribosystems under conditions of boundary lubrication. Probl. Tribol. 2021, 26, 26–33. Available online: http://tribology.khnu.km.ua/index.php/ProbTrib/article/view/794/1269 (accessed on 8 November 2022). [CrossRef]
- Kondratiev, A.V.; Gaidachuk, V.E. Mathematical analysis of technological parameters for producing superfine prepregs by flattening carbon fibers. Mech. Compos. Mater. 2021, 57, 91–100. [Google Scholar] [CrossRef]
- Li, H.; Liu, Y.; Liao, H.; Liang, Z. Accelerated Wear Test Design Based on Dissipation Wear Model Entropy Analysis under Mixed Lubrication. Lubricants 2022, 10, 71. [Google Scholar] [CrossRef]
- Ye, L.; Hu, Y.; Deng, S.; Zhang, W.; Cui, Y.; Xu, J. A Novel Model for Evaluating the Operation Performance Status of Rolling Bearings Based on Hierarchical Maximum Entropy Bayesian Method. Lubricants 2022, 10, 97. [Google Scholar] [CrossRef]
- Al-Quraan, T.M.A.; Mikosyanchik, O.O.; Mnatsakanov, R.G. Temperature resistance of the boundary lubrication layers under rolling with slippage condition. Int. J. Mech. Eng. Appl. 2017, 5, 78–86. [Google Scholar] [CrossRef][Green Version]
- Gurt, A.; Khonsari, M. The Use of Entropy in Modeling the Mechanical Degradation of Grease. Lubricants 2019, 7, 82. [Google Scholar] [CrossRef]
- Bogdanovych, O.I.; Al-Quraan, T.M.A.; Tokaruk, V.V.; Haddad, J.S. Algorithm for tribokinetic modeling tests of triboconjuc-tion materials for industrial products. Tribol. Ind. 2020, 43, 159–166. [Google Scholar] [CrossRef]
- Karl, D. Mass and Energy Balance of a Three-Body Tribosystem. Lubricants 2022, 10, 95. [Google Scholar] [CrossRef]
- Kondratiev, A.; Píštěk, V.; Smovziuk, L.; Shevtsova, M.; Fomina, A.; Kučera, P. Stress–strain behaviour of reparable composite panel with step–variable thickness. Polymers 2021, 13, 3830. [Google Scholar] [CrossRef]
- Al-Quraan, T.M.A.; Mikosyanchik, O.O.; Mnatsakanov, R.G.; Zaporozhets, O.I. Structural-Energy characteristics of tribotechnical contact in unsteady operational modes. Mod. Mech. Eng. 2016, 6, 91–97. [Google Scholar] [CrossRef][Green Version]
- Rosenkranz, A.; Marian, M.; Profito, F.J.; Aragon, N.; Shah, R. The Use of Artificial Intelligence in Tribology—A Perspective. Lubricants 2021, 9, 2. [Google Scholar] [CrossRef]
- Miroshnuk, O.O.; Tymchuk, S.O. Uniform distribution of loads in the electric system 0.38/0.22 KV using genetic algorithms. Tech. Electrodyn. 2013, 4, 67–73. Available online: http://www.scopus.com/inward/record.url?eid=2-s2.0-84885913005&partnerID=MN8TOARS (accessed on 8 November 2022).
- Argatov, I. Artificial Neural Networks (ANNs) as a Novel Modeling Technique in Tribology. Front. Mech. Eng. 2019, 5, 1074. [Google Scholar] [CrossRef]
- Joerger, A.; Reichert, S.; Wittig, C.; Aghdam, D.S.; Albers, A. An Approach for the Transfer of Real Surfaces in Finite Element Simulations. Lubricants 2021, 9, 77. [Google Scholar] [CrossRef]
- Wang, C.; Schipper, D.J. On an Elastoplastic Sliding Model for a Coated Single Asperity. Lubricants 2018, 6, 96. [Google Scholar] [CrossRef]
- Dmitriev, A.I.; Österle, W.; Wetzel, B.; Zhang, G. Mesoscale modeling of the mechanical and tribological behavior of a poly-mer matrix composite based on epoxy and 6 vol.% silica nanoparticles. Comput. Mater. Sci. 2015, 110, 204–214. [Google Scholar] [CrossRef]
- Winkler, A.; Marian, M.; Tremmel, S.; Wartzack, S. Numerical Modeling of Wear in a Thrust Roller Bearing under Mixed Elastohydrodynamic Lubrication. Lubricants 2020, 8, 58. [Google Scholar] [CrossRef]
- Terwey, J.T.; Fourati, M.A.; Pape, F.; Poll, G. Energy-Based Modelling of Adhesive Wear in the Mixed Lubrication Regime. Lubricants 2020, 8, 16. [Google Scholar] [CrossRef]
- Jacq, C.; Nelias, D.; Lormand, G.; Girodin, D. Development of a three-dimensional semi-analytical elastic-plastic contact code. J. Tribol. 2002, 124, 653–667. [Google Scholar] [CrossRef]
- Delprete, C.; Gastaldi, C.; Giorio, L. A Minimal Input Engine Friction Model for Power Loss Prediction. Lubricants 2022, 10, 94. [Google Scholar] [CrossRef]
- Wang, Z.; Yu, H.; Wang, Q. Analytical solutions for elastic fields caused by eigenstrains in two joined and perfectly bonded half-spaces and related problems. Int. J. Plast. 2016, 76, 1–28. [Google Scholar] [CrossRef]
- Orgeldinger, C.; Tremmel, S. Understanding Friction in Cam–Tappet Contacts—An Application-Oriented Time-Dependent Simulation Approach Considering Surface Asperities and Edge Effects. Lubricants 2021, 9, 106. [Google Scholar] [CrossRef]
- Yang, L.; Wang, D.; Guo, Y.; Liu, S. Tribological behaviors of quartz sand particles for hydraulic fracturing. Tribol. Int. 2016, 102, 485–496. [Google Scholar] [CrossRef]
- Scherge, M. The Running-in of Lubricated Metal-Metal Contacts—A Review on Ultra-Low Wear Systems. Lubricants 2018, 6, 54. [Google Scholar] [CrossRef]
- Vojtov, V.A.; Biekirov, A.S.; Voitov, A.V.; Tsymbal, B.M. Running-in procedures and performance tests for tribosystems. J. Frict. Wear 2019, 40, 376–383. [Google Scholar] [CrossRef]
- Kondratiev, A.; Píštěk, V.; Smovziuk, L.; Shevtsova, M.; Fomina, A.; Kučera, P.; Prokop, A. Effects of the Temperature–Time Regime of Curing of Composite Patch on Repair Process Efficiency. Polymers 2021, 13, 4342. [Google Scholar] [CrossRef]
- Wojciechowski, Ł.; Mathia, T.G. Proposal of invariant precursors for boundary lubricated scuffing. Wear 2015, 340–341, 53–62. [Google Scholar] [CrossRef]
- Wojciechowski, Ł.; Wieczorowski, M.; Mathia, T.G. Transition from the boundary lubrication to scuffing—The role of metallic surfaces morphology. Wear 2017, 392–393, 39–49. [Google Scholar] [CrossRef]
- Pusterhofer, M.; Summer, F.; Gódor, I.; Grün, F. Cumulative damage assessment of tribological durability limits. Wear 2020, 456–457, 203318. [Google Scholar] [CrossRef]
- Savolainen, M.; Lehtovaara, A. An experimental approach for investigating scuffing initiation due to overload cycles with a twin-disc test device. Tribol. Int. 2017, 109, 311–318. [Google Scholar] [CrossRef]
- Hershberger, J.; Ajayi, O.O.; Zhang, J.; Yoon, H.; Fenske, G.R. Evidence of scuffing initiation by adiabatic shear instability. Wear 2005, 258, 1471–1478. [Google Scholar] [CrossRef]
- Zhang, C.; Peng, B.; Gu, L.; Wang, T.; Wang, L. A scuffing criterion of steels based on the friction-induced adiabatic shear instability. Tribol. Int. 2020, 148, 120–134. [Google Scholar] [CrossRef]
- Wojciechowski, L.; Mathia, T.G. Focus on the concept of pressure-velocity-time (pVt) limits for boundary lubricated scuffing. Wear 2018, 402–403, 179–186. [Google Scholar] [CrossRef]
- Castro, J.; Sottomayor, A.; Seabra, J. Experimental and analystical scuffing criteria for FZG gears. Tribol. Ser. 2003, 43, 651–661. [Google Scholar] [CrossRef]
- Xue, J.-h.; Li, W.; Qin, C. The scuffing load capacity of involute spur gear systems based on dynamic loads and transient thermal elastohydrodynamic lubrication. Tribol. Int. 2014, 79, 74–83. [Google Scholar] [CrossRef]
- Im, K.; Avouac, J.-P. Linear stability analysis of the condition for vibration during frictional slip. J. Mech. Phys. Solids 2022, 167, 104993. [Google Scholar] [CrossRef]
- Sui, X.; Ding, Q. Bifurcation and stability analyses for a pad-on-disc frictional system. Int. J. Non-Linear Mech. 2018, 107, 112–125. [Google Scholar] [CrossRef]
- Onishchenko, V. Investigation of tooth wears from scuffing of heavy duty machine spur gears. Mech. Mach. Theory 2015, 83, 38–55. [Google Scholar] [CrossRef]
- Parmar, A.; Ramkumar, P.; Shankar, K. Macro geometry multi-objective optimization of planetary gearbox considering scuffing constraint. Mech. Mach. Theory 2020, 154, 104045. [Google Scholar] [CrossRef]
- Voitov, A.V. Parametric identification of the mathematical model of the functioning of tribosystems in the conditions of boundary lubrication. Probl. Tribol. 2021, 27, 6–14. [Google Scholar] [CrossRef]
- Vojtov, V.; Biekirov, A.; Voitov, A. The quality of the tribosystem as a factor of wear resistance. Int. J. Eng. Technol. 2018, 7, 25–29. [Google Scholar] [CrossRef]
- Voitov, A.; Fenenko, K.; Fenenko, O. Simulation of change in rheological properties of structure of combined materials in tribosystem. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1021, 012052. [Google Scholar] [CrossRef]
- Havrylenko, Y.; Kholodniak, Y.; Halko, S.; Vershkov, O.; Bondarenko, L.; Suprun, O.; Miroshnyk, O.; Shchur, T.; Śrutek, M.; Gackowska, M. Interpolation with Specified Error of a Point Series Belonging to a Monotone Curve. Entropy 2021, 23, 493. [Google Scholar] [CrossRef] [PubMed]
- Iegorov, O.; Iegorova, O.; Miroshnyk, O.; Savchenko, O. Improving the accuracy of determining the parameters of induction motors in transient starting modes. Energetika 2020, 66, 15–23. [Google Scholar] [CrossRef]
- Havrylenko, Y.; Kholodniak, Y.; Halko, S.; Vershkov, O.; Miroshnyk, O.; Suprun, O.; Dereza, O.; Shchur, T.; Śrutek, M. Representation of a Monotone Curve by a Contour with Regular Change in Curvature. Entropy 2021, 23, 923. [Google Scholar] [CrossRef]
- Wei, Y.; Zhao, X.; Wei, Y.; Chen, Y.Q. Lyapunov stability criteria in terms of class K functions for Riemann–Liouville nabla fractional order systems. ISA Trans. 2022, 131, 137–145. [Google Scholar] [CrossRef]
- Gokul, P.; Rakkiyappan, R. New finite-time stability for fractional-order time-varying time-delay linear systems: A Lyapunov approach. J. Frankl. Inst. 2022, 359, 7620–7631. [Google Scholar] [CrossRef]
- Mondié, S.; Egorov, A.; Gomez, M.A. Lyapunov stability tests for linear time-delay systems. Annu. Rev. Control. 2022, 54, 68–80. [Google Scholar] [CrossRef]
- Shen, C.; Li, Y.; Zhu, X.; Duan, W. Improved stability criteria for linear systems with two additive time-varying delays via a novel Lyapunov functional. J. Comput. Appl. Math. 2020, 363, 312–324. [Google Scholar] [CrossRef]
- Zhan, X.; Hu, Y. On the relation between Hurwitz stability of matrix polynomials and matrix-valued Stieltjes functions. J. Comput. Appl. Math. 2023, 417, 114614. [Google Scholar] [CrossRef]
- Zhan, X.; Dyachenko, A. On generalization of classical Hurwitz stability criteria for matrix polynomials. J. Comput. Appl. Math. 2021, 383, 113113. [Google Scholar] [CrossRef]
- El-Marhomy, A.A.; Abdel-Sattar, N.E. Stability analysis of rotor-bearing systems via Routh-Hurwitz criterion. Appl. Energy 2004, 77, 287–308. [Google Scholar] [CrossRef]
- Jin, X.-C.; Lu, J.-G. Delay-dependent criteria for robust stability and stabilization of fractional-order time-varying delay systems. Eur. J. Control. 2022, 67, 100704. [Google Scholar] [CrossRef]
- Vojtov, V.; Fenenko, K.; Voitov, A.; Hrynkiv, A.; Lyashuk, O.; Vovk, Y. Methodical Approach to Using Acoustic Emission Method for Tribosystem Monitoring. Tribol. Ind. 2022, 44, 470–481. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).