Numerical Wear Modeling in the Mixed and Boundary Lubrication Regime
Abstract
1. Introduction
1.1. State-of-the-Art
1.2. Derivation of the Need for Research
2. Numerical Modeling
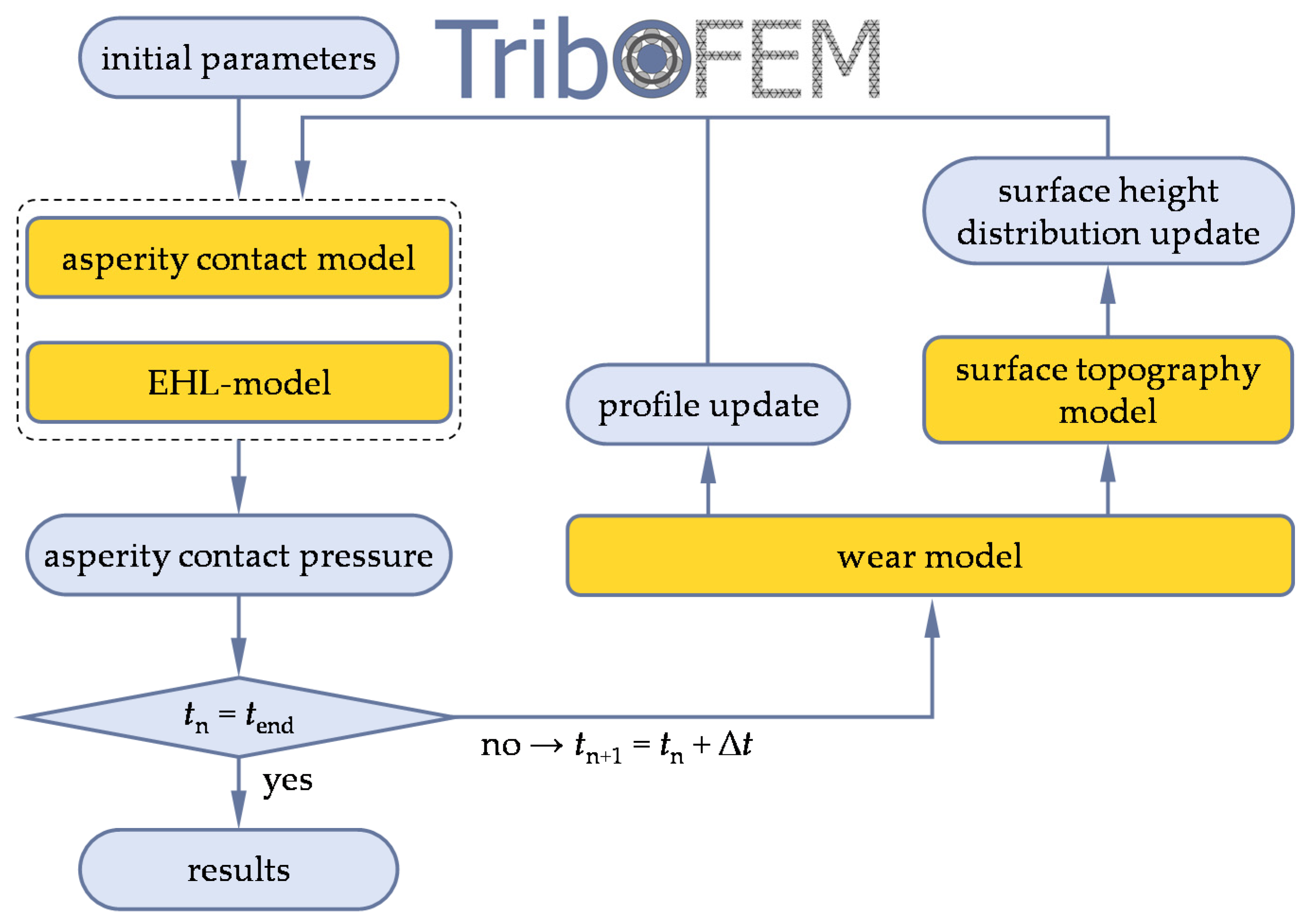
2.1. Mixed Lubrication Regime
2.1.1. Asperity Contact Model
2.1.2. EHL Model
2.1.3. Wear Model
2.1.4. Surface Topography Model
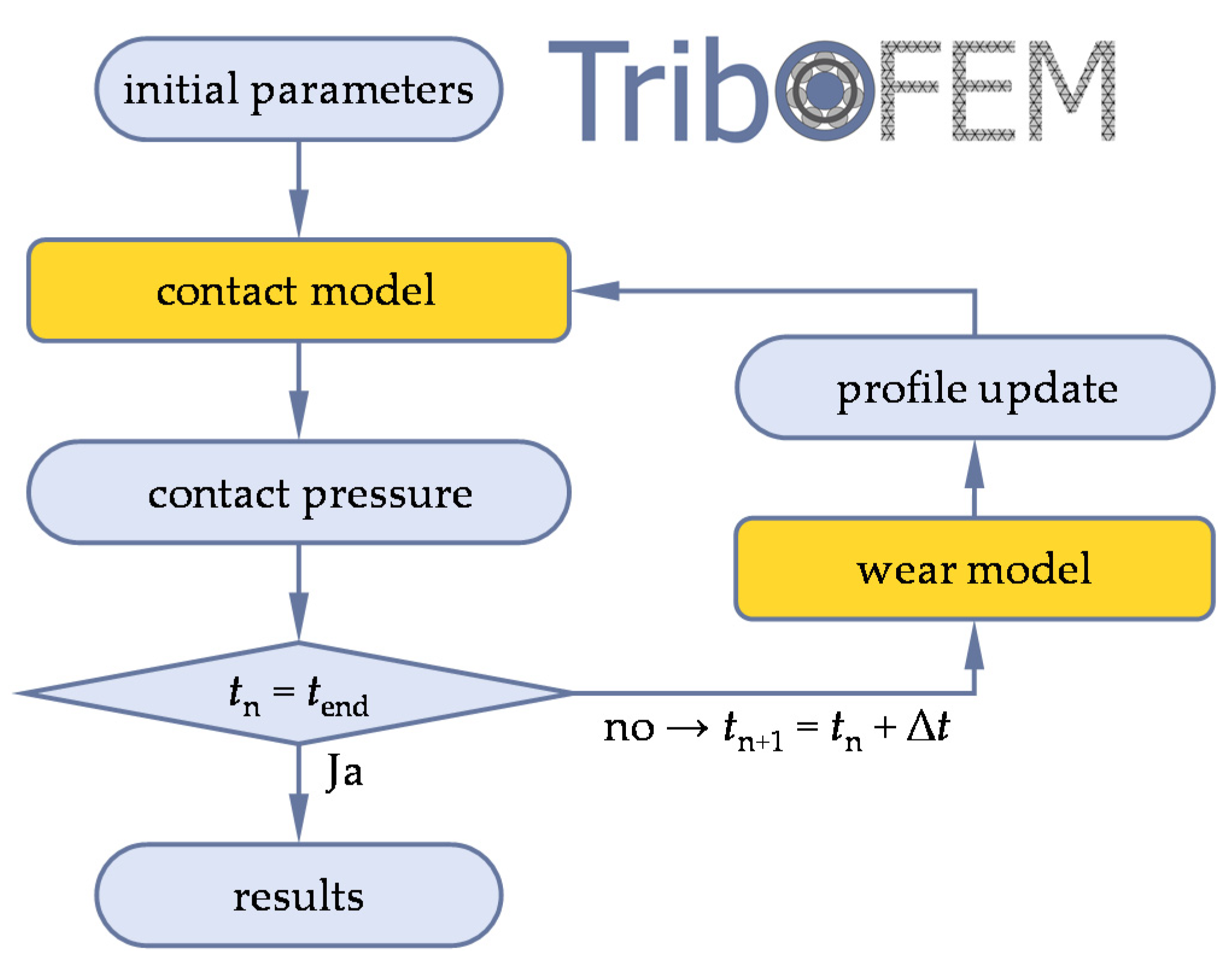
2.2. Boundary Lubrication Regime and Dry Contacts
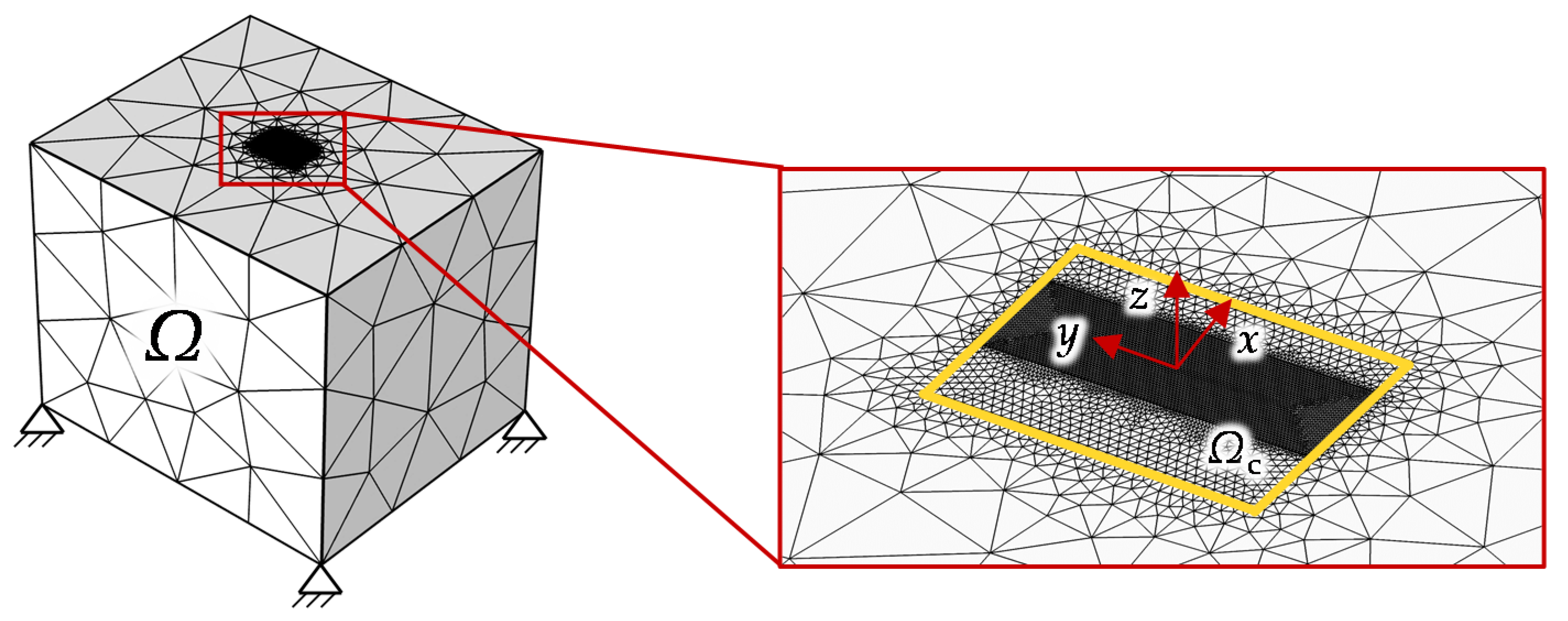
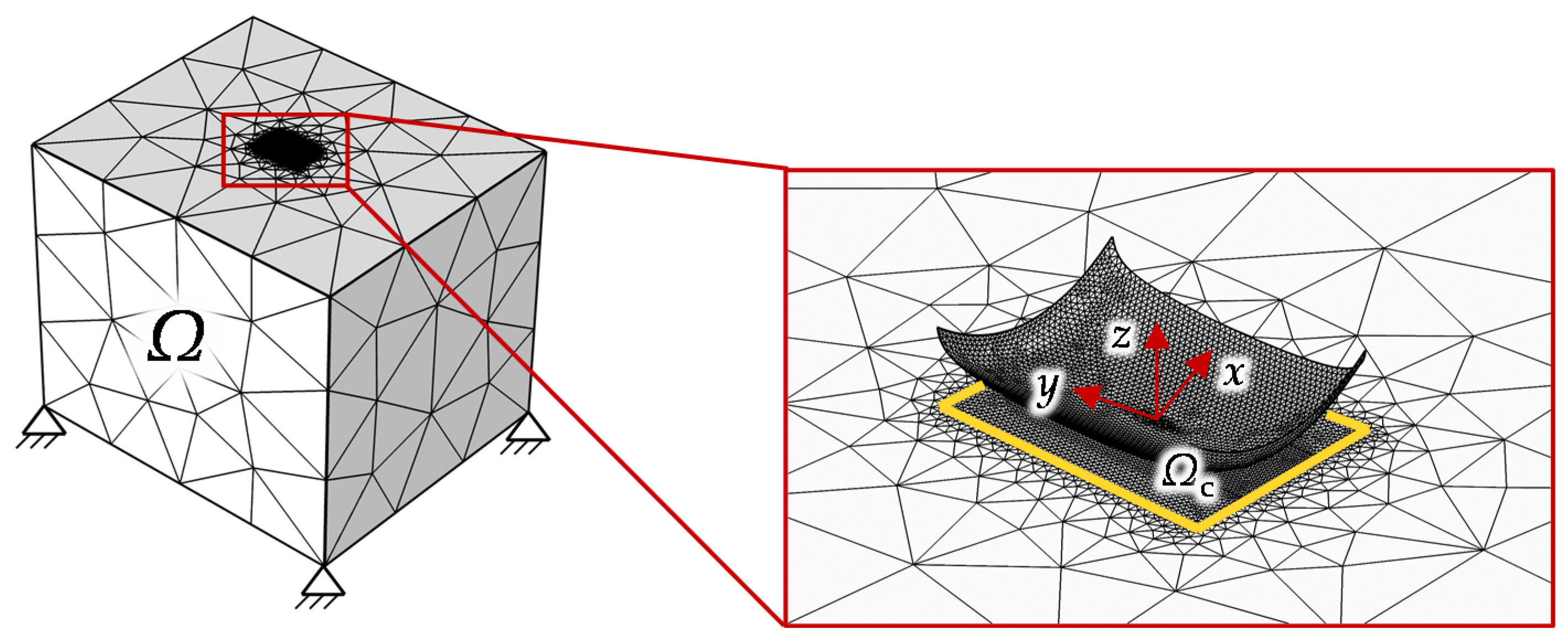
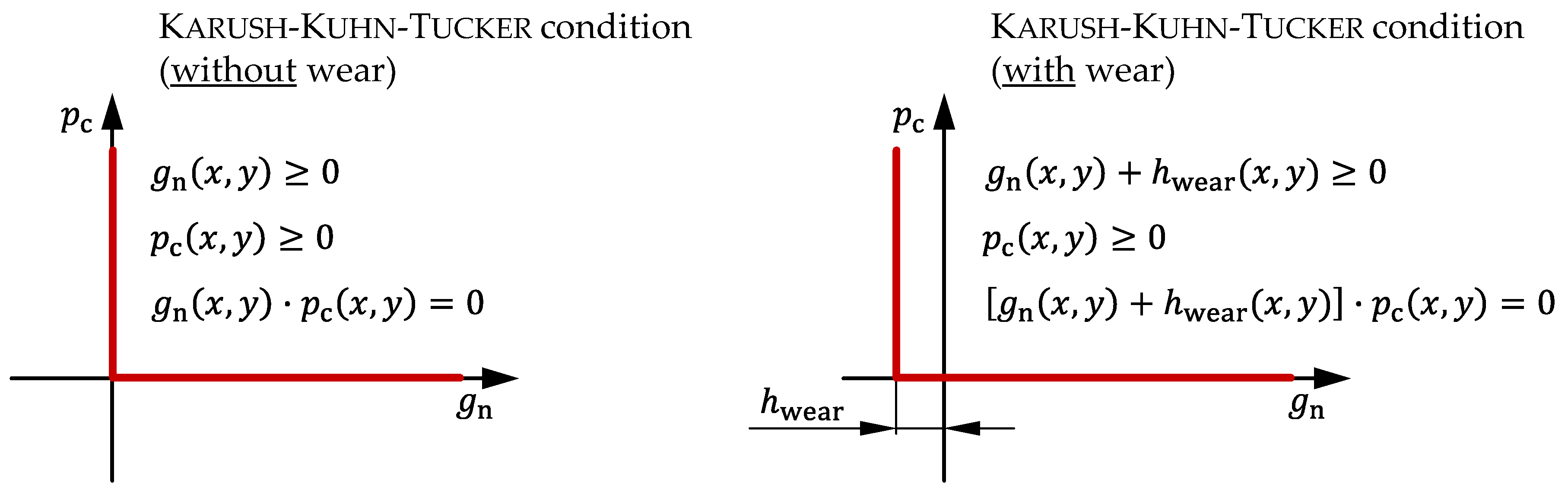
2.2.1. Contact Model
2.2.2. Wear Model
3. Experimental Determination of Wear Coefficients
4. Results and Discussion
5. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Wear cross-sectional area | |
| Parameter of the Jackson/Green asperity contact model | |
| Parameter of the Jackson/Green asperity contact model | |
| Separation based on asperity heights | |
| Diameter of roller | |
| Diameter of test discs | |
| Young’s modulus | |
| Combined Young’s modulus of two surfaces for the asperity contact model | |
| Equivalent Young’s modulus | |
| Load | |
| Distance between master and slave surfaces of FEM-based contact models | |
| Separation based on surface heights / lubricant film thickness | |
| Film thickness constant parameter | |
| Minimum lubricant film thickness | |
| Local wear depth | |
| Geometrical hardness limit according to the Jackson/Green asperity contact model | |
| Wear coefficient | |
| Length of roller | |
| Zeroth, second, and fourth spectral moment of a surface profile | |
| Masses of discs before and after two-disc tribometer tests | |
| Rotational speed | |
| Asperity contact pressure | |
| Total contact pressure in boundary lubricated or dry contacts | |
| Hydrodynamic contact pressure | |
| Critical contact force at initial yielding according to the Jackson/Green asperity contact model | |
| Elastic portion of the force acting on a single asperity | |
| Plastic portion of the force acting on a single asperity | |
| Sliding distance | |
| Geometry-function of the roller | |
| Standard deviation of surface heights | |
| Skewness of surface heights | |
| Kurtosis of surface heights | |
| Slide-to-roll ratio | |
| Time | |
| Relative velocity of the washer/roller in x direction | |
| Relative velocity of the washer/roller in y direction | |
| Sliding velocity | |
| Coordinates in and perpendicular to the rolling direction | |
| Distance between the mean height of asperities and the mean height of surface | |
| Profile coordinate based on mean height of surface | |
| Profile coordinate based on mean height of asperities | |
| Ordinate of the mean line of the composite profile | |
| Descending quantity of mean line | |
| Highest point of composite profile | |
| Moving distance of highest point | |
| Bandwidth parameter | |
| Mean summit radius | |
| Elastic deformation in z direction | |
| Dimensionless film thickness parameter | |
| Poisson’s ratio of washer/roller | |
| Equivalent Poisson’s ratio | |
| Density | |
| Area density of asperities | |
| Dynamic viscosity | |
| Standard deviation of surface heights | |
| Standard deviation of asperity heights | |
| Yield strength | |
| Probability density function of surface heights | |
| Probability density function of asperity heights | |
| Height-loss probability density function | |
| Interference | |
| Critical interference |
References
- Holmberg, K.; Erdemir, A. Influence of tribology on global energy consumption, costs and emissions. Friction 2017, 5, 263–284. [Google Scholar] [CrossRef]
- Winkler, A.; Marian, M.; Tremmel, S.; Wartzack, S. Numerical Modeling of Wear in a Thrust Roller Bearing under Mixed Elastohydrodynamic Lubrication. Lubricants 2020, 8, 58. [Google Scholar] [CrossRef]
- Põdra, P.; Andersson, S. Wear simulation with the Winkler surface model. Wear 1997, 207, 79–85. [Google Scholar] [CrossRef]
- Archard, J.F.; Hirst, W. The wear of metals under unlubricated conditions. Proc. R. Soc. Lond. Ser. A. Math. Phys. Eng. Sci. 1956, 236, 397–410. [Google Scholar] [CrossRef]
- Winkler, E. Die Lehre von der Elastizität und Festigkeit mit besonderer Rücksicht auf ihre Anwendung in der Technik: Für polytechnische Schulen, Bauakademien, Ingenieure, Maschinenbauer, Architecten, etc.; Dominicus: Prag, Czech Republic, 1867. [Google Scholar]
- Põdra, P.; Andersson, S. Simulating sliding wear with finite element method. Tribol. Int. 1999, 32, 71–81. [Google Scholar] [CrossRef]
- Hegadekatte, V.; Huber, N.; Kraft, O. Finite element based simulation of dry sliding wear. Model. Simul. Mater. Sci. Eng. 2005, 13, 57–75. [Google Scholar] [CrossRef]
- Hegadekatte, V.; Huber, N.; Kraft, O. Modeling and simulation of wear in a pin on disc tribometer. Tribol. Lett. 2006, 24, 51–60. [Google Scholar] [CrossRef]
- Hegadekatte, V.; Kurzenhäuser, S.; Huber, N.; Kraft, O. A predictive modeling scheme for wear in tribometers. Tribol. Int. 2008, 41, 1020–1031. [Google Scholar] [CrossRef]
- Sfantos, G.K.; Aliabadi, M.H. A boundary element formulation for three-dimensional sliding wear simulation. Wear 2007, 262, 672–683. [Google Scholar] [CrossRef]
- Andersson, J.; Almqvist, A.; Larsson, R. Numerical simulation of a wear experiment. Wear 2011, 271, 2947–2952. [Google Scholar] [CrossRef]
- Liu, S.; Wang, Q.; Liu, G. A versatile method of discrete convolution and FFT (DC-FFT) for contact analyses. Wear 2000, 243, 101–111. [Google Scholar] [CrossRef]
- Morales-Espejel, G.E.; Gabelli, A. Rolling bearing seizure and sliding effects on fatigue life. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2019, 233, 339–354. [Google Scholar] [CrossRef]
- Palmgren, A. Die Lebensdauer von Kugellagern: Durability of Ball Bearings. Z. Des Ver. Dtsch. Ing. 1924, 68, 339–341. [Google Scholar]
- Miner, M.A. Cumulative Damage in Fatigue. J. Appl. Mech. 1945, 12, 159–164. [Google Scholar] [CrossRef]
- Zhu, D.; Martini, A.; Wang, W.; Hu, Y.; Lisowsky, B.; Wang, Q.J. Simulation of Sliding Wear in Mixed Lubrication. J. Tribol. 2007, 129, 544–552. [Google Scholar] [CrossRef]
- Zhu, D.; Hu, Y.-Z. A Computer Program Package for the Prediction of EHL and Mixed Lubrication Characteristics, Friction, Subsurface Stresses and Flash Temperatures Based on Measured 3-D Surface Roughness. Tribol. Trans. 2001, 44, 383–390. [Google Scholar] [CrossRef]
- Hu, Y.-Z.; Zhu, D. A Full Numerical Solution to the Mixed Lubrication in Point Contacts. J. Tribol. 2000, 122, 1–9. [Google Scholar] [CrossRef]
- Lorentz, B.; Albers, A. A numerical model for mixed lubrication taking into account surface topography, tangential adhesion effects and plastic deformations. Tribol. Int. 2013, 59, 259–266. [Google Scholar] [CrossRef]
- Reichert, S.; Lorentz, B.; Heldmaier, S.; Albers, A. Wear simulation in non-lubricated and mixed lubricated contacts taking into account the microscale roughness. Tribol. Int. 2016, 100, 272–279. [Google Scholar] [CrossRef]
- Johnson, G.R.; Cook, W.H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures. Eng. Fract. Mech. 1985, 21, 31–48. [Google Scholar] [CrossRef]
- Terwey, J.T. Näherungslösungen für Reibung und Verschleiß in ölgeschmierten Wälzkontakten unter Berücksichtigung der realen Rheologie. Ph.D. Thesis, Gottfried Wilhelm Leibniz Universität Hannover, Hannover, Germany, 2020. [Google Scholar]
- Terwey, J.T.; Berninger, S.; Burghardt, G.; Jacobs, G.; Poll, G. Numerical Calculation of Local Adhesive Wear in Machine Elements Under Boundary Lubrication Considering the Surface Roughness. In Proceedings of the 7th International Conference on Fracture Fatigue and Wear; Abdel Wahab, M., Ed.; Springer: Singapore, 2019; pp. 796–807. ISBN 9789811344091. [Google Scholar]
- Terwey, J.T.; Fourati, M.A.; Pape, F.; Poll, G. Energy-Based Modelling of Adhesive Wear in the Mixed Lubrication Regime. Lubricants 2020, 8, 16. [Google Scholar] [CrossRef]
- Hamrock, B.J.; Schmid, S.R.; Jacobson, B.O. Fundamentals of Fluid Film Lubrication, 2nd ed.; Marcel Dekker: New York, NY, USA, 2004; ISBN 9780824753719. [Google Scholar]
- Fleischer, G. Verschleiß und Zuverlässigkeit; VEB: Berlin, Germany, 1980. [Google Scholar]
- Fleischer, G. Zur Energetik der Reibung. Wiss. Z. Der Tech. Univ. Otto Von Guericke Magdebg. 1990, 34, 55–66. [Google Scholar]
- Beheshti, A.; Khonsari, M.M. An engineering approach for the prediction of wear in mixed lubricated contacts. Wear 2013, 308, 121–131. [Google Scholar] [CrossRef]
- Johnson, K.L.; Greenwood, J.A.; Poon, S.Y. A simple theory of asperity contact in elastohydro-dynamic lubrication. Wear 1972, 19, 91–108. [Google Scholar] [CrossRef]
- Beheshti, A.; Khonsari, M.M. A Thermodynamic Approach for Prediction of Wear Coefficient Under Unlubricated Sliding Condition. Tribol. Lett. 2010, 38, 347–354. [Google Scholar] [CrossRef]
- Kogut, L.; Etsion, I. Elastic-Plastic Contact Analysis of a Sphere and a Rigid Flat. J. Appl. Mech. 2002, 69, 657–662. [Google Scholar] [CrossRef]
- Kogut, L.; Etsion, I. A Finite Element Based Elastic-Plastic Model for the Contact of Rough Surfaces. Tribol. Trans. 2003, 46, 383–390. [Google Scholar] [CrossRef]
- Kogut, L.; Etsion, I. A Static Friction Model for Elastic-Plastic Contacting Rough Surfaces. J. Tribol. 2004, 126, 34–40. [Google Scholar] [CrossRef]
- Zhang, Y.; Kovalev, A.; Hayashi, N.; Nishiura, K.; Meng, Y. Numerical Prediction of Surface Wear and Roughness Parameters during Running-In for Line Contacts Under Mixed Lubrication. J. Tribol. 2018, 140, 061501/1–061501/13. [Google Scholar] [CrossRef]
- Kimura, Y.; Sugimura, J. Microgeometry of sliding surfaces and wear particles in lubricated contact. Wear 1984, 100, 33–45. [Google Scholar] [CrossRef]
- Sugimura, J.; Kimura, Y. Characterization of topographical changes during lubricated wear. Wear 1984, 98, 101–116. [Google Scholar] [CrossRef]
- Sugimura, J.; Kimura, Y.; Amino, K. Analysis of the Topographical Changes Due to Wear—Geometry of the Running-In Process. J. Jpn. Soc. Lubr. Eng. 1986, 31, 813–820. [Google Scholar]
- Mukras, S.M.S. Computer Simulation/Prediction of Wear in Mechanical Components. Adv. Tribol. 2020, 2020, 1–15. [Google Scholar] [CrossRef]
- Neale, M.J. The Tribology Handbook, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 1995; ISBN 0750611987. [Google Scholar]
- Bruce, R.W. Handbook of Lubrication and Tribology: Volume II: Theory and Design, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2012; ISBN 9781420069099. [Google Scholar]
- Hansen, J.; Björling, M.; Larsson, R. Mapping of the lubrication regimes in rough surface EHL contacts. Tribol. Int. 2019, 131, 637–651. [Google Scholar] [CrossRef]
- Hansen, J.; Björling, M.; Larsson, R. Lubricant film formation in rough surface non-conformal conjunctions subjected to GPa pressures and high slide-to-roll ratios. Sci. Rep. 2020, 10, 22250/1–22250/16. [Google Scholar] [CrossRef]
- Hansen, J.; Björling, M.; Larsson, R. A New Film Parameter for Rough Surface EHL Contacts with Anisotropic and Isotropic Structures. Tribol. Lett. 2021, 69, 37/1–37/17. [Google Scholar] [CrossRef]
- Jackson, R.L.; Green, I. A Finite Element Study of Elasto-Plastic Hemispherical Contact against a Rigid Flat. J. Tribol. 2005, 127, 343–354. [Google Scholar] [CrossRef]
- Jackson, R.L.; Green, I. A statistical model of elasto-plastic asperity contact between rough surfaces. Tribol. Int. 2006, 39, 906–914. [Google Scholar] [CrossRef]
- Jackson, R.L.; Green, I. The Behavior of Thrust Washer Bearings Considering Mixed Lubrication and Asperity Contact. Tribol. Trans. 2006, 49, 233–247. [Google Scholar] [CrossRef]
- Bush, A.W.; Gibson, R.D.; Keogh, G.P. The limit of elastic deformation in the contact of rough surfaces. Mech. Res. Commun. 1976, 3, 169–174. [Google Scholar] [CrossRef]
- McCool, J.I. Relating Profile Instrument Measurements to the Functional Performance of Rough Surfaces. J. Tribol. 1987, 109, 264–270. [Google Scholar] [CrossRef]
- Beheshti, A.; Khonsari, M.M. Asperity micro-contact models as applied to the deformation of rough line contact. Tribol. Int. 2012, 52, 61–74. [Google Scholar] [CrossRef]
- Tomota, T.; Masuda, R.; Kondoh, Y.; Ohmori, T.; Yagi, K. Modeling Solid Contact between Rough Surfaces with Various Roughness Parameters. Tribol. Trans. 2021, 64, 178–192. [Google Scholar] [CrossRef]
- Johnson, N.L. Systems of Frequency Curves Generated by Methods of Translation. Biometrika 1949, 36, 149–176. [Google Scholar] [CrossRef] [PubMed]
- Elderton, W.P.; Johnson, N.L. Systems of Frequency Curves; Cambridge University Press: Cambridge, UK, 1969; ISBN 9780511569654. [Google Scholar]
- Yu, N.; Polycarpou, A.A. Contact of Rough Surfaces with Asymmetric Distribution of Asperity Heights. J. Tribol. 2002, 124, 367–376. [Google Scholar] [CrossRef]
- Habchi, W. Finite Element Modeling of Elastohydrodynamic Lubrication Problems; Wiley: Hoboken, NJ, USA, 2018; ISBN 9781119225126. [Google Scholar]
- Marian, M.; Weschta, M.; Tremmel, S.; Wartzack, S. Simulation of Microtextured Surfaces in Starved EHL Contacts Using Commercial FE Software. Mater. Perform. Charact. 2017, 6, 165–181. [Google Scholar] [CrossRef]
- Hughes, T.J.; Franca, L.P.; Hulbert, G.M. A new finite element formulation for computational fluid dynamics: VIII. The galerkin/least-squares method for advective-diffusive equations. Comput. Methods Appl. Mech. Eng. 1989, 73, 173–189. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Taylor, R.L.; Nithiarasu, P. The Finite Element Method for Fluid Dynamics, 7th ed.; Butterworth-Heinemann: Oxford, UK, 2014; ISBN 9781856176354. [Google Scholar]
- Dowson, D.; Higginson, G.R. Elasto-Hydrodynamic Lubrication: SI-Edition; Pergamon: Oxford, UK, 1977; ISBN 9780080213033. [Google Scholar]
- Roelands, C.J.A. Correlational Aspects of the Viscosity-Temperature-Pressure Relationship of Lubricating Oils. Ph.D. Thesis, Technische Hogeschool Delft, Delft, The Netherlands, 1966. [Google Scholar]
- Eyring, H. Viscosity, Plasticity, and Diffusion as Examples of Absolute Reaction Rates. J. Chem. Phys. 1936, 4, 283–291. [Google Scholar] [CrossRef]
- Wriggers, P. Computational Contact Mechanics; Wiley: New York, NY, USA, 2002; ISBN 0471496804. [Google Scholar]
- Bhushan, B. (Ed.) Modern Tribology Handbook; CRC Press: Boca Raton, FL, USA, 2001; ISBN 9780849384035. [Google Scholar]
- Jeng, Y.-R.; Gao, C.-C. Changes of Surface Topography during Wear for Surfaces with Different Height Distributions. Tribol. Trans. 2000, 43, 749–757. [Google Scholar] [CrossRef]
- Jeng, Y.-R.; Lin, Z.-W.; Shyu, S.-H. A Microscopic Wear Measurement Method for General Surfaces. J. Tribol. 2002, 124, 829–833. [Google Scholar] [CrossRef]
- Jeng, Y.-R.; Lin, Z.-W.; Shyu, S.-H. Changes of Surface Topography during Running-In Process. J. Tribol. 2004, 126, 620–625. [Google Scholar] [CrossRef]
- Hamrock, B.J.; Dowson, D. Ball Bearing Lubrication: The Elastohydrodynamics of Elliptical Contacts; Wiley: New York, NY, USA, 1981; ISBN 9780471035534. [Google Scholar]
- DIN 51819-1; Prüfung von Schmierstoffen—Mechanisch-dynamische Prüfung auf dem Wälzlagerschmierstoff-Prüfgerät FE8—Teil 1: Allgemeine Arbeitsgrundlagen. Beuth: Berlin, Germany, 2016.
- DIN 51819-3; Prüfung von Schmierstoffen—Mechanisch-dynamische Prüfung auf dem Wälzlagerschmierstoff-Prüfgerät FE8—Teil 3: Verfahren für Schmieröl–einzusetzende Prüflager: Axialzylinderrollenlager. Beuth: Berlin, Germany, 2016.

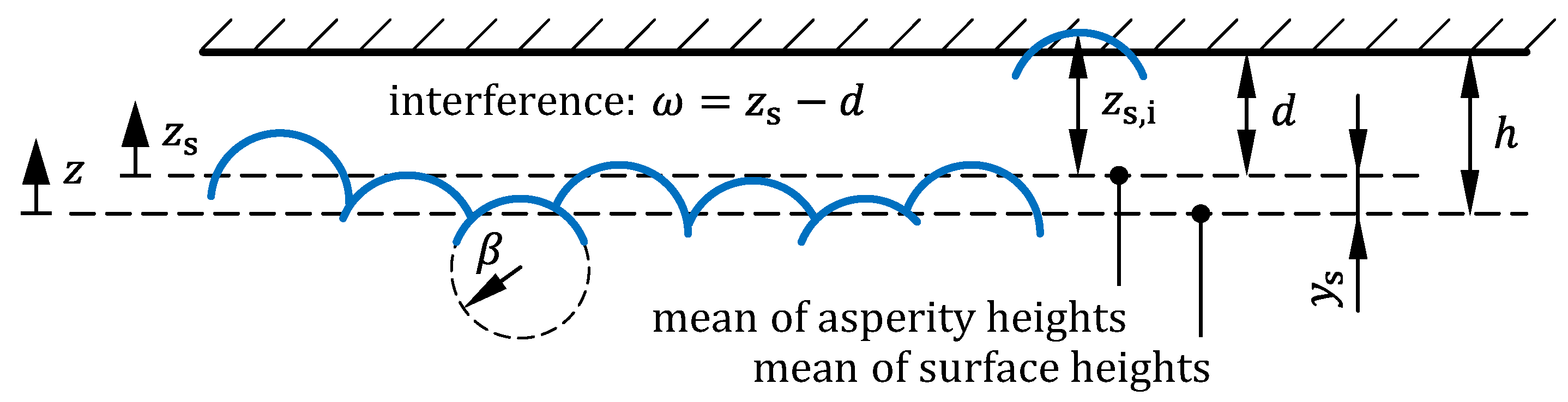





| Parameter | Value |
|---|---|
| Disc material | 100Cr6 |
| Lubricant | PAO 6 |
| Oil temperature | 80 °C |
| Disc 1 | Ø 45 mm; Crowning: 50 mm |
| Disc 2 | Ø 45 mm; Crowning: ∞ |
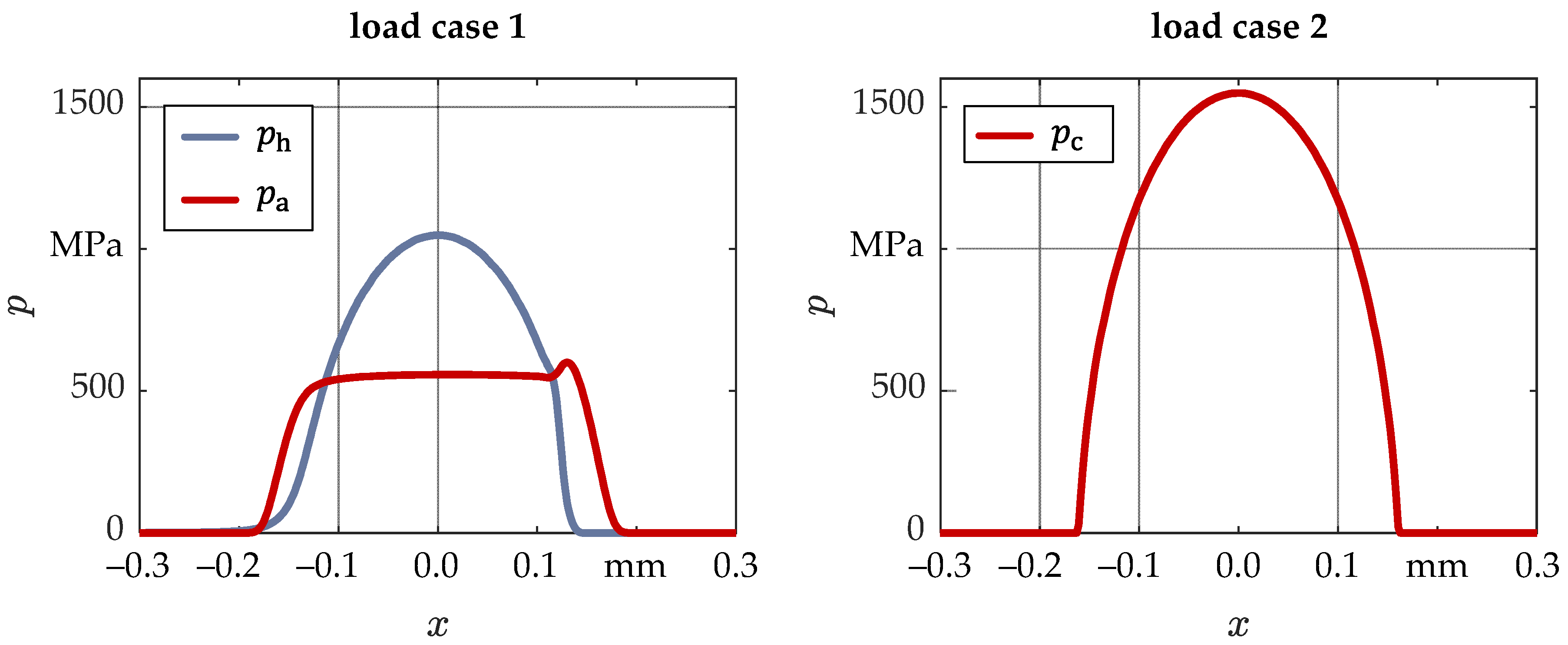
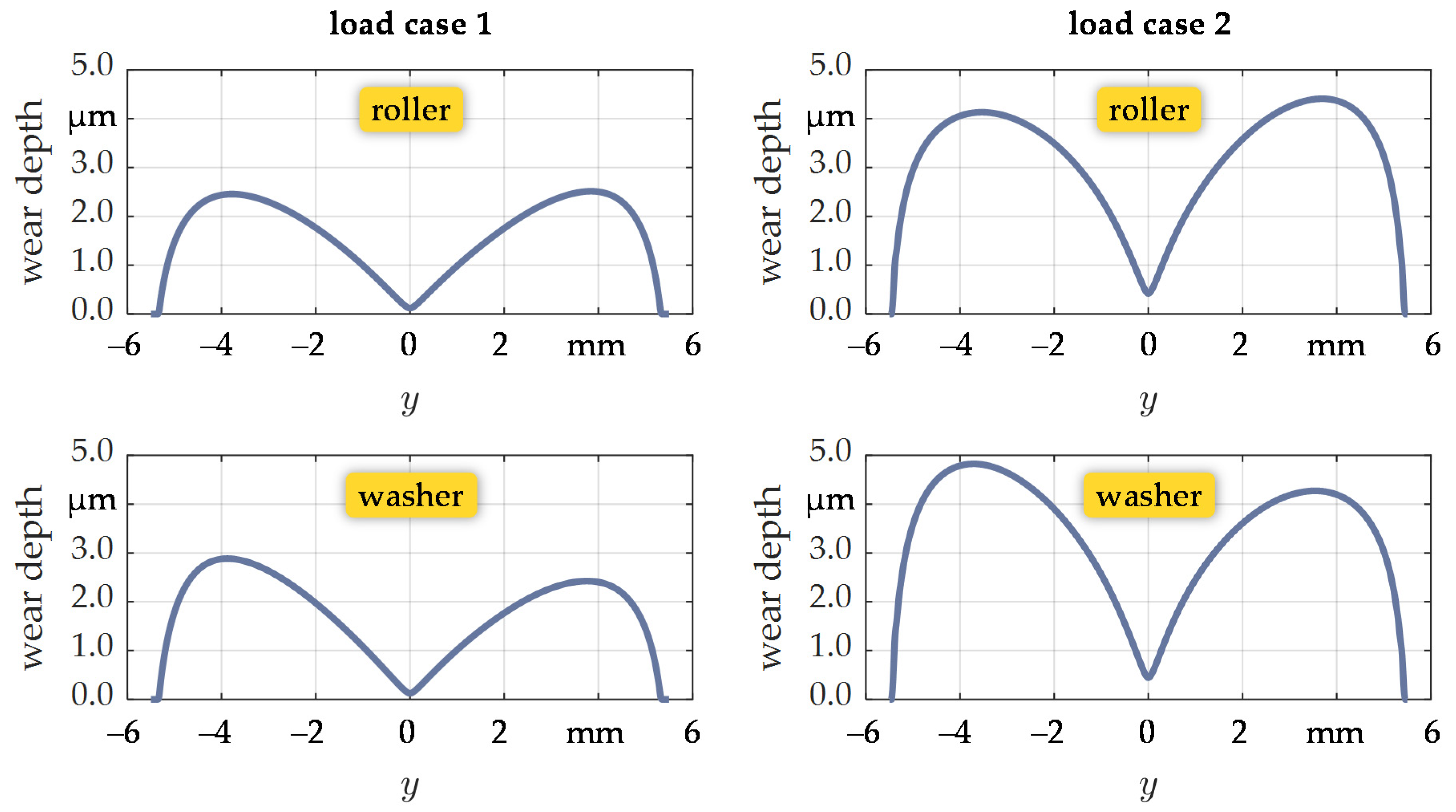
| Operating Parameters | Load Case 1 (Mixed Lubrication) | Load Case 2 (Boundary Lubrication) |
|---|---|---|
| Operating time t | 8 h | 80 h |
| Rotational speed n | 1000 min−1 | 100 min−1 |
| Load F | 50 kN | |
| Lubricant | PAO 6 at 80 °C | |
| Load Case 1 (Mixed Lubrication) | Load Case 2 (Boundary Lubrication) | |
|---|---|---|
| Wear mass | 144 mg | 280 mg |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Winkler, A.; Bartz, M.; Wartzack, S. Numerical Wear Modeling in the Mixed and Boundary Lubrication Regime. Lubricants 2022, 10, 334. https://doi.org/10.3390/lubricants10120334
Winkler A, Bartz M, Wartzack S. Numerical Wear Modeling in the Mixed and Boundary Lubrication Regime. Lubricants. 2022; 10(12):334. https://doi.org/10.3390/lubricants10120334
Chicago/Turabian StyleWinkler, Andreas, Marcel Bartz, and Sandro Wartzack. 2022. "Numerical Wear Modeling in the Mixed and Boundary Lubrication Regime" Lubricants 10, no. 12: 334. https://doi.org/10.3390/lubricants10120334
APA StyleWinkler, A., Bartz, M., & Wartzack, S. (2022). Numerical Wear Modeling in the Mixed and Boundary Lubrication Regime. Lubricants, 10(12), 334. https://doi.org/10.3390/lubricants10120334






