Effect of Engineered Roughness on the Performance of Journal Bearings Lubricated by Bingham Plastic Fluid Using Computational Fluid Dynamics (CFD)

Abstract

A journal bearing is a machine element that is used to keep the shaft rotating about its axis. The increasing demand for journal bearing applications in high-speed machines that are efficient and economical has resulted in the need for improvements to the acoustic and tribological performance of journal bearings. In order to improve the tribological and acoustic performance, this study aims to propose a novel journal bearing design by introducing a roughness condition in a specific zone of the stationary bearing surface. In addition, the impact of the application of engineered roughness on the performance of Bingham-plastic-lubricated bearings is investigated in more detail. Considering the effect of cavitation, the analysis was conducted using a 3D computational fluid dynamics (CFD) model of a journal bearing. In comparison with the Reynolds equation—which is inertialess—for lubrication analysis, the use of a 3D CFD model based on Navier–Stokes equations reflects more detailed flow characteristics. Moreover, in this work, variations in the area of surface roughness were employed, resulting in various roughness patterns on the surface of the journal bearing, so that the acoustic and tribological performances of the journal bearing were anticipated to be enhanced. The findings of this study show that under non-Newtonian lubrication of the bearing, the engineered roughness has a strong effect in altering the tribological performance. Furthermore, the well-chosen roughened surface was proven to be more pronounced in enhancing the load support and reducing the friction force. The simulation results also show that using an engineered surface has little effect on the noise of the bearing.

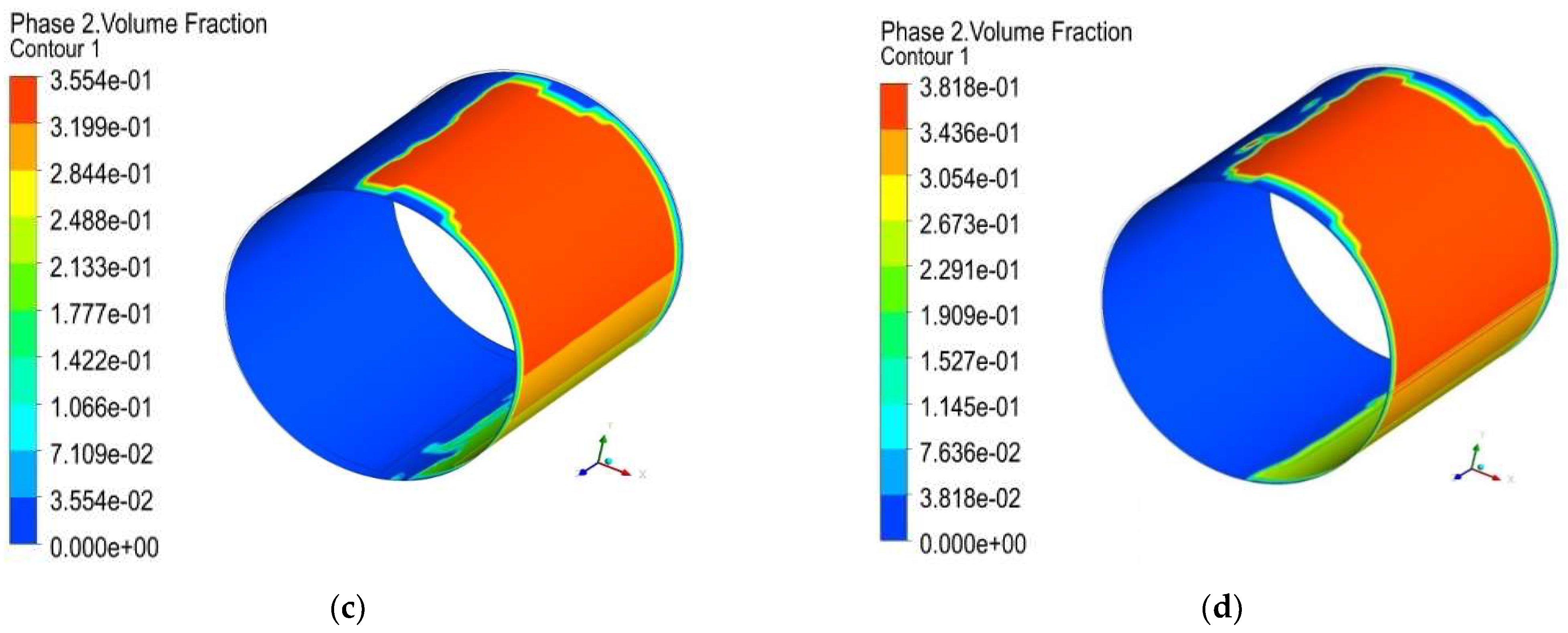
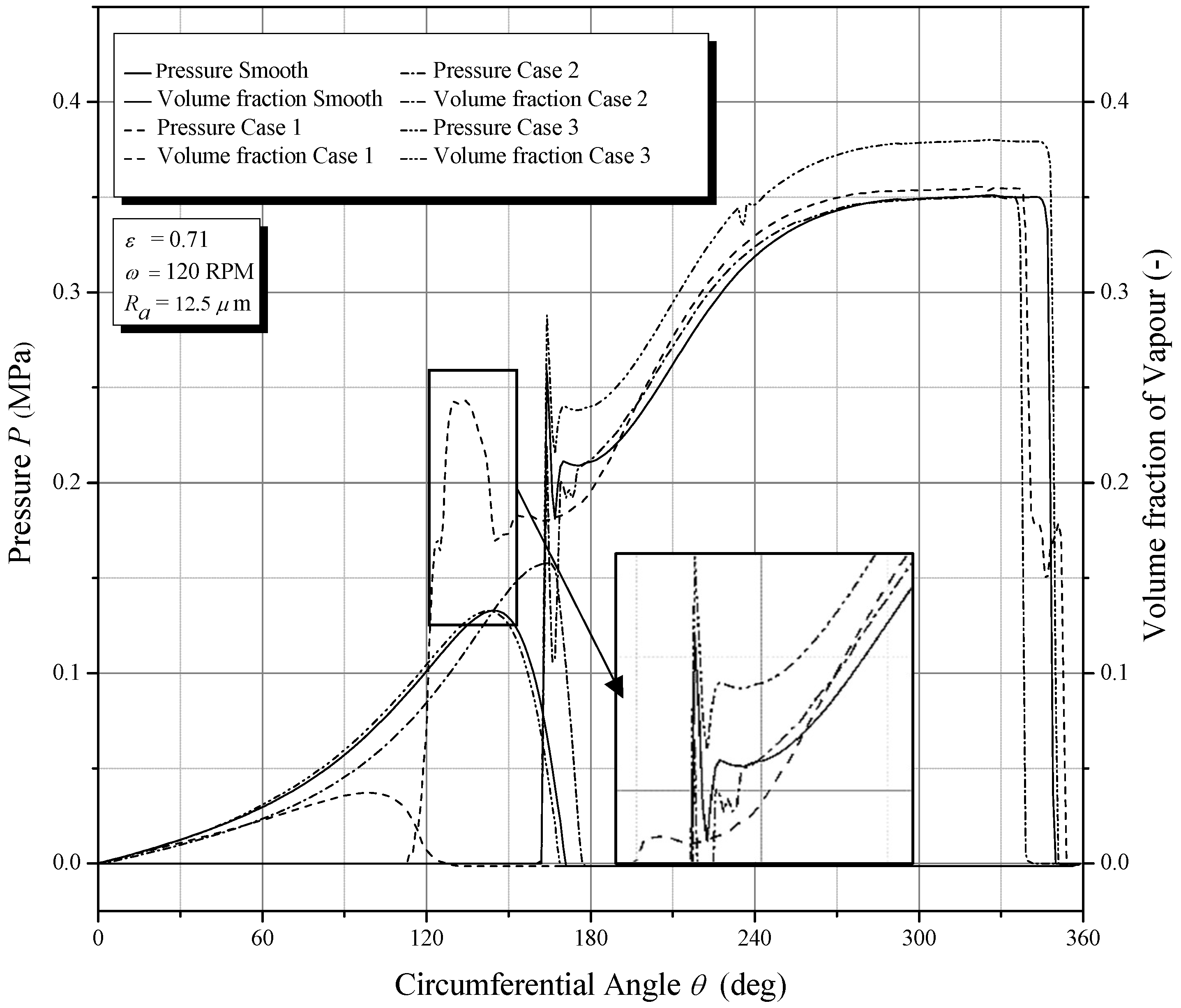
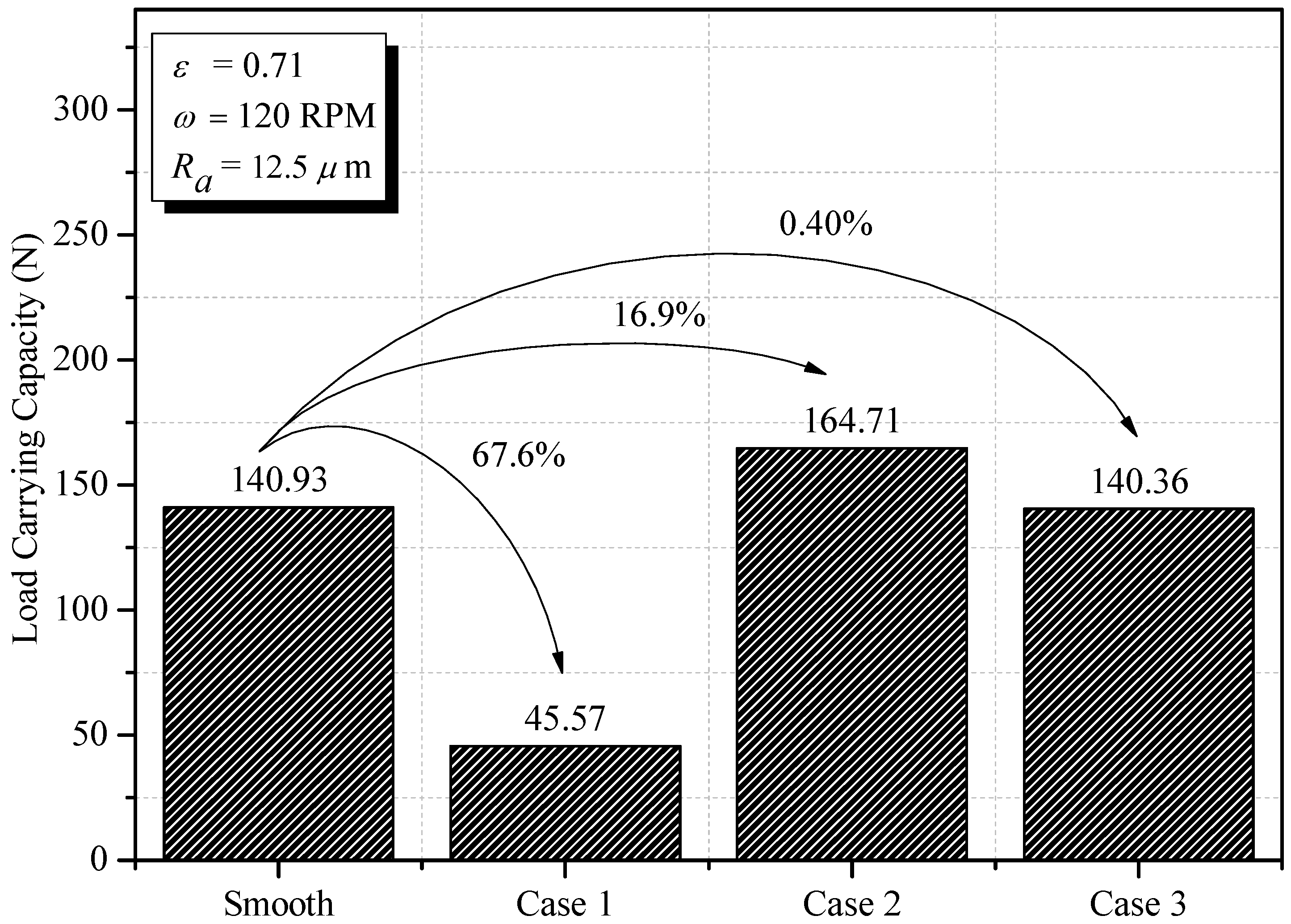
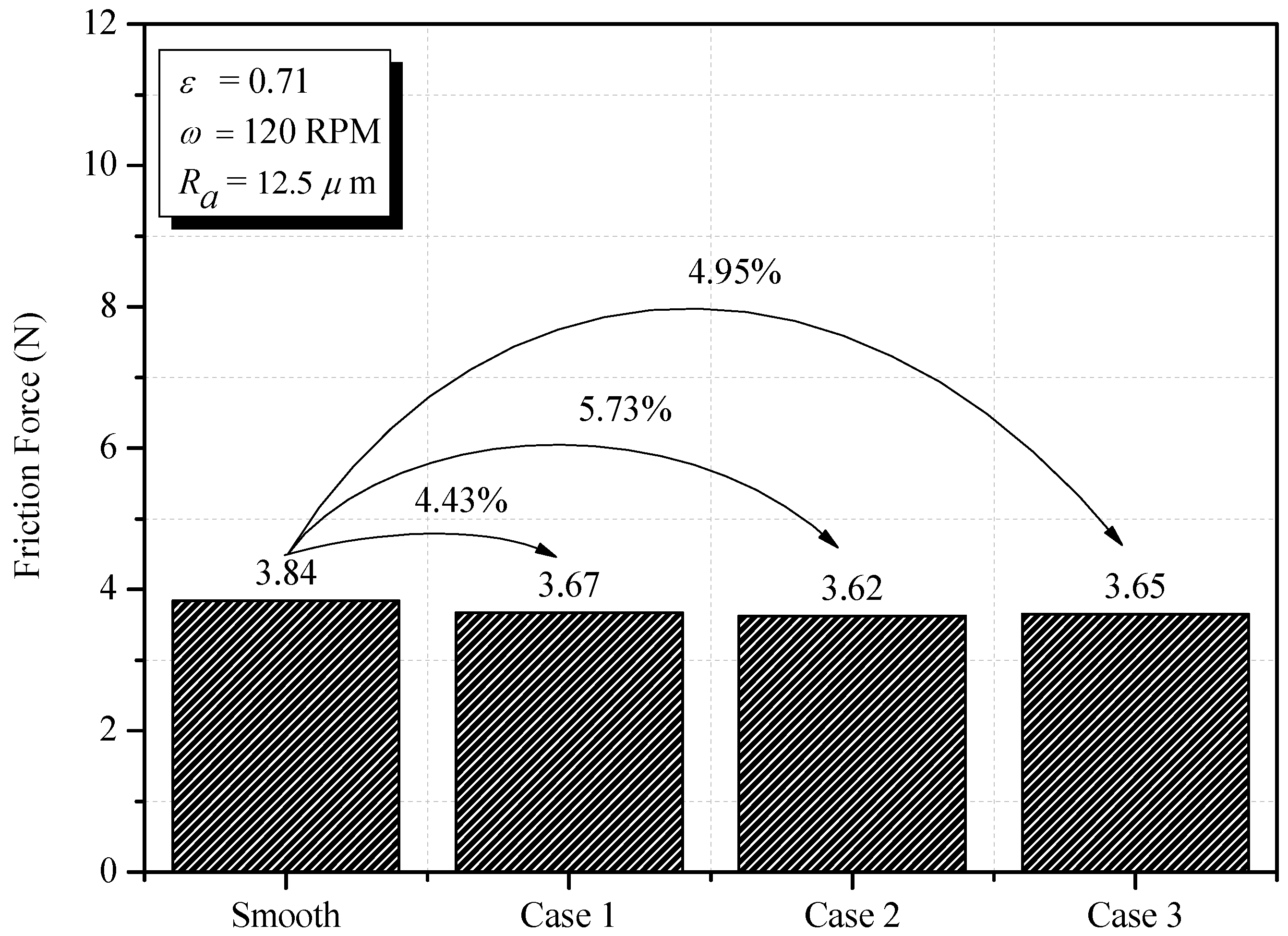
1. Introduction

In general, journal bearings are used to support high-speed rotors in turbo engines, which often operate above the critical speed acting on the rotor. These bearings provide lateral support and dynamic coefficients in the form of stiffness, damping, and mass terms, which are related to engine vibration [1]. Machining, heat treatment, assembly, destructive testing, washing, and packing are all part of the bearings’ manufacturing process. Customer satisfaction, top quality, and reliable bearing products are the primary responsibilities of any organized or disorganized bearing manufacturing unit in the current market scenario. Industry 4.0, often known as the Fourth Industrial Revolution, is a new paradigm in the digitalization of manufacturing that affords businesses a variety of benefits. Industry 4.0, which integrates numerous advancements, is an intriguing topic for nearly everyone engaged in the manufacturing sector. Future Industry 4.0 production ideas must include the development of bearing technology to maximize the added value of intelligent processes over the next decade. In order to improve the quality of a bearing, technological intervention and advancement have become essential in the manufacturing sector.

In operation, the role of lubrication in bearings is very important; one example is the selection of the lubricant. When selecting a lubricant, several criteria must be considered, including thermal properties and flow rate, both of which are mechanical parameters of the lubricating oil analyzed under different operating conditions. In general, the viscosity of the lubricant decreases with increasing temperature. For operation at high speeds and under heavy loads, oils containing highly polymeric molecules are used as viscosity index enhancers to prevent changes in viscosity with increasing temperatures. Increasing the viscosity of the lubricant also increases the bearing capacity of the modified lubricant, but the viscosity decreases with increasing shear rates. This phenomenon is called pseudoplasticity. In general, fluids that are not bound by Newton’s law of viscosity are called non-Newtonian fluids. At present, many studies in lubrication use non-Newtonian fluids. Wada et al. [2] were the first to present a significant lubrication theory for Bingham plastics in 2D lubricating films. They found that the film pressure, load-bearing capacity, and friction force of Bingham plastics were greater than those of Newtonian fluids, and that these values increased with increasing yield stress. Silva et al. [3] analyzed infinitely large plain bearings, using lubricating oils with characteristic index rheology. This index was obtained by analytical resolution of the Reynolds equation in one dimension. They showed that liquid dilatants increase the load-bearing capacity and pressure. Wang and Zhu [4] conducted a numerical study of finite journal bearings lubricated with micropolar liquids, taking into account thermal and cavitation effects. It was found that increases in load-bearing capacity and temperature values occurred in finite journal bearings compared to the use of Newtonian fluids. Gertzos et al. 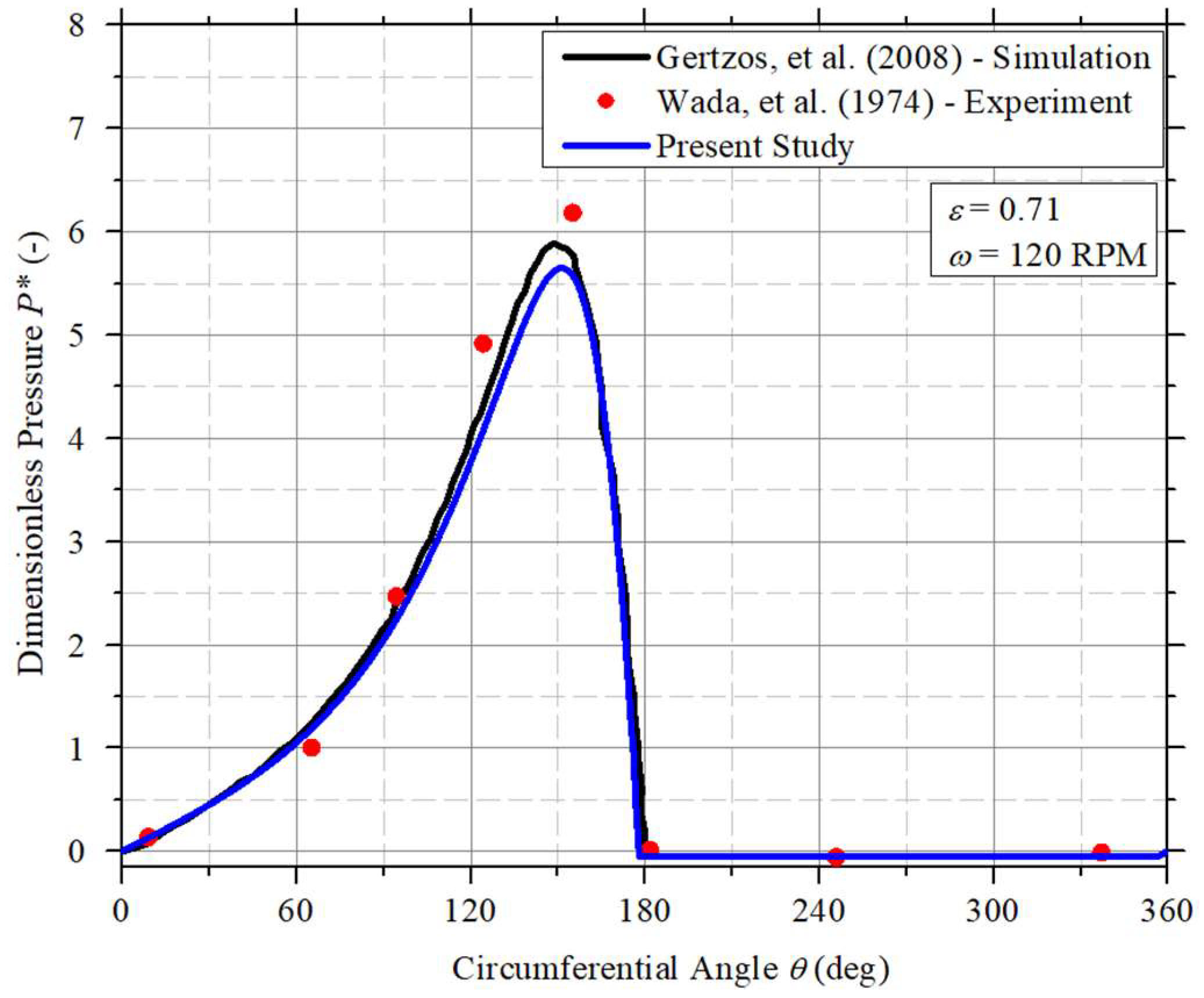[5] presented a CFD analysis of the performance characteristics of Bingham-fluid-lubricated journal bearings using different parameters. From their analysis, it can be concluded that the load-bearing capacity, film pressure, and frictional force of Bingham solids are greater than those of Newtonian fluids, and that these values increase with increasing yield stress. For low eccentricity ratios, the magnitude of the yield has little effect on the journal behavior. In electrorheological and magnetorheological fluids, the yield stress increases with changes in the electric and magnetic fields. In addition, the resulting graph can be presented in the form of a Raimondi–Boyd graph, which can be easily used in the design and analysis of Bingham-fluid-lubricated journal bearings. Garg et al. [6] investigated the thermal and rheological effects of lubricants on the performance of slot-entry hybrid journal bearing systems. Finite element analysis was used to solve the governing equations. The calculation results showed that variations in viscosity due to temperature increases and the non-Newtonian properties of the lubricant affected the bearing performance. Lin et al. [7] presented a micropolar fluid analysis of the dynamic stiffness and damping properties of parabolic-film slider bearings. The authors concluded that the non-Newtonian effect of the micropolar fluid exerts a greater influence on the increased load-bearing capacity and higher dynamic coefficient compared to Newtonian lubricants. Kango et al. [8] presented an investigation on the effects of viscous heat dissipation and non-Newtonian fluids on the performance of microtextured journal bearings with JFO (Jakobsson, Floberg, and Olsson) as the boundary condition. The authors concluded that with the presence of a micro surface texture, the average lubricant temperature decreases at low and high eccentricity ratio values. Bompos and Nikolakopoulos [9] demonstrated the use of the CFD model to analyze the effects of texture with Bingham plastic lubricants. They used two types of textures, namely, egg area and rectangular. They concluded that the egg area is promising because an increase in depth causes a 4.8% increase in eccentricity, while the performance of a rectangular area decreases. Chandra et al. [10] analyzed the performance of plain bearings with and without textures lubricated with non-Newtonian lubricants. The authors compared the characteristics of the two bearings and concluded that textured bearings provide increased stability parameters compared to journal bearings without texture. Budheeja and Verma [11] studied the stability behavior of hole-entry bearings lubricated with micropolar liquids. The influence of linear and nonlinear trajectories related to the journal motion was also studied. It was observed that micropolarity had a substantial effect on performance as a stability margin in bearings, while a fast response was achieved by nonlinear analysis. Das and Roy [12] investigated the performance parameters of four different bearing configurations and compared the results with plain journal bearings, and the analysis was carried out by considering the non-Newtonian fluids associated with the power-law model. Lambha et al. [13] considered the effects of the couple stress together with the flexibility of the bearing for elastohydrodynamic analysis of cylindrical bearings. The combined effect showed an increase in the load-bearing capacity and dynamic characteristics of JB, while the stiffness coefficient value directly increased with the increase in the variable of the couple stress. Kumar and Kakoty [14] analyzed the impact of a couple-stress lubricant on the performance of two lobe bearings by applying the Krieger–Dougherty model for viscosity calculation. The results showed a large increase in the load-bearing capacity and flow coefficient and a decrease in the friction variable. The results of the analyses conducted by the researchers mentioned above show that non-Newtonian fluids are good for improving the performance of journal bearings, with various models of approaches used—such as power-law models, Bingham, couple stress, and other performance aspects of journal bearings lubricated with non-Newtonian fluids—able to increase the load-bearing capacity and reduce the coefficient of friction in journal bearings. This is because non-Newtonian fluids have anti-wear, low-friction, and extreme pressure properties [15]. In addition, Bingham plastic lubricants were also proven to be able to enhance the stability of the bearing system and the minimum film thickness [16]. Lampaert and Ostayen [17] simulated precise thin-film lubrication for Bingham plastic fluids. The model was validated by comparing the results obtained for finite- and infinite-length journal bearings with those published in the literature, which showed good agreement. All of these studies have made significant contributions to the state of the art of non-Newtonian lubricants. However, research on Bingham plastics for journal bearings with roughness is still lacking.

Surface roughness is crucial to journal bearings’ performance and cannot be disregarded. As a result, many researchers have investigated how surface roughness affects bearings’ surfaces. The effect of surface roughness on short and long porous journal bearings lubricated with Newtonian fluids was studied by Gururajan and Prakash [18,19]. They found that there was a strong interaction between the roughness and the slip effect. Then, Naduvinamani et al. [20] studied the effects of surface roughness on porous journal bearings with couple-stress fluids. It was noted that couple-stress fluids exhibited more pronounced effects of surface roughness on the bearing characteristics than Newtonian fluids. Rahmatabadi et al. [21] conducted a study on two-lobe, three-lobe, and four-lobe hydrodynamic bearings operated with micropolar lubricants. They reported that the use of micropolar lubricants improved the static performance characteristics. The combined effects of surface roughness and non-Newtonian fluids have been studied by several authors, such as Naduvinamani et al. [22] and Ramesh et al. [23]. They found that the performance characteristics of the bearings increased with increasing roughness parameters and Hartmann number. In a study conducted by Bhaskar et al. [24], which analyzed the static characteristics of finite bearings for various L/D ratios with three types of surface roughness orientations, it was found that longitudinal surface roughness has a greater effect on the Sommerfeld number. Then, they found that the load-bearing capacity increased by 52.57% compared to journal bearings without surface roughness. Sander et al. [25] analyzed the effects of surface roughness on the dynamic properties of journal bearings ranging from hydrodynamic lubrication to mixed lubrication. They found that compared to the rough surface of the new bearing, the run-in roughness reduces the maximum contact pressure and contact area. Later, the effect of surface roughness on the transient behavior of hydrodynamic journal bearings during startup was explored by Cui et al. [26], who found that the longitudinal roughness surface configuration had a significant effect on the decrease in hydrodynamic forces. Al-Samieh [27] explored the effects of surface roughness in terms of sinusoidal waves for Newtonian and non-Newtonian lubricants. It was observed that as the wave amplitude increases, more fluctuations in the pressure distribution occur. Then, Tauviqirrahman et al. [28] revealed that the hydrodynamic pressure and load-bearing capacity decrease with surface roughness. In their case, it was assumed that the roughness was applied to the entire bushing surface. Gu et al. [29] reported that surface roughness should be taken into account in the optimization of surface texture. A study on conical hybrid journal bearings lubricated with Bingham plastics was presented by Sharma and Kumar [30]. They observed that using Bingham plastic lubricants in journal bearings enhanced the bearing performance, but at the expense of frictional power loss. Recently, Skaltsas et al. [31] demonstrated that in the case of journal bearings with stochastic roughness on the stator and rotor, the load-bearing capacity of rough bearings increases significantly—up to 14% and 10%, respectively. Furthermore, the friction coefficient of a rough bearing—defined as the ratio of friction force to load-bearing capacity—was lower than that of a smooth bearing, with a decrease reaching 5% at higher loads. The same conclusion was reached by Angadi and Naduvinamani [32], who noticed that the load-bearing capacity was enhanced by the presence of the surface roughness structure. Experimentally, it was also revealed that surface roughness has a strong effect on the friction coefficient [33]. 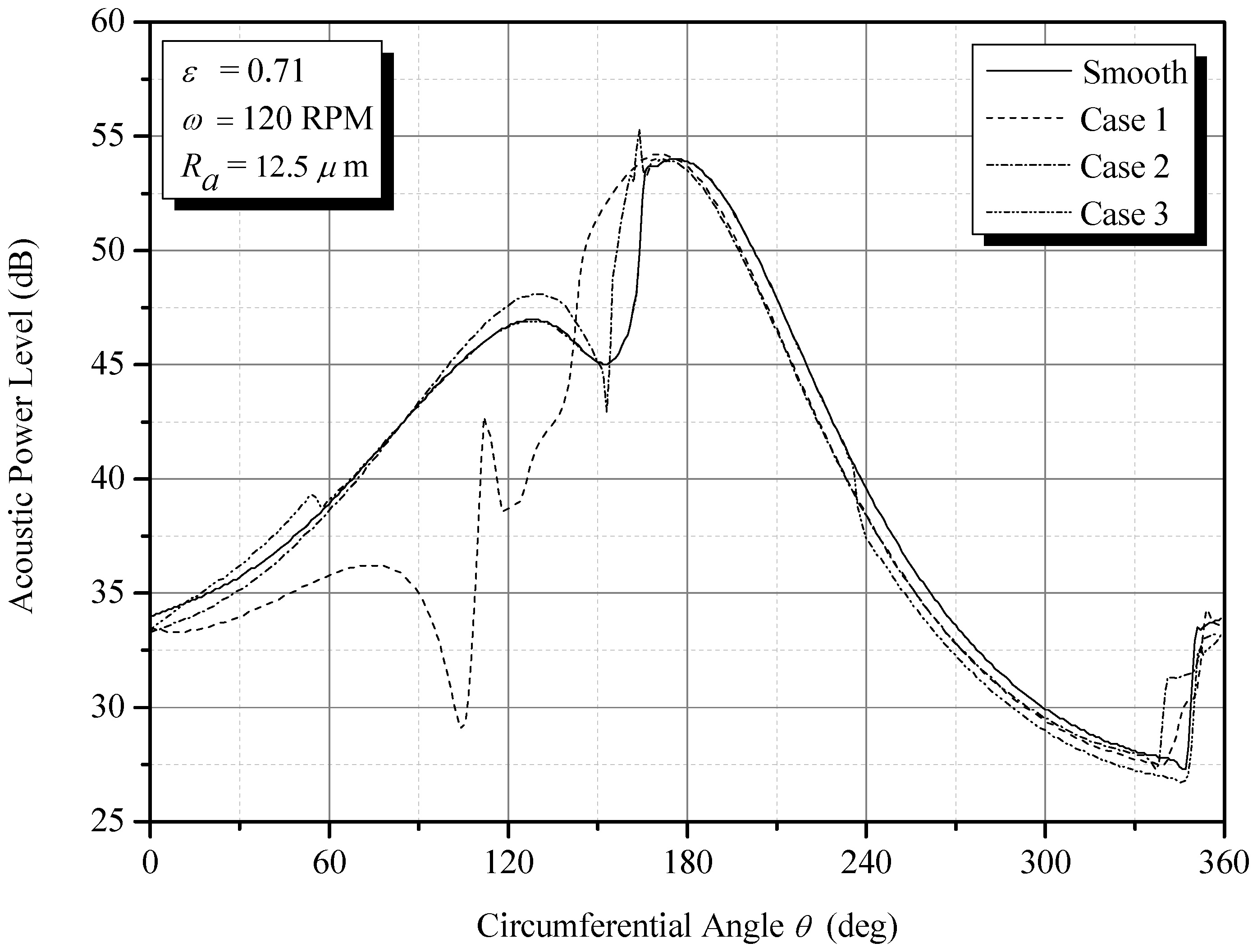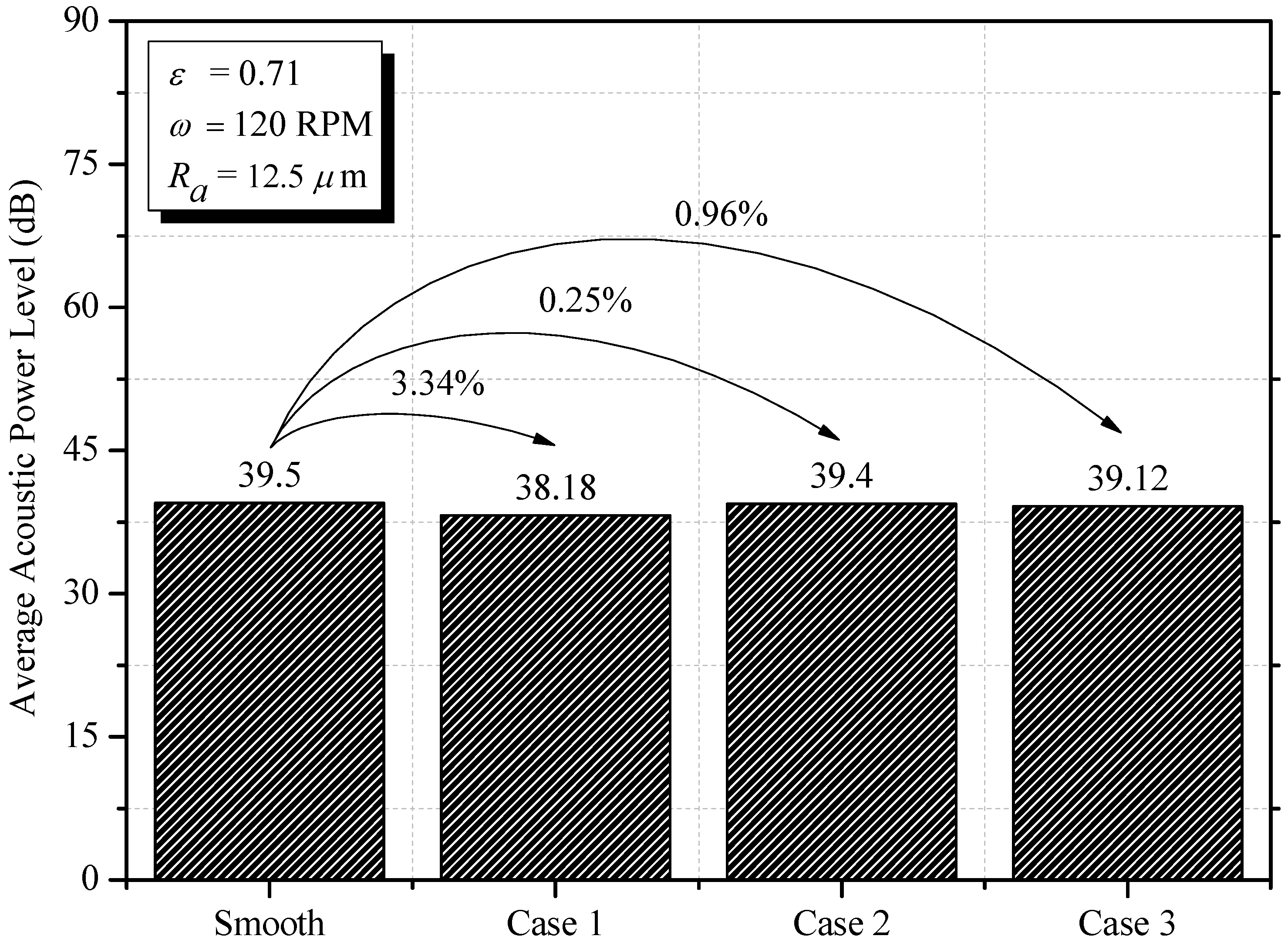Furthermore, by introducing the longitudinal roughness surface pattern, the bearing stability could be enhanced [34]. In general, a review of the relevant literature revealed that roughness characteristics have a significant impact on the tribological behavior of bearings. In addition, none of the studies on roughened journal bearings lubricated with Bingham plastics have examined acoustic behavior (noise). It remains to be seen whether engineered roughness can simultaneously achieve low noise and good tribological performance for a journal bearing.

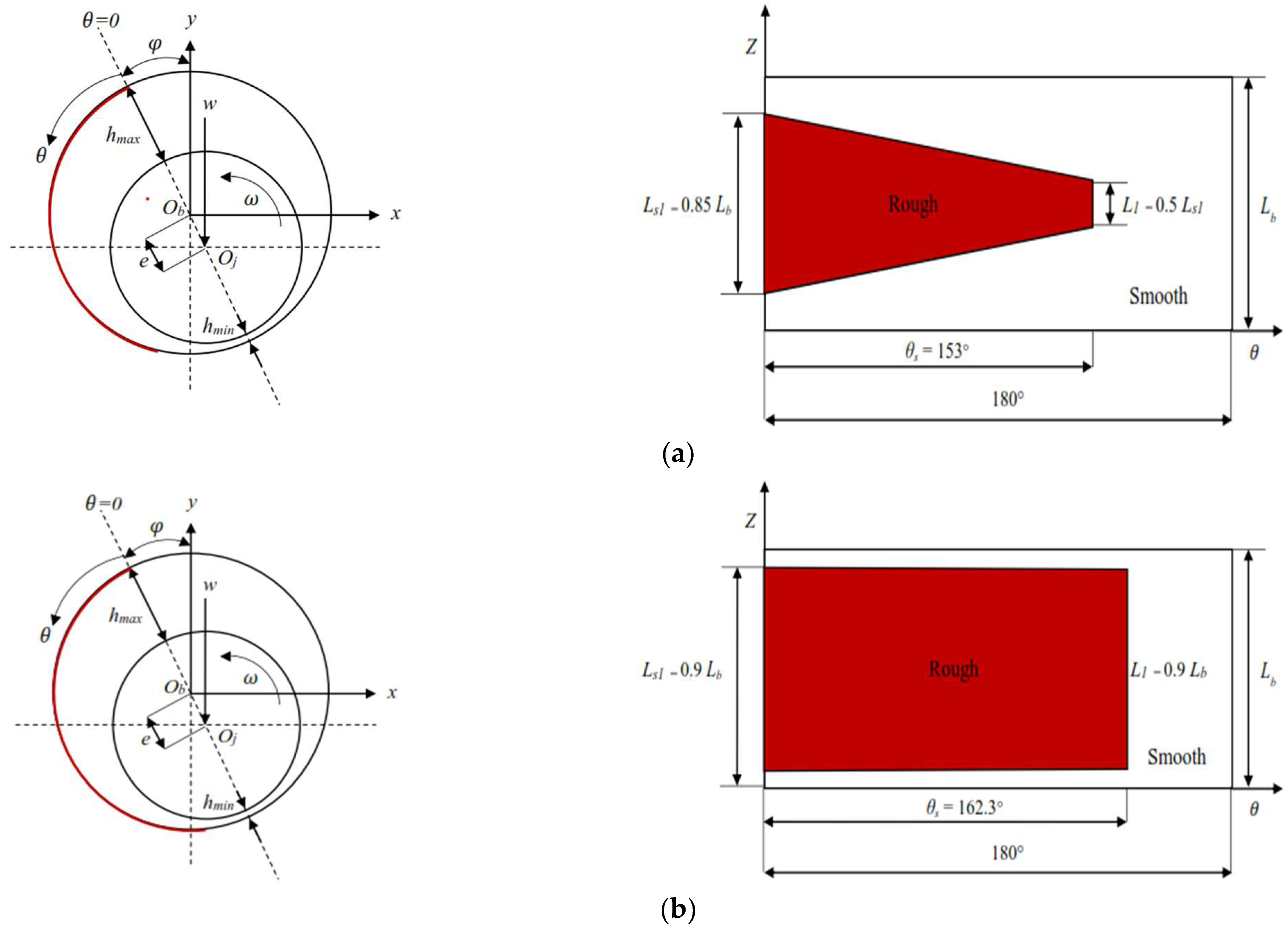
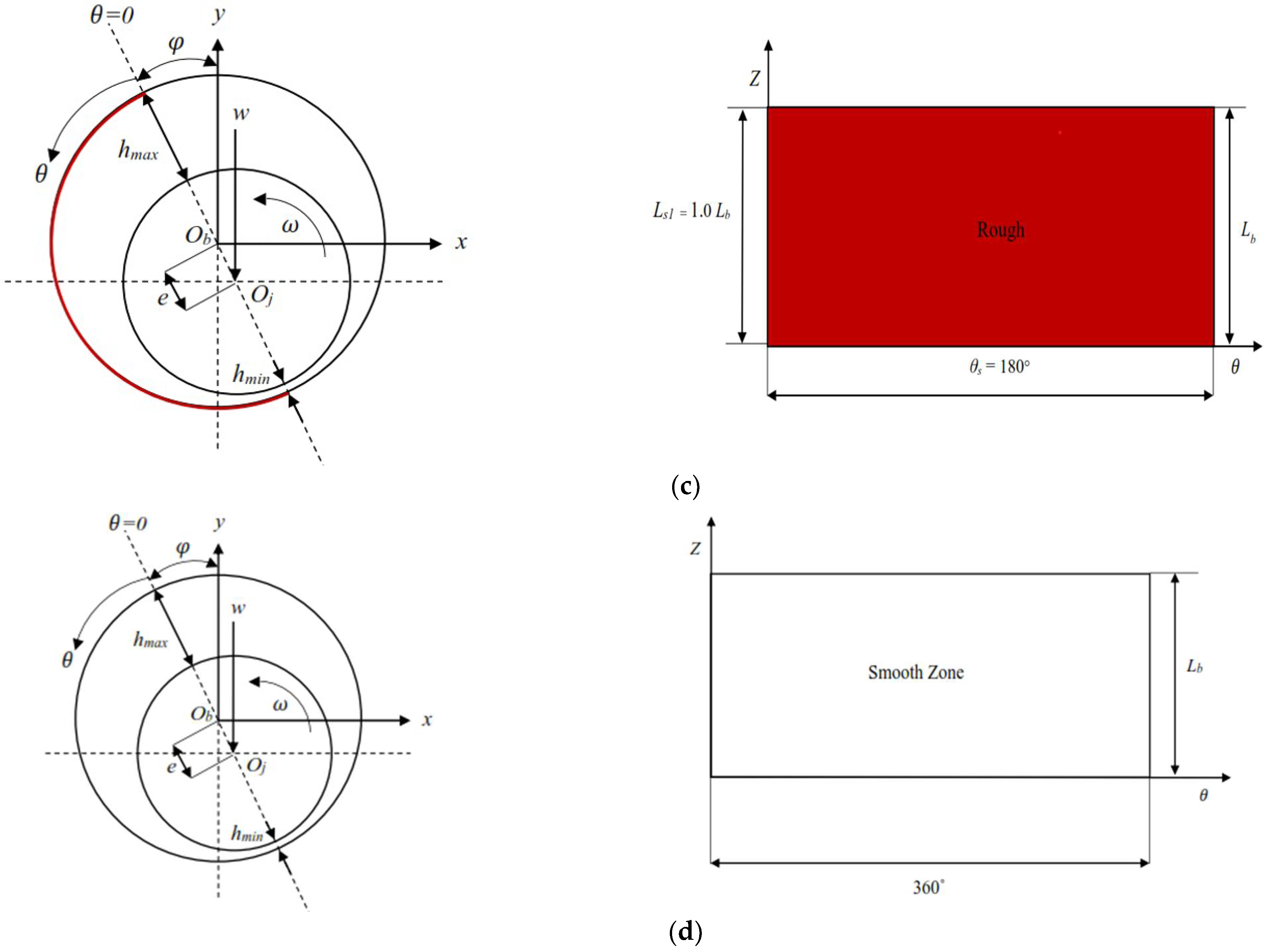
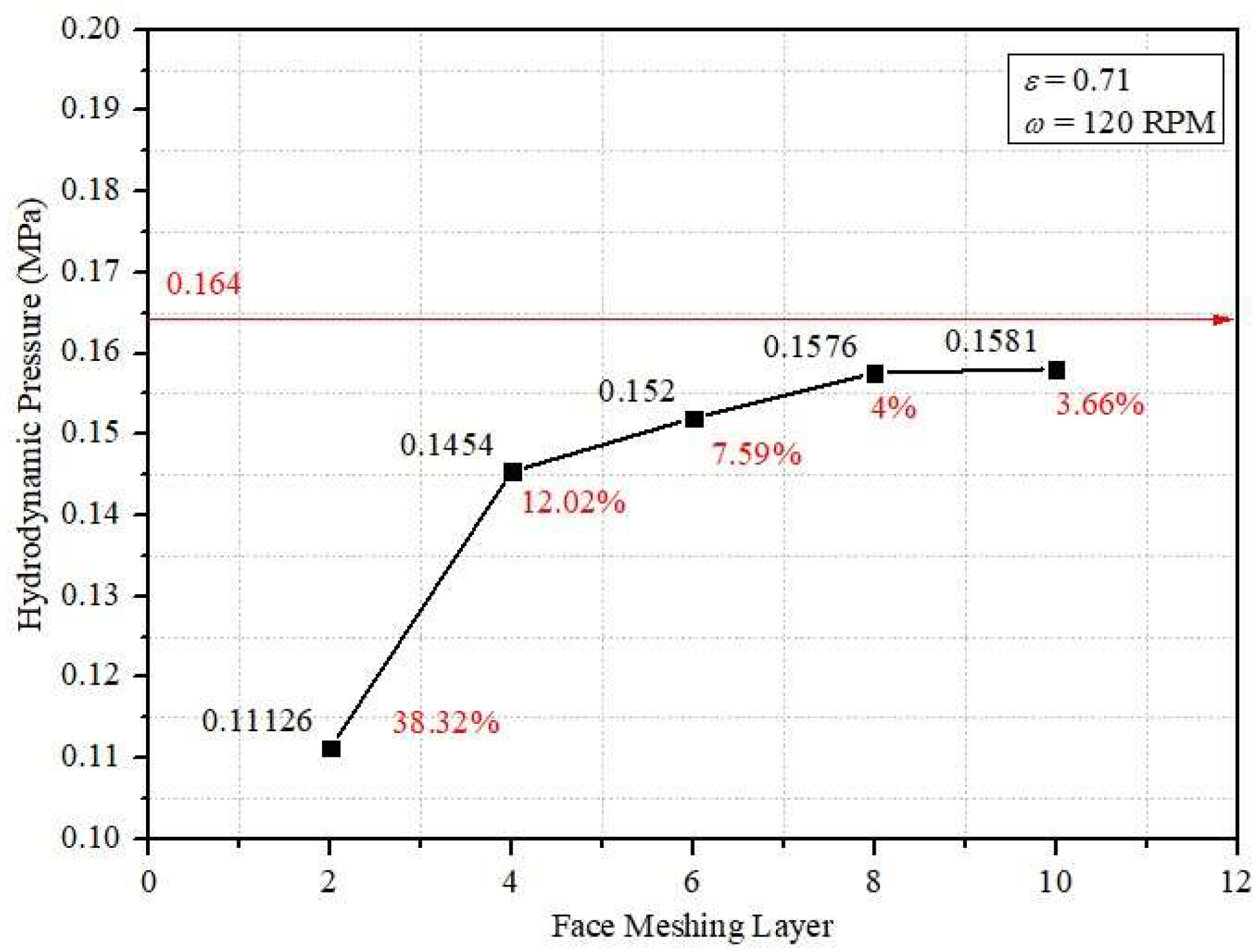
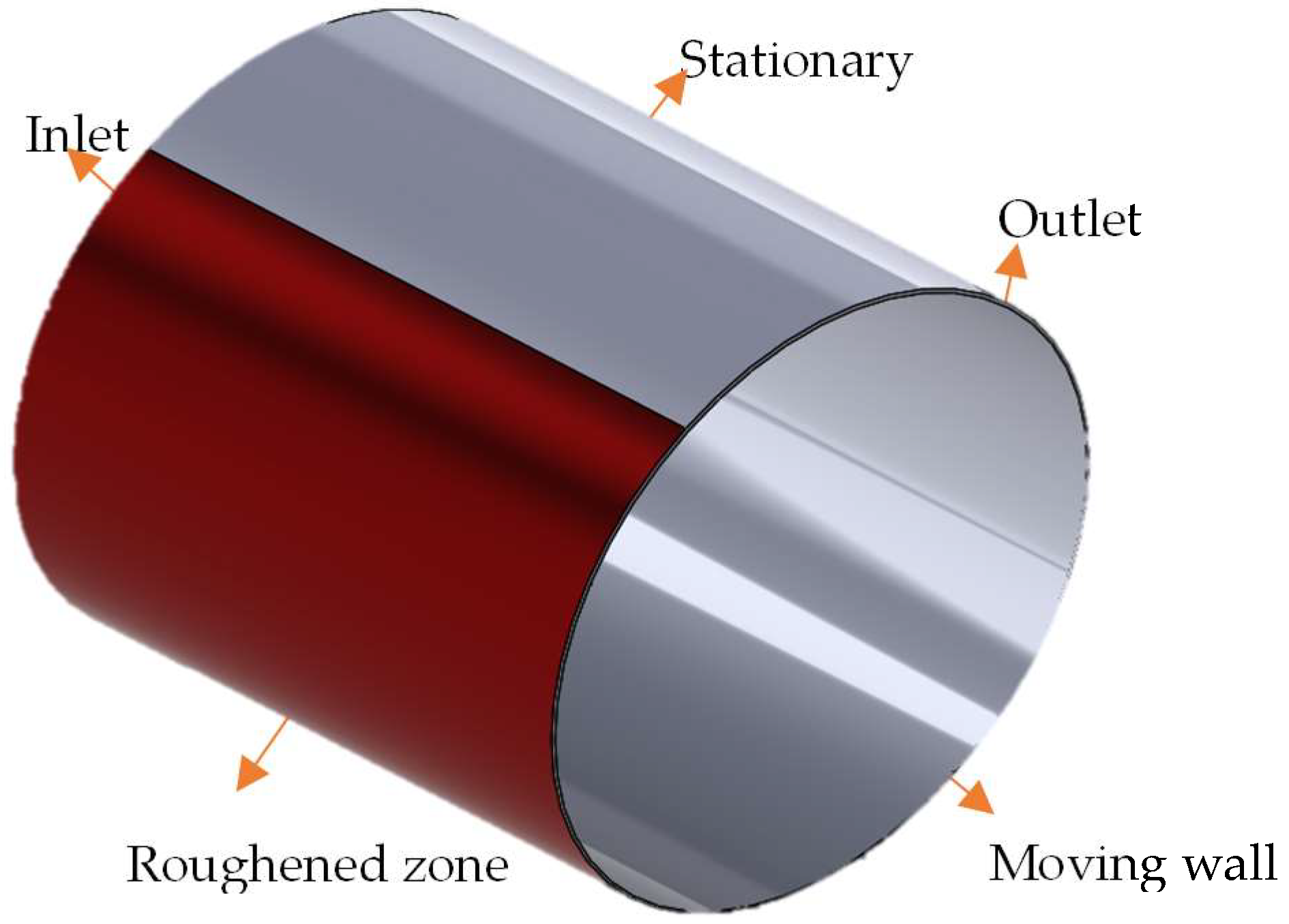
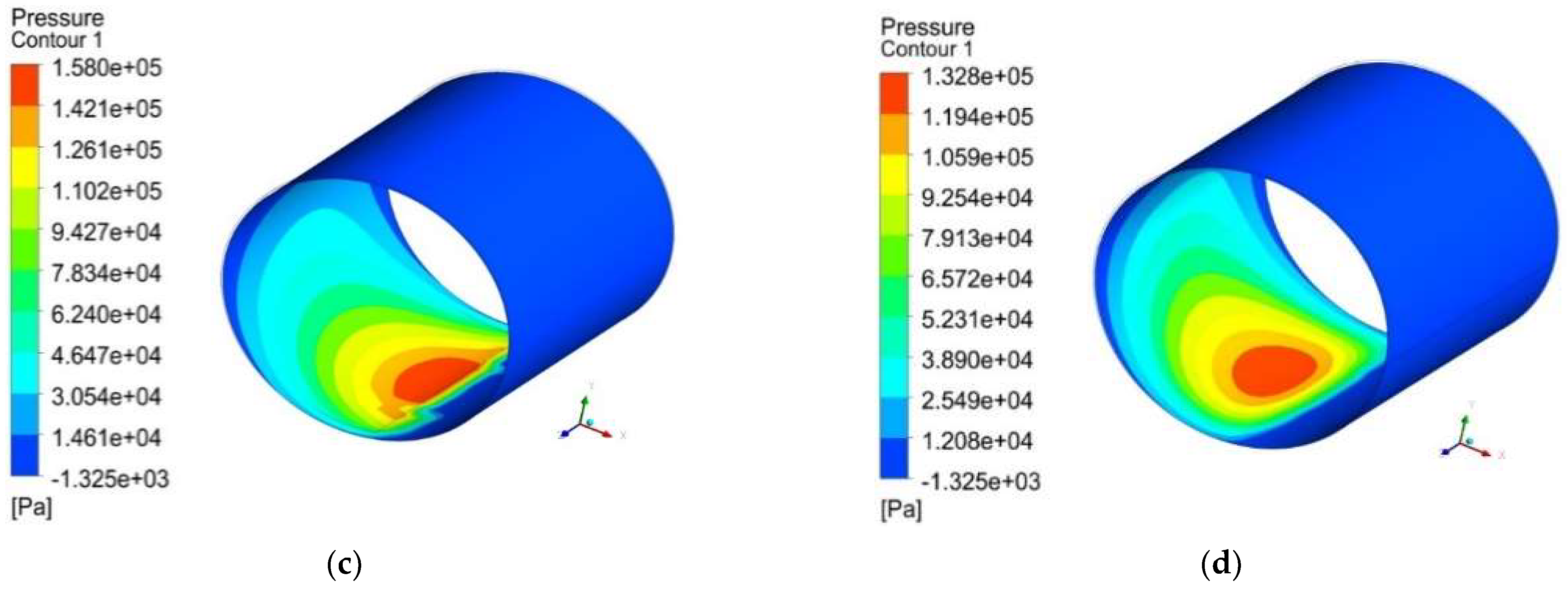
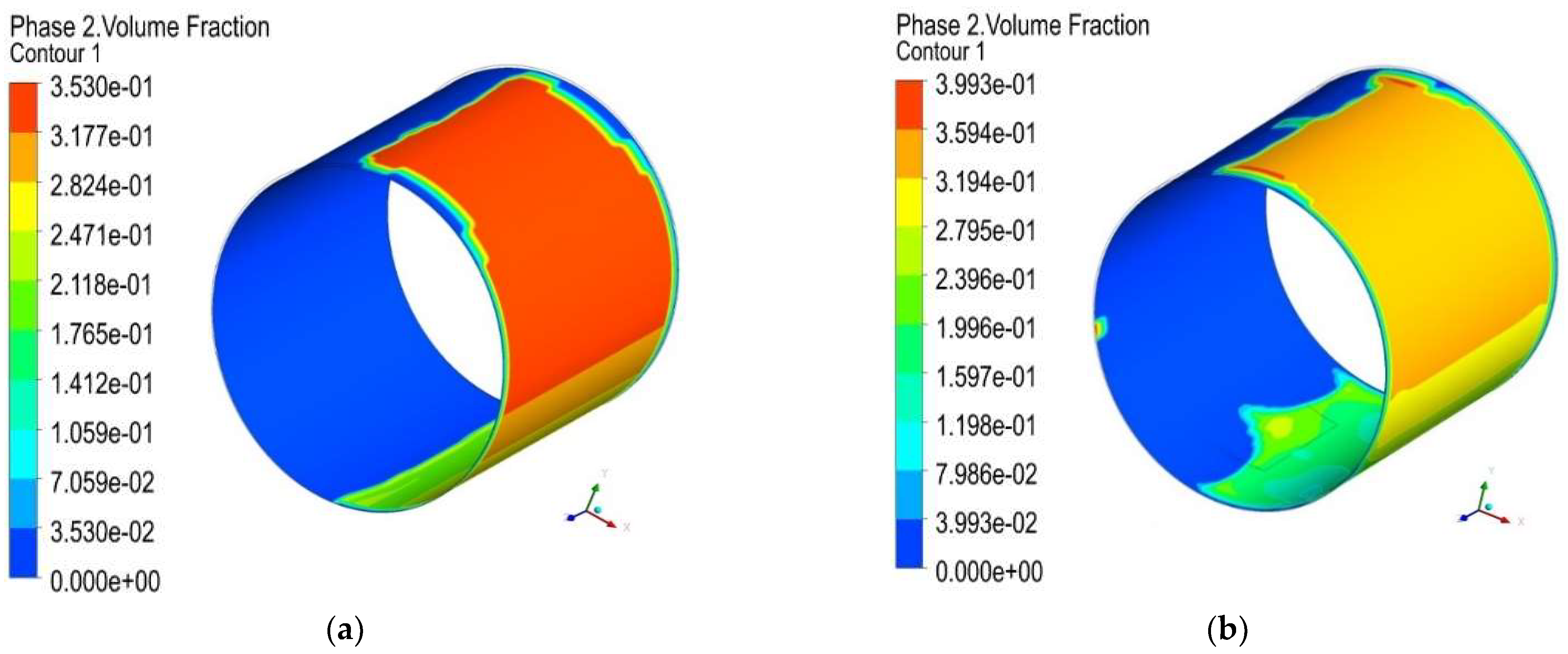
Therefore, the novelty of this study lies in the in-depth investigation of the tribological and acoustic properties of a bearing lubricated with Bingham fluids while considering roughness and cavitation. Here, in order to predict the bearing’s performance more precisely, a more thorough computational model is required. In this study, a comprehensive analysis of journal bearings lubricated with Bingham fluids with different patterns of the engineered roughness area of the bearing was carried out. Furthermore, in this work, the multiphase cavitation and turbulence were also considered to capture more realistic conditions.

2. Materials and Methods

2.1. Bingham Plastic

Non-Newtonian fluids are different from Newtonian fluids. In Newtonian fluids, the viscosity value does not depend on changes in the fluid velocity or shear rate. Meanwhile, in non-Newtonian fluids, the value of viscosity depends on changes in the fluid velocity or shear rate. Non-Newtonian fluid movements are categorized into various types, including Bingham plastic, pseudoplastic (shear thinning), and dilatant (shear thickening) [2]. A Bingham plastic is a type of time-independent viscoplastic fluid that has a yield stress. Below certain critical shear stress values, there is no permanent deformation of the fluid, and the fluid behaves like a solid. When the shear stress value passes the critical point, the material flows like a fluid. Bingham plastics are an example of viscoplastic fluids that exhibit linear shear stress behavior with respect to the shear rate after the fluid begins to flow. The viscosity equation for Bingham plastics is as follows [17]:

$${\mu }_B=\frac{\tau -{\tau }_o}{\dot{\gamma }}$$

(1)

where $\mu$_B is the viscosity of the Bingham plastic (Pa.s), $\tau$ is the shear stress (Pa), $\tau$_o is the yield stress (Pa), and $\dot{\gamma }$ is the shear rate (s⁻¹).

2.2. Surface Roughness

In this study, a sand-grain model (as shown in Figure 1) was adopted to characterize the surface roughness profile of partial coarse bearings. Here, a single layer of spheres with a diameter K_s was used to uniformly cover the surface. It should be noted that the roughness height K_s is the equivalent sand-grain roughness height and is not the same as the surface geometric roughness height. Therefore, it is necessary to use a conversion factor to convert the surface geometric roughness height to an equivalent sand-grain roughness. In this work, Ra was chosen as the parameter to represent the roughness height K_s (Figure 1). R_a represents the arithmetic mean of the roughness profile and was measured with a profilometer. For all calculations here, the value of R_a was used as the input to determine the roughness of the heterogeneous coarse/fine bearing. According to the experiment conducted by Adams et al. [35], K_s is the roughness height and R_a is the roughness level of the surface, and both have a correlation that can be defined as follows:

$$K_s=5.863R_a$$

(2)

2.3. Zwart-Gerber-Belamri Cavitation Model

In this cavitation model, all bubbles in the system are assumed to have the same size. This model assumes that the total mass transfer between phases per unit is calculated using bubble density [36,37]. The net mass transfer equation can be seen in Equation (3) below.

$$R=n\times \left(4\pi R_B^2{\rho }_v\frac{D{R}_B}{D_t}\right)$$

(3)

The vapor–liquid volume fraction (⍺) can be related to the bubble number density (n) and bubble radius (R_B) to obtain Equation (4).

$$\alpha =n\times \left(\frac{4}{3}\pi R_B^3\right)$$

(4)

By substituting Equation (3) into Equation (4), Equation (5) can be obtained.

$$R=\frac{3\alpha {\rho }_v}{R_B}\sqrt{\frac{2(P_B-P)}{3{\rho }_l}}$$

(5)

In Equation (5), the volume mass transfer value is only related to the vapor phase density 𝜌_𝑣. This equation is derived from the assumption of bubble growth (evaporation). To consider the process of disappearing bubbles (i.e., condensation), the equation can be modified as follows:

$$R_c=F\frac{3\alpha {\rho }_v}{R_B}\sqrt{\frac{2(P_B-P)}{3{\rho }_l}}sign(P_B-P)$$

(6)

where F is the empirical calibration coefficient, P_B is the bubble pressure, and P is the local pressure.

The value of the change in the mass of one bubble ($\frac{d{m}_b}{dt}$) can be seen in Equation (7) below.

$$\frac{d{m}_b}{dt}=4\pi R_B^2{\rho }_v\sqrt{\frac{2(P_v-P)}{3\rho }}$$

(7)

If n_b is the number of bubbles per unit volume, then the equation for the volume fraction of the vapor can be seen in Equation (8) below.

$$\alpha =V_b{n}_b=4\pi R_B^2{n}_b$$

(8)

As the volume of the vapor fraction increases, the nucleation density should decrease. Then, the final form of the cavitation model replaces α_v (vapor volume fraction) with α_nuc (1 − α_v) (nucleation volume fraction), as shown in Equations (9) and (10) below [32,33].

If $P\le P_v$

$$R_e=F_v\frac{3{\alpha }_{nuc}(1-{\alpha }_v){\rho }_v}{R_B}\sqrt{\frac{2(P_v-P)}{3{\rho }_l}}$$

(9)

If $P\ge P_v$

$$R_c=F_{cond}\frac{3\alpha {\rho }_v}{R_B}\sqrt{\frac{2(P-P_v)}{3{\rho }_l}}$$

(10)

where P_v is the vapor pressure, F_vap is the coefficient of evaporation (50), and F_cond is the coefficient of condensation (0.001).

2.4. Lubrication Performance

In general, many parameters can be used as guidelines in measuring the lubrication performance of journal bearings. However, in this study, the lubrication performance of journal bearings was measured by three parameters: load-bearing capacity, friction force, and acoustic power level.

The load-bearing capacity is defined as the integral of the pressure distribution profile over the journal bearing area and the total amount of load that can be supported by the distribution of film thickness on the bearing. Mathematically, the load-bearing capacity of the journal bearing can be expressed as shown in Equation (11).

$$F_{p_y}={\displaystyle \underset{A_j}{\iint }Pd{A}_j=-W}$$

(11)

where A_j is the area of the journal/shaft, p is the value of the hydrodynamic pressure generated along the surface of the journal bearing, and W is the external load.

The frictional force is defined as the integral of the shear stress along the surface of the journal bearing. It can be calculated as follows:

$$F_f={\displaystyle \underset{A}{\iint }\tau dxdz}$$

(12)

where A is the entire bearing’s area, τ is the value of the shear stress produced in the journal in the rotational direction, and dx is the integral variable indicating the differential about the x and y axes.

The acoustic power level is defined as the power per unit volume that arises due to turbulent fluid flow. Turbulence will produce sound energy as the product of the pressure and velocity components of the sound particles. The acoustic power level in decibels is 10 times the logarithm of the ratio of the sound power to the reference sound power. Equations (13) and (14) show the calculation of the acoustic power level [36].

$$L_p(dB)=10\log \left(\frac{W_p}{W_{ref}}\right)$$

(13)

$$W_p=a_{\epsilon }\rho \epsilon {\left(\frac{\sqrt{2k}}{c_0}\right)}^5$$

(14)

where L_p is the acoustic power level (dB); W_ref is the reference sound power, which is assumed to be 10–12 W/m³; W_p is the sound power produced by the bearing; k is the turbulent kinetic energy value; ɛ is the turbulent dissipation rate; and a_ɛ is a constant with a value of 0.1.

3. Simulation Methods

3.1. Model

The journal bearing geometry used in this study adopted the geometry of the journal bearing in [5].

Table 1. Journal bearing parameters.

Parameter	Symbol	Value	Unit
Bearing
Journal diameter	$D_j$	49.53	mm
Bushing diameter	Db	50	mm
Bushing length	$L_b$(Z)	50	mm
Radial clearance	$C$	0.235	mm
Roughness level	Ra	12.5	$\mathsf{\mu }$m
Lubricant
Liquid lubricant density	$\rho$	960	kg/m3
Liquid lubricant viscosity	$\mathsf{\mu }$	0.2	Pa.s
Vapor density	${\rho }_v$	0.02556	kg/m3
Vapor viscosity	${\mu }_v$	1.256 × 10−5	Pa.s

shows the dimensions of the bearing as well as the characteristics of the lubricating fluid considered here.

To create the partially roughened bearing, the roughness was engineered at the leading edge of the bearing. The area of the surface roughness was inspired by the hydrophobic journal bearing in the work of Cui et al. [38]. To determine the geometry of the surface roughness area, Equations (15)–(17) can be used.

$$\alpha =\frac{B_{Sr}}{B_l}$$

(15)

where $\alpha$ is a coefficient with a value with a range of $0\le \alpha \le 2$, B_Sr is the width of the surface roughness and B₁ is the width of the convergent area (i.e., 0.5 times the circumference of the journal bearing).

$$\gamma =\frac{L_{Sr}}{L_b}$$

(16)

where γ is a coefficient with a value with a range of 0 ≤ γ ≤ 1, L_Sr is the initial length of the surface roughness area, and L_b is the length of the bearing bushing.

$$\lambda =\frac{L_l}{L_{Sr}}$$

(17)

where λ is a coefficient with a value with a range of 0 ≤ λ, L_Sr is the initial length of the surface roughness area, and L_l is the final length of the surface roughness area. Figure 2 presents schematics of the four cases of journal bearings simulated here. In this work, there were three patterns of engineered roughness (Cases 1, 2, and 3). To determine the effects of the engineered surface on the bearings’ behavior, all patterns were compared to smooth bearings.

3.2. Meshing

In the present work, the meshing was performed using a hexahedral meshing model. The detailed meshing criteria used for constructing the meshed domain can be seen in

Table 2. Meshing criteria.

Mesh Criteria	Description
Edge sizing	360 division
Face meshing	8 layers of division
Face meshing	25 layers of division
Method	Multizone
Number of elements	72,000
Number of nodes	84,240
Maximum skewness	0.42322
Minimum skewness	5.55489 × 10−3
Average skewness	0.2647

and Figure 3.

In order to validate the model verification, it is necessary to perform a mesh-independent study. Figure 4 reveals the results of the grid test, with an eccentricity of 0.71 and a shaft speed of 120 RPM. It should be noted that additional meshing was carried out by increasing the degree of meshing on the face layer. From Figure 4, it seems that stable results began to be achieved at 8 face layers. As a result, the 8 face layers were chosen as the reference meshing configuration to be used for all subsequent simulations, with the main consideration of less computational effort but accurate results.

3.3. Defining Materials and Boundary Conditions

In this section, the definition of the boundary conditions and loading is presented. The cavitation used in this study was Zwart–Gerber–Belamri, with the vaporization pressure value (P_v) set to 100,000 Pa. Concerning the viscosity modeling, the Herschel–Bulkley model combines the Bingham and power-law effects on the fluid for a low strain rate $[\dot{\gamma }<\left(\frac{{\tau }_0}{{\mu }_0}\right)]$. When the strain rate increases and exceeds the ${\tau }_0$ limit, the fluid behavior is described by the power-law. The Herschel–Bulkley model provided by ANSYS becomes identical to the Bingham model when k = $\mu$, n = 1, and $\left(\frac{{\tau }_0}{{\mu }_0}\right)\to 0$. The equations of the Herschel–Bulkley model are as follows:

$$\tau \equiv {\mu }_a\dot{\gamma }={\tau }_0+k\left[{\dot{\gamma }}^n-{\left(\frac{{\tau }_0}{{\mu }_0}\right)}^n\right]$$

(18)

Table 3. Herschel–Bulkley model input values [5].

Model	Input	Value
Herschel–Bulkley	Consistency index (k)	0.2 kg sn−2/m
	Power-law index (n)	1
	Yield viscosity	500 Pa.s
	Yield stress	213.8 Pa

shows the material definition of the lubricant used for the simulations.

In this study, the realizable k-ε model for turbulence was adopted because it is suitable for flows with complex shear forces and involves rapid strain, sufficient eddies, vorticity, and local transitional flows with extreme pressure gradients. The journal bearing shaft moves with $\omega$ velocity with respect to the stationary housing surface. Simulations were carried out using pressure-inlet and pressure-outlet boundary conditions. The pressure values at the inlet and outlet of the journal bearing were set according to the reference journal. In this work, the roughness height Ks used was 0.073 mm. This value was obtained based on the calculations in Equation (2).

Table 4. Boundary conditions.

Boundary	Condition
Inlet	Pressure inlet (0 Pa)
Outlet	Pressure outlet (0 Pa)
Stationary wall	Partial roughness with Ra = 12.5 µm
Moving wall	Rotating wall (ω = 120 RPM)

describes the boundary conditions for the computations in detail.

In the numerical-based solver in ANSYS, two types of solver are available to solve the fluid flow simulations performed: a pressure-based solver, and a density-based solver. In this work, the pressure-based solver was adopted because it is feasible for incompressible fluid flow problems with low fluid flow rates, while density-based solvers are more specialized to solve compressible fluid flow problems with high fluid flow rates.

Table 5. Solution method used in this study.

Solution Method
Pressure–velocity coupling
Scheme	SIMPLE
Spatial discretization
Gradient	Least squares cell-based
Pressure	PRESTO!
Momentum	First-order upwind
Volume fraction	QUICK
Turbulent kinetic energy	First-order upwind
Turbulent dissipation rate	First-order upwind

provides more information on the spatial discretization used in this study for the variables of gradient, pressure, momentum, and volume fraction. In addition, to control the solution from the simulation, the under-relaxation factor (URF) must be determined. Thus,

Table 6. Solution controls for setting the under-relaxation factor.

Factors	Value
Pressure	0.2
Density	1
Body forces	1
Momentum	0.1
Volume fraction	7 × 10−5
Turbulent kinetic energy	0.5
Turbulent dissipation rate	0.5
Turbulent viscosity	0.8

shows the under-relaxation factor used in the case of this study.

4. Results

4.1. Validation

With the aim of validation, this section presents the comparison between the results of the present study and the experimental results obtained by Wada et al. [2] and by Gertzos et al. [5]. All conditions were identical to the simulation in [5]. Figure 5 shows the validation results in terms of pressure distribution. Based on Figure 6, it is evident that the CFD simulation results and the published works are in good agreement, indicating that the current numerical method is valid. It should be noted that, in Figure 6, the dimensionless parameter is used as discussed in [5], as follows:

$$P^{*}=\left(P-P_a\right)\times C^2/\left({\mu }_0\times \omega \times R_J^2\right)$$

(19)

where P is the pressure formed on the journal bearing, and P_a is the ambient pressure.

4.2. At Varied Roughness Patterns

4.2.1. Pressure Distribution

Figure 7 shows the contours of pressure distribution for each of the cases. From Figure 7, it can be seen that the maximum pressure in each case differs, indicating that when varying the surface roughness area of the journal bearing using Bingham lubricants there is a difference in the maximum pressure. In smooth bearings, the maximum pressure generated was 0.1329 MPa, while in Cases 1, 2, and 3, the maximum pressure generated was 0.0453 MPa, 0.158 MPa, and 0.1328 MPa, respectively. Figure 7 indicates that when the roughness pattern is partially applied to the rectangular zone (as in this case), the improvement of the pressure is highlighted. When the roughness zone is applied to all stationary zones, the roughness has a negative impact on pressure improvement.

4.2.2. Volume Fraction

Figure 8 depicts the contours of the vapor volume fraction inside the journal bearing in each case. Given the variation in the surface roughness area of the journal bearing, it is evident that each case of cavitation has a different trend. It seems that compared to the smooth bearing, the cavitation area of roughened journal bearings—whether in partial (i.e., Cases 1 and 2) or full (i.e., Case 3) condition—has a smaller area. In the other words, from the physical perspective, the application of the roughness tends to retard the cavitation process.

To explore the bearings’ behavior in detail, the pressure distribution and volume fraction of the vapor were evaluated in the mid-plane journal bearing area, as shown in Figure 9. It is observable that the increase in maximum pressure varies significantly between cases. In the case of a smooth bearing, the pressure increase in the journal bearing begins at 0–148°; in Case 1, the pressure increase in the journal bearing begins at 0–103°; in Case 2, the pressure increase in the journal bearing begins at 0–168°; and in Case 3, the pressure increase in the journal bearing begins at 0–147°.

According to the simulation results, the variation in the area of roughness on the journal bearing can have a significant effect on the pressure distribution and the maximum pressure value in the journal bearing. This occurs because the inner wall of the journal bearing has a non-uniform surface, which slows the fluid flow and increases the hydrodynamic pressure within the bearing. Cavitation that occurs in each case as a result of variations in the area of surface roughness produced with the Bingham lubricant in the mid-plane journal bearing area has a variety of starting points. For example, in the case of smooth bearings, the cavitation starting point begins at an angle between 170° and 60°, while for Case 1 the initial point of cavitation begins at the circumferential angle of 133–360°. The larger the cavitation in the journal bearing, the larger the pressure-generation area in the journal bearing, as depicted in Figure 9.

4.2.3. Lubrication Performance

Figure 10 compares the load-bearing capacity of the roughened journal bearings to that of the smooth bearing. It can be seen that in Cases 1, 2, and 3 with the same roughness value (R_a = 12.5 $\mathsf{\mu }$m), the load-bearing capacity varies in each case. Case 1 (α = 0.85) has a load-bearing capacity of 45.57 N, Case 2 (α = 0.9) has a load-bearing capacity of 164.71 N, Case 3 (α = 1.0) has a load-bearing carrying of 140.36 N, and the load-bearing capacity of the smooth bearing is 140.93 N.

Figure 11 shows the comparison of the friction force values in each case of the journal bearings. Observations indicate that with the same roughness value (Ra = 12.5 µm) but with variations in the area of the surface roughness in each case, the friction force values vary in such a way as to impact the performance of the journal bearing. Figure 11 demonstrates that the friction force of the heterogeneous rough/smooth bearings decreases irrespective of the roughness pattern. The reduction in frictional force ranges from 4–6%, depending on the roughness pattern. Tala-Ighil et al. [39,40] concluded that the optimal design of the journal bearing’s texture area is highly dependent on the texture geometry and operating conditions. The surface modification highlighted in [39,40] is identical to the surface roughness employed here. This study demonstrates that by varying the area of the surface roughness on the journal bearing, it is possible to reduce the friction force in the journal bearing.

Figure 12 illustrates the distribution of acoustic power levels of the journal bearings. The distributions are evaluated at the mid-plane of the bearing. In Figure 12, it can be observed that the maximum acoustic power level is achieved at an angle of 180° for the smooth bearing geometry and that of each case given variations in the area of surface roughness. According to Meng et al. [41], turbulence kinetic energy and turbulence eddy dissipation also affect acoustic power levels. Given the variation in the area of surface roughness on the journal bearing, the angle of increase in the value of acoustic power level shifts in each case where the acoustic power level increases. In Case 1, the angular shift increases the value of the acoustic power level by 20° earlier than the smooth bearing. In Cases 2 and 3, the angular shift increases the value of the acoustic power level by 20° earlier than the smooth bearing. In accordance with the research conducted by Meng et al. [42], it was found that an increase in texture or roughness would decrease the acoustic power level. This phenomenon can be explained by the speed of the lubrication distribution, where the turbulent flow of the lubricant becomes smaller overall or it becomes more difficult to experience turbulence when the surface has a high texture or roughness value, thereby reducing the acoustic magnitude that occurs in the fluid.

Figure 13 compares the trends of the average acoustic power level that occurred in each journal bearing case. From Figure 13, one can observe that the values obtained are different, with the smooth bearing having a value of 39.5 dB, Case 1 with a value of 38.18 dB, Case 2 with a value of 39.4 dB, and Case 3 with a value of 39.12 dB. Additionally, the average acoustic power level of the engineered roughened bearing is lower than that of the smooth bearing. In Cases 1, 2, and 3, the average acoustic power level decreases by 3.34%, 0.25%, and 0.96%, respectively. This is because a significant increase in turbulence will result in a decrease in the acoustic power level.

5. Conclusions

This study provides a comprehensive analysis of the tribological and acoustic behavior of engineered roughened journal bearings lubricated with a Bingham plastic lubricant. Key performance parameters such as hydrodynamic pressure, load-bearing capacity, friction force, vapor volume fraction, and acoustic power level were investigated. Here, journal bearings with different variations in their surface roughness patterns were studied and then compared with conventional smooth journal bearings. On the basis of the aforementioned results and discussion, the following conclusions can be drawn:

• Variations in the pattern of roughness on the journal bearing can have a significant impact on the pressure distribution as well as the maximum pressure value and the volume fraction of the vapor in the bearing.
• The highest tribological performance of the roughened journal bearing can be attained when the roughness pattern has a partially applied rectangular shape on the stationary surface. In comparison to a conventional smooth bearing, this engineered heterogeneous rough/smooth bearing increases the load-bearing capacity by up to 16.9% and reduces the friction force by up to 5.7%.
• Within the specified roughness level, eccentricity ratio, and rotational speed of the bearing, the engineered roughened bearing has up to 3% lower acoustic performance than the smooth bearing.