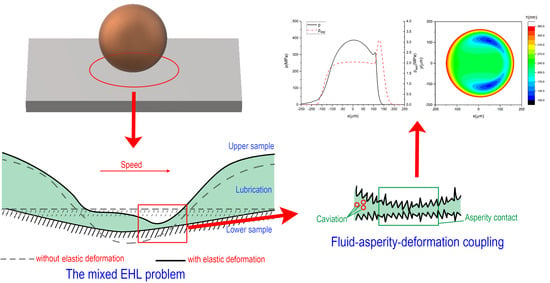
Mixed EHL Problems: An Efficient Solution to the Fluid–Solid Coupling Problem with Consideration of Elastic Deformation and Cavitation
Abstract
1. Introduction
2. Numerical Methods
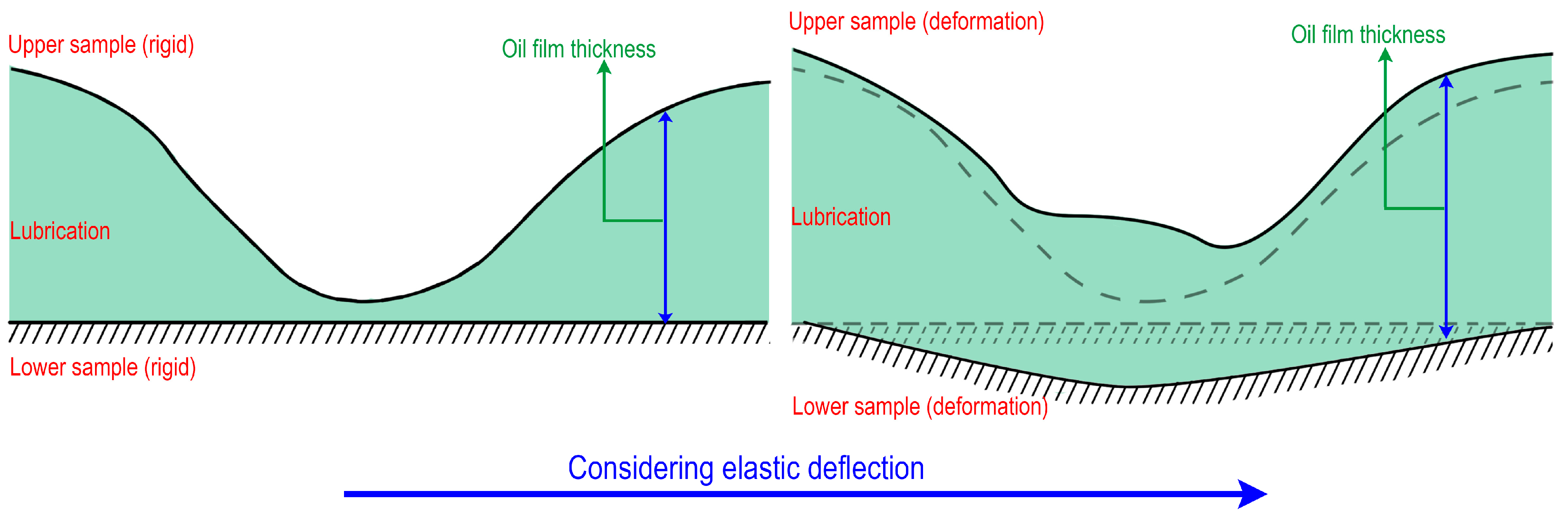
2.1. Analysis of Mixed EHL Problems
2.2. Elastic Deflection
2.3. Fluid Mechanics
2.4. Lubricant Property
2.5. Contact Mechanics
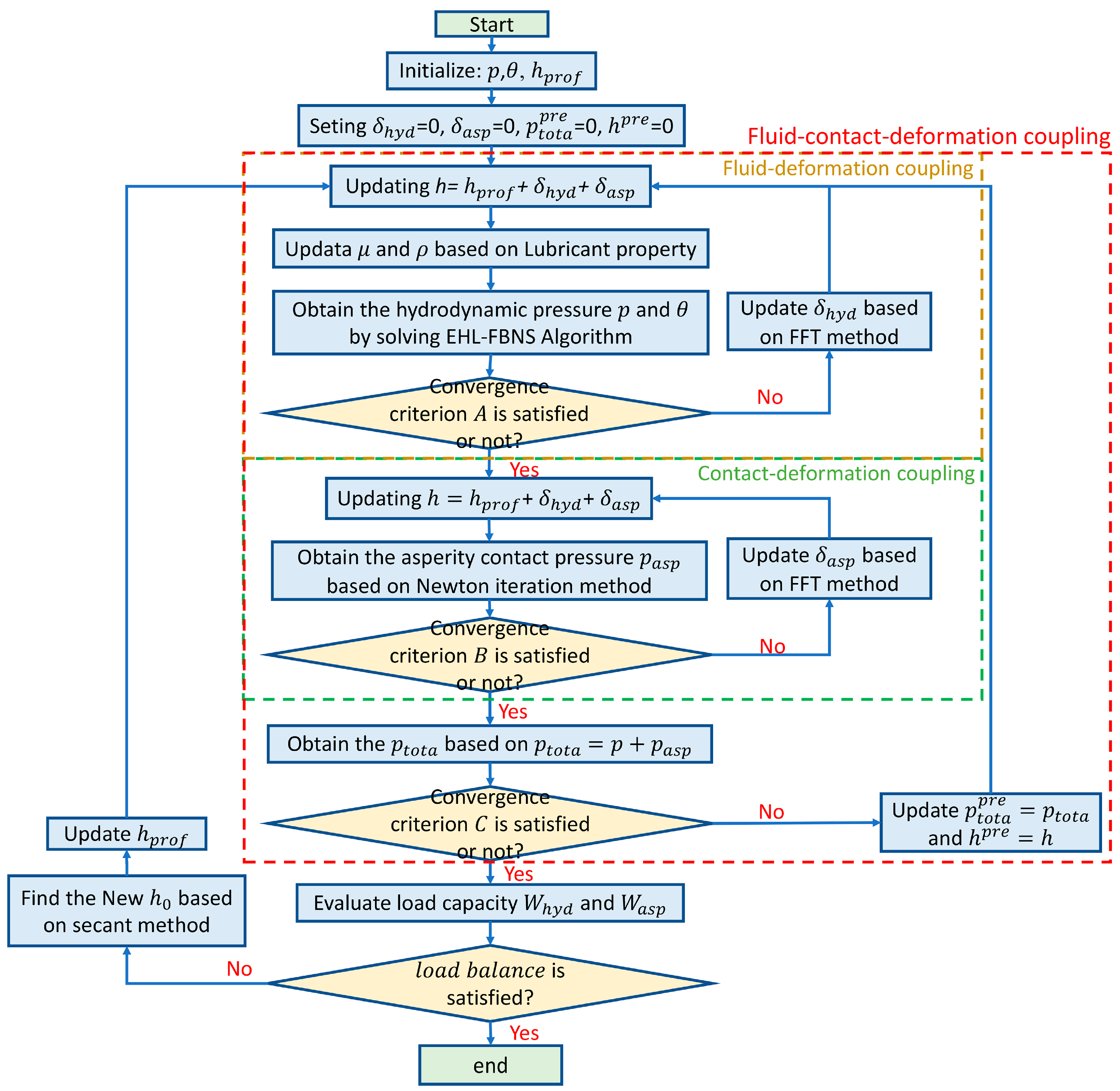
3. Method of Solution
4. Results and Discussion
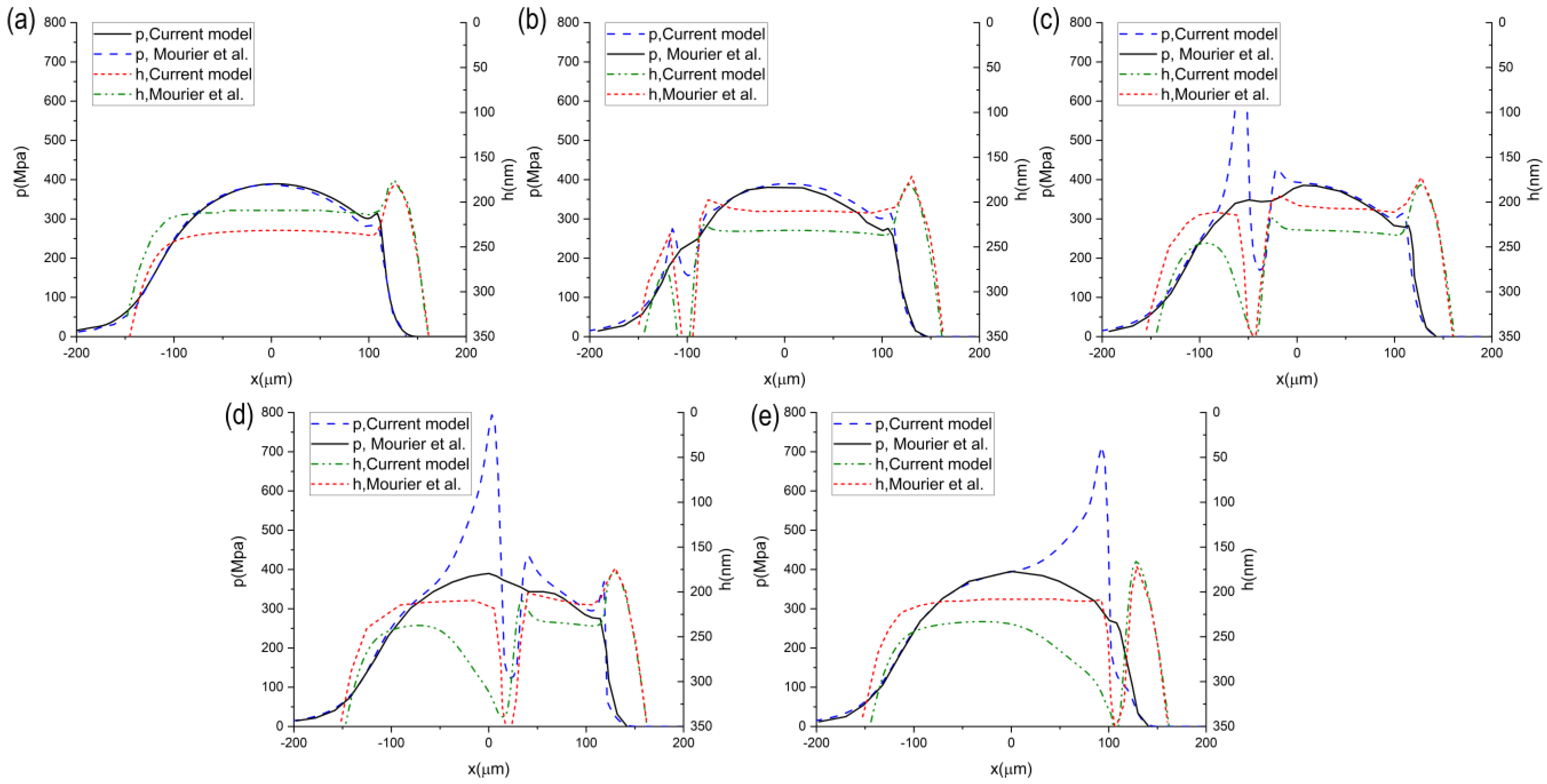
4.1. Slider with a Varying Number of Trapezoidal Pockets
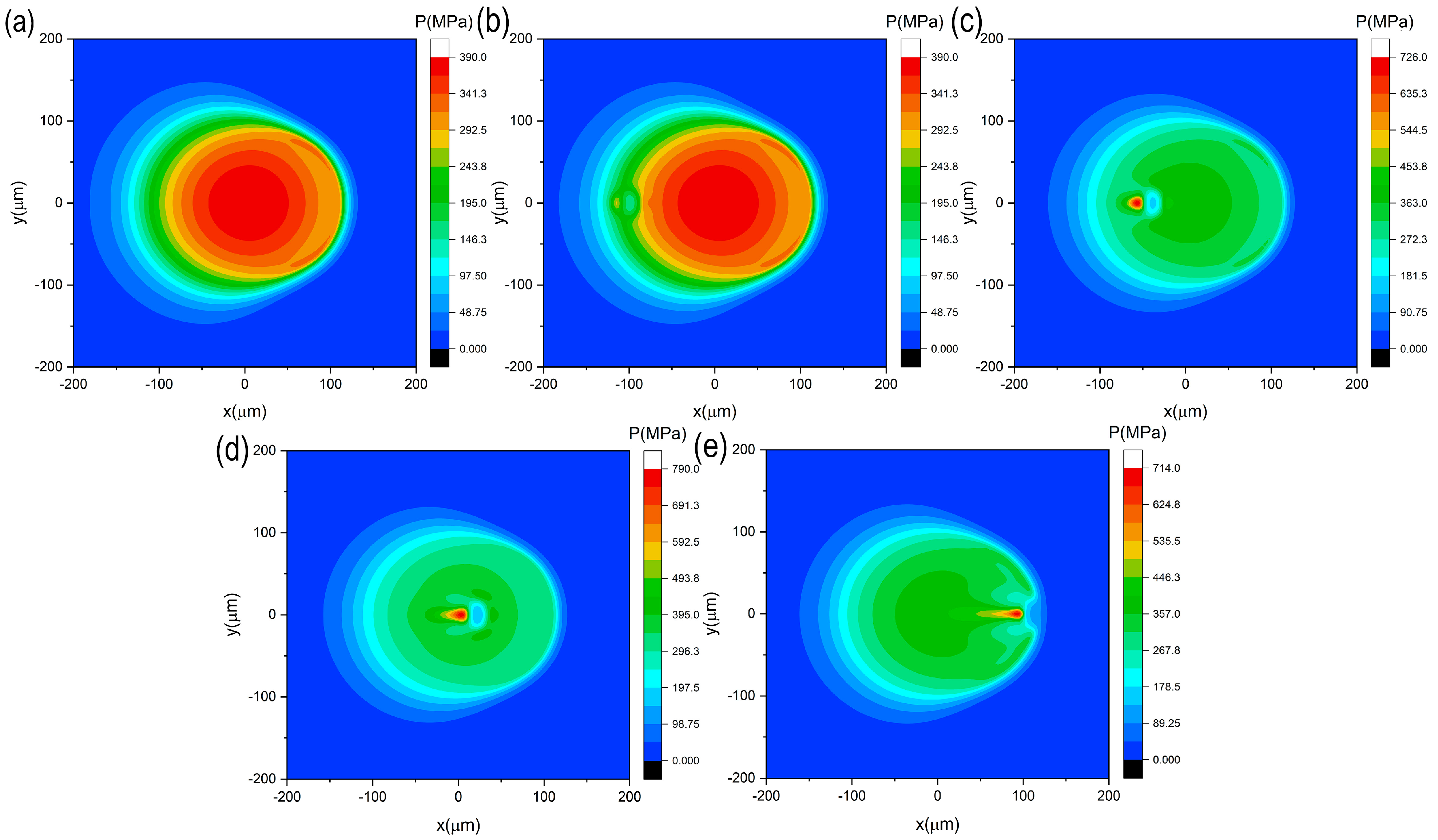
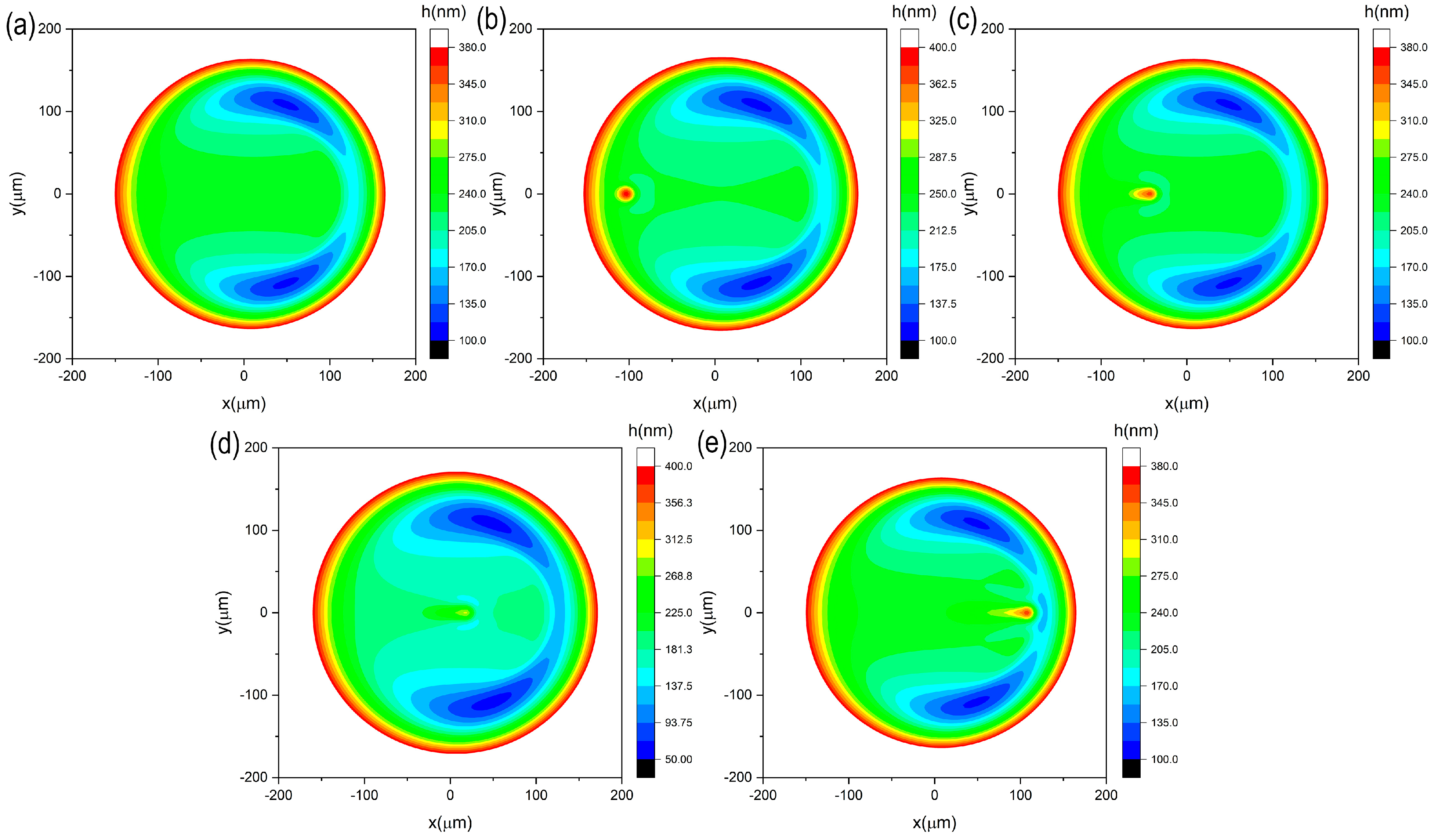
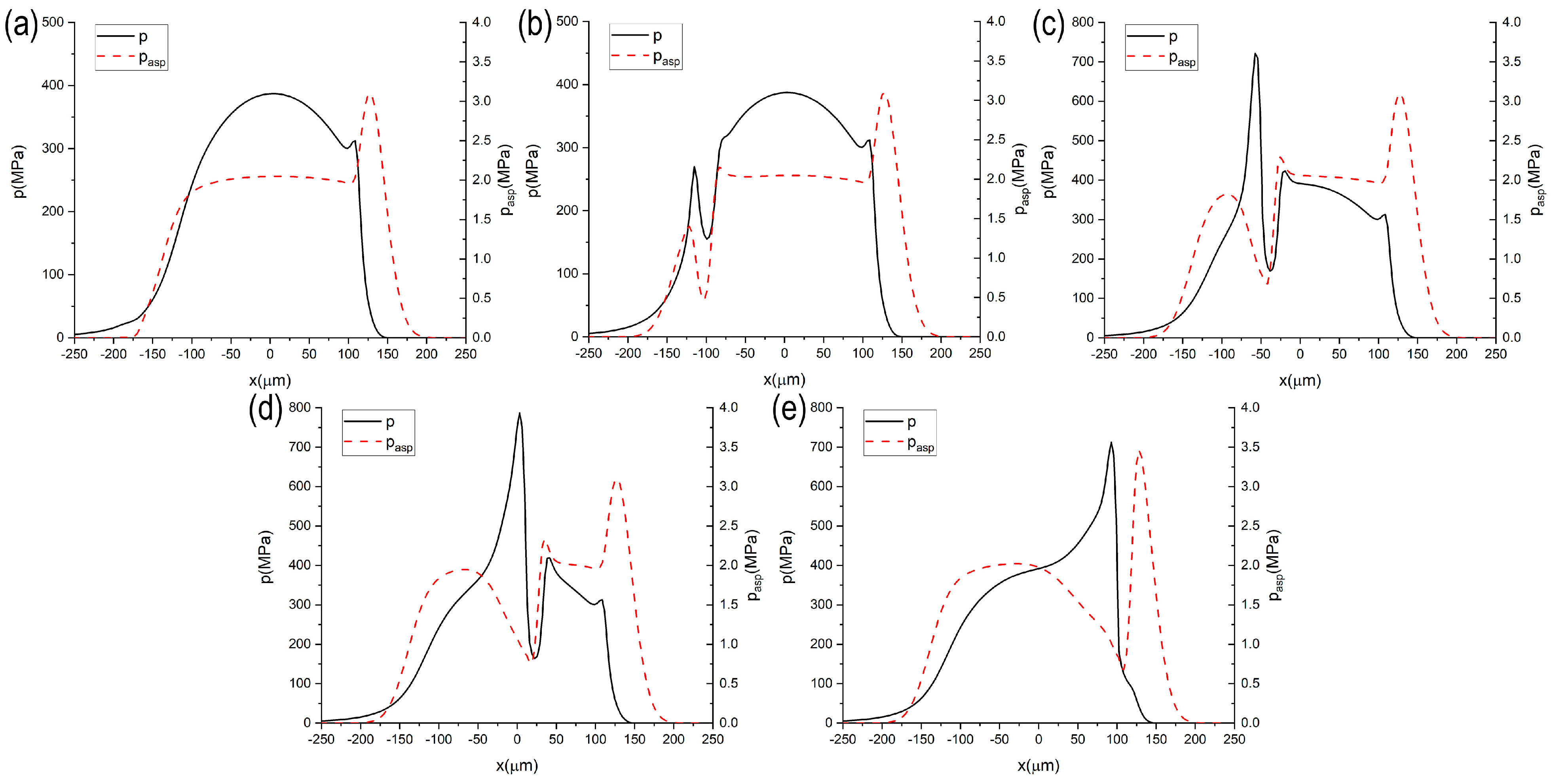
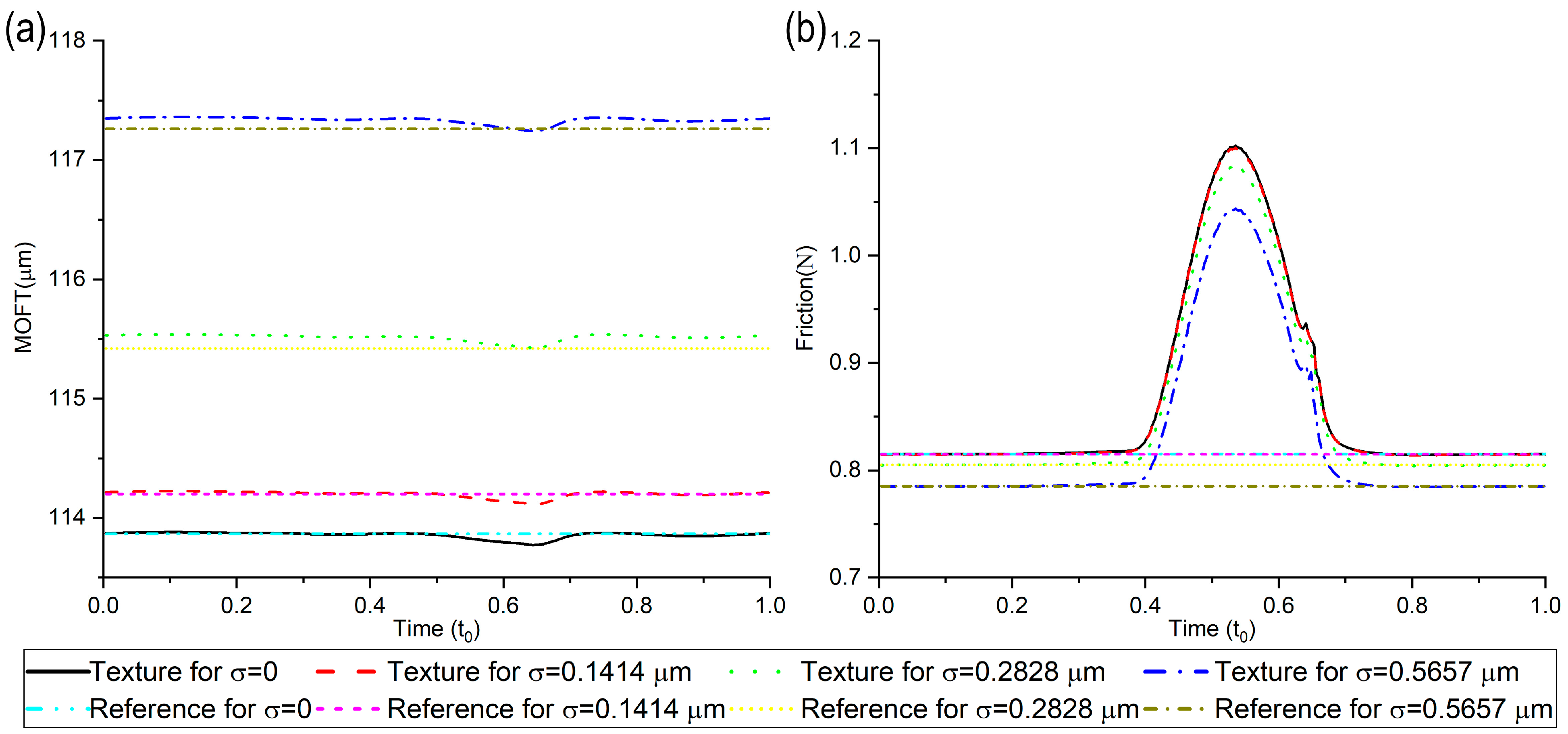
4.2. Point Contact with or without Moving Texture
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Half-width of Hertzian contact | |
| The depth of texture | |
| Influence coefficient | |
| Combined elastic modulus of the contact bodies | |
| Elastic modulus of the upper surfaces | |
| Elastic modulus of the lower surfaces | |
| Oil film thickness | |
| Rigid body displacement | |
| Oil film thickness in the case of rigid bodies | |
| Kurtosis | |
| Half-length of the rectangular integration element | |
| Length along x and y direction | |
| Hydrodynamic pressure | |
| Asperity contact pressure | |
| Hydrodynamic pressure from the current method | |
| Hydrodynamic pressure from reference | |
| The total pressure | |
| The radius of texture | |
| Equivalent radius of curvature along the direction | |
| Equivalent radius of curvature along the direction | |
| Skewness | |
| Time | |
| The velocity of moving texture | |
| The velocity of the upper surface | |
| The velocity of the lower surface | |
| Asperity contact load | |
| Hydrodynamic support | |
| Applied load | |
| , | Total number of nodes in the , directions |
| x | Direction in coordinate system |
| The location position of the moving texture | |
| y | Direction in coordinate system |
| The deflection of the solid surfaces | |
| The deflection of the solid surface due to the hydrodynamic pressure | |
| The deflection of the solid surfaces due to the asperity contact pressure | |
| The roughness-related parameters | |
| The cavity fraction | |
| The boundary friction coefficient | |
| The viscosity of the lubricant | |
| Lubricant viscosity under the atmospheric pressure | |
| The combined roughness | |
| The density of the lubricant | |
| lubricant density under the atmospheric pressure | |
| The equivalent surface roughness | |
| The roughness-related parameters | |
| The roughness of the upper surface | |
| The roughness of the lower surface | |
| Poisson’s ratio of the upper surfaces | |
| Poisson’s ratio of the lower surfaces | |
| Asperity height distribution | |
| Normalized height distribution | |
| Pressure flow factor | |
| Shear flow factor | |
| Contact factor | |
| , , | The friction-induced flow factor |
| ω0, ω1, ω2 | The relaxation factor |
References
- Chen, S.; Yin, N.; Cai, X.; Zhang, Z. Iteration framework for solving mixed lubrication computation problems. Front. Mech. Eng. 2021, 16, 635–648. [Google Scholar] [CrossRef]
- Zhu, D.; Hu, Y.-Z. The study of transition from elastohydrodynamic to mixed and boundary lubrication. In The Advancing Frontier of Engineering Tribology, Proceedings of the 1999 STLE/ASME HS Cheng Tribology Surveillance; American Society of Mechanical Engineers: New York, NY, USA, 1999; pp. 150–156. [Google Scholar]
- Hu, Y.-Z.; Zhu, D. A Full Numerical Solution to the Mixed Lubrication in Point Contacts. J. Tribol. 2000, 122, 1–9. [Google Scholar] [CrossRef]
- Wang, W.Z.; Wang, H.; Liu, Y.C.; Hu, Y.Z.; Zhu, D. A comparative study of the methods for calculation of surface elastic deformation. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2005, 217, 145–154. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Q.J.; Wang, W.; Hu, Y.; Zhu, D. Effects of Differential Scheme and Mesh Density on EHL Film Thickness in Point Contacts. J. Tribol. 2006, 128, 641–653. [Google Scholar] [CrossRef]
- Pu, W.; Wang, J.; Zhu, D. Progressive Mesh Densification Method for Numerical Solution of Mixed Elastohydrodynamic Lubrication. J. Tribol. 2016, 138, 021502. [Google Scholar] [CrossRef]
- Liu, S.B.; Qiu, L.W.; Wang, Z.J.; Chen, X.Y. Influences of Iteration Details on Flow Continuities of Numerical Solutions to Isothermal Elastohydrodynamic Lubrication with Micro-Cavitations. J. Tribol. 2021, 143, 101601. [Google Scholar] [CrossRef]
- Ferretti, A.; Giacopini, M.; Mastrandrea, L.; Dini, D. Investigation of the Influence of Different Asperity Contact Models on the Elastohydrodynamic Analysis of a Conrod Small-End/Piston Pin Coupling. SAE Int. J. Engines 2018, 11, 919–934. [Google Scholar] [CrossRef]
- Hansen, J.; Björling, M.; Larsson, R. A New Film Parameter for Rough Surface EHL Contacts with Anisotropic and Isotropic Structures. Tribol. Lett. 2021, 69, 37. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Y.; Wang, Y. A method for improving the capability of convergence of numerical lubrication simulation by using the PID controller. In Proceedings of the IFToMM World Congress on Mechanism and Machine Science, Krakow, Poland, 30 June–4 July 2019; pp. 3845–3854. [Google Scholar]
- Tošić, M.; Larsson, R.; Lohner, T. Thermal Effects in Slender EHL Contacts. Lubricants 2022, 10, 89. [Google Scholar] [CrossRef]
- Wang, Q.J.; Sun, L.L.; Zhang, X.; Liu, S.B.; Zhu, D. FFT-Based Methods for Computational Contact Mechanics. Front. Mech. Eng. Switz 2020, 6, 61. [Google Scholar] [CrossRef]
- Jakobsson, B.; Floberg, L. The Finite Journal Bearing, Considering Vaporization; Gumperts Förlag: Mississauga, ON, Canada, 1957. [Google Scholar]
- Olsson, K.-O. Cavitation in Dynamically Loaded Bearings; Scandinavian University Press: Oslo, Norway, 1965. [Google Scholar]
- Patir, N.; Cheng, H. Application of average flow model to lubrication between rough sliding surfaces. J. Tribol. 1979, 101, 220–229. [Google Scholar] [CrossRef]
- Gu, C.; Meng, X.; Xie, Y.; Zhang, D. Mixed lubrication problems in the presence of textures: An efficient solution to the cavitation problem with consideration of roughness effects. Tribol. Int. 2016, 103, 516–528. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H. An average flow model for determining effects of three-dimensional roughness on partial hydrodynamic lubrication. J. Tribol. 1978, 100, 12–17. [Google Scholar] [CrossRef]
- Roelands, C.J.A. Correlational Aspects of the Viscosity-Temperature-Pressure Relationship of Lubricating Oils. Ph.D. Thesis, Technical University of Delft, Delft, The Netherlands, 1966. [Google Scholar]
- Dowson, D.; Higginson, G.R. Elasto-Hydrodynamic Lubrication: The Fundamentals of Roller and Gear Lubrication; Pergamon Press: Oxford, UK, 1966; Volume 23. [Google Scholar]
- Greenwood, J.; Tripp, J. The contact of two nominally flat rough surfaces. Proc. Inst. Mech. Eng. 1970, 185, 625–633. [Google Scholar] [CrossRef]
- Shahmohamadi, H.; Mohammadpour, M.; Rahmani, R.; Rahnejat, H.; Garner, C.P.; Howell-Smith, S. On the boundary conditions in multi-phase flow through the piston ring-cylinder liner conjunction. Tribol. Int. 2015, 90, 164–174. [Google Scholar] [CrossRef]
- Kotwal, C.A.; Bhushan, B. Contact Analysis of Non-Gaussian Surfaces for Minimum Static and Kinetic Friction and Wear. Tribol. Trans. 1996, 39, 890–898. [Google Scholar] [CrossRef]
- Hansen, E.; Kacan, A.; Frohnapfel, B.; Codrignani, A. An EHL Extension of the Unsteady FBNS Algorithm. Tribol. Lett. 2022, 70, 80. [Google Scholar] [CrossRef]
- Woloszynski, T.; Podsiadlo, P.; Stachowiak, G.W. Efficient Solution to the Cavitation Problem in Hydrodynamic Lubrication. Tribol. Lett. 2015, 58, 18. [Google Scholar] [CrossRef]
- Mourier, L.; Mazuyer, D.; Lubrecht, A.A.; Donnet, C. Transient increase of film thickness in micro-textured EHL contacts. Tribol. Int. 2006, 39, 1745–1756. [Google Scholar] [CrossRef]
- Marian, M.; Tremmel, S.; Wartzack, S. Microtextured surfaces in higher loaded rolling-sliding EHL line-contacts. Tribol. Int. 2018, 127, 420–432. [Google Scholar] [CrossRef]


| Parameter | Value | Unit |
|---|---|---|
| 0 | Pa | |
| 15 | N | |
| 110 | GPa | |
| 0.25 | Pa.s | |
| 850 | ||
| a | 136.5 | |
| 6a | - | |
| 6a | - | |
| 0.09 | ||
| 0.09 | ||
| r | 15.5 | |
| d | 175 |
| Parameter | Case | Standard Method | Current Method | ||||
|---|---|---|---|---|---|---|---|
| Number of iterations | 1 | 1582 | 2137 | 10667 | 56 | 103 | 210 |
| 2 | 1528 | 2043 | 9982 | 231 | 460 | 941 | |
| CPU time (s) | 1 | 66.55 | 92.06 | 500.02 | 2.86 | 4.91 | 9.58 |
| 2 | 62.47 | 87.02 | 472.69 | 11.16 | 19.91 | 39.17 | |
| Parameters | Value | Unit |
|---|---|---|
| Roughness of ball | 0.1, 0.2, 0.4 | |
| Roughness of disc | 0.1, 0.2, 0.4 | |
| 0.04 | -- | |
| 0.001 | -- |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, C.; Zhang, D.; Jiang, X.; Meng, X.; Wang, S.; Ju, P.; Liu, J. Mixed EHL Problems: An Efficient Solution to the Fluid–Solid Coupling Problem with Consideration of Elastic Deformation and Cavitation. Lubricants 2022, 10, 311. https://doi.org/10.3390/lubricants10110311
Gu C, Zhang D, Jiang X, Meng X, Wang S, Ju P, Liu J. Mixed EHL Problems: An Efficient Solution to the Fluid–Solid Coupling Problem with Consideration of Elastic Deformation and Cavitation. Lubricants. 2022; 10(11):311. https://doi.org/10.3390/lubricants10110311
Chicago/Turabian StyleGu, Chunxing, Di Zhang, Xiaohui Jiang, Xianghui Meng, Shuwen Wang, Pengfei Ju, and Jingzhou Liu. 2022. "Mixed EHL Problems: An Efficient Solution to the Fluid–Solid Coupling Problem with Consideration of Elastic Deformation and Cavitation" Lubricants 10, no. 11: 311. https://doi.org/10.3390/lubricants10110311
APA StyleGu, C., Zhang, D., Jiang, X., Meng, X., Wang, S., Ju, P., & Liu, J. (2022). Mixed EHL Problems: An Efficient Solution to the Fluid–Solid Coupling Problem with Consideration of Elastic Deformation and Cavitation. Lubricants, 10(11), 311. https://doi.org/10.3390/lubricants10110311