Abstract
In a cross-country skiing competition, the time difference between the winner and the skier coming in at second place is typically very small. Since the skier spends much of the energy on overcoming resistive forces, a relatively small reduction in these forces can have a significant impact on the results. The resistive forces come partly from the friction, at the tribological interface between the ski and the snow, and as with many tribological processes, the characterisation of its origin plays an important role in determining the frictional properties. Furthermore, in cross-country ski friction, there are several scales impacting the frictional performance, with the major contributors being the ski-camber profile and ski-base structure. Macro-scale measurements of the ski-camber profile under loading are often used to determine how adequate the ski is for use under specific conditions. The characteristic properties usually assessed are the force required to collapse the ski in order to obtain a certain camber height, the topography of the kick-wax zone, and the length (determined by simple means) of the frictional interfaces associated with the rear- and front glide zones, i.e., the apparent contact length. These measurements are, however, commonly performed by loading the ski against a much stiffer counter surface than snow and this affects the quantification of the characteristic properties. To date, some mathematical models have been proposed, but there is no reliable approach for determining the macro-scale properties of the contact between a cross-country ski and a counter surface using simulations. In the present paper, an Artificial Neural Network (ANN) has been trained to predict the ski-camber profile for various loads applied at different positions. A well-established deterministic approach has been employed to simulate the contact between the ANN-predicted ski-camber profile and a linearly elastic body with a flat upper surface, representing the snow. Our findings indicate that this method is feasible for the determination of relevant macro-scale contact characteristics of different skis with snow. Moreover, we show that the apparent contact area does not linearly depend on the load and that the material properties of the counter surface also exert a large impact when quantifying the apparent contact area and the average apparent contact pressure.
1. Introduction
In the winter Olympics, solid-phase water is present in some way in every sport. Some sports are practised on top of the ice, and in these sports, the sports equipment’s contact surface is made of steel. Others are practised on snow, where the sport equipment’s contact surface is often made of polyethylene, and in alpine skiing, good control is achieved by the addition of steel edges to the polyethylene ski base with a low gliding friction. Friction on snow has fascinated researchers for years; in as early as 1939, Bowden published his ground-breaking paper [1] on this topic, and since then, many publications have followed. There has always been an interest to reduce the friction further. Eriksson [2], for instance, studied friction as a means to increase the efficiency of transporting timber on snow. In 1955, Bowden [3] started exploring friction on snow and ice; his research specifically took an interest in how to reduce friction in skiing. This opened the door to a fascinating research area, in which there are many active researchers today.
Over the years, there have been a number of theoretical studies [4,5,6,7,8,9,10] that present various equations to model the friction between the ski and snow. In order to explain what governs the friction on snow and ice, a substantial amount of research has also been produced to explore and understand the mechanisms involved. See the research of Lever et al. [11], Scherge et al. [12] and Almqvist et al. [13] for some recent work in this direction. The different friction mechanisms, i.e., snow compaction, micro-ploughing, adhesion, viscous shearing and water bridging, see [13], have been modelled by assorted equations based on different assumptions.
In most of the models available, the contact pressure is assumed to be uniformly distributed over the contact area. One of the most common assumptions is that the dry real area of contact equals the load divided by the hardness of the softer of the two contacting bodies; for example, in the work of Glenne [4]. By definition, this produces a minimum estimate of the real contact area and of the corresponding friction force. Another assumption is that the contact area comprises all of the regions that are in close proximity of contact. This is the area considered when modelling the component of wet friction in many models (e.g., see the work of Lehtovaara [5]) even though it is well known that it is countably larger than the real area of contact.
The present study serves to shed some light upon the assumptions connected to the apparent contact area and the corresponding apparent contact pressure. Since the apparent characteristics of any parameter are dependent on the scale at which the measurements are performed, the parameter should be described in a context that also defines the scales associated with the problem at hand. In the following sections, we provide our definition of the scales considered in the present investigation. Here, the macro scale encompasses the geometrical features of the ski visible to the naked eye when one’s field of vision covers the entire ski from tip to tail, which can be resolved at some tenths of a millimetre in height. If we instead were looking at it with a higher magnification, e.g., from a microscopical perspective, we would find that the real contact area was due to the ski-base structure and the grainy snow topography of the ski track. In this work, the micro scale is considered to encompass the topography of the ski base at a resolution of approximately one-hundredth of a micrometre in height and a micrometre in the lateral plane. The micro scale is, however, not included in our present analysis. (Surface roughness is in itself a multi-scale property, i.e., the resolution required to discern all relevant features depends on the procedure used to prepare the surface, as well as the tribological conditions to which the surface is exposed.) In the present situation, we also consider the meso scale (an important level intermediate to the macro- and the micro scale), which encompasses the contacts between the ski base and surface of the snow in terms of length, i.e., the rear and front glide zones of the ski. With respect to the height of the ski camber, the meso scale includes ski-camber heights within the range of about a tenth of a millimetre and down to a tenth of a micrometre.
This multi-scale nature, which is characteristic of contact mechanics in general, has been extensively studied previously—see, for example, [14,15,16,17,18,19,20,21]. Bäurle et al. [22] studied the ski–snow interaction at the micro scale and found that the real area of contact can be as small as of the apparent contact area in cold conditions, and as large as in warmer conditions. Another example is provided by Mössner et al. [23], who found that the real area of contact between a single snow grain (modelled as a sphere) and the ski base was less than of the apparent contact area. Finally, Scherge et al. [12], conducted numerical calculations to simulate the micro-scale contact mechanics between ice and measured ski-base topographies. The results they presented show that the real area of contact may be as small as , and that a perfectly plastic- and the more realistic elasto-plastic approximation of the material behaviour are significant; however, they also found that the former preserves the ranking and, therefore, may be used for qualitative analysis. Overall, this indicates that the real contact area typically covers only a small part of the area seen at the macro scale, suggesting that the corresponding real contact pressure may be significantly higher than the pressure estimate of the total load divided by the whole area of the ski base (except for the shovel and the tail). The contact pressure under a loaded ski was experimentally obtained by Bäckström et al. [24], Schindelwig et al. [25], and also by Kristiansen [26]. The contact pressure and area are, however, dependent on the stiffness of the counter surface and, to the best of the authors’ knowledge, there are no published results related to skiing for this relationship.
Measurements of the ski-camber profile can be used to evaluate ski properties with respect to several aspects, e.g., the force required to collapse the ski to a certain camber height, the topography of the kick-wax zone, and the lengths of the frictional interfaces, i.e., what we in this study regard as the apparent contact area. Breitschädel [27,28], for example, looked at the ski stiffness and its variation with temperature, and he also defined a contact criterion, based on the assumption that contact occurs wherever the ski-camber height is less than 50 m. He used this to configure the length of the frictional interfaces of cross-country skis. This contact criterion was recently used by Kalliorinne et al. [29] as a measure for comparison, when they conducted contact mechanics simulations to analyse how the length of the friction interfaces varies, as athletes execute the downhill-tucking position in different ways.
The objective of this paper was to establish a method for determining macro-scale mechanical properties of the contact between cross-country skis and snow, by conducting measurements of the ski-camber profile, a carefully designed Artificial Neural Network (ANN), and a computational contact-mechanics model. The predicted contact pressure and area are, however, mechanical properties related to meso-scale characteristics that can be observed when the virtual ski is placed in contact with virtual snow (modelled as a linear elastic half space exhibiting variable stiffness), under a given loading condition. This novel method will hopefully provide valuable new insights into the macro-scale mechanics of the contact between cross-country skis and snow, as well as of other systems exhibiting similar behaviour.
2. Theory
A model that governs the contact mechanical response that results when a cross-country ski is pressed against another body must consider the multi-scale and multi-physics nature of the processes involved. In this work, ski collapse/deformation and corresponding contact pressure are considered to involve processes at the macro-, meso- and the micro scales (with only the first two of these being included in the present analysis), as described above.
Figure 1 provides a schematic view of the scales present in the contact mechanics problem resulting when a cross-country ski is pressed against another body. The scale at the bottom is the macro scale, which represents the geometry of the ski. It encompasses both the ski-camber profile (blue solid line) of the ski base, which is in contact with the snow surface (black solid line), and the equivalent load from the athlete’s bio-mechanical input to the (grey-coloured) ski, through the (red coloured) ski boot, illustrated by the red arrow. The equivalent load (caused by the athlete’s bio-mechanical input) has two attributes, i.e., a magnitude and a location of application, which may be used to simulate specific loading conditions occurring during the different cycles used in cross-country skiing. For example, during the diagonal stride or while double polling on a classic ski, or during any one of the 7 gears used in skating [30,31]. Thus, it is of utmost importance to consider the effect of these two parameters on the ski-camber profile.
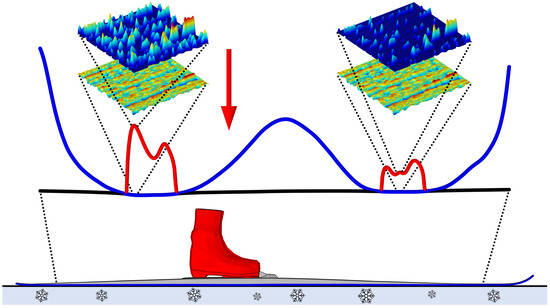
Figure 1.
A schematic view of the macro-, meso- and the micro scale of the contact occurring when a cross-country ski is pressed against another body. At the bottom, we find the macro scale, where the ski boot (coloured in red) manifests the athlete’s bio-mechanical input to the (grey coloured) ski with a ski-base surface profile, i.e., the ski-camber profile, (solid blue line), which makes contact with the surface of the snow (solid black line). Another feature appearing at the macro scale is the equivalent load, illustrated with the red arrow, from the athlete transferred through to the ski boot. Above the macro scale, we find the meso scale encompassing the contact between the ski-base, illustrated by the ski-camber profile (solid blue line), and the snow surface (solid black line), both of which are presented at a magnification in the vertical direction. At the meso scale, we also find the apparent contact pressure (solid red line), induced by the ski-camber profile measured under the equivalent load from the ski boot. Above the meso scale, encompassing both the rear- and the front-glide zones that constitute the frictional interfaces in this problem, we have two different illustrations of features belonging to the micro scale. The lower one of these illustrates the topography of the ski-base structure, and the upper one represents the corresponding real micro-scale contact pressure.
The apparent contact pressure, illustrated with the red solid line in Figure 1, is the normal stress distribution acting over the apparent contact area, observed while resolving only features appearing at the meso scale, i.e., the geometry of the rear- and the front-glide zones and the surface of the snow. These meso-scale-sized contacts constitute the frictional interfaces between the ski base, illustrated by the ski-camber profile (solid blue line), and the surface of the snow (solid black line). Nota bene, (i) these two macro-scale-sized profiles are presented at magnification in the vertical direction at this scale, (ii) the pressure distribution is highly sensitive to irregularities and therefore highlights the out-of-flatness of the contacting surfaces at the meso scale. The apparent meso-scale contact pressure can be regarded as a coupling between the scales, since it is induced by the macro-scale-sized features of the ski geometry and the equivalent load, while acting as a nominal load on the micro scale.
Features of the micro topography of the ski-base structure, the corresponding contact- pressure and area belong to the micro scale. In Figure 1, appearing above the magnified presentation of the ski-camber profile and the snow surface and the apparent (meso-scale) pressure distribution, the ski-base topography us depicted; in the figure above, the corresponding (micro-scale) pressure distribution is shown. Because of the magnitude of the corresponding apparent (meso-scale) pressure (red solid line), the load carried by a unit area of the ski-base structure is larger at the rear glide zone than it is at the front.
In practical applications, the ski-camber profile is frequently used to determine how suitable a particular cross-country ski is for an individual athlete under certain conditions. The ski-camber profile reveals, for example, what the camber height is, and approximately where the glide zones will appear. For a classic ski, this information is used to determine where the kick-wax zone should be applied. That is to determine the load required to collapse the ski to produce grip during the diagonal stride or to avoid the kick-wax zone coming into contact with the snow while performing the double-pole technique. In addition, by using Breitschädel’s contact criterion, which is based on the assumption that contact occurs whenever the ski-camber height is less than 50 m, the length of the apparent contact area of the glide zones can be estimated [28]. However, this contact criterion is based on a constant value of 50 m of the penetration depth, i.e., how deep the ski-base sinks into the snow, implying that it would always be the same, irrespectively of the prevalent conditions. The penetration depth is, however, not a constant. It is, for sure, dependent on the properties of the ski-base material and structure, the loading condition, and the properties of the snow. Both softer snow and ski-camber profiles exhibiting smaller apparent contact area will, for instance, result in a larger penetration depth. The ski-camber profile measurements are usually obtained on a plane and hard counter surface, such as the stone in the SkiSelector machine [32]. In the present analysis, it is assumed that the ski-camber profile, used as input for the contact mechanics simulations, is independent of the properties of the counter material, i.e., that the ski-camber profile would be the same if the counter surface was made of rigid stone or soft snow.
3. Method
In the present paper, a classic- and a (free style) skate cross-country ski are used for the evaluation of the skis’ contact mechanical response. The first step addresses the macro-scale deformation of the ski. This involves ski-camber profile measurements, training an Artificial Neural Network (ANN) and employing it to predict the deformation of the ski for a given loading condition. In the second step, the predicted ski deformation is used as input for numerical calculations, and for predicting the contact mechanical response of the ski in terms of the apparent meso-scale contact pressure and area.
3.1. Macro-Scale Measurement and Prediction
Together with representative material data, only a single macro-scale measurement of the ski-camber profile is required as input to execute a numerical calculation of the apparent contact pressure and area that would develop at the meso-scale between the ski and the counter material. The results obtained would, however, only represent a single loading condition, in terms of the load magnitude, m, and position, . This means that a new measurement would be needed for another (if only slightly different) loading position and this would make the procedure of tracking and predicting the contact mechanics of, e.g., a whole cycle of the diagonal stride or during double polling on a classic ski, or any one of the first 6 (of the 7) gears in skating, extremely inefficient. To circumvent this problem, the methodology proposed herein uses an ANN that is trained on a ski-camber profile dataset, obtained for various loads placed at different positions using a SkiSelector [32] ski-camber profile measuring device, as shown in Figure 2 (left). Artificial neural networks are frequently used and when successfully trained (neither under- nor over learned), an ANN, with a fit-for-purpose architecture, can be used to obtain highly accurate predictions within the domain spanned by the training data. The training data used in the present study were collected by measuring the ski-camber profile at loads ranging from 5 kg to 130 kg, positioned between 40 mm and 240 mm behind the balance point (as indicated by the ski manufacturer). See Figure 2 (middle) for the complete specification. In this way, the ANN, with the architecture depicted in Figure 3 and the ANNs available in MATLAB Central File Exchange (Data Availability Statement), is capable of making predictions with a mean error of smaller than 20 mm. Figure 2 (right) shows the tip of the classic- and the skate- ski used in this study.

Figure 2.
Measurement setup using the SkiSelector [32] to retrieve the ski-camber profile, a Fischer skate ski [33] is used, equipped with the Measurement boot developed in [29] (left). Sequences for loading, in terms of mass and positioning relative to the balance point, located at (middle). The tip of the classic- and skate ski used in the present work (right).
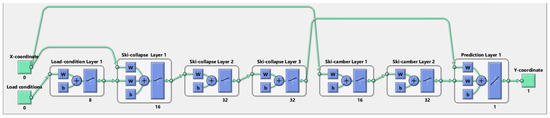
Figure 3.
Architecture of the Matlab based neural network, with 3 inputs x, m and , 7 hidden layers and 1 output “Y-coordinate”, i.e., . The inputs are separated into “X-coordinate” i.e., x and “Load conditions” i.e., m and . The fully connected hidden layers are sectioned in to 4 blocks consisting of one load-condition layer, three ski-collapse layers, two ski-camber layers and one prediction layer. The input-layer, layer-layer and layer-output connections are illustrated with green arrows. All layers have tansig activation functions, except for the prediction layer, which has a pure-lin activation function.
All the measurements are combined into a large dataset consisting of 3 inputs and 1 output. The three inputs are the coordinate running along the ski x, with at the balance point, paired with a loading condition represented by the mass m and the position , where it is applied, and the output is the ski-camber height h. The ski-camber height h may, therefore, be defined as follows:
where f is an a priori unknown function. One way of realising such an unknown function, is to represent it with a carefully designed ANN. In the present work, an ANN was constructed using the deep learning toolbox in MATLAB [34]. The final version of the ANN architecture developed herein is shown in Figure 3. In the deep learning toolbox implementation of this ANN, it is made up of 7 fully connected hidden layers sectioned into 4 blocks.
This sectioning, with each block detailed in the list below, is adopted because of the need to pass the inputs to different stages within the network and not only to the first hidden layer.
- The first block consists of a “Load-condition” layer that pre-processes the load condition inputs m and , and the output is then passed to the second block.
- The second block is designed to handle the ski collapse; thus, it requires both the x-coordinate and the output from the “Load-condition” block as the input. The block consists of 3 “Ski-collapse” layers which all employ the tansig transfer function.
- The third block, which governs the ski-camber processing, consists of two layers employing the tansig transfer function. This block only uses the x-coordinate as the input, making it independent of the loading condition.
- The fourth block is the “Prediction” block; it combines the output from the “Ski-collapse” block and the “Ski-camber” block to make the prediction. This block consists of a single layer which employs the pure-lin transfer function. The output from this block is the received y-coordinate of the ski-camber profile under the specified load-condition.
There are several benefits to employing an ANN to model this type of system. For example, because of the relatively small number of neurons compared to the number of parameters in the training data, the ANN will act as a filter for the small amount of noise in the measurement data. The most significant advantage, however, is the ability of the ANN to perform highly accurate interpolation within the parameter space spanned by the training data. In this present study, it is particularly useful for predicting the entire ski-camber profile, given an arbitrary load condition (within the specification given in Figure 2). In addition, the ski-camber profile prediction is performed on a discrete set of x-coordinate values, which can be specified at the preferred resolution, meaning that the subsequent meso-scale calculations can be realised at the required mesh resolution, independently of the original number of sampling points, collected during the ski-camber profile measurement.
3.2. Meso-Scale Calculation
The contact pressure and area are (in this work) considered to belong to the meso scale, for which encompassed features can be observed at the length scale representative of the rear- and the front glide zones. The calculations of the apparent contact pressure and area, performed in this work, were conducted with a deterministic Boundary Element Method (BEM). This method is based on a model for the contact between two semi-infinite half spaces, developed by Almqvist et al. [35] and then further improved by Sahlin et al. [36]. Since then, the model has been employed in several investigations e.g., [37,38,39,40,41,42]. With this type of dimension-reduced half-space approach, we consider the contact between two linearly elastically deformable bodies as the contact between one equivalent elastic body and a rigid plane. The elastic modulus of the equivalent elastic body is given by
where is the Poisson number, is the elastic modulus of the ski base and is the elastic modulus of the counter surface. Lintzén and Edeskär [43] investigated the uni-axial compression of snow of different types, and they estimated the elastic modulus of the snow to be between 100 and 250 MPa for new machine-made snow, and between 50 and 350 MPa for old machine-made snow. The contact mechanics calculations simulating the ski–snow contact performed in this work, are therefore conducted for elastic moduli within the range 20–400 MPa.
In the present work, the ski-camber profile is predicted by the ANN under the specified load conditions and modelled as a rigid body. That is, the BEM simulations were performed under the assumption that only the values of the load magnitude m and position have an influence on the deformation of the ski-camber profile, and not the material properties of the counter body. It is also assumed that the material of the counter body is linearly elastic, that there is no friction between the contacting surfaces, and that the height variations of the surfaces are small compared to their lateral dimensions.
An addition to the numerical solution procedure of the BEM-based model [36] was made to allow the ski to rotate around the loading point in order to fulfil both the force- and moment balance, in terms of the apparent contact pressure and the loading position , i.e.,
An initial test of the modified contact mechanics model was carried out to ascertain its feasibility. To this end, a model problem resembling the SkiSelector [32] was configured. Both a classic and a skating ski with measured ski-camber profiles were used to model the rigid bodies, which were pressed against against an elastic body with the equivalent elastic modulus 1.96 GPa calculated using = 900 MPa and = 70 GPa, with . The outcome of this initial test, as presented in Figure 4, depicts both the ANN-predicted (solid blue line) and the measured (dashed black line) ski-camber profiles for both the classic and the skating ski. Since the stone counter surface is very stiff, the load will be distributed over a relatively short length of the ski. This is also reflected by the apparent contact pressure (solid red line), exhibiting spike-like peaks at the narrow regions of contact.
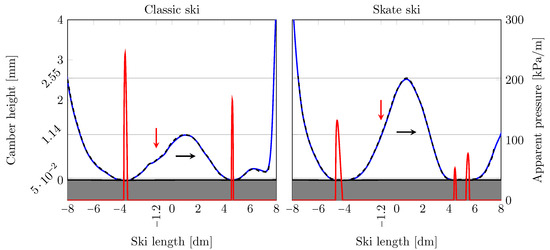
Figure 4.
The ANN-predicted (solid blue line) and measured (dashed black line) ski-camber profiles of a classic (left) and a skate ski (right) loaded with m = 30 kg at = −1.2 dm, and the corresponding apparent pressure distribution (solid red line). The vertical red arrow indicates the equivalent loading position and the horizontal black arrow indicated the gliding direction. The elastic moduli used in the simulations are 900 MPa for the ski base, and 70 GPa for the stone counter surface. According to the contact mechanics calculations, the classic ski (left) has a rear/front apparent contact length of 28.1 mm/14.9 mm with a corresponding average apparent pressure of 169 kPa/137 kPa, and the skate ski (left) was predicted to have a rear/front apparent contact length of 52.7 mm/45.7 mm with corresponding average apparent pressure of 83.7 kPa/48.1 kPa.
As can be seen in Figure 4, the BEM simulation can be considered as a good representation of the physical set-up in the Skiselector, i.e., that the contact is distributed over a relatively small area, and that the size of the deformation of the counter body (the stone) is smaller than the measurement resolution. Notably, as the elastic modulus of the counter body is reduced, the rigid ski-camber profile remains exactly the same (as measured with the SkiSelector), which is not the case in reality, where the ski-camber profile would be different if it is in contact with a less stiff counter body. Thus, the results at low stiffness should be considered as more approximate due to the error inherited from the BEM simulation with a rigid ski-camber profile. However, in the least stiff situation ( = 20 MPa) considered here, the magnitude of the deformation of the “snow” (in the rear contact zone) is less than 0.0002 mm. Assuming a snow depth of 0.2 m, the (maximum) strain would be 1/1000, which indicated that the effect of the frozen ground (beneath the snow) is negligible.
4. Results and Discussion
In this section, the results and a discussion pertaining to the influence of load magnitude, position, and the stiffness of the counter surface, on the contact mechanical response are provided. In Figure 5, Figure 6 and Figure 7, the loaded mass m, load position and elastic module of the snow counter surface were altered one at a time.
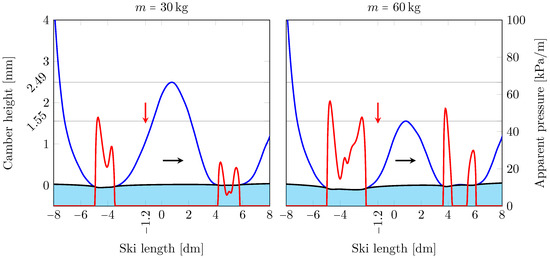
Figure 5.
The skate ski under two different loads, 30 kg (left) and 60 kg (right), and the load positioned 120 mm behind the balance point, with ski-camber profiles (blue lines), apparent pressure distributions (red lines) and elastically deformed counter surfaces (black lines). The vertical red arrow indicates the equivalent loading position and the horizontal black arrow the gliding direction. The elastic moduli used in the simulations are 900 MPa for the ski base, and 100 MPa for the (snow) counter surface. Under a 30 kg load, the ski has rear/front apparent contact lengths of 146 mm/162 mm with corresponding average apparent pressures of 30.6 KPa/13.8 KPa. Under a 60 kg load, the ski has rear/front apparent contact lengths of 288 mm/132 mm with corresponding average apparent pressures of 33.2 KPa/28.9 KPa.
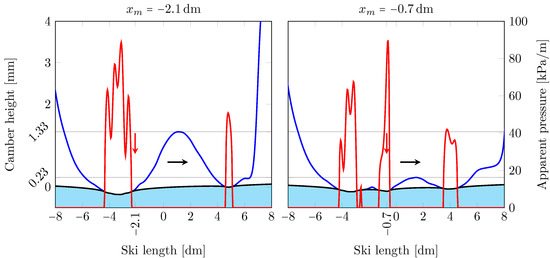
Figure 6.
The classic ski under 60 kg of load positioned at 210 mm (left) and 70 mm (right) behind the balance point, with ski-camber profiles (blue lines), apparent pressure distributions (red lines) and elastically deformed counter surfaces (black lines). The vertical red arrow indicates the equivalent loading position and the horizontal black arrow the gliding direction. The elastic moduli used in the simulations are 900 MPa, for the ski base, and 100 MPa, for the snow counter surface. With the load positioned at mm the rear/front apparent contact lengths of 200 mm/51 mm with corresponding average apparent pressures of 56.4 KPa/40.9 KPa. With the load positioned at mm, the there are three contact zones; rear/middle/front, with apparent contact lengths and corresponding average apparent pressures 146 mm/80.9 mm/105 mm and 41.1 KPa/46.6 KPa/34.3 KPa, respectively.
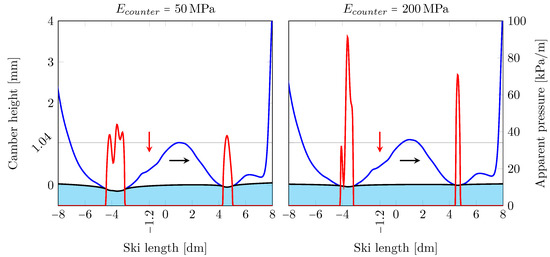
Figure 7.
The classic ski under a load of 30 kg positioned 120 mm behind the balance point, supported by snow of two different elastic modules, 50 MPa (left) and 200 MPa (right), with corresponding ski-camber profiles (blue lines), pressure distributions (red lines) and elastic deformation (black line). The vertical red arrow indicates the equivalent loading position and the horizontal black arrow the gliding direction. The elastic modulus of the ski base used in the simulations is 900 MPa. Contact with snow having elastic modulus of 50 MPa results in a rear/front apparent contact lengths of 141 mm/74 mm with corresponding average apparent pressures of 33.3 KPa/27.2 KPa. Contact with snow having elastic modulus of 200 MPa results in a rear/front apparent contact lengths of 98 mm/37 mm with corresponding average pressures of 48.2 KPa/52.7 KPa.
Figure 5 depicts the skate ski under two load cases, represented by kg (left) and kg (right), for the same load position mm and elastic modulus MPa. When the load is increased from 30 to 60 kg, the ANN predicts a different ski-camber profile. Thus, since the ski-camber profile is an input to the BEM simulation, it is not only the magnitude of load that changes when it is increased from 30 to 60 kg. As a result, the apparent contact length at the rear contact region nearly doubles, with an increase from 146 mm to 288 mm. The corresponding mean pressure does, however, only exhibit an % increase, increasing from 30.6 KPa to 33.2 KPa. The front contact region exhibits a completely different response. When the load is increased, the apparent contact length decreases moderately (≈18%), from one patch of 162 mm to two patches that amount to 132 mm, while the mean apparent contact pressure increases from 13.8 KPa to 28.9 KPa. We note that even though the overall contact topology of the skis frictional interface is very different under the two load cases, the load partitioning between the rear and front frictional interfaces remains nearly unchanged, at 67%/33% and 71%/29%, for the 30 kg and 60 kg loads, respectively.
Figure 6 illustrates how a change in the load position, i.e., , at full body load kg and with MPa, influences the frictional interface of a classic ski. The load position dm is used to represent a skier supporting their weight on the heel of the foot, and as Figure 6 (left) shows, most of the load will then be distributed over the rear frictional interface. At this load position (210 mm behind the balance point), the rear/front apparent contact lengths are 200 mm/50 mm, with corresponding average apparent pressures of 56.4 KPa/40.9 KPa, thus defining a 84%/16% load partitioning. Figure 6 (right) illustrates the case where the load is placed at dm, representing the situation where the skier transfers the load forward to collapse the ski and uses the grip of the kick-wax zone. In this case, the ski camber collapses so that a part of the load is carried inside the kick-wax zone, resulting in the following three load-carrying zones: rear/middle/front. The apparent contact lengths of the rear/middle/front zones are 146 mm/80.9 mm/105 mm with corresponding average apparent pressures of 41.1 KPa/46.6 KPa/34.3 KPa, defining a 45%/28%/27% load partitioning.
Figure 7 illustrates results simulating the effect that different snow conditions might have on the apparent contact length and pressure. To this end, contact mechanics calculations are conducted with two different elastic moduli of the counter surface, i.e., MPa and 200 MPa. Recall that the ski-camber profiles are identical for a given load case, but in order to fulfil moment balance (3), they have to be rotated slightly differently when the elastic modulus is changed. For the “softer snow condition”, simulated with MPa, the apparent pressure is lower while the apparent contact area and penetration depths are larger than for the “stiffer snow condition”, simulated with MPa. It is noted that the rear/front apparent contact area reduces from 141 mm/74 mm to 98 mm/37 mm, expressing a 31%/50% decrease. Compared with the simulations representing a counter surface made of stone, i.e., GPa, depicted in Figure 4, the rear/front apparent contact area reduces additionally from 71%/60% to 28.1 mm/14.9 mm.
As apparent contact pressure and area are closely connected to friction, it is important to know how they vary with the elastic modulus of the snow counter surface and the load exerted by the skier on the ski. Figure 8 depicts the apparent contact area (in [cm]) for the rear- (left) and front- (right) frictional interfaces, of the skate ski (with results previously presented in Figure 4 and Figure 5), as a function of the applied load on the ski (m). Each of the contours, which are spaced by 20 MPa, shows the result for different elastic modulus of the counter surface (). The thick solid black line corresponds to the apparent contact area estimate obtained with the Breitschädel contact criterion [28], based on the assumption that contact occurs whenever the ski-camber height is less than 50 m. The solid green, blue and red lines correspond to the counter surfaces with elastic modulus of 20, 260 and 400 MPa.
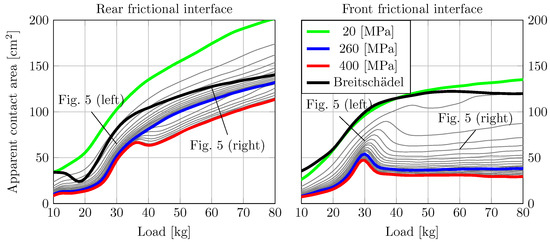
Figure 8.
The apparent contact area of the rear- (left) and front- (right) friction interface of the skate ski from Figure 5 and Figure 4. The apparent contact area of the rear- (left) and front- (right) friction interface, considered as a function of the load magnitude m. The load is placed 120 mm behind the balance point and the contours corresponds to the elastic modulus of the counter surface , which is varied from 20 to 400 MPa with increments of 20 MPa. The solid black line corresponds to the apparent contact area determined by utilising the Breitschädel contact criterion [28].
The rear frictional interface has, in general, an increasing apparent contact area with increasing load (see Figure 8 (left)). For values of higher than 260 MPa, there is, however, a local maximum at about 35 to 40 kg; thereafter, the apparent contact area attains a local minimum at about 40 to 45 kg before it begins increasing again. The estimate of the apparent contact area of the rear frictional interface, obtained using Breitschädel contact criterion, follows a similar trend for elastic moduli within the range 50–150 MPa and for loads higher than 20 kg, but exhibits a very different behaviour for lower loads than that.
According to Figure 8 (right), the apparent contact area of the front frictional interface increases with an increasing load up to about 30 kg for all loads and elastic moduli within the conditions simulated. For MPa, a local maxima appears, which converges to about 50 cm2 at 30 kg as 400 MPa. Thereafter, it decreases somewhat to flatten out at a more-or-less constant level. The explanation has to do with what can be seen in Figure 5, where the front frictional interface under a load of 30 kg consists of a single patch while at 60 kg separates into two. For MPa, the splitting from one to two patches occurs at a load of approximately 35 kg. For the front frictional interface, the Breitschädel contact criterion quite closely follows the present prediction for MPa, except for at the high end of the load range. Thus, according to the present approach, Breitschädel’s contact criterion, may be able to predict the (total) apparent contact area for “soft snow” conditions rather accurately. A notable difference between the rear- and front frictional interfaces is that the apparent contact area at the rear frictional interface increases with the load after passing the local minimum, whereas the apparent contact area at the front frictional interface remains almost constant within the same range of loads.
Figure 9 depicts the average apparent contact pressure corresponding to the apparent contact area depicted in Figure 8. For the same load where the local maximum of the apparent contact area of the rear frictional interface can be observed in Figure 8, a global minimum in the mean apparent contact pressure can be found. For the rear frictional interface, see Figure 9 (right), where the apparent contact pressure remains almost constant for loads higher than 30 kg, and this is because the apparent contact area exhibits an almost linear increase within this range of loads. Due to the steady increase in contact area, the pressure at loads higher than 30 kg does not exceed 55 MPa, even for the “stiffest snow” condition simulated using MPa. The apparent contact pressure of the front frictional interface (see Figure 9 (left)), decreases with increasing load until reaching a global minimum at approximately 30 kg. This minimum, corresponding to the local maximum in the apparent contact area, is clearly pronounced for > 200 MPa but is also existent for smaller values. After this, the pressure increases more-or-less linearly with increasing load, as suggested by the almost constant area depicted in Figure 8.
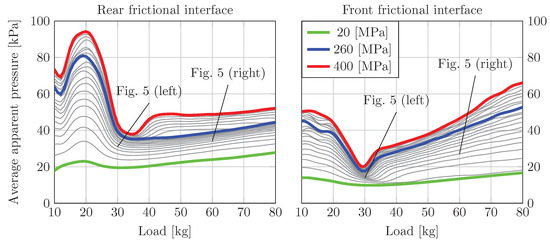
Figure 9.
The average apparent pressure of the rear- (left) and front- (right) friction interface, considered as a function of the load magnitude m, and corresponding to the apparent contact areas in Figure 8. The load is placed 120 mm behind the balance point and the contours corresponds to the elastic modulus of the counter surface , which is varied from 20 to 400 MPa with increments of 20 MPa.
The skate ski used herein has, in fact, belonged to, and been used by, an elite female skier who has a body weight of approximately 60 kg. It is, therefore, quite interesting to see that there is some sort of “sweet spot” around 30 kg, which corresponds to the situations where the athlete distributes the weight evenly on both skis. What this actually means is that at a load corresponding to half of the skier’s body weight, the apparent contact area and average apparent contact pressure remains almost the same for a large range of snow conditions, represented here by MPa − 400 MPa, whereas at full body weight, i.e., 60 kg, there will be a large difference in the apparent contact area and average apparent contact pressure.
5. Conclusions
To conclude, it can be said that a measurement sequence with a varying load magnitude and position can be used as training data for an Artificial Neural Network (ANN). A feasible ANN trained on such a dataset, consisting of measured ski-camber profiles collected with a SkiSelector [32], for various load conditions was developed. A well-established deterministic BEM-based contact mechanics model was adopted and further modified to simulate the contact between a classic- and a skate- ski with a counter surface modelled as an elastic half space. To test the feasibility of the model, an initial test, in which the contact between the ski and the stone in the SkiSelector, was carried out. Then, the model was used to predict the mechanical response between both the classic- and the skate- ski and an elastic counter surface with different elastic moduli, for a wide range of load conditions.
Our main findings were as follows:
- The apparent contact area and the apparent contact pressure for a given loading condition can be calculated reliably using the present model.
- The simulated contact mechanical response of the skate ski shows that the apparent contact area of the front frictional interface splits into two different regions as the load increases.
- The simulated contact mechanical response of the classic ski shows that the ski camber collapses when the load is moved forward and that a part of the load is then carried inside the kick-wax zone, resulting in three load-carrying zones.
- The apparent contact area of the front frictional interface has a local maximum when the load is approximately half of the skier’s body weight and remains almost constant at higher loads.
- The average apparent contact pressure at both the rear and front frictional interfaces is minimal when the load is approximately half of the skier’s body weight.
- The steady increase in apparent contact area with increasing load limits the average apparent contact pressure at loads higher than half of the skier’s body weight to below 55 MPa, even with the stiffest “snow” conditions simulated (i.e., with = 400 MPa).
Author Contributions
Conceptualization, K.K., R.L. and A.A.; methodology, K.K.; software, K.K.; validation, K.K.; formal analysis, K.K.; investigation, K.K.; resources, K.K., J.S. and G.H.; data curation, K.K.; writing—original draft preparation, K.K., J.S., G.H., R.L., H.-C.H. and A.A.; writing—review and editing, K.K., J.S., G.H., R.L., H.-C.H. and A.A.; visualization, K.K., J.S. and G.H.; supervision, R.L., H.-C.H. and A.A.; project administration, A.A.; funding acquisition, R.L., H.-C.H. and A.A. All authors have read and agreed to the published version of the manuscript.
Funding
The authors would like to acknowledge the funding from SOK (The Swedish Olympic Committee) and from VR (The Swedish Research Council): DNR 2019-04293.
Data Availability Statement
Artificial neural networks are available at: https://www.mathworks.com/matlabcentral/fileexchange, https://www.mathworks.com/matlabcentral/fileexchange/114250-fischer_speedmax_3d_classic_net_2i and https://www.mathworks.com/matlabcentral/fileexchange/114250-fischer_speedmax_3d_skate_plus_net_2i (accessed on 28 June 2022).
Acknowledgments
The authors would like to acknowledge the support from SOK (The Swedish Olympic Committee) and from VR (The Swedish Reseach Council): DNR 2019-04293.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Elastic modulus of the ski base | Pa | |
| Elastic modulus of the counter material | Pa | |
| Equivalent elastic modulus | Pa | |
| Poisson ratio | - | |
| h | Ski-camber height | mm |
| m | Load magnitude | kg |
| Loading position | mm | |
| x | x-coordinate | dm |
| p | Apparent contact pressure | Pa |
References
- Bowden, F. The mechanism of sliding on ice and snow. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1939, 172, 280–298. [Google Scholar] [CrossRef]
- Eriksson, R. Friction of Runners on Snow and Ice. In Foreningen Skogsarbetens och Kungl. Domdnstyrelsens Arbetsstudieavdelning; University of California: Los Angeles, CA, USA, 1949; pp. 34–35. [Google Scholar]
- Bowden, F.P. Some Recent Experiments in Friction: Friction on Snow and Ice and the Development of some Fast-Running Skis. Nature 1955, 176, 946–947. [Google Scholar] [CrossRef]
- Glenne, B. Sliding Friction and Boundary Lubrication of Snow. J. Tribol. 1987, 109, 614–617. [Google Scholar] [CrossRef]
- Lehtovaara, A. Kinetic Friction Between Ski and Snow. Acta Polytechn. Scandinav. Mech. Eng. Series 1989, 93, 1–52. [Google Scholar]
- Bejan, A. The Fundamentals of Sliding Contact Melting and Friction. J. Heat Transf. 1989, 111, 13–20. [Google Scholar] [CrossRef]
- Bejan, A. Contact Melting Heat Transfer and Lubrication. In Advances in Heat Transfer; Elsevier: Amsterdam, The Netherlands, 1994; Volume 24, pp. 1–38. [Google Scholar] [CrossRef]
- Makkonen, L. Application of a new friction theory to ice and snow. Ann. Glaciol. 1994, 19, 155–157. [Google Scholar] [CrossRef]
- Matveev, K.I. An analytical model for flat-ski friction in steady horizontal gliding. Sport. Eng. 2017, 20, 293–298. [Google Scholar] [CrossRef]
- Lever, J.H.; Taylor, S.; Hoch, G.R.; Daghlian, C. Evidence that abrasion can govern snow kinetic friction. J. Glaciol. 2019, 65, 68–84. [Google Scholar] [CrossRef]
- Lever, J.H.; Asenath-Smith, E.; Taylor, S.; Lines, A.P. Assessing the Mechanisms Thought to Govern Ice and Snow Friction and Their Interplay With Substrate Brittle Behavior. Front. Mech. Eng. 2021, 7, 690425. [Google Scholar] [CrossRef]
- Scherge, M.; Stoll, M.; Moseler, M. On the Influence of Microtopography on the Sliding Performance of Cross Country Skis. Front. Mech. Eng. 2021, 7, 659995. [Google Scholar] [CrossRef]
- Almqvist, A.; Pellegrini, B.; Lintzén, N.; Emami, N.; Holmberg, H.C.; Larsson, R. A Scientific Perspective on Reducing Ski-Snow Friction to Improve Performance in Olympic Cross-Country Skiing, the Biathlon and Nordic Combined. Front. Sport. Act. Living 2022, 4, 844883. [Google Scholar] [CrossRef]
- Persson, B.N.J. Elastoplastic Contact between Randomly Rough Surfaces. Phys. Rev. Lett. 2001, 87, 116101. [Google Scholar] [CrossRef]
- Yang, C.; Tartaglino, U.; Persson, B.N. A multiscale molecular dynamics approach to contact mechanics. Eur. Phys. J. E 2006, 19, 47–58. [Google Scholar] [CrossRef]
- Persson, B. Contact mechanics for randomly rough surfaces. Surf. Sci. Rep. 2006, 61, 201–227. [Google Scholar] [CrossRef]
- Goryacheva, I.G. Multiscale Modelling in Contact Mechanics. In IUTAM Symposium on Scaling in Solid Mechanics; Borodich, F., Ed.; Springer Netherlands: Dordrecht, The Netherlands, 2009; pp. 123–134. [Google Scholar] [CrossRef]
- Yastrebov, V.A.; Anciaux, G.; Molinari, J.F. The role of the roughness spectral breadth in elastic contact of rough surfaces. J. Mech. Phys. Solids 2017, 107, 469–493. [Google Scholar] [CrossRef]
- Vakis, A.; Yastrebov, V.; Scheibert, J.; Nicola, L.; Dini, D.; Minfray, C.; Almqvist, A.; Paggi, M.; Lee, S.; Limbert, G.; et al. Modeling and Simulation in Tribology across Scales: An Overview. Tribol. Int. 2018, 125, 169–199. [Google Scholar] [CrossRef]
- Aramfard, M.; Pérez-Ràfols, F.; Nicola, L. A 2D dual-scale method to address contact problems. Tribol. Int. 2022, 171, 107509. [Google Scholar] [CrossRef]
- Bonari, J.; Paggi, M.; Dini, D. A New Finite Element Paradigm to Solve Contact Problems with Roughness. Int. J. Solids Struct. 2022, 253, 111643. [Google Scholar] [CrossRef]
- Bäurle, L.; Kaempfer, T.; Szabó, D.; Spencer, N. Sliding friction of polyethylene on snow and ice: Contact area and modeling. Cold Reg. Sci. Technol. 2007, 47, 276–289. [Google Scholar] [CrossRef]
- Mössner, M.; Hasler, M.; Nachbauer, W. Calculation of the contact area between snow grains and ski base. Tribol. Int. 2021, 163, 107183. [Google Scholar] [CrossRef]
- Bäckström, M.; Dahlen, L.; Tinnsten, M. Essential Ski Characteristics for Cross-Country Skis Performance (P251). In The Engineering of Sport 7; Springer: Paris, France, 2008; pp. 543–549. [Google Scholar] [CrossRef]
- Schindelwig, K.; Hasler, M.; Van Putten, J.; Rohm, S.; Nachbauer, W. Temperature Below a Gliding Cross Country Ski. Procedia Eng. 2014, 72, 380–385. [Google Scholar] [CrossRef][Green Version]
- Kristiansen, P. Prototyping a Measurement Device for Evaluating the Performance of Cross-Country Skis Investigation of Pressure-Distribution. Master’s Thesis, University of Oslo, Oslo, Norway, 2019. [Google Scholar]
- Breitschädel, F. Effects of temperature change on cross-country ski characteristics. Procedia Eng. 2010, 2, 2913–2918. [Google Scholar] [CrossRef]
- Breitschädel, F. Variation of Nordic Classic Ski Characteristics from Norwegian national team athletes. Procedia Eng. 2012, 34, 391–396. [Google Scholar] [CrossRef]
- Kalliorinne, K. The influence of cross-country skiers’ tucking position on ski-camber profile, apparent contact area and the load partitioning. Part P J. Sport. Eng. Technol. 2022, 7. [Google Scholar]
- Pellegrini, B.; Stöggl, T.L.; Holmberg, H.C. Developments in the biomechanics and equipment of Olympic cross-country skiers. Front. Physiol. 2018, 9, 976. [Google Scholar] [CrossRef]
- Pellegrini, B.; Sandbakk, Ø.; Stöggl, T.; Supej, M.; Ørtenblad, N.; Schürer, A.; Steiner, T.; Lunina, A.; Manhard, C.; Liu, H.; et al. Methodological Guidelines Designed to Improve the Quality of Research on Cross-Country Skiing. J. Sci. Sport Exerc. 2021. [Google Scholar] [CrossRef]
- SkiSelector; SkiSelector Sportdata AB.: Piteå, Sweden, 2022.
- Speedmax 3D Classic/Skate; Fischer Sports GmbH.: Ried im Innkreis, Austria, 2020.
- MATLAB. 9.11.0 (R2021b); The MathWorks Inc.: Natick, MA, USA, 2021. [Google Scholar]
- Almqvist, A.; Sahlin, F.; Larsson, R.; Glavatskih, S. On the dry elasto-plastic contact of nominally flat surfaces. Tribol. Int. 2007, 40, 574–579. [Google Scholar] [CrossRef]
- Sahlin, F.; Larsson, R.; Almqvist, A.; Lugt, P.M.; Marklund, P. A mixed lubrication model incorporating measured surface topography. Part 1: Theory of flow factors. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2010, 224, 335–351. [Google Scholar] [CrossRef]
- Almqvist, A.; Campana, C.; Prodanov, N.; Persson, B.N.J. Interfacial Separation between Elastic Solids with Randomly Rough Surfaces: Comparison between Theory and Numerical Techniques. J. Mech. Phys. Solids 2011, 59, 2355–2369. [Google Scholar] [CrossRef]
- Ghaednia, H.; Wang, X.; Saha, S.; Xu, Y.; Sharma, A.; Jackson, R.L. A Review of Elastic–Plastic Contact Mechanics. Appl. Mech. Rev. 2017, 69, 060804. [Google Scholar] [CrossRef]
- Tiwari, A.; Almqvist, A.; Persson, B.N.J. Plastic Deformation of Rough Metallic Surfaces. Tribol. Lett. 2020, 68. [Google Scholar] [CrossRef]
- Pérez-Ràfols, F.; Almqvist, A. On the Stiffness of Surfaces with Non-Gaussian Height Distribution. Sci. Rep. 2021, 11, 1863. [Google Scholar] [CrossRef]
- Kalliorinne, K.; Larsson, R.; Pérez-Ràfols, F.; Liwicki, M.; Almqvist, A. Artificial Neural Network Architecture for Prediction of Contact Mechanical Response. Front. Mech. Eng. 2021, 6, 579825. [Google Scholar] [CrossRef]
- Huang, D.; Yan, X.; Larsson, R.; Almqvist, A. Boundary Element Method for the Elastic Contact Problem with Hydrostatic Load at the Contact Interface. Appl. Surf. Sci. Adv. 2021, 6, 100176. [Google Scholar] [CrossRef]
- Lintzén, N.; Edeskär, T. Uniaxial Strength and Deformation Properties of Machine-Made Snow. J. Cold Reg. Eng. 2015, 29, 04014020. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).