CFD-Predicted Rotordynamic Characteristics for High-Temperature Water Liquid Seal Considering Tooth Deformation
Abstract
:1. Introduction
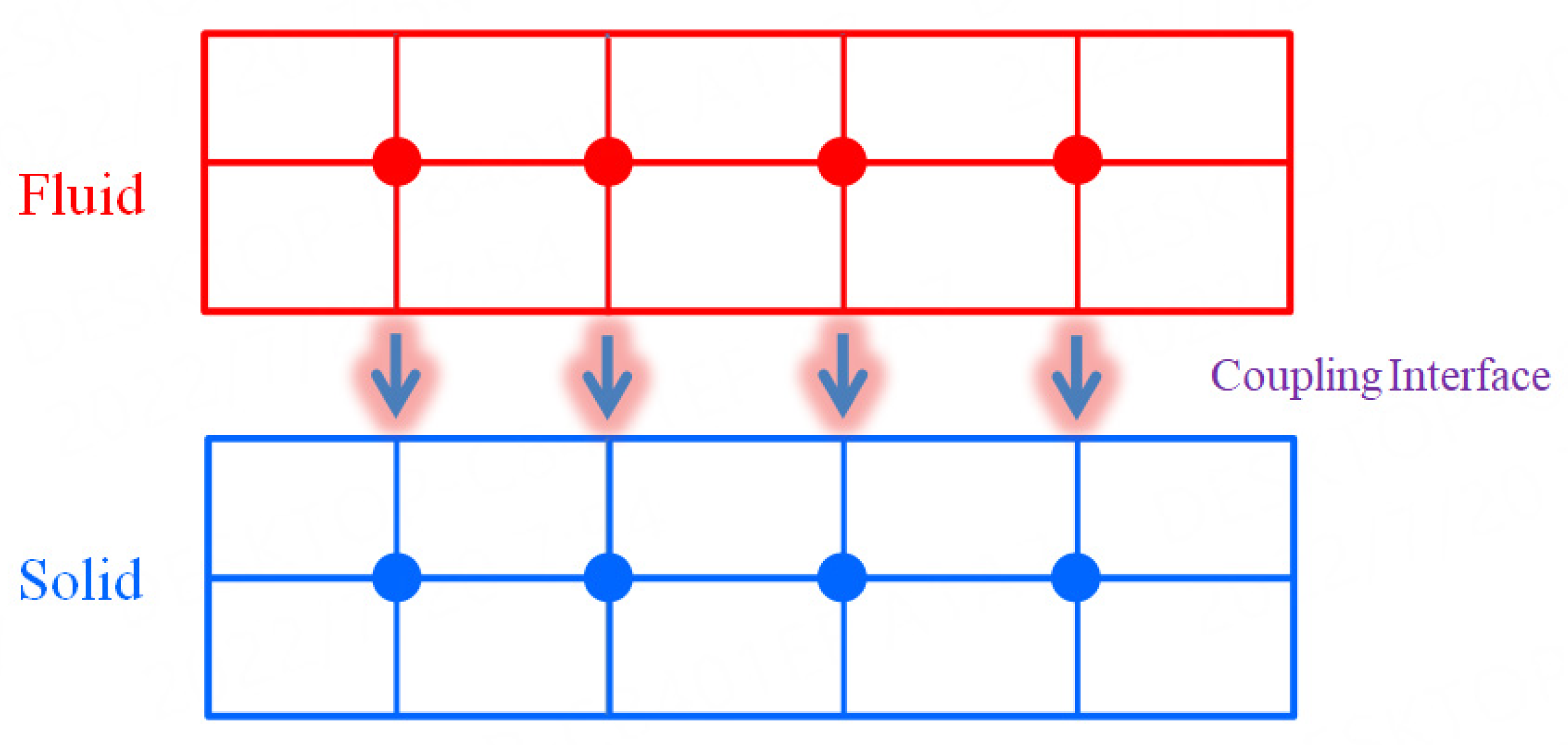
2. The Thermal-Fluid-Solid Coupling Model
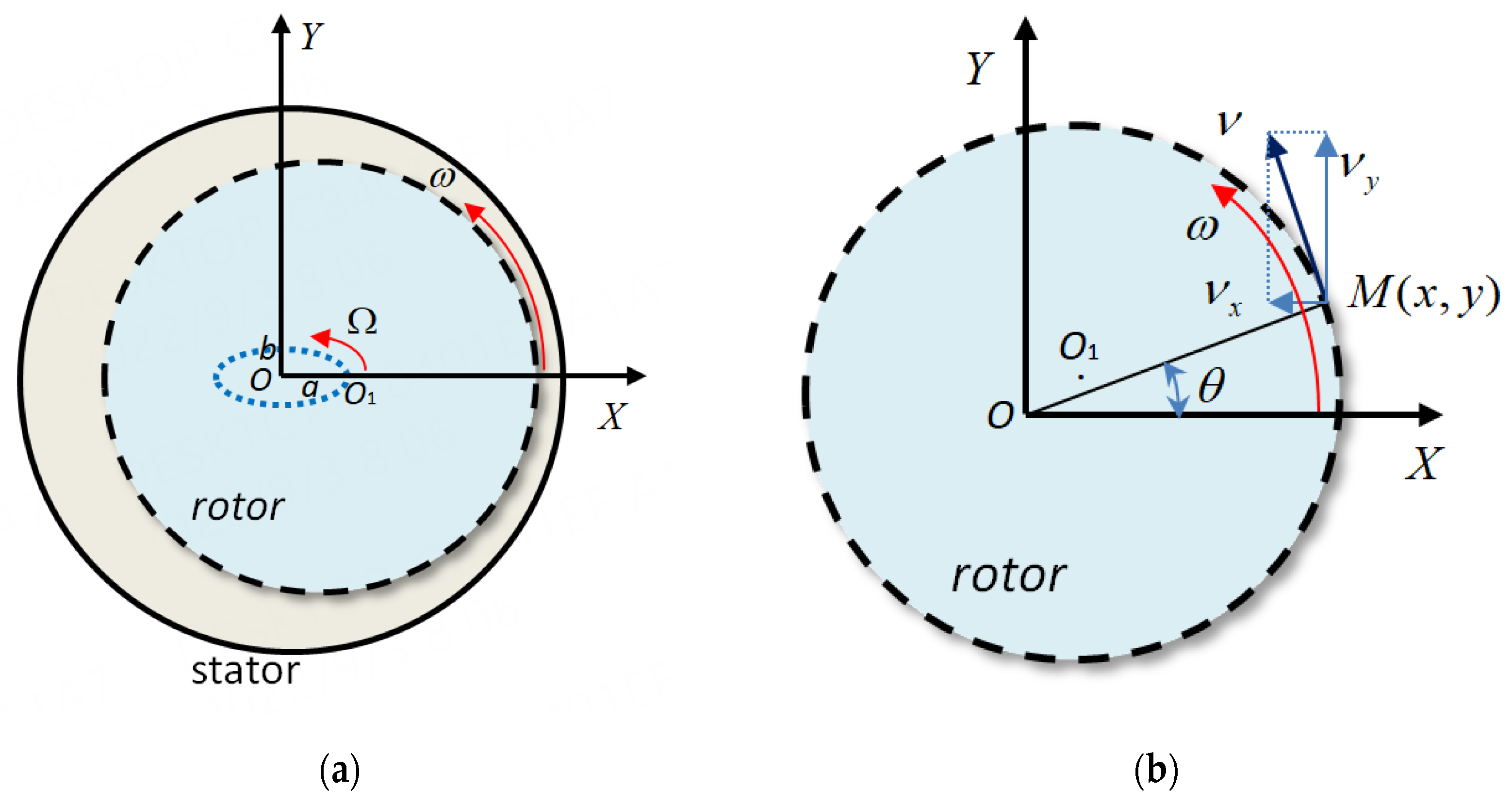
2.1. Calculation Model
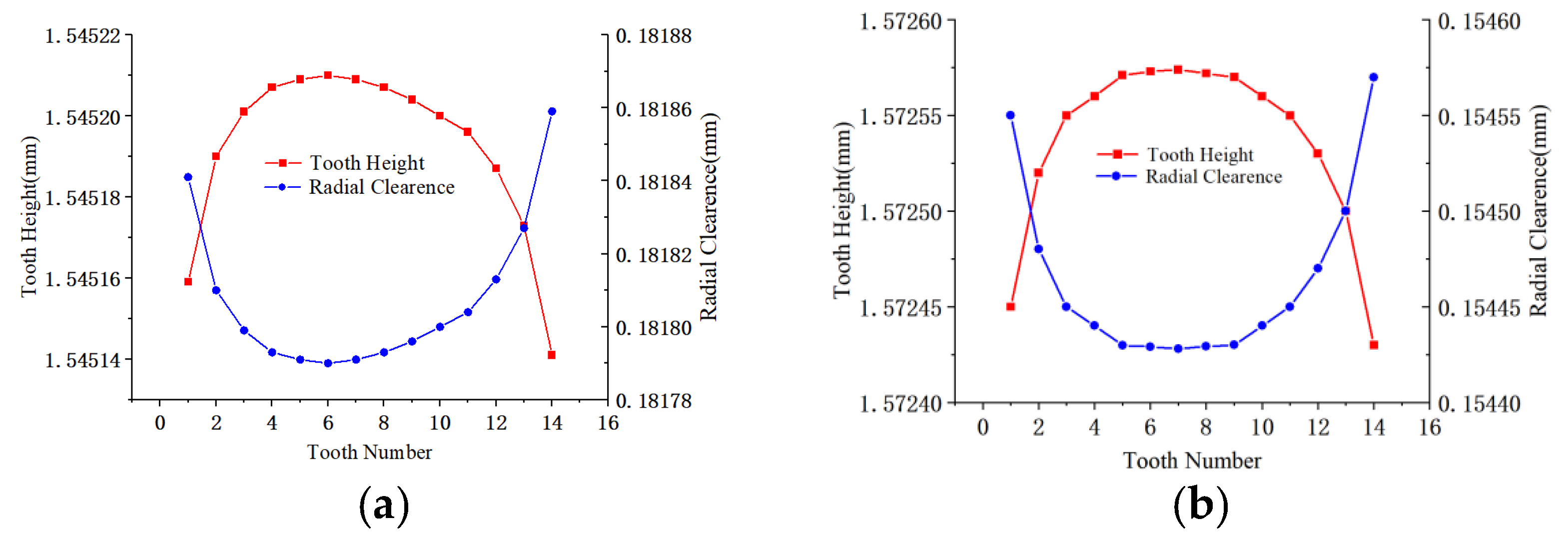
2.2. Seal Deformation Analysis
3. Dynamic Coefficients Calculation Verification
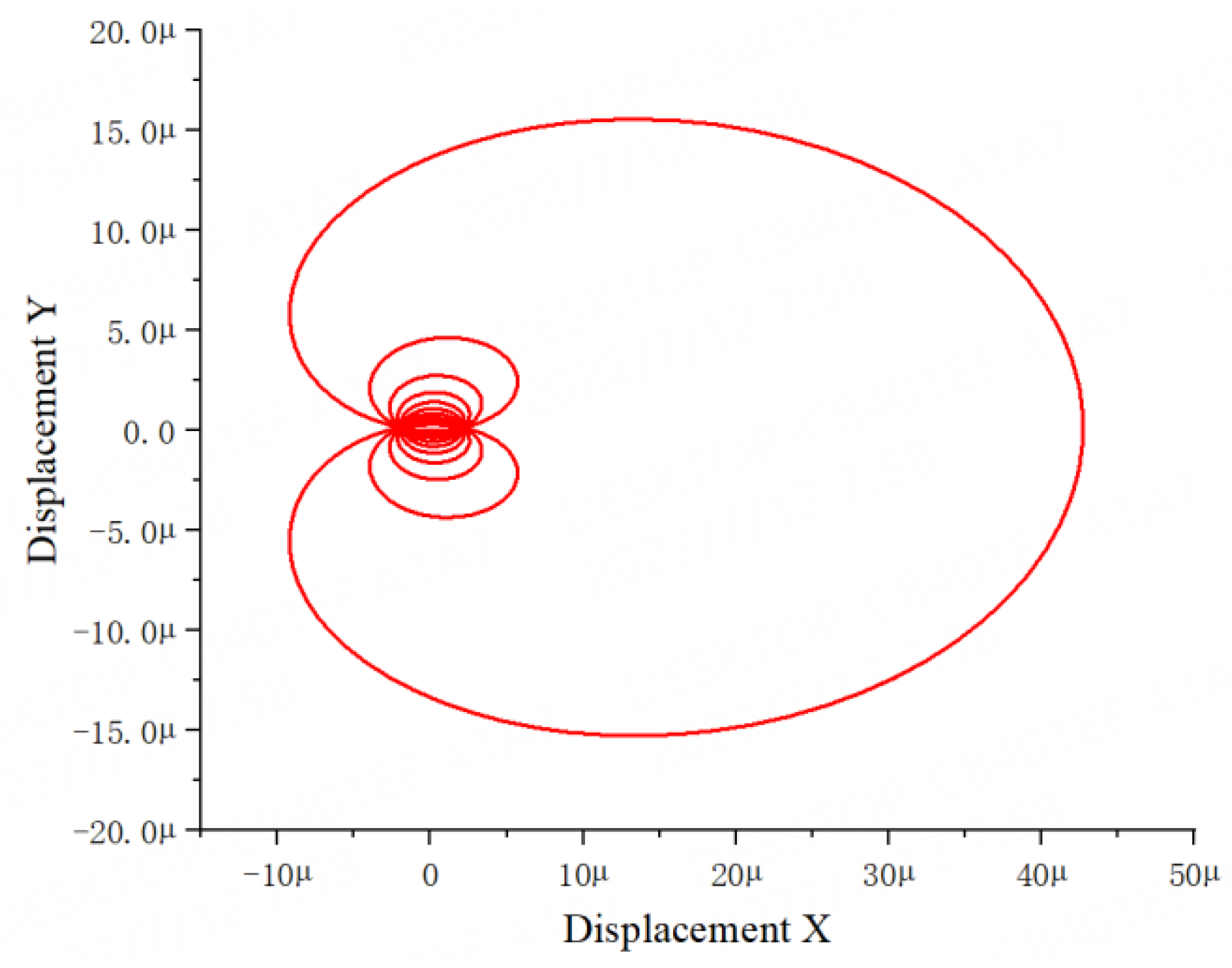
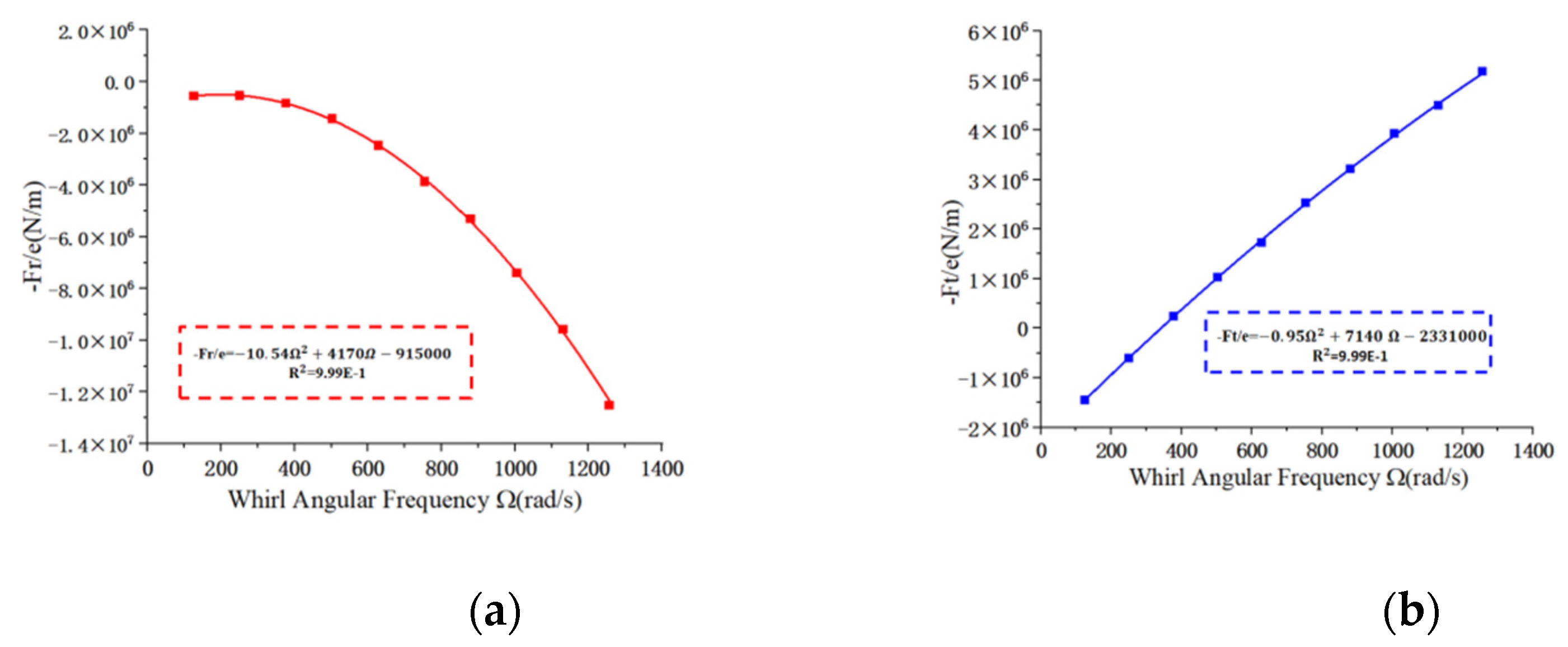
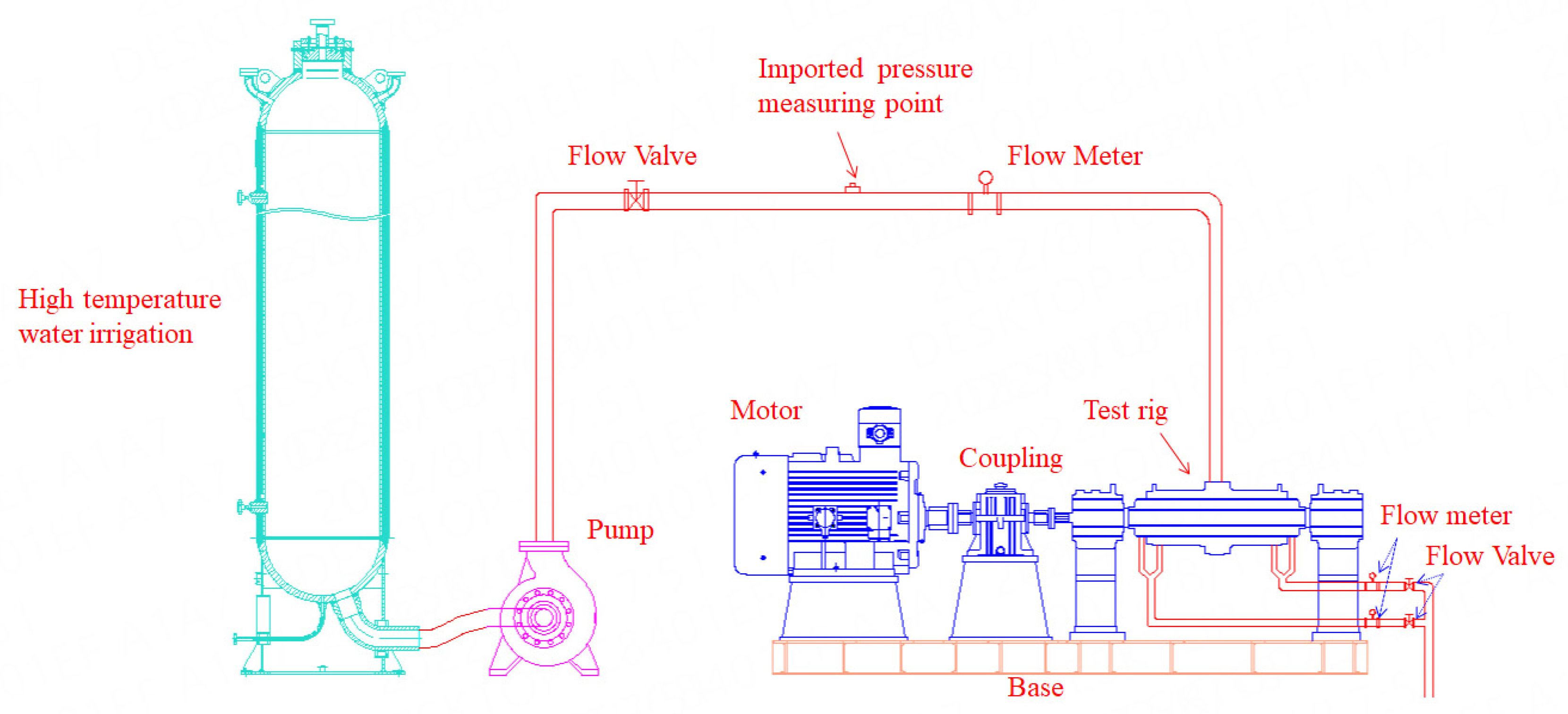
3.1. Computational Method
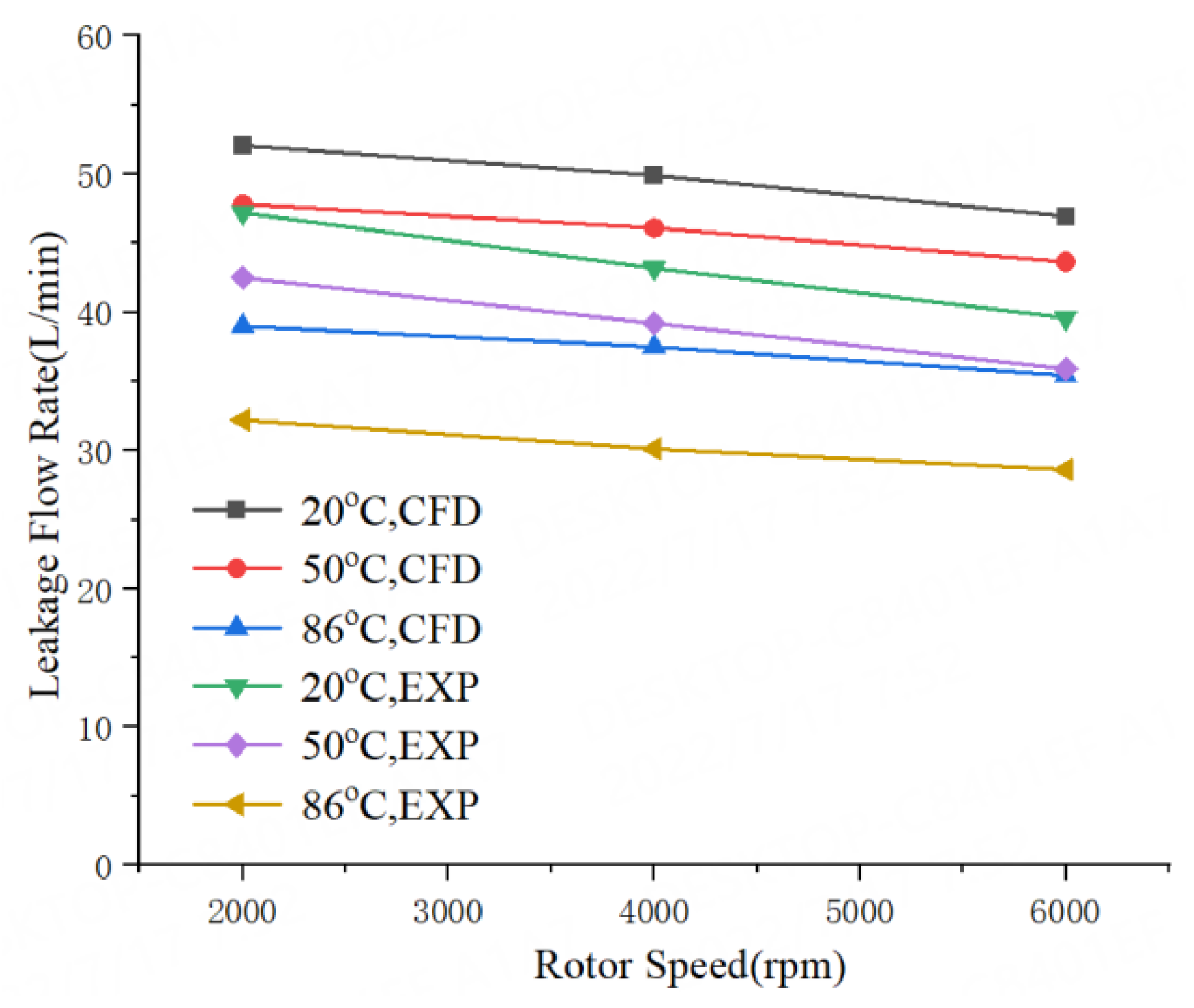
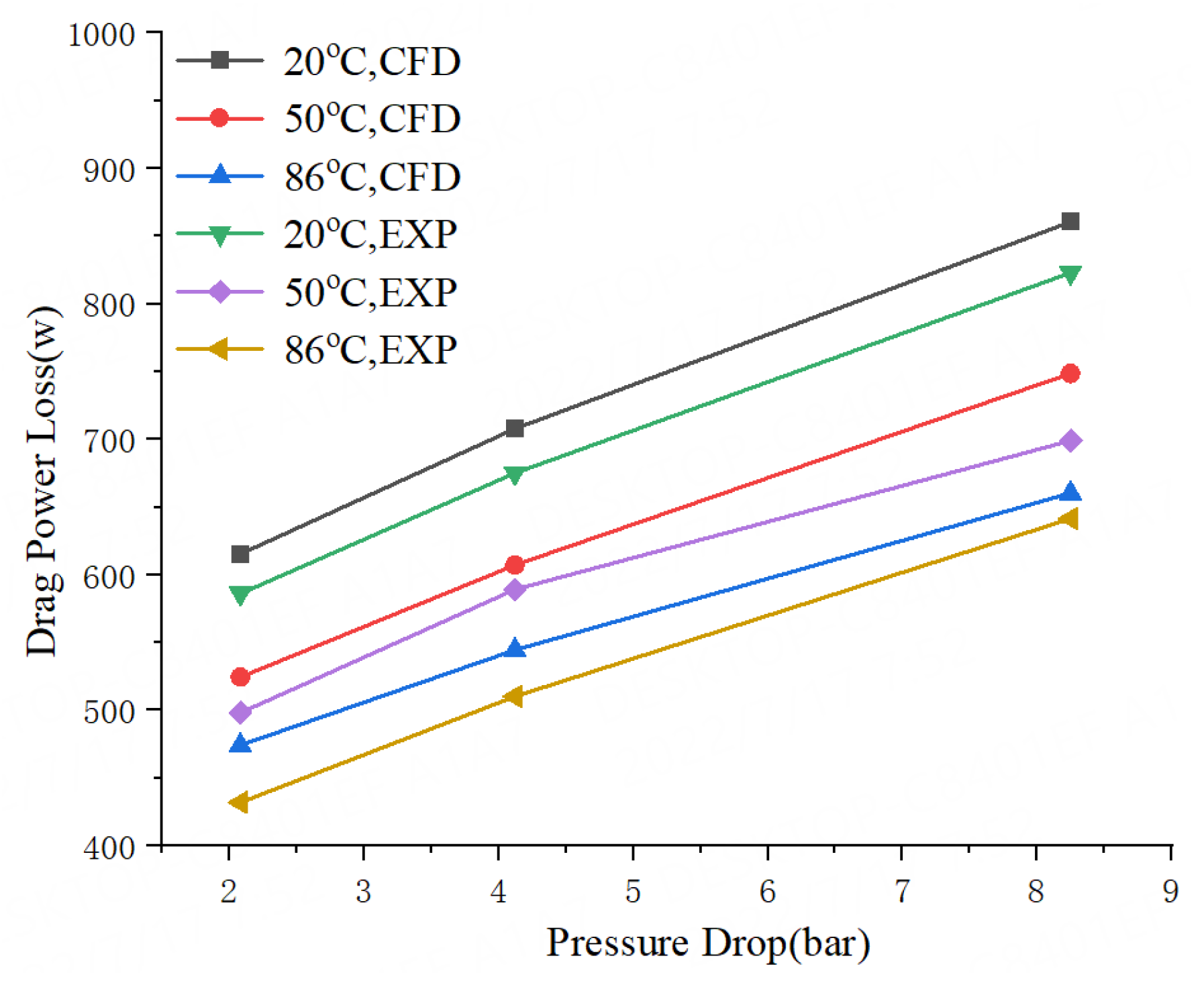
3.2. Verification
4. Calculation Model Results and Discussion
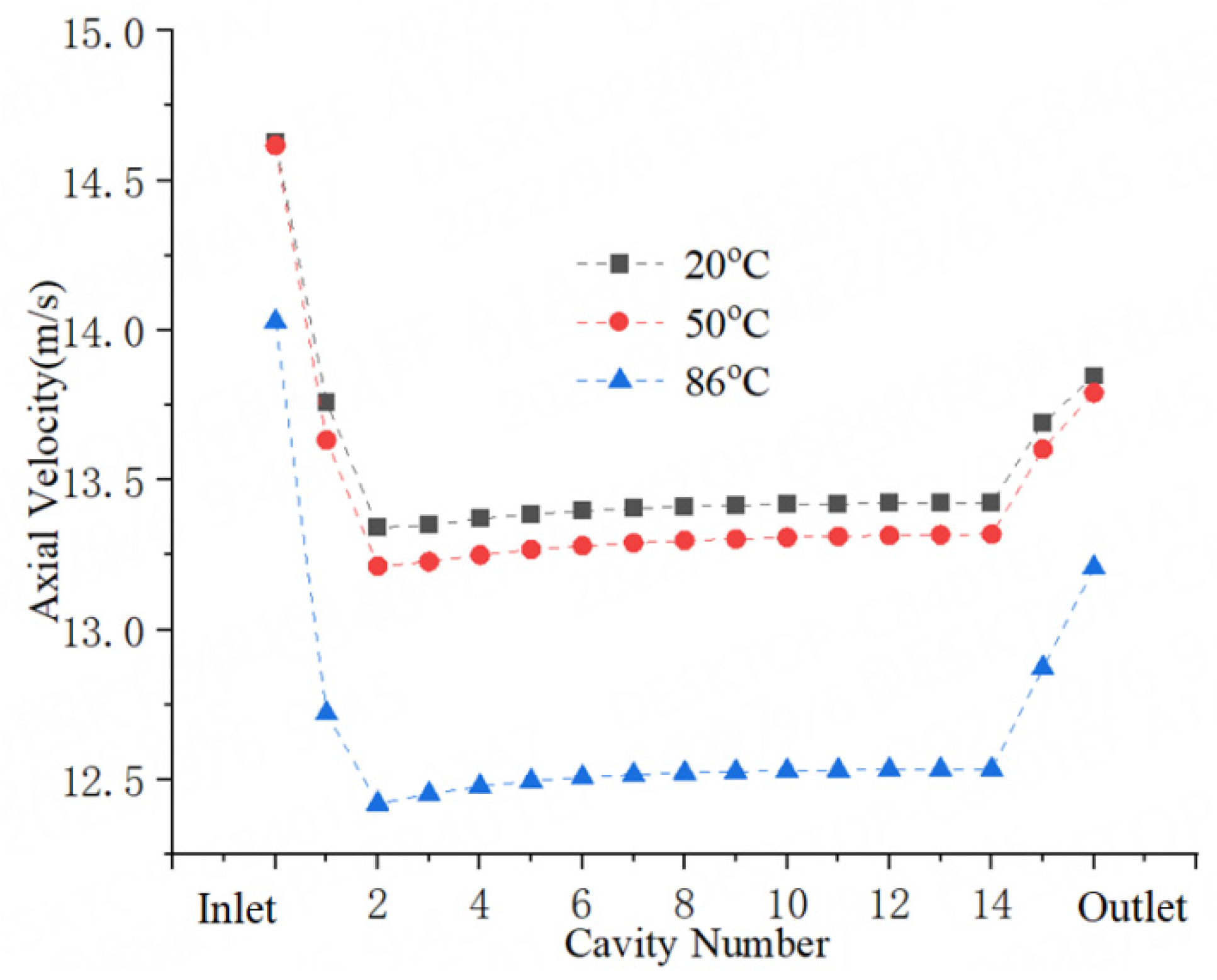
4.1. Test Results
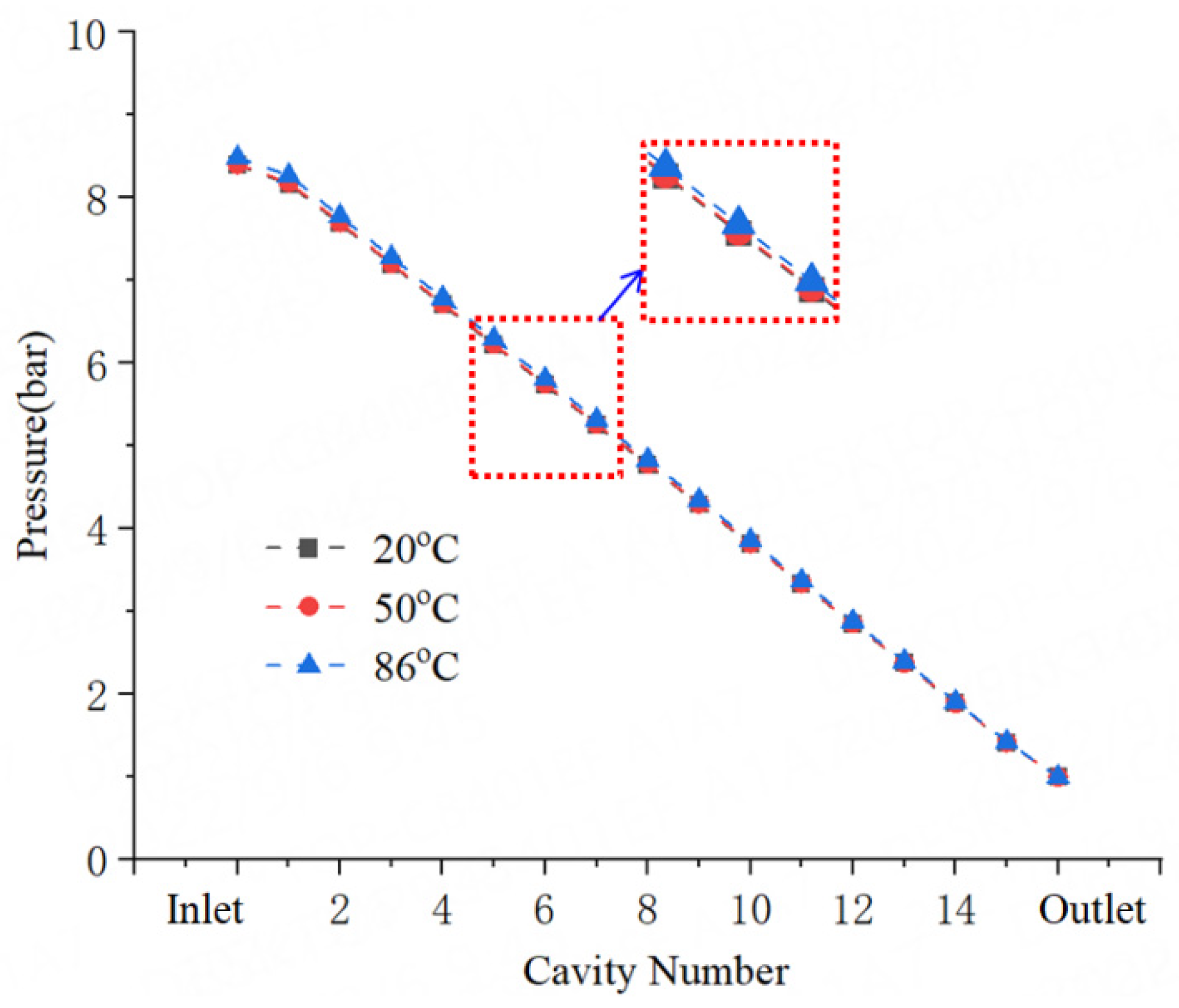
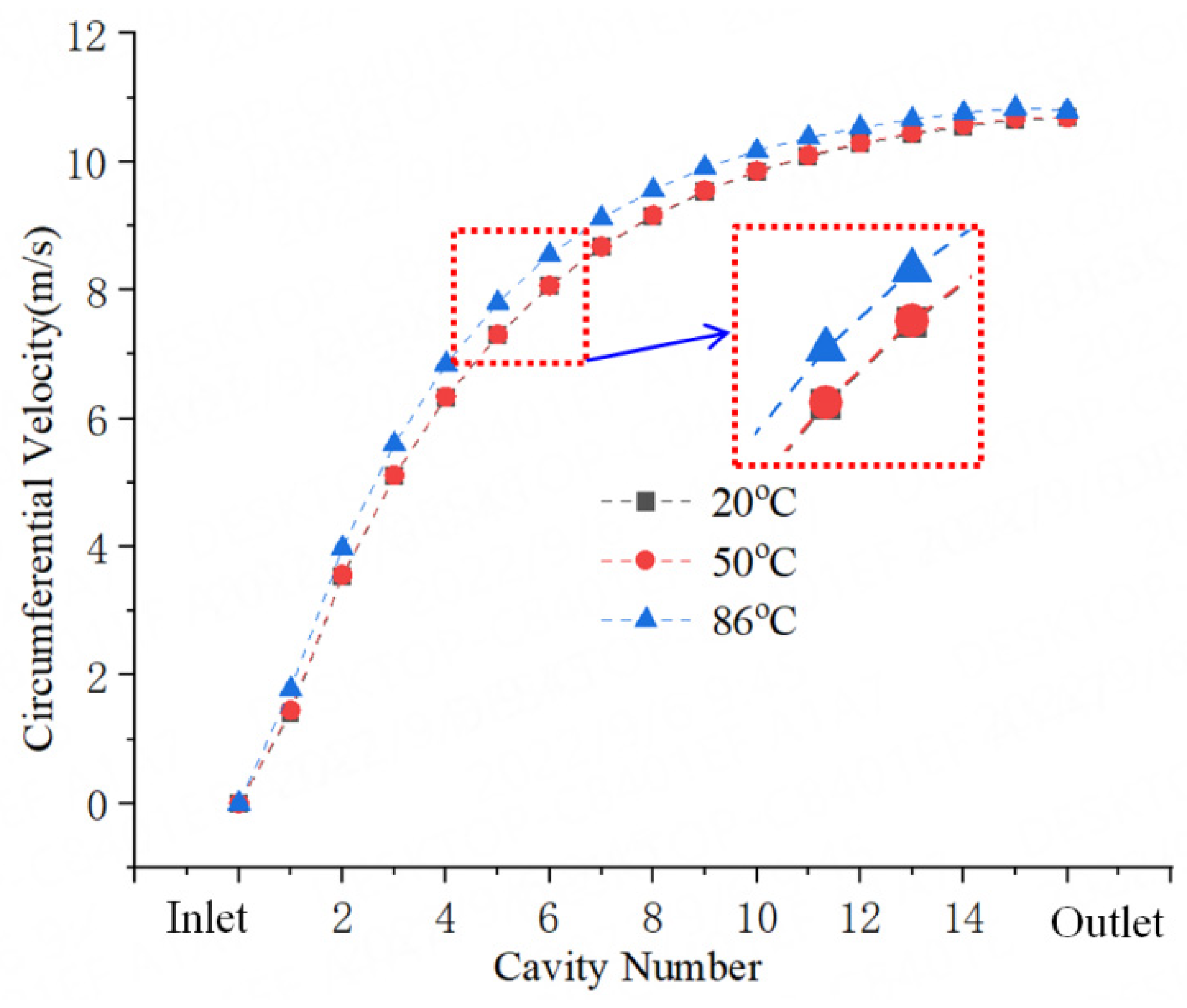
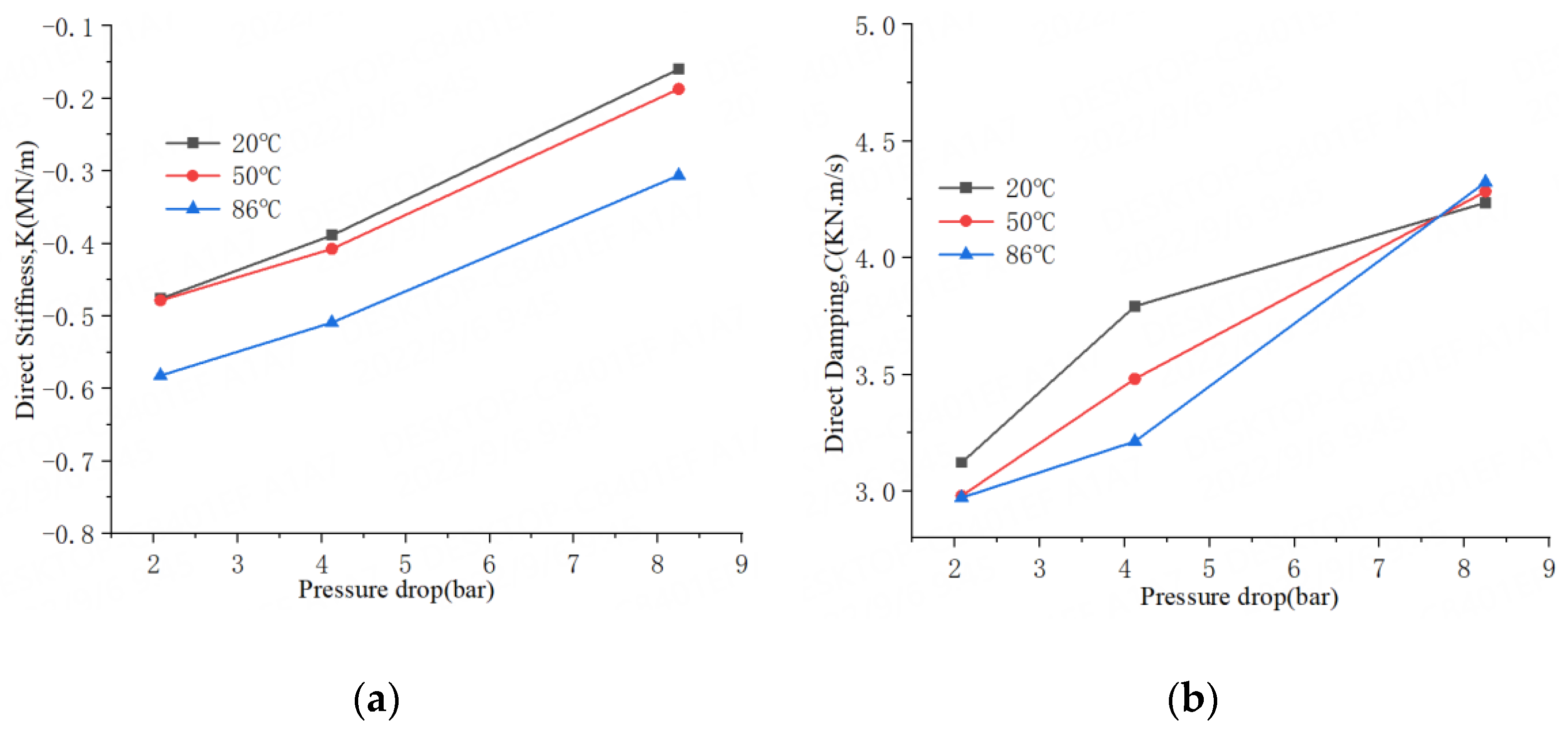
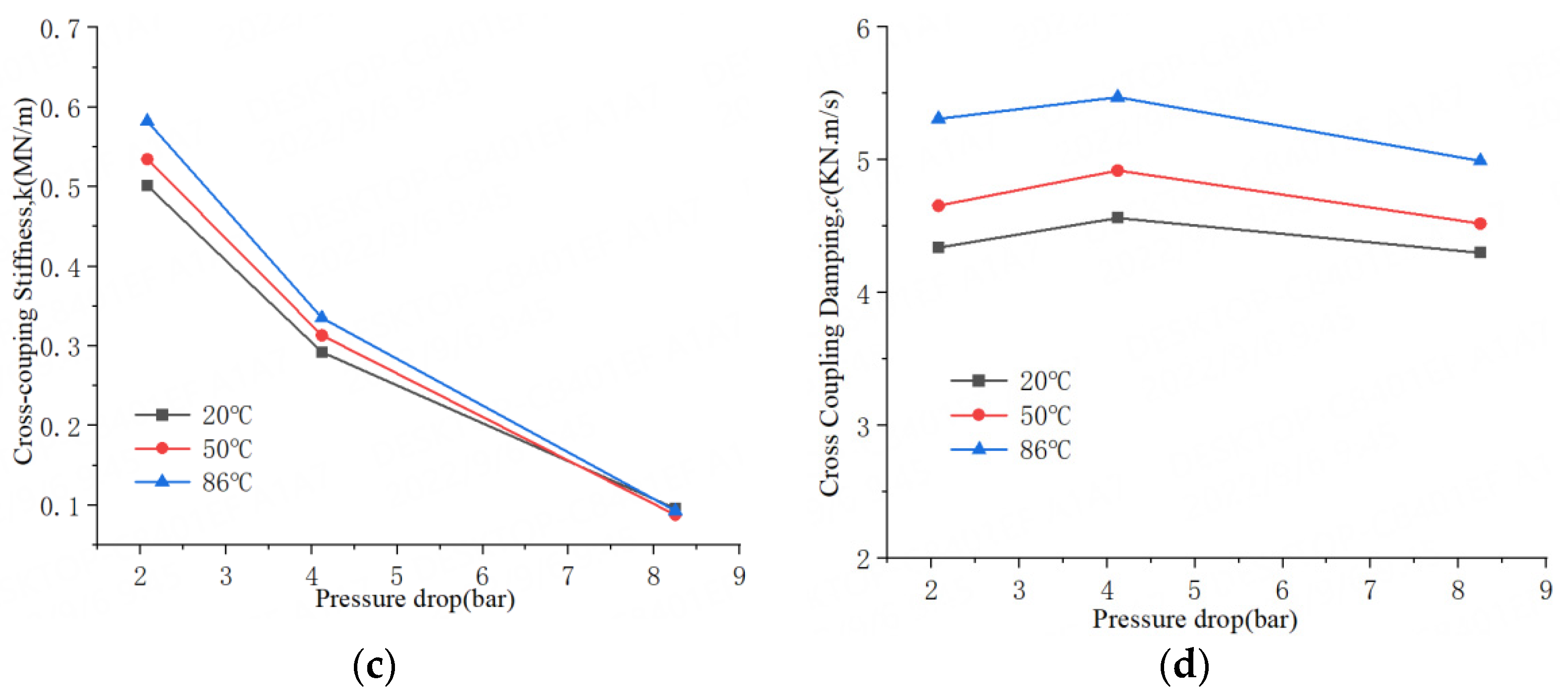
4.2. Effects of Pressure Drop
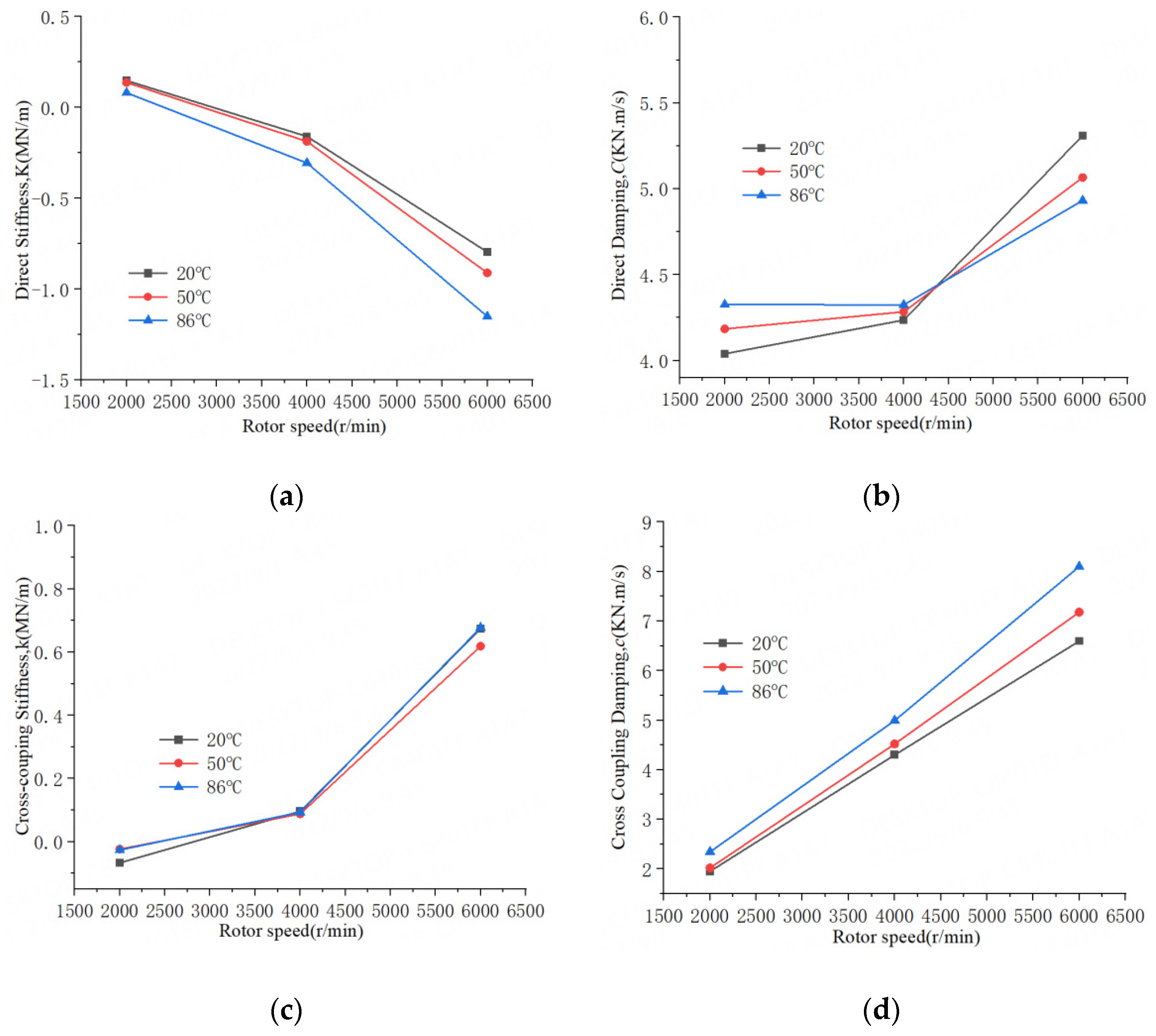
4.3. Effects of Rotational Speed
5. Conclusions
- With the increase of water temperature, the radial deformation of the seal teeth increases, and the seal clearance decreases. The leakage flow rate of water liquid seal decreases, and the power drag loss decreases too. The leakage flow rate of 86 °C water liquid seal is 25% smaller than 20 °C water liquid seal. The drag power loss of 86 °C water liquid seal is 22% smaller than 20 °C water liquid seal. The leakage flow rate decreases with the increase of the rotor speed, and the drag power loss increases with the increase of the pressure drop. This means the 86 °C water seal has a better sealing capacity.
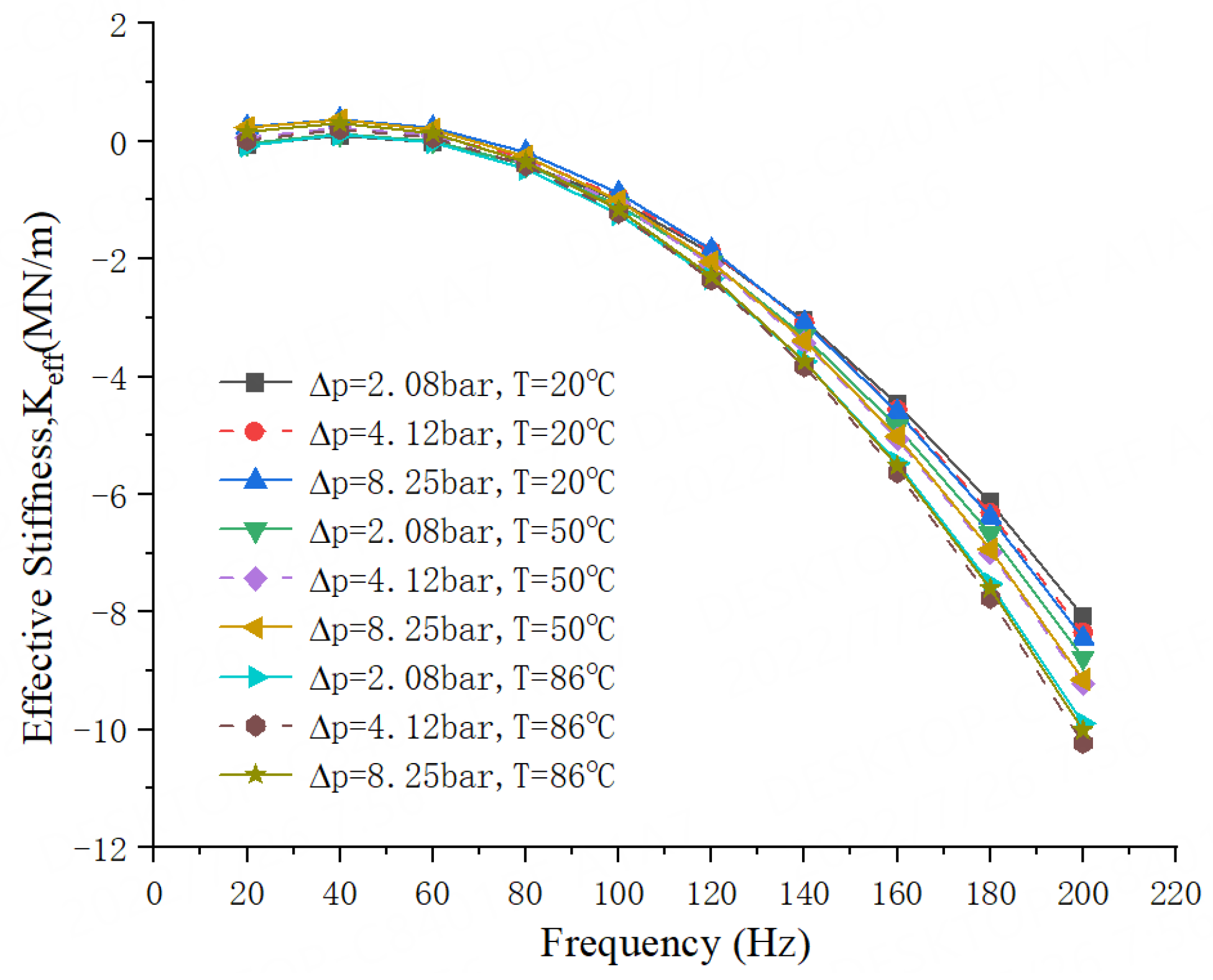
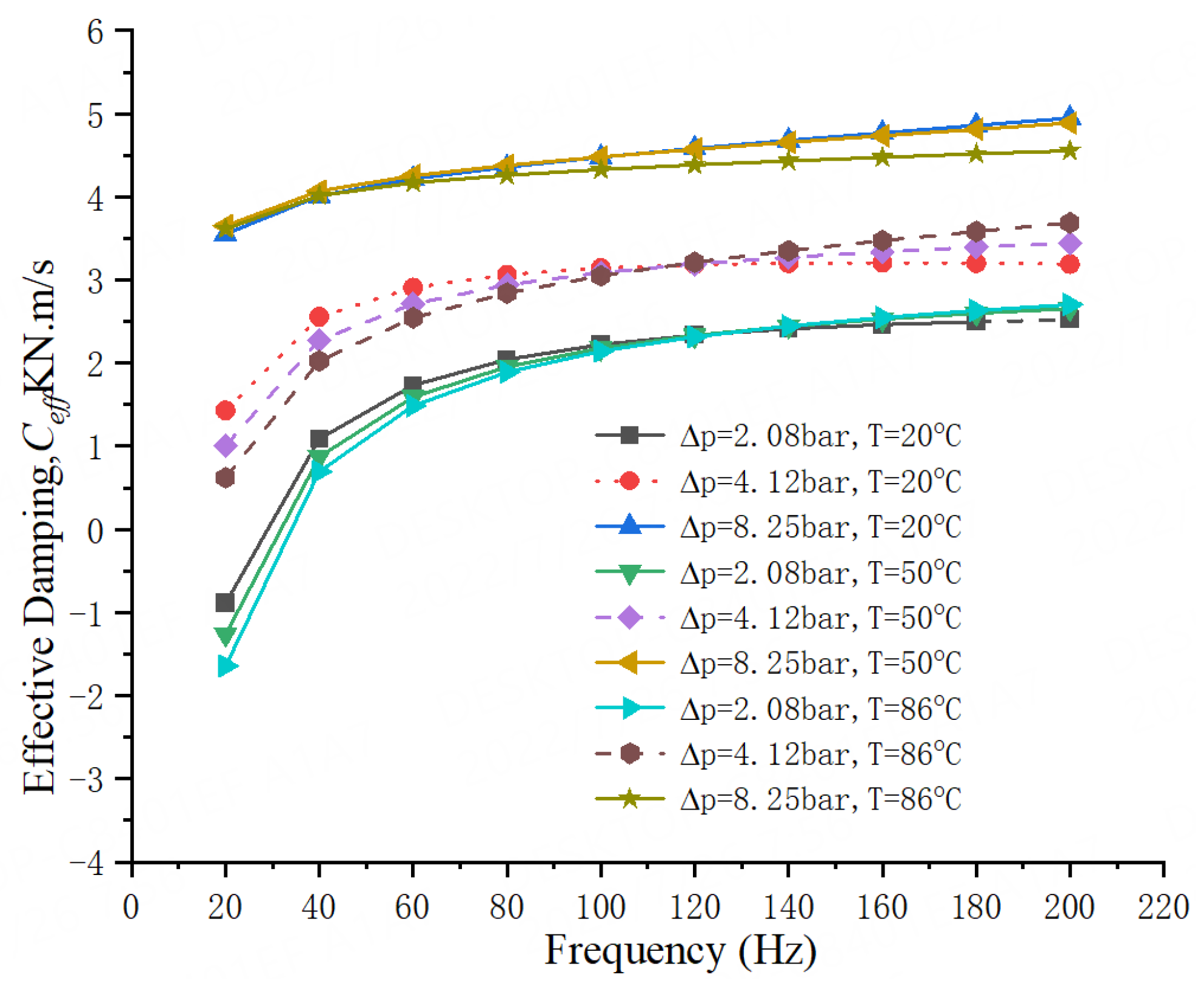
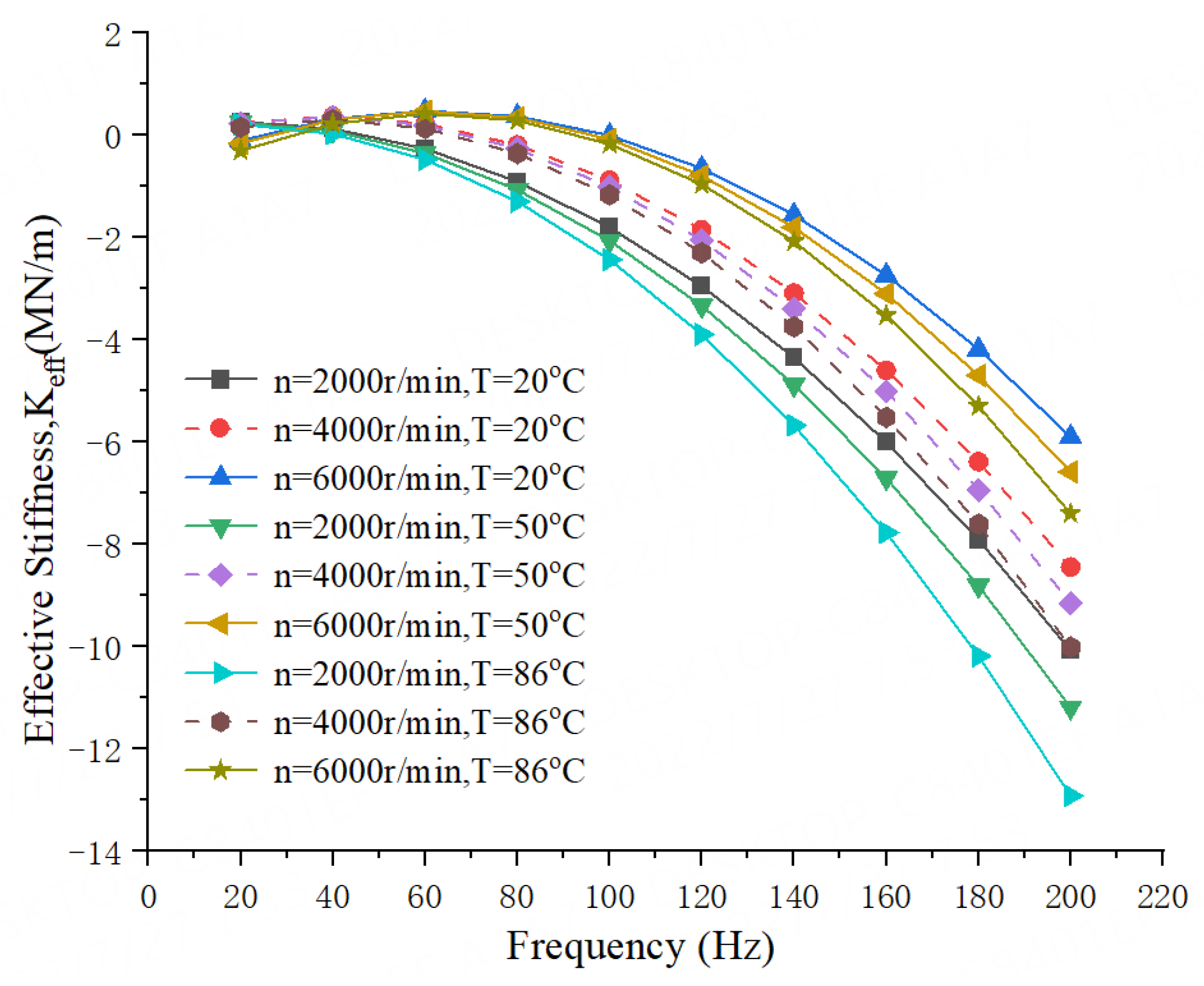
- For all operation conditions, the 20 °C water liquid seal has a relatively large direct stiffness coefficient K, followed by 50 °C water liquid seal. With the increase of water temperature, the direct stiffness coefficient decreases, and the effective stiffness coefficient Keff for 20 °C water seal possesses a better stiffness capability than the other two temperature seals.
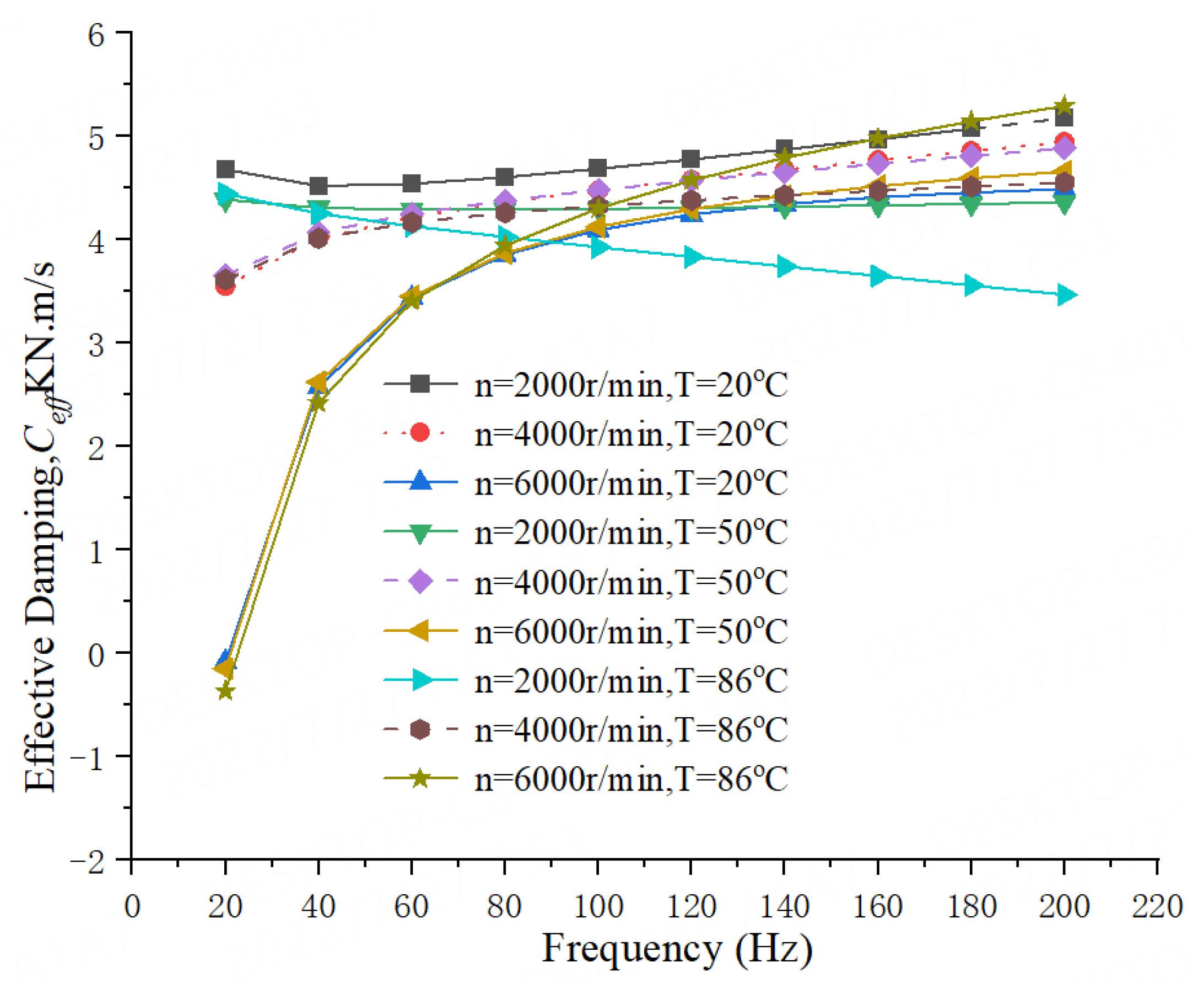
- For all operation conditions, compared to the 50 °C and 86 °C water liquid seal, the 20 °C water liquid seal has a larger effective damping coefficient Ceff in the whole whirling frequency range, it is more stable for the rotor system.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Keff | Effective stiffness (N/m) |
| Kxx | Direct stiffness in x direction (N/m) |
| Kxy | Cross coupling stiffness in x direction (N/m) |
| Kyy | Direct stiffness in y direction (N/m) |
| Kyx | Cross coupling stiffness in y direction (N/m) |
| m | Cross coupling virtual-mass (kg) |
| M | Direct virtual-mass (kg) |
| Mxx | Direct virtual-mass in x direction (kg) |
| Mxy | Cross coupling virtual-mass in x direction (kg) |
| Myy | Direct virtual-mass in y direction (kg) |
| Myx | Cross coupling virtual-mass in y direction (kg) |
| Ceff | Effective damping (Ns/m) |
| Cxx | Direct damping in x direction (Ns/m) |
| Cxy | Cross coupling damping in x direction (Ns/m) |
| Cyy | Direct damping in y direction (Ns/m) |
| Cyx | Cross coupling damping in y direction (N s/m) |
| Dxx: | Rotor motion in x direction for x direction excitation (m) |
| Dxy | Rotor motion in y direction for x direction excitation (m) |
| Dyy | Rotor motion in y direction for y direction excitation (m) |
| Dyx | Rotor motion in x direction for y direction excitation (m) |
| Fr | Response force in radial direction (N) |
| Ft | Response force in tangential direction (N) |
| Fxx | Response force in x direction for x direction excitation (N) |
| Fxy | Response force in y direction for x direction excitation (N) |
| Fyy | Response force in y direction for y direction excitation (N) |
| Fyx | Response force in x direction for y direction excitation (N) |
| Hxx | Direct force impedance in x direction (N/m) |
| Hxy | Cross coupling force impedance in x direction (N/m) |
| Hyy | Direct force impedance in y direction (N/m) |
| Hyx | Cross coupling force impedance in y direction (N/m) |
| n | Rotational speed (r/min) |
References
- Vance, J.M. Machinery Vibration and Rotordynamics; Wiley: New York, NY, USA, 2010; pp. 271–278. [Google Scholar]
- Childs, D.W.; Vance, J.M. Annular Seals and the Rotordynamics of Compressors and Turbines. In Proceedings of the 26th Turbomachinery Symposium, Houston, TX, USA, 14–18 September 1997; pp. 201–220. [Google Scholar]
- Childs, D.W. Turbomachinery Rotordynamics with Case Studies; Minter Spring Publishing: Wellborn, TX, USA, 2013. [Google Scholar]
- Xie, Z.; Wang, X.; Zhu, W. Theoretical and experimental exploration into the fluid structure coupling dynamic behaviors towards water-lubricated bearing with axial asymmetric grooves. Mech. Syst. Signal Process. 2022, 168, 108624. [Google Scholar] [CrossRef]
- Xie, Z.; Zhu, W. Theoretical and experimental exploration on the micro asperity contact load ratios and lubrication regimes transition for water-lubricated stern tube bearing. Tribol. Int. 2021, 164, 107105. [Google Scholar] [CrossRef]
- Xie, Z.; Zhu, W. An investigation on the lubrication characteristics of floating ring bearing with consideration of multi-coupling factors. Mech. Syst. Signal Process. 2022, 162, 108086. [Google Scholar] [CrossRef]
- Xie, Z.; Zhang, Y.; Zhou, J.; Zhu, W. Theoretical and experimental research on the micro interface lubrication regime of water lubricated bearing. Mech. Syst. Signal Process. 2021, 151, 107422. [Google Scholar] [CrossRef]
- Xie, Z.; Shen, N.; Zhu, W.; Tian, W.; Hao, L. Theoretical and experimental investigation on the influences of misalignment on the lubrication performances and lubrication regimes transition of water lubricated bearing. Mech. Syst. Signal Process. 2021, 149, 107211. [Google Scholar] [CrossRef]
- Lu, B.; Xuan, H.; Ma, X.; Han, F.; Hong, W.; Zhi, S. The influence of the axial rub added in the radial rub on the wear of the seal fins during the high speed rub of labyrinth-honeycomb seal. Materials 2021, 14, 1997. [Google Scholar] [CrossRef]
- Zhang, W.; Qin, P.; Zhang, X.; Ma, K.; Yin, L.; Li, C. Rotordynamic characteristics of a novel pocket damper seal with self-regulated injection. J. Mech. Sci. Technol. 2021, 35, 3421–3434. [Google Scholar] [CrossRef]
- Zhou, W.; Zhao, Z.; Wang, Y.; Shi, J.; Gan, B.; Li, B.; Qiu, N. Research on leakage performance and dynamic characteristics of a novel labyrinth seal with staggered helical teeth structure. Alex. Eng. J. 2021, 60, 3177–3187. [Google Scholar] [CrossRef]
- Zhang, W.; Gu, Q.; Wang, T. Study on the rotordynamic performance of a novel anti-stagnation labyrinth seal. J. Vib. Eng. Technol. 2020, 8, 835–846. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, J.; Li, Z.; Yan, X. Numerical comparison of leakage flow and rotordynamic characteristics for two types of labyrinth seal with baffles. J. Eng. Gas Turbines Power 2020, 142, 091008. [Google Scholar] [CrossRef]
- Moreland, J.A. Influence of Pre-Swirl and Eccentricity in Smooth Stator/Grooved Rotor Liquid Annular Seals, Measured Static and Rotordynamic Characteristics. Master’s Thesis, Texas A&M University, College Station, TX, USA, 2016. [Google Scholar]
- Childs, D.W. Turbomachinery Rotordynamics: Phenomena, Modeling and Analysis; Wiley: New York, NY, USA, 1993; p. 292. [Google Scholar]
- Iwatsubo, T.; Sheng, B. Evaluation of Dynamic Characteristics Parallel Grooved Annular Seals by Theory and Experiment. In Proceedings of the IFToMM Third International Conference on Rotordynamics, Lyon, France, 10–12 September 1990; pp. 313–318. [Google Scholar]
- Marquette, O.R.; Childs, D.W. An Extended Three-Control-Volume Theory for Circumferentially-Grooved Liquid Seals. J. Tribol. 1996, 118, 276–285. [Google Scholar] [CrossRef]
- Li, F.; Cui, B.; Zhai, L. Research on Rotordynamic Characteristics of Pump Annular Seals Based on a New Transient CFD Method. Processes 2020, 8, 227. [Google Scholar] [CrossRef]
- Jia, X.; Zheng, Q.; Jiang, Y.; Zhang, H. Leakage and rotordynamic performance of T type labyrinth seal. Aerosp. Sci. Techol. 2019, 88, 22–31. [Google Scholar] [CrossRef]
- Mortazavi, F.; Palazzolo, A. Prediction of Rotordynamic Performance of Smooth Stator-Grooved Rotor Liquid Annular Seals Utilizing CFD. J. Vib. Acoust. 2018, 140, 031002. [Google Scholar] [CrossRef]
- Kim, S.H.; Ha, T.W. Prediction of Leakage and Rotordynamic Coefficients for the Circumferential- Groove-Pump Seal Using CFD Analysis. J. Mech. Sci. Technol. 2016, 30, 2037–2043. [Google Scholar] [CrossRef]
- Andrés, L.S.; Wu, T.; Maeda, H.; Tomoki, O. A Computational fluid dynamics modified bulk flow analysis for circumferentially shallow grooved liquid seals. In Proceedings of the ASME Turbo Expo 2017: Turbomachinery Technical Conference and Exposition GT2017, Charlotte, NC, USA, 26–30 June 2017. [Google Scholar]
- Li, Z.; Fang, Z.; Li, J.; Feng, Z. Numerical Modeling of Static and Rotordynamic Characteristics for Three Types of Helically Grooved Liquid Annular Seals. J. Vib. Acoust. 2020, 142, 041001. [Google Scholar] [CrossRef]
- Iwatsubo, T.; Sheng, B.C.; Ono, M. Experiment of Static and Dynamic Characteristics of Spiral Grooved Seals. In Rotordynamic Instability Problems in High-Performance Turbomachinery; NASA, Lewis Research Center: Cleveland, OH, USA, 1990; pp. 223–233. [Google Scholar]
- Nagai, K.; Kaneko, S.; Taura, H.; Watanabe, Y. Numerical and Experimental Analyses of Dynamic Characteristics for Liquid Annular Seals With Helical Grooves in Seal Stator. J. Tribol. 2018, 140, 052201. [Google Scholar] [CrossRef]
- Zhai, L.; Zhu, Z.; Zhang, Z.; Guo, J.; Cui, B. Theoretical Solutions for Dynamic Characteristics of Spiral-Grooved Liquid Seals. Tribol. Trans. 2018, 62, 22–33. [Google Scholar] [CrossRef]
- Li, Z.; Feng, Z.; Li, J. A Comparison of Static and Rotordynamic Characteristics for Two Types of Liquid Annular Seals With Parallelly Grooved Stator/Rotor. J. Eng. Gas Turbines Power 2020, 142, 091012. [Google Scholar] [CrossRef]
- ANSYS Fluent 20.0 Theory Guide; ANSYS Inc.: Canonsburg, PA, USA, 2019.
- Moreland, J.A.; Childs, D.W.; Bullock, J.T. Measured Static and Rotordynamic Characteristics of a Smooth-Stator/Grooved-Rotor Liquid Annular Seal. J. Fluid Eng. 2018, 140, 101109. [Google Scholar] [CrossRef]
- Xie, Z.; Jiao, J.; Yang, K.; He, T.; Chen, R.; Zhu, W. Experimental and numerical exploration on the nonlinear dynamic behaviors of a novel bearing lubricated by low viscosity lubricant. Mech. Syst. Signal Process. 2023, 182, 109349. [Google Scholar] [CrossRef]
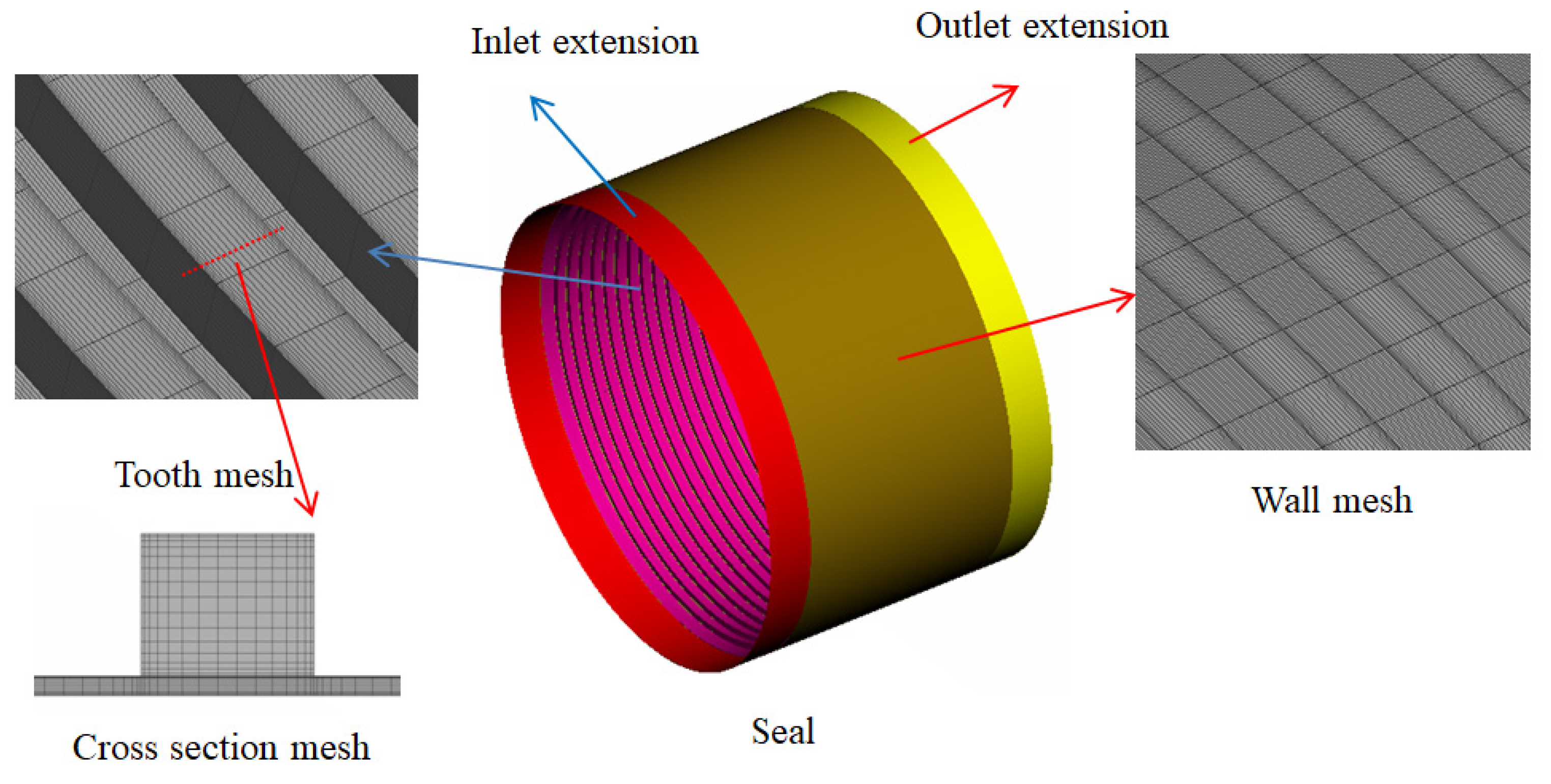
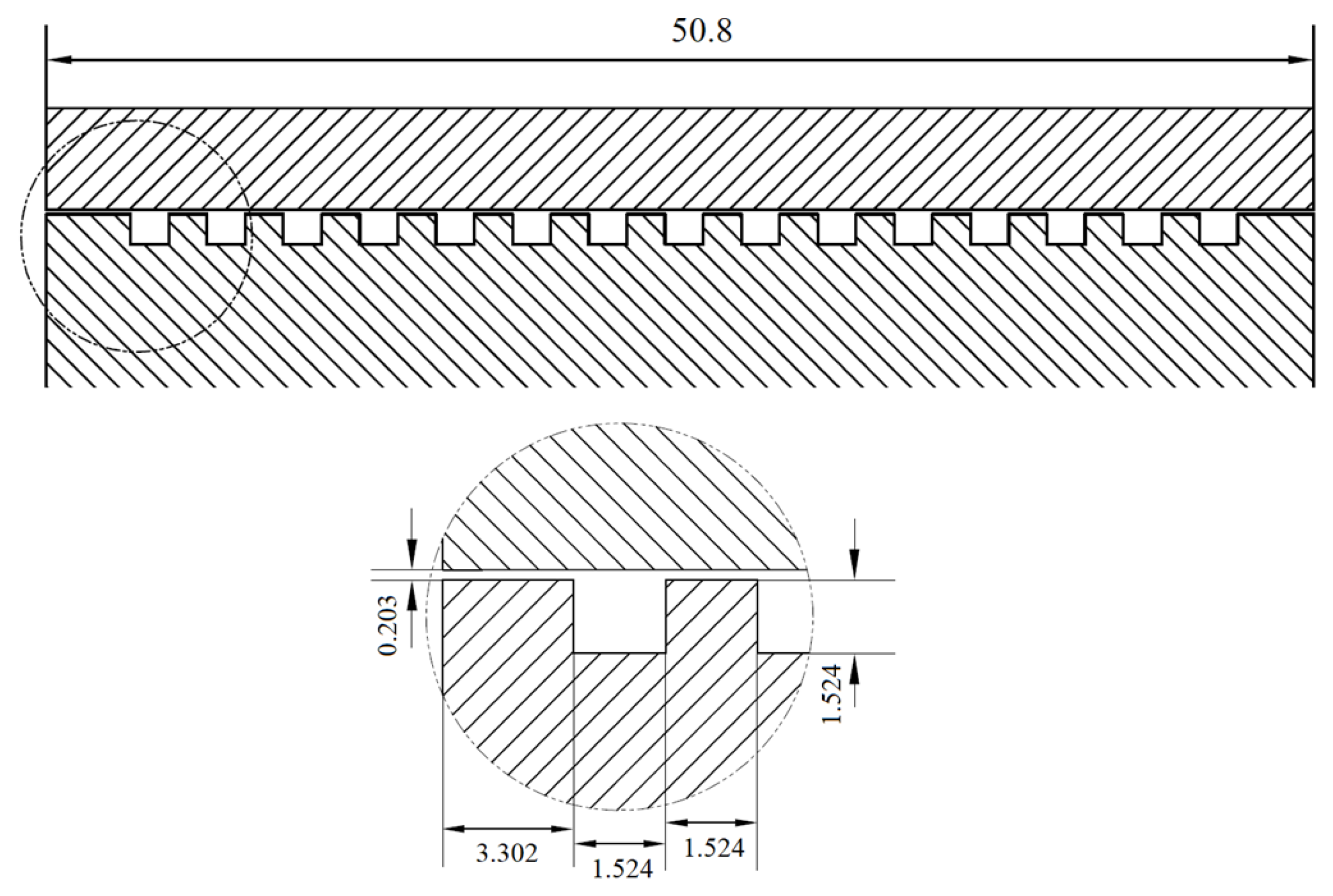
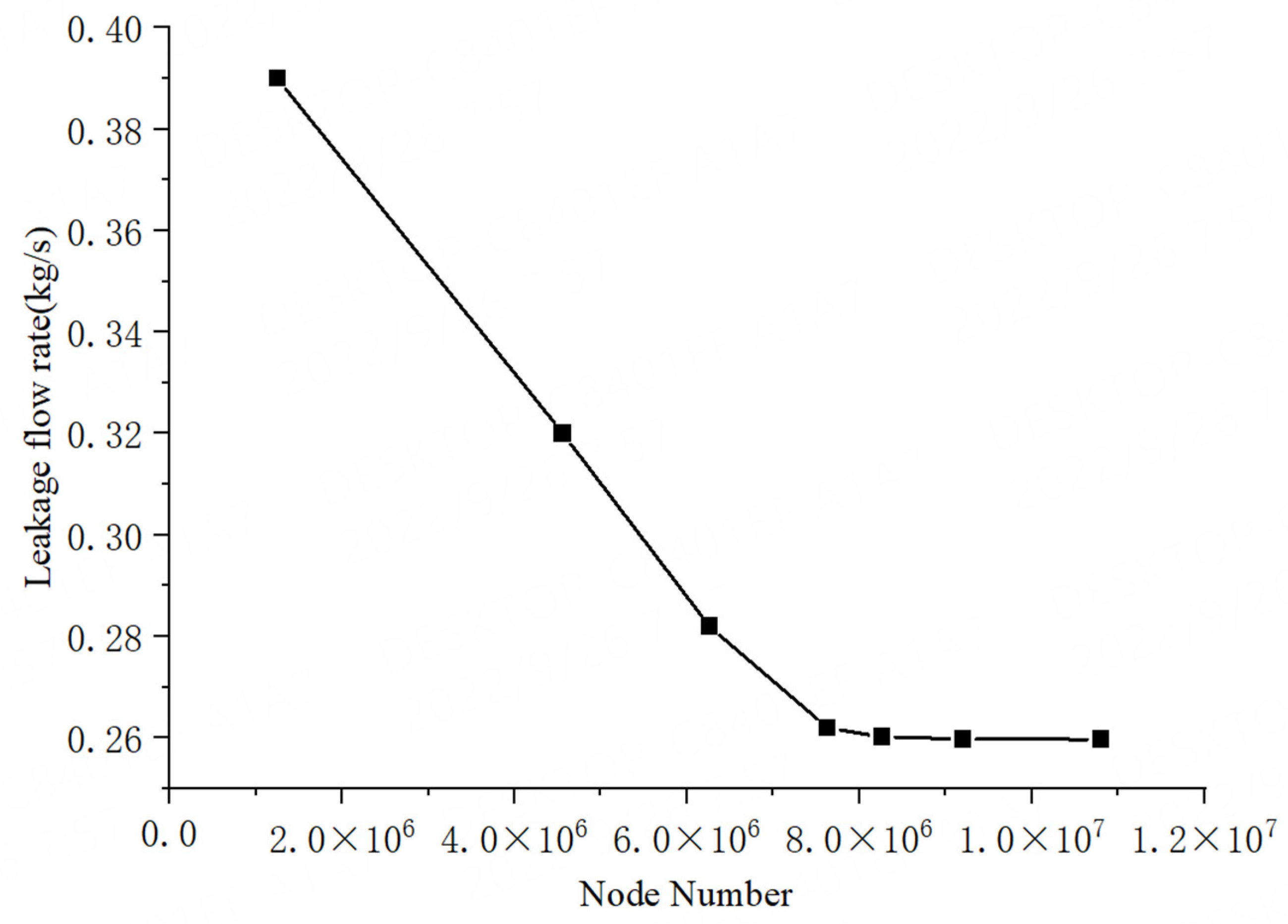
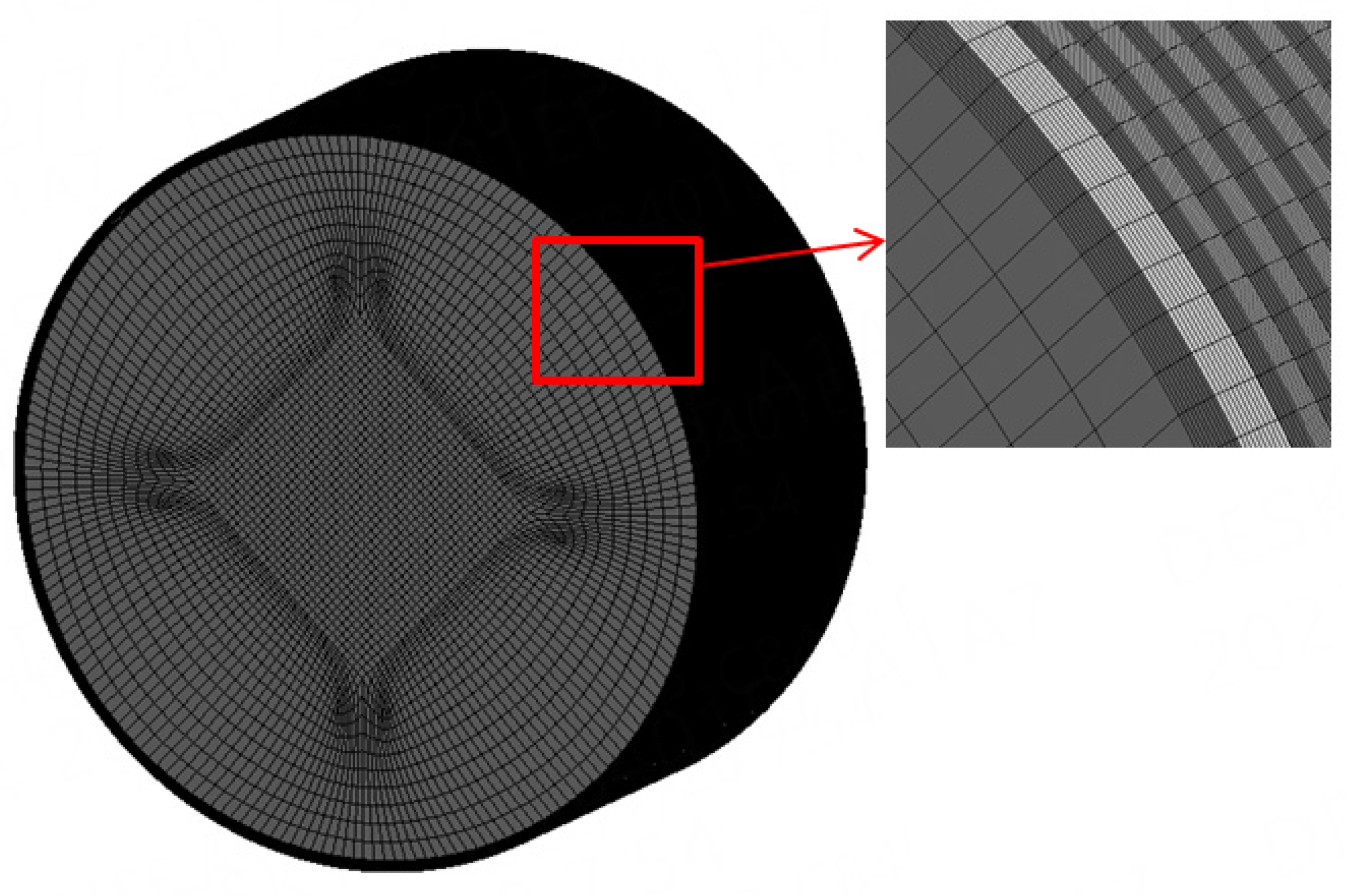




| Fluids | Water (20 °C\50 °C\86 °C) |
|---|---|
| Outlet Pressure (bar) | 1.0 |
| Inlet preswirl ratio λ | 0.0 |
| Rotational speed n (kr/min) | 2.0, 4.0, 6.0 |
| Rotor diameter D (mm) | 102 |
| Seal radial clearance cr (mm) | 0.203 |
| Groove depth d (mm) | 1.524 |
| Land width w (mm) | 1.524 |
| Groove length s (mm) | 1.524 |
| T (°C) | 20 | 50 | 86 |
|---|---|---|---|
| ρ (kg/m3) | 996.9 | 988.1 | 967.9 |
| C (J/kg/K) | 4180 | 4174 | 4203 |
| μ (Pa·s) | 0.001 | 0.0005494 | 0.000331 |
| K (W/m/K) | 0.598 | 0.648 | 0.678 |
| Loads | NO.1 Tooth | NO.7 Tooth | NO.14 Tooth | |||
|---|---|---|---|---|---|---|
| Radial | Total | Radial | Total | Radial | Total | |
| p | −3.4535 × 10−5 | 5.2086 × 10−5 | −2.3961 × 10−5 | 4.5765 × 10−5 | −1.4917 × 10−5 | 4.1742 × 10−5 |
| ω | 6.1277 × 10−5 | 6.1278 × 10−5 | 6.0835 × 10−5 | 6.0837 × 10−5 | 6.1278 × 10−5 | 6.1279 × 10−5 |
| T | −1.6365 × 10−3 | 1.6364 × 10−3 | −1.6361 × 10−3 | 1.6362 × 10−3 | −1.6348 × 10−3 | 1.6349 × 10−3 |
| p, ω, T | −1.6097 × 10−3 | 1.6102 × 10−3 | −1.5992 × 10−3 | 1.5997 × 10−3 | −1.5884 × 10−3 | 1.5889 × 10−3 |
| Loads | NO.1 Tooth | NO.7 Tooth | NO.14 Tooth | |||
|---|---|---|---|---|---|---|
| Radial | Total | Radial | Total | Radial | Total | |
| p | −3.3425 × 10−5 | 7.4469 × 10−5 | −2.3291 × 10−5 | 7.0512 × 10−5 | −1.4632 × 10−5 | 6.8145 × 10−5 |
| ω | 6.1275 × 10−5 | 6.1277 × 10−5 | 6.0835 × 10−5 | 6.0836 × 10−5 | 6.1277 × 10−5 | 6.1278 × 10−5 |
| T | 2.1284 × 10−2 | 2.1285 × 10−2 | 2.1291 × 10−2 | 2.1293 × 10−2 | 2.1279 × 10−2 | 2.1280 × 10−2 |
| p, ω, T | 2.1326 × 10−2 | 2.1327 × 10−2 | 2.1328 × 10−2 | 2.1329 × 10−2 | 2.1312 × 10−2 | 2.1313 × 10−2 |
| Loads | NO.1 Tooth | NO.7 Tooth | NO.14 Tooth | |||
|---|---|---|---|---|---|---|
| Radial | Total | Radial | Total | Radial | Total | |
| p | −3.2746 × 10−5 | 3.918 × 10−5 | −2.2987 × 10−5 | 3.1463 × 10−5 | −1.4778 × 10−5 | 2.6051 × 10−5 |
| ω | 6.3653 × 10−5 | 6.3658 × 10−5 | 6.3224 × 10−5 | 6.3228 × 10−5 | 6.3676 × 10−5 | 6.3669 × 10−5 |
| T | 4.8397 × 10−2 | 4.8401 × 10−2 | 4.8533 × 10−2 | 4.8535 × 10−2 | 4.8396 × 10−2 | 4.8401 × 10−2 |
| p, ω, T | 4.8428 × 10−2 | 4.8431 × 10−2 | 4.8574 × 10−2 | 4.8575 × 10−2 | 4.8447 × 10−2 | 4.8449 × 10−2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, P.; Wang, T.; Ma, W.; Xie, Z.; Yu, G. CFD-Predicted Rotordynamic Characteristics for High-Temperature Water Liquid Seal Considering Tooth Deformation. Lubricants 2022, 10, 240. https://doi.org/10.3390/lubricants10100240
Chen P, Wang T, Ma W, Xie Z, Yu G. CFD-Predicted Rotordynamic Characteristics for High-Temperature Water Liquid Seal Considering Tooth Deformation. Lubricants. 2022; 10(10):240. https://doi.org/10.3390/lubricants10100240
Chicago/Turabian StyleChen, Pingwei, Tong Wang, Wensheng Ma, Zhongliang Xie, and Guangbin Yu. 2022. "CFD-Predicted Rotordynamic Characteristics for High-Temperature Water Liquid Seal Considering Tooth Deformation" Lubricants 10, no. 10: 240. https://doi.org/10.3390/lubricants10100240
APA StyleChen, P., Wang, T., Ma, W., Xie, Z., & Yu, G. (2022). CFD-Predicted Rotordynamic Characteristics for High-Temperature Water Liquid Seal Considering Tooth Deformation. Lubricants, 10(10), 240. https://doi.org/10.3390/lubricants10100240






