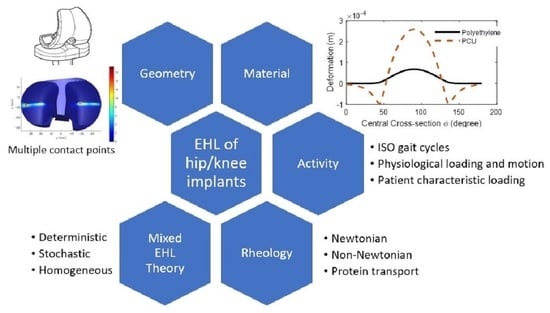
Lubrication Modelling of Artificial Joint Replacements: Current Status and Future Challenges
Abstract
:1. Introduction
2. Lubrication Modelling of Hip and Knee Replacements
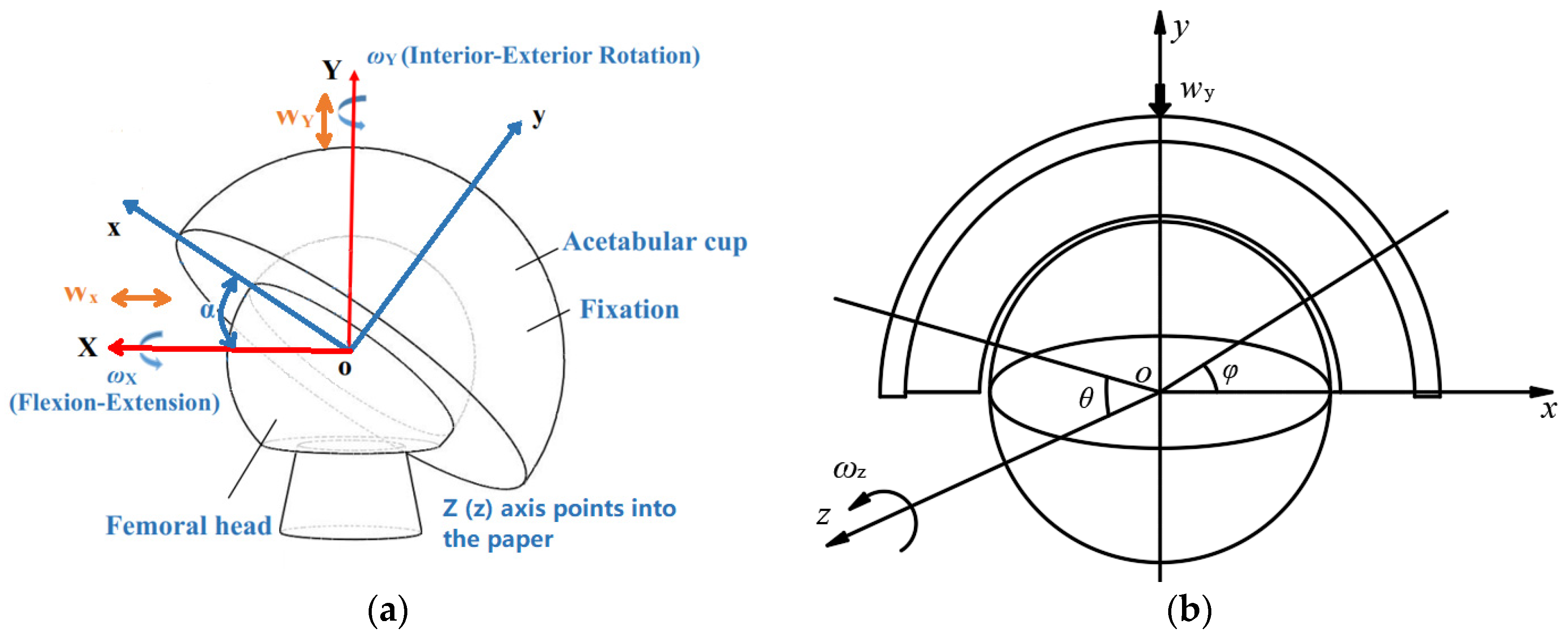
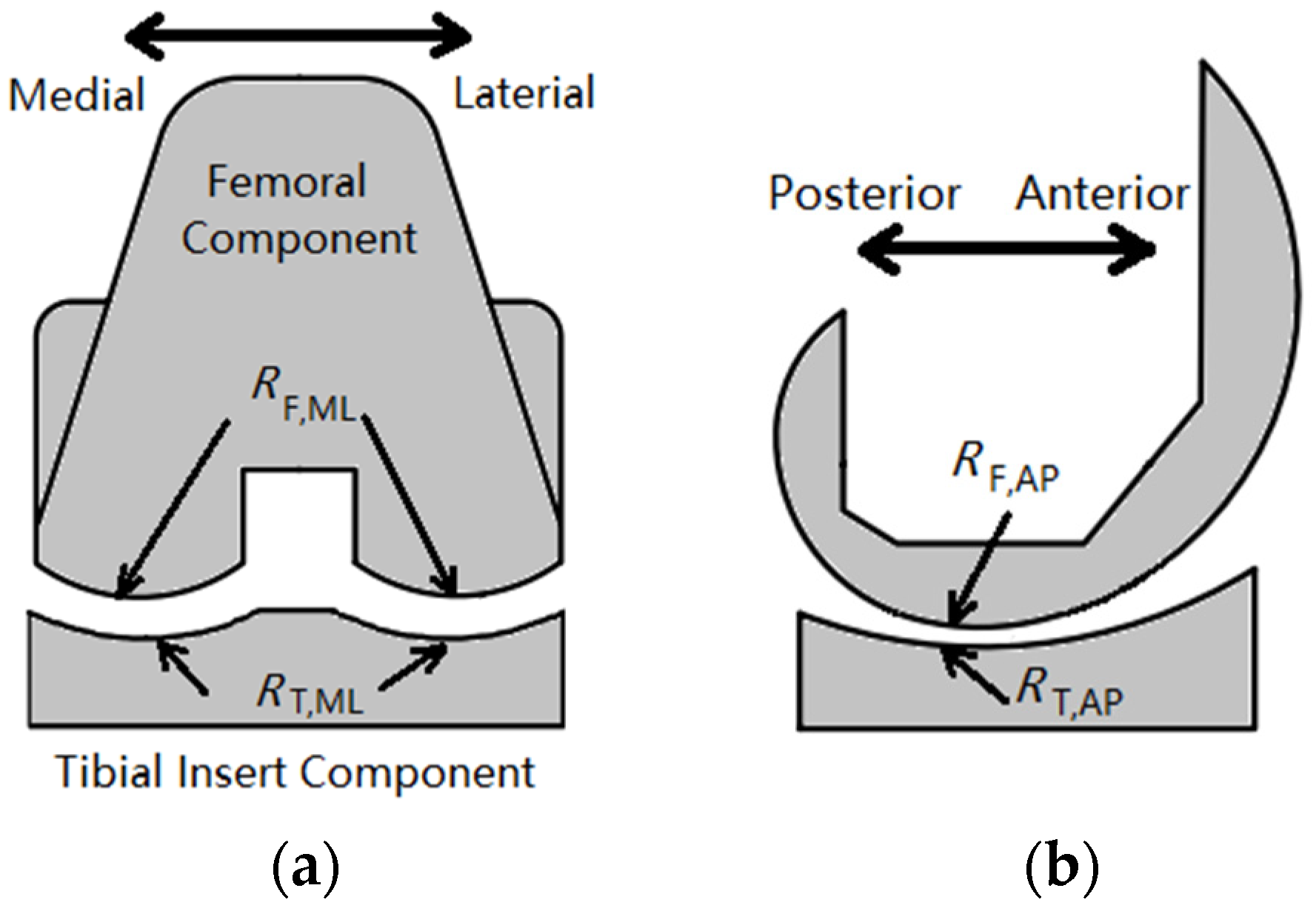
2.1. Geometries of Contact Surfaces
2.2. Materials
2.3. The Bearing Surface Deformations
2.4. Loading and Motions of Human Daily Activities
2.5. Measurement of Film Thickness
2.6. The Synovial Fluids and Rheology Models
3. Mixed Lubrication Modelling of Hip and Knee Replacements
3.1. The Mixed Lubrication Regime
3.2. The Mixed Lubrication Models
3.2.1. Deterministic Model
3.2.2. Stochastic Models
3.2.3. Homogenisation Methods
4. Discussion
4.1. The Mixed Lubrication Theory
- (1)
- Is the negative film thickness proper to determine the asperity contact?
- (2)
- Is the unified Reynolds equation adequate to solve the micro-EHL problems?
4.2. Methods to Address the Realistic Geometry, Design, and Materials
4.3. Individual Physiological Diversities
4.4. Lubrication Analysis towards Design Optimisation
4.5. Joint Simulators and Validation of Numerical Models
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- National Joint Registry. National Joint Registry the 18th Annual Report; National Joint Registry: London, UK, 2021. [Google Scholar]
- Evans, J.T.; Walker, R.W.; Blom, A.W.; Whitehouse, M.R.; Sayers, A. How long does a hip replacement last? A systematic review and meta-analysis of case series and national registry reports with more than 15 years of follow-up. Lancet 2019, 393, 647–654. [Google Scholar] [CrossRef]
- Revell, P.A. The combined role of wear particles, macrophages and lymphocytes in the loosening of total joint prostheses. J. R. Soc. Interface 2008, 5, 1263–1278. [Google Scholar] [CrossRef]
- Dowson, D. Review Paper 2: Whither Tribology? Proc. Inst. Mech. Eng. Conf. Proc. 1969, 184, 181–185. [Google Scholar] [CrossRef]
- Dowson, D.; Wright, V. Bio-tribology. In The Rheology of Lubricants; Davenport, T.C., Ed.; Applied Science Publishers: Barking, UK, 1973; pp. 81–88. [Google Scholar]
- Dowson, D.; Jin, Z.-M. Metal-on-metal hip joint tribology. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2006, 220, 107–118. [Google Scholar] [CrossRef] [PubMed]
- Hamrock, B.J.; Dowson, D. Elastohydrodynamic Lubrication of Elliptical Contacts for Materials of Low Elastic Modulus I—Fully Flooded Conjunction. J. Lubr. Technol. 1978, 100, 236–245. [Google Scholar] [CrossRef]
- Nečas, D.; Vrbka, M.; Rebenda, D.; Gallo, J.; Galandáková, A.; Wolfová, L.; Křupka, I.; Hartl, M. In situ observation of lubricant film formation in THR considering real conformity: The effect of diameter, clearance and material. J. Mech. Behav. Biomed. Mater. 2017, 69, 66–74. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.; Nečas, D.; Meng, Q.; Rebenda, D.; Vrbka, M.; Hartl, M.; Jin, Z. Towards the direct validation of computational lubrication modelling of hip replacements. Tribol. Int. 2020, 146, 106240. [Google Scholar] [CrossRef]
- Dowson, D.; Higginson, G.R. A Numerical Solution to the Elasto-Hydrodynamic Problem. J. Mech. Eng. Sci. 1959, 1, 6–15. [Google Scholar] [CrossRef]
- Hamrock, B.J.; Dowson, D. Isothermal Elastohydrodynamic Lubrication of Point Contacts: Part III—Fully Flooded Results. J. Lubr. Technol. 1977, 99, 264–276. [Google Scholar] [CrossRef]
- Hamrock, B.J.; Dowson, D. Isothermal Elastohydrodynamic Lubrication of Point Contacts: Part 1—Theoretical Formulation. J. Lubr. Technol. 1976, 98, 223–228. [Google Scholar] [CrossRef]
- Hamrock, B.J.; Dowson, D. Isothermal Elastohydrodynamic Lubrication of Point Contacts: Part II—Ellipticity Parameter Results. J. Lubr. Technol. 1976, 98, 375–381. [Google Scholar] [CrossRef]
- Hamrock, B.J.; Dowson, D. Isothermal Elastohydrodynamic Lubrication of Point Contacts: Part IV—Starvation Results. J. Lubr. Technol. 1977, 99, 15–23. [Google Scholar] [CrossRef]
- Dowson, D. Paper 12: Modes of Lubrication in Human Joints. Proc. Inst. Mech. Eng. Conf. Proc. 1966, 181, 45–54. [Google Scholar] [CrossRef]
- Dowson, D. Tribological principles in metal-on-metal hip joint design. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2006, 220, 161–171. [Google Scholar] [CrossRef] [PubMed]
- Nečas, D.; Vrbka, M.; Rebenda, D.; Gallo, J.; Galandáková, A.; Wolfová, L.; Křupka, I.; Hartl, M. In situ observation of lubricant film formation in THR considering real conformity: The effect of model synovial fluid composition. Tribol. Int. 2018, 117, 206–216. [Google Scholar] [CrossRef]
- Myant, C.; Cann, P. In contact observation of model synovial fluid lubricating mechanisms. Tribol. Int. 2013, 63, 97–104. [Google Scholar] [CrossRef]
- Myant, C.; Cann, P. On the matter of synovial fluid lubrication: Implications for Metal-on-Metal hip tribology. J. Mech. Behav. Biomed. Mater. 2014, 34, 338–348. [Google Scholar] [CrossRef] [PubMed]
- Fan, J.; Myant, C.W.; Underwood, R.; Cann, P.M.; Hart, A. Inlet protein aggregation: A new mechanism for lubricating film formation with model synovial fluids. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2011, 225, 696–709. [Google Scholar] [CrossRef]
- Liu, F.; Wang, F.C.; Jin, Z.M.; Hirt, F.; Rieker, C.; Grigoris, P. Steady-state elastohydrodynamic lubrication analysis of a metal-on-metal hip implant employing a metallic cup with an ultra-high molecular weight polyethylene backing. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2004, 218, 261–270. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.C.; Liu, F.; Jin, Z.M. A general elastohydrodynamic lubrication analysis of artificial hip joints employing a compliant layered socket under steady state rotation. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2004, 218, 283–291. [Google Scholar] [CrossRef]
- Jin, Z.M.; Dowson, D. A full numerical analysis of hydrodynamic lubrication in artificial hip joint replacements constructed from hard materials. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 1999, 213, 355–370. [Google Scholar] [CrossRef]
- Jalali-Vahid, D.; Jagatia, M.; Jin, Z.; Dowson, D. Prediction of lubricating film thickness in UHMWPE hip joint replacements. J. Biomech. 2001, 34, 261–266. [Google Scholar] [CrossRef]
- Jalali-Vahid, D.; Jagatia, M.; Jin, Z.M.; Dowson, D. Prediction of lubricating film thickness in a ball-in-socket model with a soft lining representing human natural and artificial hip joints. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2001, 215, 363–372. [Google Scholar] [CrossRef]
- Dowson, D.; Hardaker, C.; Flett, M.; Isaac, G.H. A hip joint simulator study of the performance of metal-on-metal joints: Part II: Design. J. Arthroplast. 2004, 19, 124–130. [Google Scholar] [CrossRef]
- Okazaki, Y. Effect of head size on wear properties of metal-on-metal bearings of hip prostheses, and comparison with wear properties of metal-on-polyethylene bearings using hip simulator. J. Mech. Behav. Biomed. Mater. 2014, 31, 152–163. [Google Scholar] [CrossRef]
- Wang, F.C.; Brockett, C.; Williams, S.; Udofia, I.; Fisher, J.; Jin, Z.M. Lubrication and friction prediction in metal-on-metal hip implants. Phys. Med. Biol. 2008, 53, 1277–1293. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.C.; Zhao, S.X.; Quiñonez, A.F.; Xu, H.; Mei, X.S.; Jin, Z.M. Nonsphericity of bearing geometry and lubrication in hip joint implants. J. Tribol. 2009, 131, 31201. [Google Scholar] [CrossRef]
- Wang, L.; Liu, X.; Li, D.; Liu, F.; Jin, Z. Contact mechanics studies of an ellipsoidal contact bearing surface of metal-on-metal hip prostheses under micro-lateralization. Med Eng. Phys. 2014, 36, 419–424. [Google Scholar] [CrossRef]
- Fisher, J. Acetabular. Cup. Patent WO 95/23566, 8 September 1995. [Google Scholar]
- Gao, L.M.; Meng, Q.E.; Liu, F.; Fisher, J.; Jin, Z.M. The effect of aspherical geometry and surface texturing on the elastohydrodynamic lubrication of metal-on-metal hip prostheses under physiological loading and motions. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2010, 224, 2627–2636. [Google Scholar] [CrossRef]
- Meng, Q.; Gao, L.; Liu, F.; Yang, P.; Fisher, J.; Jin, Z. Contact mechanics and elastohydrodynamic lubrication in a novel metal-on-metal hip implant with an aspherical bearing surface. J. Biomech. 2010, 43, 849–857. [Google Scholar] [CrossRef] [Green Version]
- Gao, L.; Hua, Z.; Hewson, R. Can a ‘pre-worn’ bearing surface geometry reduce the wear of metal-on-metal hip replacements?—A numerical wear simulation study. WEAR 2018, 406, 13–21. [Google Scholar] [CrossRef]
- Mattei, L.; Di Puccio, F.; Piccigallo, B.; Ciulli, E. Lubrication and wear modelling of artificial hip joints: A review. Tribol. Int. 2011, 44, 532–549. [Google Scholar] [CrossRef]
- Chan, F.W.; Bobyn, J.D.; Medley, J.B.; Krygier, J.J.; Tanzer, M. The Otto Aufranc Award—Wear and lubrication of metal-on-metal hip implants. Clin. Orthop. Relat. Res. 1999, 369, 10–24. [Google Scholar] [CrossRef] [PubMed]
- Jin, Z.M. Theoretical studies of elastohydrodynamic lubrication of artificial hip joints. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2006, 220, 719–727. [Google Scholar] [CrossRef]
- Roussot, M.A.; Haddad, F.S. The evolution of patellofemoral prosthetic design in total knee arthroplasty: How far have we come? EFORT Open Rev. 2019, 4, 503–512. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Chen, Z.; Jin, Z.; Muratoglu, O.K.; Varadarajan, K.M. Patient-specific musculoskeletal models as a framework for comparing ACL function in unicompartmental versus bicruciate retaining arthroplasty. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2021, 235, 861–872. [Google Scholar] [CrossRef]
- Marian, M.; Orgeldinger, C.; Rothammer, B.; Nečas, D.; Vrbka, M.; Křupka, I.; Hartl, M.; Wimmer, M.A.; Tremmel, S.; Wartzack, S. Towards the understanding of lubrication mechanisms in total knee replacements—Part II: Numerical modeling. Tribol. Int. 2021, 156, 106809. [Google Scholar] [CrossRef]
- Su, Y.; Fu, Z.; Yang, P.; Wang, C. A Full Numerical Analysis of Elastohydrodynamic Lubrication in Knee Prosthesis under Walking Condition. J. Mech. Med. Biol. 2010, 10, 621–641. [Google Scholar] [CrossRef]
- Di Puccio, F.; Mattei, L. Biotribology of artificial hip joints. World J. Orthop. 2015, 6, 77–94. [Google Scholar] [CrossRef]
- Inagaki, K.; Iida, S.; Miyamoto, S.; Suzuki, C.; Nakatani, T.; Shinada, Y.; Kawarai, Y.; Hagiwara, S.; Nakamura, J.; Orita, S.; et al. Natural history of noise and squeaking in cementless ceramic-on-ceramic total hip arthroplasty. J. Orthop. 2020, 21, 544–549. [Google Scholar] [CrossRef]
- Jin, Z.; Zheng, J.; Li, W.; Zhou, Z. Tribology of medical devices. Biosurface Biotribol. 2016, 2, 173–192. [Google Scholar] [CrossRef]
- Dowson, D. Elastohydrodynamic lubrication in ‘soft-on-soft’ natural synovial joints; ‘hard-on-soft’ cushion and ‘hard-on-hard’ metal-on-metal total joint replacements. In Proceedings of the IUTAM Symposium on Elastohydrodynamics and Micro-elastohydrodynamics, Cardiff, UK, 1–3 September 2004; Springer: Dordrecht, The Netherlands, 2006; pp. 297–308. [Google Scholar]
- Ebramzadeh, E.; Campbell, P.A.; Takamura, K.M.; Lu, Z.; Sangiorgio, S.N.; Kalma, J.J.; De Smet, K.A.; Amstutz, H.C. Failure Modes of 433 Metal-on-Metal Hip Implants: How, Why, and Wear. Orthop. Clin. N. Am. 2011, 42, 241–250. [Google Scholar] [CrossRef] [PubMed]
- Dowson, D.; Fisher, J.; Jin, Z.M.; Auger, D.D.; Jobbins, B. Design Considerations for Cushion Form Bearings in Artificial Hip Joints. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 1991, 205, 59–68. [Google Scholar] [CrossRef] [PubMed]
- Meng, Q.; Wang, J.; Yang, P.; Jin, Z.; Fisher, J. The lubrication performance of the ceramic-on-ceramic hip implant under starved conditions. J. Mech. Behav. Biomed. Mater. 2015, 50, 70–76. [Google Scholar] [CrossRef]
- Ford, A.; Hua, Z.; Ferguson, S.J.; Pruitt, L.A.; Gao, L. A 3D-transient elastohydrodynamic lubrication hip implant model to compare ultra high molecular weight polyethylene with more compliant polycarbonate polyurethane acetabular cups. J. Mech. Behav. Biomed. Mater. 2021, 119, 104472. [Google Scholar] [CrossRef]
- Ren, S.; Huang, J.; Cui, M.; Pu, J.; Wang, L. Improved adaptability of polyaryl-ether-ether-ketone with texture pattern and graphite-like carbon film for bio-tribological applications. Appl. Surf. Sci. 2017, 400, 24–37. [Google Scholar] [CrossRef]
- Cacopardo, L. Biomaterials for orthopedic devices. In Human Orthopaedic Biomechanics; Innocenti, B., Galbusera, F., Eds.; Elsevier: Amsterdam, The Netherlands, 2022; p. 345. [Google Scholar]
- Wang, F.C.; Jin, Z.M. Prediction of elastic deformation of acetabular cups and femoral heads for lubrication analysis of artificial hip joints. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2004, 218, 201–209. [Google Scholar] [CrossRef]
- Bartel, D.L.; Burstein, A.H.; Toda, M.D.; Edwards, D.L. The Effect of Conformity and Plastic Thickness on Contact Stresses in Metal-Backed Plastic Implants. J. Biomech. Eng. 1985, 107, 193–199. [Google Scholar] [CrossRef]
- Jin, Z.; Dowson, D.; Fisher, J. A parametric analysis of the contact stress in ultra-high molecular weight polyethylene acetabular cups. Med. Eng. Phys. 1994, 16, 398–405. [Google Scholar] [CrossRef]
- Gao, L.; Hua, Z.; Hewson, R.; Andersen, M.S.; Jin, Z. Elastohydrodynamic lubrication and wear modelling of the knee joint replacements with surface topography. Biosurface Biotribol. 2018, 4, 18–23. [Google Scholar] [CrossRef]
- Jagatia, M.; Jalali-Vahid, D.; Jin, Z.M. Elastohydrodynamic lubrication analysis of ultra-high molecular weight polyethylene hip joint replacements under squeeze-film motion. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2001, 215, 141–151. [Google Scholar] [CrossRef] [PubMed]
- Gao, L.M.; Meng, Q.; Wang, F.C.; Yang, P.R.; Jin, Z.M. Comparison of numerical methods for elastohydrodynamic lubrication analysis of metal-on-metal hip implants: Multi-grid verses Newton-Raphson. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2007, 221, 133–140. [Google Scholar] [CrossRef]
- Habchi, H. A Full-System Finite Element Approach to Elastohydrodynamic Lubrication Problems: Application to Ultralow-viscosity Fluids. Ph.D. Thesis, L’Institut National des Sciences Appliquées de Lyon, Lyon, France, 2008. [Google Scholar]
- Tian, Q.; Lou, J.; Mikkola, A. A new elastohydrodynamic lubricated spherical joint model for rigid-flexible multibody dynamics. Mech. Mach. Theory 2017, 107, 210–228. [Google Scholar] [CrossRef]
- Tan, X.C.; Goodyer, C.; Jimack, P.K.; Taylor, R.I.; Walkley, M.A. Computational approaches for modelling elastohydrodynamic lubrication using multiphysics software. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2012, 226, 463–480. [Google Scholar] [CrossRef]
- Noori-Dokht, H.; Niroomand-Oscuii, H.; Jalali-Vahid, D.; Jin, Z. Finite element analysis of elastohydrodynamic lubrication in an artificial hip joint under squeeze film motion using fluid–structure interaction method. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2017, 231, 1171–1183. [Google Scholar] [CrossRef]
- Lu, X.; Meng, Q.; Wang, J.; Jin, Z. Transient viscoelastic lubrication analyses of UHMWPE hip replacements. Tribol. Int. 2018, 128, 271–278. [Google Scholar] [CrossRef]
- Gao, L.M.; Meng, Q.E.; Wang, F.C.; Yang, P.R.; Jin, Z.M. Numerical solutions for the elastic deformation of spherical bearing surfaces of metal-on-metalhip joint implants. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2010, 224, 797–805. [Google Scholar] [CrossRef]
- ISO 14242-1:2012; Implants for Surgery—Wear of Total Hip-Joint Prostheses. ISO: Geneva, Switzerland, 2002.
- ISO 14243-3:2014; Implants for Surgery—Wear of Total Knee-Joint Prostheses—Part 3. ISO: Geneva, Switzerland, 2014.
- Marra, M.A.; Vanheule, V.; Fluit, R.; Koopman, B.H.F.J.M.; Rasmussen, J.; Verdonschot, N.; Andersen, M.S. A Subject-Specific Musculoskeletal Modeling Framework to Predict In Vivo Mechanics of Total Knee Arthroplasty. J. Biomech. Eng. 2015, 137, 20904. [Google Scholar] [CrossRef] [PubMed]
- De Pieri, E.; Lunn, D.E.; Chapman, G.J.; Rasmussen, K.P.; Ferguson, S.J.; Redmond, A.C. Patient characteristics affect hip contact forces during gait. Osteoarthr. Cartil. 2019, 27, 895–905. [Google Scholar] [CrossRef]
- Lunn, D.E.; De Pieri, E.; Chapman, G.J.; Lund, M.E.; Redmond, A.C.; Ferguson, S.J. Current Preclinical Testing of New Hip Arthroplasty Technologies Does Not Reflect Real-World Loadings: Capturing Patient-Specific and Activity-Related Variation in Hip Contact Forces. J. Arthroplast. 2020, 35, 877–885. [Google Scholar] [CrossRef] [Green Version]
- Damm, P.; Kutzner, I.; Bergmann, G.; Rohlmann, A.; Schmidt, H. Comparison of in vivo measured loads in knee, hip and spinal implants during level walking. J. Biomech. 2017, 51, 128–132. [Google Scholar] [CrossRef]
- Bergmann, G.; Deuretzbacher, G.; Heller, M.; Graichen, F.; Rohlmann, A.; Strauss, J.; Duda, G. Hip contact forces and gait patterns from routine activities. J. Biomech. 2001, 34, 859–871. [Google Scholar] [CrossRef]
- Bergmann, G.; Graichen, F.; Rohlmann, A. Hip joint contact forces during stumbling. Langenbecks Arch. Surg. 2004, 389, 53–59. [Google Scholar] [CrossRef]
- Fregly, B.J.; Besier, T.; Lloyd, D.; Delp, S.L.; Banks, S.; Pandy, M.; D’Lima, D. Grand challenge competition to predict in vivo knee loads. J. Orthop. Res. 2012, 30, 503–513. [Google Scholar] [CrossRef]
- Dowson, D.; McNie, C.M.; Goldsmith, A.A.J. Direct experimental evidence of lubrication in a metal-on-metal total hip replacement tested in a joint simulator. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2000, 214, 75–86. [Google Scholar] [CrossRef]
- Hesketh, J.; Meng, Q.; Dowson, D.; Neville, A. Biotribocorrosion of metal-on-metal hip replacements: How surface degradation can influence metal ion formation. Tribol. Int. 2013, 65, 128–137. [Google Scholar] [CrossRef]
- Choudhury, D.; Rebenda, D.; Sasaki, S.; Hekrle, P.; Vrbka, M.; Zou, M. Enhanced lubricant film formation through micro-dimpled hard-on-hard artificial hip joint: An in-situ observation of dimple shape effects. J. Mech. Behav. Biomed. Mater. 2018, 81, 120–129. [Google Scholar] [CrossRef]
- Nissim, L.; Butt, H.; Gao, L.; Myant, C.; Hewson, R. Role of protein concentration on transient film thickness in synovial fluid lubricated joints. J. Biotribol. 2021, 28, 100191. [Google Scholar] [CrossRef]
- Nečas, D.; Sadecká, K.; Vrbka, M.; Gallo, J.; Galandáková, A.; Křupka, I.; Hartl, M. Observation of lubrication mechanisms in knee replacement: A pilot study. Biotribology 2019, 17, 1–7. [Google Scholar] [CrossRef]
- Myant, C.W.; Cann, P. The effect of transient conditions on synovial fluid protein aggregation lubrication. J. Mech. Behav. Biomed. Mater. 2014, 34, 349–357. [Google Scholar] [CrossRef] [Green Version]
- Myant, C.; Underwood, R.; Fan, J.; Cann, P. Lubrication of metal-on-metal hip joints: The effect of protein content and load on film formation and wear. J. Mech. Behav. Biomed. Mater. 2012, 6, 30–40. [Google Scholar] [CrossRef]
- Mavraki, A.; Cann, P. Lubricating film thickness measurements with bovine serum. Tribol. Int. 2011, 44, 550–556. [Google Scholar] [CrossRef]
- Nečas, D.; Vrbka, M.; Marian, M.; Rothammer, B.; Tremmel, S.; Wartzack, S.; Galandáková, A.; Gallo, J.; Wimmer, M.A.; Křupka, I.; et al. Towards the understanding of lubrication mechanisms in total knee replacements—Part I: Experimental investigations. Tribol. Int. 2021, 156, 106874. [Google Scholar] [CrossRef]
- Mazzucco, D.; McKinley, G.; Scott, R.D.; Spector, M. Rheology of joint fluid in total knee arthroplasty patients. J. Orthop. Res. 2002, 20, 1157–1163. [Google Scholar] [CrossRef]
- Cooke, A.F.; Dowson, D.; Wright, V. The Rheology of Synovial Fluid and Some Potential Synthetic Lubricants for Degenerate Synovial Joints. Eng. Med. 1978, 7, 66–72. [Google Scholar] [CrossRef]
- Cross, M.M. Rheology of non-Newtonian fluids: A new flow equation for pseudoplastic systems. J. Colloid Sci. 1965, 20, 417–437. [Google Scholar] [CrossRef]
- Gao, L.; Dowson, D.; Hewson, R.W. A numerical study of non-Newtonian transient elastohydrodynamic lubrication of metal-on-metal hip prostheses. Tribol. Int. 2016, 93, 486–494. [Google Scholar] [CrossRef]
- Wonerow, T.; Uhler, M.; Nuppnau, J.; Kretzer, J.; Mantwill, F. Rheologic Behavior of Bovine Calf Serum. Materials 2021, 14, 2538. [Google Scholar] [CrossRef]
- Jacobson, B. The Stribeck memorial lecture. Tribol. Int. 2003, 36, 781–789. [Google Scholar] [CrossRef]
- Barber, H.; Kelly, C.N.; Abar, B.; Allen, N.; Adams, S.B.; Gall, K. Rotational Wear and Friction of Ti-6Al-4V and CoCrMo against Polyethylene and Polycarbonate Urethane. Biotribology 2021, 26, 100167. [Google Scholar] [CrossRef]
- Topolovec, M.; Cör, A.; Milošev, I. Metal-on-metal vs. metal-on-polyethylene total hip arthroplasty tribological evaluation of retrieved components and periprosthetic tissue. J. Mech. Behav. Biomed. Mater. 2014, 34, 243–252. [Google Scholar] [CrossRef]
- Hu, Y.-Z.; Zhu, D. A Full Numerical Solution to the Mixed Lubrication in Point Contacts. J. Tribol. 1999, 122, 1–9. [Google Scholar] [CrossRef]
- Gao, L.; Yang, P.; Dymond, I.; Fisher, J.; Jin, Z. Effect of surface texturing on the elastohydrodynamic lubrication analysis of metal-on-metal hip implants. Tribol. Int. 2010, 43, 1851–1860. [Google Scholar] [CrossRef]
- Gao, L.; Dowson, D.; Hewson, R.W. Predictive wear modeling of the articulating metal-on-metal hip replacements. J. Biomed. Mater. Res. Part B Appl. Biomater. 2017, 105, 497–506. [Google Scholar] [CrossRef] [PubMed]
- Mattei, L.; Di Puccio, F.; Ciulli, E. A comparative study of wear laws for soft-on-hard hip implants using a mathematical wear model. Tribol. Int. 2013, 63, 66–77. [Google Scholar] [CrossRef]
- Ruggiero, A.; Sicilia, A. Lubrication modeling and wear calculation in artificial hip joint during the gait. Tribol. Int. 2020, 142, 105993. [Google Scholar] [CrossRef]
- Ruggiero, A.; Sicilia, A.; Affatato, S. In silico total hip replacement wear testing in the framework of ISO 14242-3 accounting for mixed elasto-hydrodynamic lubrication effects. Wear 2020, 460–461, 203420. [Google Scholar] [CrossRef]
- Srivastava, G.; Christian, N.; Higgs, C.F. A predictive framework of the tribological impact of physical activities on metal-on-plastic hip implants. Biotribology 2021, 25, 100156. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H.S. An Average Flow Model for Determining Effects of Three-Dimensional Roughness on Partial Hydrodynamic Lubrication. J. Lubr. Technol. 1978, 100, 12–17. [Google Scholar] [CrossRef]
- Chyr, A.; Qiu, M.; Speltz, J.W.; Jacobsen, R.L.; Sanders, A.P.; Raeymaekers, B. A patterned microtexture to reduce friction and increase longevity of prosthetic hip joints. Wear 2014, 315, 51–57. [Google Scholar] [CrossRef] [Green Version]
- Butt, H.; Nissim, L.; Gao, L.; Myant, C.; de Boer, G.; Hewson, R. Transient mixed lubrication model of the human knee implant. Biosurface Biotribol. 2021, 7, 206–218. [Google Scholar] [CrossRef]
- Almqvist, A.; Essel, E.K.; Fabricius, J.; Wall, P. Reiterated homogenization applied in hydrodynamic lubrication. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2008, 222, 827–841. [Google Scholar] [CrossRef]
- Almqvist, A.; Essel, E.; Persson, L.-E.; Wall, P. Homogenization of the unstationary incompressible Reynolds equation. Tribol. Int. 2007, 40, 1344–1350. [Google Scholar] [CrossRef]
- Almqvist, A.; Fabricius, J.; Spencer, A.; Wall, P. Similarities and Differences Between the Flow Factor Method by Patir and Cheng and Homogenization. J. Tribol. 2011, 133, 031702. [Google Scholar] [CrossRef]
- Almqvist, A. Homogenization of the Reynolds Equation Governing Hydrodynamic Flow in a Rotating Device. J. Tribol. 2011, 133, 021705. [Google Scholar] [CrossRef]
- Sahlin, F.; Larsson, R.; Almqvist, A.; Lugt, P.M.; Marklund, P. A mixed lubrication model incorporating measured surface topography. Part 1: Theory of flow factors. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2010, 224, 335–351. [Google Scholar] [CrossRef]
- Sahlin, F.; Larsson, R.; Almqvist, A.; Lugt, P.M.; Marklund, P. A mixed lubrication model incorporating measured surface topography. Part 2: Roughness treatment, model validation, and simulation. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2010, 224, 353–365. [Google Scholar] [CrossRef]
- Gao, L.; Hewson, R. A Multiscale Framework for EHL and Micro-EHL. Tribol. Trans. 2012, 55, 713–722. [Google Scholar] [CrossRef]
- De Boer, G.; Gao, L.; Hewson, R.; Thompson, H. Heterogeneous Multiscale Methods for modelling surface topography in Elastohydrodynamic Lubrication line contacts. Tribol. Int. 2017, 113, 262–278. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, C. A New Deterministic Model for Mixed Lubricated Point Contact with High Accuracy. J. Tribol. 2021, 143, 102201. [Google Scholar] [CrossRef]
- Zhu, D. On some aspects of numerical solutions of thin-film and mixed elastohydrodynamic lubrication. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2007, 221, 561–579. [Google Scholar] [CrossRef]
- Venner, C.H. EHL Film Thickness Computations at Low Speeds: Risk of Artificial Trends as a Result of Poor Accuracy and Implications for Mixed Lubrication Modelling. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2005, 219, 285–290. [Google Scholar] [CrossRef]
- Desai, P.S.; Granja, V.; Higgs, C.F., III. Lifetime Prediction Using a Tribology-Aware, Deep Learning-Based Digital Twin of Ball Bearing-Like Tribosystems in Oil and Gas. Processes 2021, 9, 922. [Google Scholar] [CrossRef]
- Marian, M.; Tremmel, S. Current Trends and Applications of Machine Learning in Tribology—A Review. Lubricants 2021, 9, 86. [Google Scholar] [CrossRef]
- Jia, D.; Duan, H.; Zhan, S.; Jin, Y.; Cheng, B.; Li, J. Design and Development of Lubricating Material Database and Research on Performance Prediction Method of Machine Learning. Sci. Rep. 2019, 9, 20277. [Google Scholar] [CrossRef] [PubMed]
- Suggs, J.F.; Hanson, G.R.; Li, G. In-Vivo Tibiofemoral Contact Stress in the Knee After TKA. In Proceedings of the ASME 2007 Summer Bioengineering Conference, Keystone, CO, USA, 20–24 June 2007; pp. 661–662. [Google Scholar]
- Li, J.; Lu, Y.; Miller, S.C.; Jin, Z.; Hua, X. Development of a finite element musculoskeletal model with the ability to predict contractions of three-dimensional muscles. J. Biomech. 2019, 94, 230–234. [Google Scholar] [CrossRef] [PubMed]
- Damm, P.; Bender, A.; Duda, G.; Bergmann, G. In vivo measured joint friction in hip implants during walking after a short rest. PLoS ONE 2017, 12, e0174788. [Google Scholar] [CrossRef]
- Damm, P.; Bender, A.; Bergmann, G. Postoperative Changes in In Vivo Measured Friction in Total Hip Joint Prosthesis during Walking. PLoS ONE 2015, 10, e0120438. [Google Scholar] [CrossRef]
- Roy, T.; Choudhury, D.; Ghosh, S.; Bin Mamat, A.; Pingguan-Murphy, B. Improved friction and wear performance of micro dimpled ceramic-on-ceramic interface for hip joint arthroplasty. Ceram. Int. 2015, 41, 681–690. [Google Scholar] [CrossRef]
- Shen, G.; Zhang, J.; Melentiev, R.; Fang, F. Study on tribological performance of groove-textured bioimplants. J. Mech. Behav. Biomed. Mater. 2021, 119, 104514. [Google Scholar] [CrossRef]
- Ghosh, S.; Choudhury, D.; Roy, T.; Bin Mamat, A.; Masjuki, H.H.; Pingguan-Murphy, B. Tribological investigation of diamond-like carbon coated micro-dimpled surface under bovine serum and osteoarthritis oriented synovial fluid. Sci. Technol. Adv. Mater. 2015, 16, 035002. [Google Scholar] [CrossRef] [PubMed]
- Rebenda, D.; Vrbka, M.; Nečas, D.; Toropitsyn, E.; Yarimitsu, S.; Čípek, P.; Pravda, M.; Hartl, M. Rheological and frictional analysis of viscosupplements towards improved lubrication of human joints. Tribol. Int. 2021, 160, 107030. [Google Scholar] [CrossRef]
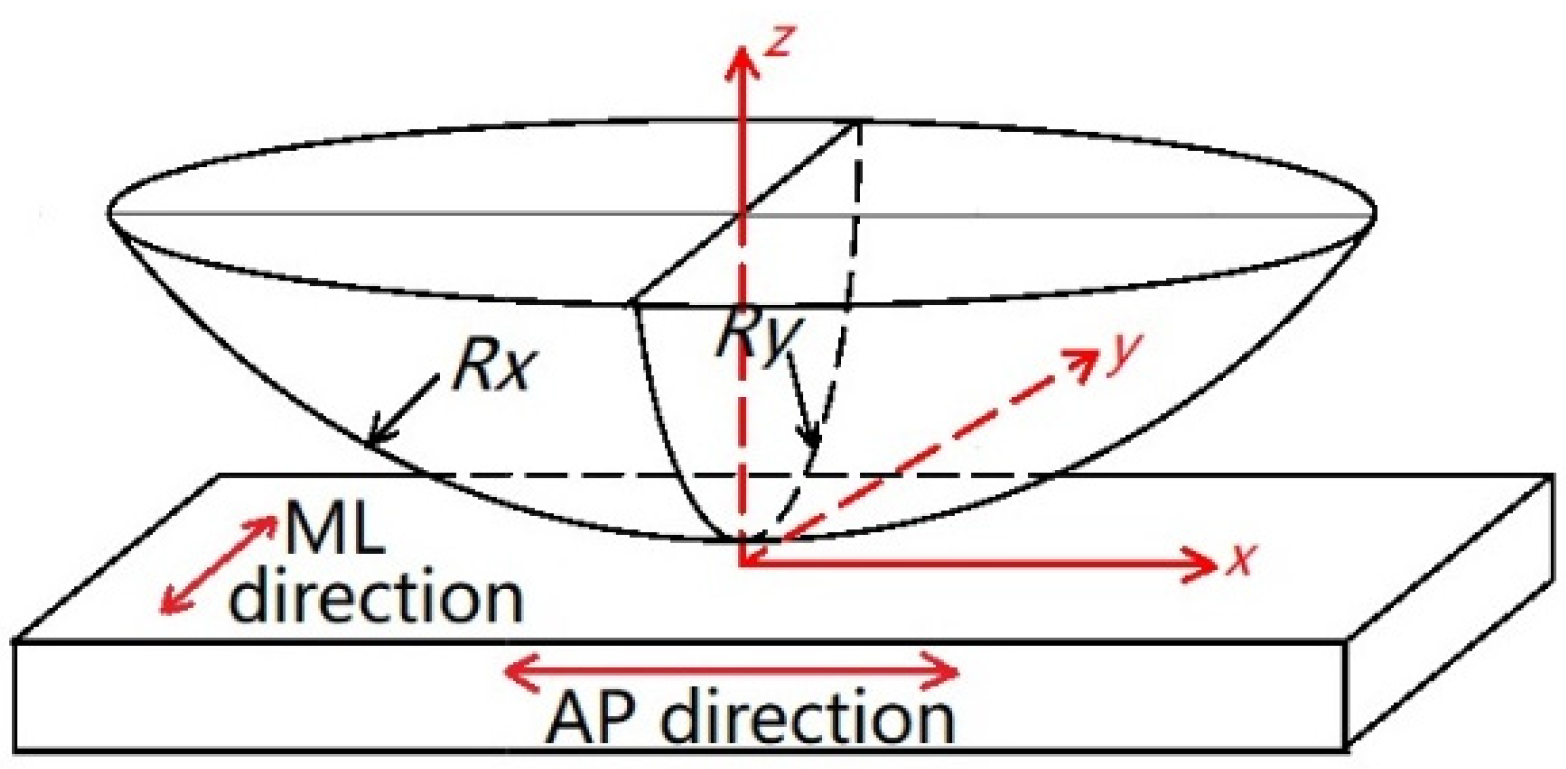
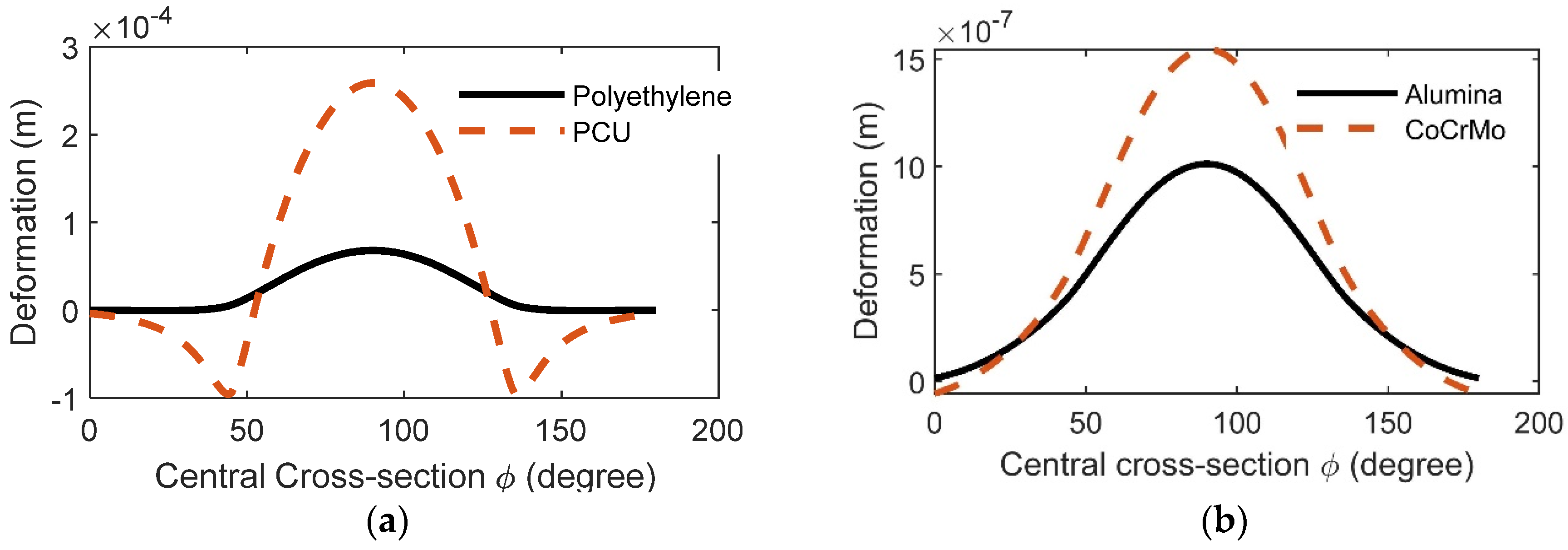

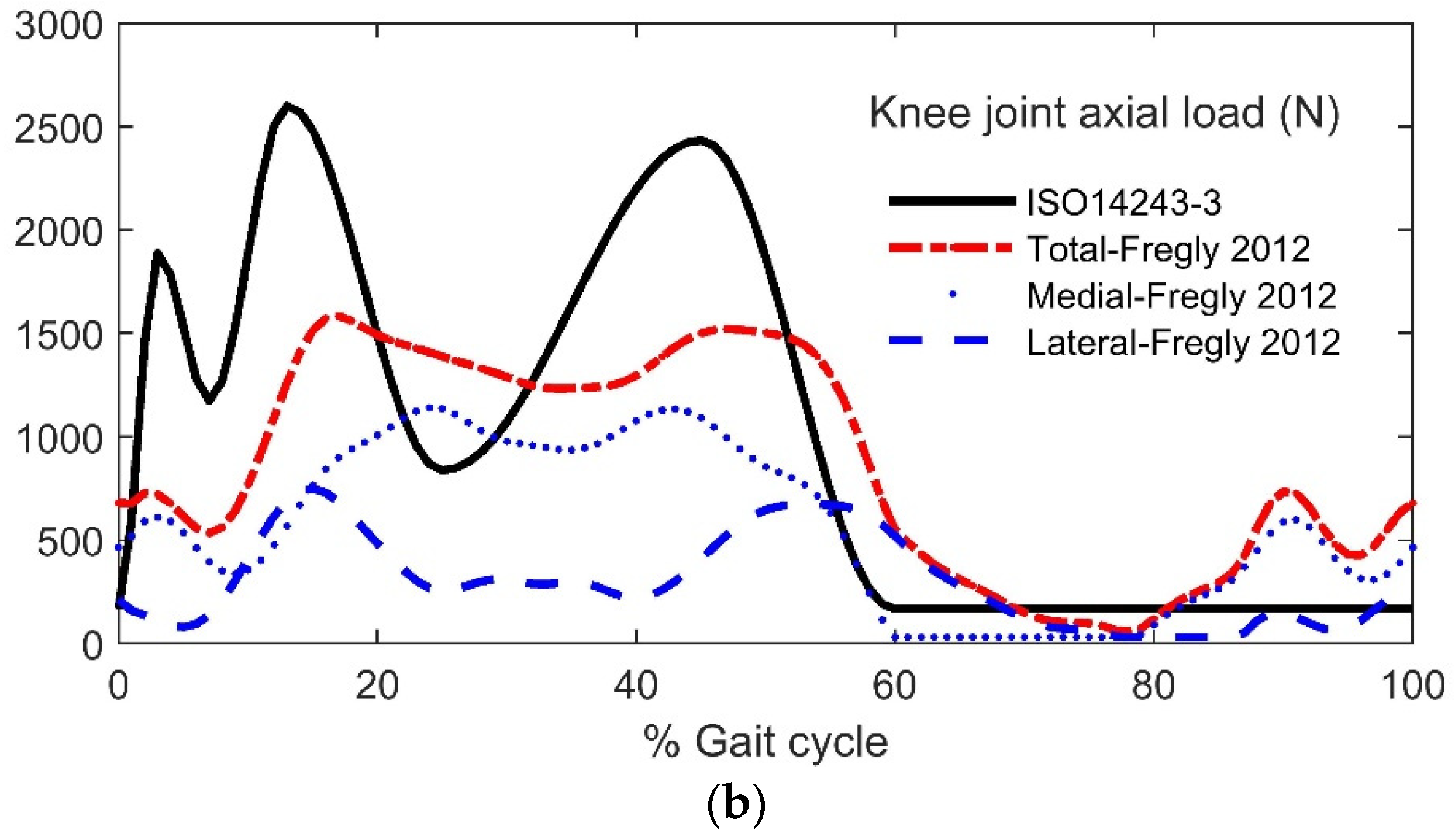
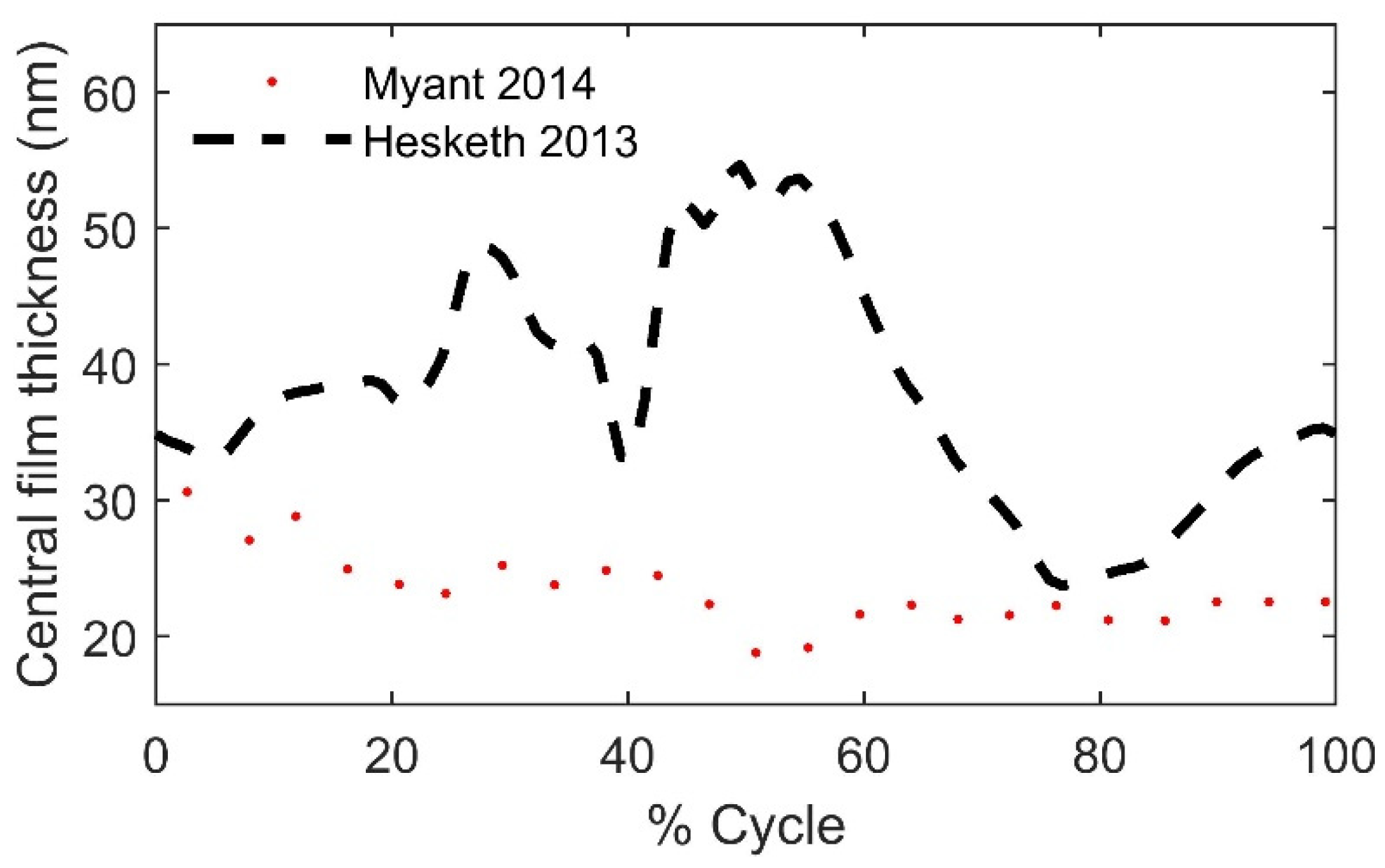
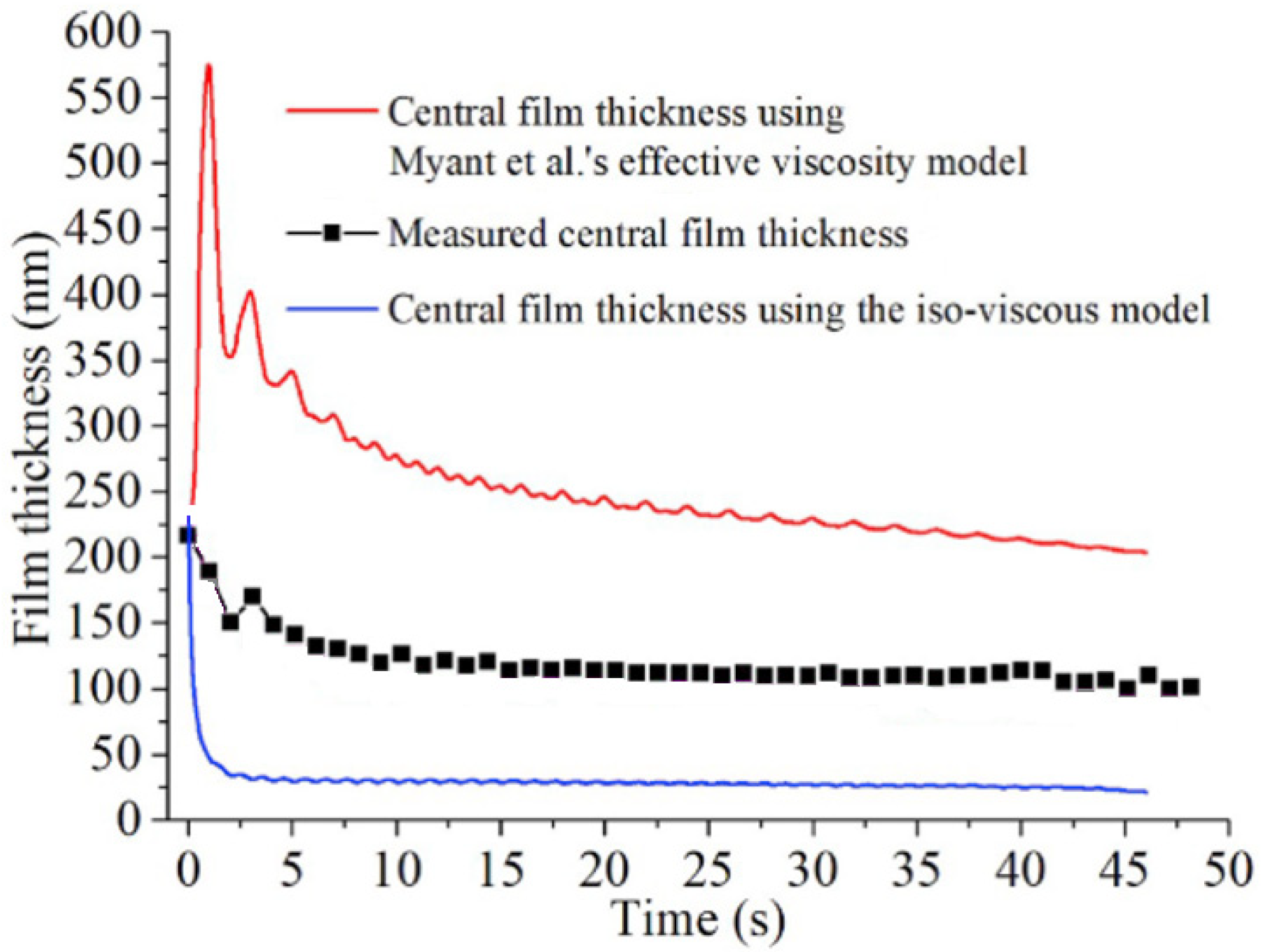
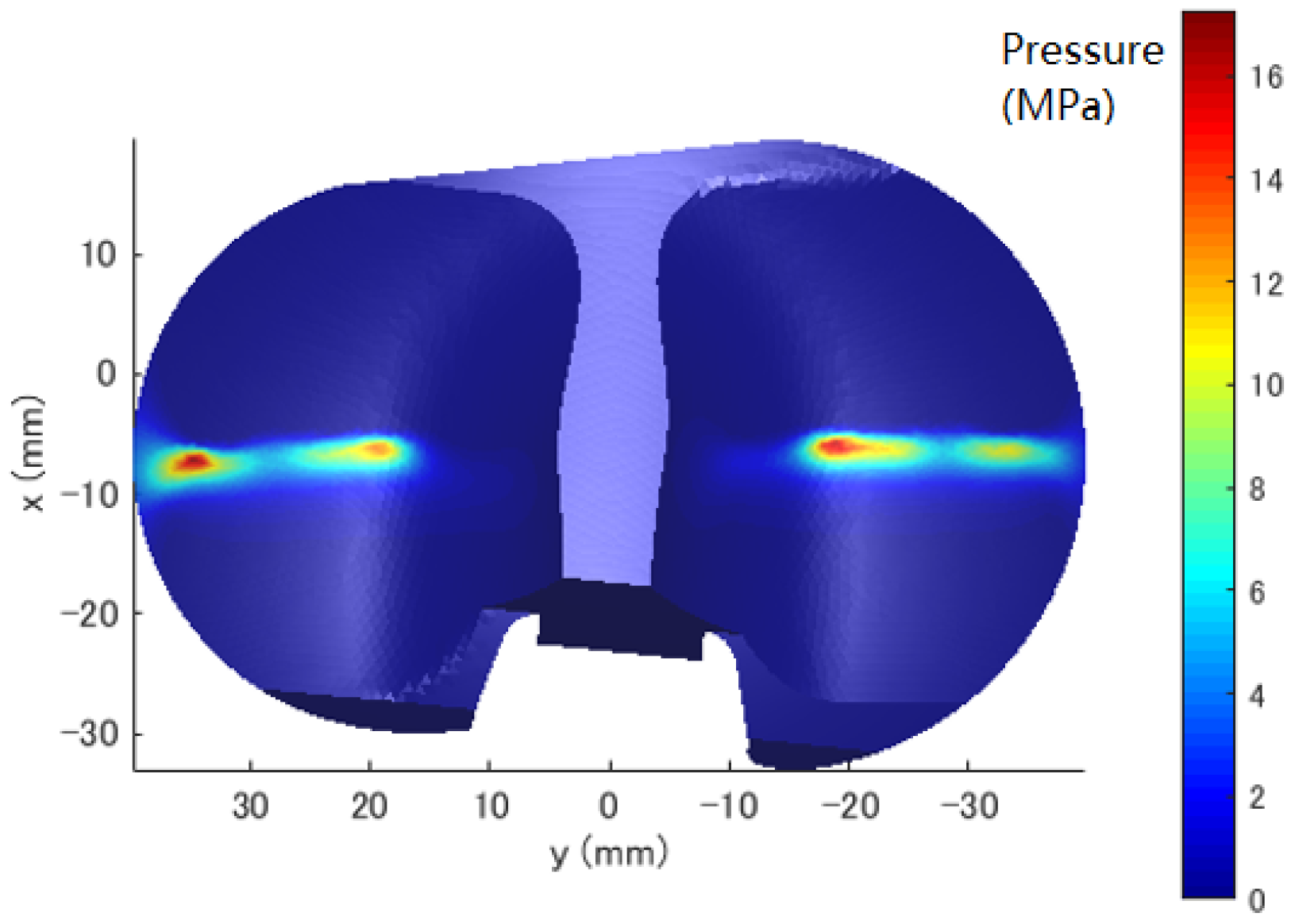
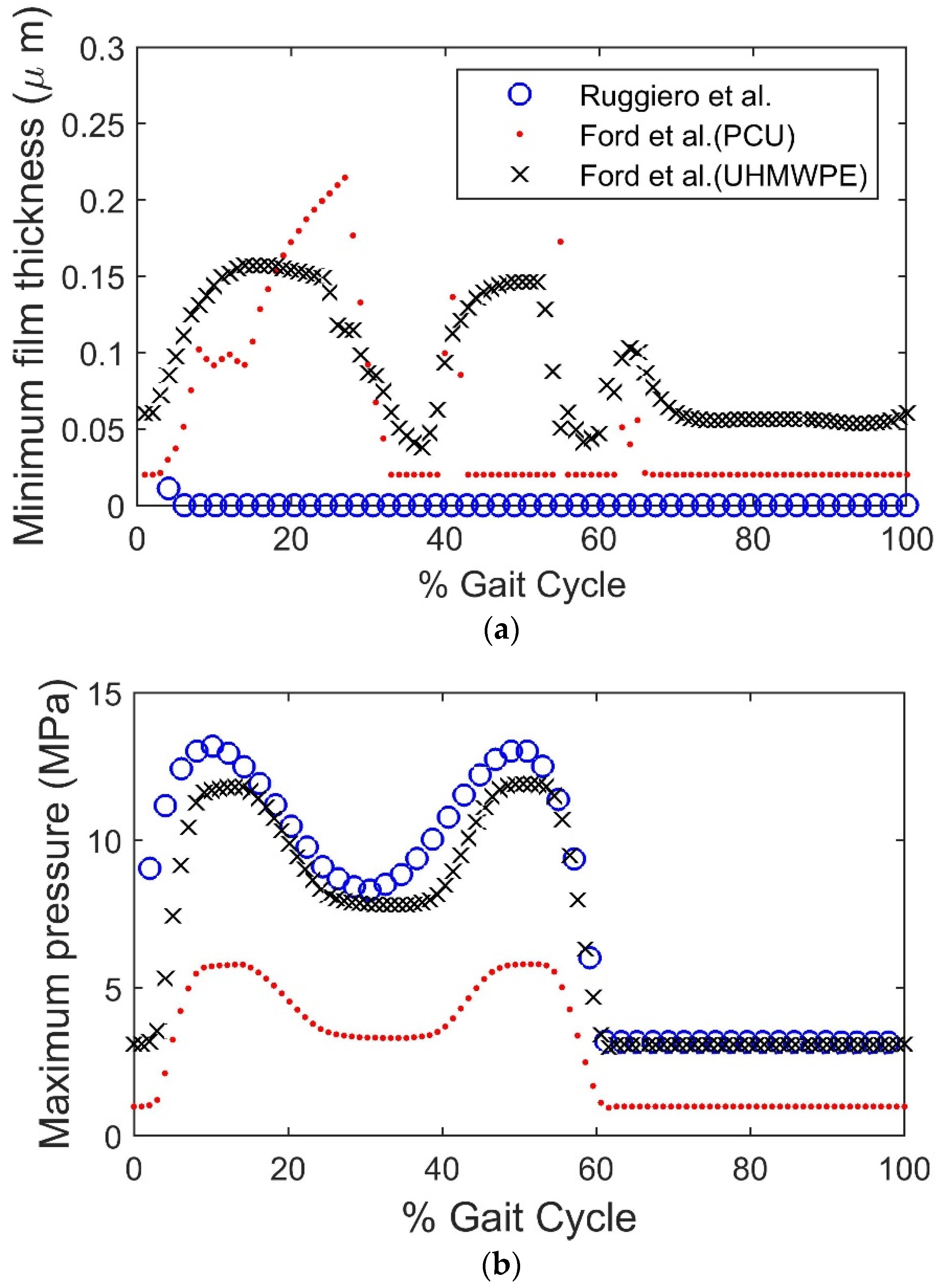

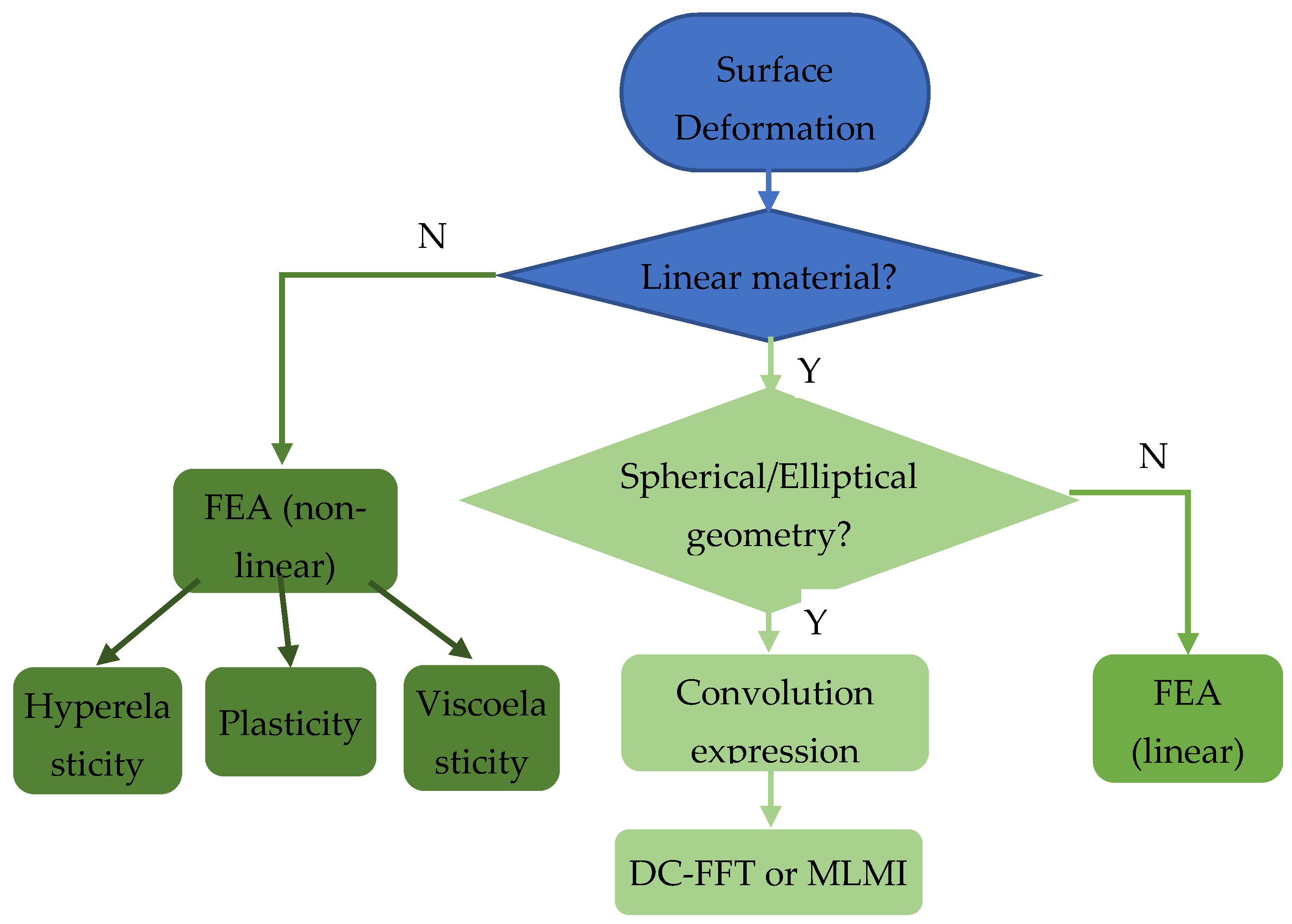
| Component | Femoral Head Radius R (mm) | Radial Clearance (μm) | |
|---|---|---|---|
| Spherical bearing [27,35,36,37] | MoP | 11–18 | 80–200 |
| MoM | 14–24 | 30–150 | |
| CoC | 14–18 | 10–50 | |
| MoMR | 20–30 | 75–150 | |
| Ellipsoidal surface [29] | a, b, c are the three semi-axis lengths of an ellipsoid | ||
| Alpharabola surface [33] | a is the parameter to control the variation rate of the radius of curvature | ||
| Pre-worn surface [34] | are curve-fitted parameters based on rotational Gaussian distribution function. | ||
| Components | Magnitudes (mm) |
|---|---|
| Femoral radius in ML direction, RF, ML | 18 |
| Femoral radius in AP direction, RF, AP | 24–33 |
| Tibial radius in ML direction, RT, ML | 21 |
| Tibial radius in AP direction, RT, AP | 45 |
| Tibial liner thickness, d | 10 |
| Materials | Example | Elastic Modulus (GPa) | Poisson’s Ratio | Density (kg/m3) | Advantages | Disadvantages |
|---|---|---|---|---|---|---|
| Metals | Stainless steel | 210 | 0.3 | 7900 |
|
|
| Titanium alloys | 110 | 0.3 | 4500 | |||
| CoCrMo/CoCr alloys | 230 | 0.3 | 8900 | |||
| Ceramics | Alumina | 380 | 0.26 | 3900 |
|
|
| Zirconia | 210 | 0.3 | 5600 | |||
| Polymers | PEEK | 3–4 | 0.25 | 1300 |
|
|
| UHMWPE | 0.5–1 | 0.4–0.46 | 900 | |||
| PCU | 0.024 | 0.49 | 1200 |
| Approaches | Speed for a Full Steady-State Solution | Accuracy | Applicable Geometries |
|---|---|---|---|
| Column model [24,54] | A few seconds to minutes | Good accuracy for hard-on-soft bearings | Ball-in-socket; large conformity |
| Multi-Grid [63] | Minutes to hours | High | Ball-on-plan or ball-in-socket |
| Spherical FFT [63] | Minutes to hours | High | Ball-in-socket |
| FEA [60] | Hours | High | Ball-on-plan or ball-in-socket |
| Lubricants | Zero Shear-rate Viscosity (Pa·s) | Plateau Viscosity (Pa·s) | (the Constant, Unit·s) | (the Rate Index Constant) |
|---|---|---|---|---|
| Healthy synovial fluid [83,85] | 40 | 0.0009 | 9.54 | 0.73 |
| TKA [82] | 0.087–25 | 0.0094–11 | 0.047–35 | 0.44–0.64 |
| Revision TKA [82] | 0.0087–4.0 | 0.0043–0.77 | 0.0043–10.8 | 0.37–0.59 |
| Calf serum (protein concentration 20 g/L for knee wear test) [86] | 0.018 | 0.00085 | 13 | 0.85 |
| Calf serum (protein concentration 30 g/L for hip wear test) [86] | 0.004 | 0.00088 | 11 | 0.6 |
| References | Geometry Type | Material Combination/Young’s Modulus (GPa)/Poisson’s Ratio | Fluid Rheology Properties/Viscosity (Pa·s) | Operating Conditions | Further Details |
|---|---|---|---|---|---|
| Hip implants | |||||
| Ruggiero and Sicilia [10] | Ball-in-Socket | MoP/cup: 1.05/0.4 | Non-Newtonian/40 (base) and 0.0009 (plateau) | ISO 14242-3 | Deterministic; wear model |
| Ruggiero and Sicilia [9] | Ball-in-Socket | CoP/cup: 1.0/0.47 | Non-Newtonian/ 0.0015 (base)– (plateau) | Measured from patients [70] | Deterministic; wear model |
| Ford et al. [49] | Ball-in-Socket | MoP/cup: 0.024/0.49; 0.7/0.4; 1.0/0.4 | Newtonian/0.002 | ISO 14242-1 | Deterministic model |
| Gao et al. [85] | Ball-in-Socket | MoM 210/0.3 | Non-Newtonian/40 (base) and 0.0009 (plateau) | Leeds ProSim; Measured from patients [70] | Deterministic model |
| Gao et al. [92] | Ball-in-Socket | MoM 210/0.3 | Newtonian/0.0009 | ISO 14242-1 | Deterministic; wear model |
| Gao et al. [91] | Ball-in-Socket | MoM 210/0.3 | Newtonian/0.001 | ISO 14242-1 | Deterministic model; surface texturing |
| Chyr et al. [98] | Ball-on-Plane | MoP (no deformation in modelling) | Newtonian/not explicitly specified | Steady-state | Stochastic model |
| Knee implants | |||||
| Butt et al. [99] | Real geometry from CAD model | MoP/cup: 1.0/0.4 | Newtonian/0.1 | ISO 14243-3 | Stochastic model |
| Marian et al. [40] | Elliptical ball-in-socket | MoP/cup: 3.5/0.34; 0.66/0.46 | Non-Newtonian/0.05 (base) and 0.002 (plateau) | ISO 14243-3 | Deterministic model |
| Gao et al. [55] | Spherical ball-in-socket | MoP/cup: 1.0/0.4 | Non-Newtonian/40 (base) and 0.005 (plateau) | Subject-specific gait cycle [66] | Deterministic; wear model |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, L.; Lu, X.; Zhang, X.; Meng, Q.; Jin, Z. Lubrication Modelling of Artificial Joint Replacements: Current Status and Future Challenges. Lubricants 2022, 10, 238. https://doi.org/10.3390/lubricants10100238
Gao L, Lu X, Zhang X, Meng Q, Jin Z. Lubrication Modelling of Artificial Joint Replacements: Current Status and Future Challenges. Lubricants. 2022; 10(10):238. https://doi.org/10.3390/lubricants10100238
Chicago/Turabian StyleGao, Leiming, Xianjiu Lu, Xiaogang Zhang, Qingen Meng, and Zhongmin Jin. 2022. "Lubrication Modelling of Artificial Joint Replacements: Current Status and Future Challenges" Lubricants 10, no. 10: 238. https://doi.org/10.3390/lubricants10100238
APA StyleGao, L., Lu, X., Zhang, X., Meng, Q., & Jin, Z. (2022). Lubrication Modelling of Artificial Joint Replacements: Current Status and Future Challenges. Lubricants, 10(10), 238. https://doi.org/10.3390/lubricants10100238