Accounting for Selection Bias and Redshift Evolution in GRB Radio Afterglow Data
Abstract
1. Introduction
2. Methods
2.1. Variables of Interest
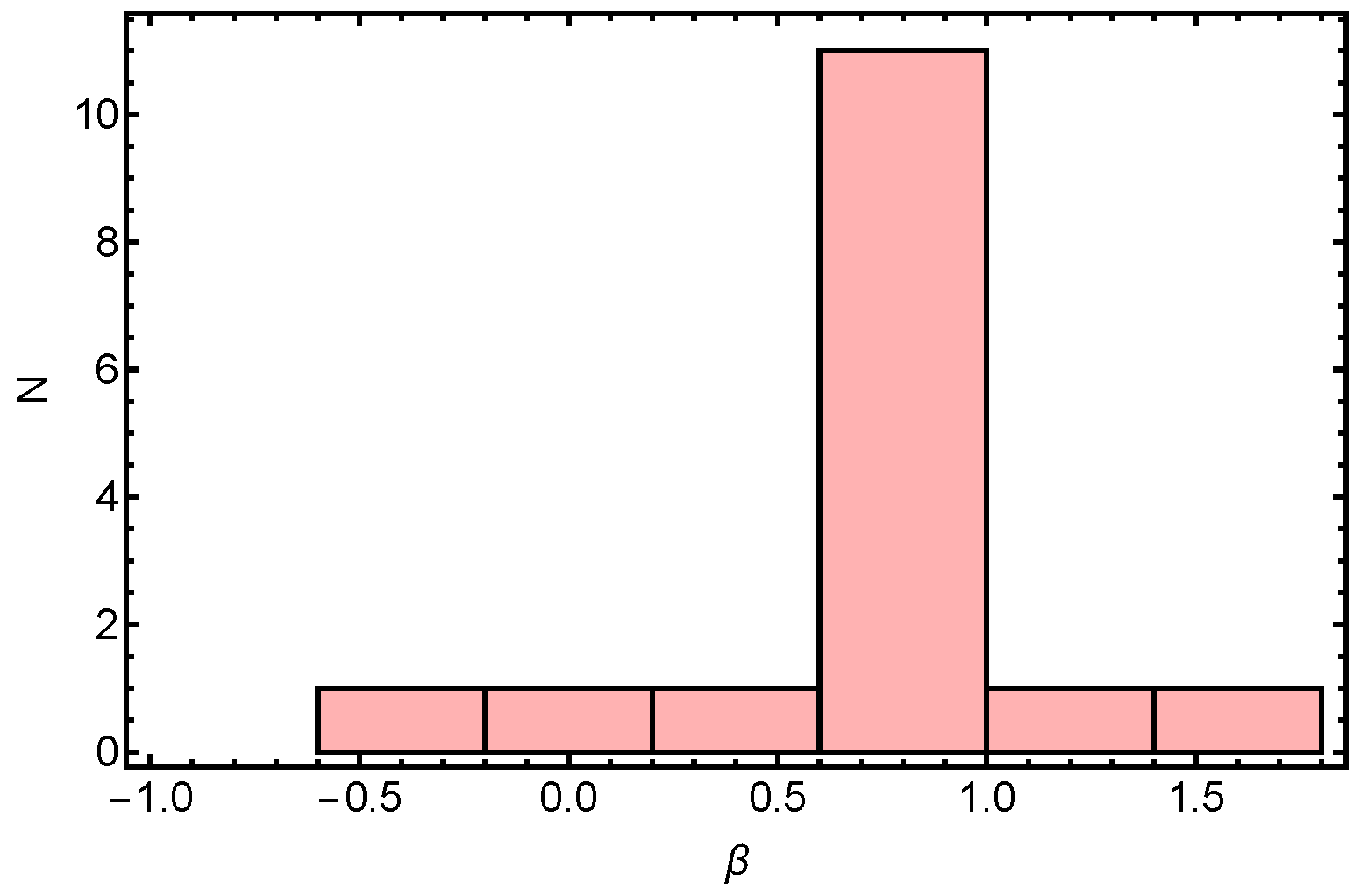
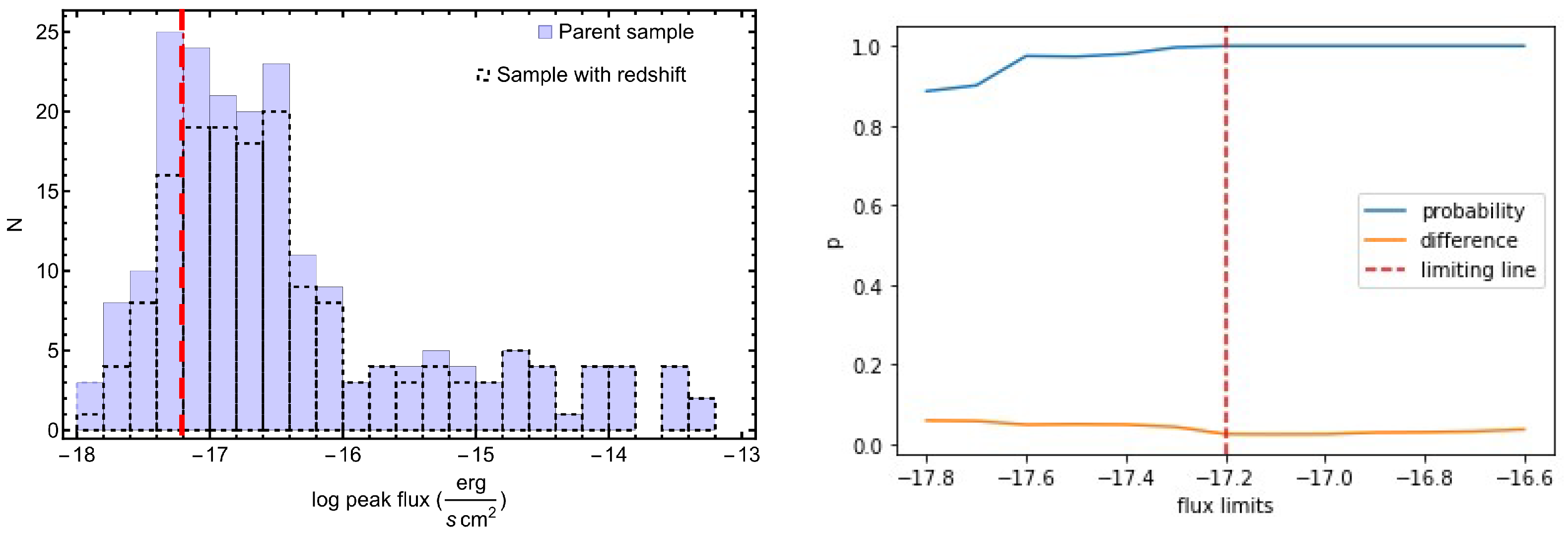
2.2. Limiting Fluxes, Fluences, and Times
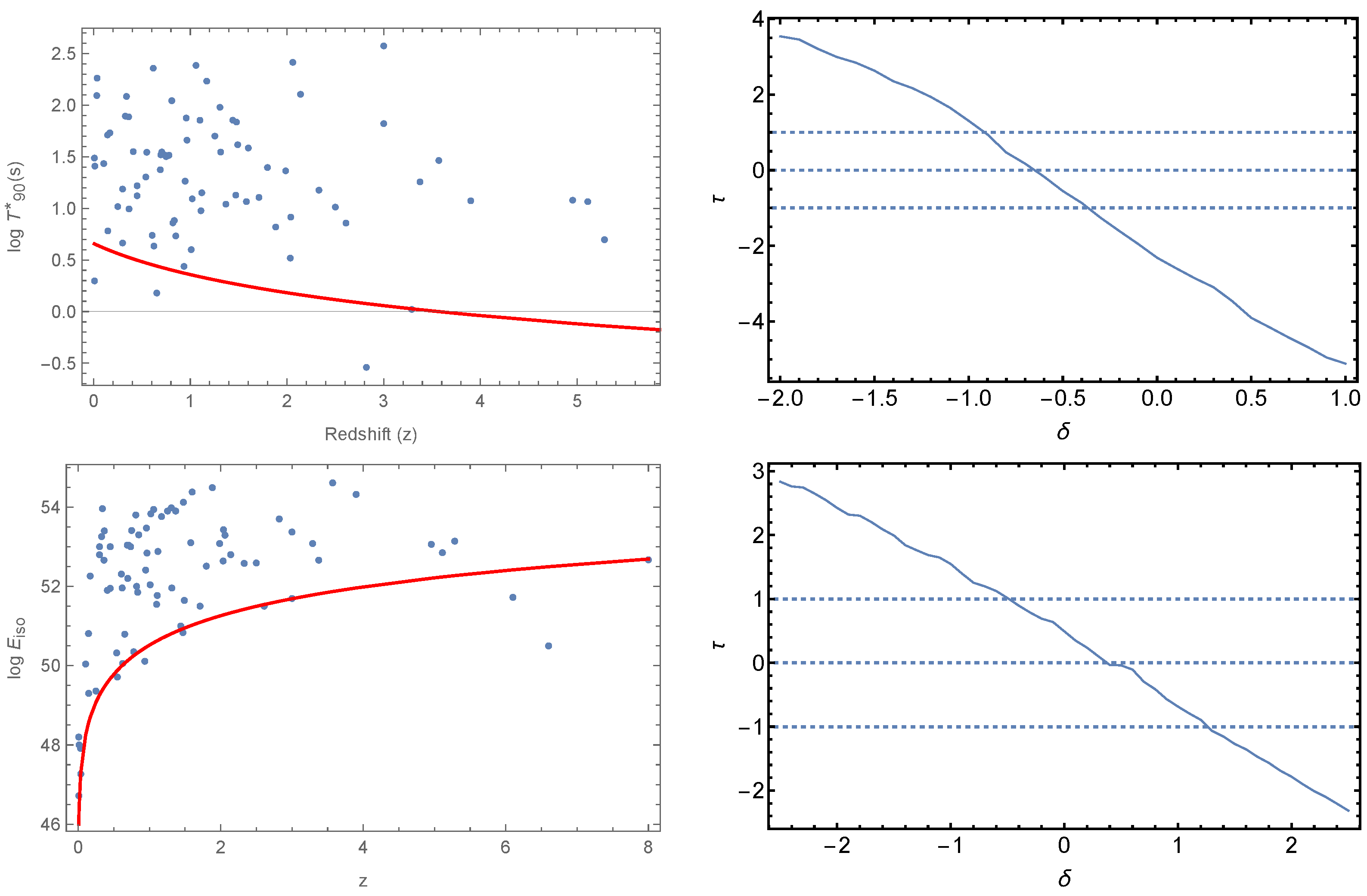
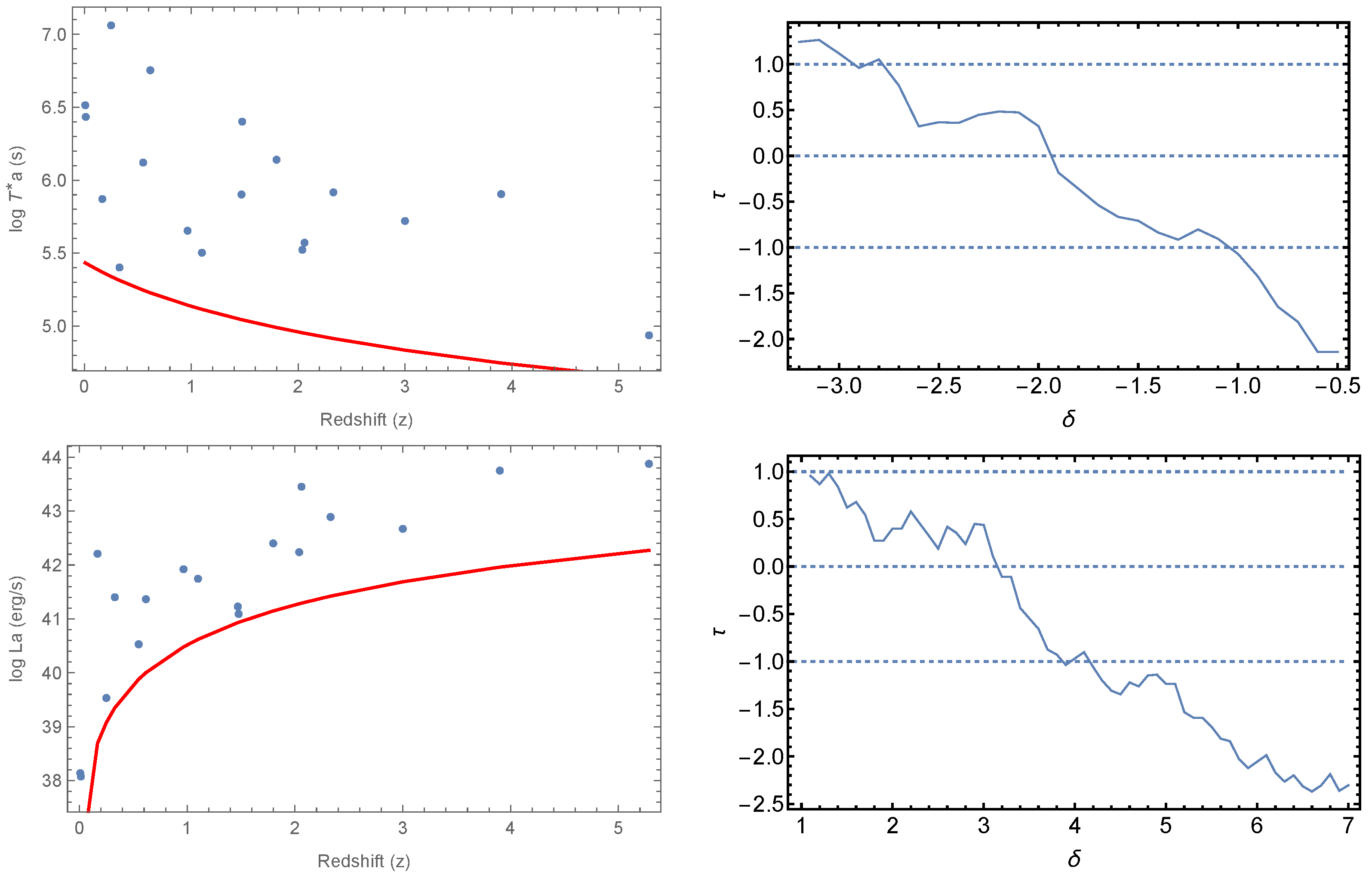
2.3. Removing Selection Bias and Redshift Evolution
3. Results
4. Discussion and Conclusions
- 1.
- After testing intrinsic properties of a GRB, such as and , as well as properties such as and , we see , and present strong correlation with redshift, thus indicating that they are susceptible to redshift evolution.
- 2.
- The values obtained in this work agree with those of previous studies, indicating that this trend of strong correlation with redshift still holds true in radio wavelengths.
- 3.
- The study of these evolutionary functions is the first necessary step to determine the true intrinsic nature of the correlations, object of our study.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cucchiara, A.; Levan, A.J.; Fox, D.B.; Tanvir, N.R.; Ukwatta, T.N.; Berger, E.; Krühler, T.; Küpcü Yoldaş, A.; Wu, X.F.; Toma, K.; et al. A Photometric Redshift of z~9.4 for GRB 090429B. Astrophys. J. 2011, 736, 7. [Google Scholar] [CrossRef]
- Cardone, V.F.; Capozziello, S.; Dainotti, M.G. An updated gamma-ray bursts Hubble diagram. Mon. Not. R. Astron. Soc. 2009, 400, 775–790. [Google Scholar] [CrossRef]
- Salvaterra, R.; Della Valle, M.; Campana, S.; Chincarini, G.; Covino, S.; D’Avanzo, P.; Fernández-Soto, A.; Guidorzi, C.; Mannucci, F.; Margutti, R.; et al. GRB090423 at a redshift of z~8.1. Nature 2009, 461, 1258–1260. [Google Scholar] [CrossRef] [PubMed]
- Tanvir, N.R.; Fox, D.B.; Levan, A.J.; Berger, E.; Wiersema, K.; Fynbo, J.P.U.; Cucchiara, A.; Krühler, T.; Gehrels, N.; Bloom, J.S.; et al. A γ-ray burst at a redshift of z~8.2. Nature 2009, 461, 1254–1257. [Google Scholar] [CrossRef]
- Cardone, V.F.; Dainotti, M.G.; Capozziello, S.; Willingale, R. Constraining cosmological parameters by gamma-ray burst X-ray afterglow light curves. Mon. Not. R. Astron. Soc. 2010, 408, 1181–1186. [Google Scholar] [CrossRef]
- Postnikov, S.; Dainotti, M.G.; Hernandez, X.; Capozziello, S. Nonparametric Study of the Evolution of the Cosmological Equation of State with SNeIa, BAO, and High-redshift GRBs. Astrophys. J. 2014, 783, 126. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Petrosian, V.; Singal, J.; Ostrowski, M. Determination of the Intrinsic Luminosity Time Correlation in the X-ray Afterglows of Gamma-ray Bursts. Astrophys. J. 2013, 774, 157. [Google Scholar] [CrossRef]
- Littlejohns, O.M.; Tanvir, N.R.; Willingale, R.; Evans, P.A.; O’Brien, P.T.; Levan, A.J. Are gamma-ray bursts the same at high redshift and low redshift? Mon. Not. R. Astron. Soc. 2013, 436, 3640–3655. [Google Scholar] [CrossRef]
- Laskar, T.; Berger, E.; Tanvir, N.; Zauderer, B.A.; Margutti, R.; Levan, A.; Perley, D.; Fong, W.F.; Wiersema, K.; Menten, K.; et al. GRB 120521C at z~6 and the Properties of High-redshift γ-Ray Bursts. Astrophys. J. 2014, 781, 1. [Google Scholar] [CrossRef]
- McGuire, J.T.W.; Tanvir, N.R.; Levan, A.J.; Trenti, M.; Stanway, E.R.; Shull, J.M.; Wiersema, K.; Perley, D.A.; Starling, R.L.C.; Bremer, M.; et al. Detection of Three Gamma-ray Burst Host Galaxies at z~6. Astrophys. J. 2016, 825, 135. [Google Scholar] [CrossRef]
- Tanvir, N.R.; Laskar, T.; Levan, A.J.; Perley, D.A.; Zabl, J.; Fynbo, J.P.U.; Rhoads, J.; Cenko, S.B.; Greiner, J.; Wiersema, K.; et al. The Properties of GRB 120923A at a Spectroscopic Redshift of z≈7.8. Astrophys. J. 2018, 865, 107. [Google Scholar] [CrossRef]
- Gehrels, N.; Razzaque, S. Gamma-ray bursts in the swift-Fermi era. Front. Phys. 2013, 8, 661–678. [Google Scholar] [CrossRef]
- Norris, J.P.; Bonnell, J.T. Short Gamma-ray Bursts with Extended Emission. Astrophys. J. 2006, 643, 266–275. [Google Scholar] [CrossRef]
- Norris, J.P.; Gehrels, N.; Scargle, J.D. Heterogeneity in Short Gamma-ray Bursts. Astrophys. J. 2011, 735, 23. [Google Scholar] [CrossRef]
- Woosley, S.E. Gamma-ray Bursts from Stellar Mass Accretion Disks around Black Holes. Astrophys. J. 1993, 405, 273. [Google Scholar] [CrossRef]
- Paczyński, B. Are Gamma-ray Bursts in Star-Forming Regions? Astrophys. J. 1998, 494, L45–L48. [Google Scholar] [CrossRef]
- Usov, V.V. Millisecond pulsars with extremely strong magnetic fields as a cosmological source of gamma-ray bursts. Nature 1992, 357, 472–474. [Google Scholar] [CrossRef]
- Duncan, R.C.; Thompson, C. Formation of Very Strongly Magnetized Neutron Stars: Implications for Gamma-ray Bursts. Astrophys. J. 1992, 392, L9. [Google Scholar] [CrossRef]
- Metzger, B.D.; Giannios, D.; Thompson, T.A.; Bucciantini, N.; Quataert, E. The protomagnetar model for gamma-ray bursts. Mon. Not. R. Astron. Soc. 2011, 413, 2031–2056. [Google Scholar] [CrossRef]
- Gehrels, N.; Chincarini, G.; Giommi, P.; Mason, K.O.; Nousek, J.A.; Wells, A.A.; White, N.E.; Barthelmy, S.D.; Burrows, D.N.; Cominsky, L.R.; et al. The Swift Gamma-ray Burst Mission. Astrophys. J. 2004, 611, 1005–1020. [Google Scholar] [CrossRef]
- Sakamoto, T.; Hill, J.E.; Yamazaki, R.; Angelini, L.; Krimm, H.A.; Sato, G.; Swindell, S.; Takami, K.; Osborne, J.P. Evidence of Exponential Decay Emission in the Swift Gamma-ray Bursts. Astrophys. J. 2007, 669, 1115–1129. [Google Scholar] [CrossRef]
- O’Brien, P.T.; Willingale, R.; Osborne, J.; Goad, M.R.; Page, K.L.; Vaughan, S.; Rol, E.; Beardmore, A.; Godet, O.; Hurkett, C.P.; et al. The Early X-ray Emission from GRBs. Astrophys. J. 2006, 647, 1213–1237. [Google Scholar] [CrossRef]
- Willingale, R.; O’Brien, P.T.; Osborne, J.P.; Godet, O.; Page, K.L.; Goad, M.R.; Burrows, D.N.; Zhang, B.; Rol, E.; Gehrels, N.; et al. Testing the Standard Fireball Model of Gamma-ray Bursts Using Late X-ray Afterglows Measured by Swift. Astrophys. J. 2007, 662, 1093–1110. [Google Scholar] [CrossRef]
- Pe’er, A. Physics of Gamma-ray Bursts Prompt Emission. Adv. Astron. 2015, 2015, 907321. [Google Scholar] [CrossRef]
- Yonetoku, D.; Murakami, T.; Nakamura, T.; Yamazaki, R.; Inoue, A.K.; Ioka, K. Gamma-ray Burst Formation Rate Inferred from the Spectral Peak Energy-Peak Luminosity Relation. Astrophys. J. 2004, 609, 935–951. [Google Scholar] [CrossRef]
- Dai, Z.G.; Wang, F.Y. Recent progress on GRB cosmology. Adv. Space Res. 2007, 40, 1244–1249. [Google Scholar] [CrossRef]
- Ghirlanda, G. Gamma-ray bursts spectral correlations and their cosmological use. Philos. Trans. R. Soc. Lond. Ser. A 2007, 365, 1385–1394. [Google Scholar] [CrossRef] [PubMed]
- Dainotti, M.G.; Cardone, V.F.; Capozziello, S. A time-luminosity correlation for γ-ray bursts in the X-rays. Mon. Not. R. Astron. Soc. 2008, 391, L79–L83. [Google Scholar] [CrossRef]
- Amati, L.; Guidorzi, C.; Frontera, F.; Della Valle, M.; Finelli, F.; Landi, R.; Montanari, E. Measuring the cosmological parameters with the Ep,i − Eiso correlation of gamma-ray bursts. Mon. Not. R. Astron. Soc. 2008, 391, 577–584. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Willingale, R.; Capozziello, S.; Fabrizio Cardone, V.; Ostrowski, M. Discovery of a Tight Correlation for Gamma-ray Burst Afterglows with “Canonical” Light Curves. Astrophys. J. 2010, 722, L215–L219. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Fabrizio Cardone, V.; Capozziello, S.; Ostrowski, M.; Willingale, R. Study of Possible Systematics in the L*X-T*a Correlation of Gamma-ray Bursts. Astrophys. J. 2011, 730, 135. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Ostrowski, M.; Willingale, R. Towards a standard gamma-ray burst: Tight correlations between the prompt and the afterglow plateau phase emission. Mon. Not. R. Astron. Soc. 2011, 418, 2202–2206. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Postnikov, S.; Hernandez, X.; Ostrowski, M. A Fundamental Plane for Long Gamma-ray Bursts with X-ray Plateaus. Astrophys. J. 2016, 825, L20. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Nagataki, S.; Maeda, K.; Postnikov, S.; Pian, E. A study of gamma ray bursts with afterglow plateau phases associated with supernovae. Astron. Astrophys. 2017, 600, A98. [Google Scholar] [CrossRef]
- Dainotti, M. Gamma-ray Burst Correlations: Current Status and Open Questions; IOP Publishing Ltd.: Bristol, UK, 2019. [Google Scholar] [CrossRef]
- Kocevski, D.; Butler, N.; Bloom, J.S. Pulse Width Evolution of Late-Time X-ray Flares in Gamma-ray Bursts. Astrophys. J. 2007, 667, 1024–1032. [Google Scholar] [CrossRef]
- Shahmoradi, A.; Nemiroff, R.J. The possible impact of gamma-ray burst detector thresholds on cosmological standard candles. Mon. Not. R. Astron. Soc. 2011, 411, 1843–1856. [Google Scholar] [CrossRef][Green Version]
- Shahmoradi, A.; Nemiroff, R.J. Short versus long gamma-ray bursts: A comprehensive study of energetics and prompt gamma-ray correlations. Mon. Not. R. Astron. Soc. 2015, 451, 126–143. [Google Scholar] [CrossRef]
- Coward, D.M.; Howell, E.J.; Wan, L.; MacPherson, D. Selection biases in the gamma-ray burst Eiso-Lopt, X correlation. Mon. Not. R. Astron. Soc. 2015, 449, L6–L10. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Cardone, V.F.; Piedipalumbo, E.; Capozziello, S. Slope evolution of GRB correlations and cosmology. Mon. Not. R. Astron. Soc. 2013, 436, 82–88. [Google Scholar] [CrossRef]
- Efron, B.; Petrosian, V. A Simple Test of Independence for Truncated Data with Applications to Redshift Surveys. Astrophys. J. 1992, 399, 345. [Google Scholar] [CrossRef]
- Lynden-Bell, D. A method of allowing for known observational selection in small samples applied to 3CR quasars. Mon. Not. R. Astron. Soc. 1971, 155, 95. [Google Scholar] [CrossRef]
- Efron, B.; Petrosian, V. Nonparametric Methods for Doubly Truncated Data. arXiv 1998, arXiv:astro-ph/9808334. [Google Scholar] [CrossRef]
- Lloyd, N.M.; Petrosian, V.; Mallozzi, R.S. Cosmological versus Intrinsic: The Correlation between Intensity and the Peak of the νFν Spectrum of Gamma-ray Bursts. Astrophys. J. 2000, 534, 227–238. [Google Scholar] [CrossRef]
- Singal, J.; Petrosian, V.; Lawrence, A.; Stawarz, Ł. On the Radio and Optical Luminosity Evolution of Quasars. Astrophys. J. 2011, 743, 104. [Google Scholar] [CrossRef]
- Lloyd-Ronning, N.M.; Aykutalp, A.; Johnson, J.L. On the cosmological evolution of long gamma-ray burst properties. Mon. Not. R. Astron. Soc. 2019, 488, 5823–5832. [Google Scholar] [CrossRef]
- Lloyd-Ronning, N.; Hurtado, V.U.; Aykutalp, A.; Johnson, J.; Ceccobello, C. The evolution of gamma-ray burst jet opening angle through cosmic time. Mon. Not. R. Astron. Soc. 2020, 494, 4371–4381. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Petrosian, V.; Bowden, L. Cosmological Evolution of the Formation Rate of Short Gamma-ray Bursts with and without Extended Emission. Astrophys. J. 2021, 914, L40. [Google Scholar] [CrossRef]
- Amati, L.; Frontera, F.; Tavani, M.; In’t Zand, J.J.M.; Antonelli, A.; Costa, E.; Feroci, M.; Guidorzi, C.; Heise, J.; Masetti, N.; et al. Intrinsic spectra and energetics of BeppoSAX Gamma-ray Bursts with known redshifts. Astron. Astrophys. 2002, 390, 81–89. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Livermore, S.; Kann, D.A.; Li, L.; Oates, S.; Yi, S.; Zhang, B.; Gendre, B.; Cenko, B.; Fraija, N. The Optical Luminosity-Time Correlation for More than 100 Gamma-ray Burst Afterglows. Astrophys. J. 2020, 905, L26. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Del Vecchio, R. Gamma ray Burst afterglow and prompt-afterglow relations: An overview. nar 2017, 77, 23–61. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Del Vecchio, R.; Tarnopolski, M. Gamma-ray Burst Prompt Correlations. Adv. Astron. 2018, 2018, 4969503. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Amati, L. Gamma-ray Burst Prompt Correlations: Selection and Instrumental Effects. Adv. Astron. 2018, 130, 051001. [Google Scholar] [CrossRef]
- Titarchuk, L.; Farinelli, R.; Frontera, F.; Amati, L. An Upscattering Spectral Formation Model for the Prompt Emission of Gamma-ray Bursts. Astrophys. J. 2012, 752, 116. [Google Scholar] [CrossRef]
- Beloborodov, A.M.; Mészáros, P. Photospheric Emission of Gamma-ray Bursts. Space Sci. Rev. 2017, 207, 87–110. [Google Scholar] [CrossRef]
- Dereli-Bégué, H.; Pe’er, A.; Ryde, F. Classification of Photospheric Emission in Short GRBs. Astrophys. J. 2020, 897, 145. [Google Scholar] [CrossRef]
- Toma, K.; Wu, X.F.; Mészáros, P. Photosphere-internal shock model of gamma-ray bursts: Case studies of Fermi/LAT bursts. Mon. Not. R. Astron. Soc. 2011, 415, 1663–1680. [Google Scholar] [CrossRef]
- Zheng, Z.; Lu, Y.; Zhao, Y.H. A Comptonization Model for the Prompt Optical and Infrared Emission of GRB 041219A. Astrophys. J. 2006, 646, L25–L28. [Google Scholar] [CrossRef][Green Version]
- Ito, H.; Matsumoto, J.; Nagataki, S.; Warren, D.C.; Barkov, M.V.; Yonetoku, D. The photospheric origin of the Yonetoku relation in gamma-ray bursts. Nat. Commun. 2019, 10, 1504. [Google Scholar] [CrossRef]
- Ahlgren, B.; Larsson, J.; Nymark, T.; Ryde, F.; Pe’er, A. Confronting GRB prompt emission with a model for subphotospheric dissipation. Mon. Not. R. Astron. Soc. 2015, 454, L31–L35. [Google Scholar] [CrossRef]
- Ghirlanda, G.; Pescalli, A.; Ghisellini, G. Photospheric emission throughout GRB 100507 detected by Fermi. Mon. Not. R. Astron. Soc. 2013, 432, 3237–3244. [Google Scholar] [CrossRef][Green Version]
- Ito, H.; Nagataki, S.; Matsumoto, J.; Lee, S.H.; Tolstov, A.; Mao, J.; Dainotti, M.; Mizuta, A. Spectral and Polarization Properties of Photospheric Emission from Stratified Jets. Astrophys. J. 2014, 789, 159. [Google Scholar] [CrossRef]
- Dall’Osso, S.; Stratta, G.; Guetta, D.; Covino, S.; De Cesare, G.; Stella, L. Gamma-ray bursts afterglows with energy injection from a spinning down neutron star. Astron. Astrophys. 2011, 526, A121. [Google Scholar] [CrossRef]
- Rowlinson, A.; O’Brien, P.T.; Metzger, B.D.; Tanvir, N.R.; Levan, A.J. Signatures of magnetar central engines in short GRB light curves. Mon. Not. R. Astron. Soc. 2013, 430, 1061–1087. [Google Scholar] [CrossRef]
- Fraija, N.; Veres, P.; Beniamini, P.; Galvan-Gamez, A.; Metzger, B.D.; Barniol Duran, R.; Becerra, R.L. On the Origin of the Multi-GeV Photons from the Closest Burst with Intermediate Luminosity: GRB 190829A. Astrophys. J. 2021, 918, 12. [Google Scholar] [CrossRef]
- Rowlinson, A.; Gompertz, B.P.; Dainotti, M.; O’Brien, P.T.; Wijers, R.A.M.J.; van der Horst, A.J. Constraining properties of GRB magnetar central engines using the observed plateau luminosity and duration correlation. Mon. Not. R. Astron. Soc. 2014, 443, 1779–1787. [Google Scholar] [CrossRef]
- Rea, N.; Gullón, M.; Pons, J.A.; Perna, R.; Dainotti, M.G.; Miralles, J.A.; Torres, D.F. Constraining the GRB-Magnetar Model by Means of the Galactic Pulsar Population. Astrophys. J. 2015, 813, 92. [Google Scholar] [CrossRef]
- Stratta, G.; Dainotti, M.G.; Dall’Osso, S.; Hernandez, X.; De Cesare, G. On the Magnetar Origin of the GRBs Presenting X-ray Afterglow Plateaus. Astrophys. J. 2018, 869, 155. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Del Vecchio, R.; Shigehiro, N.; Capozziello, S. Selection Effects in Gamma-ray Burst Correlations: Consequences on the Ratio between Gamma-ray Burst and Star Formation Rates. Astrophys. J. 2015, 800, 31. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Hernandez, X.; Postnikov, S.; Nagataki, S.; O’brien, P.; Willingale, R.; Striegel, S. A Study of the Gamma-ray Burst Fundamental Plane. Astrophys. J. 2017, 848, 88. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Lenart, A.Ł.; Sarracino, G.; Nagataki, S.; Capozziello, S.; Fraija, N. The X-ray Fundamental Plane of the Platinum Sample, the Kilonovae, and the SNe Ib/c Associated with GRBs. Astrophys. J. 2020, 904, 97. [Google Scholar] [CrossRef]
- Dainotti, M.G.; De Simone, B.; Schiavone, T.; Montani, G.; Rinaldi, E.; Lambiase, G. On the Hubble Constant Tension in the SNe Ia Pantheon Sample. Astrophys. J. 2021, 912, 150. [Google Scholar] [CrossRef]
- Lloyd-Ronning, N.M.; Gompertz, B.; Pe’er, A.; Dainotti, M.; Fruchter, A. A Comparison between Radio Loud and Quiet Gamma-ray Bursts, and Evidence for a Potential Correlation between Intrinsic Duration and Redshift in the Radio Loud Population. Astrophys. J. 2019, 871, 118. [Google Scholar] [CrossRef]
- Bryant, C.M.; Osborne, J.A.; Shahmoradi, A. How unbiased statistical methods lead to biased scientific discoveries: A case study of the Efron-Petrosian statistic applied to the luminosity-redshift evolution of gamma-ray bursts. Mon. Not. R. Astron. Soc. 2021, 504, 4192–4203. [Google Scholar] [CrossRef]
- Piran, T. Gamma-ray bursts and the fireball model. Phys. Rep. 1999, 314, 575–667. [Google Scholar] [CrossRef]
- Sari, R.; Piran, T. GRB 990123: The Optical Flash and the Fireball Model. Astrophys. J. 1999, 517, L109–L112. [Google Scholar] [CrossRef]
- Dainotti, M.; Petrosian, V.; Willingale, R.; O’Brien, P.; Ostrowski, M.; Nagataki, S. Luminosity-time and luminosity-luminosity correlations for GRB prompt and afterglow plateau emissions. Mon. Not. R. Astron. Soc. 2015, 451, 3898–3908. [Google Scholar] [CrossRef]
- Petrosian, V.; Kitanidis, E.; Kocevski, D. Cosmological Evolution of Long Gamma-ray Bursts and the Star Formation Rate. Astrophys. J. 2015, 806, 44. [Google Scholar] [CrossRef]
- Lloyd-Ronning, N.M.; Petrosian, V. Interpreting the Behavior of Time-resolved Gamma-ray Burst Spectra. Astrophys. J. 2002, 565, 182–194. [Google Scholar] [CrossRef][Green Version]
- Chandra, P.; Frail, D.A. A Radio-selected Sample of Gamma-ray Burst Afterglows. Astrophys. J. 2012, 746, 156. [Google Scholar] [CrossRef]
- Zauderer, B.A.; Berger, E.; Margutti, R.; Levan, A.J.; Olivares, E.F.; Perley, D.A.; Fong, W.; Horesh, A.; Updike, A.C.; Greiner, J.; et al. Illuminating the Darkest Gamma-ray Bursts with Radio Observations. Astrophys. J. 2013, 767, 161. [Google Scholar] [CrossRef]
- Laskar, T.; Berger, E.; Margutti, R.; Perley, D.; Zauderer, B.A.; Sari, R.; Fong, W.F. Energy Injection in Gamma-ray Burst Afterglows. Astrophys. J. 2015, 814, 1. [Google Scholar] [CrossRef]
- Laskar, T.; van Eerten, H.; Schady, P.; Mundell, C.G.; Alexander, K.D.; Barniol Duran, R.; Berger, E.; Bolmer, J.; Chornock, R.; Coppejans, D.L.; et al. A Reverse Shock in GRB 181201A. Astrophys. J. 2019, 884, 121. [Google Scholar] [CrossRef]
- Cucchiara, A.; Veres, P.; Corsi, A.; Cenko, S.B.; Perley, D.A.; Lien, A.; Marshall, F.E.; Pagani, C.; Toy, V.L.; Capone, J.I.; et al. Happy Birthday Swift: Ultra-long GRB 141121A and Its Broadband Afterglow. Astrophys. J. 2015, 812, 122. [Google Scholar] [CrossRef]
- Bright, J.S.; Horesh, A.; van der Horst, A.J.; Fender, R.; Anderson, G.E.; Motta, S.E.; Cenko, S.B.; Green, D.A.; Perrott, Y.; Titterington, D. A detailed radio study of the energetic, nearby, and puzzling GRB 171010A. Mon. Not. R. Astron. Soc. 2019, 486, 2721–2729. [Google Scholar] [CrossRef]
- Anderson, G.E.; van der Horst, A.J.; Staley, T.D.; Fender, R.P.; Wijers, R.A.M.J.; Scaife, A.M.M.; Rumsey, C.; Titterington, D.J.; Rowlinson, A.; Saunders, R.D.E. Probing the bright radio flare and afterglow of GRB 130427A with the Arcminute Microkelvin Imager. Mon. Not. R. Astron. Soc. 2014, 440, 2059–2065. [Google Scholar] [CrossRef][Green Version]
- Singer, L.P.; Kasliwal, M.M.; Cenko, S.B.; Perley, D.A.; Anderson, G.E.; Anupama, G.C.; Arcavi, I.; Bhalerao, V.; Bue, B.D.; Cao, Y.; et al. The Needle in the 100 deg2 Haystack: Uncovering Afterglows of Fermi GRBs with the Palomar Transient Factory. Astrophys. J. 2015, 806, 52. [Google Scholar] [CrossRef]
- Laskar, T.; Berger, E.; Margutti, R.; Zauderer, B.A.; Williams, P.K.G.; Fong, W.F.; Sari, R.; Alexander, K.D.; Kamble, A. A VLA Study of High-redshift GRBs. II. The Complex Radio Afterglow of GRB 140304A: Shell Collisions and Two Reverse Shocks. Astrophys. J. 2018, 859, 134. [Google Scholar] [CrossRef]
- Kangas, T.; Fruchter, A.S.; Cenko, S.B.; Corsi, A.; de Ugarte Postigo, A.; Pe’er, A.; Vogel, S.N.; Cucchiara, A.; Gompertz, B.; Graham, J.; et al. The Late-time Afterglow Evolution of Long Gamma-ray Bursts GRB 160625B and GRB 160509A. Astrophys. J. 2020, 894, 43. [Google Scholar] [CrossRef]
- Laskar, T.; Alexander, K.D.; Berger, E.; Fong, W.F.; Margutti, R.; Shivvers, I.; Williams, P.K.G.; Kopač, D.; Kobayashi, S.; Mundell, C.; et al. A Reverse Shock in GRB 160509A. Astrophys. J. 2016, 833, 88. [Google Scholar] [CrossRef]
- Chen, W.J.; Urata, Y.; Huang, K.; Takahashi, S.; Petitpas, G.; Asada, K. Two-component Jets of GRB 160623A as Shocked Jet Cocoon Afterglow. Astrophys. J. 2020, 891, L15. [Google Scholar] [CrossRef]
- Bhalerao, V.; Kasliwal, M.M.; Bhattacharya, D.; Corsi, A.; Aarthy, E.; Adams, S.M.; Blagorodnova, N.; Cantwell, T.; Cenko, S.B.; Fender, R.; et al. A Tale of Two Transients: GW 170104 and GRB 170105A. Astrophys. J. 2017, 845, 152. [Google Scholar] [CrossRef]
- Hallinan, G.; Corsi, A.; Mooley, K.P.; Hotokezaka, K.; Nakar, E.; Kasliwal, M.M.; Kaplan, D.L.; Frail, D.A.; Myers, S.T.; Murphy, T.; et al. A radio counterpart to a neutron star merger. Science 2017, 358, 1579–1583. [Google Scholar] [CrossRef] [PubMed]
- Mooley, K.P.; Nakar, E.; Hotokezaka, K.; Hallinan, G.; Corsi, A.; Frail, D.A.; Horesh, A.; Murphy, T.; Lenc, E.; Kaplan, D.L.; et al. A mildly relativistic wide-angle outflow in the neutron-star merger event GW170817. Nature 2018, 554, 207–210. [Google Scholar] [CrossRef] [PubMed]
- Resmi, L.; Schulze, S.; Ishwara-Chandra, C.H.; Misra, K.; Buchner, J.; De Pasquale, M.; Sánchez-Ramírez, R.; Klose, S.; Kim, S.; Tanvir, N.R.; et al. Low-frequency View of GW170817/GRB 170817A with the Giant Metrewave Radio Telescope. Astrophys. J. 2018, 867, 57. [Google Scholar] [CrossRef]
- Margutti, R.; Alexander, K.D.; Xie, X.; Sironi, L.; Metzger, B.D.; Kathirgamaraju, A.; Fong, W.; Blanchard, P.K.; Berger, E.; MacFadyen, A.; et al. The Binary Neutron Star Event LIGO/Virgo GW170817 160 Days after Merger: Synchrotron Emission across the Electromagnetic Spectrum. Astrophys. J. 2018, 856, L18. [Google Scholar] [CrossRef]
- Maity, B.; Chandra, P. 1000 Days of the Lowest-frequency Emission from the Low-luminosity GRB 171205A. Astrophys. J. 2021, 907, 60. [Google Scholar] [CrossRef]
- Rhodes, L.; van der Horst, A.J.; Fender, R.; Monageng, I.M.; Anderson, G.E.; Antoniadis, J.; Bietenholz, M.F.; Böttcher, M.; Bright, J.S.; Green, D.A.; et al. Radio afterglows of very high-energy gamma-ray bursts 190829A and 180720B. Mon. Not. R. Astron. Soc. 2020, 496, 3326–3335. [Google Scholar] [CrossRef]
- Bloom, J.S.; Frail, D.A.; Sari, R. The Prompt Energy Release of Gamma-ray Bursts using a Cosmological [ITAL]k[/ITAL]-Correction. Astron. J. 2001, 121, 2879–2888. [Google Scholar] [CrossRef]
- Avni, Y. Parameter estimation for X-ray sources: Positions. Astron. Astrophys. 1978, 66, 307–309. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dainotti, M.; Levine, D.; Fraija, N.; Chandra, P. Accounting for Selection Bias and Redshift Evolution in GRB Radio Afterglow Data. Galaxies 2021, 9, 95. https://doi.org/10.3390/galaxies9040095
Dainotti M, Levine D, Fraija N, Chandra P. Accounting for Selection Bias and Redshift Evolution in GRB Radio Afterglow Data. Galaxies. 2021; 9(4):95. https://doi.org/10.3390/galaxies9040095
Chicago/Turabian StyleDainotti, Maria, Delina Levine, Nissim Fraija, and Poonam Chandra. 2021. "Accounting for Selection Bias and Redshift Evolution in GRB Radio Afterglow Data" Galaxies 9, no. 4: 95. https://doi.org/10.3390/galaxies9040095
APA StyleDainotti, M., Levine, D., Fraija, N., & Chandra, P. (2021). Accounting for Selection Bias and Redshift Evolution in GRB Radio Afterglow Data. Galaxies, 9(4), 95. https://doi.org/10.3390/galaxies9040095





