Abstract
The orbital period of Nova-like variable RW Tri is expected to experience a long-term evolution due to a stable mass transfer from the red dwarf to the white dwarf. By adding 297 new eclipse timings obtained from our own observations and a cross-identification of many databases, we fully reinvestigated the variations in orbital period of RW Tri, based on a total of 658 data points spanning over 80 years. The new O-C diagram demonstrates a more complicate pattern than a pure sinusoidal modulation shown in the previous O-C analyses. The best fit of the O-C variations is a quadratic-plus-sinusoidal curve with a period of 22.66 (2) years and a typical decrease rate of = .32(4) × 10 yr. To explain secular orbital period decrease, the magnetic braking effect is required to cause the orbital angular moment loss in RW Tri with a mass ratio less than unity, while a conserved mass transfer is also enough for RW Tri with a mass ratio larger than unity. No matter what the mass ratio is, a slightly enhanced mass transfer rate, 2.4–5.3 × 10 M yr, derived from our O-C diagram, providing an evidence supporting the disk instability model and the standard/revised models of cataclysmic variable evolution, is almost the same as that obtained from the light-curve modeling. This further confirms our observed orbital period decrease and the controversial system parameter, mass transfer rate. Our updated O-C analysis further verifies the claimed cyclical changes of orbital period with a period range of 21–24 years, which is approximately one half of the results in the literature. In accordance with the light-travel time effect, this periodical variation shown in our new O-C diagram indicates a brown dwarf hidden in RW Tri at a coplanar orbit. Note that the large scatter in the data range of 0–3 × 10 cycles requires the high-precision photometry in the longer base line in the future.
1. Introduction
RW Tri was first discovered as an Algol-type eclipsing binary with an orbital period of ∼334 min [1]. However, Walker [2,3] showed the strong Balmer and weaker HeII emission lines. This is similar to those of UX Ursae Majoris and DQ Herculis stars. Later, RW Tri was classified as a nova-like (NL) variable, a subclass of cataclysmic variables (CVs; [4]) and shows a number of features as that of SW Sex-type stars [5], a special subtype with orbital period in a range of 3–4 h [6,7]. The magnitudes of RW Tri in out-of-eclipse and mid-eclipse are 13.74 mag and 15.83 mag, respectively [8]. This indicates that RW Tri is a bright object and it has been extensively studied in photometry (e.g., [1,9,10]) and spectroscopy (e.g., [5,11,12]). Based on these observations, the absolute parameters of RW Tri have been discussed for many years. The considerably large distinctions in system parameters indicate that RW Tri is still a mysterious NL variable. In spite of this, the masses of two components recently obtained by Smak [13] and Subebekova et al. [14] are basically consistent.
According to the theories on accretion disk [15], RW Tri is a stable accretion system. Horne and Cook [16], Rutter et al. [17], and Halevin and Henden [8] reconstructed the steady-state accretion disk of RW Tri from the eclipsing light curves. Due to the mass transfer between the two components, the orbital period evolution of RW Tri is suitable to be studied in detail. Although RW Tri is one of the earliest known cataclysmic variables, the orbital period variations have only received little attention. The early analysis showed a periodic variation with a period shorter than 15 years (e.g., ∼5.2 years in Halevin and Henden [8]; ∼7.6 years and ∼13.6 years in Africano et al. [1] and ∼6.1 years in Still et al. [11]). Based on the possible orbital period decrease, Robinson et al. [18] derived a mass transfer with a rate of 1.15 × 10 M yr from the Roche-lobe filling star to white dwarf. However, they never presented an available quadratic ephemeris and the corresponding O-C diagram due to the large error of the calculated decrease rate. Polsgrove et al. [19] showed an O-C diagram fitting by a secular orbital period decrease with a rate of .8(3) × 10 yr. Moreover, they never found any cyclical change claimed in the previous O-C analyses. By adding many new data points, the two recent O-C diagrams [14,20] again show a pure cyclical variation with a period approaching 40 years, without any secular change. Therefore, a careful verification for all the data including the historic and new observed data they used to carry out their own O-C analyses and the more supplemental new high-precision data may be helpful to solve this apparent controversy.
In this paper, 297 new light minimum times spanning from 1978 to 2019 are presented in Section 2 (although parts of data were published before, we carried out a cross-identification for all of them; the similar data taken in the different band, observatory or observers marked in Table A2 of Appendix A were averaged in our O-C analysis). Section 3 deals with the O-C analysis for RW Tri in detail. The discussions of the possible mechanisms for the orbital period changes are presented in Section 4.
2. New Light Minimum Times
Table 1 provides a log of the new observations in photometry and surveys.

Table 1.
Details of new observations.
2.1. Photometry
Two new light minimum times are obtained from our CCD photometric observations with the PI 1024 TKB CCD photometric system attached to the 1.0-m reflecting telescope at Yunnan Observatories in China. Two nearby stars with the similar brightness in the same viewing field of telescope are chosen as the comparison and check star, respectively. All CCD images were reduced by using PHOT routine measuring magnitudes for a list of stars in aperture photometry package of IRAF (IRAF (Image Reduction and Analysis Facility) is distributed by the National Optical Astronomy Observatory, which is operated by the Association of Universities for Research in Astronomy, under cooperative agreement with the National Science Foundation). In Appendix A, the three differential light curves are shown in Figure A1, and their corresponding photometry data are listed in Table A1 of Appendix A.
Due to the smooth and symmetrical eclipse profile, the light minimum times corresponding to the eclipsing time of the center part of the accretion disk (i.e., the white dwarf and the inner disk) can be derived by using a least-squares fitting method to a parabolic curve. The fitting errors derived by using the bootstrap method and the time-resolution of CCD observations were combined to estimate the uncertainties of light minimum times (these two methods were also applied to all eclipsing light curves obtained from the American Association of Variable Star Observers (AAVSO), the NASA’s Transiting Exoplanet Survey Satellite (TESS) and the UK’s Wide Angle Search for Planets (SuperWASP)). In the first observation, the two similar light minimum times in R- and V-bands are averaged. Thus, the two CCD light minimum times in Heliocentric Julian Day (HJD) are listed in Table A2 of Appendix A.
2.2. Data from AAVSO
AAVSO is famous for its abundant information and data on variable stars. The data from the AAVSO International Database (AID) are well-calibrated and accurate (the original data format can be found on the webpage: https://www.aavso.org/aavso-international-database-aid, accessed on 20 October 2021).
At present, a total of 36,916 observations for RW Tri have been recorded in AID. From this database, we extracted 130 available orbital light curves in different optical bands covering one primary minimum at least, of which 21 were observed within the different orbital phase ranges on the same night by the different observers. All of them have an average of ∼13 mag at the outside part of eclipse. Compared with the other databases and the published data, the similar out-of-eclipse magnitude of the AAVSO light curve indicates that RW Tri always maintains a steady-state accretion disk during the AAVSO observations. A total of 107 new and available light minimum times were obtained, of which 10 are the averages observed by the different observer, including 2 approaching the times obtained by Subebekova et al. [14].
2.3. Data from TESS
The archived data of TESS are primarily designed to search transiting exoplanets from an all-sky survey using a set of four wide-field cameras (four CCDs in each camera), covering a field of 24 96 of the sky [21]. Although the CCDs produce a continuous stream of images with an exposure time of 2 s, the final data products of TESS provided a cadence observation with an effective exposure time of 2 min similar to the long- and short-cadence data collected by Kepler (documentation of TESS can be found on the webpage: https://archive.stsci.edu/missions-and-data/tess, accessed on 20 October 2021). In 2019 November, the TESS carried out a continuous observations for RW Tri lasting ∼25 days. Considering that our O-C analysis only focuses on the variations in eclipsing time rather than the system light, Simple Aperture photometry (SAP) flux light curves (one of the two types of the TESS data) was used to derive the light minimum times listed in Table A2 of Appendix A. To estimate the luminosity state of RW Tri observed by TESS, SAP flux was roughly transformed to the magnitude (TESS Instrument Handbook told that the TESS cameras create 15,000 e/s for a 10 mag star). The averaged out-of-eclipse magnitude is basically consistent with the AAVSO data. This indicates the almost same luminosity state of RW Tri during the TESS observations. Thus, all 96 new light minimum times were combined with the other datasets to carry out the following O-C analysis (the timestamps of the TESS light curve is in Dynamical Time(TDB); to match with the historical light minimum times, the light minimum times were transformed to HJD).
2.4. Data from SuperWASP
With the purpose of searching transiting exo-planets, the SuperWASP project was established by a consortium of eight academic institutions in 2000 [22] (the details of this project can be found on the homepage: https://www.superwasp.org/, accessed on 20 October 2021). Since 2004 and 2006, SuperWASP conducted wide-field time photometry observations in the northern and southern hemisphere, respectively [19,23]. Like TESS, the SuperWASP data can also be used for the study of variable stars [24]. For RW Tri, SuperWASP obtained 137 light curves with the non-uniformity time resolutions (i.e., the interval time of two continuous data points is different in the different light curves) lasting over 4 years, of which 67 cover the light minimum. However, the four low-time-resolution light curves (the interval time is larger than 5 min) were removed from our O-C analysis. Hence, there are 63 new and available light minimum times added to our O-C diagram. Compared with the other datasets, all light minimum times in HJD are identified to be new data. Like the AAVSO and TESS data, the averaged out-of-eclipse magnitude is also close to 13 mag.
2.5. Cross-Identification of Data from the Literature
Since the previous O-C analyses (e.g., [14,20]) never carried out a detailed verification for all datapoints, but only made the collections for the historical light minimum times available in the literature, a possibility that the data points with the large deviations (many were clearly seen in the historical O-C diagrams) resulted from the incorrect light minimum times, cannot be ruled out. A cross-identification for all the light minimum times from the literature found that some with the small differences are caused by the different observatories and filters, while some listed in O-C gateway [25] are different from the data published in the literature. The averages and primary data were preferred in these two cases, respectively. Finally, 28 revised light minimum times are listed in Table A2 of Appendix A. They are helpful for clarifying the authentic variations in eclipsing times. Considering that most of the precisions of CCD light minimum times are 4 significant digits, we inferred that the previous photoelectric/CCD eclipsing times lack of the errors also have similar precisions (i.e., 0.0001).
3. Orbital Period Changes
3.1. New Ephemeris
Mandel [26], Africano et al. [1], and Subebekova et al. [14] regarded that a sine fit with a period of 6–19 years plotting in their O-C diagrams is formally significant, but the following O-C analysis including the low-precision data [19] only showed a secular decrease without an appropriate explanation. The recent two O-C analyses [14,20] again indicated that the eclipsing times of RW Tri should contain a cyclical change with a longer period of ∼40 years than before. Therefore, a new O-C analysis by adding our new data is expected to further verify this controversial periodical variation in eclipsing times.
Since the photographic and visual data published in many BBSAG Bulls with the large scatter almost completely occult the possible changes of O-Cs [19], all these low-precision data are excluded our O-C analysis, but shown in the O-C diagram together with the high-precision data for demonstrating the goodness of fit. The ephemeris of Robinson et al. [18] was published ∼30 years ago. Therefore, an updated ephemeris is required for the calculation of the new O-Cs (658 data points shown in Figure 1 are comprise of 200 low-precision data and 458 high-precision data). A significant decrease is shown in the upper panel of Figure 1. Using a linear fitting to the high-precision O-Cs, a revised ephemeris with the new epoch and orbital period was derived as
with a variance of 1.7 × 10. The linear fitting coefficients are listed in Table 2. The difference in epoch between the new and old ephemeris is ∼2 min. However, the precisions of the new epoch and orbital period have been improved by over an order of magnitude. In the lower panel of Figure 1, the residuals of this linear fitting (i.e., O-C) show a complicated variation, and the low-precision O-Cs with the greater scatter are consistent with the variations in high-precision O-Cs.
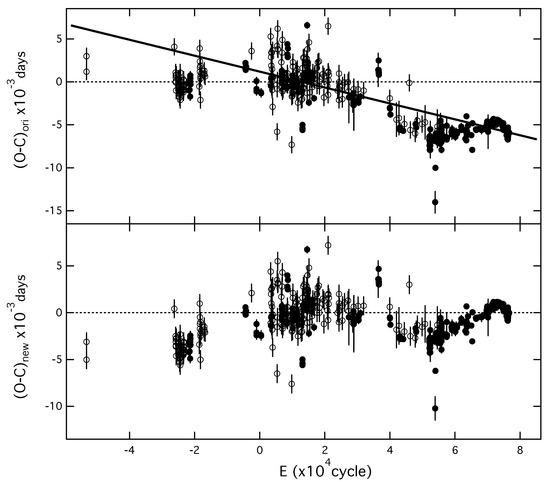
Figure 1.
Upper panel: (O-C) are calculated from the ephemeris derived by Robinson et al. [18]. The solid line refers to the best-fit linear curve. The open and solid circles denote the low- and high-precision O-Cs, respectively. Lower panel: (O-C) are the residuals of the linear fitting.

Table 2.
The best least-squares fitting parameters for the high-precision O-Cs of RW Tri.
3.2. O-C Analysis
Since the variations in O-C obviously cannot be simply described by a quadratic or sine curve like those in the previous O-C diagrams (e.g., [1,11,14,19,20,26]), 7 nonlinear fitting formulae—constant-plus-sinusoidal, linear-plus-sinusoidal, quadratic-plus-sinusoidal, linear-plus-dual-sinusoidal, quadratic-plus-dual-sinusoidal, linear-plus-light travel time effect (LITE), and quadratic-plus-LITE—were attempted to describe the O-C. The fitting formula of LITE was described by Irwin [27],
where , e, , , M, EE, , , and t are semi-amplitude, eccentricity, longitude of periastron, true anomaly, mean anomaly, eccentric anomaly, time of periastron passage, orbital period of the third body, and light minimum times, respectively. To carry out the non-linear least-squares fittings, we used our routine, OCFIT, combining a Levenberg–Marquadt algorithm with an improved Nelder–Mead simplex method [28], which was successfully applied to the non-linear fittings for the complicate O-C variations of the polar AM Her [29].
Using the parameter , F-test proposed by Pringle [30] confirms their high confidence levels (all seven non-linear fittings have the significant level of 100%). The best convergent solutions are listed in Table 2, and the corresponding best-fit curves and residuals are shown in Figure 2. The new data (E > 52,000 cycles) obtained from our photometry, AAVSO, TESS, and SuperWASP prominently determine the best-fit curves of the O-C diagram due to their highest precisions. Hence, the residuals of the low-precision data located at the range of E = 0–52,000 cycles becomes a good indicator to specify the deviations from the best-fit curves. Using the fitting parameter as a judgment of the best fit, the linear- and quadratic-plus-dual-sinusoidal fittings with the minimal of ∼33 seem to be the best fits for the high-precision O-Cs. However, the residuals of low-precision O-Cs in these two fittings demonstrate the conspicuous variations. Compared with these fittings, the quadratic-plus-sinusoidal fitting residuals shown in Figure 2 are flat, indicating a probably better description for both high- and low-precision data than the others. Considering that the corresponding 41 is approaching the minimal of ∼33, we preferred that the best-fit for O-C be a quadratic-plus-sinusoidal curve, based on the current data quality of O-Cs. This is because, although more complicate formulae with a large number of fitting parameters can give the better in mathematics, a simple formula with a general fitting trend may be enough to describe a logical and physical process. Like the O-C diagrams of the post-nova T Aur [31] and the long-period dwarf nova (DN) EM Cyg [32], the orbital period of RW Tri experiences a cyclical variation with a period of 22.66(2) years and a semi-amplitude of 199.721(2) s, superimposed on a secular quadratic decrease with a period decrease rate of = .32(4) × 10 yr, slightly smaller than that of Polsgrove et al. [19]. This newly derived cyclical period is about one half of the periods recently derived by Boyd [20] and Subebekova et al. [14], but far larger than the periods previously derived by Mandel [26], Africano et al. [1], and Still et al. [11]. In considering the large scatter in the data range of E = 0–3 × 10 cycles, the high-precision photometry in the longer base line is needed to provide other more convincing evidence on measurement of the estimated period decrease rate and cyclical variations.
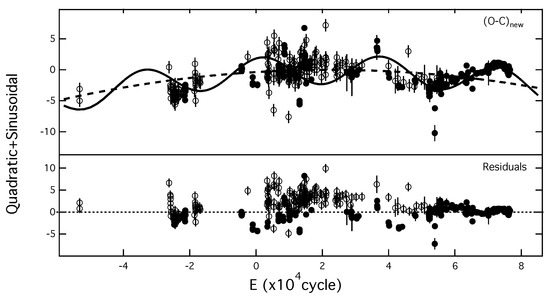
Figure 2.
The quadratic-plus-sinusoidal fitting curves denoted by the solid lines, including their corresponding fitting residuals, are shown from top to bottom. The dash lines refer to the quadratic fitting curve. The symbols of the data points and the y-axes are the same as those used in Figure 1.
4. Discussion
4.1. Secular Orbital Period Decrease
The standard theory of CV evolution (e.g., [33,34]) indicates that the CVs above the period gap are expected to decrease their orbital period due to the angular momentum loss. Although the O-C diagrams of dwarf nova (DN) U Gem [35] and intermediate polar (IP) DQ Her [36] show the secular orbital period increases, conflicting with the prediction of the standard theory of CV evolution, the new observations may revise the increase trends of their O-C diagrams to some extent. Polsgrove et al. [19] first detected the orbital period decrease of RW Tri. However, they simply attributed this decrease to a decreasing branch of a sine curve, rather than a secular evolution of orbital period. Thus, a detailed and complete investigation for the orbital period decrease of RW Tri is expected.
According to the CV model [37,38], the mass transfer from the red dwarf to the white dwarf causes the orbital shrinking or expansion depending on the mass ratio of binary system. However, the mass ratios of RW Tri derived from the spectroscopic data [5,12,17,39]) is obviously inconsistent with that from the photometric data [9,10]. Therefore, it is necessary to discuss two cases of mass ratio: MM (i.e., q < 1), and MM (i.e., q > 1).
4.1.1. Case1: q < 1
Although Still et al. [11] never obtained the accurate system parameters of RW Tri from the radial velocity measurement of the white dwarf due to the spectral contamination from accretion flow, hot spot, and the red dwarf, Subebekova et al. [14] derived a complete set of system parameters by modeling the eclipsing light curves. Taking advantage of these updated physical parameters, conservation of mass transfer from the red dwarf (M = 0.42 M) to the massive white dwarf (M = 0.7 M) with a rate of 4.3 × 10 M yr can only result in the orbital period increase rather than decrease. Thus, an efficient mechanism for dissipating angular momentum in RW Tri is required to interpret the observed orbital period decrease, = .32(4) × 10 yr, which corresponds to an angular momentum loss rate of = −2.28(4) × 10 dyn cm.
Three possible explanations that involve gravitational radiation, magnetic braking, and systematic mass loss are proposed for solving this apparent paradox. Since the orbital period of RW Tri is ∼5.6 h above the CV period gap, the effect of gravitational radiation can be neglected. Since RW Tri is a non-outburst-type CV, there is no evidence supporting systematic mass loss in this steady system. In accordance with the standard theory of CV evolution [33,34], magnetic braking is a most likely explanation.
We calculated two magnetic braking models, denoted as MB1 and MB2 proposed by Rappaport et al. [40] and Tout and Hall [41], respectively. MB1 with index parameter = 3 and MB2 produce two similar angular momentum loss rates: 10 dyn cm and 10 dyn cm, respectively. Both have the same order of magnitude as . The mass transfer rate, , estimated from MB1 is 2.4 × 10 M yr, while that from MB2 is 4.3 × 10M yr. The latter is almost the same as that derived by Subebekova et al. [14]. Inspection of Figure 3 indicates that MB2 is a better explanation for the secular orbital period decrease of RW Tri, since the derived mass transfer rate aligns with the predictions of the standard/revised models of CV evolution [42]. This is similar to the mass transfer rates of T Aur and EM Cyg derived from their O-C diagrams [31,32]. In Figure 3, a group of CVs near RW Tri with orbital periods in a range of 5–6 h, as listed in Table 3, clearly demonstrate that the mass transfer rates of NL and IP are higher than that of DN. Except for the two DN, CZ Ori and HL CMa, the mass transfer rates of many other U Gem-type DN appear to be overestimated; oppositely, those of NL and IP are underestimated by the standard/revised models. Considering that many U Gem-type DN with orbital periods in the range of 3–5 h have lower mass transfer rates than those predicted by the standard/revised models at the same orbital periods [43], we suspected that the overestimations of the mass transfer rates may be common for the U Gem-type DN.
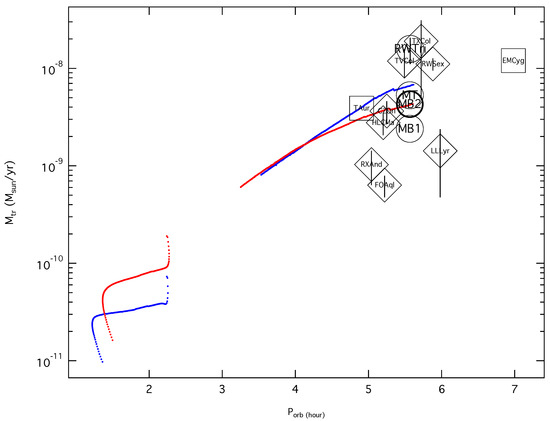
Figure 3.
Mass transfer rates as a function of the orbital period. The red and blue lines refer to the mass transfer rates derived by the standard and revised models [42], respectively. The CV names represent the CVs with the orbital periods similar to that of RW Tri listed in Table 3. The texts of MT, MB1, and MB2 inside the open circles represent , and of RW Tri calculated in this paper, respectively. The mass transfer rates denoted by the diamonds are listed in Table A.2 in Dubus et al. [44], while those denoted by the rectangles are derived from their corresponding O-C diagrams.

Table 3.
Mass transfer rates of the CVs with the orbital periods similar to that of RW Tri.
Smak [45] proved that accretion in RW Tri is stable. The eclipse map [8] further indicated that RW Tri is a typically NL lack of outburst. This means that the mass transfer rate must be high enough to maintain a high-state accretion disk. A critical mass transfer rate specified in the disk instability model (DI; [15,46]) can be estimated using an empirical formula [47],
where P and M are the orbital period in unit of hour and the white dwarf mass in unit of solar mass, respectively. For RW Tri, (0.7 M, 5.565 h) ∼ 7.4 × 10 M yr, slightly larger than the mass transfer rates calculated from the two magnetic braking models.
4.1.2. Case: q
Smak [10] presents another possibility that the mass ratio larger than unity (i.e., q ≈ 1.4) can directly interpret the observed orbital period decrease. Supposing that the mass and angular moment are conserved, we attempted to estimate the mass transfer rate, denoted as MT, using the formula
Considering the combined masses of 0.45 M + 0.63 M for the eclipsing pair of RW Tri [10], the mass transfer rate can be derived as = 5.3 × 10 Myr, which is similar to those derived from the two magnetic braking models, and much closer to the revised model of CV evolution shown in Figure 3.
In accordance with the reconstructions of disk map [8,17,39], the analysis of the eclipsing light curves [10] and spectrophotometric study [5], the predicted range of the mass transfer rate is from 10 Myr to 10 Myr. Compared with the mass transfer rate of RW Tri listed in Dubus et al. [44], which is obviously beyond this range, our derived mass transfer rate is consistent with MB2 and the theoretical prediction derived by the standard/revised models [42], while being far lower than the other NL.
Based on the effective temperature of the red dwarf [14], the Kelvin–Helmholtz timescale of the red dwarf is 2.0 × 10 years, larger than the mass loss timescales of the red dwarf (using M/, the three derived mass transfer rates: 2.4 × 10 Myr, 4.3 × 10 Myr and 5.3 × 10 Myr correspond to 1.8 × 10 years, 9.8 × 10 years and 7.9 × 10 years, respectively). This means that the mass transfer rate of RW Tri may be enhanced, since the Roche-lobe filling red dwarf deviating from thermal equilibrium is expanded due to the donor mass loss.
4.2. Cyclical Variation
A strong solar-type magnetic activity cycle in the K5-M0 type secondary star of RW Tri may explain the prominent cyclical variation with a semi-amplitude of 199.721(2) s, shown in the O-C diagram (Figure 2). The variation of the quadrupole momentum ∆Q for the secondary star of RW Tri is calculated to be ∼−2.15(1) × 10 g cm, corresponding to a minimum energy of 1.1 × 10 erg required to drive the observed period oscillation. However, this energy is almost comparable to the total radiation energy of an K5-M0 type red dwarf during a period of 22.6 years. Thus, the red dwarf of RW Tri cannot afford sufficient energy to force the periodic modulation shown in the O-C diagram.
Considering that the light minimum times are the eclipsing times of white dwarf (or the central part of the disk), the cyclical modulation in the O-C diagram can be attributed to an orbital perturbation from a tertiary component hidden in the RW Tri system (i.e., LITE), like several other CVs (e.g., [29,48,49,50]). Although the quadratic-plus-sinusoidal curve with a period of 22.66(2) years is the best fit for the O-C diagram, the optimized parameters of the sine-like modulation listed in Table 2 for the other six nonlinear fittings also present the similar periods within a narrow range of 21–24 years. Note that the period of the quadratic-plus-sinusoidal formula is close to the mean value of this range. A set of quadratic-plus-sinusoidal fitting coefficients was used to estimate the projected distance from the binary to mass center of this triple system, A 0.401(2) AU, and the mass function of the third component, f(M)∼ 1.25(2) × 10 M. A newly combined mass of 0.7 M + 0.42 M [14] is used to calculate two relationships of M vs. i and A vs. i. Both relationships shown in Figure 4 clearly indicate that this third component in RW Tri may be a brown dwarf with a mass of M 0.057 M located at an orbit of A 8 AU (over ten times of the binary separation) away from the binary, as all of them are in coplanar orbit. In addition, this third component can be a red dwarf as long as the orbital inclination of the third component, i lower than 51.
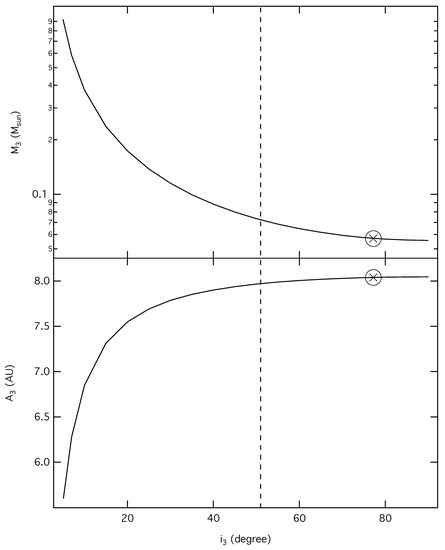
Figure 4.
Masses and separations of the third component in RW Tri depending on the different orbital inclination are plotted in the upper and lower panels, respectively. The cross denotes the mass and separation of a brown dwarf hidden in a coplanar orbit of RW Tri.
5. Conclusions
From the archived data of AAVSO, TESS, and SuperWASP, 107, 96, and 63 new light minimum times were derived, respectively. A cross-identification for all of the light minimum times collected in the literature corrects 28 light minimum times. Combining with two light minimum times observed from our photometry, a total of 658 light minimum times including 297 new data covering over 80 years are compiled, and an updated O-C diagram of RW Tri is obtained. The 658 light minimum times are composed of 200 low- and 458 high-precision data points.
Using our combined routine, we carried out a linear and seven nonlinear least-squares fittings for the 458 high-precision O-Cs. The linear fitting improved the precisions of the epoch and orbital period of RW Tri listed in the old ephemeris [18] over an order of magnitude, while the seven nonlinear fittings for the residuals of this linear fitting demonstrated that the best fit is a quadratic-plus-sinusoidal curve with a period of 22.66(2) years and a decrease rate of = .32(4) × 10 yr similar to that of Polsgrove et al. [19].
The detailed investigations on the magnetic braking effect in RW Tri indicate a high consistence of the mass transfer rate obtained from our O-C analysis and the light-curve modeling [14]. This consistence not only verifies the secular decrease shown in our O-C diagram, but also confirms some of the controversial system parameters of RW Tri. The slightly enhanced mass transfer rate, comparable with the empirical , seems to be a weak evidence that the accretion disk of RW Tri basically satisfies the predictions of the DI model [15]. The red dwarf of RW Tri cannot supply enough energy to drive the observed periodical changes shown in the O-C diagram, while a brown dwarf with a mass of ∼0.057 M, hidden in a coplanar orbit, ∼8 AU away from the central binary, perfectly gives rise to an orbital perturbation within a period range of 21–24 years demonstrated by all seven nonlinear fittings.
Author Contributions
Conceptualization, Z.D. and S.Q.; methodology, Z.D. and S.Q.; software, Z.D.; validation, Z.D., S.Q. and I.M.; formal analysis, Z.D.; investigation, Z.D.; resources, Z.D. and S.Q.; data curation, Z.D., S.Q. and I.M.; writing—original draft preparation, Z.D.; writing—review and editing, Z.D., S.Q. and I.M.; visualization, Z.D., S.Q. and I.M.; supervision, Z.D.; project administration, Z.D.; funding acquisition, Z.D. and S.Q. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partly funded by Yunnan Natural Science Foundation (No. 2016FB007) and Chinese Natural Science Foundation (No.11933008).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Three survey datasets from AAVSO (https://www.aavso.org/aavso-international-database-aid, accessed on 22 October 2021), TESS (https://archive.stsci.edu/missions-and-data/tess, accessed on 22 October 2021), SuperWASP (https://www.superwasp.org/, accessed on 22 October 2021), and one archived dataset of the O-C gateway (http://var2.astro.cz/ocgate, accessed on 22 October 2021) provided parts of original and historical data supporting our results.
Acknowledgments
This work is partly supported by Yunnan Natural Science Foundation (No. 2016FB007)) and Chinese Natural Science Foundation (No.11933008). CCD photometric observations of RW Tri were obtained with the 1.0 m telescope at Yunnan Observatories, Chinese Academy of Sciences. We acknowledge with thanks the variable star observations from the AAVSO International Database, contributed by observers worldwide. The TESS data presented in this paper were obtained from the Mikulski Archive for Space Telescopes (MAST) at the Space Telescope Science Institute (STScI). STScI is operated by the Association of Universities for Research in Astronomy, Inc. Support to MAST for these data is provided by the NASA Office of Space Science. Funding for the TESS mission is provided by the NASA Explorer Program. We thank the anonymous referee for valuable comments and suggestions, which have improved the manuscript greatly. This paper makes use of data from the DR1 of the WASP data as provided by the WASP consortium, and the computing and storage facilities at the CERIT Scientific Cloud, reg. no. CZ.1.05/3.2.00/08.0144, which is operated by Masaryk University, Czech Republic.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Table A1 lists the photometry data plotted on Figure A1, obtained by using the 1.0 m reflecting telescope located at Yunnan Observatories in China. Table A2 lists a total of 297 new mid-eclipsing times and their corresponding O-C values plotted on the upper panel of Figure 1.
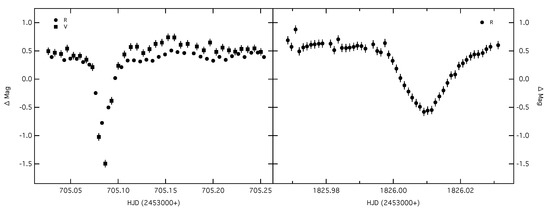
Figure A1.
Three differential light curves of RW Tri in R and V bands. The error bars indicate the standard deviation (STD) of the magnitude difference between the comparison and check stars.

Table A1.
The ground-based photometry data of RW Tri.
Table A1.
The ground-based photometry data of RW Tri.
| 30 November 2005 | 25 December 2008 | ||||||
|---|---|---|---|---|---|---|---|
| R Band | V Band | R Band | |||||
| HJD | Mag | HJD | Mag | HJD | Mag | HJD | Mag |
| 24530000+ | 24530000+ | 24530000+ | 24530000+ | ||||
| 705.0300 | 0.391 | 705.0265 | 0.495 | 1825.9686 | 0.689 | 1825.9697 | 0.572 |
| 705.0432 | 0.338 | 705.0333 | 0.468 | 1825.9709 | 0.880 | 1825.9720 | 0.491 |
| 705.0497 | 0.364 | 705.0399 | 0.447 | 1825.9732 | 0.562 | 1825.9743 | 0.581 |
| 705.0564 | 0.360 | 705.0464 | 0.541 | 1825.9755 | 0.608 | 1825.9766 | 0.617 |
| 705.0631 | 0.303 | 705.0530 | 0.415 | 1825.9778 | 0.626 | 1825.9789 | 0.632 |
| 705.0697 | 0.257 | 705.0598 | 0.411 | 1825.9813 | 0.628 | 1825.9824 | 0.514 |
| 705.0763 | −0.246 | 705.0665 | 0.346 | 1825.9836 | 0.706 | 1825.9847 | 0.553 |
| 705.0830 | −0.775 | 705.0730 | 0.213 | 1825.9859 | 0.552 | 1825.9870 | 0.558 |
| 705.0898 | −0.502 | 705.0796 | −1.022 | 1825.9882 | 0.571 | 1825.9893 | 0.591 |
| 705.0969 | 0.020 | 705.0865 | −1.496 | 1825.9905 | 0.585 | 1825.9917 | 0.540 |
| 705.1035 | 0.213 | 705.0931 | −0.384 | 1825.9940 | 0.616 | 1825.9952 | 0.499 |
| 705.1100 | 0.330 | 705.1001 | 0.238 | 1825.9963 | 0.475 | 1825.9975 | 0.639 |
| 705.1166 | 0.334 | 705.1066 | 0.437 | 1825.9986 | 0.435 | 1825.9998 | 0.325 |
| 705.1232 | 0.312 | 705.1132 | 0.570 | 1826.0009 | 0.186 | 1826.0021 | 0.020 |
| 705.1297 | 0.345 | 705.1198 | 0.575 | 1826.0033 | −0.110 | 1826.0045 | −0.219 |
| 705.1363 | 0.325 | 705.1264 | 0.462 | 1826.0056 | −0.328 | 1826.0068 | −0.424 |
| 705.1428 | 0.394 | 705.1330 | 0.534 | 1826.0079 | −0.489 | 1826.0091 | −0.579 |
| 705.1494 | 0.437 | 705.1395 | 0.624 | 1826.0102 | −0.557 | 1826.0114 | −0.547 |
| 705.1560 | 0.507 | 705.1461 | 0.647 | 1826.0125 | −0.411 | 1826.0137 | −0.305 |
| 705.1625 | 0.479 | 705.1526 | 0.741 | 1826.0149 | −0.200 | 1826.0161 | −0.066 |
| 705.1696 | 0.463 | 705.1592 | 0.739 | 1826.0172 | 0.067 | 1826.0184 | 0.083 |
| 705.1796 | 0.457 | 705.1658 | 0.610 | 1826.0195 | 0.235 | 1826.0207 | 0.280 |
| 705.1868 | 0.398 | 705.1732 | 0.625 | 1826.0218 | 0.341 | 1826.0230 | 0.404 |
| 705.1935 | 0.360 | 705.1829 | 0.578 | 1826.0241 | 0.438 | 1826.0253 | 0.441 |
| 705.2001 | 0.327 | 705.1902 | 0.510 | 1826.0266 | 0.463 | 1826.0277 | 0.532 |
| 705.2067 | 0.394 | 705.1968 | 0.648 | 1826.0289 | 0.574 | 1826.0312 | 0.602 |
| 705.2133 | 0.341 | 705.2034 | 0.483 | ||||
| 705.2199 | 0.407 | 705.2100 | 0.559 | ||||
| 705.2266 | 0.447 | 705.2167 | 0.511 | ||||
| 705.2331 | 0.392 | 705.2232 | 0.488 | ||||
| 705.2402 | 0.468 | 705.2298 | 0.535 | ||||
| 705.2470 | 0.471 | 705.2365 | 0.528 | ||||
| 705.2536 | 0.391 | 705.2435 | 0.544 | ||||
| 705.2503 | 0.484 | ||||||

Table A2.
New light minimum times of RW Tri.
Table A2.
New light minimum times of RW Tri.
| JD.Hel. | Error | Type | E | O-C | Ref. | JD.Hel. | Error | Type | E | O-C | Ref. |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2400000+ | Days | Cycles | Days | 2400000+ | Days | Cycles | Days | ||||
| 43780.94990 | 0.0004 | pe | 11435 | −0.00047 | (1,2) | 44170.04510 | - | pe | 13113 | −0.00544 | (3) |
| 44171.90000 | - | pe | 13121 | −0.00561 | (3) | 44173.06000 | - | pe | 13126 | −0.00503 | (3) |
| 44491.4410 | - | vis | 14499 | +0.00021 | (4) | 44497.4715 | - | vis | 14525 | +0.00174 | (4) |
| 44499.5585 | - | vis | 14534 | +0.00179 | (4) | 45341.2955 | - | vis | 18164 | +0.00242 | (4) |
| 47792.52930 | - | ccd | 28735 | −0.00211 | (5) | 47793.68950 | - | ccd | 28740 | −0.00133 | (5) |
| 47794.61610 | - | ccd | 28744 | −0.00226 | (5) | 47795.54440 | - | ccd | 28748 | −0.00149 | (5) |
| 47801.57360 | - | ccd | 28774 | −0.00126 | (5) | 47802.50020 | - | ccd | 28778 | −0.00219 | (5) |
| 49598.90483 | - | pe | 36525 | +0.00254 | (6) | 49599.83122 | - | pe | 36529 | +0.00139 | (6) |
| 49600.99038 | - | pe | 36534 | +0.00114 | (6) | 49602.84540 | - | pe | 36542 | +0.00109 | (6) |
| 49604.00488 | - | pe | 36547 | +0.00115 | (6) | 49604.93229 | - | pe | 36551 | +0.00103 | (6) |
| 49605.85991 | - | pe | 36555 | +0.00112 | (6) | 49607.94677 | - | pe | 36564 | +0.00103 | (6) |
| 49608.87435 | - | pe | 36568 | +0.00108 | (6) | 49610.96118 | - | pe | 36577 | +0.00096 | (6) |
| 49611.88859 | - | pe | 36581 | +0.00083 | (6) | 50391.4764 | 0.0002 | ccd | 39943 | −0.00300 | (7) |
| 50403.5342 | 0.0004 | ccd | 39995 | −0.00313 | (7) | 50437.3885 | 0.0003 | ccd | 40141 | −0.00380 | (7) |
| 51119.3558 | 0.0006 | ccd | 43082 | −0.00527 | (7) | 51124.4569 | 0.0003 | ccd | 43104 | −0.00560 | (7) |
| 51353.09375 | - | ccd | 44090 | −0.00568 | (4,8) | 53201.6667 | 0.0008 | ccd | 52062 | −0.00638 | (9) |
| 53204.6809 | 0.0002 | ccd | 52075 | −0.00666 | (9) | 53207.6955 | 0.0002 | ccd | 52088 | −0.00654 | (9) |
| 53217.6662 | 0.0003 | ccd | 52131 | −0.00683 | (9) | 53220.6801 | 0.0004 | ccd | 52144 | −0.00741 | (9) |
| 53229.7243 | 0.0001 | ccd | 52183 | −0.00666 | (9) | 53230.6521 | 0.0002 | ccd | 52187 | −0.00639 | (9) |
| 53236.6806 | 0.0003 | ccd | 52213 | −0.00686 | (9) | 53237.6075 | 0.0006 | ccd | 52217 | −0.00749 | (9) |
| 53239.6952 | 0.0003 | ccd | 52226 | −0.00674 | (9) | 53240.6216 | 0.0004 | ccd | 52230 | −0.00787 | (9) |
| 53242.7095 | 0.0004 | ccd | 52239 | −0.00692 | (9) | 53243.6370 | 0.0003 | ccd | 52243 | −0.00696 | (9) |
| 53245.7237 | 0.0003 | ccd | 52252 | −0.00720 | (9) | 53246.6518 | 0.0003 | ccd | 52256 | −0.00664 | (9) |
| 53247.5789 | 0.0005 | ccd | 52260 | −0.00707 | (9) | 53248.7389 | 0.0006 | ccd | 52265 | −0.00649 | (9) |
| 53249.6665 | 0.0005 | ccd | 52269 | −0.00642 | (9) | 53250.5942 | 0.0003 | ccd | 52273 | −0.00625 | (9) |
| 53254.5353 | 0.0005 | ccd | 52290 | −0.00717 | (9) | 53256.6231 | 0.0008 | ccd | 52299 | −0.00632 | (9) |
| 53258.7090 | 0.0006 | ccd | 52308 | −0.00737 | (9) | 53259.6374 | 0.0009 | ccd | 52312 | −0.00650 | (9) |
| 53260.5644 | 0.0006 | ccd | 52316 | −0.00704 | (9) | 53261.7240 | 0.001 | ccd | 52321 | −0.00685 | (9) |
| 53266.5933 | 0.0007 | ccd | 52342 | −0.00710 | (9) | 53275.6360 | 0.001 | ccd | 52381 | −0.00785 | (9) |
| 53276.5659 | 0.0001 | ccd | 52385 | −0.00548 | (9) | 53277.4915 | 0.0004 | ccd | 52389 | −0.00742 | (9) |
| 53672.62145 | 0.00006 | ccd | 54093 | −0.00660 | (7) | 53705.08523 | 0.00086 | ccd | 54233 | −0.00649 | (10) |
| 53770.7090 | 0.001 | vis | 54516 | −0.00569 | (7) | 53773.7240 | 0.002 | vis | 54529 | −0.00517 | (7) |
| 53777.6660 | 0.001 | vis | 54546 | −0.00519 | (7) | 53778.5920 | 0.001 | vis | 54550 | −0.00672 | (7) |
| 53979.63600 | 0.0008 | ccd | 55417 | −0.00554 | (9) | 53995.63600 | 0.001 | ccd | 55486 | −0.00549 | (9) |
| 53997.72380 | 0.0009 | ccd | 55495 | −0.00464 | (9) | 53998.65140 | 0.001 | ccd | 55499 | −0.00457 | (9) |
| 54001.66410 | 0.0004 | ccd | 55512 | −0.00635 | (9) | 54003.51970 | 0.0006 | ccd | 55520 | −0.00582 | (9) |
| 54007.69330 | 0.0003 | ccd | 55538 | −0.00612 | (9) | 54008.62100 | 0.0004 | ccd | 55542 | −0.00595 | (9) |
| 54011.63690 | 0.0006 | ccd | 55555 | −0.00453 | (9) | 54023.69300 | 0.001 | ccd | 55607 | −0.00637 | (9) |
| 54030.64950 | 0.0002 | ccd | 55637 | −0.00637 | (9) | 54031.57680 | 0.0007 | ccd | 55641 | −0.00660 | (9) |
| 54032.50390 | 0.0008 | ccd | 55645 | −0.00703 | (9) | 54050.59170 | 0.0004 | ccd | 55723 | −0.00613 | (9) |
| 54056.38910 | 0.0009 | ccd | 55748 | −0.00581 | (9) | 54057.54880 | 0.001 | ccd | 55753 | −0.00553 | (9) |
| 54066.35950 | 0.0005 | ccd | 55791 | −0.00639 | (9) | 54066.59270 | 0.0008 | ccd | 55792 | −0.00508 | (9) |
| 54067.52010 | 0.0005 | ccd | 55796 | −0.00521 | (9) | 54068.44580 | 0.0005 | ccd | 55800 | −0.00704 | (9) |
| 54069.37500 | 0.001 | ccd | 55804 | −0.00538 | (9) | 54069.60560 | 0.0009 | ccd | 55805 | −0.00666 | (9) |
| 54070.53380 | 0.0005 | ccd | 55809 | −0.00599 | (9) | 54075.40140 | 0.0004 | ccd | 55830 | −0.00794 | (9) |
| 54076.33140 | 0.0005 | ccd | 55834 | −0.00547 | (9) | 54076.56280 | 0.0004 | ccd | 55835 | −0.00596 | (9) |
| 54077.48990 | 0.0005 | ccd | 55839 | −0.00639 | (9) | 54083.51970 | 0.0003 | ccd | 55865 | −0.00556 | (9) |
| 54084.44660 | 0.0002 | ccd | 55869 | −0.00619 | (9) | 54085.37420 | 0.0005 | ccd | 55873 | −0.00612 | (9) |
| 54092.33080 | 0.0002 | ccd | 55903 | −0.00602 | (9) | 54093.48990 | 0.0003 | ccd | 55908 | −0.00634 | (9) |
| 54095.34490 | 0.0003 | ccd | 55916 | −0.00641 | (9) | 54103.46100 | 0.0002 | ccd | 55951 | −0.00622 | (9) |
| 54826.00982 | 0.0001 | ccd | 59067 | −0.0058 | (10) | 55768.846500 | 0.00020 | ccd | 63133 | −0.00656 | (7) |
| 55780.905400 | 0.00010 | ccd | 63185 | −0.00559 | (7) | 56206.410600 | 0.00010 | ccd | 65020 | −0.00624 | (7) |
| 56265.539200 | 0.00010 | ccd | 65275 | −0.00788 | (7) | 57314.350030 | 0.00007 | ccd | 69798 | −0.00520 | (7) |
| 57315.741510 | 0.00007 | ccd | 69804 | −0.00502 | (7) | 57317.596450 | 0.00009 | ccd | 69812 | −0.00515 | (7) |
| 57319.683350 | 0.00004 | ccd | 69821 | −0.00520 | (7) | 57321.306500 | 0.0001 | ccd | 69828 | −0.00523 | (7) |
| 57321.538400 | 0.0001 | ccd | 69829 | −0.00522 | (7) | 57322.697600 | 0.0001 | ccd | 69834 | −0.00543 | (7) |
| 57324.321500 | 0.0003 | ccd | 69841 | −0.00472 | (7) | 57324.552810 | 0.00007 | ccd | 69842 | −0.00529 | (7) |
| 57326.40801 | 0.00006 | ccd | 69850 | −0.00516 | (7) | 57326.639845 | 0.000055 | ccd | 69851 | −0.00520 | (7) |
| 57327.335425 | 0.000075 | ccd | 69854 | −0.00527 | (7,11) | 57327.567370 | 0.00007 | ccd | 69855 | −0.00521 | (7) |
| 57327.799250 | 0.00008 | ccd | 69856 | −0.00522 | (7) | 57328.263020 | 0.00006 | ccd | 69858 | −0.00521 | (7) |
| 57328.726700 | 0.0001 | ccd | 69860 | −0.00530 | (7) | 57329.422420 | 0.00006 | ccd | 69863 | −0.00523 | (7) |
| 57329.654330 | 0.00006 | ccd | 69864 | −0.00520 | (7) | 57329.654770 | 0.00005 | ccd | 69864 | −0.00476 | (7) |
| 57329.886680 | 0.00005 | ccd | 69865 | −0.00473 | (7) | 57330.582430 | 0.00003 | ccd | 69868 | −0.00463 | (7) |
| 57330.813785 | 0.000075 | ccd | 69869 | −0.00516 | (7) | 57331.277610 | 0.00006 | ccd | 69871 | −0.00510 | (7) |
| 57331.509520 | 0.00005 | ccd | 69872 | −0.00508 | (7) | 57331.741260 | 0.0001 | ccd | 69873 | −0.00522 | (7) |
| 57332.6688945 | 0.00009 | ccd | 69877 | −0.00512 | (7) | 57332.900810 | 0.00008 | ccd | 69878 | −0.00509 | (7) |
| 57333.364730 | 0.00009 | ccd | 69880 | −0.00493 | (7) | 57334.292090 | 0.00005 | ccd | 69884 | −0.00511 | (7) |
| 57334.523950 | 0.00006 | ccd | 69885 | −0.00513 | (7) | 57334.75609 | 0.00005 | ccd | 69886 | −0.00487 | (7) |
| 57335.451510 | 0.00006 | ccd | 69889 | −0.00510 | (7) | 57335.683300 | 0.0001 | ccd | 69890 | −0.00520 | (7) |
| 57335.915180 | 0.00008 | ccd | 69891 | −0.00520 | (7) | 57336.379070 | 0.00004 | ccd | 69893 | −0.00508 | (7) |
| 57336.610820 | 0.000075 | ccd | 69894 | −0.00521 | (7) | 57336.842710 | 0.00008 | ccd | 69895 | −0.00520 | (7) |
| 57337.538410 | 0.00006 | ccd | 69898 | −0.00515 | (7) | 57338.697690 | 0.0001 | ccd | 69903 | −0.00529 | (7) |
| 57339.393480 | 0.00004 | ccd | 69906 | −0.00515 | (7) | 57340.320970 | 0.00004 | ccd | 69910 | −0.00519 | (7) |
| 57342.407900 | 0.00006 | ccd | 69919 | −0.00521 | (7) | 57342.408030 | 0.00005 | ccd | 69919 | −0.00508 | (7) |
| 57343.335500 | 0.00005 | ccd | 69923 | −0.00515 | (7) | 57344.263060 | 0.00006 | ccd | 69927 | −0.00512 | (7) |
| 57345.422440 | 0.00004 | ccd | 69932 | −0.00516 | (7) | 57346.349800 | 0.0002 | ccd | 69936 | −0.00533 | (7) |
| 57361.654400 | 0.0002 | ccd | 70002 | −0.00503 | (7) | 57380.436840 | 0.00004 | ccd | 70083 | −0.00513 | (7) |
| 57383.219200 | 0.00008 | ccd | 70095 | −0.00537 | (7) | 57383.451400 | 0.0002 | ccd | 70096 | −0.00506 | (7) |
| 57384.378965 | 0.000075 | ccd | 70100 | −0.00502 | (7,11) | 57385.306380 | 0.00004 | ccd | 70104 | −0.00514 | (7) |
| 57385.538270 | 0.00006 | ccd | 70105 | −0.00514 | (7) | 57386.465770 | 0.00004 | ccd | 70109 | −0.00517 | (7) |
| 57389.712180 | 0.00008 | ccd | 70123 | −0.00513 | (7) | 57390.639000 | 0.002 | ccd | 70127 | −0.00584 | (7) |
| 57391.799070 | 0.0001 | ccd | 70132 | −0.00519 | (7) | 57397.828200 | 0.00006 | ccd | 70158 | −0.00502 | (7) |
| 57399.683340 | 0.00008 | ccd | 70166 | −0.00495 | (7) | 57399.6841 | 0.0003 | ccd | 70166 | −0.00419 | (7) |
| 57400.379000 | 0.0001 | ccd | 70169 | −0.00494 | (7) | 57400.610840 | 0.00007 | ccd | 70170 | −0.00498 | (7) |
| 57401.538270 | 0.00009 | ccd | 70174 | −0.00508 | (7) | 57401.770020 | 0.00008 | ccd | 70175 | −0.00522 | (7) |
| 57402.697710 | 0.00007 | ccd | 70179 | −0.00506 | (7) | 57403.625230 | 0.0001 | ccd | 70183 | −0.00507 | (7) |
| 57407.567215 | 0.00009 | ccd | 70200 | −0.00510 | (7) | 57408.726680 | 0.00007 | ccd | 70205 | −0.00506 | (7) |
| 57409.654150 | 0.00007 | ccd | 70209 | −0.00512 | (7) | 57410.581950 | 0.00009 | ccd | 70213 | −0.00485 | (7) |
| 57414.291890 | 0.00009 | ccd | 70229 | −0.00505 | (7) | 57414.755660 | 0.00007 | ccd | 70231 | −0.00504 | (7) |
| 57415.683190 | 0.00006 | ccd | 70235 | −0.00504 | (7) | 57416.610670 | 0.00008 | ccd | 70239 | −0.00510 | (7) |
| 57417.770020 | 0.00007 | ccd | 70244 | −0.00516 | (7) | 57419.393140 | 0.00005 | ccd | 70251 | −0.00523 | (7) |
| 57420.320740 | 0.00005 | ccd | 70255 | −0.00516 | (7) | 57421.480140 | 0.00007 | ccd | 70260 | −0.00518 | (7) |
| 57422.407720 | 0.00005 | ccd | 70264 | −0.00513 | (7) | 57423.335450 | 0.00007 | ccd | 70268 | −0.00493 | (7) |
| 57424.494670 | 0.00009 | ccd | 70273 | −0.00513 | (7) | 57424.726400 | 0.00009 | ccd | 70274 | −0.00528 | (7) |
| 57684.899790 | 0.00008 | ccd | 71396 | −0.00495 | (7) | 57685.595760 | 0.00007 | ccd | 71399 | −0.00463 | (7) |
| 57685.827800 | 0.0001 | ccd | 71400 | −0.00448 | (7) | 57686.754820 | 0.00008 | ccd | 71404 | −0.00499 | (7) |
| 58048.725200 | 0.0001 | ccd | 72965 | −0.00444 | (7) | 58428.781200 | 0.0002 | ccd | 74604 | −0.00516 | (7) |
| 58431.332210 | 0.00008 | ccd | 74615 | −0.00487 | (7) | 58479.331640 | 0.00009 | ccd | 74822 | −0.00528 | (7) |
| 58479.564000 | 0.0001 | ccd | 74823 | −0.00480 | (7) | 58749.938710 | 0.0001 | ccd | 75989 | −0.00602 | (7) |
| 58790.750428 | 0.0002 | ccd | 76165 | −0.00576 | (12) | 58790.982028 | 0.0002 | ccd | 76166 | −0.00604 | (12) |
| 58791.446029 | 0.0001 | ccd | 76168 | −0.00581 | (12) | 58791.678029 | 0.0002 | ccd | 76169 | −0.00569 | (12) |
| 58791.909730 | 0.0001 | ccd | 76170 | −0.00587 | (12) | 58792.141530 | 0.0002 | ccd | 76171 | −0.00596 | (12) |
| 58792.373730 | 0.0002 | ccd | 76172 | −0.00564 | (12) | 58792.605831 | 0.0002 | ccd | 76173 | −0.00542 | (12) |
| 58792.837631 | 0.0002 | ccd | 76174 | −0.00550 | (12) | 58793.068731 | 0.0001 | ccd | 76175 | −0.00629 | (12) |
| 58793.300732 | 0.0001 | ccd | 76176 | −0.00617 | (12) | 58793.532662 | 0.00006 | ccd | 76177 | −0.00612 | (12) |
| 58793.764353 | 0.00004 | ccd | 76178 | −0.00632 | (12) | 58793.996323 | 0.00004 | ccd | 76179 | −0.00623 | (12) |
| 58794.228133 | 0.0002 | ccd | 76180 | −0.00630 | (12) | 58794.460364 | 0.00009 | ccd | 76181 | −0.00596 | (12) |
| 58794.692034 | 0.0002 | ccd | 76182 | −0.00617 | (12) | 58794.924134 | 0.0001 | ccd | 76183 | −0.00595 | (12) |
| 58795.155735 | 0.0002 | ccd | 76184 | −0.00623 | (12) | 58795.387835 | 0.0002 | ccd | 76185 | −0.00602 | (12) |
| 58795.619515 | 0.00009 | ccd | 76186 | −0.00622 | (12) | 58795.851245 | 0.00007 | ccd | 76187 | −0.00637 | (12) |
| 58796.083606 | 0.00009 | ccd | 76188 | −0.00590 | (12) | 58796.315346 | 0.00007 | ccd | 76189 | −0.00604 | (12) |
| 58796.547136 | 0.0002 | ccd | 76190 | −0.00613 | (12) | 58796.778937 | 0.00006 | ccd | 76191 | −0.00622 | (12) |
| 58797.010897 | 0.00005 | ccd | 76192 | −0.00614 | (12) | 58797.243337 | 0.0002 | ccd | 76193 | −0.00558 | (12) |
| 58797.475038 | 0.0002 | ccd | 76194 | −0.00576 | (12) | 58797.706698 | 0.00009 | ccd | 76195 | −0.00599 | (12) |
| 58797.937898 | 0.00009 | ccd | 76196 | −0.00667 | (12) | 58798.170739 | 0.0001 | ccd | 76197 | −0.00571 | (12) |
| 58798.402539 | 0.0002 | ccd | 76198 | −0.00580 | (12) | 58798.634639 | 0.0002 | ccd | 76199 | −0.00558 | (12) |
| 58798.866040 | 0.0001 | ccd | 76200 | −0.00606 | (12) | 58799.097950 | 0.0001 | ccd | 76201 | −0.00603 | (12) |
| 58799.329820 | 0.00009 | ccd | 76202 | −0.00605 | (12) | 58799.561910 | 0.00009 | ccd | 76203 | −0.00584 | (12) |
| 58799.793761 | 0.0001 | ccd | 76204 | −0.00587 | (12) | 58800.025541 | 0.0001 | ccd | 76205 | −0.00598 | (12) |
| 58800.257441 | 0.0001 | ccd | 76206 | −0.00596 | (12) | 58800.489332 | 0.00008 | ccd | 76207 | −0.00595 | (12) |
| 58800.721142 | 0.0002 | ccd | 76208 | −0.00603 | (12) | 58801.649043 | 0.0001 | ccd | 76212 | −0.00566 | (12) |
| 58801.880863 | 0.00008 | ccd | 76213 | −0.00572 | (12) | 58802.111843 | 0.0002 | ccd | 76214 | −0.00662 | (12) |
| 58803.503745 | 0.0001 | ccd | 76220 | −0.00602 | (12) | 58803.735645 | 0.0002 | ccd | 76221 | −0.00601 | (12) |
| 58803.967945 | 0.0002 | ccd | 76222 | −0.00559 | (12) | 58804.199546 | 0.0002 | ccd | 76223 | −0.00587 | (12) |
| 58804.431286 | 0.00009 | ccd | 76224 | −0.00601 | (12) | 58804.663246 | 0.0001 | ccd | 76225 | −0.00594 | (12) |
| 58804.895346 | 0.0001 | ccd | 76226 | −0.00572 | (12) | 58805.127147 | 0.0001 | ccd | 76227 | −0.00580 | (12) |
| 58805.358947 | 0.0001 | ccd | 76228 | −0.00589 | (12) | 58805.590247 | 0.0001 | ccd | 76229 | −0.00647 | (12) |
| 58805.822527 | 0.00005 | ccd | 76230 | −0.00607 | (12) | 58806.054447 | 0.0002 | ccd | 76231 | −0.00604 | (12) |
| 58806.286048 | 0.0001 | ccd | 76232 | −0.00632 | (12) | 58806.518348 | 0.0002 | ccd | 76233 | −0.00590 | (12) |
| 58806.750098 | 0.00009 | ccd | 76234 | −0.00604 | (12) | 58806.981998 | 0.00009 | ccd | 76235 | −0.00602 | (12) |
| 58807.213648 | 0.0001 | ccd | 76236 | −0.00625 | (12) | 58807.445609 | 0.00006 | ccd | 76237 | −0.00617 | (12) |
| 58807.677949 | 0.0001 | ccd | 76238 | −0.00572 | (12) | 58807.909409 | 0.00006 | ccd | 76239 | −0.00614 | (12) |
| 58808.142049 | 0.0002 | ccd | 76240 | −0.00538 | (12) | 58808.374049 | 0.0002 | ccd | 76241 | −0.00527 | (12) |
| 58808.605550 | 0.0001 | ccd | 76242 | −0.00565 | (12) | 58808.837640 | 0.00008 | ccd | 76243 | −0.00544 | (12) |
| 58809.069250 | 0.0002 | ccd | 76244 | −0.00572 | (12) | 58809.300480 | 0.00005 | ccd | 76245 | −0.00637 | (12) |
| 58809.532540 | 0.00008 | ccd | 76246 | −0.00619 | (12) | 58809.764550 | 0.0001 | ccd | 76247 | −0.00607 | (12) |
| 58809.996451 | 0.0002 | ccd | 76248 | −0.00605 | (12) | 58810.228751 | 0.0002 | ccd | 76249 | −0.00563 | (12) |
| 58810.460751 | 0.0002 | ccd | 76250 | −0.00552 | (12) | 58810.692551 | 0.0002 | ccd | 76251 | −0.00560 | (12) |
| 58810.924551 | 0.0002 | ccd | 76252 | −0.00548 | (12) | 58811.155651 | 0.0001 | ccd | 76253 | −0.00626 | (12) |
| 58811.387652 | 0.0002 | ccd | 76254 | −0.00615 | (12) | 58811.619452 | 0.0001 | ccd | 76255 | −0.00623 | (12) |
| 58811.851352 | 0.0001 | ccd | 76256 | −0.00621 | (12) | 58812.083552 | 0.0002 | ccd | 76257 | −0.00590 | (12) |
| 58812.314952 | 0.0002 | ccd | 76258 | −0.00638 | (12) | 58812.547152 | 0.0002 | ccd | 76259 | −0.00606 | (12) |
| 58812.778853 | 0.0002 | ccd | 76260 | −0.00625 | (12) | 58813.010853 | 0.0001 | ccd | 76261 | −0.00613 | (12) |
| 58813.242923 | 0.00008 | ccd | 76262 | −0.00594 | (12) | 58813.474853 | 0.0001 | ccd | 76263 | −0.00590 | (12) |
| 58813.706853 | 0.0001 | ccd | 76264 | −0.00578 | (12) | 58813.938653 | 0.0001 | ccd | 76265 | −0.00586 | (12) |
| 58814.170453 | 0.0001 | ccd | 76266 | −0.00595 | (12) | 58814.402553 | 0.0002 | ccd | 76267 | −0.00573 | (12) |
| 58814.634454 | 0.0002 | ccd | 76268 | −0.00571 | (12) | 58814.866154 | 0.0002 | ccd | 76269 | −0.00590 | (12) |
| 58828.315435 | 0.0001 | ccd | 76327 | −0.00585 | (11) | 58866.344145 | 0.0001 | ccd | 76491 | −0.00600 | (11) |
| 58892.315190 | 0.0001 | ccd | 76603 | −0.00588 | (11) |
a vis: Visual, pe: Photoelectric, ccd: CCD. b Average data obtained in the different observation band. References: (1) [51]; (2) [18]; (3) [9]; (4) O-C gateway data; (5) [17]; (6) [10]; (7) AAVSO; (8) ROTSE; (9) SuperWASP; (10) This paper; (11) [14]; (12) TESS.
References
- Africano, J.L.; Nather, R.E.; Patterson, J.; Robinson, E.L.; Warner, B. Eclipse timings of RW Tri. Publ. Astron. Soc. Pac. 1978, 90, 568. [Google Scholar] [CrossRef][Green Version]
- Walker, M.F. Photoelectric Observations of RW Tri. Astrophys. J. 1963, 137, 485. [Google Scholar] [CrossRef]
- Walker, M.F. Simultaneous Spectroscopic and Photometric Observations of Short Period Binary Systems. IAU Colloq. 1971, 15, 243. [Google Scholar]
- Warner, B. Nova-Like Variables and Nova Remnants. In Cataclysmic Variable Stars; King, A., Lin, D., Maran, S., Pringle, J., Ward, M., Eds.; Cambridge Univ. Press: Cambridge, UK, 1995; pp. 216–256. [Google Scholar]
- Groot, P.J.; Rutten, R.G.M.; van Paradijs, J. A spectrophotometric study of RW Tri. Astron. Astrophys. 2004, 417, 283. [Google Scholar] [CrossRef]
- Groot, P.J.; Rutten, R.F.; van Paradijs, J. SW Sextantis in an excited, low state. Astron. Astrophys. 2001, 368, 183. [Google Scholar] [CrossRef]
- Araujo-Betancor, S.; Knigge, C.; Long, K.S.; Hoard, D.W.; Szkody, P.; Rodgers, B.; Krisciunas, K.; Dhillon, V.S.; Hynes, R.I.; Patterson, J. The System Parameters of DW Ursae Majoris. Astrophys. J. 2003, 583, 437. [Google Scholar] [CrossRef][Green Version]
- Halevin, A.V.; Henden, A.A. Eclipse mapping of RW Tri in the low luminositity state. Inf. Bull. Var. Stars 2008, 5861, 1. [Google Scholar]
- Longmore, A.J.; Lee, T.J.; Allen, D.A.; Adams, D.J. Infrared observations of the cataclysmic variable RW Tri. Mon. Not. R. Astron. Soc. 1981, 195, 825. [Google Scholar]
- Smak, J. Eclipses in Cataclysmic Variables with Stationary Accretion Disks. V. RW Tri. Acta Astron. 1995, 45, 259. [Google Scholar]
- Still, M.D.; Dhillon, V.S.; Jones, D.H. Spectrophotometry of the nova-like variable RW Tri in a high-state. Mon. Not. R. Astron. Soc. 1995, 273, 849. [Google Scholar]
- Poole, T.; Mason, K.O.; Ramsay, G.; Drew, J.E.; Smith, R.C. The component star masses in RW Tri. Mon. Not. R. Astron. Soc. 2003, 340, 499. [Google Scholar] [CrossRef]
- Smak, J. RW Tri-its Negative Superhumps and System Parameters. Acta Astron. 2019, 69, 79. [Google Scholar]
- Subebekova, G.; Zharikov, S.; Tovmassian, G.; Neustroev, V.; Wolf, M.; Hernandez, M.-S.; Kučáková, H.; Khokhlov, S. Structure of accretion flows in the nova-like cataclysmic variable RWTri. Mon. Not. R. Astron. Soc. 2020, 497, 1475. [Google Scholar] [CrossRef]
- Lasota, J.-P. The disc instability model of dwarf novae and low-mass X-ray binary transients. New Astron. Rev. 2001, 45, 449. [Google Scholar] [CrossRef]
- Horne, K.; Cook M., C. UBV images of the Z Cha accretion disc in outburst. Mon. Not. R. Astron. Soc. 1985, 214, 307. [Google Scholar]
- Rutter, R.G.M.; van Paradijs, J.; Tinbergen, J. Reconstruction of the accretion disk in six cataclysmic variable stars. Astron. Astrophys. 1992, 260, 213. [Google Scholar]
- Robinson, E.L.; Shetrone, M.D.; Africano, J.L. New Eclipse Timings and an Upper Limit to the Rate of Mass Transfer in the Novalike Variable RW Tri. Astron. J. 1991, 102, 1176. [Google Scholar] [CrossRef]
- Polsgrove, D.E.; Wetterer, C.J.; Bloomer, R.H.; Newton, J.D. CCD photometry of DF Lyr, BY Peg, CW Peg, and RW Tri. Inf. Bull. Var. Stars 2006, 5710, 1. [Google Scholar]
- Boyd, D. A Study of the Orbital Periods of Deeply Eclipsing SW Sextantis Stars. J. AAVSO 2012, 40, 295. [Google Scholar]
- Ricker, G.R.; Winn, J.N.; Vanderspek, R.; Ennico, K.A.; Bakos, G.; Brown, T.M.; Burgasser, A.J.; Charbonneau, D.; Clampin, M.; Deming, L.D.; et al. Transiting Exoplanet Survey Satellite (TESS). Astrophys. J. 2015, 1, 014003. [Google Scholar]
- Paunzen, E.; Kuba, M.; West, R.G.; Zejda, M. SuperWASP data release 1 public again. Inf. Bull. Var. Stars 2014, 6090, 1. [Google Scholar]
- Butters, O.W.; West, R.G.; Anderson, D.R.; Cameron, C.; Clarkson, W.I.; Enoch, B.; Haswell, C.A.; Hellier, C.; Horne, K.; Joshi, Y.; et al. The first WASP public data release. Astron. Astrophys. 2010, 520, L10. [Google Scholar] [CrossRef]
- Norton, A.J.; Wheatley, P.J.; West, R.G.; Haswell, C.A.; Street, R.A.; Cameron, A.C.; Christian, D.J.; Clarkson, W.I.; Enoch, B.; Gallaway, M.; et al. New periodic variable stars coincident with ROSAT sources discovered using SuperWASP. Astron. Astrophys. 2007, 467, 785. [Google Scholar] [CrossRef]
- Paschke, A.; Brat, L. Extrema timings of some short-period variable stars. Open Eur. J. Var. Star 2006, 23, 13. [Google Scholar]
- Mandel, O.E. On the Periods of RW Tri and UX UMa. Perem. Zvezdy 1965, 15, 474. [Google Scholar]
- Irwin, J.B. The Determination of a Light-Time Orbit. Astrophys. J. 1952, 116, 211. [Google Scholar]
- Nelder, J.A.; Mead, R. A Simplex Method for Function Minimization. Comput. J. 1965, 7, 308. [Google Scholar] [CrossRef]
- Dai, Z.B.; Qian, S.B.; Li, L.J. Updated Photometry and Orbital Period Analysis for the Polar AM Herculis on the Upper Edge of the Period Gap. Astrophys. J. 2013, 774, 153. [Google Scholar] [CrossRef]
- Pringle, J.E. Period changes in eruptive binaries. Mon. Not. R. Astron. Soc. 1975, 170, 633. [Google Scholar]
- Dai, Z.B.; Qian, S.B. Orbital period analysis of eclipsing post-novae T Aurigae: Evidence of magnetic braking and an unseen companion. New Astron. 2010, 15, 380. [Google Scholar] [CrossRef]
- Dai, Z.B.; Qian, S.B. Orbital Period Analysis of Eclipsing Z Cam-Type Dwarf Nova EM Cygni: Evidence of Magnetic Braking and a Third Body. Publ. Astron. Soc. Jpn. 2010, 62, 965. [Google Scholar] [CrossRef]
- Robinson, E.L.; Barker, E.S.; Cochran, A.L.; Cochran, W.D.; Nather, R.E. MV Lyrae-Spectrophotometric properties of minimum light: Or on MV Lyrae off. Astrophys. J. 1981, 251, 611. [Google Scholar]
- Spruit, H.C.; Ritter, H. Stellar activity and the period gap in cataclysmic variables. Astron. Astrophys. 1983, 124, 267. [Google Scholar]
- Dai, Z.B.; Qian, S.B. Orbital period analysis of eclipsing dwarf novae: U Geminorum. Astrophys. Space Sci. 2009, 321, 91. [Google Scholar] [CrossRef]
- Dai, Z.B.; Qian, S.B. Plausible explanations for the variations of orbital period in the old nova DQ Herculis. Astron. Astrophys. 2009, 503, 883. [Google Scholar]
- Warner, B.; Nather, R.E. Observations of rapid blue variables-II. U Geminorum. Mon. Not. R. Astron. Soc. 1971, 152, 219. [Google Scholar] [CrossRef][Green Version]
- Smak, J. Eruptive Binaries. II. U Geminorum. Acta Astron. 1971, 21, 15. [Google Scholar]
- Frank, J.; King, A.R. A standard accretion disc model for RW Tri. Mon. Not. R. Astron. Soc. 1981, 195, 227. [Google Scholar] [CrossRef]
- Rappaport, S.; Verbunt, F.; Joss, P.C. A new technique for calculations of binary stellar evolution application to magnetic braking. Astrophys. J. 1983, 275, 713. [Google Scholar] [CrossRef]
- Tout, C.A.; Hall, D.S. Wind driven mass transfer in interacting binary systems. Mon. Not. R. Astron. Soc. 1991, 253, 9. [Google Scholar] [CrossRef]
- Knigge, C.; Baraffe, I.; Patterson, J. The Evolution of Cataclysmic Variables as Revealed by Their Donor Stars. Astrophys. J. Suppl. Ser. 2011, 194, 28. [Google Scholar] [CrossRef]
- Dai, Z.B.; Szkody, P.; Garnavich, P.M. Evolution of the Quiescent Disk Surrounding a Superoutburst of the Dwarf Nova TW Virginis. Astrophys. J. 2021, 161, 34. [Google Scholar]
- Dubus, G.; Otulakowska-Hypka, M.; Lasota, J.-P. Testing the disk instability model of cataclysmic variables. Astron. Astrophys. 2018, 617, A26. [Google Scholar] [CrossRef]
- Smak, J. Eclipses in Cataclysmic Variables with Stationary Accretion Disks. VI. Is Accretion in UX UMa and RW Tri Really Stationary? Acta Astron. 1998, 48, 59. [Google Scholar]
- Osaki, Y. An Accretion Model for the Outbursts of U Geminorum Stars. Publ. Astron. Soc. Jpn. 1974, 26, 429. [Google Scholar]
- Shafter, A.W.; Wheeler, J.C.; Cannizzo, J.K. Mass Transfer in Cataclysmic Variables: Clues from the Dwarf Nova Period Distribution. Astrophys. J. 1986, 305, 261. [Google Scholar]
- Dai, Z.B.; Qian, S.B.; Fernández Lajús, E. Evidence of a Brown Dwarf in the Eclipsing Dwarf Nova Z Chamaeleonis. Astrophys. J. 2009, 703, 109. [Google Scholar]
- Dai, Z.B.; Qian, S.B.; Fernández Lajús, E.; Baume, G.L. A cyclical period variation detected in the updated orbital period analysis of TV Columbae. Astrophys. Space Sci. 2010, 330, 243. [Google Scholar] [CrossRef][Green Version]
- Dai, Z.B.; Qian, S.B.; Fernández Lajús, E.; Baume, G.L. Orbital period analyses for two cataclysmic variables: UZ Fornacis and V348 Puppis inside the period gap. Mon. Not. R. Astron. Soc. 2010, 409, 1195. [Google Scholar]
- Winkler, L. New features in RW Tri. Astron. J. 1977, 82, 1008. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).