A Roadmap to Gamma-Ray Bursts: New Developments and Applications to Cosmology
Abstract
1. Introduction
2. GRB Classification and Properties
2.1. Classification: Short and Long GRBs
- short–hard ( s) GRBs, hereafter SGRBs,
- long–soft ( s) GRBs, hereafter LGRBs.
2.2. Intermediate GRBs?
2.3. Ultra-Long GRBs and X-ray Flashes
- (a)
- their observed prompt emission spectrum that peaks at energies which are an order of magnitude lower than those of standard LGRBs;
- (b)
- their time integrated flux in the 2–30 keV X-ray band greater than that in the 30–400 keV -ray band.
2.4. Progenitors and Open Questions
- I:
- LGRBs could arise from the core-collapse of a massive star or collapsar [23],
- II:
- SGRBs could originate from the binary neutron star-black hole (NS-BH) or NS-NS mergers [24].
- an “on-axis” observer detects the prompt emission and then, as the jet decelerates, the afterglow emission and finally a jet-break due to the faster spreading of the emitted radiation;
- an “off-axis” observer cannot detect the prompt emission but detects an orphan afterglow, namely an afterglow without a preceding GRB.
2.4.1. The LGRB-Supernova Connection
2.4.2. SGRBs, Macronovae, and Gravitational Waves
2.5. Observable Quantities from GRBs
- (1)
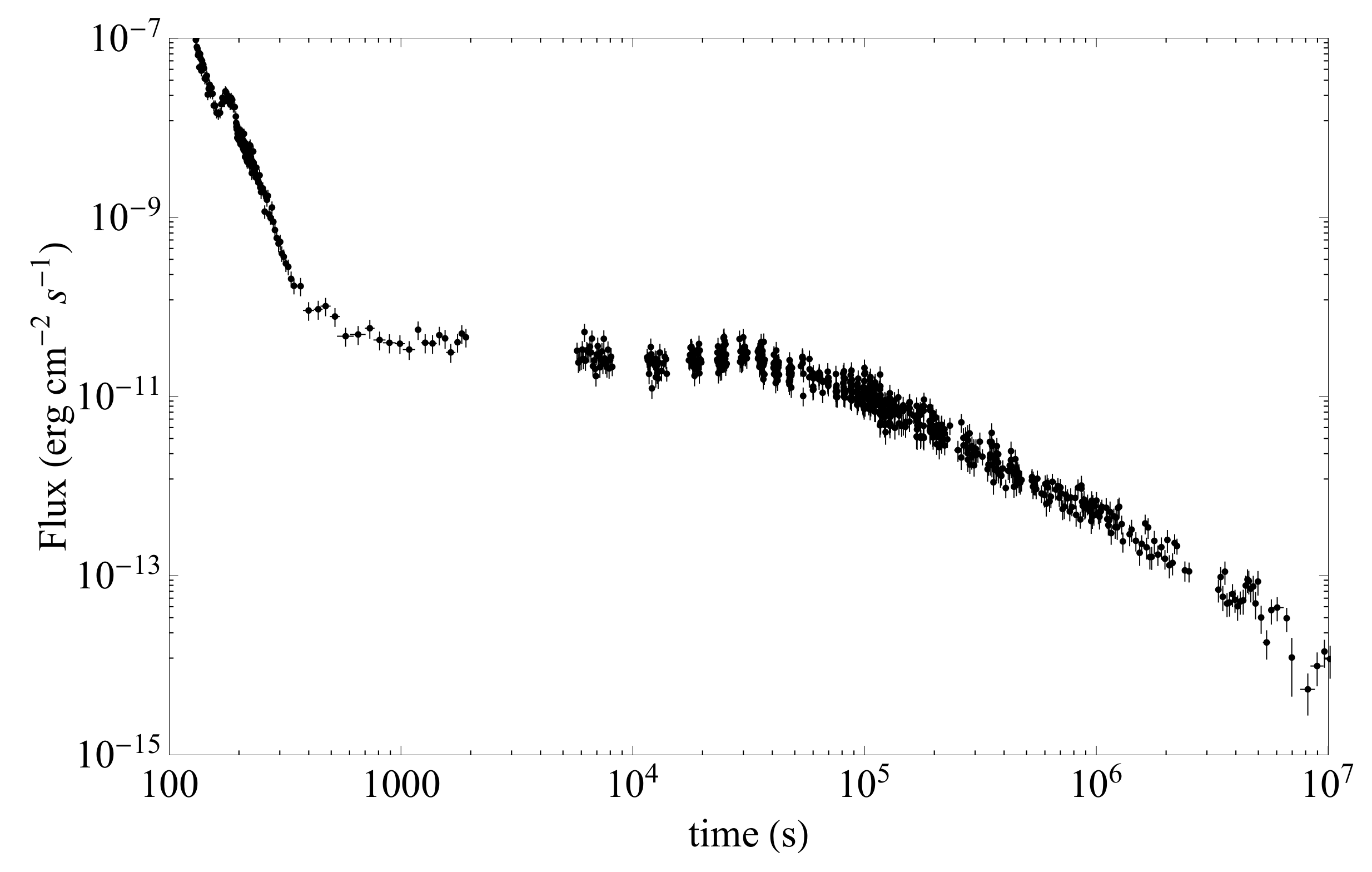
- an early steep decay, interpreted as the tail of the prompt emission at large angles, followed by a very shallow decay, called the plateau, usually accompanied by spectral parameter variations, and
- (2)
- a final decay, less steep than the first one.
Timescales and Characteristic Energy as Observable Signature of GRBs
- , the time at which the late X-ray afterglow power-law decline suddenly steepens due to the slowing down of the jet until the relativistic beaming angle roughly equals the jet opening angle .
- , the time lag is computed as the difference of arrival times to the observer of the high energy photons () and low energy photons (25–50)12.
- , the rest-frame time, defined by a broken power-law fit of the X-ray afterglow light curve, at which a late power-law decay after the plateau phase is established.
- , the rest-frame time marking the end of the plateau phase, defined from a fit of the X-ray afterglow with a smooth function given in Ref. [68].
- and are the observed X-ray fluxes respective to and , whereas the corresponding rest-frame –10 keV luminosities and are computed as follows:13where we used the fact that X-ray data are observed by the Swift-XRT in the –10 keV energy band and the SED is in general a power-law spectrum with and power-law index .
- V, the variability of the GRB light curve. It is computed by taking the difference between the observed light curve and its smoothed version, squaring this difference, summing these squared differences over time intervals, and appropriately normalizing the resulting sum.
3. Theory of GRB Progenitors
- -
- GRB progenitors harbor a BH14 which acts as a central engine powering the GRB emission.
- -
- The burst energy must be gravitational, and it is released in a very short time and from a compact region.
- -
- Substantial part of this energy is converted into kinetic energy and a relativistic jetted outflow is formed.
- -
- The acceleration process and the role played by magnetic fields are still unclear.
- -
- The dissipation of part of the kinetic energy produces the observed prompt emission.
- -
- The thermal emission of the prompt emission may be the relic of the photons emitted during the initial explosion, whose energy has not been converted into kinetic form.
- -
- Afterward, relativistic jets interact with the CBM, gradual energy conversion occurs, and the afterglow (from X-ray down to radio) is produced.
3.1. The Fireball Model
3.1.1. Photon-Dominated Scenario
3.1.2. Internal Shock Scenario and Photospheric Emission
- 1.
- Light curve variability. The time delay between the photons produced by the collisions and a photon emitted from the central engine towards the observer, i.e., , is similar to the central engine variability and can explain the observed variability ( ms).
- 2.
- Particle acceleration. Shell collisions generate internal shock waves, which can accelerate particles to high energies via Fermi mechanism and produce -rays.
- 3.
- Thermal radiation. Equation (13) states the fireball is optically thick [48,49,76]. For , an effective photosphere radius can defined by requesting [77]. Internal shocks take place at . In a more realistic picture, photons decouple the plasma on “photospheric surface” [78] and the emerging emission is a convolution of different Doppler boosts and different adiabatic energy losses of photons [62,78]. This emission explains the thermal-like emission embedded in the non-thermal spectra of some GRBs [62,79,80].
- 1.
- Efficiency. From the energy and momentum conservation, the kinetic energy dissipation is highly efficient only if two shells have masses and Lorentz factors . The average over several collisions leads to a low global efficiency of 1-[81,82], which contrasts with the much higher efficiency inferred from afterglow measurements [31,33]. Higher efficiency up to the can be attained by considering larger contrasts [82]. However, these Lorentz factor contrasts unlikely occur within the traditional collapsar or the merger scenarios.
- 2.
- Observed spectra. This model does not explain the observed spectra and needs further assumptions on how the dissipated energy produces photons (i.e., involving standard radiative processes such as synchrotron emission or Compton scattering).
3.1.3. Magnetized (or Poynting-Flux Dominated) Outflows
3.1.4. Particle Acceleration
3.1.5. Radiative Processes
- Synchrotron Emission
- (1)
- requires energetic particles and strong magnetic fields, both expected in shock waves;
- (2)
- has a broad-band spectrum with characteristic peak, associated with the observed peak energy;
- (3)
- for typical parameters, energetic electrons radiate nearly 100% of their energy.
- Photospheric Emission
- (1)
- similar to the Rayleigh–Jeans part of the thermal spectrum, for ;
- (2)
- (or ) because of multiple Compton scattering, for ;
- (3)
- an exponential cutoff, for for .
- (1)
- low energy spectral slopes less steep than the Rayleigh—Jeans part of a Planck spectrum;
- (2)
- the observed GeV emission, which may originate from some dissipation above the photosphere.
4. Reconciling Cosmological Indicators to GRBs
4.1. Distance Indicators
- Absolute measures, as they are computed through previously known information, e.g., trigonometric parallax.
- Relative measures, as they involve empirical relations based on indirect or direct probes, e.g., Cepheids period–luminosity relation, for which the distance measures are calibrated against an absolute method to enable those measurements to be somehow anchored.
4.2. Standard Candles
4.3. Classifying Standard Candles
- Standard candles as primary distance indicators, which can be calibrated within the Milky Way galaxy.
- Standard candles as secondary distance indicators, which can be observed at larger distances than Milky Way scales. However, they require calibration, typically performed using known primary distance indicators within distant galaxies.
4.3.1. Primary Distance Indicators
4.3.2. Secondary Distance Indicators
5. Going Ahead with Standard Indicators: The Analysis
5.1. Probability Distribution
5.2. The SNe Ia Measurements
5.3. BAO Measurements
5.4. Differential Age and Hubble Measurements
5.5. The Parameter
5.6. Confidence Levels and Uncertainties
5.7. Binning Procedure
6. Standardizing GRBs
- (1)
- Computing the luminosity function for GRBs, constructing it from the prompt emission as well as afterglows. This treatment is analogous to what we do for SNe Ia.
- (2)
- Computing the redshift distribution of GRBs. This enables one to use GRBs as tracers for the cosmic star-formation history. Consequently, spotting very high redshift GRBs will shed light on their distribution at intermediate epochs of the universe evolution.
- (3)
- Studying the host galaxies, in particular those faint, high-redshift galaxies that are unlikely to be found and studied with other methods, characterizing the dust extinction curves of high-z galaxies.
- (4)
- Studying GRB-selected absorption line systems and probing cosmic chemical evolution with GRBs.
- (5)
- Studying if and how much GRBs can be used for determining the cosmological parameters of dark energy models and/or to rule out a few models. Analogously, the use of GRBs can be tested in view of determining cosmographic parameters, i.e., getting model independent bounds over the cosmic evolution.
6.1. GRB Correlations and Related Issues
6.2. Prompt Emission GRB Correlations
6.2.1. – Correlation
6.2.2. –V Correlation
6.2.3. Amati or – Correlation
6.2.4. Yonetoku or – Correlation
6.2.5. Ghirlanda or – Correlation
6.3. Prompt and Afterglow Emission Correlations
6.3.1. Liang–Zhang or –– Correlation
6.3.2. Dainotti or – Correlation
6.3.3. –– Correlation
6.3.4. Combo Correlation
6.3.5. L–T–E Correlation
7. Further Issues Related to Constructing GRB Correlations
7.1. Evolution Effects
7.2. Instrumental Selection Effects
7.3. Systematic Errors
7.4. Issues and Interpretation of Prompt Emission GRB Correlations
7.4.1. – Correlation
7.4.2. –V Correlation
7.4.3. Amati or – Correlation
7.4.4. Ghirlanda or – Correlation
7.4.5. Yonetoku or – Correlation
7.5. Issues and Interpretation of Prompt and Afterglow Emission GRB Correlations
7.5.1. Liang–Zhang or –– Correlation
7.5.2. Dainotti or – Correlation
7.5.3. –– Correlation
7.5.4. Combo Correlation
7.5.5. L–T–E Correlation
8. Circularity or Not Circularity?
8.1. Calibration Versus Non-Calibration
8.2. Fitting Procedures with Calibration
8.2.1. SN Calibration
8.2.2. Model Dependent Calibration
8.2.3. Model Independent Calibration
- 1.
- 2.
- .
- 3.
- .
8.3. The Use of Bézier Polynomials
8.3.1. Simultaneous Fits
8.3.2. Narrow Calibration
8.4. Fitting Procedures without Calibration
9. Recent Developments of Cosmology with Gamma-Ray Bursts
9.1. Numerical Results Using Correlations
9.2. Applications of Statistical Analysis with GRBs
- -
- GRB . Here, we definewhere and are the experimental and theoretical GRB distance moduli.
- -
- SN . Here, by virtue of the above discussion concerning SN statistical analysis, we rewrite the chi square function in Equation (25) bywhere is the module of the vector of residuals, and the covariance matrix.In particular, we prompt the distance modulus for the most recent SN catalog, named Pantheon Sample. This represents the current largest SN sample consisting of 1048 SNe Ia lying on [180]. The corresponding magnitudes readHere, and are the B-band absolute and apparent magnitudes, respectively. The above distance moduli also depend upon other quantities required to standardize/correct the light curves of SNe Ia. The quantities and are the light curve shape and color parameters, respectively, whereas and are the coefficients of the luminosity–stretch and luminosity–color relationships, respectively. is a distance correction determined on host galaxy mass of SNe, while a distance correction that is built up from predicted biases determined by means of simulations.By marginalizing over through a flat prior, it is possible to demonstrate that SN uncertainties do not depend on , and this permits one to simplify the chi square function throughwhere , , .
- -
9.2.1. Bézier Polynomials and Cosmographic Series
9.2.2. Bézier Polynomials and CDM and CDM Cosmological Models
9.3. The Role of Spatial Curvature
- I.
- the terms and are obtained from small GRB sub-samples with almost the same redshift;
- II.
- is determined from the use of SNe Ia limited to the lowest redshift of the GRBs of the Combo data set, in which the calibration of SNe Ia is negligible [140].
10. Further Application of GRBs as Probes of the High-Redshift Universe
10.1. Star Formation Rate from GRBs
10.2. High-Redshift GRB Rate Excess
10.3. Gravitationally-Lensed GRBs
11. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | New data come from the newly born gravitational wave, neutrino, and BH astronomy. We remark that precision cosmology is essential to shed light on the mysteries that jeopardize the standard cosmological puzzle. In this respect, GRBs could play a significant role since they represent outstanding explosions whose nature can trace the dark energy (DE) and BH natures. |
| 2 | GRBs approximately span in the range –10. |
| 3 | Like the long-lived GeV emission, which is consistent with the afterglow emission of a blast wave in adiabatic expansion |
| 4 | For a different perspective, see, e.g., [26] |
| 5 | Hereafter the bulk Lorentz factor is indicated with to avoid confusion with the power-law photon index , describing simple power-law GRB spectra. |
| 6 | In the observer frame. |
| 7 | The GW signal, originating from the shell elliptical galaxy NGC 4993, had a duration of s. By the characteristics in intensity and frequency, GW 170817 has been unambiguously associated with the inspiraling of a binary NS-SN merger of total mass M, which is consistent with the masses of all known binary NS systems. |
| 8 | Typically dubbed time-integrated and time-resolved analyses, respectively. |
| 9 | However, in this case the spectral break is very likely below or above the detector bandpass. |
| 10 | This energy band is the one established in the original work by Ref. [65]. |
| 11 | Additional details on will be summarized later in this review. Here, we stress that this definition has been written for spatially flat DE models. |
| 12 | The time lag is historically computed in these energy bands which are the BATSE energy channels 3 and 1, respectively. |
| 13 | As a convention, the X-ray luminosities are computed in a rest-frame energy band with similar extrema with respect to the observed one; with this prescription, their expressions are simple, as portrayed in Equation (11). |
| 14 | An alternative scenario proposes that an NS remnant could be left after a GRB emission, though this issue is still under debate. For details, see Refs. [15,70,71] and Section 3.1.3. |
| 15 | Astrophysical fireballs include also some baryons from the surrounding medium, remnant of the progenitor system. |
| 16 | However, both B and are much higher than the ones inferred from the fit with the synchrotron model of the GRB afterglow, whose microphysics of particle acceleration and magnetic field generation should be similar to that of the prompt emission environment [105]. |
| 17 | Examples are main sequence fitting method, variable stars, Tully–Fisher and Faber–Jackson relations, etc. |
| 18 | Examples are SNe Ia, Cosmic Microwave Background (CMB) measurements, Baryonic Acoustic Oscillations (BAO), etc. |
| 19 | They refer to “Type Ia” for the absence of hydrogen and the presence of once ionized silicon (SiII) in their early-time spectra. |
| 20 | Weak similarities between GRBs and SNe Ia may occur at the level of formal computation, although the GRB nature is absolutely different from SNe. The core idea is to write a GRB luminosity distance as well and proceed analogously. |
| 21 | We here focus on vanishing spatial curvature, i.e., [122]. |
| 22 | The flare-filtered luminosity light curves are iteratively fitted with the above function: at every iteration, data points with the largest positive residual are discarded, until a final fit with a p-value is obtained. |
| 23 | Where their luminosity distance is essentially independent from the choice of the cosmological model |
| 24 | The cosmological model under exam, or background cosmology, is intimately determined by knowing the functional form and evolution of . |
| 25 | For the sake of completeness, this problem is not related to GRB redshifts only, but it remains an open issue of cosmography. |
| 26 | Similar conclusions have been reached in Ref. [213], who confirmed that only the Ghirlanda correlation has no redshift dependence, and determined in the flat CDM model from SNeIa calibrated GRB data. |
| 27 | Possibly including those associated with detector sensitivity, and the differences in estimated spectral parameters determined from measurements taken with different detectors or from different models. |
| 28 | Here, the brackets indicate the average over the posterior distribution. |
| 29 | By construction, these sub-samples exhibit the same correlation with the same and but involve different normalizations. |
| 30 | |
| 31 | |
| 32 | In the case of strong lensing, the time delay between the images is larger than the duration of the burst. |
References
- Piron, F. Gamma-ray bursts at high and very high energies. Comptes Rendus Phys. 2016, 17, 617–631. [Google Scholar] [CrossRef]
- Nakar, E. Short-hard gamma-ray bursts. Phys. Rep. 2007, 442, 166–236. [Google Scholar] [CrossRef]
- Kouveliotou, C.; Meegan, C.A.; Fishman, G.J.; Bhat, N.P.; Briggs, M.S.; Koshut, T.M.; Paciesas, W.S.; Pendleton, G.N. Identification of two classes of gamma-ray bursts. Astrophys. J. Lett. 1993, 413, L101. [Google Scholar] [CrossRef]
- von Kienlin, A.; Meegan, C.A.; Paciesas, W.S.; Bhat, P.N.; Bissaldi, E.; Briggs, M.S.; Burgess, J.M.; Byrne, D.; Chaplin, V.; Cleveland, W.; et al. The Second Fermi GBM Gamma-Ray Burst Catalog: The First Four Years. Astrophys. J. Suppl. 2014, 211, 13. [Google Scholar] [CrossRef]
- D’Avanzo, P. The link between short gamma-ray bursts and gravitational waves: Perspectives for the THESEUS mission. Mem. Soc. Ast. It. 2018, 89, 213. [Google Scholar]
- Ghirlanda, G.; Salafia, O.S.; Pescalli, A.; Ghisellini, G.; Salvaterra, R.; Chassande-Mottin, E.; Colpi, M.; Nappo, F.; D’Avanzo, P.; Melandri, A.; et al. Short gamma-ray bursts at the dawn of the gravitational wave era. Astron. Astrophys. 2016, 594, A84. [Google Scholar] [CrossRef]
- Berger, E.; Kulkarni, S.R.; Fox, D.B.; Soderberg, A.M.; Harrison, F.A.; Nakar, E.; Kelson, D.D.; Gladders, M.D.; Mulchaey, J.S.; Oemler, A.; et al. Afterglows, Redshifts, and Properties of Swift Gamma-Ray Bursts. Astrophys. J. 2005, 634, 501. [Google Scholar] [CrossRef]
- Rodney, S.A.; Riess, A.G.; Scolnic, D.M.; Jones, D.O.; Hemmati, S.; Molino, A.; McCully, C.; Mobasher, B.; Strolger, L.G.; Graur, O.; et al. Two SNe Ia at Redshift ∼2: Improved Classification and Redshift Determination with Medium-band Infrared Imaging. Astron. J. 2015, 150, 156. [Google Scholar] [CrossRef]
- Capozziello, S.; D’Agostino, R.; Luongo, O. Extended gravity cosmography. Int. J. Mod. Phys. D 2019, 28, 1930016. [Google Scholar] [CrossRef]
- Khadka, N.; Luongo, O.; Muccino, M.; Ratra, B. Do gamma-ray burst measurements provide a useful test of cosmological models? arXiv 2021, arXiv:2105.12692. [Google Scholar]
- Lin, H.N.; Li, X.; Wang, S.; Chang, Z. Are long gamma-ray bursts standard candles? Mon. Not. R. Astron. Soc. 2015, 453, 128–132. [Google Scholar] [CrossRef]
- Demianski, M.; Piedipalumbo, E.; Sawant, D.; Amati, L. Cosmology with gamma-ray bursts. I. The Hubble diagram through the calibrated Ep,I-Eiso correlation. Astron. Astrophys. 2017, 598, A112. [Google Scholar] [CrossRef]
- Demianski, M.; Lusso, E.; Paolillo, M.; Piedipalumbo, E.; Risaliti, G. Investigating dark energy equation of state with high redshift Hubble diagram. Front. Astron. Space Sci. 2020, 7, 69. [Google Scholar] [CrossRef]
- Mazets, E.P.; Golenetskii, S.V.; Ilinskii, V.N.; Panov, V.N.; Aptekar, R.L.; Gurian, I.A.; Proskura, M.P.; Sokolov, I.A.; Sokolova, Z.I.; Kharitonova, T.V. Catalog of cosmic gamma-ray bursts from the KONUS experiment data. I. Astrophys. Space Sci. 1981, 80, 3–83. [Google Scholar] [CrossRef]
- Kouveliotou, C.; Wijers, R.A.M.J.; Woosley, S. Gamma-Ray Bursts; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Norris, J.P.; Bonnell, J.T. Short Gamma-Ray Bursts with Extended Emission. Astrophys. J. 2006, 643, 266. [Google Scholar] [CrossRef]
- Lü, H.J.; Zhang, B.; Lei, W.H.; Li, Y.; Lasky, P.D. The Millisecond Magnetar Central Engine in Short GRBs. Astrophys. J. 2015, 805, 89. [Google Scholar] [CrossRef]
- Levan, A.J.; Tanvir, N.R.; Starling, R.L.C.; Wiersema, K.; Page, K.L.; Perley, D.A.; Schulze, S.; Wynn, G.A.; Chornock, R.; Hjorth, J.; et al. A New Population of Ultra-long Duration Gamma-Ray Bursts. Astrophys. J. 2014, 781, 13. [Google Scholar] [CrossRef]
- Zhang, B.B.; Zhang, B.; Murase, K.; Connaughton, V.; Briggs, M.S. How Long does a Burst Burst? Astrophys. J. 2014, 787, 66. [Google Scholar] [CrossRef]
- Heise, J.; in’t Zand, J.; Kippen, R.M.; Woods, P.M. X-ray Flashes and X-ray Rich Gamma Ray Bursts. In Gamma-ray Bursts in the Afterglow Era; Costa, E., Frontera, F., Hjorth, J., Eds.; Springer: Berlin, Heidelberg, 2001; p. 16. [Google Scholar]
- Piran, T.; Bromberg, O.; Nakar, E.; Sari, R. The long, the short and the weak: The origin of gamma-ray bursts. R. Soc. Lond. Philos. Trans. Ser. A 2013, 371, 20273. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Zhang, B.B.; Liang, E.W.; Gehrels, N.; Burrows, D.N.; Mészáros, P. Making a Short Gamma-Ray Burst from a Long One: Implications for the Nature of GRB 060614. Astrophys. J. Lett. 2007, 655, L25–L28. [Google Scholar] [CrossRef]
- Woosley, S.E.; Bloom, J.S. The Supernova Gamma-Ray Burst Connection. Annu. Rev. Astron. Astrophys. 2006, 44, 507–556. [Google Scholar] [CrossRef]
- Berger, E. Short-Duration Gamma-Ray Bursts. Annu. Rev. Astron. Astrophys. 2014, 52, 43–105. [Google Scholar] [CrossRef]
- Piran, T.; Sari, R.; Zou, Y.C. Observational limits on inverse Compton processes in gamma-ray bursts. Mon. Not. R. Astron. Soc. 2009, 393, 1107. [Google Scholar] [CrossRef]
- Ruffini, R.; Vereshchagin, G.; Xue, S.S. Electron-positron pairs in physics and astrophysics: From heavy nuclei to black holes. Phys. Rep. 2010, 487, 1. [Google Scholar] [CrossRef]
- Panaitescu, A.; Mészáros, P. Dynamical Evolution, Light Curves, and Spectra of Spherical and Collimated Gamma-Ray Burst Remnants. Astrophys. J. 1999, 526, 707. [Google Scholar] [CrossRef]
- Sari, R.; Piran, T.; Halpern, J.P. Jets in Gamma-Ray Bursts. Astrophys. J. Lett. 1999, 519, L17. [Google Scholar] [CrossRef]
- Racusin, J.L.; Liang, E.W.; Burrows, D.N.; Falcone, A.; Sakamoto, T.; Zhang, B.B.; Zhang, B.; Evans, P.; Osborne, J. Jet Breaks and Energetics of Swift Gamma-Ray Burst X-Ray Afterglows. Astrophys. J. 2009, 698, 43–74. [Google Scholar] [CrossRef]
- Lamb, G.P.; Kann, D.A.; Fernández, J.J.; Mandel, I.; Levan, A.J.; Tanvir, N.R. GRB jet structure and the jet break. Mon. Not. R. Astron. Soc. 2021, 506, 4163–4174. [Google Scholar] [CrossRef]
- Nousek, J.A.; Kouveliotou, C.; Grupe, D.; Page, K.L.; Granot, J.; Ramirez-Ruiz, E.; Patel, S.K.; Burrows, D.N.; Mangano, V.; Barthelmy, S.; et al. Evidence for a Canonical Gamma-Ray Burst Afterglow Light Curve in the Swift XRT Data. Astrophys. J. 2006, 642, 389. [Google Scholar] [CrossRef]
- Panaitescu, A.; Mészáros, P.; Burrows, D.; Nousek, J.; Gehrels, N.; O’Brien, P.; Willingale, R. Evidence for chromatic X-ray light-curve breaks in Swift gamma-ray burst afterglows and their theoretical implications. Mon. Not. R. Astron. Soc. 2006, 369, 2059. [Google Scholar] [CrossRef]
- Zhang, B.; Fan, Y.Z.; Dyks, J.; Kobayashi, S.; Mészáros, P.; Burrows, D.N.; Nousek, J.A.; Gehrels, N. Physical Processes Shaping Gamma-Ray Burst X-Ray Afterglow Light Curves: Theoretical Implications from the Swift X-Ray Telescope Observations. Astrophys. J. 2006, 642, 354. [Google Scholar] [CrossRef]
- Chincarini, G.; Moretti, A.; Romano, P.; Falcone, A.D.; Morris, D.; Racusin, J.; Campana, S.; Covino, S.; Guidorzi, C.; Tagliaferri, G.; et al. The First Survey of X-Ray Flares from Gamma-Ray Bursts Observed by Swift: Temporal Properties and Morphology. Astrophys. J. 2007, 671, 1903. [Google Scholar] [CrossRef]
- Kumar, P.; Narayan, R.; Johnson, J.L. Mass fall-back and accretion in the central engine of gamma-ray bursts. Mon. Not. R. Astron. Soc. 2008, 388, 1729–1742. [Google Scholar] [CrossRef]
- Hjorth, J. The supernova-gamma-ray burst-jet connection. Philos. Trans. R. Soc. Lond. Ser. A 2013, 371, 20120275. [Google Scholar] [CrossRef]
- Galama, T.J.; Vreeswijk, P.M.; van Paradijs, J.; Kouveliotou, C.; Augusteijn, T.; Böhnhardt, H.; Brewer, J.P.; Doublier, V.; Gonzalez, J.; Leibundgut, B.; et al. An unusual supernova in the error box of the γ-ray burst of 25 April 1998. Nature 1998, 395, 670. [Google Scholar] [CrossRef]
- Hjorth, J.; Sollerman, J.; Møller, P.; Fynbo, J.P.U.; Woosley, S.E.; Kouveliotou, C.; Tanvir, N.R.; Greiner, J.; Andersen, M.I.; Castro-Tirado, A.J.; et al. A very energetic supernova associated with the γ-ray burst of 29 March 2003. Nature 2003, 423, 847. [Google Scholar] [CrossRef] [PubMed]
- Soderberg, A.M.; Kulkarni, S.R.; Nakar, E.; Berger, E.; Cameron, P.B.; Fox, D.B.; Frail, D.; Gal-Yam, A.; Sari, R.; Cenko, S.B.; et al. Relativistic ejecta from X-ray flash XRF 060218 and the rate of cosmic explosions. Nature 2006, 442, 1014–1017. [Google Scholar] [CrossRef]
- MacFadyen, A.I.; Woosley, S.E.; Heger, A. Supernovae, Jets, and Collapsars. Astrophys. J. 2001, 550, 410–425. [Google Scholar] [CrossRef]
- Zhang, W.; Woosley, S.E.; MacFadyen, A.I. Relativistic Jets in Collapsars. Astrophys. J. 2003, 586, 356–371. [Google Scholar] [CrossRef]
- Greiner, J.; Mazzali, P.A.; Kann, D.A.; Krühler, T.; Pian, E.; Prentice, S.; Olivares E., F.; Rossi, A.; Klose, S.; Taubenberger, S.; et al. A very luminous magnetar-powered supernova associated with an ultra-long γ-ray burst. Nature 2015, 523, 189–192. [Google Scholar] [CrossRef] [PubMed]
- Gal-Yam, A. Luminous Supernovae. Science 2012, 337, 927. [Google Scholar] [CrossRef]
- Fynbo, J.P.U.; Watson, D.; Thöne, C.C.; Sollerman, J.; Bloom, J.S.; Davis, T.M.; Hjorth, J.; Jakobsson, P.; Jørgensen, U.G.; Graham, J.F.; et al. No supernovae associated with two long-duration γ-ray bursts. Nature 2006, 444, 1047–1049. [Google Scholar] [CrossRef]
- Della Valle, M.; Chincarini, G.; Panagia, N.; Tagliaferri, G.; Malesani, D.; Testa, V.; Fugazza, D.; Campana, S.; Covino, S.; Mangano, V.; et al. An enigmatic long-lasting γ-ray burst not accompanied by a bright supernova. Nature 2006, 444, 1050. [Google Scholar] [CrossRef]
- Gal-Yam, A.; Fox, D.B.; Price, P.A.; Ofek, E.O.; Davis, M.R.; Leonard, D.C.; Soderberg, A.M.; Schmidt, B.P.; Lewis, K.M.; Peterson, B.A.; et al. A novel explosive process is required for the γ-ray burst GRB 060614. Nature 2006, 444, 1053–1055. [Google Scholar] [CrossRef]
- Gehrels, N.; Sarazin, C.L.; O’Brien, P.T.; Zhang, B.; Barbier, L.; Barthelmy, S.D.; Blustin, A.; Burrows, D.N.; Cannizzo, J.; Cummings, J.R.; et al. A short γ-ray burst apparently associated with an elliptical galaxy at redshift z = 0.225. Nature 2005, 437, 851. [Google Scholar] [CrossRef]
- Goodman, J. Are gamma-ray bursts optically thick? Astrophys. J. Lett. 1986, 308, L47. [Google Scholar] [CrossRef]
- Paczynski, B. Gamma-ray bursters at cosmological distances. Astrophys. J. Lett. 1986, 308, L43. [Google Scholar] [CrossRef]
- Eichler, D.; Livio, M.; Piran, T.; Schramm, D.N. Nucleosynthesis, neutrino bursts and gamma-rays from coalescing neutron stars. Nature 1989, 340, 126–128. [Google Scholar] [CrossRef]
- Taylor, J.H.; Weisberg, J.M. Further experimental tests of relativistic gravity using the binary pulsar PSR 1913 + 16. Astrophys. J. 1989, 345, 434. [Google Scholar] [CrossRef]
- Li, L.X.; Paczyński, B. Transient Events from Neutron Star Mergers. Astrophys. J. Lett. 1998, 507, L59–L62. [Google Scholar] [CrossRef]
- Tanvir, N.R.; Levan, A.J.; Fruchter, A.S.; Hjorth, J.; Hounsell, R.A.; Wiersema, K.; Tunnicliffe, R.L. A ‘kilonova’ associated with the short-duration γ-ray burst GRB 130603B. Nature 2013, 500, 547–549. [Google Scholar] [CrossRef]
- Lamb, G.P.; Tanvir, N.R.; Levan, A.J.; de Ugarte Postigo, A.; Kawaguchi, K.; Corsi, A.; Evans, P.A.; Gompertz, B.; Malesani, D.B.; Page, K.L.; et al. Short GRB 160821B: A Reverse Shock, a Refreshed Shock, and a Well-sampled Kilonova. Astrophys. J. 2019, 883, 48. [Google Scholar] [CrossRef]
- Troja, E.; Castro-Tirado, A.J.; Becerra González, J.; Hu, Y.; Ryan, G.S.; Cenko, S.B.; Ricci, R.; Novara, G.; Sánchez-Rámirez, R.; Acosta-Pulido, J.A.; et al. The afterglow and kilonova of the short GRB 160821B. Mon. Not. R. Astron. Soc. 2019, 489, 2104–2116. [Google Scholar] [CrossRef]
- Fong, W.; Laskar, T.; Rastinejad, J.; Escorial, A.R.; Schroeder, G.; Barnes, J.; Kilpatrick, C.D.; Paterson, K.; Berger, E.; Metzger, B.D.; et al. The Broadband Counterpart of the Short GRB 200522A at z = 0.5536: A Luminous Kilonova or a Collimated Outflow with a Reverse Shock? Astrophys. J. 2021, 906, 127. [Google Scholar] [CrossRef]
- Gompertz, B.P.; Levan, A.J.; Tanvir, N.R.; Hjorth, J.; Covino, S.; Evans, P.A.; Fruchter, A.S.; González-Fernández, C.; Jin, Z.P.; Lyman, J.D.; et al. The Diversity of Kilonova Emission in Short Gamma-Ray Bursts. Astrophys. J. 2018, 860, 62. [Google Scholar] [CrossRef]
- LIGO Scientific Collaboration; Virgo Collaboration; Fermi Gamma-ray Burst Monitor; INTEGRAL. Gravitational Waves and Gamma-Rays from a Binary Neutron Star Merger: GW170817 and GRB 170817A. Astrophys. J. Lett. 2017, 848, L13. [Google Scholar] [CrossRef]
- Troja, E.; Ryan, G.; Piro, L.; van Eerten, H.; Cenko, S.B.; Yoon, Y.; Lee, S.K.; Im, M.; Sakamoto, T.; Gatkine, P.; et al. A luminous blue kilonova and an off-axis jet from a compact binary merger at z = 0.1341. Nat. Commun. 2018, 9, 4089. [Google Scholar] [CrossRef]
- Band, D.; Matteson, J.; Ford, L.; Schaefer, B.; Palmer, D.; Teegarden, B.; Cline, T.; Briggs, M.; Paciesas, W.; Pendleton, G.; et al. BATSE observations of gamma-ray burst spectra. I—Spectral diversity. Astrophys. J. 1993, 413, 281. [Google Scholar] [CrossRef]
- Ryde, F.; Axelsson, M.; Zhang, B.B.; McGlynn, S.; Pe’er, A.; Lundman, C.; Larsson, S.; Battelino, M.; Zhang, B.; Bissaldi, E.; et al. Identification and Properties of the Photospheric Emission in GRB090902B. Astrophys. J. Lett. 2010, 709, L172. [Google Scholar] [CrossRef]
- Ryde, F.; Pe’er, A.; Nymark, T.; Axelsson, M.; Moretti, E.; Lundman, C.; Battelino, M.; Bissaldi, E.; Chiang, J.; Jackson, M.S.; et al. Observational evidence of dissipative photospheres in gamma-ray bursts. Mon. Not. R. Astron. Soc. 2011, 415, 3693–3705. [Google Scholar] [CrossRef]
- Guiriec, S.; Connaughton, V.; Briggs, M.S.; Burgess, M.; Ryde, F.; Daigne, F.; Mészáros, P.; Goldstein, A.; McEnery, J.; Omodei, N.; et al. Detection of a Thermal Spectral Component in the Prompt Emission of GRB 100724B. Astrophys. J. Lett. 2011, 727, L33. [Google Scholar] [CrossRef]
- Ghirlanda, G.; Ghisellini, G.; Nava, L. Short and long gamma-ray bursts: Same emission mechanism? Mon. Not. R. Astron. Soc. 2011, 418, L109–L113. [Google Scholar] [CrossRef]
- Yonetoku, D.; Murakami, T.; Nakamura, T.; Yamazaki, R.; Inoue, A.K.; Ioka, K. Gamma-Ray Burst Formation Rate Inferred from the Spectral Peak Energy-Peak Luminosity Relation. Astrophys. J. 2004, 609, 935–951. [Google Scholar] [CrossRef]
- Burlon, D.; Ghirlanda, G.; Ghisellini, G.; Lazzati, D.; Nava, L.; Nardini, M.; Celotti, A. Precursors in Swift Gamma Ray Bursts with Redshift. Astrophys. J. Lett. 2008, 685, L19. [Google Scholar] [CrossRef]
- Ajello, M.; Arimoto, M.; Axelsson, M.; Baldini, L.; Barbiellini, G.; Bastieri, D.; Bellazzini, R.; Bhat, P.N.; Bissaldi, E.; Blandford, R.D.; et al. A Decade of Gamma-Ray Bursts Observed by Fermi-LAT: The Second GRB Catalog. Astrophys. J. 2019, 878, 52. [Google Scholar] [CrossRef]
- Ruffini, R.; Muccino, M.; Bianco, C.L.; Enderli, M.; Izzo, L.; Kovacevic, M.; Penacchioni, A.V.; Pisani, G.B.; Rueda, J.A.; Wang, Y. On binary-driven hypernovae and their nested late X-ray emission. Astron. Astrophys. 2014, 565, L10. [Google Scholar] [CrossRef]
- Piran, T. The physics of gamma-ray bursts. Rev. Mod. Phys. 2005, 76, 1143. [Google Scholar] [CrossRef]
- Usov, V.V. Millisecond pulsars with extremely strong magnetic fields as a cosmological source of gamma-ray bursts. Nature 1992, 357, 472–474. [Google Scholar]
- Bucciantini, N.; Quataert, E.; Arons, J.; Metzger, B.D.; Thompson, T.A. Relativistic jets and long-duration gamma-ray bursts from the birth of magnetars. Mon. Not. R. Astron. Soc. 2008, 383, L25–L29. [Google Scholar] [CrossRef]
- Pe’er, A.; Zhang, B.B.; Ryde, F.; McGlynn, S.; Zhang, B.; Preece, R.D.; Kouveliotou, C. The Connection Between Thermal and Non-Thermal Emission in Gamma-ray Bursts: General Considerations and GRB090902B as a Case Study. Mon. Not. R. Astron. Soc. 2012, 420, 468–482. [Google Scholar] [CrossRef]
- Meszaros, P.; Laguna, P.; Rees, M.J. Gasdynamics of relativistically expanding gamma-ray burst sources - Kinematics, energetics, magnetic fields, and efficiency. Astrophys. J. 1993, 415, 181. [Google Scholar] [CrossRef]
- Rees, M.J.; Meszaros, P. Relativistic fireballs - Energy conversion and time-scales. Mon. Not. R. Astron. Soc. 1992, 258, 41. [Google Scholar] [CrossRef]
- Sari, R.; Piran, T. Variability in Gamma-Ray Bursts: A Clue. Astrophys. J. 1997, 485, 270. [Google Scholar] [CrossRef]
- Shemi, A.; Piran, T. The appearance of cosmic fireballs. Astrophys. J. Lett. 1990, 365, L55. [Google Scholar] [CrossRef]
- Paczynski, B. Cosmological gamma-ray bursts. Acta Astron. 1991, 41, 257–267. [Google Scholar]
- Pe’er, A. Temporal Evolution of Thermal Emission from Relativistically Expanding Plasma. Astrophys. J. 2008, 682, 463. [Google Scholar] [CrossRef]
- Ryde, F. The Cooling Behavior of Thermal Pulses in Gamma-Ray Bursts. Astrophys. J. 2004, 614, 827. [Google Scholar] [CrossRef]
- Ryde, F.; Pe’er, A. Quasi-blackbody Component and Radiative Efficiency of the Prompt Emission of Gamma-ray Bursts. Astrophys. J. 2009, 702, 1211. [Google Scholar] [CrossRef]
- Kobayashi, S.; Piran, T.; Sari, R. Can Internal Shocks Produce the Variability in Gamma-Ray Bursts? Astrophys. J. 1997, 490, 92. [Google Scholar] [CrossRef]
- Kobayashi, S.; Sari, R. Ultraefficient Internal Shocks. Astrophys. J. 2001, 551, 934. [Google Scholar] [CrossRef]
- Blandford, R.D.; Znajek, R.L. Electromagnetic extraction of energy from Kerr black holes. Mon. Not. R. Astron. Soc. 1977, 179, 433–456. [Google Scholar] [CrossRef]
- Blandford, R.D.; Payne, D.G. Hydromagnetic flows from accretion disks and the production of radio jets. Mon. Not. R. Astron. Soc. 1982, 199, 883–903. [Google Scholar] [CrossRef]
- Giannios, D.; Spruit, H.C. Spectra of Poynting-flux powered GRB outflows. Astron. Astrophys. 2005, 430, 1. [Google Scholar] [CrossRef]
- Giannios, D. Prompt emission spectra from the photosphere of a GRB. Astron. Astrophys. 2006, 457, 763. [Google Scholar] [CrossRef]
- Zhang, B.; Yan, H. The Internal-collision-induced Magnetic Reconnection and Turbulence (ICMART) Model of Gamma-ray Bursts. Astrophys. J. 2011, 726, 90. [Google Scholar] [CrossRef]
- Fermi, E. On the Origin of the Cosmic Radiation. Phys. Rev. 1949, 75, 1169–1174. [Google Scholar] [CrossRef]
- Ellison, D.C.; Double, G.P. Diffusive shock acceleration in unmodified relativistic, oblique shocks. Astropart. Phys. 2004, 22, 323–338. [Google Scholar] [CrossRef]
- Pe’er, A. Physics of Gamma-Ray Bursts Prompt Emission. Adv. Astron. 2015, 2015, 907321. [Google Scholar] [CrossRef]
- Sironi, L.; Spitkovsky, A. Particle Acceleration in Relativistic Magnetized Collisionless Electron-Ion Shocks. Astrophys. J. 2011, 726, 75. [Google Scholar] [CrossRef]
- Meszaros, P.; Rees, M.J. Relativistic fireballs and their impact on external matter—Models for cosmological gamma-ray bursts. Astrophys. J. 1993, 405, 278. [Google Scholar] [CrossRef]
- Tavani, M. A Shock Emission Model for Gamma-Ray Bursts. II. Spectral Properties. Astrophys. J. 1996, 466, 768. [Google Scholar] [CrossRef]
- Sari, R. Hydrodynamics of Gamma-Ray Burst Afterglow. Astrophys. J. Lett. 1997, 489, L37. [Google Scholar] [CrossRef]
- Daigne, F.; Mochkovitch, R. Gamma-ray bursts from internal shocks in a relativistic wind: Temporal and spectral properties. Mon. Not. R. Astron. Soc. 1998, 296, 275. [Google Scholar] [CrossRef]
- Chiang, J.; Dermer, C.D. Synchrotron and Synchrotron Self-Compton Emission and the Blast-Wave Model of Gamma-Ray Bursts. Astrophys. J. 1999, 512, 699. [Google Scholar] [CrossRef]
- Stern, B.E.; Poutanen, J. Gamma-ray bursts from synchrotron self-Compton emission. Mon. Not. R. Astron. Soc. 2004, 352, L35–L39. [Google Scholar] [CrossRef]
- Nakar, E.; Ando, S.; Sari, R. Klein-Nishina Effects on Optically Thin Synchrotron and Synchrotron Self-Compton Spectrum. Astrophys. J. 2009, 703, 675–691. [Google Scholar] [CrossRef]
- Ryde, F. Is Thermal Emission in Gamma-Ray Bursts Ubiquitous? Astrophys. J. Lett. 2005, 625, L95. [Google Scholar] [CrossRef]
- Mészáros, P.; Rees, M.J. Steep Slopes and Preferred Breaks in Gamma-Ray Burst Spectra: The Role of Photospheres and Comptonization. Astrophys. J. 2000, 530, 292. [Google Scholar] [CrossRef]
- Pe’er, A.; Mészáros, P.; Rees, M.J. The Observable Effects of a Photospheric Component on GRB and XRF Prompt Emission Spectrum. Astrophys. J. 2006, 642, 995. [Google Scholar] [CrossRef]
- Rybicki, G.B.; Lightman, A.P. Radiative Processes in Astrophysics; A Wiley-Interscience Publication: New York, NY, USA, 1979. [Google Scholar]
- Meszaros, P.; Rees, M.J. Gamma-Ray Bursts: Multiwaveband Spectral Predictions for Blast Wave Models. Astrophys. J. Lett. 1993, 418, L59. [Google Scholar] [CrossRef]
- Spitkovsky, A. On the Structure of Relativistic Collisionless Shocks in Electron-Ion Plasmas. Astrophys. J. Lett. 2008, 673, L39. [Google Scholar] [CrossRef]
- Kumar, P.; Panaitescu, A. Afterglow Emission from Naked Gamma-Ray Bursts. Astrophys. J. Lett. 2000, 541, L51. [Google Scholar] [CrossRef]
- Sari, R. The Observed Size and Shape of Gamma-Ray Burst Afterglow. Astrophys. J. Lett. 1998, 494, L49. [Google Scholar] [CrossRef]
- Sari, R.; Piran, T.; Narayan, R. Spectra and Light Curves of Gamma-Ray Burst Afterglows. Astrophys. J. Lett. 1998, 497, L17. [Google Scholar] [CrossRef]
- Kumar, P.; McMahon, E. A general scheme for modelling γ-ray burst prompt emission. Mon. Not. R. Astron. Soc. 2008, 384, 33. [Google Scholar] [CrossRef]
- Granot, J.; Piran, T.; Sari, R. The Synchrotron Spectrum of Fast Cooling Electrons Revisited. Astrophys. J. Lett. 2000, 534, L163. [Google Scholar] [CrossRef]
- Panaitescu, A.; Mészáros, P. Gamma-Ray Bursts from Upscattered Self-absorbed Synchrotron Emission. Astrophys. J. Lett. 2000, 544, L17. [Google Scholar] [CrossRef]
- Pe’er, A.; Zhang, B. Synchrotron Emission in Small-Scale Magnetic Fields as a Possible Explanation for Prompt Emission Spectra of Gamma-Ray Bursts. Astrophys. J. 2006, 653, 454. [Google Scholar] [CrossRef]
- Gupta, N.; Zhang, B. Diagnosing the site of gamma-ray burst prompt emission with spectral cut-off energy. Mon. Not. R. Astron. Soc. 2008, 384, L11–L15. [Google Scholar] [CrossRef]
- Asano, K.; Mészáros, P. Delayed Onset of High-energy Emissions in Leptonic and Hadronic Models of Gamma-Ray Bursts. Astrophys. J. 2012, 757, 115. [Google Scholar] [CrossRef]
- Pe’er, A.; Waxman, E. Prompt Gamma-Ray Burst Spectra: Detailed Calculations and the Effect of Pair Production. Astrophys. J. 2004, 613, 448–459. [Google Scholar] [CrossRef]
- Pe’er, A.; Mészáros, P.; Rees, M.J. Peak Energy Clustering and Efficiency in Compact Objects. Astrophys. J. 2005, 635, 476. [Google Scholar] [CrossRef]
- Gao, H.; Zhang, B. Photosphere Emission from a Hybrid Relativistic Outflow with Arbitrary Dimensionless Entropy and Magnetization in GRBs. Astrophys. J. 2015, 801, 103. [Google Scholar] [CrossRef]
- Weinberg, S. Cosmology; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- Phillips, M.M. The absolute magnitudes of Type IA supernovae. Astrophys. J. Lett. 1993, 413, L105–L108. [Google Scholar] [CrossRef]
- Silk, J. Cosmic Black-Body Radiation and Galaxy Formation. Astrophys. J. 1968, 151, 459. [Google Scholar] [CrossRef]
- Peebles, P.J.E.; Yu, J.T. Primeval Adiabatic Perturbation in an Expanding Universe. Astrophys. J. 1970, 162, 815. [Google Scholar] [CrossRef]
- Eisenstein, D.J.; Zehavi, I.; Hogg, D.W.; Scoccimarro, R.; Blanton, M.R.; Nichol, R.C.; Scranton, R.; Seo, H.J.; Tegmark, M.; Zheng, Z.; et al. Detection of the Baryon Acoustic Peak in the Large-Scale Correlation Function of SDSS Luminous Red Galaxies. Astrophys. J. 2005, 633, 560–574. [Google Scholar] [CrossRef]
- Planck Collaboration; Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; et al. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar]
- Amati, L.; D’Agostino, R.; Luongo, O.; Muccino, M.; Tantalo, M. Addressing the circularity problem in the Ep-Eiso correlation of gamma-ray bursts. Mon. Not. R. Astron. Soc. 2019, 486, L46–L51. [Google Scholar] [CrossRef]
- Jimenez, R.; Loeb, A. Constraining Cosmological Parameters Based on Relative Galaxy Ages. Astrophys. J. 2002, 573, 37–42. [Google Scholar] [CrossRef]
- Moresco, M.; Pozzetti, L.; Cimatti, A.; Jimenez, R.; Maraston, C.; Verde, L.; Thomas, D.; Citro, A.; Tojeiro, R.; Wilkinson, D. A 6% measurement of the Hubble parameter at z~0.45: Direct evidence of the epoch of cosmic re-acceleration. J. Cosmology Astropart. Phys. 2016, 2016, 014. [Google Scholar] [CrossRef]
- Bond, J.R.; Efstathiou, G. Cosmic background radiation anisotropies in universes dominated by nonbaryonic dark matter. Astrophys. J. Lett. 1984, 285, L45–L48. [Google Scholar] [CrossRef]
- Bond, J.R.; Efstathiou, G.; Tegmark, M. Forecasting cosmic parameter errors from microwave background anisotropy experiments. Mon. Not. R. Astron. Soc. 1997, 291, L33–L41. [Google Scholar]
- Hu, W.; Sugiyama, N. Small-Scale Cosmological Perturbations: An Analytic Approach. Astrophys. J. 1996, 471, 542. [Google Scholar] [CrossRef]
- Norris, J.P.; Scargle, J.D.; Bonnell, J.T. Pulses, spectral lags, durations, and hardness ratios in long GRBs. In Gamma 2001: Gamma-Ray Astrophysics; Ritz, S., Gehrels, N., Shrader, C.R., Eds.; American Institute of Physics Conference Series; American Institute of Physics: College Park, MD, USA, 2001; Volume 587, pp. 176–180. [Google Scholar]
- Dainotti, M.G.; Del Vecchio, R.; Tarnopolski, M. Gamma-Ray Burst Prompt Correlations. Adv. Astron. 2018, 2018, 4969503. [Google Scholar] [CrossRef]
- Fenimore, E.E.; Ramirez-Ruiz, E. Redshifts For 220 BATSE Gamma-Ray Bursts Determined by Variability and the Cosmological Consequences. arXiv 2000, arXiv:astroph:0004176. [Google Scholar]
- Amati, L.; Frontera, F.; Tavani, M.; in’t Zand, J.J.M.; Antonelli, A.; Costa, E.; Feroci, M.; Guidorzi, C.; Heise, J.; Masetti, N.; et al. Intrinsic spectra and energetics of BeppoSAX Gamma-Ray Bursts with known redshifts. Astron. Astrophys. 2002, 390, 81. [Google Scholar] [CrossRef]
- Calderone, G.; Ghirlanda, G.; Ghisellini, G.; Bernardini, M.G.; Campana, S.; Covino, S.; D’Elia, V.; Melandri, A.; Salvaterra, R.; Sbarufatti, B.; et al. There is a short gamma-ray burst prompt phase at the beginning of each long one. Mon. Not. R. Astron. Soc. 2015, 448, 403–416. [Google Scholar] [CrossRef]
- Ghirlanda, G.; Ghisellini, G.; Lazzati, D. The Collimation-corrected Gamma-Ray Burst Energies Correlate with the Peak Energy of Their νFν Spectrum. Astrophys. J. 2004, 616, 331. [Google Scholar] [CrossRef]
- Liang, E.; Zhang, B. Model-independent Multivariable Gamma-Ray Burst Luminosity Indicator and Its Possible Cosmological Implications. Astrophys. J. 2005, 633, 611–623. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Cardone, V.F.; Capozziello, S. A time-luminosity correlation for γ-ray bursts in the X-rays. Mon. Not. R. Astron. Soc. 2008, 391, L79–L83. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Ostrowski, M.; Willingale, R. Towards a standard gamma-ray burst: Tight correlations between the prompt and the afterglow plateau phase emission. Mon. Not. R. Astron. Soc. 2011, 418, 2202–2206. [Google Scholar] [CrossRef]
- Bernardini, M.G.; Margutti, R.; Zaninoni, E.; Chincarini, G. A universal scaling for short and long gamma-ray bursts: EX,iso-E?,iso-Epk. Mon. Not. R. Astron. Soc. 2012, 425, 1199–1204. [Google Scholar] [CrossRef]
- Margutti, R.; Zaninoni, E.; Bernardini, M.G.; Chincarini, G.; Pasotti, F.; Guidorzi, C.; Angelini, L.; Burrows, D.N.; Capalbi, M.; Evans, P.A.; et al. The prompt-afterglow connection in gamma-ray bursts: A comprehensive statistical analysis of Swift X-ray light curves. Mon. Not. R. Astron. Soc. 2013, 428, 729–742. [Google Scholar] [CrossRef]
- Izzo, L.; Muccino, M.; Zaninoni, E.; Amati, L.; Della Valle, M. New measurements of Ωm from gamma-ray bursts. Astron. Astrophys. 2015, 582, A115. [Google Scholar] [CrossRef]
- Muccino, M.; Izzo, L.; Luongo, O.; Boshkayev, K.; Amati, L.; Della Valle, M.; Pisani, G.B.; Zaninoni, E. Tracing Dark Energy History with Gamma-Ray Bursts. Astrophys. J. 2021, 908, 181. [Google Scholar] [CrossRef]
- Tang, C.H.; Huang, Y.F.; Geng, J.J.; Zhang, Z.B. Statistical Study of Gamma-Ray Bursts with a Plateau Phase in the X-Ray Afterglow. Astrophys. J. Suppl. 2019, 245, 1. [Google Scholar] [CrossRef]
- Basilakos, S.; Perivolaropoulos, L. Testing gamma-ray bursts as standard candles. Mon. Not. R. Astron. Soc. 2008, 391, 411–419. [Google Scholar] [CrossRef]
- Nava, L.; Ghirlanda, G.; Ghisellini, G. Selection effects on GRB spectral-energy correlations. In Gamma-Ray Burst: Sixth Huntsville Symposium; Meegan, C., Kouveliotou, C., Gehrels, N., Eds.; American Institute of Physics Conference Series; American Institute of Physics: College Park, MD, USA, 2009; Volume 1133, pp. 350–355. [Google Scholar]
- Schaefer, B.E. The Hubble Diagram to Redshift >6 from 69 Gamma-Ray Bursts. Astrophys. J. 2007, 660, 16. [Google Scholar] [CrossRef]
- Wang, Y. Model-independent distance measurements from gamma-ray bursts and constraints on dark energy. Phys. Rev. D 2008, 78, 123532. [Google Scholar] [CrossRef]
- Margutti, R.; Guidorzi, C.; Chincarini, G.; Bernardini, M.G.; Genet, F.; Mao, J.; Pasotti, F. Lag-luminosity relation in γ-ray burst X-ray flares: A direct link to the prompt emission. Mon. Not. R. Astron. Soc. 2010, 406, 2149–2167. [Google Scholar] [CrossRef]
- Sultana, J.; Kazanas, D.; Fukumura, K. Luminosity Correlations for Gamma-Ray Bursts and Implications for Their Prompt and Afterglow Emission Mechanisms. Astrophys. J. 2012, 758, 32. [Google Scholar] [CrossRef]
- Shahmoradi, A.; Nemiroff, R.J. A Catalog of Redshift Estimates for 1366 BATSE Long-Duration Gamma-Ray Bursts: Evidence for Strong Selection Effects on the Phenomenological Prompt Gamma-Ray Correlations. arXiv 2019, arXiv:1903.06989. [Google Scholar]
- Salmonson, J.D.; Galama, T.J. Discovery of a Tight Correlation between Pulse Lag/Luminosity and Jet-Break Times: A Connection between Gamma-Ray Bursts and Afterglow Properties. Astrophys. J. 2002, 569, 682–688. [Google Scholar] [CrossRef]
- Amati, L.; Della Valle, M. Measuring Cosmological Parameters with Gamma Ray Bursts. Int. J. Mod. Phys. D 2013, 22, 1330028. [Google Scholar] [CrossRef]
- D’Agostini, G. Fits, and especially linear fits, with errors on both axes, extra variance of the data points and other complications. arXiv 2005, arXiv:physics/0511182. [Google Scholar]
- Thompson, C.; Mészáros, P.; Rees, M.J. Thermalization in Relativistic Outflows and the Correlation between Spectral Hardness and Apparent Luminosity in Gamma-Ray Bursts. Astrophys. J. 2007, 666, 1012–1023. [Google Scholar] [CrossRef]
- Butler, N.R.; Kocevski, D.; Bloom, J.S.; Curtis, J.L. A Complete Catalog ofSwiftGamma-Ray Burst Spectra and Durations: Demise of a Physical Origin for Pre-Swift High-Energy Correlations. Astrophys. J. 2007, 671, 656–677. [Google Scholar] [CrossRef]
- Ghirlanda, G.; Nava, L.; Ghisellini, G.; Firmani, C.; Cabrera, J.I. The Epeak-Eiso plane of long gamma-ray bursts and selection effects. Mon. Not. R. Astron. Soc. 2008, 387, 319–330. [Google Scholar] [CrossRef]
- Nava, L.; Ghirlanda, G.; Ghisellini, G.; Firmani, C. Peak energy of the prompt emission of long gamma-ray bursts versus their fluence and peak flux. Mon. Not. R. Astron. Soc. 2008, 391, 639–652. [Google Scholar] [CrossRef][Green Version]
- Amati, L.; Frontera, F.; Guidorzi, C. Extremely energetic Fermi gamma-ray bursts obey spectral energy correlations. Astron. Astrophys. 2009, 508, 173–180. [Google Scholar] [CrossRef]
- Yonetoku, D.; Murakami, T.; Tsutsui, R.; Nakamura, T.; Morihara, Y.; Takahashi, K. Possible Origins of Dispersion of the Peak Energy-Brightness Correlations of Gamma-Ray Bursts. Publ. Astron. Soc. Jpn. 2010, 62, 1495. [Google Scholar] [CrossRef]
- Shahmoradi, A.; Nemiroff, R.J. The possible impact of gamma-ray burst detector thresholds on cosmological standard candles. Mon. Not. R. Astron. Soc. 2011, 411, 1843–1856. [Google Scholar] [CrossRef][Green Version]
- Band, D.L.; Preece, R.D. Testing the Gamma-Ray Burst Energy Relationships. Astrophys. J. 2005, 627, 319–323. [Google Scholar] [CrossRef]
- Friedman, A.S.; Bloom, J.S. Toward a More Standardized Candle Using Gamma-Ray Burst Energetics and Spectra. Astrophys. J. 2005, 627, 1–25. [Google Scholar] [CrossRef]
- Ito, H.; Matsumoto, J.; Nagataki, S.; Warren, D.C.; Barkov, M.V.; Yonetoku, D. The photospheric origin of the Yonetoku relation in gamma-ray bursts. Nat. Commun. 2019, 10, 1504. [Google Scholar] [CrossRef] [PubMed]
- Lu, R.J.; Wei, J.J.; Qin, S.F.; Liang, E.W. Selection Effects on the Observed Redshift Dependence of Gamma-Ray Burst Jet Opening Angles. Astrophys. J. 2012, 745, 168. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Del Vecchio, R. Gamma Ray Burst afterglow and prompt-afterglow relations: An overview. New Astron. Rev. 2017, 77, 23–61. [Google Scholar] [CrossRef]
- Muccino, M.; Boshkayev, K. Physical insight into the Combo-relation. Mon. Not. R. Astron. Soc. 2017, 468, 570–576. [Google Scholar] [CrossRef]
- Kodama, Y.; Yonetoku, D.; Murakami, T.; Tanabe, S.; Tsutsui, R.; Nakamura, T. Gamma-ray bursts in 1.8<z<5.6 suggest that the time variation of the dark energy is small. Mon. Not. R. Astron. Soc. 2008, 391, L1–L4. [Google Scholar]
- Soderberg, A.M.; Berger, E.; Page, K.L.; Schady, P.; Parrent, J.; Pooley, D.; Wang, X.Y.; Ofek, E.O.; Cucchiara, A.; Rau, A.; et al. An extremely luminous X-ray outburst at the birth of a supernova. Nature 2008, 453, 469–474. [Google Scholar] [CrossRef] [PubMed]
- Liang, N.; Xiao, W.K.; Liu, Y.; Zhang, S.N. A Cosmology-Independent Calibration of Gamma-Ray Burst Luminosity Relations and the Hubble Diagram. Astrophys. J. 2008, 685, 354–360. [Google Scholar] [CrossRef]
- Wei, H. Observational constraints on cosmological models with the updated long gamma-ray bursts. J. Cosmology Astropart. Phys. 2010, 2010, 020. [Google Scholar] [CrossRef]
- Gruber, C.; Luongo, O. Cosmographic analysis of the equation of state of the universe through Padé approximations. Phys. Rev. D 2014, 89, 103506. [Google Scholar] [CrossRef]
- Ghirlanda, G.; Ghisellini, G.; Lazzati, D.; Firmani, C. Gamma-Ray Bursts: New Rulers to Measure the Universe. Astrophys. J. Lett. 2004, 613, L13–L16. [Google Scholar] [CrossRef]
- Wang, F.Y.; Dai, Z.G.; Zhu, Z.H. Measuring Dark Energy with Gamma-Ray Bursts and Other Cosmological Probes. Astrophys. J. 2007, 667, 1–10. [Google Scholar] [CrossRef][Green Version]
- Liang, E.; Zhang, B. Calibration of gamma-ray burst luminosity indicators. Mon. Not. R. Astron. Soc. 2006, 369, L37–L41. [Google Scholar] [CrossRef]
- Ghirlanda, G.; Ghisellini, G.; Firmani, C.; Nava, L.; Tavecchio, F.; Lazzati, D. Cosmological constraints with GRBs: Homogeneous medium vs. wind density profile. Astron. Astrophys. 2006, 452, 839–844. [Google Scholar] [CrossRef]
- Khadka, N.; Ratra, B. Constraints on cosmological parameters from gamma-ray burst peak photon energy and bolometric fluence measurements and other data. Mon. Not. R. Astron. Soc. 2020, 499, 391–403. [Google Scholar] [CrossRef]
- Peebles, P.J.E. Tests of cosmological models constrained by inflation. Astrophys. J. 1984, 284, 439–444. [Google Scholar] [CrossRef]
- Di Valentino, E.; Mena, O.; Pan, S.; Visinelli, L.; Yang, W.; Melchiorri, A.; Mota, D.F.; Riess, A.G.; Silk, J. In the Realm of the Hubble tension—A Review of Solutions. arXiv 2021, arXiv:2103.01183. [Google Scholar]
- Perivolaropoulos, L.; Skara, F. Challenges for ΛCDM: An update. arXiv 2021, arXiv:2105.05208. [Google Scholar]
- Farooq, O.; Ranjeet Madiyar, F.; Crandall, S.; Ratra, B. Hubble Parameter Measurement Constraints on the Redshift of the Deceleration-Acceleration Transition, Dynamical Dark Energy, and Space Curvature. Astrophys. J. 2017, 835, 26. [Google Scholar] [CrossRef]
- Scolnic, D.M.; Jones, D.O.; Rest, A.; Pan, Y.C.; Chornock, R.; Foley, R.J.; Huber, M.E.; Kessler, R.; Narayan, G.; Riess, A.G.; et al. The Complete Light-curve Sample of Spectroscopically Confirmed SNe Ia from Pan-STARRS1 and Cosmological Constraints from the Combined Pantheon Sample. Astrophys. J. 2018, 859, 101. [Google Scholar] [CrossRef]
- eBOSS Collaboration. The Completed SDSS-IV extended Baryon Oscillation Spectroscopic Survey: Cosmological Implications from two Decades of Spectroscopic Surveys at the Apache Point observatory. arXiv 2020, arXiv:2007.08991.
- Mania, D.; Ratra, B. Constraints on dark energy from H II starburst galaxy apparent magnitude versus redshift data. Phys. Lett. B 2012, 715, 9–14. [Google Scholar] [CrossRef]
- Chávez, R.; Terlevich, R.; Terlevich, E.; Bresolin, F.; Melnick, J.; Plionis, M.; Basilakos, S. The L-σ relation for massive bursts of star formation. Mon. Not. R. Astron. Soc. 2014, 442, 3565–3597. [Google Scholar] [CrossRef]
- González-Morán, A.L.; Chávez, R.; Terlevich, R.; Terlevich, E.; Bresolin, F.; Fernández-Arenas, D.; Plionis, M.; Basilakos, S.; Melnick, J.; Telles, E. Independent cosmological constraints from high-z H II galaxies. Mon. Not. R. Astron. Soc. 2019, 487, 4669–4694. [Google Scholar] [CrossRef]
- González-Morán, A.L.; Chávez, R.; Terlevich, E.; Terlevich, R.; Fernández-Arenas, D.; Bresolin, F.; Plionis, M.; Melnick, J.; Basilakos, S.; Telles, E. Independent cosmological constraints from high-z HII galaxies: New results from VLT-KMOS data. arXiv 2021, arXiv:2105.04025. [Google Scholar]
- Cao, S.; Ryan, J.; Ratra, B. Cosmological constraints from H II starburst galaxy apparent magnitude and other cosmological measurements. Mon. Not. R. Astron. Soc. 2020, 497, 3191–3203. [Google Scholar] [CrossRef]
- Cao, S.; Ryan, J.; Khadka, N.; Ratra, B. Cosmological constraints from higher redshift gamma-ray burst, H II starburst galaxy, and quasar (and other) data. Mon. Not. R. Astron. Soc. 2021, 501, 1520–1538. [Google Scholar] [CrossRef]
- Johnson, J.P.; Sangwan, A.; Shankaranarayanan, S. Cosmological perturbations in the interacting dark sector: Observational constraints and predictions. arXiv 2021, arXiv:2102.12367. [Google Scholar]
- Cao, S.; Zheng, X.; Biesiada, M.; Qi, J.; Chen, Y.; Zhu, Z.H. Ultra-compact structure in intermediate-luminosity radio quasars: Building a sample of standard cosmological rulers and improving the dark energy constraints up to z 3. Astron. Astrophys. 2017, 606, A15. [Google Scholar] [CrossRef]
- Ryan, J.; Chen, Y.; Ratra, B. Baryon acoustic oscillation, Hubble parameter, and angular size measurement constraints on the Hubble constant, dark energy dynamics, and spatial curvature. Mon. Not. R. Astron. Soc. 2019, 488, 3844–3856. [Google Scholar] [CrossRef]
- Cao, S.; Ryan, J.; Ratra, B. Using Pantheon and DES supernova, baryon acoustic oscillation, and Hubble parameter data to constrain the Hubble constant, dark energy dynamics, and spatial curvature. Mon. Not. R. Astron. Soc. 2021, 504, 300–310. [Google Scholar] [CrossRef]
- Zheng, X.; Cao, S.; Biesiada, M.; Li, X.; Liu, T.; Liu, Y. Multiple measurements of quasars acting as standard probes: Model independent calibration and exploring the dark energy equation of states. Sci. China Physics, Mech. Astron. 2021, 64, 259511. [Google Scholar] [CrossRef]
- Lian, Y.; Cao, S.; Biesiada, M.; Chen, Y.; Zhang, Y.; Guo, W. Probing modified gravity theories with multiple measurements of high-redshift quasars. arXiv 2021, arXiv:2105.04992. [Google Scholar]
- Risaliti, G.; Lusso, E. A Hubble Diagram for Quasars. Astrophys. J. 2015, 815, 33. [Google Scholar] [CrossRef]
- Risaliti, G.; Lusso, E. Cosmological Constraints from the Hubble Diagram of Quasars at High Redshifts. Nat. Astron. 2019, 3, 272–277. [Google Scholar] [CrossRef]
- Khadka, N.; Ratra, B. Quasar X-ray and UV flux, baryon acoustic oscillation, and Hubble parameter measurement constraints on cosmological model parameters. Mon. Not. R. Astron. Soc. 2020, 492, 4456–4468. [Google Scholar] [CrossRef]
- Khadka, N.; Ratra, B. Using quasar X-ray and UV flux measurements to constrain cosmological model parameters. Mon. Not. R. Astron. Soc. 2020, 497, 263–278. [Google Scholar] [CrossRef]
- Khadka, N.; Ratra, B. Determining the range of validity of quasar X-ray and UV flux measurements for constraining cosmological model parameters. Mon. Not. R. Astron. Soc. 2021, 502, 6140–6156. [Google Scholar] [CrossRef]
- Yang, T.; Banerjee, A.; Ó Colgáin, E. Cosmography and flat Λ CDM tensions at high redshift. Phys. Rev. D 2020, 102, 123532. [Google Scholar] [CrossRef]
- Lusso, E.; Risaliti, G.; Nardini, E.; Bargiacchi, G.; Benetti, M.; Bisogni, S.; Capozziello, S.; Civano, F.; Eggleston, L.; Elvis, M.; et al. Quasars as standard candles. III. Validation of a new sample for cosmological studies. Astron. Astrophys. 2020, 642, A150. [Google Scholar] [CrossRef]
- Li, X.; Keeley, R.E.; Shafieloo, A.; Zheng, X.; Cao, S.; Biesiada, M.; Zhu, Z.H. Hubble diagram at higher redshifts: Model independent calibration of quasars. arXiv 2021, arXiv:2103.16032. [Google Scholar]
- Cucchiara, A.; Levan, A.J.; Fox, D.B.; Tanvir, N.R.; Ukwatta, T.N.; Berger, E.; Krühler, T.; Küpcü Yoldaş, A.; Wu, X.F.; Toma, K.; et al. A Photometric Redshift of z 9.4 for GRB 090429B. Astrophys. J. 2011, 736, 7. [Google Scholar] [CrossRef]
- Amati, L.; Guidorzi, C.; Frontera, F.; Della Valle, M.; Finelli, F.; Landi, R.; Montanari, E. Measuring the cosmological parameters with the Ep,i–Eiso correlation of gamma-ray bursts. Mon. Not. R. Astron. Soc. 2008, 391, 577. [Google Scholar] [CrossRef]
- Capozziello, S.; Izzo, L. Cosmography by gamma ray bursts. Astron. Astrophys. 2008, 490, 31–36. [Google Scholar] [CrossRef]
- Izzo, L.; Capozziello, S.; Covone, G.; Capaccioli, M. Extending the Hubble diagram by gamma ray bursts. Astron. Astrophys. 2009, 508, 63–67. [Google Scholar] [CrossRef]
- Wei, J.J.; Wu, X.F.; Melia, F.; Wei, D.M.; Feng, L.L. Cosmological tests using gamma-ray bursts, the star formation rate and possible abundance evolution. Mon. Not. R. Astron. Soc. 2014, 439, 3329–3341. [Google Scholar] [CrossRef]
- Schaefer, B.E. Gamma-Ray Burst Hubble Diagram to z=4.5. Astrophys. J. Lett. 2003, 583, L67–L70. [Google Scholar] [CrossRef]
- Dai, Z.G.; Liang, E.W.; Xu, D. Constraining ΩM and Dark Energy with Gamma-Ray Bursts. Astrophys. J. Lett. 2004, 612, L101–L104. [Google Scholar] [CrossRef]
- Samushia, L.; Ratra, B. Constraining Dark Energy with Gamma-ray Bursts. Astrophys. J. 2010, 714, 1347–1354. [Google Scholar] [CrossRef][Green Version]
- Liu, J.; Wei, H. Cosmological models and gamma-ray bursts calibrated by using Padé method. Gen. Relativ. Gravit. 2015, 47, 141. [Google Scholar] [CrossRef]
- Lin, H.N.; Li, X.; Chang, Z. Model-independent distance calibration of high-redshift gamma-ray bursts and constrain on the ΛCDM model. Mon. Not. R. Astron. Soc. 2016, 455, 2131–2138. [Google Scholar] [CrossRef]
- Huang, L.; Huang, Z.; Luo, X.; He, X.; Fang, Y. Revisiting the Redshift Evolution of GRB Luminosity Correlation with PAge Approximation. arXiv 2020, arXiv:2012.02474. [Google Scholar]
- Tang, L.; Li, X.; Lin, H.N.; Liu, L. Model-independently Calibrating the Luminosity Correlations of Gamma-Ray Bursts Using Deep Learning. Astrophys. J. 2021, 907, 121. [Google Scholar] [CrossRef]
- Demianski, M.; Piedipalumbo, E.; Sawant, D.; Amati, L. Cosmology with gamma-ray bursts. II. Cosmography challenges and cosmological scenarios for the accelerated Universe. Astron. Astrophys. 2017, 598, A113. [Google Scholar] [CrossRef]
- Demianski, M.; Piedipalumbo, E.; Sawant, D.; Amati, L. High redshift constraints on dark energy models and tension with the flat LambdaCDM model. arXiv 2019, arXiv:1911.08228. [Google Scholar]
- Luongo, O.; Muccino, M. Kinematic constraints beyond z≃0 using calibrated GRB correlations. Astron. Astrophys. 2020, 641, 15. [Google Scholar] [CrossRef]
- Luongo, O.; Muccino, M. Model independent calibrations of gamma ray bursts using machine learning. arXiv 2020, arXiv:2011.13590. [Google Scholar]
- Rezaei, M.; Pour-Ojaghi, S.; Malekjani, M. A Cosmography Approach to Dark Energy Cosmologies: New Constraints Using the Hubble Diagrams of Supernovae, Quasars, and Gamma-Ray Bursts. Astrophys. J. 2020, 900, 70. [Google Scholar] [CrossRef]
- Lusso, E.; Piedipalumbo, E.; Risaliti, G.; Paolillo, M.; Bisogni, S.; Nardini, E.; Amati, L. Tension with the flat ΛCDM model from a high-redshift Hubble diagram of supernovae, quasars, and gamma-ray bursts. Astron. Astrophys. 2019, 628, L4. [Google Scholar] [CrossRef]
- Kumar, D.; Jain, D.; Mahajan, S.; Mukherjee, A.; Rani, N. Constraining cosmological and galaxy parameters using strong gravitational lensing systems. Phys. Rev. D 2021, 103, 063511. [Google Scholar] [CrossRef]
- Montiel, A.; Cabrera, J.I.; Hidalgo, J.C. Improving sampling and calibration of gamma-ray bursts as distance indicators. Mon. Not. R. Astron. Soc. 2021, 501, 3515–3526. [Google Scholar]
- Riess, A.G.; Casertano, S.; Yuan, W.; Macri, L.M.; Scolnic, D. Large Magellanic Cloud Cepheid Standards Provide a 1% Foundation for the Determination of the Hubble Constant and Stronger Evidence for Physics beyond ΛCDM. Astrophys. J. 2019, 876, 85. [Google Scholar] [CrossRef]
- Fana Dirirsa, F.; Razzaque, S.; Piron, F.; Arimoto, M.; Axelsson, M.; Kocevski, D.; Longo, F.; Ohno, M.; Zhu, S. Spectral Analysis of Fermi-LAT Gamma-Ray Bursts with Known Redshift and their Potential Use as Cosmological Standard Candles. Astrophys. J. 2019, 887, 13. [Google Scholar] [CrossRef]
- Wang, J.S.; Wang, F.Y.; Cheng, K.S.; Dai, Z.G. Measuring dark energy with the Eiso - Ep correlation of gamma-ray bursts using model-independent methods. Astron. Astrophys. 2016, 585, A68. [Google Scholar] [CrossRef]
- Yang, T.; Banerjee, A.; Colgáin, E.Ó. On cosmography and flat ΛCDM tensions at high redshift. arXiv 2019, arXiv:1911.01681. [Google Scholar]
- Betoule, M.; Kessler, R.; Guy, J.; Mosher, J.; Hardin, D.; Biswas, R.; Astier, P.; El-Hage, P.; Konig, M.; Kuhlmann, S.; et al. Improved cosmological constraints from a joint analysis of the SDSS-II and SNLS supernova samples. Astron. Astrophys. 2014, 568, A22. [Google Scholar] [CrossRef]
- Akaike, H. A New Look at the Statistical Model Identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Kunz, M.; Trotta, R.; Parkinson, D. Measuring the effective complexity of cosmological models. Phys. Rev. 2006, D74, 023503. [Google Scholar] [CrossRef]
- Liddle, A.R. Information criteria for astrophysical model selection. Mon. Not. Roy. Astron. Soc. 2007, 377, L74–L78. [Google Scholar] [CrossRef]
- Stanek, K.Z.; Matheson, T.; Garnavich, P.M.; Martini, P.; Berlind, P.; Caldwell, N.; Challis, P.; Brown, W.R.; Schild, R.; Krisciunas, K.; et al. Spectroscopic Discovery of the Supernova 2003dh Associated with GRB 030329. Astrophys. J. Lett. 2003, 591, L17. [Google Scholar] [CrossRef]
- Totani, T. Cosmological Gamma-Ray Bursts and Evolution of Galaxies. Astrophys. J. Lett. 1997, 486, L71–L74. [Google Scholar] [CrossRef]
- Wijers, R.A.M.J.; Bloom, J.S.; Bagla, J.S.; Natarajan, P. Gamma-ray bursts from stellar remnants: Probing the Universe at high redshift. Mon. Not. R. Astron. Soc. 1998, 294, L13–L17. [Google Scholar] [CrossRef]
- Lamb, D.Q.; Reichart, D.E. Gamma-Ray Bursts as a Probe of the Very High Redshift Universe. Astrophys. J. 2000, 536, 1. [Google Scholar] [CrossRef]
- Porciani, C.; Madau, P. On the Association of Gamma-Ray Bursts with Massive Stars: Implications for Number Counts and Lensing Statistics. Astrophys. J. 2001, 548, 522–531. [Google Scholar] [CrossRef]
- Bromm, V.; Loeb, A. The Expected Redshift Distribution of Gamma-Ray Bursts. Astrophys. J. 2002, 575, 111–116. [Google Scholar] [CrossRef]
- Wanderman, D.; Piran, T. The luminosity function and the rate of Swift’s gamma-ray bursts. Mon. Not. R. Astron. Soc. 2010, 406, 1944–1958. [Google Scholar] [CrossRef]
- Cao, X.F.; Yu, Y.W.; Cheng, K.S.; Zheng, X.P. The luminosity function of Swift long gamma-ray bursts. Mon. Not. R. Astron. Soc. 2011, 416, 2174–2181. [Google Scholar] [CrossRef][Green Version]
- Tan, W.W.; Cao, X.F.; Yu, Y.W. Determining the Luminosity Function of Swift Long Gamma-Ray Bursts with Pseudo-redshifts. Astrophys. J. Lett. 2013, 772, L8. [Google Scholar] [CrossRef]
- Pescalli, A.; Ghirlanda, G.; Salvaterra, R.; Ghisellini, G.; Vergani, S.D.; Nappo, F.; Salafia, O.S.; Melandri, A.; Covino, S.; Götz, D. The rate and luminosity function of long gamma ray bursts. Astron. Astrophys. 2016, 587, A40. [Google Scholar] [CrossRef]
- Virgili, F.J.; Zhang, B.; O’Brien, P.; Troja, E. Are All Short-hard Gamma-ray Bursts Produced from Mergers of Compact Stellar Objects? Astrophys. J. 2011, 727, 109. [Google Scholar] [CrossRef]
- Wang, F.Y.; Dai, Z.G.; Liang, E.W. Gamma-ray burst cosmology. New Astron. Rev. 2015, 67, 1–17. [Google Scholar] [CrossRef]
- Wang, F.Y. The high-redshift star formation rate derived from gamma-ray bursts: Possible origin and cosmic reionization. Astron. Astrophys. 2013, 556, A90. [Google Scholar] [CrossRef]
- Le, T.; Dermer, C.D. On the Redshift Distribution of Gamma-Ray Bursts in the Swift Era. Astrophys. J. 2007, 661, 394–415. [Google Scholar] [CrossRef]
- Salvaterra, R.; Chincarini, G. The Gamma-Ray Burst Luminosity Function in the Light of the Swift 2 Year Data. Astrophys. J. Lett. 2007, 656, L49–L52. [Google Scholar] [CrossRef]
- Kistler, M.D.; Yüksel, H.; Beacom, J.F.; Stanek, K.Z. An Unexpectedly Swift Rise in the Gamma-Ray Burst Rate. Astrophys. J. Lett. 2008, 673, L119. [Google Scholar] [CrossRef]
- Wang, F.Y.; Dai, Z.G.; Qi, S. Constraints on generalized Chaplygin gas model including gamma-ray bursts. Res. Astron. Astrophys. 2009, 9, 547–557. [Google Scholar] [CrossRef][Green Version]
- Robertson, B.E.; Ellis, R.S. Connecting the Gamma Ray Burst Rate and the Cosmic Star Formation History: Implications for Reionization and Galaxy Evolution. Astrophys. J. 2012, 744, 95. [Google Scholar] [CrossRef]
- Bouwens, R.J.; Illingworth, G.D.; Bradley, L.D.; Ford, H.; Franx, M.; Zheng, W.; Broadhurst, T.; Coe, D.; Jee, M.J. Z 7-10 Galaxies Behind Lensing Clusters: Contrast with Field Search Results. Astrophys. J. 2009, 690, 1764. [Google Scholar] [CrossRef][Green Version]
- Levesque, E.M.; Kewley, L.J.; Berger, E.; Zahid, H.J. The Host Galaxies of Gamma-ray Bursts. II. A Mass-metallicity Relation for Long-duration Gamma-ray Burst Host Galaxies. Astron. J. 2010, 140, 1557–1566. [Google Scholar] [CrossRef]
- Niino, Y. Revisiting the metallicity of long-duration gamma-ray burst host galaxies: The role of chemical inhomogeneity within galaxies. Mon. Not. R. Astron. Soc. 2011, 417, 567–572. [Google Scholar] [CrossRef][Green Version]
- Marani, G.F.; Nemiroff, R.J.; Norris, J.P.; Bonnell, J.T. A new gravitational lens search for gamma ray bursts. In Gamma-Ray Bursts: 3rd Huntsville Symposium; Kouveliotou, C., Briggs, M.F., Fishman, G.J., Eds.; American Institute of Physics Conference Series; American Institute of Physics: College Park, MD, USA, 1996; Volume 384, pp. 487–491. [Google Scholar]
- Davidson, R.; Bhat, P.N.; Li, G. Are there Gravitationally Lensed Gamma-ray Bursts detected by GBM? In Gamma Ray Bursts 2010; McEnery, J.E., Racusin, J.L., Gehrels, N., Eds.; American Institute of Physics Conference Series; American Institute of Physics: College Park, MD, USA, 2011; Volume 1358, pp. 17–20. [Google Scholar]
- Li, C.; Li, L. Search for strong gravitational lensing effect in the current GRB data of BATSE. Sci. China Physics, Mech. Astron. 2014, 57, 1592–1599. [Google Scholar] [CrossRef]
- Hurley, K.; Tsvetkova, A.E.; Svinkin, D.S.; Aptekar, R.L.; Frederiks, D.D.; Golenetskii, S.V.; Kokomov, A.A.; Kozlova, A.V.; Lysenko, A.L.; Ulanov, M.V.; et al. A Search for Gravitationally Lensed Gamma-Ray Bursts in the Data of the Interplanetary Network and Konus-Wind. Astrophys. J. 2019, 871, 121. [Google Scholar] [CrossRef]
- Ahlgren, B.; Larsson, J. A Search for Lensed Gamma-Ray Bursts in 11 yr of Observations by Fermi GBM. Astrophys. J. 2020, 897, 178. [Google Scholar] [CrossRef]
- Ougolnikov, O.S. A Search for Possible Mesolensing of Cosmic Gamma-Ray Bursts: II. Double and Triple Bursts in the BATSE Catalog. Cosm. Res. 2003, 41, 141–146. [Google Scholar] [CrossRef]
- Hirose, Y.; Umemura, M.; Yonehara, A.; Sato, J. Imprint of Gravitational Lensing by Population III Stars in Gamma-Ray Burst Light Curves. Astrophys. J. 2006, 650, 252–260. [Google Scholar] [CrossRef][Green Version]
- Ji, L.; Kovetz, E.D.; Kamionkowski, M. Strong lensing of gamma ray bursts as a probe of compact dark matter. Phys. Rev. D 2018, 98, 123523. [Google Scholar] [CrossRef]
- Paynter, J.; Webster, R.; Thrane, E. Evidence for an intermediate-mass black hole from a gravitationally lensed gamma-ray burst. Nat. Astron. 2021, 5, 560–568. [Google Scholar] [CrossRef]
- Kalantari, Z.; Ibrahim, A.; Rahimi Tabar, M.R.; Rahvar, S. Imprints of Gravitational Microlensing on the Light Curve of GRBs. arXiv 2021, arXiv:2105.00585. [Google Scholar]
- Marani, G.F.; Nemiroff, R.J.; Norris, J.P.; Hurley, K.; Bonnell, J.T. Gravitationally Lensed Gamma-Ray Bursts as Probes of Dark Compact Objects. Astrophys. J. Lett. 1999, 512, L13–L16. [Google Scholar] [CrossRef]

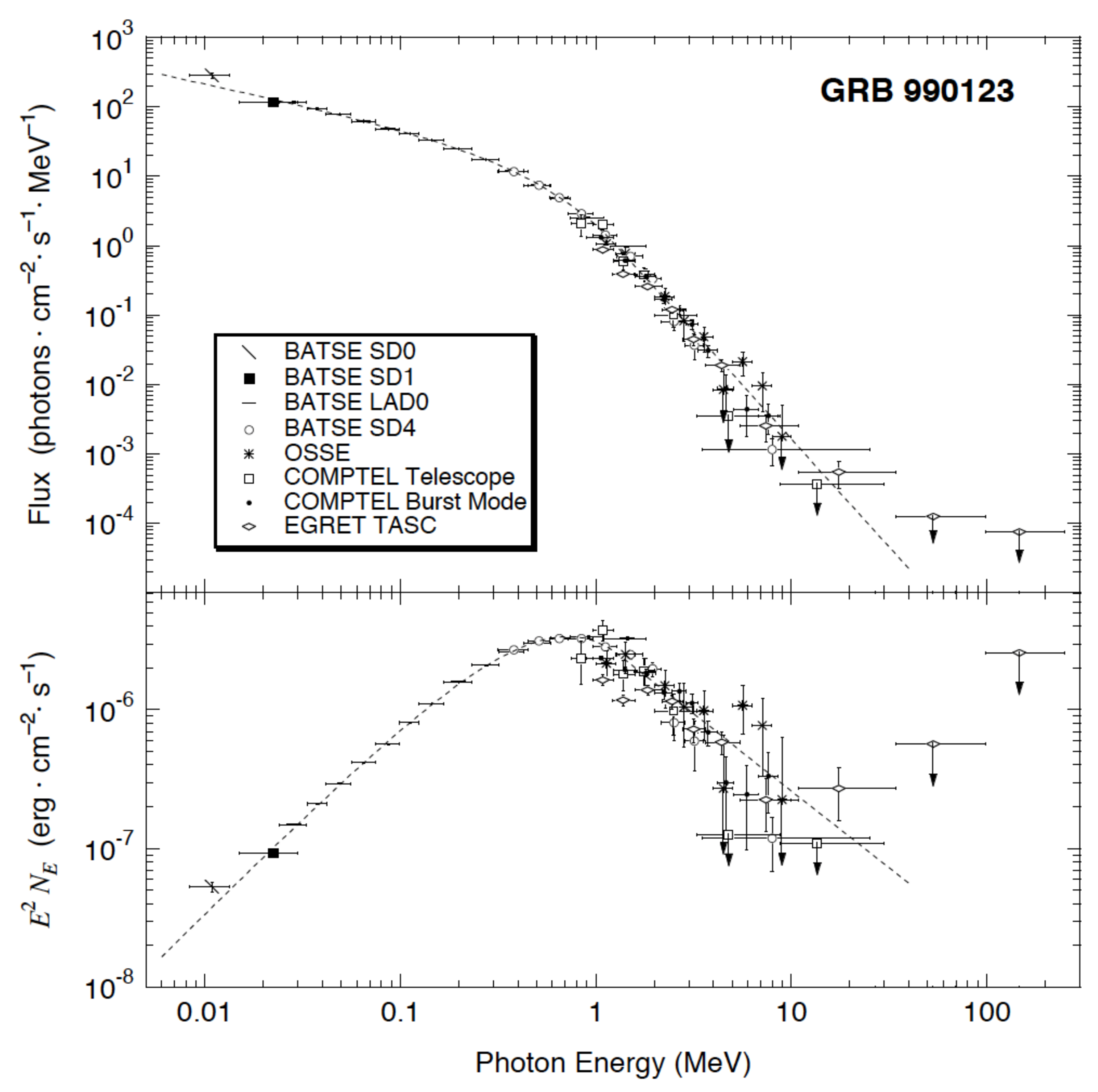
| Correlation | N | Update | Parameters | ||
|---|---|---|---|---|---|
| Amati | 193 | 2015 | |||
| Ghirlanda | 27 | 2007 | |||
| Yonetoku | 101 | 2018 | |||
| Combo | 60 | 2015 | |||
| Correlation | Sample | (km sMpc) | Reference | |||
|---|---|---|---|---|---|---|
| Amati (193) | GRB + SNIa | 0 | [123] | |||
| Amati (74) | GRB + SNIa + BAO + CMB | 0 | [221] | |||
| Combo (174) | GRB | 0 | [141] | |||
| 0 | ||||||
| Amati (118) | GRB + + BAO | 0 | [175] | |||
| Amati (118) | GRB + + BAO + QSO + HIIG | 0 | [186] |
| Taylor Fits | |||||||
|---|---|---|---|---|---|---|---|
| Hierarchy1 | Hierarchy2 | ||||||
| A | |||||||
| G | |||||||
| Y | |||||||
| C | |||||||
| Fits | |||||||
|---|---|---|---|---|---|---|---|
| Hierarchy1 | Hierarchy2 | ||||||
| A | |||||||
| G | |||||||
| Y | |||||||
| C | |||||||
| Padé Fits | |||
|---|---|---|---|
| Hierarchy1 | |||
| A | |||
| G | |||
| Y | |||
| C | |||
| Sample | DoF | Hierarchy | Approximant | ||
|---|---|---|---|---|---|
| Taylor | Function | Padé | |||
| Combo | 1113 | 1 | |||
| 1112 | 2 | ||||
| Ghirlanda | 1080 | 1 | |||
| 1079 | 2 | ||||
| Yonetoku | 1154 | 1 | |||
| 1153 | 2 | ||||
| Amati | 1246 | 1 | |||
| 1245 | 2 | ||||
| Model | AIC | DIC | ||
|---|---|---|---|---|
| CDM | −1 | 0 | 0 | |
| wCDM |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luongo, O.; Muccino, M. A Roadmap to Gamma-Ray Bursts: New Developments and Applications to Cosmology. Galaxies 2021, 9, 77. https://doi.org/10.3390/galaxies9040077
Luongo O, Muccino M. A Roadmap to Gamma-Ray Bursts: New Developments and Applications to Cosmology. Galaxies. 2021; 9(4):77. https://doi.org/10.3390/galaxies9040077
Chicago/Turabian StyleLuongo, Orlando, and Marco Muccino. 2021. "A Roadmap to Gamma-Ray Bursts: New Developments and Applications to Cosmology" Galaxies 9, no. 4: 77. https://doi.org/10.3390/galaxies9040077
APA StyleLuongo, O., & Muccino, M. (2021). A Roadmap to Gamma-Ray Bursts: New Developments and Applications to Cosmology. Galaxies, 9(4), 77. https://doi.org/10.3390/galaxies9040077






