1. Introduction
The universe is opaque to the propagation of radiation in particular of its most energetic component, that is cosmic rays (CRs). This part of the extraterrestrial radiation is composed of charged particles, protons and heavier (bare) nuclei, most likely of extragalactic origin. Since the universe opacity is more pronounced at the highest energies, in this work we deal with Ultra High Energy Cosmic Rays (UHECRs) that is the most energetic fraction of CR with energies larger than ∼10
eV. CRs during their propagation may interact with background radiation fields in particular with the Extragalactic Background Light (EBL) and at sufficiently high energies with the Cosmic Microwave Background (CMB) being attenuated in a way that depends on their energy and nature. The UHECR’s lightest component, protons with energies above the photopion threshold ∼5 × 10
eV, dissipate energy mainly via pair production or photopion creation, instead the heavier component composed of bare nuclei can also undergo photodissociation processes. A CR can be generated with a limited energy proportional to the product of the magnetic field and the dimension of any candidate source:
, following the so-called
Hillas criterion [
1]. Since UHECRs’ free propagation path is finite and their energy is limited, they can be detected on Earth only under a determined energy threshold if they propagate for long enough distances. This phenomenon poses an upper limit on the detectable UHECRs energy and in the case of the lightest component is named GZK cut-off from the name of the physicists Greisen, Zatsepin and Kuzmin [
2,
3].
The physics correlated with the UHECR propagation can be exploited to investigate new phenomena, such as the supposed quantum structure of the spacetime [
4,
5,
6,
7,
8,
9]. Astroparticle physics can be a useful framework to conduct searches for possible departures from the Lorentz covariance since in some theoretical models the quantum gravity (QG) effects are supposed to be more visible in the high-energy limit as Lorentz Invariance Violation (LIV) effects. UHECRs propagate for cosmic distances and reach extremely high energies, therefore they can open a window on the Planck scale physics.
Currently, there is no definitive theory that unifies quantum physics with gravity. The greatest challenge in formulating such a unified theory is the actual impossibility of obtaining the energies needed to probe the Planck scale realm. It is commonly believed that the Planck energy represents the threshold that separates the classical formulation of physics, which is General Relativity (GR), from the quantum realm, represented by Quantum Field Theory (QFT). Nevertheless some QG signatures may become manifest in a low-energy regime as residual effects and these perturbations of standard physics may give access to the possible phenomenology induced by QG.
In this work, we investigate the possibility to detect QG signatures as departures from the Lorentz covariance in the UHECR sector. Indeed, the introduction of QG motivated modifications could modify the threshold of physical processes in UHECR physics, influencing the generation of hadronic showers in the atmosphere at the detection. Moreover, QG can perturb at sufficiently high energies the free particle kinematics reducing the interaction with the background fields, mainly the CMB, and the related energy dissipation caused by the GZK effect and photodissociation process, resulting in an enlargement of the volume of the universe accessible at UHECRs. A natural way of looking for QG signals involves the determination of UHECR propagation length. This result can be obtained by finding out the source of these particles, for instance, detecting anisotropies in their flux. Indeed, anisotropy searches will require a better knowledge of the supposed UHECR sources distribution.
The comprehension of UHECR physics must be improved in order to conduct the anisotropy analysis that underlies all the potential QG studies in the CR propagation sector. Indeed, this analysis can be spoiled by the presence of Galactic (GMF) and Extragalactic Magnetic Fields (EGMF). Since CR are charged particles, their trajectories are affected by magnetic fields and the measure of the deflection can be obtained evaluating the particle rigidity, that is the ratio of CR energy and charge:
, for higher rigidity values the resulting deflections are smaller:
, where
is the average deflection angle. The theoretical and experimental uncertainties about EBL, GMF [
10,
11] and particularly EGMF can spoil this analysis. Posing constraints on the magnitude of EGMF, for instance, is extremely complicated since the universe is mostly composed of cosmic void, therefore the EGMF magnitude evaluation ranges from ∼×10
G [
12] to ∼×10
G [
13]. Most of the studies about EGMF effects on UHECR propagation are conducted by simulating the cosmological structure formation, but with conflicting and inconclusive results [
14,
15]. A last remark about the necessity of better understanding the nature of the primary CR in order to discriminate the lighter UHECR component from the heavier one on a particle-by-particle basis. Recent studies of the Pierre Auger collaboration indicate that above the energy threshold of ∼×10
eV the CR flux is dominated by the light primaries, nevertheless as the energy increases the lightest fraction (protons) seems to be partially replaced by an intermediate mass component (He-N) with a Fe contribution above ∼×10
eV [
16,
17].
The phenomenological analysis conducted to detect the presumed QG effects in the present study is limited to the lightest component of the UHECRs, that is protons. This component is interesting since it is the least deflected one by magnetic fields during propagation. In fact, UHE protons can reach rigidities beyond ∼20 × 10 eV presenting ballistic trajectories, which can allow for small-scale anisotropies searches.
For a more exhaustive and complete introduction on the CR physics and the related issues, we suggest the lecture of the review [
18].
There are many theoretical models that investigate the possibility of modifications as QG-induced perturbations [
4,
19,
20,
21,
22,
23,
24,
25], but we conduct our investigation in the context of Homogeneously Modified Special Relativity (HMSR) [
26]. In this theoretical framework the covariance is modified and not broken as in Doubly Special Relativity (DSR) [
22,
23,
24,
25]. Hence, the kinematical symmetry is again valid in an amended formulation and the introduction of a privileged reference frame is not required. In this context a minimal extension of the Standard Model (SM) of particle physics can be formulated preserving the modified covariance. The QG perturbations are introduced in the free particle kinematics modifying the dispersion relations (DRs). This idea is motivated by the hypothesis that the effects induced by the quantum structure of the background can be geometrized requiring a more general structure to set the theory than the usual Riemann geometry, that is the Finsler one. The introduction of QG kinematical perturbations can modify the allowed phase space for the interaction with the CMB and the pion creation process. The phenomenological effects are evaluated via numerical simulations conducted using an ad hoc version of the software
SimProp [
27], modified in order to include the QG kinematical perturbations [
8]. The introduction of Lorentz covariance modifications induce an opacity horizon enlargement [
7,
8], as foreseen even in the case of pure LIV [
4,
5,
6].
This work is structured as follows: first we introduce the theoretical framework motivated by the QG perspective, geometrizing the interaction of a free particle with the background. Then, we introduce a minimal extension of the Standard Model of particle physics in an amended covariant formulation. In the following we introduce the physics related with the UHECRs propagation explaining where the QG effects can manifest themselves. Afterwards, we present the numerical results obtained via the modified SimProp software. Finally, we analyze the results with particular emphasis on the possibility of obtaining detectable phenomenological effects in this sector in the context of a covariant framework, that retains a modified version of the kinematical symmetry group (the Lorentz/Poincaré one).
3. Finsler Geometry
We give now a brief introduction to Finsler geometry that will be useful in the following. A Finsler geometric structure can be defined as a manifold M where in every tangent space a norm function F is defined not necessarily starting from an inner product. F is a positively homogeneous norm only if the Hessian of is positive definite. The norm must be a real and positive definite function of the section of the tangent space , which depends on the point x and on a vector . The norm must be 1-degree homogeneous with respect to the vectors satisfying the relations:
.
In Finsler geometry the norm can define a local metric via the equation:
which requires that
and
. In this way, it is possible to reobtain a vector norm:
As in Riemann geometry it is possible to define a duality relation between vectors and dual forms defining the Legendre transform. Using the metric the resulting bijection is given by:
The previous definition is valid for a Finsler structure with a definite signature of the metric, but it must be generalized in order to deal with the physical spacetime, which exhibits a Minkowski-type underlying metric of indefinite-signature. A systematical introduction to this issue and the so-called pseudo-Finsler geometry can be found in [
32,
33,
34,
35,
36,
37]. Here, we follow the definition given in [
33,
35] and pose a pseudo-Finsler geometric structure modifying the previous definition and requiring that:
there exists a connected component T of the pre-image of , such that on T the metric defined by the Hessian exists, is smooth and has Lorentzian signature .
A typical difference between Finsler and Riemann geometry consists in the necessity to consider the fiber bundle since in the first case objects exist on
, whereas in the second, they do so on the manifold
M. This fact implies that in Finsler geometry, vectors and covectors must be studied in
and
, respectively. Moreover, it is necessary to introduce the horizontal-vertical decomposition and the related nonlinear connection for the
and
structures, as in [
38].
Considering
, one can introduce the
vertical distribution generated by the derivative
as:
Given the vertical distribution, it is possible to identify a complementary structure, the
horizontal distribution, named
nonlinear connection, for which the Whitney decomposition is valid [
39]:
The nonlinear connection is a collection of homogeneous functions of degree 1, locally defined on the manifold, such that:
In this work, we follow [
38] and as nonlinear connection we choose the usual General Relativity (GR) form:
where
represents the GR affine connection. The choice for a nonlinear connection is not uniquely defined, but this particular formulation is the most convenient one in this context.
Analogously, the cotangent space is spanned by the differential basis defined by:
In the context of Finsler geometry, it is possible to generalize the definition of the affine connection via the general Christoffel symbols:
and the geodesic equations become:
The study conducted in this work can be generalized with these prescriptions in a curved spacetime. In the following, we will consider a geometry with no matter induced curvature for the investigation of the phenomenology introduced in the propagation of UHECRs. Hence, the nonlinear connection Equation (
12) is zero and the derivative Equation (
11) reduces to the usual partial derivative.
4. Finsler Geometry and HMSR
The MDR (
1) can be interpreted as the Finsler pseudo-norm characterizing the spacetime (momentum space) structure. In HMSR, the standard physics is modified in a CPT-even scenario, the MDRs, indeed, do not exhibit any dependence on helicities, for instance, and are supposed to be equal for particles and the related antiparticles. A well-known result about fundamental physics symmetry states that in a CPT-odd scenario the Lorentz symmetry as usually formulated must be violated, whereas the opposite statement is not automatically true, and therefore it is possible to violate or modify covariance, while preserving the CPT symmetry [
40,
41]. A review on the implications of the CPT symmetry in particle and astroparticle physics and its relation to the Lorentz/Poincaré symmetry is presented, for instance, in [
42].
Following the idea presented in [
26], the MDR Equation (
1) are promoted to the role of a Finsler norm and the related momentum space metric is obtained as the Hessian of the squared norm:
Since the function
is 2-degree homogeneous, the computation produces a 0-homogeneous tensor that can be written as:
with a diagonal matrix
D:
The matrix
D is the associated generalized Hamilton’s space metric that effectively contributes to the computation of the MDR Equation (
1). Indeed, by direct calculation it is straightforward to demonstrate the relation:
The complete Finsler metric tensor is written including the matrix
A Equation (
17) and satisfies the Finsler requirement of a totally symmetric associated Cartan’s tensor:
The matrix
A has both diagonal and nondiagonal entries and thanks to the explicit form acquired by the metric tensor
it is simple to find out that this matrix gives no contribution to the norm of a covector:
Equation (
19). For the following computations, it is important to emphasize that the entries of this matrix are first-order perturbations under the assumption that the functions
and their derivatives have a perturbative character See
Appendix A, hence
.
From the Finsler co-metric, one can derive the metric associated with coordinate space as the inverse one, via the defining equation:
obtaining the explicit form of the coordinate space metric:
and the diagonal matrix
:
where
indicates a second-order perturbation with respect to the scale fixed by the function
h and
k Equation (
1).
Lagrangian and Hamilton Finsler Geometry
In this work, we present a precise insight of the existing correlation between coordinate and momentum space in the context of HMSR starting from the action:
where the Lagrangian
is defined using a Lagrange multiplier
to pose the constraint that the MDR,
, must be satisfied [
43]. The action
S is obtained integrating the Lagrangian
with respect to the proper time
.
The equations of motion can be obtained varying the Lagrangian
. Hence, one can obtain the partial derivatives with respect to the velocity
and the Lagrange multiplier
:
The variation calculated with respect to the momentum
gives:
A simple application of the Euler’s theorem on homogeneous functions implies that the second term on the right-hand side of the previous relation is zero thanks to the 0-homogeneity of the metric tensor. Therefore, the velocity can be written in the simple form:
Inverting the previous relation, the momentum can be expressed as:
The momentum can be expressed as a function of the velocity solving Equation (
28), for instance, perturbatively. As a consequence, the coordinate space metric
, defined as the inverse of the momentum space metric
, can be written as a function of coordinate
x and velocity
:
The Lagrangian can be computed substituting Equation (
26) in the action Equation (
24):
The variation of the previous relation with respect to the parameter
gives:
and then the Lagrangian can be written as:
From the Legendre transform of action Equation (
24), it is possible to compute the energy
E solving the following equation for
:
It is important to underline that this equation is equivalent to the mass-shell constraint obtained from the MDR Equation (
1). The energy
E can finally be considered as the Hamiltonian of the system:
The relation between the Lagrangian and the Hamiltonian formulation has been established and it is possible to compute the norm for the velocity
. This function is associated with the momentum space norm
F which is defined via the MDR Equation (
1). The coordinate space norm can be determined starting from the metric Equation (
21):
As a final remark it is possible to state that the resulting structure is a Finsler geometry.
5. HMSR Generalized Finsler Spacetime
In the following we will consider a generalized Finsler geometry model to set the stage of the HMSR formulation. In this context, we will obtain an extension of the Standard Model (SM) of particle physics and will conduct the computations related with the GZK cutoff phenomenon.
The generalized Finsler geometry is a less restrictive structure which does not require a totally symmetric Cartan’s tensor associated to the metric Equation (
20), therefore, the construction of the geometry is easier. In this context the spacetime and the momentum metrics Equations (
17) and (
21) can be simplified taking into account only the diagonal parts Equations (
18) and (
23):
In this way, the coordinate and momentum metrics are reduced to the parts that really contribute in evaluating the squared norm of a vector or a covector, respectively.
Starting from the defining equations:
it is possible to compute the generalized associated vierbein, which can be written as:
It is simple to determine the perturbative order of part of these matrix entries using the approximation , valid for .
The form of the vierbein Equation (39) will be used in all the following computations, for instance, when evaluating the kinematical invariants (the Mandelstam s variable of the reactions involved in the GZK cut-off phenomenon).
5.1. Generalized Covariance
In the HMSR model [
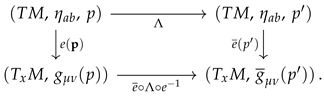
26] every particle has its personal modified spacetime, which is parameterized by the particle momentum. This means that every physical quantity related with a given particle is generalized and lives in a spacetime that acquires an explicit dependence on the particle energy. It is therefore necessary to introduce an original formalism to correlate different local spaces, using the generalized vierbein elements as projectors from every spacetime to a common flat Minkowski support space. Here, we report a scheme of how the correlation between different local spaces is established:
![Galaxies 09 00103 i001]() |
The Greek indices refer to the local curved geometric structures, whereas the Latin ones refer to the common Minkowski support space. Referring to the previous scheme, using the vierbein elements as projectors, the generalized Lorentz transformations can be obtained:
where the elements
belong to the Lorentz group and are defined in the flat Minkowski spacetime and the used vierbein is defined in Equation (39) and includes all terms up to the perturbative order under consideration. The Lorentz covariance is promoted to a diffeomorphism invariance and the introduced class of
Modified Lorentz Transformations (MLT) represent the isometries of the MDR of Equation (
1). We point out that the previous construction about the generalization of covariance is valid if the spacetime is metrizable and admits a vierbein, hence the result is valid even in different contexts. Therefore, the present prescription can be used to pose analogous definitions and set the stage of the model in the context of the more restrictive Finsler geometry.
5.2. Affine and Spinorial Connections
The geometrical structure is characterized by the
affine and the
spinorial connections. In Finsler geometry, the affine connection, that is the Christoffel symbol, can be defined using Equation (
14). In the case of zero spacetime curvature, the nonlinear connection Equation (
12) is
and therefore the derivative Equation (
12) reduces to the ordinary one:
Since in the case of absence of curvature, the metric depends only on the momentum (or equivalently on the velocity) and not on the coordinates, the Christoffel symbol Equation (
14) becomes:
The explicit form of the covariant derivative is a consequence of this result and it is equal to the ordinary derivative in flat spacetime:
Now it is possible to define the spinorial connection using the covariant derivative:
It is trivial to demonstrate that all the connection coefficients vanish since the vierbein depends on the momentum but not on the coordinates. Finally, we obtain the total geometric covariant derivative, which will be useful in defining the minimal extension of the Standard Model (SM) of particle physics:
The resulting spacetime geometry is therefore a flat Finsler pseudo-structure [
43,
44,
45,
46,
47,
48], whereas the associated momentum space is asymptotically flat.
5.3. Modified Poincaré Brackets
As a final result about the geometrical structure introduced by HMSR, we report the modified Poincaré brackets, computed for the local structure using the vierbein projectors:
where
are the local coordinates and
since the vierbein
is a function of the momentum
. Hence, time and space coordinates do not commute anymore [
31]. Using the explicit form of the vierbein Equation (39) and admitting for the perturbation functions the approximations (See
Appendix A) :
it is possible to obtain the following relations valid at the first perturbative order:
with the antisymmetric matrix
that satisfies the relations:
in the high energy limit, proving that the spacetime coordinates do not commute anymore [
49] if the parameters
and
are different, that is
Equation (
1).
The relation existing between noncommutative field theory and LIV was analyzed in [
50]; here we introduced a framework to investigate this point in the context of modified covariance.
6. Minimal Extension of the Standard Model in Covariance-Preserving Scenario
In the HMSR framework, the SM of particle physics can be amended in order to include the QG-caused perturbations preserving the covariance of the theory, even if in an amended formulation. Following, for instance, a strategy analogous to that used for the isotropic sector of the
Standard Model Extension (SME) [
19], the theory formulation requires the definition of the modified Dirac matrices with the related Clifford algebra and spinors.
6.1. Modified Clifford Algebra and Spinors
The Dirac matrices acquire an explicit dependence on the particle momentum and again using the vierbein projectors Equation (39) they can be written as:
The matrix is constant and this means that the chiral projectors are not affected.
The Dirac matrices modified via Equation (
51) satisfy the defining relation of the Clifford algebra:
The definition of spinor fields is now amended preserving the usual plane-wave formulation:
The normalization of the spinors
and
is modified since these are defined using the newly introduced metric Equation (
21) and the related internal product.
From the previous definitions the modified Dirac equation can be derived:
An important consistency check of the new formalism can be obtained verifying that Equation (
54) implies the MDR Equation (
1).
As a final result, a minimal extension of the SM can be obtained from the formalism here introduced. Indeed using the vierbein elements to project to a common Minkowski support spacetime the physical quantities related to different interacting particles and using the explicit form of the total covariant derivative Equation (
45), the minimal extension of the SM can be formulated for a flat spacetime. Here we illustrate the amended formulation of quantum electrodynamics (QED), whose Lagrangian can be written in the form:
where the term
is borrowed from the formulation of QFT in curved spacetime. The vierbein element
is related to the gauge field
. The gauge field is supposed as Lorentz-covariant in the usual meaning, that is, the MAV of photons is the usual speed of light
c. The gauge field therefore is set on a Minkowski spacetime
and the vierbein is given by:
. The QG corrections can be introduced in the generic gauge boson sector modifying the definition of the vierbein related to the gauge field, as done for the massive fermion fields.
The interaction is governed by the conserved current.
In the low-energy scenario, the covariance perturbations in the conserved current are negligible, whereas in the high-energy limit the formulation admits a constant form, since one can consider the incoming and outgoing momenta with the same constant high-energy limit.
6.2. Gauge Symmetry
The SM minimal extension obtained in the context of HMSR preserves the classic internal gauge symmetry
. This result can be stated formulating an amended version of the Coleman–Mandula theorem [
26]. The modified gauge symmetry group acquires the explicit form:
where
is the kinematical symmetry group and is given by the direct product of the momentum-dependent Poincaré groups associated with the different particle species.
and
is the internal gauge symmetry group, in this case the usual SM gauge group:
6.3. Modified Kinematics
HMSR theory perturbs the kinematics geometrizing the interaction of free propagating particles with the supposed quantized structure of the spacetime. In this work, we investigate the phenomenological effects introduced by QG in the UHECRs propagation, where the main effects are caused by the modification of the kinematics. The detectable effects are caused by the interaction of different particle species, which modify in a proper way the related spacetime.
Introducing a generalized internal product in the momentum space for more than two different interacting particle species, it is possible to obtain a generalized formulation for the Mandelstam variables s, t and u, which are the dynamical invariant quantities linked to a reaction.
Considering
p and
q as the momenta of two interacting particles of different species, the internal product of their sum can be defined as:
where the vierbeins
and
are associated, respectively, with the two different particle species. The formulation of the modified internal product can be simplified in the form:
using the generalized metric:
The inner product defined in Equation (
62) is invariant with respect to the
Modified Lorentz Transformations (MLT) introduced in HMSR:
The inner product remains invariant under the action of such generalized Lorentz transformations, indeed one can obtain:
is the metric evaluated for the two particle momenta
,
.
The new formalism here introduced guarantees that HMSR theory can deal with the interaction of different particle species in the context of a QG-modified kinematics without the necessity of the introduction of a preferred reference frame.
7. Ultra-High-Energy Cosmic Ray Propagation
Before investigating the QG-induced phenomenology in UHECRs physics, it is useful to illustrate the standard physics predictions for these highly energetic particles. During their propagation, at sufficiently high energies, UHECRs can interact with the CMB and depending on their nature and energy their flux is attenuated. For instance, a propagating CR bare nucleus
X with atomic number
A can undergo a photo-dissociation process interacting with the CMB and emitting one or more nucleons:
where
is a generic nucleon. The proton propagation is influenced by different interaction processes with the CMB, hence it can undergo, for instance, a pair production process:
This process is the main interaction mechanism with the CMB for CR protons with an energy lower than the threshold
. The dominant process for UHECR protons with an energy exceeding this threshold is the
particle resonance photopion production process:
These dissipation mechanisms make the universe opaque to the propagation of CR, particularly for the most energetic component (UHECR), with an energy that exceeds the threshold
. In this work, we are particularly interested in the UHECRs propagation since CRs can be useful in investigating QG phenomenology thanks to their huge energy and propagation length. QG effects in some theories are expected as more evident at high energies and their perturbations can sum up during the propagation of this kind of particles. The photopion production is the main attenuation interaction of UHECRs and is the core mechanism for the so-called GZK cut-off phenomenon for protons [
2,
3]. This effect poses an upper limit on the energy of protons detected at ground and coming from distant sources. Since through this effect a particle dissipates energy, but is not annihilated, a proton with enough energy can undergo the same interaction process again, and can undergo what is known as a stochastic dissipation process. This way, it becomes possible to evaluate the
attenuation length, defined as the average distance that the proton has to travel in order to reduce its energy by a factor of
. The inverse of the attenuation length is given by [
51]:
where
is the proton–photon interaction cross section as a function of the squared center of mass energy (the Mandelstam
s variable),
represents the background photon density per unit volume and photon energy
,
is the impact parameter and
is the interaction threshold energy.
represents the reaction inelasticity, that is, the energy fraction available for secondary-particle production during the reaction. Complementary to the inelasticity is the elasticity function, defined as the energy fraction preserved by the primary particle after the interaction,
with the incoming particle energy
and the residual energy
. Elasticity and inelasticity are connected by the simple relation:
.
The Mandelstam
s can be computed introducing the photon four-momentum
defined in the rest frame of the nucleus. In the high-energy limit approximation for the proton velocity
, with
, the following relations hold:
hence, the inverse of the attenuation length Equation (
69) can be written as:
where the primed quantities are defined in the proton rest frame, whereas the other quantities are defined in the laboratory rest frame. Since the
distribution is a Planckian function of the temperature
T, a further simplification of the previous relation of Equation (
73) is possible, obtaining the explicit form for the inverse of the attenuation length [
5]:
The inelasticity computed for the standard physics case is given by the relation [
51]:
8. QG Introduced Phenomenology in UHECR Propagation
In this work, we present a review of the QG presumed effects in the UHECR sector as predicted in the context of the HMSR model [
26]. The results, already presented in a previous work [
8], are better justified by a generalized formulation of the model, that indicates a strategy to set the investigation in curved spacetime. Moreover, in this work we conduct our analysis in the HMSR framework, but in the context of a Finsler geometry structure obtained by starting from a MDR written in a more general form Equation (
1) than the one given by Equation (
3) and used in previous works [
7,
8].
Following the theoretical framework introduced by HMSR, the kinematics of free particles are modified in order to include the QG effects. The kinematical perturbations modify the allowed phase space for the reaction and may therefore influence the processes involved in UHECR propagation. The introduction of QG phenomenology can indeed affect the photopion production mechanism, the core reaction underlying the GZK phenomenon [
5,
6,
7,
8]. The QG-caused reduction of the allowed phase space can modify the inelasticity
K Equation (
75). The consequent reduction of the inelasticity means that the incoming UHECR proton dissipates less energy during the GZK process and therefore the resulting opacity horizon is enlarged with respect to the standard model physics prediction.
8.1. Constraints from Resonance Creation
The photopion production requires a
particle creation (Equation (
68)) and can occur passing through a real
particle, in the case of the dominant process, or alternatively through a virtual one. The introduction of QG phenomenology can presumably modify only the GZK cut-off phenomenon, enlarging the foreseen opacity sphere without a complete suppression. The observed UHECR flux suppression can be caused by the exhaustion of the sources energy or by the Universe opacity to the propagation of CR [
52,
53]. In the last scenario, an uncertainty exists about the dimension of the foreseen opacity horizon. The production of the real
particle must therefore be preserved in order to foresee only small QG-induced deviations from the standard physics predictions for the GZK process. The four-momenta used in the following computations are considered as covariant vectors in order to simplify the use of the MLT for changing the reference frame. In the proton-CMB interaction process the production of a
particle is allowed if the proton-CMB interaction free energy, that is the Mandelstam
variable, exceeds the rest energy of the particle resonance. As a consequence of this threshold energy consideration, a first constraint on the magnitude of the QG perturbation parameters can be posed. Using the generalized internal product and the formalism developed for the modified kinematics in the Equations (
61) and (
62) one can write the Mandelstam
s variable as a function of the proton and the photon four-momenta, respectively,
and
:
The vierbein Equation (39) has been used to project the momenta of different particles to the common support Minkowski spacetime and the symmetry of the mixed product of
and
has been used. Photons are assumed to be Lorentz-invariant, hence the related vierbein is defined as usual:
. Using the explicit form of the squared Finsler norm
given in Equation (
35), the following inequality can be derived reordering the terms of the previous relation in an opportune manner:
where
and
are the proton QG perturbation functions taken from the MDR Equation (39). The following inequality can be derived from the previous Equation (
77) using the MDR Equation (
1):
where
,
. The covariant formulation of the model is fundamental since it allows the change of the reference frame. Indeed, in order to simplify the computation, it is possible to choose the more suitable reference frame, where the involved energy scales ratio allows the suppression of some perturbative terms. One can therefore consider the laboratory frame, where the proton energy is much higher than the CMB one. Considering that the UHECR proton energy has an upper limit
[
1] and taking into account the tiny average value of the CMB energy
, one can neglect the
contributions in the second term obtaining:
Defining the function
the result obtained is comparable with the one presented in [
7,
8]. The derived inequality must be satisfied in order to produce a
resonance, otherwise the QG perturbations totally suppress the GZK effect. Imposing the validity of the previous relation the following constraint can be derived:
Substituting the approximated average value of the CMB energy in the previous inequality one can obtain the approximated constraint:
where
and
. The obtained constraint is consistent with the upper limit
obtained numerically in [
5] for the QG perturbation magnitude.
As a final remark from the relations Equations (
78) and (
80), it follows that in order to generate visible effects on the GZK phenomenon, the QG perturbation function
must satisfy the relation:
Indeed from Equation (
78) the high-energy limit excludes the possibility of any suppression of the GZK cut-off in the case of a negative function
. We underline that the choice of positive values of the perturbation
corresponds to the introduction of an effective MAV in the MDR of Equation (
1) for every massive particle, which is lower than the standard speed of light.
8.2. Modified Inelasticity
The introduction of QG perturbations can modify the phase space allowed for the photopion production process, determining a modification of the inelasticity function
Equation (
75). In this work, we evaluate the new inelasticity in the context of the generalized Finsler geometry here introduced following the approach of [
7,
8], originally inspired by [
5,
6]. In the following, all the computations are conducted again considering the four-momenta as covariant vectors, in order to simplify the computations transforming the reference frame with the MLT. The introduction of the center-of-mass (CM) reference frame is useful and it is defined via the relation:
where the momenta are defined on the common Minkowski support spacetime
and * labels the quantities related to the CM frame.
The next element necessary in evaluating the change from the CM to a generic reference frame is the
Lorentz factor. Starting from the free energy available for the photopion production
one can obtain the relation:
Using the CM definition Equation (
83) the relation
follows and the four-momentum of the photopion can be written in the CM reference frame as
. From the latter, the free energy necessary to produce a photopion in the CM frame can be computed using the squared Finsler norm Equation (
35):
and
are the perturbation functions of the proton MDR of Equation (
1) and
and
are the analogous functions for the pion MDR,
p and
label, respectively, the elements related to the proton and the pion.
We underline that the computation made here for the modifications induced on the inelasticity are still valid in the context of the more restrictive Finsler geometry. Indeed, the computation is conducted using the MDR Equation (
1), that is the norm Equation (
35).
From the previous equation and neglecting the
perturbations in Equation (
35), the following equality can be obtained:
where
and
are the QG perturbation parameters. Considering the high-energy limit
in the previous relation the residual proton energy after the photopion reaction can be increased if the QG parameters satisfy the inequality
and therefore the relation
. The proton-dominant correction
must be larger than the pion one
in order to produce a dilatation of the GZK sphere. In this work, we assume the gravitational nature of the perturbation effects caused by the supposed quantum structure of the background, hence the heavier particles have a bigger QG-induced modification. As a consequence, the correction factors of the pion can be considered negligible and it is possible to pose
and
.
Now the following approximations can be introduced:
represents the initial free total energy and and are the final energies of the proton and the pion, respectively.
Using the Lorentz transformations for changing reference frames, one can obtain the following:
where
is the pion inelasticity depending on the impact angle.
In the high-energy limit, where for ultra-relativistic particles
and the velocity factor
and
is approximated by Equation (
84), the following equation can be derived:
Posing
in the previous relation, it is possible to obtain the following one:
where the latter result was obtained in [
7,
8]. The previous equation can be numerically solved in order to evaluate the inelasticity as a function of the collision angle
. The numerical computation is conducted in the high-energy limit, hence by using Equation (87) and
is the initial energy for the process.
The free energy
s can be written as:
introducing the energy of the photon
defined in the proton rest frame
.
The inelasticity is finally averaged over the interval
:
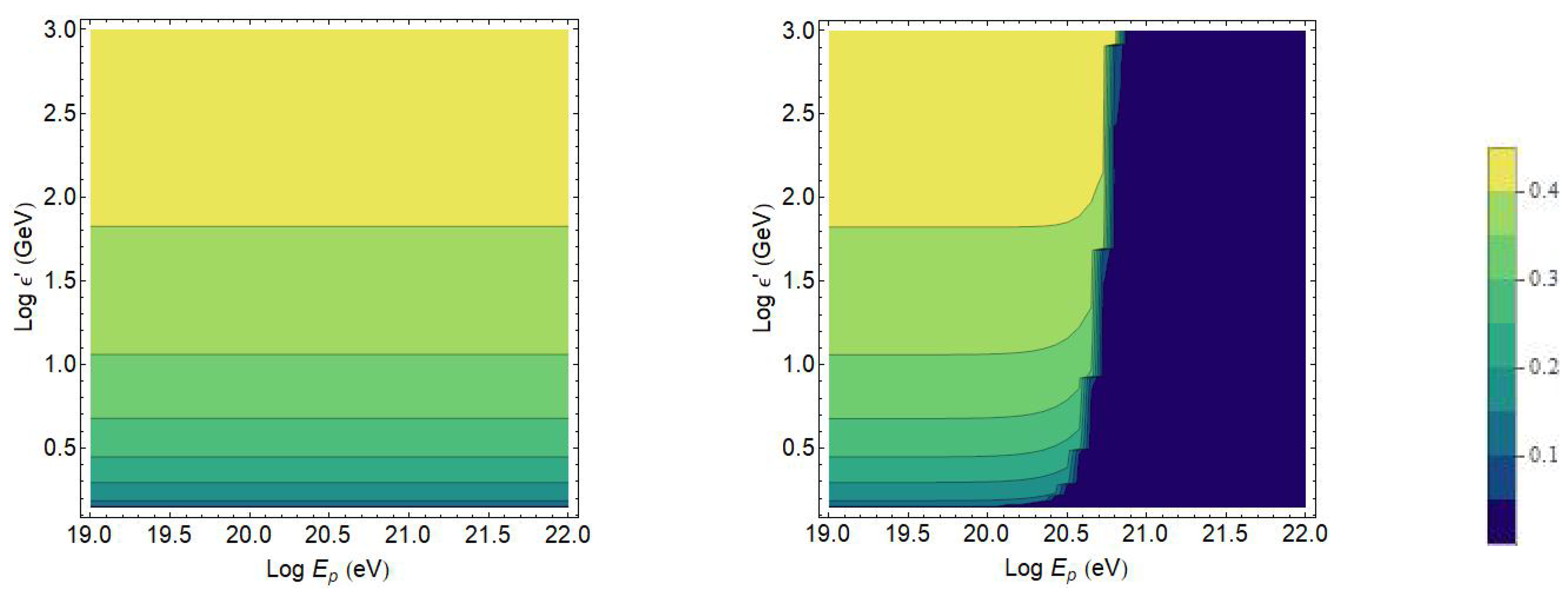
In the following, we plot in
Figure 1 and
Figure 2 the inelasticity for different choices of the parameter
in order to compare the standard physics predicted result with the QG induced modifications. The parameter
is constrained to be positive in order to guarantee detectable QG effects. This hypothesis corresponds to the introduction of a MAV inferior to the classical speed of light
c for every massive particle species. The parameter is even constrained from above by the limit obtained in the previous section Equation (
81), hence the plausible parameter must be included in the interval
. The inelasticity is plotted as a function of the proton energy
, defined in the laboratory reference frame, and the photon energy
, defined in the proton rest frame. Under these hypotheses, the QG perturbations cause a dramatic drop of the inelasticity value, which is more visible for increasing values of the parameter
. This implies a reduction of the allowed phase space for the photopion production process, and an enlargement of the foreseen proton opacity horizon for an increasing magnitude of the QG perturbation.
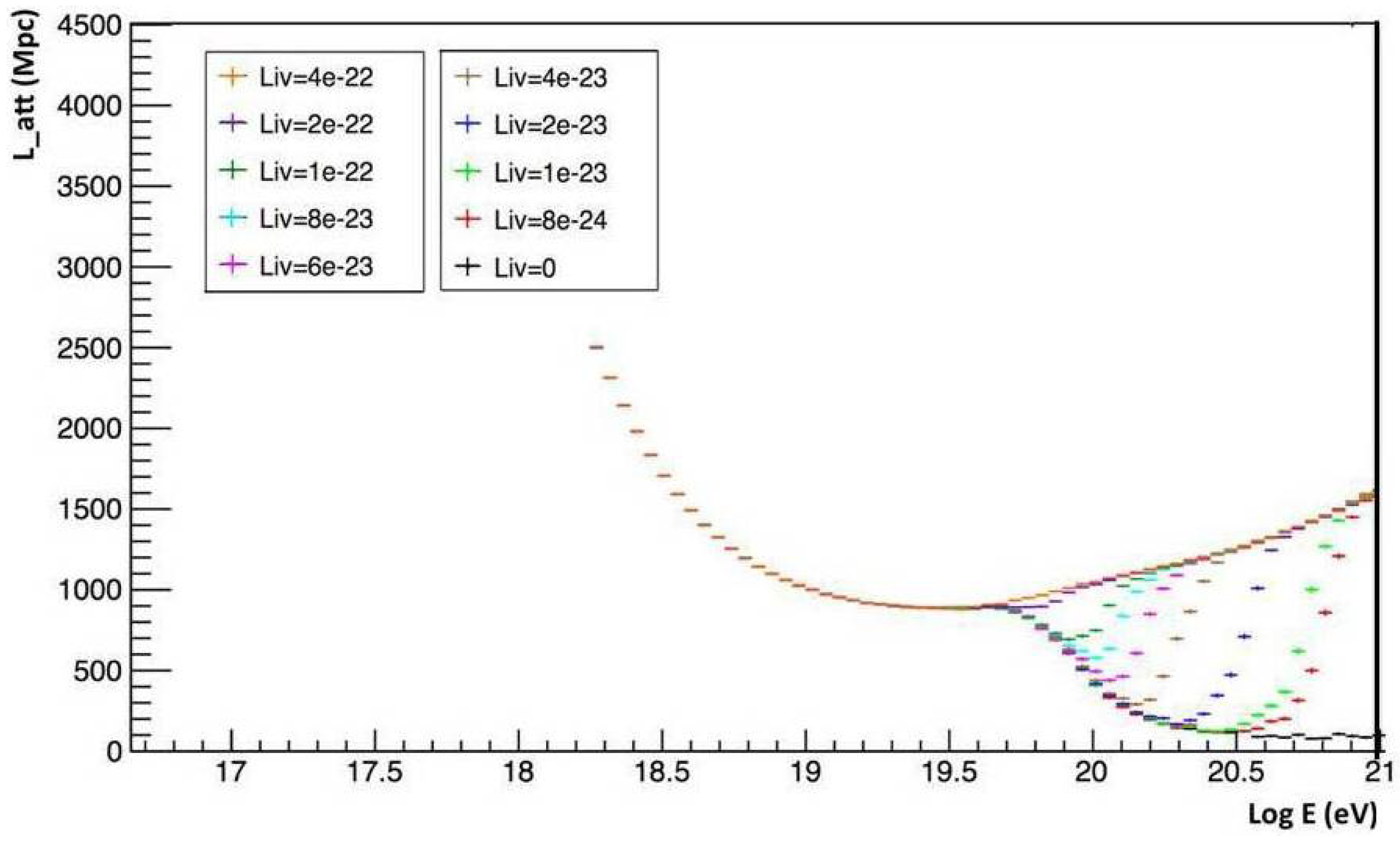
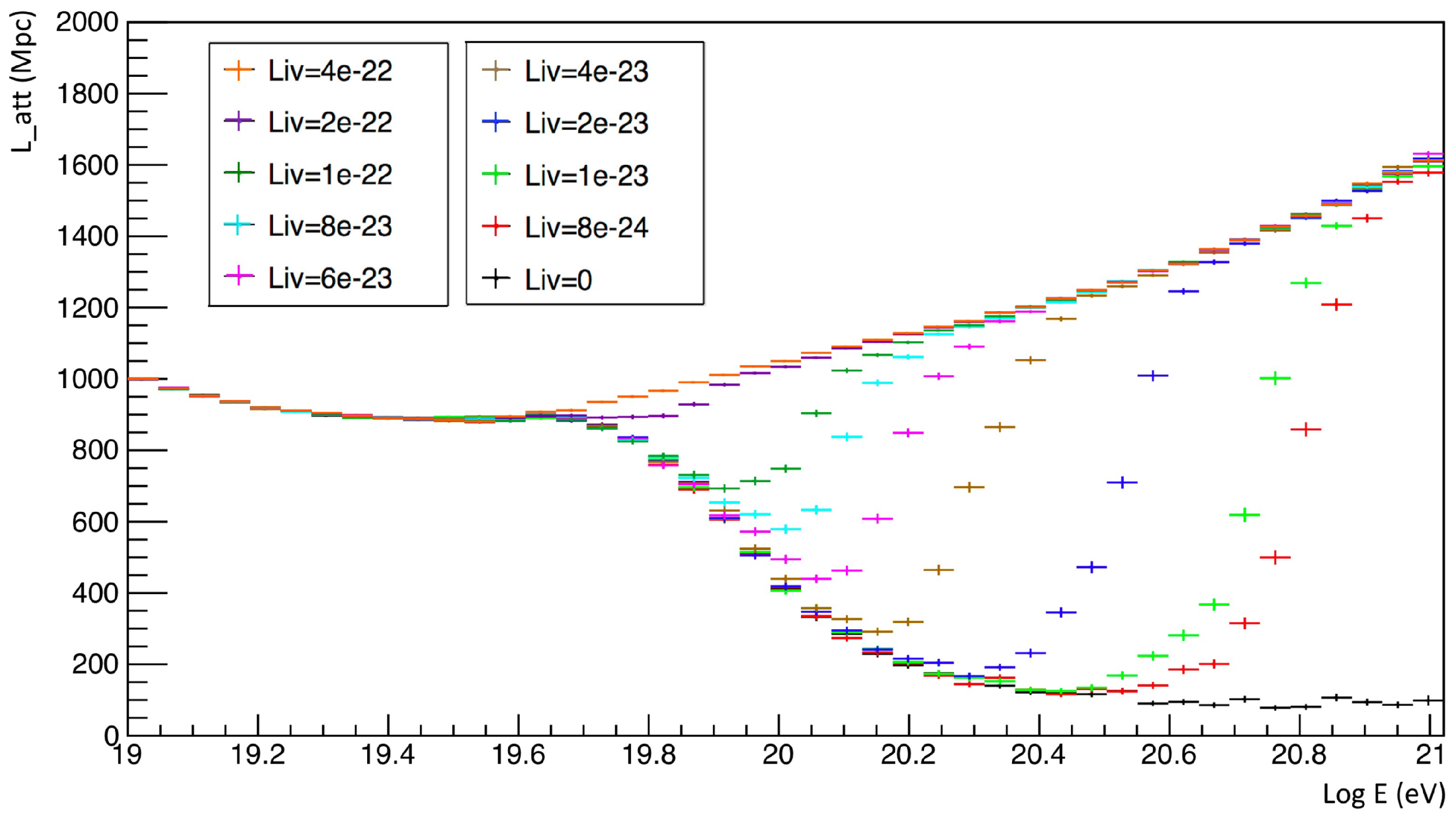
9. Simulated Attenuation Length
The impact of the QG perturbations on the UHECR free propagation can be evaluated computing the value of the attenuation length as a function of the modified inelasticity
K in Equation (
74). In this work, we present the attenuation length, as in a previous work [
8], obtained using an ad hoc modified version of the simulation software
SimProp [
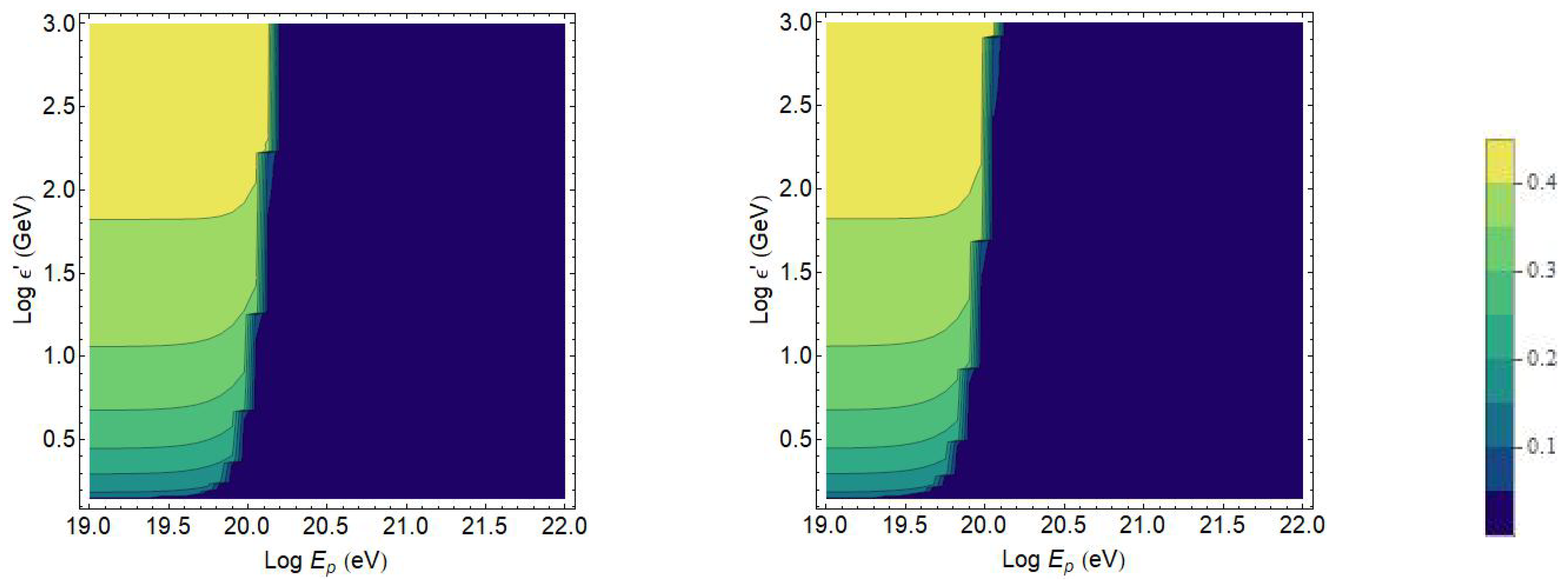
27]. In this software version, we substituted the inelasticity predicted by the standard model physics with the modified one, being a function not only of the proton and the CMB energy but also of the QG parameter. The analysis is conducted neglecting the interaction of the UHE protons with the EBL. This interaction is dominant at energies below ∼5 × 10
eV. Slightly above this threshold the ELB interaction might give a
contribution in determining the attenuation length [
54]. Hence the prediction presented in
Figure 3 and
Figure 4 can be affected by ELB interaction at energies below the photopion production threshold (∼5 × 10
19 eV). For UHE protons exceeding this energy limit the effect produced seems to be a negligible reduction of the mean free path. In
Figure 3 and
Figure 4 it is visible that the increase of the opacity horizon can be caused by the QG-induced modification of Lorentz covariance. In the QG-less scenario the attenuation length decreases for increasing CR energy values. In the presence of QG, the interaction length at first decreases with the energy, but then after an inflection point, which depends on the energy, this quantity starts rising for increasing energy values. This effect is caused by the reduction of the average energy lost for every proton-CMB interaction caused by the reduction of the inelasticity. For a QG parameter of
the modifications in the attenuation length are appreciable starting from an energy
of the incoming proton, instead for a parameter
the perturbation starts being appreciable yet at an energy
. The analysis can be improved taking into account even the electron–positron pair production. This effect is not dominant at the highest energies, but would presumably further increase the energy loss process.
10. Conclusions
In this work, we investigated the possibility of exploiting the UHECR physics to detect supposed signatures of the quantum structure of spacetime. Nowadays, the Lorentz covariance stands at the base of our physics knowledge, but QG can introduce small departures from the classic scenario. We studied these supposed departures simulating UHECRs propagation in a framework of Lorentz covariance modification. In this research, we generalize the results of previous works [
7,
8] in the context of a more complete formulation of the HMSR model [
26]. Indeed, in our proposal a way is outlined to generalize HMSR theory in curved spacetime introducing a formalism that defines the threshold energy of reactions in a modified covariant framework. The model foresees a minimal extension of the particle SM, preserves the usual gauge symmetry
and does not introduce exotic particles or reactions. The resulting geometry is a generalized Finsler spacetime and all the GZK cutoff modification effects have been computed in this context. We underline that the methodology here introduced can be used to set the stage of the model in the context of the more restrictive Finsler geometry and we have demonstrated that the inelasticity modification that underlies the opacity sphere enlargement can be still computed in the Finsler spacetime. Moreover, a generalized analysis framework for the possible QG induced effects is introduced investigating a more general form of the MDRs. Finally, we can state that all the presented results are obtained in the context of a more complete theoretical model formulation.
Our proposal is analogous to that of [
4], but is based on a covariant formulation, such as in DSR theories [
55,
56]. The kinematical solution presented in our work is based on the hypothesis that the QG induced corrections are particle species depending and are caused by the particle interplay with the QG structure of spacetime. The introduced QG phenomenology is limited to the free particle kinematics since nowadays it is not totally clear how DSR theories can affect the process dynamics, since the related computations are incredibly complicated [
57]. However, the kinematic perturbation here introduced can modify the allowed phase space for different particle interaction processes amending the related threshold energies. Hence, in this scenario QG may affect the interaction of different particle species, such as in the case of the GZK cut-off phenomenon.
The conducted simulations foresee an enlargement of the attenuation length in accordance with other works [
5,
6,
7,
8,
58,
59], but are obtained in a covariance-preserving scenario as proposed in [
60].
We emphasize the importance of preserving covariance in the HMSR model, even if in an amended formulation, which allows the definition of relativistic kinematical invariants. As a direct consequence, it is possible to choose the most suitable reference frame to simplify the computations, suppressing some perturbation terms thanks to the involved energy scale ratios. Furthermore, in the astroparticle sector, covariance can be a great experimental advantage, since all the obtained data can be collected without the necessity to introduce any sidereal discrimination related to the orientation of the detector with respect to a fixed privileged reference frame.
The analysis strategy presented in this work can be improved including a heavier UHECR component, which is a more realistic CR composition, as indicated by the Pierre Auger collaboration [
16]. The QG perturbations are expected to be larger for a CR component heavier than protons. Indeed, the kinematical perturbations can affect the propagation of bare nuclei in a more significant way, amending the threshold processes underlying the heavy UHECR photodissociation. This improvement of the analysis will be necessary since presently the measured UHECR composition suggests that the spectrum end is not caused only by the GZK cut-off.