Abstract
Precursor emissions are found in some short gamma-ray bursts (SGRBs). In this paper, we review the theories and observations of the SGRB precursor and discuss its prospect as an electromagnetic counterpart of the gravitational wave event produced by neutron star (NS) mergers. The observed luminosity, spectrum, and duration of precursors are explained by the magnetospheric interaction model during the inspiral or the cocoon/jet shock breakout model during the jet propagation. In general, these two models predict that the precursor will be weaker than the main GRB, but will be of a larger opening angle, which makes it an advantageous gamma-ray counterpart for NS mergers in the local Universe, especially for NS - black hole mergers with very low mass ratios, in which the main GRBs are not expected. The joint observation of the precursor, SGRB, and gravitational wave will help to reveal the jet launch mechanism and post-merger remnant.
1. Introduction
On 17 August 2017, the Fermi/gamma-ray burst monitor (GBM) was triggered by a short gamma-ray burst (SGRB)-GRB 170817A [1,2,3]. Independently, the gravitational-wave (GW) event GW170817 produced by the double neutron star (NS) merger was detected by the advanced LIGO and Virgo detectors [4,5]. The joint detection of GW170817/GRB 170817A confirms that at least some SGRBs originate from NS mergers, and herald the multi-messenger astronomy [1,2,3,4,5]. It also enables better localization, which benefited the multi-wavelength follow-up observations. The detection of the associated kilonova, AT 2017gfo, led to the discovery of the host-galaxy NGC 4993 at a distance of ∼40 Mpc, which shed light on the physics of nucleosynthesis [1,6,7,8,9,10,11].
Joint detection can provide abundant information to study some fundamental physics. Using the GW data alone, constraints on the NS equation of state can be obtained (e.g., [4]). Combining with the electromagnetic (EM) observations, (1) the GW event can be treated as a standard siren to study cosmology [12]; (2) one can also constrain the difference between the speed of gravity and the light speed, test the violation of Lorentz invariance and the equivalence principle [5,13]. It can also be used to study the launching mechanism, structure, composition, and radiation mechanism of GRB jets (e.g., [3,14,15,16,17,18,19,20,21,22,23]).
Since the discovery of GW170817/GRB 170817A, many efforts have been put into the follow-up observations of GW events to search for their EM counterparts. No new confident joint detection is observed, except for a sub-threshold event: the sub-threshold GRB (GBM-190816) [20,24] was found to be possibly associated with a sub-threshold NS merger event GW190425 [25]. But in the archived Fermi/GBM data, a small sample of GRB 170817A-like events has been found [26]. In theory, many EM signals are expected for the NS merger. The observation and theory of SGRBs, afterglows, and kilonova were summarized in many reviews [27,28,29,30,31,32]. However, little attention has been placed on the pre-merger EM radiation. As a complement, we focused on the precursor emissions of SGRB in this review.
Precursors were initially identified as weak signals in long GRBs (e.g., [33,34,35,36,37,38,39]). Later precursors of SGRBs were found in the Swift/Burst Alert Telescope (BAT) data [40]. Within the standard fireball scenario, precursors are suggested to be associated with the transition of the fireball from optically thick to optically thin, leading to photospheric blackbody emissions [29,41,42,43,44]. This applies to both long and short GRBs. It is also suggested that a precursor can be generated by the shock breakout (SBO) of a jet or a cocoon. For long GRBs, this links to the SBO from the stellar surface [32,45,46,47,48,49,50], some research proposed that breakout of a radiation mediated shocks train can naturally generate a band-like spectrum [51,52]. For SGRB, this relates to the SBO from the ejecta produced during the NS merger [32,50,53,54]. Besides, there are two more scenarios proposed only for SGRB precursors. During the inspiral phase of the NS–NS/black hole (BH) binary, the magnetospheric interaction of the binary [55,56,57,58,59,60,61,62,63], or the crust crack of the NS [64,65,66] may also generate gamma-ray emissions. As such, precursors of SGRBs may shed light on the physical processes right before or shortly after the merger.
Moreover, the magnetospheric interaction model [62] and the SBO model [32,53,54] predict the precursor, although fainter than the main GRB, would have a much larger opening angle, as the radiation is generated by a mild relativistic component. In this case, the precursor can serve as an independent EM counterpart for GWs, even though the prompt GRB points away from the line of sight. It has been suggested that GRB 170817A can be such a case [32,53,54]. This feature would be greatly appreciated for follow-up observations. Thus, research on precursors is important for multi-messenger astronomy. This review aims to summarize the current understanding of SGRB precursors and discuss the possibility for future observations. In the next section, we review the feasible precursor models. Observations are summarized in Section 3. In Section 4, the discussion and prospects are presented.
2. Precursor Models
Various research studies have shown that a gamma-ray precursor event can be produced prior to the main GRB event. Here, we divide the precursor models into two categories based on their relative time to the merger: pre-merger models and post-merger models. More specifically, in the pre-merger phase, magnetospheric interaction in the NS binary and the crustal failure triggered by tidal interactions could lead to precursor emissions. While during the post-merger phase, it is suggested that the photospheric emission from the fireball and the SBO can also result in precursors.
We summarize the luminosity, spectrum, duration, and opening angle of these precursor models below, which relate to their detectability. To make sure the precursor is detectable at an extra-galactic distance, its luminosity should satisfy , where S is the sensitivity of the detector, and D is the distance. Recently, researchers have searched for SGRBs in the local Universe in the Swift catalog and found that the four closest SGRBs could locate at 100–200 Mpc [67]. Thus we adopt Mpc. For sensitivity, we use the gravitational wave high-energy electromagnetic counterpart all-sky monitor (GECAM) as an example, which has in keV [68]. The corresponding lower limit on luminosity is then
2.1. Pre-Merger Models
2.1.1. Magnetospheric Interactions of NS–NS/BH Binaries
It has long been suggested that the magnetospheric interactions in compact star binaries can lead to energy dissipation (e.g., [55]). Following [62,69], three cases are considered in this review as shown in Figure 1: case 0 with , case 1 with , and case 2 with , where the subscripts (∗, c) represent the NS and its companion, respectively. The magnetic dipole moment is , where B is the surface magnetic field and R is the radius. We consider the binary to be of a separation a, a mass ratio , and an orbital angular velocity . Within this framework, the energy dissipation rate of the NS binary system can be well formulated.
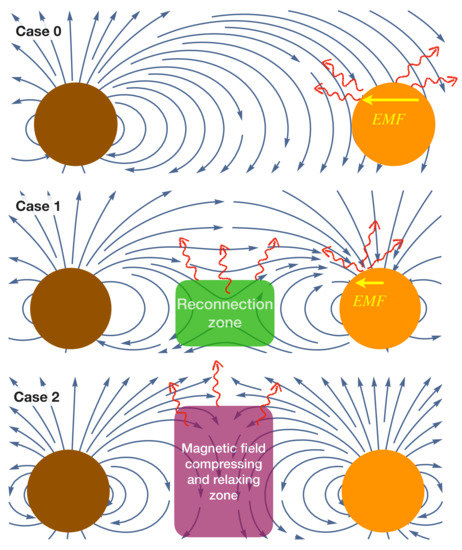
Figure 1.
We show the schematics of three typical magnetic field configurations in inspiraling NS binaries: case 0 with , case 1 with , and case 2 with . The red winding arrows represent the emitted photons.
Case 0 can be well understood within the unipolar induction directcurrent (DC) circuit model, i.e., the weakly magnetized NS or non-magnetic BH is moving across the magnetic field lines inside the magnetosphere of the NS. This generates an electromotive force (EMF) on the two poles of the companion, where , , and is the spin of the NS. This EMF can drive currents along the magnetic field lines, which makes a closed DC circuit. Note this DC circuit may not always be stable [56]. The resistance of the magnetosphere is [70]. The luminosity can then be estimated as [56],
where the mass is in units of solar mass . Note that, here and below, we adopt the approximation of , this is appropriate, as we are considering the last few seconds before the merger. Simulations of inspiraling NS–NS/BH binaries indicate that the main features are well captured by this model (e.g., [58,59,61,63,71,72]).
The other cases are more complicated. During the shrinking of the orbit, the magnetospheres of NSs would interact with each other, dissipating the orbital kinetic energy. The location of the interaction is around , where and . If the magnetic field lines from two stars are anti-parallel with each other (Case 1), magnetic reconnection is expected. After the reconnection, the magnetic field lines would connect the two stars directly, leading to the formation of a DC circuit, such as in Case 0 driven by the EMF with an electric field . We find that the energy dissipation rate from the DC circuit is generally larger than that in the magnetic reconnection in the last few seconds before the merger, and it can be formulated as [62],
If the magnetic field lines are parallel with each other (Case 2), the field lines would experience compressing at , and the compression location would rotate around the main star at an angular speed . When the compression location moves away, the compressed field lines will relax. This alternate compression and relaxation would lead to an electric field and an energy dissipation rate [62],
where is the width of the compression region.
It can be found that the energy dissipation rate increases non-linearly with time. Comparing with Equation (1), we found that it would be detectable only in the last few milliseconds to seconds depending on the magnetic field and distance to the observer. In general, Case 1 would have the highest energy dissipation rate, while Case 0 would have the lowest. We noticed that, for real cases, the magnetic axis may have an inclination angle with respect to the orbital axis, and in these cases, the energy dissipation rate would lie in between the above scenarios. As the poloidal field is the dominant component, we ignored the contribution of the toroidal magnetic field, which are caused by the revolution of the binary system and are observed in many simulations (e.g., [58,59,61,63,71,72]).
The opening angle of the radiation depends on the actual magnetic configuration and the orbital phase. In all cases, the generated acceleration electric field is not parallel to the B field. The radiation process would then be dominated by the synchrotron radiation [62]. Based on the threshold (Equation (1)), the magnetic field should be G. While in such a high magnetic field, the high-energy photon will be absorbed, leading to a synchrotron-pair cascade. Using Monte-Carlo simulations, we find the spectral energy distribution (SED) can be well described by a cutoff-power law, with a photon index around and peak energy at <MeV [62,73]. This could be understood as the synchrotron radiation by the mildly relativistic electrons with , as high-energy photons emitted by higher-energy electrons will be absorbed to produce pairs. Therefore, the radiation cone will be of half opening-angle , and this radiation cone is rotating with an angular speed at . Note that the magnetospheric interaction can create more open field lines than the isolated NSs, we would expect the outer gap acceleration to operate at around , and so the curvature radiation may dominate after the electrons/positrons, losing their perpendicular moment. Overall, in these cases, the radiation opening angle will be much larger than that of jetted GRBs [62]. This can also be seen from the Poynting flux direction from magneto-hydrodynamics simulations (e.g., [57,58]).
2.1.2. NS Crust Crack Model
During the inspiral of the NS binary, tidal interactions can distort the NS, inducing ellipticities. Once the ellipticity becomes large enough that after the crystalline structure of the NS crust cannot respond linearly, a crust failure may be induced [40,64]. It has been suggested that the crust breaking strain is around [74], which corresponds to a critical ellipticity of , where is the elongated NS radius. This can be easily reached by the tidally-induced f-mode oscillation in the last seconds before the merger [65] (see also Figure 3 of Reference [75]). Recent works show that the g-mode can also lead to the breaking of the NS crust [66].
If the energy is dissipated into heat, the crust can be heated up to keV with erg/K [76] and erg. The corresponding thermal luminosity from the crust surface with cm is then [69],
where is the Stefan–Boltzmann constant. This is too faint to be observed at an extra-galactic distance.
It has also been proposed that, if the NS is highly magnetized, i.e., being a magnetar with G, the crust failure may trigger a violent reconstruction of magnetic fields, leading to a magnetar-giant-flare-like event (e.g., [40,66]). However, it should be noted that for magnetar giant flares, the crust failure is believed to be caused by the sudden rearrangement of magnetic field [77]. It is unclear whether a crust failure could lead to the amplification and rearrangement of magnetar magnetic field. Nevertheless, in this case, the luminosity may be estimated as
where is the duration of the flare. The SED and opening angle in this case would be similar to observed giant flares.
2.2. Post-Merger Models
Within the standard fireball model for GRBs, a photospheric blackbody precursor can be produced when the fireball changes from optically thick regime to optically thin (see Section 7.3.3 of Reference [29], and references therein). The luminosity is determined by the transition radius. However, it has been found that, to fit the observation, the fireball Lorentz factor should be ∼30, much smaller than the expected value (>100) [40,69]. Therefore, this is unlikely to be responsible for the precursors, and we mainly focus on the SBO model for post-merger models.
SBO Model
Both NS–NS and NS–BH mergers can launch relativistic jets. As the relativistic jet propagates through the sub-relativistic expanding merger ejecta, a high-pressure bubble would be generated, which engulfs the jet and affects its propagation. This will lead to the formation of a jet-cocoon system, which is a structured relativistic outflow with a wide-angle. A successful SGRB jet is expected to penetrate through this ejecta and produce gamma-rays by the internal dissipation processes within the jet. It has been proposed that when the shock driven by a mildly relativistic cocoon breaks out of the ejecta, gamma-ray emission would also be produced [53,54]. This process differs significantly from what occurs in ordinary SGRBs.
For a low-power and short-duration jet, it may not penetrate through the ejecta, and the jet is choked. Both successful jet and chocked jet can drive an at least mildly relativistic SBO from the expanding merger ejecta [53]. The SBO of the relativistic jet or the mildly relativistic cocoon from the sub-relativistic expanding merger ejecta could release a tiny fraction, e.g., , of the total kinetic energy of the outflow into gamma-ray.
Two key physical parameters, the final Lorentz factor of the breakout layer and the radius of the SBO , determine the main properties of the observed emissions. The SBO occurring in a sub-relativistic expanding ejecta is very different from that occurring in a static stellar envelope. The shock velocity in the lab frame would determine the boost of the emission to the observer, and the shock velocity in the ejecta frame would determine the strength of the shock. The SBO from the breakout layer would have an optical depth , where is the shock velocity seen in the ejecta frame. The shock quantities seen in the unshocked merger ejecta frame are marked with a prime. The mass of the breakout layer can be estimated to be
where the opacity is expected for fully ionized heavy elements, .
If the shock is fast enough (e.g., ), the radiation temperature behind the shock reaches keV at which pair production becomes important [49]. In this case, the mean photon energy is in the -ray regime. The observed energy from the breakout layer can be roughly estimated by the internal energy of the shocked breakout layer and boosted to the observer frame as [32,50]
In the case of a spherical breakout, the difference between the light travel time of photons emitted along the line of sight determines the duration of the breakout signal
The bolometric luminosity of an SBO could then be roughly estimated as [69]
where is the total kinetic energy of the outflow, and is the fraction of the total explosion energy emitted in -rays.
In the framework of the SBO scenario, three SBO parameters: the breakout radius , the ejecta Lorentz factor , and the shock Lorentz factor , are related with three main observables: the total observed isotropic equivalent energy , the duration , and the breakout temperature . The SBO temperature is roughly the immediate downstream temperature of the breakout layer, as observed in the observer frame. The rest-frame temperature at the time that the photons are released is keV, the observed temperature of SBO can be estimated as
The three breakout observed quantities, , and , satisfy a closure relation [32,49]
This closure relation can be used to see if the detected -ray flash is consistent with a relativistic SBO origin. It is worth noting that this relation is strongly dependent on the breakout temperature , which is difficult to determine precisely because the SBO spectrum could deviate from a blackbody spectrum.
There are three generic properties of a relativistic SBO from a moving ejecta: (1) the light curve is smooth; (2) only a tiny fraction of the total energy would be emitted at the SBO stage; (3) the spectrum shows a hard to soft evolution [49,53]. Thus for precursors produced by SBO, the observed energies could be orders of magnitude lower, but depend on the viewing angle of the jet. Note, interestingly, all of these properties are observed in GRB 170817A. Therefore, a mildly relativistic cocoon shock breaking out from the merger ejecta provides a natural explanation of the observational properties of GRB 170817A.
3. Observational Results
Searching SGRB precursors has been performed in various space observatories, such as INTEGRAL [78], Swift [40,79], and Fermi/GBM [69,79]. Detecting weak signals before SGRBs will be subject to instrumental biases (the energy range and sensitivity). For example, although Fermi/GBM covers a broad energy range (∼8 keV–40 MeV), Swift/BAT has a higher sensitive in the 15–150 keV band. Thus Swift will be stronger to detect soft weak precursors, consistent with observations.
In the pioneer research, precursors are searched by visual inspection in binned light curves with a certain fixed bin width (e.g., [33]). Later, wavelet analysis is introduced to analyze such binned light curves [34,40]. Recently, the Bayesian block algorithm [80] has been widely applied in both the binned light curve and the time-tagged event data [69,79,81]. Yet in the Bayesian block algorithm, the false alarm probability is adopted; thus, additional analysis is required to obtain the significance of the precursor [69,79]. By applying these methods, precursors are found in both long GRBs and SGRBs, and the detection rate of precursor is higher in long GRBs (e.g., [35,81]).
For SGRBs, the fraction of precursor events is less than for INTEGRAL [78], and is ∼8–10% for Swift/BAT [40]. For the combined Swift and Fermi/GBM sample, the fraction is found to be [79]. Applying the Bayesian block algorithm in the Fermi/GBM sample alone, we found a fraction of SGRBs are associated with precursor activities [69], while only a fraction of is found in Reference [81]. The major difference in the detection fraction may arise from the selection criteria for the precursors. The precursor events provided in Reference [69] are found of the signal-to-noise ratio (SNR) , where the SNR is obtained in the optimized energy range for the precursor. Thus, we adopt this precursor sample for Fermi/GBM in the following analysis. In Table 1, we list the SGRBs with precursors detected by Fermi/GBM [69] and/or Swift/BAT [40,79], where we show the duration of the precursor (), waiting time (), and the main SGRB (). For the Fermi/GBM sample [69], the duration is provided following the common definition of , during which 90% of the total counts have been detected. However, for the Swift/BAT sample, the duration is directly provided by the wavelet analysis or Bayesian block analysis following References [40,79].

Table 1.
The durations of the precursor (), waiting time (), and the main SGRB () are taken from [69] for Fermi/GBM detected bursts, and from [40,79] for Swift detected bursts (marked with ‘’). For the events only detected by Fermi/GBM, their names are provided following the Fermi GBM Burst Catalog. The redshift is for GRB060502B, and GRB090510 for 0.903.
Precursors of SGRBs are usually too faint to perform spectral analysis. Therefore, the hardness ratio is often used to indicate the spectral properties [35,40,69,79]. Previous research found that there is no significant spectral difference between the precursors and the main GRBs for Swift/BAT events [35,40], while for Fermi/GBM events, a slight difference is found [79]. There could be two possibilities for precursor events having similar spectra to the main GRBs. On the observational side, this might be caused by the narrow bandpass of Swift/BAT and the lack of photon counts [40]. On the theoretical side, there is a possibility that the precursor and the main GRB are mimicked by two episodes of activities produced by collapsars with only the “tip-of-the-iceberg” of the light curve being observed, which makes them have similar spectral shapes [36,82,83,84,85]. However, the latter possibility is disfavored by the f-factor analysis [85] for most of the events in Table 1; thus, we focus here on the scenario that precursors have different origins from the main GRBs.
For the Fermi/GBM events, there are several events that have enough photon counts to do spectral analyses as shown in Table 1 of Reference [69]. The precursors of GRB111117A and GRB160804180 are found to be in favor of non-thermal spectra and can be well explained by the magnetospheric interaction model; the precursors of GRB081216 and GRB141102A favor thermal spectra and can be explained by the SBO model [69]. For the magnetospheric interaction model, the precursor duration relates to the chirp signal time of GW radiation. For the SBO model, this relates to the radius and Lorentz factor of the shock. Note that for GRB090510, there are two precursors, and the second one may be described by the thermal SBO model [69], while the first one could then originate from magnetospheric interactions.
The GRB duration is usually described as , where is the jet dissipation radius, is the bulk Lorentz factor at , and z is the redshift of the source. For the magnetospheric interaction model, the waiting time consists of the jet launch time () and the jet propagation time (). For the SBO model, the waiting time relates to the jet propagation from the SBO radius to the jet dissipation radius, i.e., . For the cases with and , we would expect . Yet there is an exception case for magnetospheric interaction model, in which the NS merger remnant is a stable NS (SNS) formed after the spin-down of the initially-formed uniform-rotation-supported supramassive NS with [19,86]. Note that for the SBO model, one can constrain the ratio of the radii from observations.
Previous results based on Fermi/GBM events have indicated that can be generally satisfied [69]; here, in Figure 2, we show the updated diagram, which includes both Fermi/GBM and Swift/BAT events. The fitting of the data (red line) shows that , largely consistent with theories and previous results [69]. However, note here that the fitting errors are not provided, as the errors of the data points are not available for the Swift events [40,79]. However, there are two outliers, GRB090510 (the first precursor event) and GRB191221802, with . This might suggest that SNSs are formed in these two events.
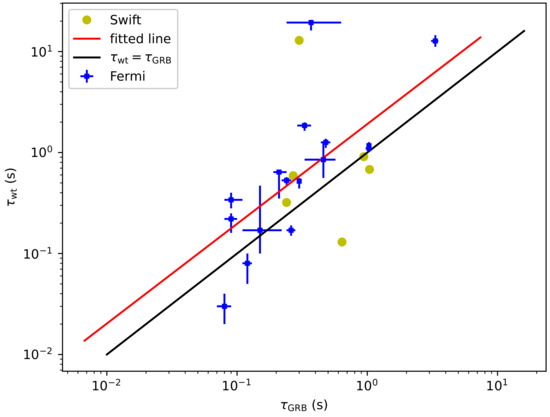
Figure 2.
The waiting time and GRB duration are taken from [69] for Fermi detected bursts, and from [40,79] for Swift detected bursts. The black is the line, and the red line is the fitting of the data.
4. Discussion and Prospects
Precursors have been detected for a small fraction of SGRBs. Here, we briefly review the models for precursors, mainly focusing on the magnetospheric interaction model and the SBO model, while the crust crack model and the fireball photospheric radiation model are found to be less likely based on current observations [69]. We focused on the explanation of the major physical processes in these models. To directly compare with observations, we estimated the luminosity, spectrum, duration, and opening angle for these models.
For the magnetospheric interaction model, the precursor will be produced simultaneously with GWs. A cutoff-power-law spectrum is expected with a photon index ∼−2/3 and a cutoff at MeV. Moreover, fast radio bursts (FRBs) are suggested to be produced during the magnetospheric interaction (e.g., [60,63]). It should be noted that for NS–BH binaries with mass ratio <0.2, the NS would be swallowed by the BH without producing a GRB and, thus, only the precursor is available.
While for the SBO model, the precursor is produced after the merger, but before the main GRB. Although GRB 170817A was classified as an SGRB, with a duration ≈0.5 s, it was fainter than the faintest SGRB previously detected by roughly three orders of magnitude, with the isotropic equivalent energy of erg. The delay time between the GW signal and the -rays, s. The peak energy of the observed integrated spectrum is eV [2,3]. The breakout layer parameter that could produce the observables of GRB 170817A are cm and . SBO emissions from the jet-cocoon system seems to provide a natural explanation for this observed event because of the low radiation efficiency and the wide emission angle. However, the event rate for cocoon-SBO-induced GRBs should be very small, considering that most GRBs are observed at cosmological distances [87].
Compared with the main GRBs, we found that precursors are usually much weaker, but with a larger opening angle. Thus, for the NS mergers that occurred within several hundred Mpc, the detection of precursors is very likely. This will greatly benefit the search for gamma-ray counterparts of GW events and FRBs, which can be well tested by the current and near-future observatories, e.g., Fermi/GBM and Swift/BAT, GECAM [68], and the space-based multi-band astronomical variable objects monitor (SVOM) [88]. Furthermore, the time delay between precursors and GRBs or GW can be used to constrain the jet launch mechanism and post-merger remnant [19,69]. For the magnetospheric interaction model, photon splitting could be important, and it might significantly change the polarization state of emitted photons [89,90]. This can also be tested by the future gamma-ray polarimeter detector POLAR-2 [91].
Funding
J.W. acknowledges the sponsorship of the Alexander von Humboldt Foundation.
Data Availability Statement
No new data were created or analyzed in this study.
Acknowledgments
The authors thank the reviewers for the valuable comments and suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Multi-messenger Observations of a Binary Neutron Star Merger. Astrophys. J. Lett. 2017, 848, L12. [Google Scholar] [CrossRef]
- Goldstein, A.; Veres, P.; Burns, E.; Briggs, M.S.; Hamburg, R.; Kocevski, D.; Wilson-Hodge, C.A.; Preece, R.D.; Poolakkil, S.; Roberts, O.J.; et al. An Ordinary Short Gamma-Ray Burst with Extraordinary Implications: Fermi-GBM Detection of GRB 170817A. Astrophys. J. Lett. 2017, 848, L14. [Google Scholar] [CrossRef]
- Zhang, B.B.; Zhang, B.; Sun, H.; Lei, W.H.; Gao, H.; Li, Y.; Shao, L.; Zhao, Y.; Hu, Y.D.; Lü, H.J.; et al. A peculiar low-luminosity short gamma-ray burst from a double neutron star merger progenitor. Nat. Commun. 2018, 9, 447. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Gravitational Waves and Gamma-Rays from a Binary Neutron Star Merger: GW170817 and GRB 170817A. Astrophys. J. Lett. 2017, 848, L13. [Google Scholar] [CrossRef]
- Coulter, D.A.; Foley, R.J.; Kilpatrick, C.D.; Drout, M.R.; Piro, A.L.; Shappee, B.J.; Siebert, M.R.; Simon, J.D.; Ulloa, N.; Kasen, D.; et al. Swope Supernova Survey 2017a (SSS17a), the Optical Counterpart to a Gravitational Wave Source. arXiv 2017, arXiv:astro-ph.HE/1710.05452. [Google Scholar] [CrossRef] [PubMed]
- Soares-Santos, M.; Holz, D.E.; Annis, J.; Chornock, R.; Herner, K.; Berger, E.; Brout, D.; Chen, H.Y.; Kessler, R.; Sako, M.; et al. The Electromagnetic Counterpart of the Binary Neutron Star Merger LIGO/Virgo GW170817. I. Discovery of the Optical Counterpart Using the Dark Energy Camera. Astrophys. J. Lett. 2017, 848, L16. [Google Scholar] [CrossRef]
- Valenti, S.; Sand, D.J.; Yang, S.; Cappellaro, E.; Tartaglia, L.; Corsi, A.; Jha, S.W.; Reichart, D.E.; Haislip, J.; Kouprianov, V. The Discovery of the Electromagnetic Counterpart of GW170817: Kilonova AT 2017gfo/DLT17ck. Astrophys. J. Lett. 2017, 848, L24. [Google Scholar] [CrossRef]
- Arcavi, I.; Hosseinzadeh, G.; Howell, D.A.; McCully, C.; Poznanski, D.; Kasen, D.; Barnes, J.; Zaltzman, M.; Vasylyev, S.; Maoz, D.; et al. Optical emission from a kilonova following a gravitational-wave-detected neutron-star merger. Nature 2017, 551, 64–66. [Google Scholar] [CrossRef]
- Tanvir, N.R.; Levan, A.J.; González-Fernández, C.; Korobkin, O.; Mandel, I.; Rosswog, S.; Hjorth, J.; D’Avanzo, P.; Fruchter, A.S.; Fryer, C.L.; et al. The Emergence of a Lanthanide-rich Kilonova Following the Merger of Two Neutron Stars. Astrophys. J. Lett. 2017, 848, L27. [Google Scholar] [CrossRef]
- Lipunov, V.M.; Gorbovskoy, E.; Kornilov, V.G.; Tyurina, N.; Balanutsa, P.; Kuznetsov, A.; Vlasenko, D.; Kuvshinov, D.; Gorbunov, I.; Buckley, D.A.H.; et al. MASTER Optical Detection of the First LIGO/Virgo Neutron Star Binary Merger GW170817. Astrophys. J. Lett. 2017, 850, L1. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. A gravitational-wave standard siren measurement of the Hubble constant. Nature 2017, 551, 85–88. [Google Scholar] [CrossRef]
- Wei, J.J.; Zhang, B.B.; Wu, X.F.; Gao, H.; Mészáros, P.; Zhang, B.; Dai, Z.G.; Zhang, S.N.; Zhu, Z.H. Multimessenger tests of the weak equivalence principle from GW170817 and its electromagnetic counterparts. J. Cosmol. Astropart. Phys. 2017, 2017, 035. [Google Scholar] [CrossRef]
- Troja, E.; Piro, L.; van Eerten, H.; Wollaeger, R.T.; Im, M.; Fox, O.D.; Butler, N.R.; Cenko, S.B.; Sakamoto, T.; Fryer, C.L.; et al. The X-ray counterpart to the gravitational-wave event GW170817. Nature 2017, 551, 71–74. [Google Scholar] [CrossRef]
- Hallinan, G.; Corsi, A.; Mooley, K.P.; Hotokezaka, K.; Nakar, E.; Kasliwal, M.M.; Kaplan, D.L.; Frail, D.A.; Myers, S.T.; Murphy, T.; et al. A radio counterpart to a neutron star merger. Science 2017, 358, 1579–1583. [Google Scholar] [CrossRef]
- Mooley, K.P.; Nakar, E.; Hotokezaka, K.; Hallinan, G.; Corsi, A.; Frail, D.A.; Horesh, A.; Murphy, T.; Lenc, E.; Kaplan, D.L.; et al. A mildly relativistic wide-angle outflow in the neutron-star merger event GW170817. Nature 2018, 554, 207–210. [Google Scholar] [CrossRef]
- Mooley, K.P.; Deller, A.T.; Gottlieb, O.; Nakar, E.; Hallinan, G.; Bourke, S.; Frail, D.A.; Horesh, A.; Corsi, A.; Hotokezaka, K. Superluminal motion of a relativistic jet in the neutron-star merger GW170817. Nature 2018, 561, 355–359. [Google Scholar] [CrossRef] [PubMed]
- Gill, R.; Nathanail, A.; Rezzolla, L. When Did the Remnant of GW170817 Collapse to a Black Hole? Astrophys. J. 2019, 876, 139. [Google Scholar] [CrossRef]
- Zhang, B. The delay time of gravitational wave—Gamma-ray burst associations. Front. Phys. 2019, 14, 64402. [Google Scholar] [CrossRef]
- Yang, Y.S.; Zhong, S.Q.; Zhang, B.B.; Wu, S.; Zhang, B.; Yang, Y.H.; Cao, Z.; Gao, H.; Zou, J.H.; Wang, J.S.; et al. Physical Implications of the Subthreshold GRB GBM-190816 and Its Associated Subthreshold Gravitational-wave Event. Astrophys. J. 2020, 899, 60. [Google Scholar] [CrossRef]
- Troja, E.; van Eerten, H.; Ryan, G.; Ricci, R.; Burgess, J.M.; Wieringa, M.H.; Piro, L.; Cenko, S.B.; Sakamoto, T. A year in the life of GW 170817: The rise and fall of a structured jet from a binary neutron star merger. Mon. Notices Royal Astron. Soc. 2019, 489, 1919–1926. [Google Scholar] [CrossRef]
- Ryan, G.; van Eerten, H.; Piro, L.; Troja, E. Gamma-Ray Burst Afterglows in the Multimessenger Era: Numerical Models and Closure Relations. Astrophys. J. 2020, 896, 166. [Google Scholar] [CrossRef]
- Balasubramanian, A.; Corsi, A.; Mooley, K.P.; Brightman, M.; Hallinan, G.; Hotokezaka, K.; Kaplan, D.L.; Lazzati, D.; Murphy, E.J. Continued Radio Observations of GW170817 3.5 yr Post-merger. Astrophys. J. Lett. 2021, 914, L20. [Google Scholar] [CrossRef]
- Goldstein, A.; Hamburg, R.; Wood, J.; Hui, C.M.; Cleveland, W.H.; Kocevski, D.; Littenberg, T.; Burns, E.; Dal Canton, T.; Veres, P.; et al. Updates to the Fermi GBM Targeted Sub-threshold Search in Preparation for the Third Observing Run of LIGO/Virgo. arXiv 2019, arXiv:astro-ph.HE/1903.12597. [Google Scholar]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. GW190425: Observation of a Compact Binary Coalescence with Total Mass ∼3.4 M⊙. Astrophys. J. Lett. 2020, 892, L3. [Google Scholar] [CrossRef]
- von Kienlin, A.; Veres, P.; Roberts, O.J.; Hamburg, R.; Bissaldi, E.; Briggs, M.S.; Burns, E.; Goldstein, A.; Kocevski, D.; Preece, R.D.; et al. Fermi-GBM GRBs with Characteristics Similar to GRB 170817A. Astrophys. J. 2019, 876, 89. [Google Scholar] [CrossRef]
- Berger, E. Short-Duration Gamma-Ray Bursts. Annu. Rev. Astron. Astrophys. 2014, 52, 43–105. [Google Scholar] [CrossRef]
- Fernández, R.; Metzger, B.D. Electromagnetic Signatures of Neutron Star Mergers in the Advanced LIGO Era. Annu. Rev. Nucl. Part. Sci. 2016, 66, 23–45. [Google Scholar] [CrossRef]
- Zhang, B. The Physics of Gamma-Ray Bursts; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar] [CrossRef]
- Metzger, B.D. Kilonovae. Living Rev. Relativ. 2019, 23, 1. [Google Scholar] [CrossRef] [PubMed]
- Burns, E. Neutron star mergers and how to study them. Living Rev. Relativ. 2020, 23, 4. [Google Scholar] [CrossRef]
- Nakar, E. The electromagnetic counterparts of compact binary mergers. Phys. Rep. 2020, 886, 1–84. [Google Scholar] [CrossRef]
- Koshut, T.M.; Kouveliotou, C.; Paciesas, W.S.; van Paradijs, J.; Pendleton, G.N.; Briggs, M.S.; Fishman, G.J.; Meegan, C.A. Gamma-Ray Burst Precursor Activity as Observed with BATSE. Astrophys. J. 1995, 452, 145. [Google Scholar] [CrossRef]
- Lazzati, D. Precursor activity in bright, long BATSE gamma-ray bursts. Mon. Notices Royal Astron. Soc. 2005, 357, 722–731. [Google Scholar] [CrossRef]
- Burlon, D.; Ghirlanda, G.; Ghisellini, G.; Lazzati, D.; Nava, L.; Nardini, M.; Celotti, A. Precursors in Swift Gamma Ray Bursts with Redshift. Astrophys. J. Lett. 2008, 685, L19. [Google Scholar] [CrossRef]
- Burlon, D.; Ghirlanda, G.; Ghisellini, G.; Greiner, J.; Celotti, A. Time resolved spectral behavior of bright BATSE precursors. Astron. Astrophys. 2009, 505, 569–575. [Google Scholar] [CrossRef]
- Hu, Y.D.; Liang, E.W.; Xi, S.Q.; Peng, F.K.; Lu, R.J.; Lü, L.Z.; Zhang, B. Internal Energy Dissipation of Gamma-Ray Bursts Observed with Swift: Precursors, Prompt Gamma-Rays, Extended Emission, and Late X-ray Flares. Astrophys. J. 2014, 789, 145. [Google Scholar] [CrossRef]
- Lan, L.; Lü, H.J.; Zhong, S.Q.; Zhang, H.M.; Rice, J.; Cheng, J.G.; Du, S.S.; Li, L.; Lin, J.; Lu, R.J.; et al. Characteristics of Two-episode Emission Patterns in Fermi Long Gamma-Ray Bursts. Astrophys. J. 2018, 862, 155. [Google Scholar] [CrossRef]
- Zhang, B.B.; Zhang, B.; Castro-Tirado, A.J.; Dai, Z.G.; Tam, P.H.T.; Wang, X.Y.; Hu, Y.D.; Karpov, S.; Pozanenko, A.; Zhang, F.W.; et al. Transition from fireball to Poynting-flux-dominated outflow in the three-episode GRB 160625B. Nat. Astron. 2018, 2, 69–75. [Google Scholar] [CrossRef]
- Troja, E.; Rosswog, S.; Gehrels, N. Precursors of Short Gamma-ray Bursts. Astrophys. J. 2010, 723, 1711–1717. [Google Scholar] [CrossRef]
- Paczynski, B. Gamma-ray bursters at cosmological distances. Astrophys. J. Lett. 1986, 308, L43–L46. [Google Scholar] [CrossRef]
- Mészáros, P.; Rees, M.J. Steep Slopes and Preferred Breaks in Gamma-Ray Burst Spectra: The Role of Photospheres and Comptonization. Astrophys. J. 2000, 530, 292–298. [Google Scholar] [CrossRef]
- Daigne, F.; Mochkovitch, R. The expected thermal precursors of gamma-ray bursts in the internal shock model. Mon. Notices Royal Astron. Soc. 2002, 336, 1271–1280. [Google Scholar] [CrossRef]
- Ruffini, R.; Aksenov, A.G.; Bernardini, M.G.; Bianco, C.L.; Caito, L.; Dainotti, M.G.; de Barros, G.; Guida, R.; Vereshchagin, G.V.; Xue, S.S. The canonical Gamma-ray Bursts and their “precursors”. In Proceedings of the 2008 Nanjing Gamma-ray Burst Conference, Nanjing, China, 11 November 2008; Huang, Y.F., Dai, Z.G., Zhang, B., Eds.; American Institute of Physics Conference Series. Volume 1065, pp. 219–222. [Google Scholar] [CrossRef][Green Version]
- Ramirez-Ruiz, E.; MacFadyen, A.I.; Lazzati, D. Precursors and e+/− pair loading from erupting fireballs. Mon. Notices Royal Astron. Soc. 2002, 331, 197–202. [Google Scholar] [CrossRef]
- Waxman, E.; Mészáros, P. Collapsar Uncorking and Jet Eruption in Gamma-Ray Bursts. Astrophys. J. 2003, 584, 390–398. [Google Scholar] [CrossRef]
- Zhang, W.; Woosley, S.E.; MacFadyen, A.I. Relativistic Jets in Collapsars. Astrophys. J. 2003, 586, 356–371. [Google Scholar] [CrossRef]
- Lazzati, D.; Begelman, M.C. Universal GRB Jets from Jet-Cocoon Interaction in Massive Stars. Astrophys. J. 2005, 629, 903–907. [Google Scholar] [CrossRef]
- Nakar, E.; Sari, R. Relativistic Shock Breakouts—A Variety of Gamma-Ray Flares: From Low-luminosity Gamma-Ray Bursts to Type Ia Supernovae. Astrophys. J. 2012, 747, 88. [Google Scholar] [CrossRef]
- Levinson, A.; Nakar, E. Physics of radiation mediated shocks and its applications to GRBs, supernovae, and neutron star mergers. Phys. Rep. 2020, 866, 1–46. [Google Scholar] [CrossRef]
- Keren, S.; Levinson, A. Sub-photospheric, Radiation-mediated Shocks in Gamma-Ray Bursts: Multiple Shock Emission and the Band Spectrum. Astrophys. J. 2014, 789, 128. [Google Scholar] [CrossRef][Green Version]
- Ito, H.; Matsumoto, J.; Nagataki, S.; Warren, D.C.; Barkov, M.V.; Yonetoku, D. The photospheric origin of the Yonetoku relation in gamma-ray bursts. Nat. Commun. 2019, 10, 1504. [Google Scholar] [CrossRef]
- Gottlieb, O.; Nakar, E.; Piran, T.; Hotokezaka, K. A cocoon shock breakout as the origin of the γ-ray emission in GW170817. Mon. Notices Royal Astron. Soc. 2018, 479, 588–600. [Google Scholar] [CrossRef]
- Bromberg, O.; Tchekhovskoy, A.; Gottlieb, O.; Nakar, E.; Piran, T. The γ-rays that accompanied GW170817 and the observational signature of a magnetic jet breaking out of NS merger ejecta. Mon. Notices Royal Astron. Soc. 2018, 475, 2971–2977. [Google Scholar] [CrossRef]
- Hansen, B.M.S.; Lyutikov, M. Radio and X-ray signatures of merging neutron stars. Mon. Notices Royal Astron. Soc. 2001, 322, 695–701. [Google Scholar] [CrossRef]
- Lai, D. DC Circuit Powered by Orbital Motion: Magnetic Interactions in Compact Object Binaries and Exoplanetary Systems. Astrophys. J. Lett. 2012, 757, L3. [Google Scholar] [CrossRef]
- Palenzuela, C.; Lehner, L.; Ponce, M.; Liebling, S.L.; Anderson, M.; Neilsen, D.; Motl, P. Electromagnetic and Gravitational Outputs from Binary-Neutron-Star Coalescence. Phys. Rev. Lett. 2013, 111, 061105. [Google Scholar] [CrossRef] [PubMed]
- Palenzuela, C.; Lehner, L.; Liebling, S.L.; Ponce, M.; Anderson, M.; Neilsen, D.; Motl, P. Linking electromagnetic and gravitational radiation in coalescing binary neutron stars. Phys. Rev. D 2013, 88, 043011. [Google Scholar] [CrossRef]
- Paschalidis, V.; Etienne, Z.B.; Shapiro, S.L. General-relativistic simulations of binary black hole-neutron stars: Precursor electromagnetic signals. Phys. Rev. D 2013, 88, 021504. [Google Scholar] [CrossRef]
- Wang, J.S.; Yang, Y.P.; Wu, X.F.; Dai, Z.G.; Wang, F.Y. Fast Radio Bursts from the Inspiral of Double Neutron Stars. Astrophys. J. Lett. 2016, 822, L7. [Google Scholar] [CrossRef]
- Paschalidis, V. General relativistic simulations of compact binary mergers as engines for short gamma-ray bursts. Class. Quantum Gravity 2017, 34, 084002. [Google Scholar] [CrossRef]
- Wang, J.S.; Peng, F.K.; Wu, K.; Dai, Z.G. Pre-merger Electromagnetic Counterparts of Binary Compact Stars. Astrophys. J. 2018, 868, 19. [Google Scholar] [CrossRef]
- Most, E.R.; Philippov, A.A. Electromagnetic Precursors to Gravitational-wave Events: Numerical Simulations of Flaring in Pre-merger Binary Neutron Star Magnetospheres. Astrophys. J. Lett. 2020, 893, L6. [Google Scholar] [CrossRef]
- Tsang, D.; Read, J.S.; Hinderer, T.; Piro, A.L.; Bondarescu, R. Resonant Shattering of Neutron Star Crusts. Phys. Rev. Lett. 2012, 108, 011102. [Google Scholar] [CrossRef] [PubMed]
- Suvorov, A.G.; Kokkotas, K.D. Precursor flares of short gamma-ray bursts from crust yielding due to tidal resonances in coalescing binaries of rotating, magnetized neutron stars. Phys. Rev. D 2020, 101, 083002. [Google Scholar] [CrossRef]
- Kuan, H.J.; Suvorov, A.G.; Kokkotas, K.D. General-relativistic treatment of tidal g-mode resonances in coalescing binaries of neutron stars—II. As triggers for precursor flares of short gamma-ray bursts. Mon. Notices Royal Astron. Soc. 2021, 508, 1732–1744. [Google Scholar] [CrossRef]
- Dichiara, S.; Troja, E.; O’Connor, B.; Marshall, F.E.; Beniamini, P.; Cannizzo, J.K.; Lien, A.Y.; Sakamoto, T. Short gamma-ray bursts within 200 Mpc. Mon. Notices Royal Astron. Soc. 2020, 492, 5011–5022. [Google Scholar] [CrossRef]
- Zhang, D.; Li, X.; Xiong, S.; Li, Y.; Sun, X.; An, Z.; Xu, Y.; Zhu, Y.; Peng, W.; Wang, H.; et al. Energy response of GECAM gamma-ray detector based on LaBr3:Ce and SiPM array. Nucl. Instruments Methods Phys. Res. A 2019, 921, 8–13. [Google Scholar] [CrossRef]
- Wang, J.S.; Peng, Z.K.; Zou, J.H.; Zhang, B.B.; Zhang, B. Stringent Search for Precursor Emission in Short GRBs from Fermi/GBM Data and Physical Implications. Astrophys. J. Lett. 2020, 902, L42. [Google Scholar] [CrossRef]
- Mottez, F.; Heyvaerts, J. Magnetic coupling of planets and small bodies with a pulsar wind. Astron. Astrophys. 2011, 532, A21. [Google Scholar] [CrossRef]
- Ponce, M.; Palenzuela, C.; Lehner, L.; Liebling, S.L. Interaction of misaligned magnetospheres in the coalescence of binary neutron stars. Phys. Rev. D 2014, 90, 044007. [Google Scholar] [CrossRef]
- Carrasco, F.; Shibata, M.; Reula, O. Magnetospheres of black hole-neutron star binaries. arXiv 2021, arXiv:2106.09081. [Google Scholar] [CrossRef]
- Wang, J.S.; Liu, R.Y.; Aharonian, F.; Dai, Z.G. Analytical treatment for the development of electromagnetic cascades in intense magnetic fields. Phys. Rev. D 2018, 97, 103016. [Google Scholar] [CrossRef]
- Horowitz, C.J.; Kadau, K. Breaking Strain of Neutron Star Crust and Gravitational Waves. Phys. Rev. Lett. 2009, 102, 191102. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.S.; Lai, D. Evolution of inspiralling neutron star binaries: Effects of tidal interactions and orbital eccentricities. Phys. Rev. D 2020, 102, 083005. [Google Scholar] [CrossRef]
- Yakovlev, D.G.; Levenfish, K.P.; Shibanov, Y.A. Cooling of neutron stars and superfluidity in their cores. Phys. Usp. 1999, 42, 737. [Google Scholar] [CrossRef]
- Thompson, C.; Duncan, R.C. The Giant Flare of 1998 August 27 from SGR 1900+14. II. Radiative Mechanism and Physical Constraints on the Source. Astrophys. J. 2001, 561, 980–1005. [Google Scholar] [CrossRef]
- Minaev, P.; Pozanenko, A.; Molkov, S. Precursors of short gamma-ray bursts detected by the INTEGRAL observatory. Int. J. Mod. Phys. D 2018, 27, 1844013. [Google Scholar] [CrossRef]
- Zhong, S.Q.; Dai, Z.G.; Cheng, J.G.; Lan, L.; Zhang, H.M. Precursors in Short Gamma-Ray Bursts as a Possible Probe of Progenitors. Astrophys. J. 2019, 884, 25. [Google Scholar] [CrossRef]
- Scargle, J.D.; Norris, J.P.; Jackson, B.; Chiang, J. Studies in Astronomical Time Series Analysis. VI. Bayesian Block Representations. Astrophys. J. 2013, 764, 167. [Google Scholar] [CrossRef]
- Coppin, P.; de Vries, K.D.; van Eijndhoven, N. Identification of gamma-ray burst precursors in Fermi-GBM bursts. Phys. Rev. D 2020, 102, 103014. [Google Scholar] [CrossRef]
- Zhang, B.; Zhang, B.B.; Virgili, F.J.; Liang, E.W.; Kann, D.A.; Wu, X.F.; Proga, D.; Lv, H.J.; Toma, K.; Mészáros, P.; et al. Discerning the Physical Origins of Cosmological Gamma-ray Bursts Based on Multiple Observational Criteria: The Cases of z = 6.7 GRB 080913, z = 8.2 GRB 090423, and Some Short/Hard GRBs. Astrophys. J. 2009, 703, 1696–1724. [Google Scholar] [CrossRef]
- Virgili, F.J.; Zhang, B.; O’Brien, P.; Troja, E. Are All Short-hard Gamma-ray Bursts Produced from Mergers of Compact Stellar Objects? Astrophys. J. 2011, 727, 109. [Google Scholar] [CrossRef]
- Bromberg, O.; Nakar, E.; Piran, T.; Sari, R. Short versus Long and Collapsars versus Non-collapsars: A Quantitative Classification of Gamma-Ray Bursts. Astrophys. J. 2013, 764, 179. [Google Scholar] [CrossRef]
- Lü, H.J.; Zhang, B.; Liang, E.W.; Zhang, B.B.; Sakamoto, T. The ‘amplitude’ parameter of gamma-ray bursts and its implications for GRB classification. Mon. Notices Royal Astron. Soc. 2014, 442, 1922–1929. [Google Scholar] [CrossRef]
- Metzger, B.D.; Giannios, D.; Thompson, T.A.; Bucciantini, N.; Quataert, E. The protomagnetar model for gamma-ray bursts. Mon. Notices Royal Astron. Soc. 2011, 413, 2031–2056. [Google Scholar] [CrossRef]
- Matsumoto, T.; Piran, T. On short GRBs similar to GRB 170817A detected by Fermi-GBM. Mon. Notices Royal Astron. Soc. 2020, 492, 4283–4290. [Google Scholar] [CrossRef]
- Yu, S.; Gonzalez, F.; Wei, J.; Zhang, S.; Cordier, B. SVOM: A Joint Gamma-ray Burst Detection Mission. Chin. Astron. Astrophys. 2020, 44, 269–282. [Google Scholar] [CrossRef]
- Adler, S.L. Photon splitting and photon dispersion in a strong magnetic field. Ann. Phys. 1971, 67, 599–647. [Google Scholar] [CrossRef]
- Baring, M.G.; Harding, A.K. Photon Splitting and Pair Creation in Highly Magnetized Pulsars. Astrophys. J. 2001, 547, 929–948. [Google Scholar] [CrossRef]
- De Angelis, N.; Burgess, J.M.; Cadoux, F.; Greiner, J.; Hulsman, J.; Kole, M.; Li, H.C.; Mianowski, S.; Pollo, A.; Produit, N.; et al. Development and science perspectives of the POLAR-2 instrument: A large scale GRB polarimeter. arXiv 2021, arXiv:2109.02978. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).