Detectability of Continuous Gravitational Waves from Magnetically Deformed Neutron Stars
Abstract
:1. Introduction
2. Materials and Methods
3. Results
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
| 1 | The XNS code solves simultaneously and self-consistently the Einstein equations for the metric, the GRMHD-Euler Equation for the plasma, and the GR-Maxwell Equations for the magnetic field distribution, using the XCFC formalism. |
| 2 | The aLIGO design densitivity curves can be found at https://dcc.ligo.org/LIGO-T1800044/public, (accessed on 14 September 2021). |
| 3 | The ET sensitivity curves can be found at http://www.et-gw.eu/index.php/etsensitivities, (accessed on 14 September 2021). |
References
- Landau, L.D. To the theory of energy transmission in collissions. II. Phys. Zs. Sowjet 1932, 2, 46. [Google Scholar]
- Baade, W.; Zwicky, F. On Super-novae. Proc. Natl. Acad. Sci. USA 1934, 20, 254–259. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pacini, F. Energy Emission from a Neutron Star. Nature 1967, 216, 567–568. [Google Scholar] [CrossRef]
- Hewish, A.; Bell, S.J.; Pilkington, J.D.H.; Scott, P.F.; Collins, R.A. Observation of a Rapidly Pulsating Radio Source. Nature 1968, 217, 709–713. [Google Scholar] [CrossRef]
- Gold, T. Rotating Neutron Stars as the Origin of the Pulsating Radio Sources. Nature 1968, 218, 731–732. [Google Scholar] [CrossRef]
- Duncan, R.C.; Thompson, C. Formation of Very Strongly Magnetized Neutron Stars: Implications for Gamma-Ray Bursts. ApJ 1992, 392, L9. [Google Scholar] [CrossRef]
- Thompson, C.; Duncan, R.C. Neutron Star Dynamos and the Origins of Pulsar Magnetism. ApJ 1993, 408, 194. [Google Scholar] [CrossRef]
- Thompson, C.; Duncan, R.C. The soft gamma repeaters as very strongly magnetized neutron stars—I. Radiative mechanism for outbursts. MNRAS 1995, 275, 255–300. [Google Scholar] [CrossRef]
- Thompson, C.; Duncan, R.C. The Soft Gamma Repeaters as Very Strongly Magnetized Neutron Stars. II. Quiescent Neutrino, X-Ray, and Alfven Wave Emission. ApJ 1996, 473, 322. [Google Scholar] [CrossRef]
- Kouveliotou, C.; Dieters, S.; Strohmayer, T.; van Paradijs, J.; Fishman, G.J.; Meegan, C.A.; Hurley, K.; Kommers, J.; Smith, I.; Frail, D.; et al. An X-ray pulsar with a superstrong magnetic field in the soft γ-ray repeater SGR1806 - 20. Nature 1998, 393, 235–237. [Google Scholar] [CrossRef]
- Gavriil, F.P.; Kaspi, V.M.; Woods, P.M. Magnetar-like X-ray bursts from an anomalous X-ray pulsar. Nature 2002, 419, 142–144. [Google Scholar] [CrossRef] [PubMed]
- Mereghetti, S.; Pons, J.; Melatos, A. Magnetars: Properties, Origin and Evolution. Space Sci. Rev. 2015, 191, 315–338. [Google Scholar] [CrossRef] [Green Version]
- Olausen, S.A.; Kaspi, V.M. The McGill Magnetar Catalog. ApJS 2014, 212, 6. [Google Scholar] [CrossRef] [Green Version]
- Kaspi, V.M.; Beloborodov, A.M. Magnetars. ARA&A 2017, 55, 261–301. [Google Scholar] [CrossRef] [Green Version]
- Asseo, E.; Khechinashvili, D. The role of multipolar magnetic fields in pulsar magnetospheres. MNRAS 2002, 334, 743–759. [Google Scholar] [CrossRef] [Green Version]
- Spruit, H.C. The source of magnetic fields in (neutron-) stars. In Cosmic Magnetic Fields: From Planets, to Stars and Galaxies; Strassmeier, K.G., Kosovichev, A.G., Beckman, J.E., Eds.; Cambridge University Press: Cambridge, UK, 2009; Volume 259, pp. 61–74. [Google Scholar] [CrossRef] [Green Version]
- Ferrario, L.; Melatos, A.; Zrake, J. Magnetic Field Generation in Stars. Space Sci. Rev. 2015, 191, 77. [Google Scholar] [CrossRef] [Green Version]
- Popov, S.B. Origins of magnetars in binary systems. Astron. Astrophys. Trans. 2016, 29, 183–192. [Google Scholar]
- Del Zanna, L.; Bucciantini, N. Covariant and 3 + 1 equations for dynamo-chiral general relativistic magnetohydrodynamics. MNRAS 2018, 479, 657–666. [Google Scholar] [CrossRef]
- Ciolfi, R.; Kastaun, W.; Kalinani, J.V.; Giacomazzo, B. First 100 ms of a long-lived magnetized neutron star formed in a binary neutron star merger. Phys. Rev. D 2019, 100, 023005. [Google Scholar] [CrossRef] [Green Version]
- Franceschetti, K.; Del Zanna, L. General Relativistic Mean-Field Dynamo Model for Proto-Neutron Stars. Universe 2020, 6, 83. [Google Scholar] [CrossRef]
- Prendergast, K.H. The Equilibrium of a Self-Gravitating Incompressible Fluid Sphere with a Magnetic Field. I. ApJ 1956, 123, 498. [Google Scholar] [CrossRef]
- Chandrasekhar, S.; Prendergast, K.H. THE EQUILIBRIUM OF MAGNETIC STARS. Proc. Natl. Acad. Sci. USA 1956, 42, 5–9. [Google Scholar] [CrossRef] [Green Version]
- Chandrasekhar, S.; Kendall, P.C. On Force-Free Magnetic Fields. ApJ 1957, 126, 457. [Google Scholar] [CrossRef]
- Tayler, R.J. The adiabatic stability of stars containing magnetic fields-I.Toroidal fields. MNRAS 1973, 161, 365. [Google Scholar] [CrossRef]
- Markey, P.; Tayler, R.J. The adiabatic stability of stars containing magnetic fields. II. Poloidal fields. MNRAS 1973, 163, 77–91. [Google Scholar] [CrossRef]
- Markey, P.; Tayler, R.J. The adiabatic stability of stars containing magnetic fields-III. Additional results for poloidal fields. MNRAS 1974, 168, 505–514. [Google Scholar] [CrossRef] [Green Version]
- Tayler, R.J. The adiabatic stability of stars containing magnetic fields. IV—Mixed poloidal and toroidal fields. MNRAS 1980, 191, 151–163. [Google Scholar] [CrossRef]
- Ciolfi, R.; Rezzolla, L. Twisted-torus configurations with large toroidal magnetic fields in relativistic stars. MNRAS 2013, 435, L43–L47. [Google Scholar] [CrossRef] [Green Version]
- Uryū, K.; Gourgoulhon, E.; Markakis, C.M.; Fujisawa, K.; Tsokaros, A.; Eriguchi, Y. Equilibrium solutions of relativistic rotating stars with mixed poloidal and toroidal magnetic fields. Phys. Rev. D 2014, 90, 101501. [Google Scholar] [CrossRef]
- Pili, A.G.; Bucciantini, N.; Del Zanna, L. Axisymmetric equilibrium models for magnetized neutron stars in general relativity under the conformally flat condition. MNRAS 2014, 439, 3541–3563. [Google Scholar] [CrossRef] [Green Version]
- Samuelsson, L.; Andersson, N. Neutron star asteroseismology. Axial crust oscillations in the Cowling approximation. MNRAS 2007, 374, 256–268. [Google Scholar] [CrossRef]
- Sotani, H. Torsional oscillations of neutron stars with highly tangled magnetic fields. Phys. Rev. D 2015, 92, 104024. [Google Scholar] [CrossRef] [Green Version]
- Page, D.; Lattimer, J.M.; Prakash, M.; Steiner, A.W. Minimal Cooling of Neutron Stars: A New Paradigm. ApJS 2004, 155, 623–650. [Google Scholar] [CrossRef] [Green Version]
- Aguilera, D.N.; Pons, J.A.; Miralles, J.A. The Impact of Magnetic Field on the Thermal Evolution of Neutron Stars. ApJ 2008, 673, L167. [Google Scholar] [CrossRef] [Green Version]
- Haskell, B.; Samuelsson, L.; Glampedakis, K.; Andersson, N. Modelling magnetically deformed neutron stars. MNRAS 2008, 385, 531–542. [Google Scholar] [CrossRef] [Green Version]
- Eslam Panah, B.; Bordbar, G.H.; Hendi, S.H.; Ruffini, R.; Rezaei, Z.; Moradi, R. Expansion of Magnetic Neutron Stars in an Energy (in)Dependent Spacetime. ApJ 2017, 848, 24. [Google Scholar] [CrossRef] [Green Version]
- Gomes, R.O.; Pais, H.; Dexheimer, V.; Providência, C.; Schramm, S. Limiting magnetic field for minimal deformation of a magnetized neutron star. A&A 2019, 627, A61. [Google Scholar] [CrossRef] [Green Version]
- Kandel, D.; Romani, R.W. Atmospheric Circulation on Black Widow Companions. ApJ 2020, 892, 101. [Google Scholar] [CrossRef] [Green Version]
- Fonseca, E.; Cromartie, H.T.; Pennucci, T.T.; Ray, P.S.; Kirichenko, A.Y.; Ransom, S.M.; Demorest, P.B.; Stairs, I.H.; Arzoumanian, Z.; Guillemot, L.; et al. Refined Mass and Geometric Measurements of the High-Mass PSR J0740+6620. arXiv 2021, arXiv:2104.00880. [Google Scholar]
- Pang, P.T.H.; Tews, I.; Coughlin, M.W.; Bulla, M.; Van Den Broeck, C.; Dietrich, T. Nuclear-Physics Multi-Messenger Astrophysics Constraints on the Neutron-Star Equation of State: Adding NICER’s PSR J0740+6620 Measurement. arXiv 2021, arXiv:2105.08688. [Google Scholar]
- Zhang, N.B.; Li, B.A. Impacts of NICER’s Radius Measurement of PSR J0740+6620 on Nuclear Symmetry Energy at Suprasaturation Densities. arXiv 2021, arXiv:2105.11031. [Google Scholar]
- Collaboration, T.L.S.; Collaboration, V. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef] [Green Version]
- The LIGO Scientific Collaboration; The Virgo Collaboration. GW170817: Measurements of Neutron Star Radii and Equation of State. Phys. Rev. Lett. 2018, 121, 161101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cai, B.J.; Fattoyev, F.J.; Li, B.A.; Newton, W.G. Critical density and impact of Δ (1232 ) resonance formation in neutron stars. Phys. Rev. C 2015, 92, 015802. [Google Scholar] [CrossRef] [Green Version]
- Drago, A.; Lavagno, A.; Pagliara, G.; Pigato, D. The scenario of two families of compact stars. Eur. Phys. J. A 2016, 52, 40. [Google Scholar] [CrossRef] [Green Version]
- Zdunik, J.L.; Haensel, P. Maximum mass of neutron stars and strange neutron-star cores. A&A 2013, 551, A61. [Google Scholar] [CrossRef]
- Chatterjee, D.; Vidaña, I. Do hyperons exist in the interior of neutron stars? Eur. Phys. J. A 2016, 52, 29. [Google Scholar] [CrossRef] [Green Version]
- Avancini, S.S.; Menezes, D.P.; Pinto, M.B.; Providência, C. QCD critical end point under strong magnetic fields. Phys. Rev. D 2012, 85, 091901. [Google Scholar] [CrossRef] [Green Version]
- Ferreira, M.; Costa, P.; Menezes, D.P.; Providência, C.; Scoccola, N.N. Deconfinement and chiral restoration within the SU(3) Polyakov-Nambu-Jona-Lasinio and entangled Polyakov-Nambu-Jona-Lasinio models in an external magnetic field. Phys. Rev. D 2014, 89, 016002. [Google Scholar] [CrossRef] [Green Version]
- Costa, P.; Ferreira, M.; Hansen, H.; Menezes, D.P.; Providência, C. Phase transition and critical end point driven by an external magnetic field in asymmetric quark matter. Phys. Rev. D 2014, 89, 056013. [Google Scholar] [CrossRef]
- Roark, J.; Dexheimer, V. Deconfinement phase transition in proto-neutron-star matter. Phys. Rev. C 2018, 98, 055805. [Google Scholar] [CrossRef] [Green Version]
- Lugones, G.; Grunfeld, A.G. Surface tension of hot and dense quark matter under strong magnetic fields. Phys. Rev. C 2019, 99, 035804. [Google Scholar] [CrossRef] [Green Version]
- Ruderman, M. Spin-driven changes in neutron star magnetic fields. J. Astrophys. Astron. 1995, 16, 207–216. [Google Scholar] [CrossRef]
- Lander, S.K. Magnetic Fields in Superconducting Neutron Stars. Phys. Rev. Lett. 2013, 110, 071101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Haskell, B.; Sedrakian, A. Superfluidity and Superconductivity in Neutron Stars. In The Physics and Astrophysics of Neutron Stars; Rezzolla, L., Pizzochero, P., Jones, D.I., Rea, N., Vidaña, I., Eds.; Springer: Cham, Switzerland, 2018; Volume 457, p. 401. [Google Scholar] [CrossRef] [Green Version]
- Bocquet, M.; Bonazzola, S.; Gourgoulhon, E.; Novak, J. Rotating neutron star models with a magnetic field. A&A 1995, 301, 757. [Google Scholar]
- Cutler, C. Gravitational waves from neutron stars with large toroidal B fields. Phys. Rev. D 2002, 66, 084025. [Google Scholar] [CrossRef] [Green Version]
- Oron, A. Relativistic magnetized star with poloidal and toroidal fields. Phys. Rev. D 2002, 66, 023006. [Google Scholar] [CrossRef]
- Dall’Osso, S.; Shore, S.N.; Stella, L. Early evolution of newly born magnetars with a strong toroidal field. MNRAS 2009, 398, 1869–1885. [Google Scholar] [CrossRef] [Green Version]
- Frieben, J.; Rezzolla, L. Equilibrium models of relativistic stars with a toroidal magnetic field. MNRAS 2012, 427, 3406. [Google Scholar] [CrossRef] [Green Version]
- Breu, C.; Rezzolla, L. Maximum mass, moment of inertia and compactness of relativistic stars. MNRAS 2016, 459, 646–656. [Google Scholar] [CrossRef] [Green Version]
- Soldateschi, J.; Bucciantini, N.; Del Zanna, L. Quasi-universality of the magnetic deformation of neutron stars in general relativity and beyond. arXiv 2021, arXiv:2106.00603. [Google Scholar]
- Soldateschi, J.; Bucciantini, N.; Del Zanna, L. Axisymmetric equilibrium models for magnetised neutron stars in scalar-tensor theories. A&A 2020, 640, A44. [Google Scholar] [CrossRef]
- Soldateschi, J.; Bucciantini, N.; Del Zanna, L. Magnetic deformation of neutron stars in scalar-tensor theories. A&A 2021, 645, A39. [Google Scholar] [CrossRef]
- Manchester, R.N.; Hobbs, G.B.; Teoh, A.; Hobbs, M. The Australia Telescope National Facility Pulsar Catalogue. Astron. J. 2005, 129, 1993–2006. [Google Scholar] [CrossRef]
- Pili, A.G.; Bucciantini, N.; Del Zanna, L. General relativistic neutron stars with twisted magnetosphere. MNRAS 2015, 447, 2821–2835. [Google Scholar] [CrossRef] [Green Version]
- Bucciantini, N.; Del Zanna, L. General relativistic magnetohydrodynamics in axisymmetric dynamical spacetimes: The X-ECHO code. A&A 2011, 528, A101. [Google Scholar] [CrossRef] [Green Version]
- Gourgoulhon, E. An introduction to the theory of rotating relativistic stars. arXiv 2010, arXiv:1003.5015. [Google Scholar]
- Gourgoulhon, É. 3+1 Formalism in General Relativity: Bases of Numerical Relativity; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Eslam Panah, B.; Yazdizadeh, T.; Bordbar, G.H. Contraction of cold neutron star due to in the presence a quark core. Eur. Phys. J. C 2019, 79, 815. [Google Scholar] [CrossRef]
- Akmal, A.; Pandharipande, V.R.; Ravenhall, D.G. Equation of state of nucleon matter and neutron star structure. Phys. Rev. C 1998, 58, 1804–1828. [Google Scholar] [CrossRef] [Green Version]
- Typel, S.; Oertel, M.; Klaehn, T. CompOSE—CompStar Online Supernovae Equations of State. arXiv 2013, arXiv:1307.5715. [Google Scholar]
- Horowitz, C.J.; Piekarewicz, J. Neutron Star Structure and the Neutron Radius of 208Pb. Phys. Rev. Lett. 2001, 86, 5647–5650. [Google Scholar] [CrossRef] [Green Version]
- Fortin, M.; Providencia, C.; Raduta, A.R.; Gulminelli, F.; Zdunik, J.L.; Haensel, P.; Bejger, M. Neutron star radii and crusts: uncertainties and unified equations of state. Phys. Rev. C 2016, 94, 035804. [Google Scholar] [CrossRef] [Green Version]
- Antoniadis, J.; Tauris, T.M.; Ozel, F.; Barr, E.; Champion, D.J.; Freire, P.C.C. The millisecond pulsar mass distribution: Evidence for bimodality and constraints on the maximum neutron star mass. arXiv 2016, arXiv:1605.01665. [Google Scholar]
- Faucher-Giguère, C.A.; Kaspi, V.M. Birth and Evolution of Isolated Radio Pulsars. ApJ 2006, 643, 332–355. [Google Scholar] [CrossRef]
- Bisnovatyi-Kogan, G.S.; Komberg, B.V. Pulsars and close binary systems. SvA 1974, 18, 217. [Google Scholar]
- Romani, R.W. A unified model of neutron-star magnetic fields. Nature 1990, 347, 741–743. [Google Scholar] [CrossRef]
- Cruces, M.; Reisenegger, A.; Tauris, T.M. On the weak magnetic field of millisecond pulsars: does it decay before accretion? MNRAS 2019, 490, 2013–2022. [Google Scholar] [CrossRef] [Green Version]
- Alsing, J.; Silva, H.O.; Berti, E. Evidence for a maximum mass cut-off in the neutron star mass distribution and constraints on the equation of state. MNRAS 2018, 478, 1377–1391. [Google Scholar] [CrossRef] [Green Version]
- Farrow, N.; Zhu, X.J.; Thrane, E. The Mass Distribution of Galactic Double Neutron Stars. ApJ 2019, 876, 18. [Google Scholar] [CrossRef] [Green Version]
- Narayan, R. The Birthrate and Initial Spin Period of Single Radio Pulsars. ApJ 1987, 319, 162. [Google Scholar] [CrossRef]
- Lorimer, D.R.; Bailes, M.; Dewey, R.J.; Harrison, P.A. Pulsar statistics: the birthrate and initial spin periods of radio pulsars. Mon. Not. R. Astron. Soc. 1993, 263, 403–415. [Google Scholar] [CrossRef] [Green Version]
- Lorimer, D.R.; Faulkner, A.J.; Lyne, A.G.; Manchester, R.N.; Kramer, M.; McLaughlin, M.A.; Hobbs, G.; Possenti, A.; Stairs, I.H.; Camilo, F.; et al. The Parkes Multibeam Pulsar Survey—VI. Discovery and timing of 142 pulsars and a Galactic population analysis. Mon. Not. R. Astron. Soc. 2006, 372, 777–800. [Google Scholar] [CrossRef] [Green Version]
- Kiel, P.D.; Hurley, J.R. Populating the Galaxy with pulsars – II. Galactic dynamics. Mon. Not. R. Astron. Soc. 2009, 395, 2326–2346. [Google Scholar] [CrossRef] [Green Version]
- Faucher-Giguère, C.A.; Loeb, A. The pulsar contribution to the gamma-ray background. J. Cosmology Astropart. Phys. 2010, 2010, 005. [Google Scholar] [CrossRef] [Green Version]
- Lorimer, D.R. The Galactic Millisecond Pulsar Population. Proc. Int. Astron. Union 2012, 8, 237–242. [Google Scholar] [CrossRef] [Green Version]
- Grégoire, T.; Knödlseder, J. Constraining the Galactic millisecond pulsar population using Fermi Large Area Telescope. A&A 2013, 554, A62. [Google Scholar] [CrossRef] [Green Version]
- Hooper, D.; Cholis, I.; Linden, T.; Siegal-Gaskins, J.M.; Slatyer, T.R. Millisecond pulsars cannot account for the inner Galaxy’s GeV excess. Phys. Rev. D 2013, 88, 083009. [Google Scholar] [CrossRef] [Green Version]
- Ronchi, M.; Graber, V.; Garcia-Garcia, A.; Rea, N.; Pons, J.A. Analyzing the Galactic Pulsar Distribution with Machine Learning. ApJ 2021, 916, 100. [Google Scholar] [CrossRef]
- Bonazzola, S.; Gourgoulhon, E. Gravitational waves from pulsars: emission by the magnetic-field-induced distortion. A&A 1996, 312, 675–690. [Google Scholar]
- Buikema, A.; Cahillane, C.; Mansell, G.L.; Blair, C.D.; Abbott, R.; Adams, C.; Adhikari, R.X.; Ananyeva, A.; Appert, S.; Arai, K.; Areeda, J.S.; et al. Sensitivity and performance of the Advanced LIGO detectors in the third observing run. Phys. Rev. D 2020, 102, 062003. [Google Scholar] [CrossRef]
- Hild, S.; Abernathy, M.; Acernese, F.; Amaro-Seoane, P.; Andersson, N.; Arun, K.; Barone, F.; Barr, B.; Barsuglia, M.; Beker, M.; et al. Sensitivity studies for third-generation gravitational wave observatories. Class. Quantum Gravity 2011, 28, 094013. [Google Scholar] [CrossRef]
- Watts, A.L.; Krishnan, B.; Bildsten, L.; Schutz, B.F. Detecting gravitational wave emission from the known accreting neutron stars. Mon. Not. R. Astron. Soc. 2008, 389, 839–868. [Google Scholar] [CrossRef] [Green Version]
- Yusifov, I.; Küçük, I. Revisiting the radial distribution of pulsars in the Galaxy. A&A 2004, 422, 545–553. [Google Scholar] [CrossRef] [Green Version]
- Lorimer, D.R. Binary and Millisecond Pulsars. Living Rev. Relativ. 2008, 11, 8. [Google Scholar] [CrossRef] [PubMed] [Green Version]
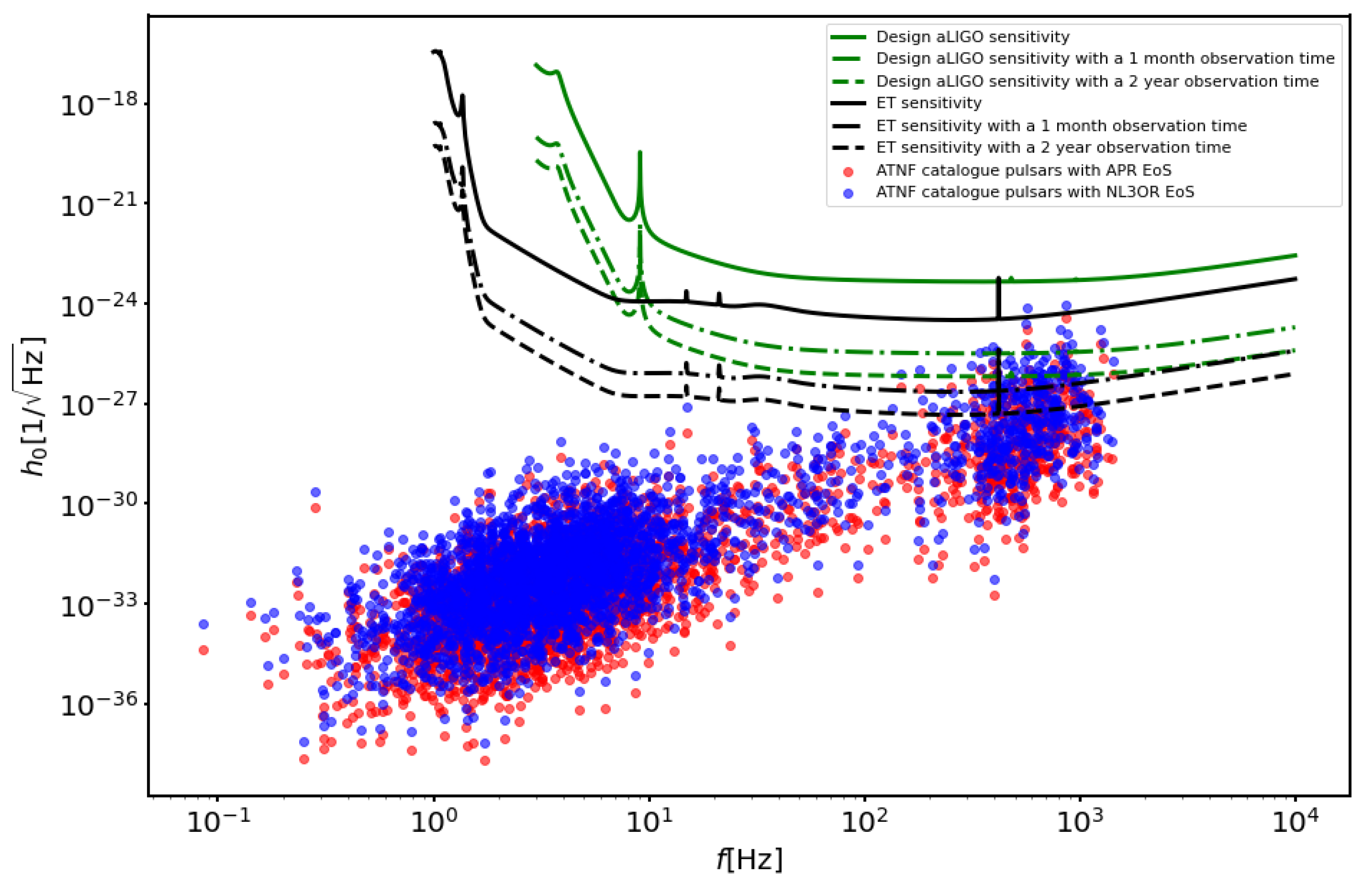
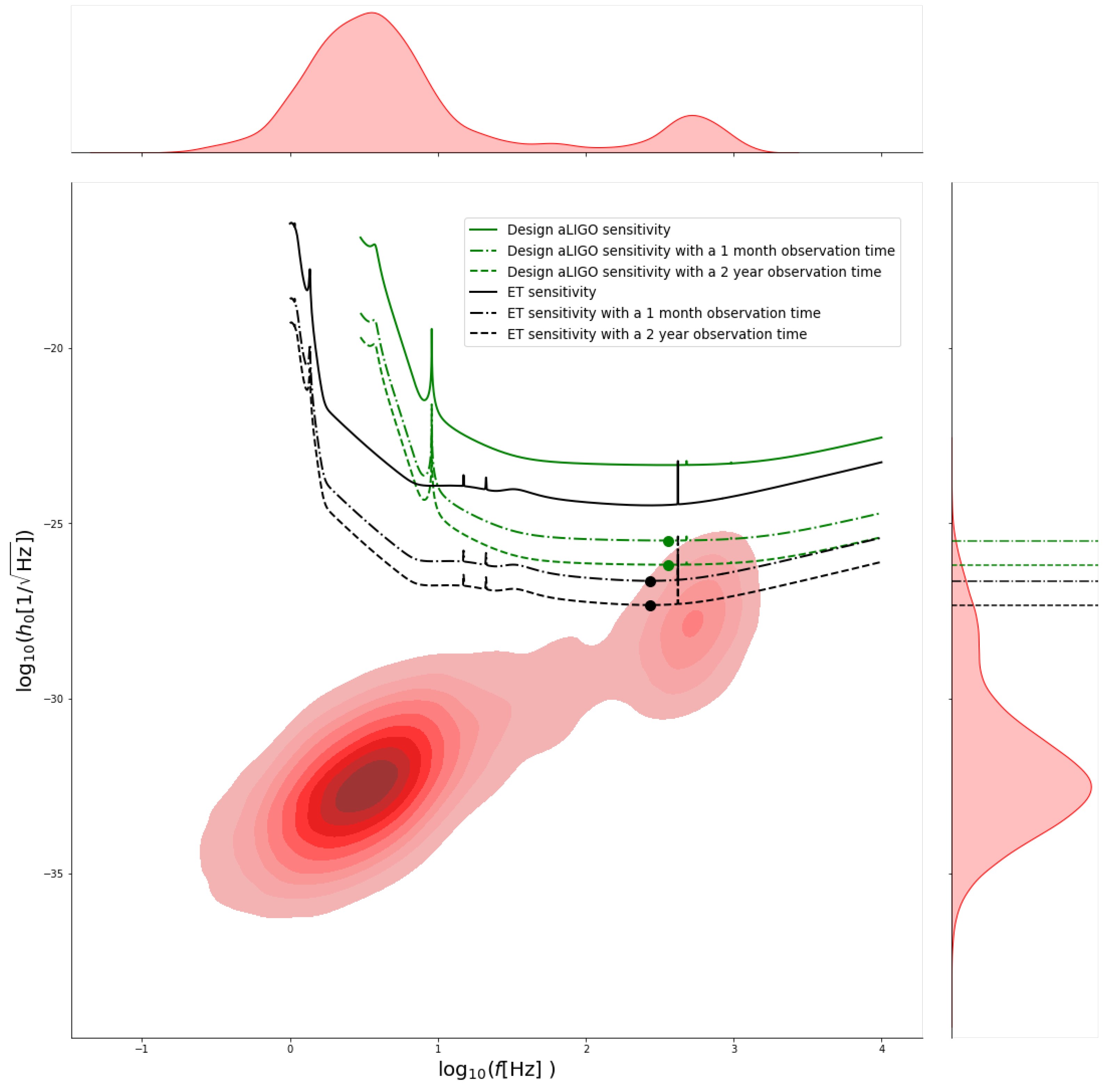
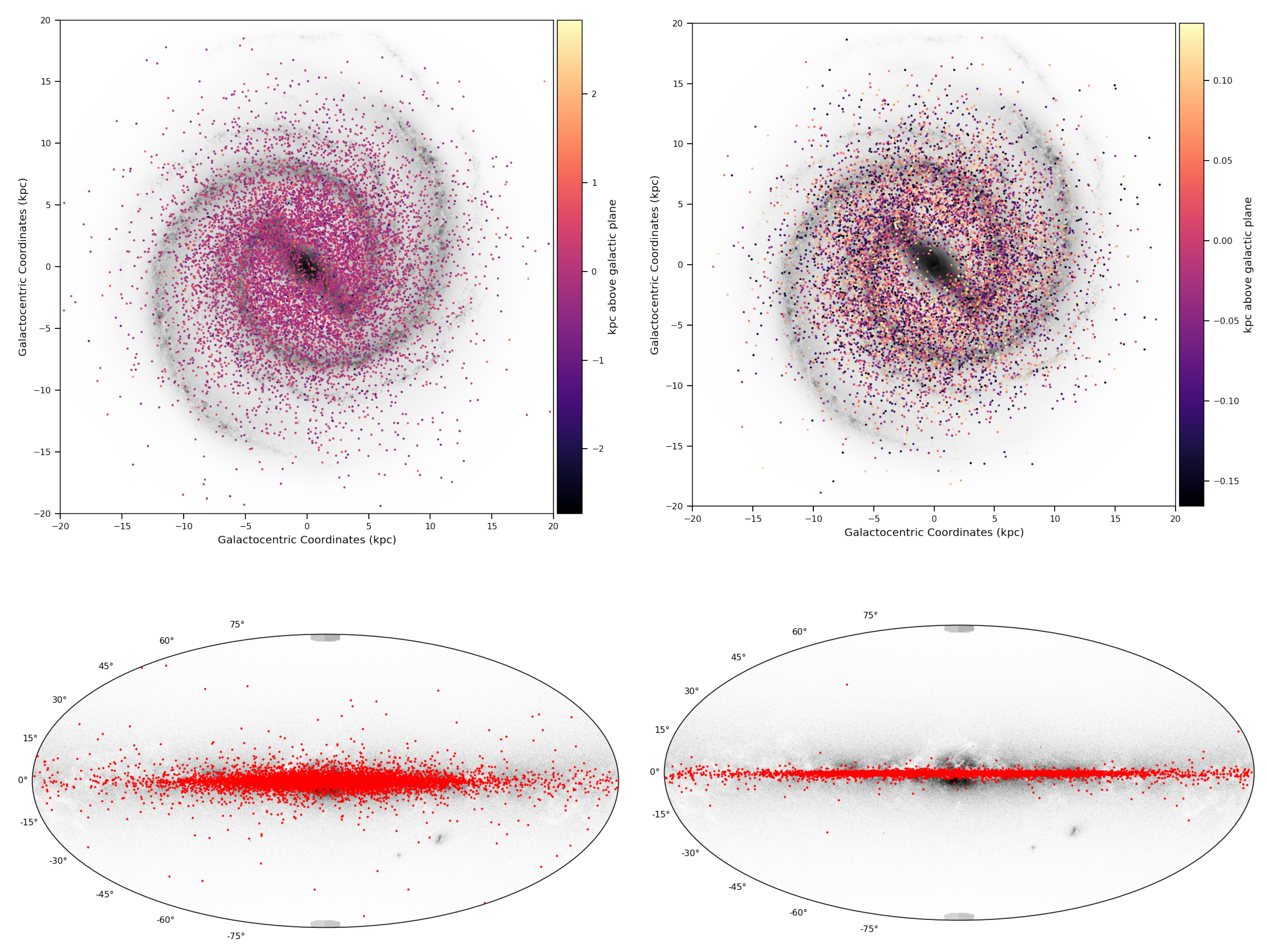
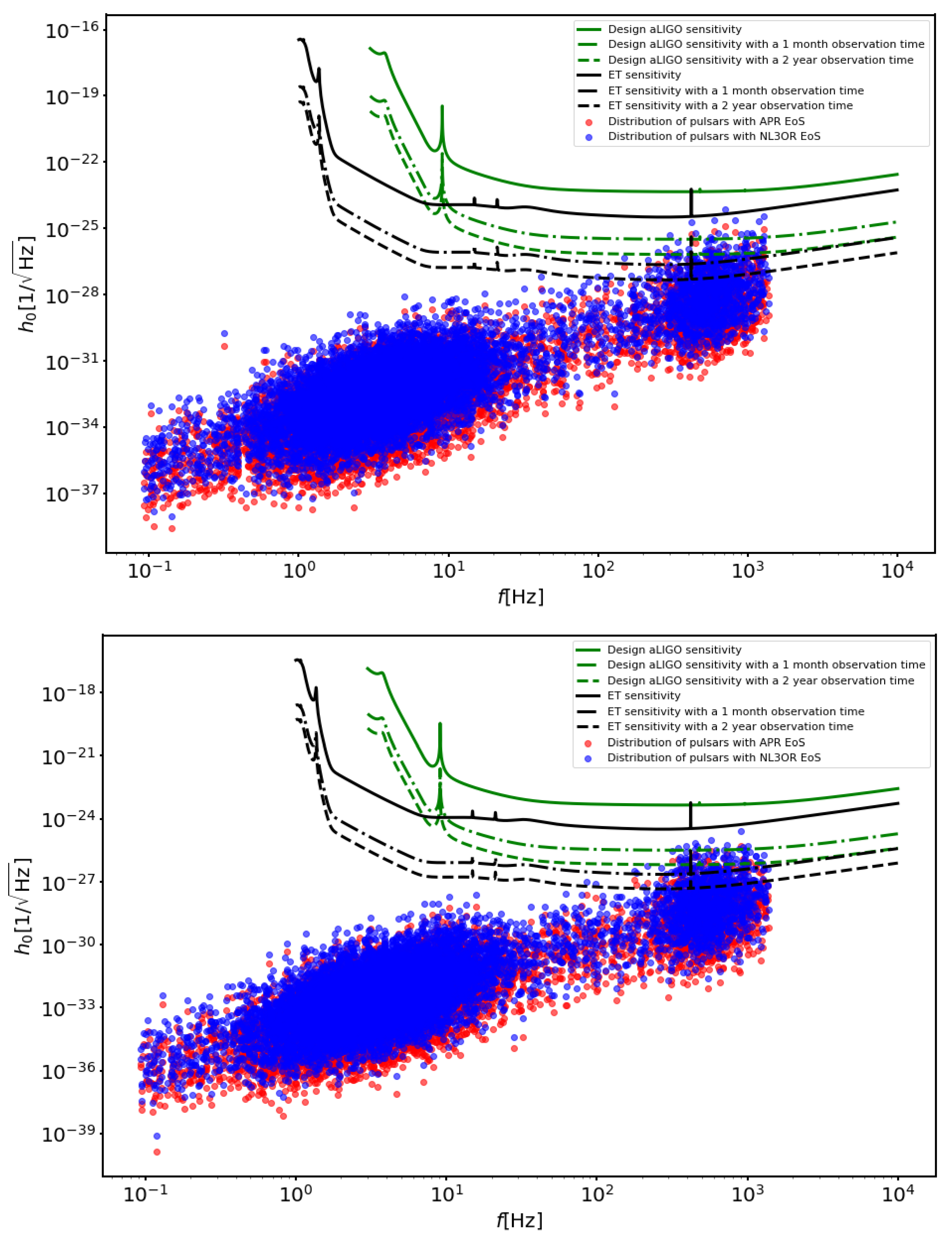
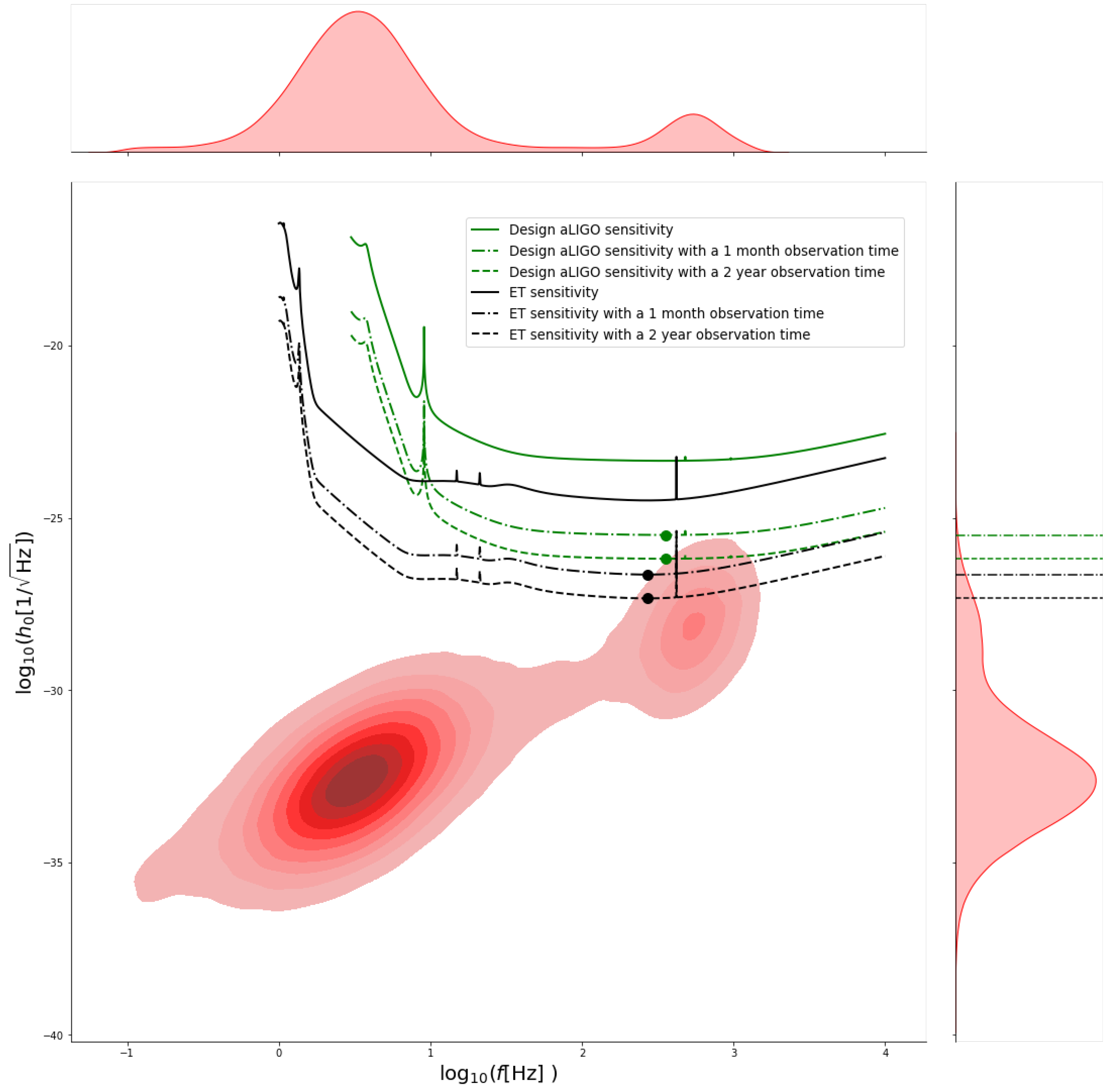

| Name | Distance [kpc] | Period [s] | Median Strain | Detection Probability |
|---|---|---|---|---|
| J0605+3757 | 0.215 | 0.002728 | 3.21 × | 18% (36%) |
| J0636+5129 | 0.210 | 0.002869 | 3.57 × | 15% (33%) |
| J0034-0534 | 1.348 | 0.001877 | 1.57 × | 14% (30%) |
| J1400-1431 | 0.278 | 0.003084 | 1.91 × | 13% (30%) |
| J1653-0158 | 0.840 | 0.001968 | 3.58 × | 12% (28%) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soldateschi, J.; Bucciantini, N. Detectability of Continuous Gravitational Waves from Magnetically Deformed Neutron Stars. Galaxies 2021, 9, 101. https://doi.org/10.3390/galaxies9040101
Soldateschi J, Bucciantini N. Detectability of Continuous Gravitational Waves from Magnetically Deformed Neutron Stars. Galaxies. 2021; 9(4):101. https://doi.org/10.3390/galaxies9040101
Chicago/Turabian StyleSoldateschi, Jacopo, and Niccolò Bucciantini. 2021. "Detectability of Continuous Gravitational Waves from Magnetically Deformed Neutron Stars" Galaxies 9, no. 4: 101. https://doi.org/10.3390/galaxies9040101
APA StyleSoldateschi, J., & Bucciantini, N. (2021). Detectability of Continuous Gravitational Waves from Magnetically Deformed Neutron Stars. Galaxies, 9(4), 101. https://doi.org/10.3390/galaxies9040101






