A Broadband Signal Recycling Scheme for Approaching the Quantum Limit from Optical Losses
Abstract
1. Introduction
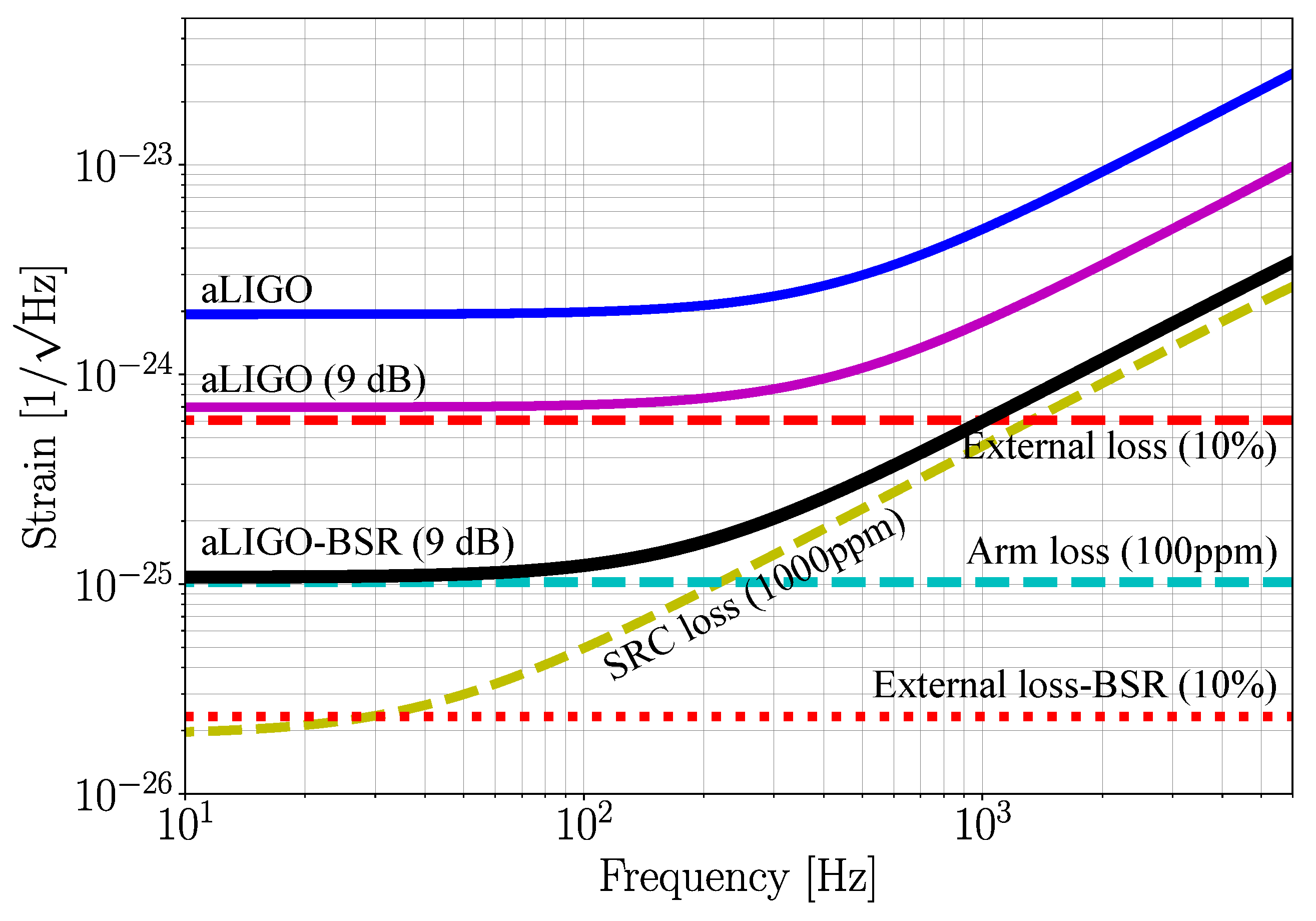
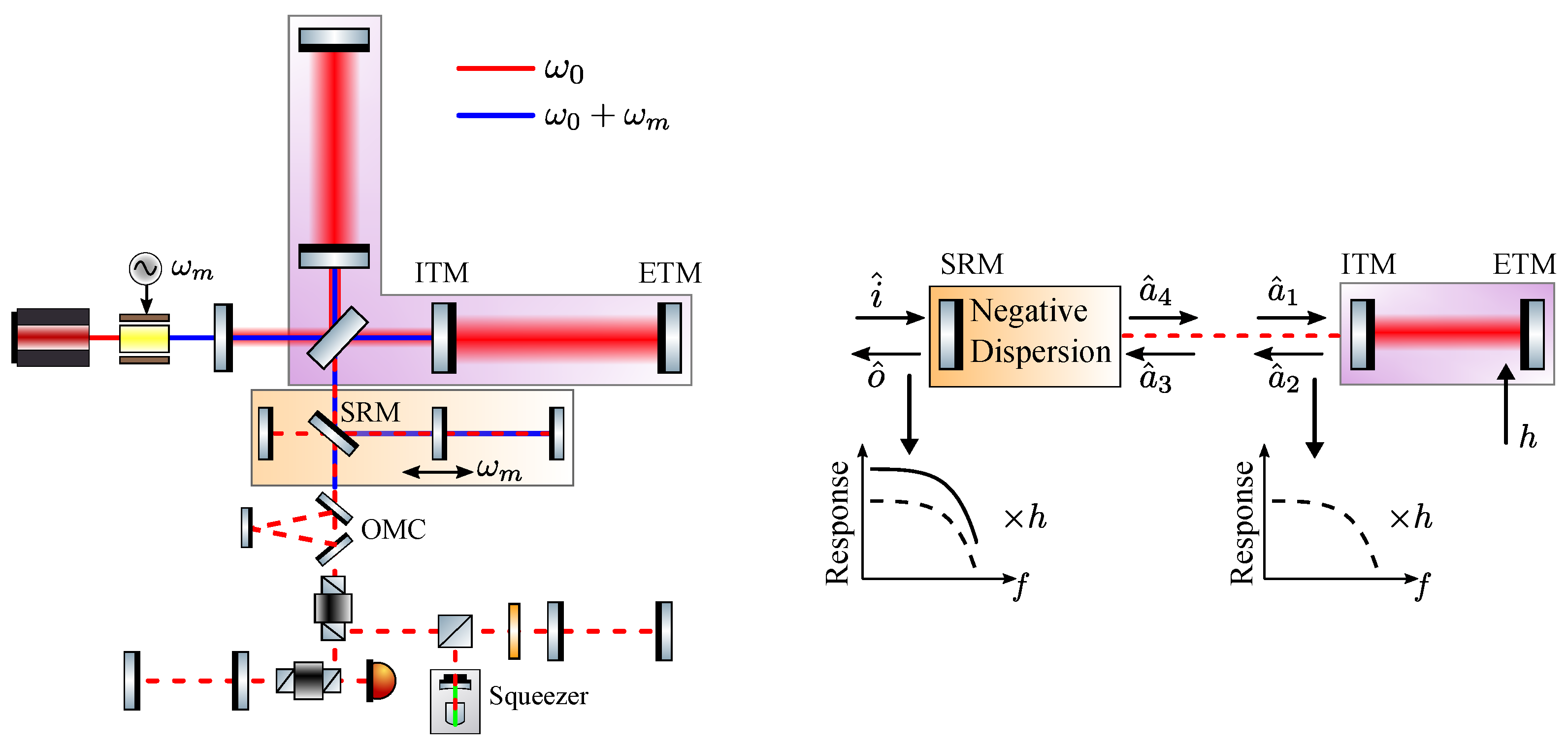
2. Design Concept and Quantum Noise
3. Summary and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Braginsky, V.B.; Khalili, F.Y.; Thorne, K.S. Quantum Measurement; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar] [CrossRef]
- Helstrom, C. Minimum mean-squared error of estimates in quantum statistics. Phys. Lett. A 1967, 25, 101–102. [Google Scholar] [CrossRef]
- Braginsky, V.B.; Gorodetsky, M.L.; Khalili, F.Y.; Thorne, K.S. Energetic quantum limit in large-scale interferometers. AIP Conf. Proc. 2000, 523, 180–190. [Google Scholar] [CrossRef]
- Tsang, M.; Wiseman, H.M.; Caves, C.M. Fundamental Quantum Limit to Waveform Estimation. Phys. Rev. Lett. 2011, 106, 090401. [Google Scholar] [CrossRef] [PubMed]
- Miao, H.; Adhikari, R.X.; Ma, Y.; Pang, B.; Chen, Y. Towards the Fundamental Quantum Limit of Linear Measurements of Classical Signals. Phys. Rev. Lett. 2017, 119, 050801. [Google Scholar] [CrossRef] [PubMed]
- Miao, H.; Smith, N.D.; Evans, M. Quantum Limit for Laser Interferometric Gravitational-Wave Detectors from Optical Dissipation. Phys. Rev. X 2019, 9, 011053. [Google Scholar] [CrossRef]
- Aasi, J.; Abbott, B.P.; Abbott, R.; Abbott, T.; Abernathy, M.R.; Ackley, K.; Ackley, C.; Adams, T.; Addesso, P.; Adhikari, P.X.; et al. Advanced LIGO. Class. Quantum Gravity 2015, 32, 074001. [Google Scholar] [CrossRef]
- Miao, H.; Yang, H.; Martynov, D. Towards the design of gravitational-wave detectors for probing neutron-star physics. Phys. Rev. D 2018, 98, 044044. [Google Scholar] [CrossRef]
- Martynov, D.; Miao, H.; Yang, H.; Vivanco, F.H.; Thrane, E.; Smith, R.; Lasky, P.; East, W.E.; Adhikari, R.; Bauswein, A.; et al. Exploring the sensitivity of gravitational wave detectors to neutron star physics. Phys. Rev. D 2019, 99, 102004. [Google Scholar] [CrossRef]
- Braginsky, V.B.; Vorontsov, Y.I.; Thorne, K.S. Quantum Nondemolition Measurements. Science 1980, 209, 547–557. [Google Scholar] [CrossRef]
- Chen, Y.; Danilishin, S.L.; Khalili, F.Y.; Müller-Ebhardt, H. QND measurements for future gravitational-wave detectors. Gen. Relativ. Gravit. 2011, 43, 671–694. [Google Scholar] [CrossRef][Green Version]
- Kimble, H.J.; Levin, Y.; Matsko, A.B.; Thorne, K.S.; Vyatchanin, S.P. Conversion of conventional gravitational-wave interferometers into quantum nondemolition interferometers by modifying their input and/or output optics. Phys. Rev. D 2001, 65, 022002. [Google Scholar] [CrossRef]
- Adya, V.B.; Yap, M.J.; Töyrä, D.; McRae, T.G.; Altin, P.A.; Sarre, L.K.; Meijerink, M.; Kijbunchoo, N.; Slagmolen, B.J.J.; Ward, R.L.; et al. Quantum enhanced kHz gravitational wave detector with internal squeezing. Class. Quantum Gravity 2020, 37, 07LT02. [Google Scholar] [CrossRef]
- Korobko, M.; Kleybolte, L.; Ast, S.; Miao, H.; Chen, Y.; Schnabel, R. Beating the Standard Sensitivity-Bandwidth Limit of Cavity-Enhanced Interferometers with Internal Squeezed-Light Generation. Phys. Rev. Lett. 2017, 118, 143601. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Aritomi, N.; Capocasa, E.; Leonardi, M.; Eisenmann, M.; Guo, Y.; Polini, E.; Tomura, A.; Arai, K.; Aso, Y.; et al. Frequency-Dependent Squeezed Vacuum Source for Broadband Quantum Noise Reduction in Advanced Gravitational-Wave Detectors. Phys. Rev. Lett. 2020, 124, 171101. [Google Scholar] [CrossRef] [PubMed]
- McCuller, L.; Whittle, C.; Ganapathy, D.; Komori, K.; Tse, M.; Fernandez-Galiana, A.; Barsotti, L.; Fritschel, P.; MacInnis, M.; Matichard, F.; et al. Frequency-Dependent Squeezing for Advanced LIGO. Phys. Rev. Lett. 2020, 124, 171102. [Google Scholar] [CrossRef] [PubMed]
- Ackley, K.; Adya, V.B.; Agrawal, P.; Altin, P.; Ashton, G.; Bailes, M.; Baltinas, E.; Barbuio, A.; Beniwal, D.; Blair, C.; et al. Neutron Star Extreme Matter Observatory: A kilohertz-band gravitational-wave detector in the global network. arXiv 2020, arXiv:2007.03128. [Google Scholar] [CrossRef]
- Rinkleff, R.H.; Wicht, A. The Concept of White Light Cavities Using Atomic Phase Coherence. Phys. Scr. 2005, 85. [Google Scholar] [CrossRef]
- Miao, H.; Ma, Y.; Zhao, C.; Chen, Y. Enhancing the Bandwidth of Gravitational-Wave Detectors with Unstable Optomechanical Filters. Phys. Rev. Lett. 2015, 115, 211104. [Google Scholar] [CrossRef]
- Page, M.A.; Goryachev, M.; Miao, H.; Chen, Y.; Ma, Y.; Mason, D.; Rossi, M.; Blair, C.D.; Ju, L.; Blair, D.G.; et al. Gravitational wave detectors with broadband high frequency sensitivity. arXiv 2020, arXiv:2007.08766. [Google Scholar]
- Mason, D.; Chen, J.; Rossi, M.; Tsaturyan, Y.; Schliesser, A. Continuous force and displacement measurement below the standard quantum limit. Nat. Phys. 2019, 15, 745–749. [Google Scholar] [CrossRef]
- Danilishin, S.L.; Khalili, F.Y.; Miao, H. Advanced quantum techniques for future gravitational-wave detectors. Living Rev. Relativ. 2019, 22, 2. [Google Scholar] [CrossRef]
- Adhikari, R.X.; Arai, K.; Brooks, A.F.; Wipf, C.; Aguiar, O.; Altin, P.; Barr, B.; Barsotti, L.; Bassiri, R.; Bell, A.; et al. A cryogenic silicon interferometer for gravitational-wave detection. Class. Quantum Gravity 2020, 37, 165003. [Google Scholar] [CrossRef]
- The ET Science Team. Einstein Gravitational Wave Telescope Conceptual Design; European Commission: Luxembourg, 2011. [Google Scholar]
- ET Steering Committee Editorial Team. Einstein Telescope Design Report Update 2020; Einstein Telescope Collaboration: Cascina, Italy, 2020. [Google Scholar]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Ackley, K.; Adams, C.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. Exploring the sensitivity of next generation gravitational wave detectors. Class. Quantum Gravity 2017, 34, 044001. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, T.; Bentley, J.; Miao, H. A Broadband Signal Recycling Scheme for Approaching the Quantum Limit from Optical Losses. Galaxies 2021, 9, 3. https://doi.org/10.3390/galaxies9010003
Zhang T, Bentley J, Miao H. A Broadband Signal Recycling Scheme for Approaching the Quantum Limit from Optical Losses. Galaxies. 2021; 9(1):3. https://doi.org/10.3390/galaxies9010003
Chicago/Turabian StyleZhang, Teng, Joe Bentley, and Haixing Miao. 2021. "A Broadband Signal Recycling Scheme for Approaching the Quantum Limit from Optical Losses" Galaxies 9, no. 1: 3. https://doi.org/10.3390/galaxies9010003
APA StyleZhang, T., Bentley, J., & Miao, H. (2021). A Broadband Signal Recycling Scheme for Approaching the Quantum Limit from Optical Losses. Galaxies, 9(1), 3. https://doi.org/10.3390/galaxies9010003




