Abstract
We investigate the dark matter distribution in the spiral galaxy ESO0140040, employing the most widely used density profiles: the pseudo-isothermal, exponential sphere, Burkert, Navarro-Frenk-White, Moore and Einasto profiles. We infer the model parameters and estimate the total dark matter content from the rotation curve data. For simplicity, we assume that dark matter distribution is spherically symmetric without accounting for the complex structure of the galaxy. Our predictions are compared with previous results and the fitted parameters are statistically confronted for each profile. We thus show that although one does not include the galaxy structure it is possible to account for the same dynamics assuming that dark matter provides a non-zero pressure in the Newtonian approximation. In this respect, we solve the hydrostatic equilibrium equation and construct the dark matter pressure as a function for each profile. Consequently, we discuss the dark matter equation of state and calculate the speed of sound in dark matter. Furthermore, we interpret our results in view of our approach and we discuss the role of the refractive index as an observational signature to discriminate between our approach and the standard one.
1. Introduction
Understanding the nature and properties of dark matter (DM) is a challenging conundrum of our current Universe. Unlike ordinary matter, DM weakly interacts with other constituents via gravity only, so far being inaccessible to direct observations. Recent observations certify that DM amounts for about 26.8% of the total energy budget of the Universe [1], while from theoretical point of view it has been proposed that DM is made of some experimentally as yet undiscovered particles [2,3] coming from extensions of the standard model of particle physics1. The number of approaches related to the DM problem is steadily growing, reflecting a noticeable interest in comprehending its nature [4,5,6], which constitutes the 85% of all the matter i.e., DM+baryons, and state function of baryons in the Universe.
One of the most striking proofs of the existence of DM is the rotation curves (RCs) of galaxies, i.e., the dependence of the speed of rotation (linear speed) v of stars and gas in a galaxy on the distance r from the center to the halo. Spiral galaxies are commonly used to better understand DM. Therefore, DM is thought to be made of non-relativistic and collisionless particles whose cross sections between DM and baryons lie on ∼ cm [7]. Broadly speaking, the RCs of such galaxies have amplitude that remains constant with increasing distance, even beyond the stellar disc, which is not expected in Newtonian gravity (NG) [8,9].
In this paper, we focus on the physics of the disk galaxy ESO0140040. In this framework we assume Newtonian gravity only and we investigate dark matter’s distributions using well-consolidated density profiles, among them: pseudo-isothermal (ISO), Burkert, Navarro-Frenk-White (NFW), Moore, Einasto and exponential sphere ones. This heuristic choice is motivated by the fact that most DM candidates cannot be distinguished by large-scale observations leaving a wide range of potential candidates2 Using data from ESO140040 rotational curve, we fit the free parameters of each profile and we compute: (1) the total dark matter content, (2) the speed of sound in DM perturbations and (3) the refractive index, under the hypothesis that DM has a non-zero pressure. We statistically confront our results among them, and we do not consider the complex structure of the galaxy itself on purpose. In fact, we demonstrate that the only use of is enough to predict RCs in good agreement with observations. It is, therefore, possible to account for the same dynamics assuming that dark matter provides a non-zero pressure in Newtonian approximation, by solving the hydrostatic equilibrium equation. Furthermore, we discuss the dark matter equation of state and we interpret our results in view of future observations on other galaxies.
The paper is organized as follows. In Section 2, the main features of our work are formulated. In Section 3, the observational data of ESO0140040 RCs are statistically analyzed and moreover the equation of state, the speed of sound and the refractive index are investigated. In Section 3.1, the major results of the paper are presented. In Section 4, we report the conclusions and perspectives of our work.
2. DM Distribution in Spirals
The standard cosmological model can broadly fit the large-scale evolution of the Universe [10,11]. N-body simulations can be used to resolve the current structure of virialized objects from galaxy clusters to dwarf galaxies. Those simulations combined with the property that DM is collisionless lead to a cuspy dark halo density profile that scales like , providing dark halos around galaxies.
The sharp central cusp of the DM density distribution disagrees with the overwhelming evidence for cored dark halo distributions emphasizing a decisive support in favor of the DM halo cored distribution. Supported by these reasons we need to include different approaches to the DM density profiles. In particular, we soon notice that DM distribution in galaxy halos is non-uniform, concentrating at their centers and dropping off to the periphery.
The way to get profiles is usually found by the methods of numerical modeling of the dynamics of stars in galaxies and so, in this respect we select the mostly used phenomenological DM profiles: ISO, exponential sphere, Burkert, NFW, Moore and Einasto. All these profiles have as model parameters the DM density at galactic centers or characteristic density and the scale radius ; only the Einasto profile has an additional extra free parameter3.
Inferring bounds over free parameters turns out to be essential to investigating galactic dynamics and, in addition, to reconciling DM abundance with the dark energy contribution in the present epoch4. Thus, a successfully implemented paradigm can be naturally worked out within the Newtonian approximation [13], for the slow motions of stars as commonly adopted in the literature.
Thus, we employ the following models:
- 1.
- The ISO profile [14]:where r is the radial coordinate/distance. The model depends upon the two constants and .
- 2.
- Exponential sphere [15]:The model depends on the same constants as in the ISO profile.
- 3.
- Burkert profile [16]:The model depends upon the same constants as above and overcomes the issue related to the cusp in galaxies. Despite its experimental triumph, the Burkert profile is not theoretically motivated and remains a phenomenological approach to face the DM problem.
- 4.
- The NFW profile [17]which was originally found as consequence of simulated halo formation in which the cosmological model is fixed.
- 5.
- Moore profile [18]:which is motivated by the fact that several studies claimed that simulated DM halos show significantly steeper cusps than NFW profile. This leads to a phenomenological reconstruction of DM profile, alternative to the NFW profile.
- 6.
- Einasto profile [19]:where is the Einasto free parameter. This extra parameter determines the degree of curvature (shape) of the profile. If are identified with cuspy halos, while for presents a cored-like behavior. The Einasto profile is quite different from the other models, whose slope is a power-law function. The larger , the more rapidly the slope varies with radius [20].
Every DM halo profile well adapts to slightly flat RCs, enabling the baryonic contribution for each galaxy and providing a dependence over the free coefficients illustrated in Figure 1 (left panel).
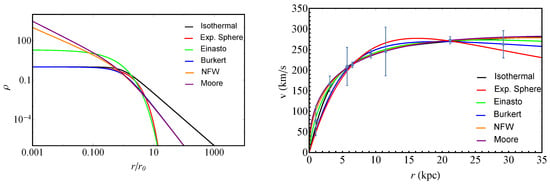
Figure 1.
Color online. Left panel: Different phenomenological DM density profiles and we choose for the Einasto profile. Right panel: RCs of galaxy ESO0140040 and fitted profiles.
As stated above, our computations are performed in the NG regime to fulfill the simplest assumptions over star motions in disk galaxies. In the next subsection, we enter deeply the strategy adopted to fit galactic data of ESO140040 [21,22].
2.1. Galaxy Eso140040 within Newtonian Gravity
The main purpose of this paper is to introduce the idea that pressure can mimic the overall effects due to morphology of a galaxy. We assume that DM pressure is therefore able to mimic the complex structure of the underlying galaxy here involved, within the weak field approximation. To do so and to guarantee NG approximation and we start with the standard Newtonian hydrostatic equilibrium equations, given by [23,24]
where is the mass profile enclosed inside the sphere of radius r, is the DM pressure and is the gravitational potential. Our strategy consists of obtaining the expressions for the pressure in this approximation. To do so, the density profiles Equations (1)–(6) are plugged in Equations (7) and (8). Afterwards, we integrate employing as boundary conditions the fact that P vanishes as one approaches infinity.
It should be noted that due to the complexity for the Einasto, Moore, NFW and Burkert profiles all computations are carried out numerically, while for the ISO and exponential sphere profiles are performed analytically. Therefore, The DM halo pressure formulas for the ISO and exponential sphere profiles in Equations (1) and (2) are given by, respectively
where the gamma function is defined by , with .
2.2. Perturbations and Optical Properties
Perturbations due to the DM fluid can be accounted by means of the speed of sound . Its definition in case of adiabatic perturbations is [25]
Furthermore, from Equations (12) and (13), we obtain the speed of sound for ISO and exponential sphere profiles
For all profiles, the speed of sound decreases with increasing density. This is a unique feature of DM that plays a key role in shaping the structure of the Universe. It is known from cosmology that if the speed of sound in the central part of the dark matter distribution is less than in its outer parts, then it allows the formation of large-scale structures of the Universe [26].
To study the optical properties of the considered galaxy, it is easy to notice that DM produces a refractive index which necessarily differs from a pure vacuum. Thus, we here consider the refractive index of DM halo of galaxy ESO040140 for the ISO, exponential sphere, Burkert, NFW, Moore and Einasto profiles. The refractive index in the field of DM in NG is given by [27]
In Figure 2 we plot the refractive index n as a function of the radial coordinate in the DM distribution for the above considered profiles in galaxy ESO0140040. As expected, the value of the index is very small in halo region. Here by “halo” we mean the spherical component of the galaxy beyond its disk. In the core region the refractive index grows slowly, but remains extremely small, growing less than 1 part in 10!.

Figure 2.
Color online. The refractive index for DM in galaxy ESO0140040. Left panel: The refractive index of the Einasto, NFW and Moore profiles. Right panel: The refractive index of the ISO, exponential sphere and Burkert profiles.
The DM refractive index for different profiles is plotted in Figure 2. At distances within 1–29.2 kpc which corresponds to RC data points, the DM refractive index is slightly greater than vacuum for all the involved profiles. In general, its use can be invoked even to investigate the light propagation process in the DM dominance epoch using a non-stationary equation of state [28].
2.3. The Role of the Dm Equation of State
For a given fluid, its equation of state shows the physical properties of the fluid itself and how it evolves in case it is not at equilibrium. The thermodynamic properties of the fluid are thus hidden the equation of state, defined by [29]
often known also with the name of state or barotropic parameter. Here c is the speed of light in vacuum. The same assumption is made in genuine cosmological scenarios in which the term driving the Universe dynamics is related to the Universe equation of state and to its kinematics [30]. It is possible to show, indeed, that its functional form is related to the deceleration parameter and consequently to the overall cosmological dynamics [31].
For our case, since we are interested in assuming a non-vanishing pressure, the corresponding expressions for the equation of state turn out to be complicated for every profile. Nevertheless, one can immediately demonstrate Equation (18) could be written as a function of radial coordinate r or density as illustrated in Figure 3.
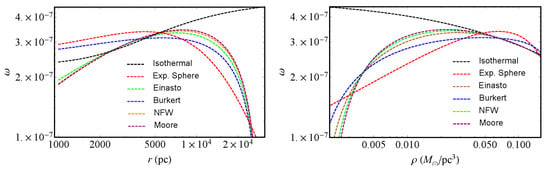
Figure 3.
Color online. Left panel: Dimensionless state parameter as a function of radial coordinate r. Right panel: Dimensionless state parameter as a function of density .
It is thus intriguing to investigate the radial behavior of the equation of state. Immediately it follows for large distances, or low densities, tends to zero (except for the isothermal profile, where it becomes constant. Instead for small distances, or high densities, tends to constant) for the cored profiles and to low values close to zero for cuspy profiles, at least in the considered range of distances provided by the rotation curve data points.
The last considerations are intimately related to the physics of our galaxy [32]. Hence, to better clarify this point let us consider two limiting regimes and . The first case for the cored profiles turns out to be unphysical as is the central density for the DM distribution and by construction it is maximum. Thus, for cored profiles it is impossible to fulfill the condition . However, for the cuspy profiles is the characteristic density and the condition is achievable since close to the center the densities can be larger than and tends to zero as the density goes up faster than the pressure (see Figure 4).

Figure 4.
Color online. Left panel: Logarithmic density profiles of DM in the halo. Right panel: Logarithmic pressure profiles of DM in the halo.
The case corresponds to large distances. Only for the isothermal profile tends to a constant value and for other profiles tends to zero. This can be observed in both panels of Figure 3, where one can see that in the halo region the pressure goes down faster than the density. One intriguing thing is noticing that from our procedures no negative pressures have been found. This is in contrast with cosmological [33] and astronomical evidence [34]. Recently, for example, the idea of negative pressure for DM contribution has been introduced, to unify DM and dark energy [35,36]. Even though this possibility is plausible, we do not have any evidence for it from our studies. Refined analysis would better highlight hints toward the sign of DM pressure.
We can also consider the effects of general relativity in our calculations. Obviously, at large distances or general relativity corrections can be neglected. However, close to the central part of the galaxy its deviations from NG would be significantly noticeable since general relativity corrections over pressure are clearly much larger than in the NG [37]. This is straightforward as consequence of the Tolman–Oppenheimer–Volkoff solution.
3. Methods and Analyses
We aim to show that as a result of our analysis, by testing different profiles for such a galaxy, DM halo density law can be accounted for the kinematics of the whole family of disk galaxies like ESO140040. There the internal structure is not known and so the strategy is to get the maximum rotational velocity by means of pressure.
The galaxy ESO0140040 has been chosen even for the fact that the visible matter contribution is small and thus we can check whether the pressure alone is able to reproduce the morphology of the galaxy itself much simpler than a galaxy whose morphology is complicated.
For the sake of completeness, it is remarkable to stress that the contributions of gas, luminosity and size are absolutely essential to characterize the RCs. However, we expect fairly viable results mimicking such contributions with pressure5.
In turn, the RC allows one to determine the distribution of the galaxy’s mass along the radial distance. In the standard approach, in the circular velocity model, the total circular velocity i.e., RC is approximated by
where is the disk velocity and is the contributions of the DM halo profile velocity. The disk velocity in most cases can be neglected due to its small contribution to the RC. Therefore by equating the centrifugal and gravitational forces for a star moving in a circular orbit at a distance r from the center of the galaxy one can find and :
where the DM mass has been obtained from Equation (20), by simply integrating Equation (7) and making use of , i.e., the DM density profile taken from Equations (1) through (6).
For the sake of completeness, the next step will be to work out the visible matter contribution within our prescription. Therefore, in the future efforts we will give an answer to the question: does the pressure reproduce the morphology of galaxies even when visible matter contribution is not negligible? Below we report our numerical analysis on this single case only, on which we introduce the idea that DM pressure plays a prominent role in spiral galaxies.
3.1. Numerical Results
We apply the Levenberg-Marquardt nonlinear least squares method6 [39,40] to find the minimum of the function defined as
where and are the N data points of ESO0140040 RC and their corresponding errors, respectively (see Figure 1, right panel), while is given by Equation (20) and describes the RCs for each DM profile. The best fit parameters, minimizing the for each DM profile are listed in Table 1 and shown in Figure 1 (right panel). The and parameters listed in Table 1 agree with the results of Ref. [41]. The amount of DM mass in the galaxy, computed by using different profiles, is also shown in Table 1 and it is shown to be consistent with the results of Ref. [41]. For the Einasto profile we obtained . The values are also shown in the last column of Table 1.

Table 1.
Model parameters for the analyzed galaxy ESO0140040. We reported for each profile the density , and the masses expressed in terms of . For every column we report the error bars. The last two columns report the BIC statistical outputs and the corresponding chi squares used for computing the BIC values.
To compare the considered 6 profiles, which have different number of parameters and are not nested into each other, we employ the Bayesian Information Criterion (BIC)7 [44]. Starting from the definition, the BIC is defined as
where k is the number of model parameters. For the Einasto profile , while for all the other profiles . A profile with a minimum BIC value is favored, according to Ref. [45]. As one can see from Table 1 for galaxy ESO0140040 the BIC value is minimum for the Einasto profile and is maximum for the exponential sphere profile, though the difference between the values is not large.
In Figure 1 (right panel) the gray thick points show the observational data points with their error bars for galaxy ESO0140040; solid curves show ISO (black), exponential sphere (red), Einasto (green), Burkert (blue), NFW (orange) and Moore (purple) profiles.
In Figure 4 we plotted (left panel) and (right panel) for galaxy ESO0140040, using Equations (1)–(6) and (10) and (11), respectively.
Using Equations (12) and (13) we plotted the equation of state for ISO and exponential sphere profiles in Figure 5 (left panel). Moreover, in Figure 5 (right panel) we plotted the speed of sound according to Equations (15) and (16) for ISO and exponential sphere profiles.
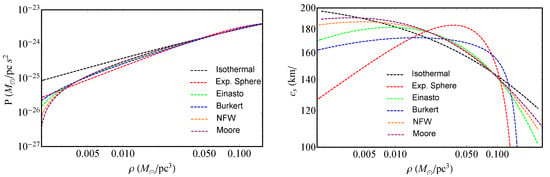
Figure 5.
Color online. Left panel: The equation of state of DM halo. Right panel: The speed of sound for the DM fluid for different DM profiles.
In Figure 4 (right panel) and Figure 5 (left panel) one can adopt different units by using the following conversion factors: /pc = 6.77 g/cm = 38.05 GeV/cm.
It should be recalled that for ISO, exponential sphere and Burkert profiles is the central density. However, for the Einasto, Moore and NFW profiles is the characteristic density, i.e., one can choose arbitrary large central density. As can be seen from Figure 5, the behaviors are very different, some of them change drastically as a function of the density. Our results are similar to the ones of Ref. [21], but for another galaxy. Even though it seems that there are small differences in framing out the net equation of state of DM for each profiles, the NFW and Moore profiles are less appropriate to describe the DM distribution of this galaxy for statistical reasons, as has been pointed out using the BIC information criterion. This does not mean that the same could be found also if visible matter contribution is added and/or for other galaxies. We thus intend to check this byproduct of our analysis in next works where we are going to test the equation of state of DM for other Spirals. In addition, it should be mentioned that the density and correspondingly the pressure diverge when r tends to zero, causing the cuspy halo problem, which is not applicable for considering the equation of state.
4. Final Outlooks and Perspectives
We analyzed the RC of galaxy ESO0140040 and inferred the free parameters of the considered profiles by means of the least square method. We used the well-known DM density profiles from the literature, and, in addition, we considered the exponential sphere profile for comparison. The exponential sphere profile is usually applied to study the inner parts of galaxies [15] and, in fact, for galaxy ESO0140040 it showed weak results. This can be seen from the analyses of the RC: exponential sphere does not produce a flat RC and its BIC (or ) is the largest.
We considered also NFW and Moore profiles for completeness, though these density profiles diverge as causing the cuspy halo problem. Indeed, in examining the equation of state of DM these two profiles are not appropriate, though at large distances they give flat RCs. It turned out that only three profiles, namely ISO, Burkert and Einasto profiles are suitable for the analysis of the DM equation of state as , where the density tends to be finite avoiding cusps. Out of the three profiles, the Einasto possesses the minimum BIC number and the Burkert profile possesses the maximum BIC number. The same is true also for the , though ISO profile value is closer to unity. The difference in BIC between Einasto (with three free parameters) and ISO (with two free parameters) profiles is BIC and exhibits a positive (though not definitive) evidence against the model with the higher BIC (in this case ISO). Therefore, for our purposes the Einasto and ISO profiles are the most convenient profiles to study the DM equation of state. Although from the analyses of , and it is seen that the behavior of the profiles is similar, the degeneracy among the profiles is completely broken by looking at the diagram of the speed of sound. Here the behavior of ISO profile is analogous to NFW and Moore profiles, though the latter two cause cusps. Nevertheless, the speed of sound decreases with the increasing density for all profiles. This is a unique feature/signature of DM and it plays a key role in the structure formation.
Future applications will be devoted to analyzing the same features of this work but adding other contributions, as due e.g., to gas. Moreover, it would be interesting to proceed with a back-scattering strategy to infer from data the most suitable profile instead of postulating them at the beginning. In this respect the universal RCs already known in the literature [46] could be compared with our future expectations. Future studies will be necessary to test whether the possibility here investigated can also be checked in view of wider galaxy samples. This will permit one to generalize the procedure we introduced and to see whether DM shows a universal pressure in spiral galaxies.
Author Contributions
All the authors have contributed in the same way to write the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
The work was supported by the Ministry of Education and Science of the Republic of Kazakhstan, Target Program ’Center of Excellence for Fundamental and Applied Physics’ IRN: BR05236454, Grants: IRN AP08052311 and IRN AP05134454.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ade, P.A.R.; Aghanim, N.; Alves, M.I.R.; Armitage-Caplan, C.; Arnaud, M.; Ashdown, M.; Atrio-Barandela, F.; Aumont, J.; Aussel, H.; Baccigalupi, C.; et al. Planck 2013 results. I. Overview of products and scientific results. Astron. Astrophys. 2014, 571, A1. [Google Scholar] [CrossRef]
- Bertone, G.; Hooper, D.; Silk, J. Particle dark matter: Evidence, candidates and constraints. Phys. Rep. 2005, 405, 279–390. [Google Scholar] [CrossRef]
- Schumann, M. Direct detection of WIMP dark matter: Concepts and status. J. Phys. Nucl. Part. Phys. 2019, 46, 103003. [Google Scholar] [CrossRef]
- Tam, S.I.; Jauzac, M.; Massey, R.; Harvey, D.; Eckert, D.; Ebeling, H.; Ellis, R.S.; Ghirardini, V.; Klein, B.; Kneib, J.P.; et al. The distribution of dark matter and gas spanning 6 Mpc around the post-merger galaxy cluster MS 0451–03. Mon. Not. R. Astron. Soc. 2020, 496, 4032–4050. [Google Scholar] [CrossRef]
- Ablimit, I.; Zhao, G.; Flynn, C.; Bird, S.A. The Rotation Curve, Mass Distribution, and Dark Matter Content of the Milky Way from Classical Cepheids. Astrophys. J. Lett. 2020, 895, L12. [Google Scholar] [CrossRef]
- Epinat, B.; Adamczyk, P.; Bounissou, S.; Amram, P.; Neichel, B. Dark matter distribution in distant galaxies with HARMONI. In Proceedings of the SF2A-2019: Proceedings of the Annual meeting of the French Society of Astronomy and Astrophysics, Paris, Nice, France, 14–17 May 2019. [Google Scholar]
- Jungman, G.; Kamionkowski, M.; Griest, K. Supersymmetric dark matter. Phys. Rep. 1996, 267, 195–373. [Google Scholar] [CrossRef]
- Einasto, J.; Kaasik, A.; Saar, E. Dynamic evidence on massive coronas of galaxies. Nature 1974, 250, 309–310. [Google Scholar] [CrossRef]
- Rubin, V.C.; Burstein, D.; Ford, W.K.J.; Thonnard, N. Rotation velocities of 16 SA galaxies and a comparison of Sa, SB and SC rotation properties. Astrophys. J. 1985, 289, 81–104. [Google Scholar] [CrossRef]
- Davis, M.; Efstathiou, G.; Frenk, C.S.; White, S.D.M. The evolution of large-scale structure in a universe dominated by cold dark matter. Astrophys. J. 1985, 292, 371–394. [Google Scholar] [CrossRef]
- Bode, P.; Bahcall, N.A.; Ford, E.B.; Ostriker, J.P. Evolution of the Cluster Mass Function: GPC3 Dark Matter Simulations. Astrophys. J. 2001, 551, 15–22. [Google Scholar] [CrossRef]
- Boshkayev, K.; Zhumakhanova, G.; Mutalipova, K.; Muccino, M. Investigation of different dark matter profiles. News Natl. Acad. Sci. Repub. Kazakhstan. Phys. Math. Ser. 2019, 6, 25–33. [Google Scholar] [CrossRef]
- Chechin, L.M.; Konysbayev, T.K. Searching the Parameters of Dark Matter Halos on the Basis of Dwarf Galaxies’ Dynamics. J. Mod. Phys. 2016, 7, 982–988. [Google Scholar] [CrossRef]
- Jimenez, R.; Verde, L.; Oh, S.P. Dark halo properties from rotation curves. Mon. Not. R. Astron. Soc. 2003, 339, 243–259. [Google Scholar] [CrossRef]
- Sofue, Y. Rotation Curve and Mass Distribution in the Galactic Center - From Black Hole to Entire Galaxy. Publ. Astron. Soc. Jpn. 2013, 65, 118. [Google Scholar] [CrossRef]
- Burkert, A. The Structure of Dark Matter Halos in Dwarf Galaxies. Astrophys. J. Lett. 1995, 447, L25–L28. [Google Scholar] [CrossRef]
- Navarro, J.F.; Frenk, C.S.; White, S.D.M. The Structure of Cold Dark Matter Halos. Astrophys. J. 1996, 462, 563. [Google Scholar] [CrossRef]
- Moore, B.; Governato, F.; Quinn, T.; Stadel, J.; Lake, G. Resolving the Structure of Cold Dark Matter Halos. Astrophys. J. Lett. 1998, 499, L5–L8. [Google Scholar] [CrossRef]
- Merritt, D.; Graham, A.W.; Moore, B.; Diemand, J.; Terzić, B. Empirical Models for Dark Matter Halos. I. Nonparametric Construction of Density Profiles and Comparison with Parametric Models. Astron. J. 2006, 132, 2685–2700. [Google Scholar] [CrossRef]
- Einasto, J. On the Construction of a Composite Model for the Galaxy and on the Determination of the System of Galactic Parameters. Trudy Astrofiz. Inst.-Alma-Ata 1965, 5, 87–100. [Google Scholar]
- Barranco, J.; Bernal, A.; Núñez, D. Dark matter equation of state from rotational curves of galaxies. Mon. Not. R. Astron. Soc. 2015, 449, 403–413. [Google Scholar] [CrossRef]
- de Blok, W.J.G.; McGaugh, S.S.; Rubin, V.C. High-Resolution Rotation Curves of Low Surface Brightness Galaxies. II. Mass Models. Astron. J. 2001, 122, 2396–2427. [Google Scholar] [CrossRef]
- Shapiro, S.L.; Teukolsky, S.A. Black Holes, White Dwarfs and Neutron Stars: The Physics of Compact Objects; Wiley-VCH: Weinheim, Germany, 1986. [Google Scholar]
- Misner, C.W.; Thorne, K.S.; Wheeler, J.A. Gravitation Volume 2; W. H. Freeman & Company: San Francisco, CA, USA, 1977; Volume 2. [Google Scholar]
- Capozziello, S.; D’Agostino, R.; Luongo, O. Extended gravity cosmography. Int. J. Mod. Phys. D 2019, 28, 1930016. [Google Scholar] [CrossRef]
- Del Popolo, A. Dark matter, density perturbations, and structure formation. Astron. Rep. 2007, 51, 169–196. [Google Scholar] [CrossRef]
- Perlick, V. Gravitational Lensing from a Spacetime Perspective. Living Rev. Relativ. 2004, 7, 9. [Google Scholar] [CrossRef]
- Chechin, L.M.; Kurmanov, E.B.; Konysbaev, T.K. Geometrical Optics in a Universe with Dominance of Dark Matter. Russ. Phys. J. 2020, 63, 58–63. [Google Scholar] [CrossRef]
- Capozziello, S.; De Laurentis, M.; Luongo, O.; Ruggeri, A. Cosmographic Constraints and Cosmic Fluids. Galaxies 2013, 1, 216–260. [Google Scholar] [CrossRef]
- Dunsby, P.K.S.; Luongo, O. On the theory and applications of modern cosmography. Int. J. Geom. Methods Mod. Phys. 2016, 13, 1630002–1630606. [Google Scholar] [CrossRef]
- Aviles, A.; Gruber, C.; Luongo, O.; Quevedo, H. Cosmography and constraints on the equation of state of the Universe in various parametrizations. Phys. Rev. D 2012, 86, 123516. [Google Scholar] [CrossRef]
- Salucci, P. Dark Matter in Galaxies: Evidences and Challenges. Found. Phys. 2018, 48, 1517–1537. [Google Scholar] [CrossRef]
- Copeland, E.J.; Sami, M.; Tsujikawa, S. Dynamics of Dark Energy. Int. J. Mod. Phys. D 2006, 15, 1753–1935. [Google Scholar] [CrossRef]
- Faber, T.; Visser, M. Combining rotation curves and gravitational lensing: How to measure the equation of state of dark matter in the galactic halo. Mon. Not. R. Astron. Soc. 2006, 372, 136–142. [Google Scholar] [CrossRef]
- Luongo, O.; Muccino, M. Speeding up the Universe using dust with pressure. Phys. Rev. D 2018, 98, 103520. [Google Scholar] [CrossRef]
- Campos, J.P.; Fabris, J.C.; Perez, R.; Piattella, O.F.; Velten, H. Does Chaplygin gas have salvation? Eur. Phys. J. C 2013, 73, 2357. [Google Scholar] [CrossRef]
- Will, C.M. The Confrontation between General Relativity and Experiment. Living Rev. Relativ. 2014, 17, 4. [Google Scholar] [CrossRef]
- Yegorova, I.A.; Babic, A.; Salucci, P.; Spekkens, K.; Pizzella, A. Rotation curves of luminous spiral galaxies. Astron. Astrophys. Trans. 2012, 27, 335–338. [Google Scholar] [CrossRef]
- Levenberg, K. A method for the solution of certain non-linear problems in least squares. Q. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef]
- Marquardt, D. An algorithm for least-squares estimation of nonlinear parameters. J. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Garcia-Aspeitia, M.A.; Lopez-Dominguez, J.C.; Ortiz, C.; Hinojosa-Ruiz, S.; Rodriguez-Meza, M.A. Energy density profile inspired by noncommutativity. arXiv 2015, arXiv:1511.06740. [Google Scholar]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control. 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Kunz, M.; Trotta, R.; Parkinson, D.R. Measuring the effective complexity of cosmological models. Phys. Rev. D 2006, 74, 023503. [Google Scholar] [CrossRef]
- Schwarz, G.D. Estimating the Dimension of a Model. Ann. Stat. 1963, 6, 461–464. [Google Scholar] [CrossRef]
- Siutsou, I.; Argüelles, C.R.; Ruffini, R. Dark matter massive fermions and Einasto profiles in galactic haloes. Astron. Rep. 2015, 59, 656–666. [Google Scholar] [CrossRef]
- Salucci, P.; Lapi, A.; Tonini, C.; Gentile, G.; Yegorova, I.; Klein, U. The universal rotation curve of spiral galaxies—II. The dark matter distribution out to the virial radius. Mon. Not. R. Astron. Soc. 2007, 378, 41–47. [Google Scholar] [CrossRef]
| 1. | One is forced to exclude dark baryons since the numerical simulations provide radically different large-scale structure of the Universe. |
| 2. | As morphological and clustering properties of galaxies, abundances of rich clusters, halo masses degenerate if we consider cold, warm or collisional DM. We therefore seek tests of DM’s nature that could be sensitive to its presumed microphysics and/or to its interaction properties and we can assume to consider density profiles only without taking care at this stage of other velocity corrections. |
| 3. | In general, all model parameters can be estimated by analyzing galaxies, albeit with a strong unvoidable degeneracy [12]. |
| 4. | With increasing interests, models that aim to unify DM with dark energy are always more studied. A final goal could be to unify the dark Universe under the same standards. |
| 5. | For a review of galaxy morphology and properties of DM see [38]. |
| 6. | The Levenberg-Marquardt algorithm is an iterative technique that locates the minimum of a function that is expressed as the sum of squares of nonlinear functions. It consists of a combination of the Gauss–Newton algorithm and the method of the steepest descent gradient. |
| 7. | BIC is a selection criterion among a finite set of models, conceived to solve the overfitting issue when increasing the number of parameters in the fitting function. For the sake of completeness, please notice that other selection criteria could be used, e.g., the Akaike information and/or DIC criteria [42,43]. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).