Abstract
In the Newtonian limit of general relativity a force acting on a test mass in a central gravitational field is conventionally defined by the attractive Newtonian gravity (inverse square) term plus a small repulsive cosmological force, which is proportional to the slow acceleration of the universe expansion. In this paper we considered the cosmological-force correction due to fast quantum oscillations of the universe scale factor as a potential solution of the cosmological constant problem. These fast fluctuations of the cosmological scale factor violate Lorentz invariance at the Planck scale, and they induce strong changes to the current sign and magnitude of the average cosmological force, thus making it one of the potential probable causes for the modification of Newtonian dynamics in galaxy-scale systems. The modified cosmological force may be responsible for the recently discovered “cosmic-clock” behavior of disk galaxies in the low-redshift universe. The obtained results have strong implications for astroparticle physics since they demonstrate that typical galaxy rotation curves may be obtained without (or almost without) dark-matter particles.
1. Introduction
The discrepancy between visible masses in galaxies and galaxy clusters and their dynamics predicted by the application of Newton’s laws was first noticed by Fritz Zwicky almost a hundred years ago [1]. The proposed solutions to this mystery range from dark-matter halos around galaxy centers [2] to various modifications of Newton’s laws themselves [3,4] and even optical cloaking [5]. However, despite almost a hundred years of experimental and theoretical studies, the ultimate solution of this mystery remains elusive [6]. The recently discovered “cosmic-clock” behavior [7] of disk galaxies in the low-redshift universe further underlines this discrepancy. It appears that despite spanning a factor of 30 in size and velocity (from small irregular dwarf galaxies to the largest spirals) the galaxies behave as “clocks”, rotating roughly once in a billion years at the very outskirts of their discs. While this behavior strongly contradicts conventional Newtonian dynamics in the absence of dark-matter halos, it would also require a very special fine tuning of the dark-matter halos around each galaxy. As we will try to demonstrate below, quite unexpectedly, a solution to this old problem may come from considerations of a Lorentz invariance violation at the Planck scale.
It has been well established for quite a while [8,9] that in an expanding universe the equations of motion of a test body in a central gravitational field must be modified even in the Newtonian limit of general relativity. The easiest way to see it is to write down the metric that describes the spacetime in the vicinity of a point mass M placed in an expanding flat background [10]:
where G is the gravitational constant, a(t) is the cosmological scale factor, and ρ is the comoving radial coordinate, which relates to the proper radial coordinate r as
The proper radial coordinate r measures the distance between a test body and the position of a point mass M. The geodesics corresponding to the line element (1) are defined by
Introducing L as the constant angular momentum per unit mass
The radial equation of motion for a test body in the Newtonian limit may be written as
As we can see from Equation (5), the Newtonian equation of motion in an expanding universe is modified by an additional small cosmological force [8,9]:
where m is the mass of the test body. The current value of is believed to be positive based on the experimental measurements of the universe deceleration parameter:
where H is the Hubble parameter. According to the Planck spacecraft data, in the current epoch [11], which results in a small repulsive addition to the attractive Newtonian gravity term in Equation (5):
At large distances from the center, the velocity distribution of the test bodies would be modified as
leading to an apparent upper limit on the radius RM of a gravitationally bound system at a given M:
Assuming the mass of the Milky Way to be M~1012 solar masses, the projected RM for the Milky Way should be about 3 × 106 light years, or about 30 times larger than its radius. This should mean that the so determined cosmological force plays a very little role in the dynamics of the Milky Way, and it cannot be responsible for the observed flattening of the rotation curves in a typical galaxy [2].
2. Methods
Fortunately, this may not be the end of the story for the cosmological force. In a very recent development, Wang et al. suggested that very fast quantum fluctuations of the universe scale factor a(t,x) may considerably alter the universe dynamics, thus providing a potential solution to the cosmological constant problem [12]. While these fast quantum fluctuations of the cosmological scale factor would violate Lorentz invariance at the Planck scale, the large-scale structure of the physical spacetime would remain Lorentz-invariant. Basically, the approach developed in [12] results in a scale-dependent magnitude of the observed effective cosmological constant. At the microscopic (Planck) scale, the “true” magnitude of the cosmological constant is very large. Its magnitude is defined by the vacuum energy density predicted by quantum mechanics, and it is about 120 orders of magnitude larger than the value observed at cosmological scales, which is inferred by cosmological observations of the accelerating cosmic expansion. According to [12], the vacuum energy density is still huge at sufficiently small (Planck) scales, but its effect at macroscopic scales is largely canceled. Moreover, due to the weak parametric resonance of those oscillations, expansion outweighs contraction a little bit during each oscillation. This effect accumulates at sufficiently large scales (cosmological scale), resulting in an observable effect—the slow accelerating expansion of the universe. As a result, the effective cosmological constant observed at these large cosmological scales equals its currently measured value of Λ=1.11 × 10−52 m−2 [11]. The observed value of Λ changes continuously in between the Planck scale and the cosmological scale.
Let us demonstrate that these fast fluctuations of the cosmological scale factor may also induce strong changes of the current sign and magnitude of the average cosmological force. As a result, the re-defined average cosmological force may contribute substantially to the modification of Newtonian dynamics in galaxy-scale systems.
Wang et al. [12] assumed the global metric of the universe to have the cosmology’s standard Friedmann–Lemaître–Robertson–Walker (FLRW) form:
while allowing spatio-temporal inhomogeneity in the scale factor a(t,x). After solving the full coordinate-dependent Einstein field equations, they have obtained the following dynamic evolution equation for a(t,x):
where ω2 > 0 for the quantum fluctuations of the matter fields (see Equations (41) and (42) from [12]). Due to the stochastic nature of these fast quantum fluctuations, ω(t,x) is not strictly periodic. However, as demonstrated in [12], its effect on the gravitating system is still similar to a periodic function (see also further refinements of these arguments in [13]). We should also note that cosmological solutions exhibiting fast scale factor oscillations appear quite generically in many other situations, such as semiclassical quantum gravity [14], cosmological models with oscillating dark energy [15] and various modified gravity theories [16]. In some of these situations (for example in Ref. [12]) the scale factor oscillations do not necessarily decay due to re-heating [17]. In addition, experimental evidence of relatively fast scale factor oscillations also started to emerge very recently [18]. Therefore, it makes sense to consider the effect of fast fluctuations of the cosmological scale factor on the sign and magnitude of the cosmological force described by Equations (5) and (6).
Following the standard analysis of system dynamics under the influence of a fast oscillating force [19], let us consider a toy cosmological model in which the evolution of the scale factor of the universe is separated into slow and fast components:
In this decomposition, a0(t) represents the observed slow cosmological evolution of the universe, while positive represents the typical (potentially also time-dependent) amplitude of the scale factor fluctuations introduced in [12] (in order to simplify our consideration we have neglected a spatial dependence of α by replacing α(x) with its spatial average). We will assume that ω−1 is much faster than the typical time scales of galaxy evolution and the evolution of the universe as a whole, since, as suggested in [12], the physical origin of these fluctuations is due to quantum effects. We will also assume ω−1 to be much faster than any possible time dependence of α, so its time derivative may be neglected. Under these assumptions, the radial equation of motion of a test body in a central gravitational field will be modified as follows:
which indicates that the cosmological force experiences fast oscillations. If these oscillations are fast enough, the αω2 term may not be neglected compared to the term. Following the standard treatment in [19], the proper radial coordinate of the test body should be expressed as
where ξ(t) represents small oscillations of the test body with respect to its slowly evolving radial position r0(t). By separating the fast and slow motion in Equation (14), and by expanding to leading order in small quantities, the amplitude of these small oscillations may be defined from:
thus, leading to:
As usual (see [19]), we will assume that the average kinetic energy of the fast oscillations of the test body contributes to its effective potential energy:
(similar to the introduction of the effective potential energy for an inverted (Kapitza) pendulum [19]), so that the average effective cosmological force in Equation (5) must be re-defined as
Note that the newly derived component of the cosmological force (due to the fast scale factor fluctuations) is always attractive. The total overall cosmological force will also become attractive if:
If the origin of the fast scale factor fluctuations is due to Lorentz-violating quantum gravity, and both their characteristic amplitude α and frequency ω are defined by the Planck scale, the right-hand side of Equation (20) is expected to be of order unity. The left-hand side of Equation (20) has the same order of magnitude, which means that it is plausible that the overall sign of the cosmological force is attractive. Therefore, let us assume that:
where A~1 is a dimensionless positive constant, whose exact magnitude needs to be determined either from the future theory of quantum gravity, or from astronomical observations. Such an attractive cosmological force will result in the following velocity distribution of test bodies far from the compact central mass:
and at very large distances from the center, a slow linear velocity increase will be observed as a function of radial distance.
As illustrated in Figure 1, the measured rotation curve in a typical spiral galaxy such as M33 indeed shows a slow linear increase in the rotation velocity with the radial distance. This behavior is consistent with the expectations based on Equations (22) and (23) for A1/2~0.05. The observed rotation curve of the Milky Way [20] (also shown in Figure 1) exhibits a similar linear dependence of the rotation speed at large distances from the center.
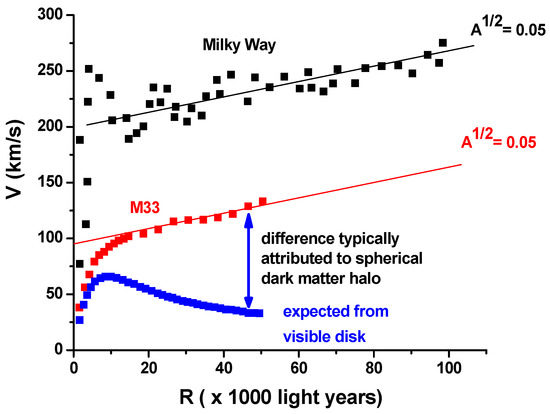
Figure 1.
Comparison of the observed rotation curve (red) with the computed rotation curve (blue) obtained based on the unmodified Newtonian dynamics and the visible mass distribution for the typical spiral galaxy M33 [2]. Note that at large distances from the galactic center the observed rotation curve exhibits a slow linear dependence on the radial distance, which is consistent with the expectations based on Equations (22) and (23) for A1/2~0.05. The observed rotation curve of the Milky Way (black) [20] exhibits a similar linear dependence of the rotation speed at large distances from the center.
3. Results
The difference between the measured rotation curve and the rotation curve calculated based on the Newtonian dynamics of visible matter is typically attributed to a spherical dark-matter halo [2,6], which is assumed to exist around virtually every galaxy. If such a spherical halo has an approximately constant density, its mass distribution would be:
leading to similar linear dependencies of the gravitational and cosmological forces on the radial coordinate. This means that the effect of the dark-matter halo and the effect of the cosmological force may mimic each other, and that the total amount of dark matter in a typical galaxy needs to be carefully re-examined. A good strategy to differentiate between the effects of dark-matter halos and the cosmological force is to carefully re-evaluate the galaxy rotation curves at very large distances from the galactic centers. If these rotation curves show signs of a universal linear increase far from the galaxy center (see Equation (23)), such an effect may turn out to become a very important observational evidence of quantum gravity. The comparison of the rotation curves at large distances from the center for the M33 and the Milky Way galaxy shown in Figure 1 indicates that this research direction may indeed be very promising. The slopes of the rotation curves look nearly identical at large distances from the respective galactic centers.
In fact, recent detailed observations indicate that this is not a mere coincidence. It appears that disk galaxies in the low-redshift universe exhibit the “cosmic-clock” behavior [7] illustrated in Figure 2. Despite spanning a factor of 30 in size and velocity (from small irregular dwarf galaxies to the largest spirals), the disk galaxies behave as “clocks”, rotating roughly once a billion years at the very outskirts of their discs. While this behavior strongly contradicts conventional Newtonian dynamics in the absence of dark-matter halos, it would also require a very special fine tuning of the dark-matter halos around each galaxy (see [21] as an example). It has to be assumed that the mass and the angular momentum of the visible matter disks must be fixed fractions of those of its surrounding dark-matter halos. On the other hand, the “cosmic-clock” behavior finds a very simple and natural explanation if the universal attractive cosmological force defined by Equation (21) is responsible for the observed galaxy rotation curves at large distances from the centers. The universal linear long-distance rotation curve defined by Equation (23) leads to a universal “clock-like” periodicity of galactic rotations:
which does not depend on the galaxy shape or dimensions. Indeed, the low scatter around the “universal slope” dv/dr = 1.84 × 10−3 km/s/ly seen in Figure 2 implies that this relationship is generic to disc galaxies in the low-redshift universe. As a result, the galaxies behave as “cosmic clocks”, rotating with a periodicity of roughly one billion years.
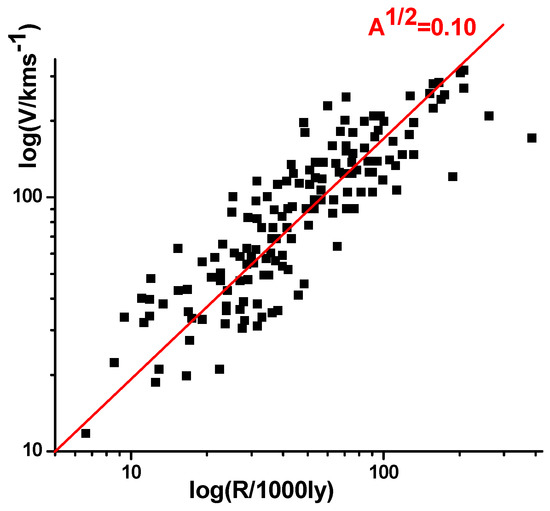
Figure 2.
Log–log plot of the observed circular velocity V as a function of the maximum radius R for low-redshift disk galaxies re-plotted using data from Figure 4 of Ref. [7]. Low scatter around the “universal slope” 1.84 × 10−3 km/s/ly indicated by the red line implies that this relationship is generic for disc galaxies in the low-redshift universe. As a result, the galaxies behave as “cosmic clocks”, rotating roughly once a billion years at the very outskirts of their discs. This “universal slope” corresponds to A1/2~0.10.
The magnitude of the “universal” dv/dr stemming from the data in Figure 2 indicates that the true value of A1/2 in Equation (23) may be about twice as large as the A1/2~0.05 value indicated by the data shown in Figure 1. In order to clarify this issue and to re-examine the assumed amount of dark matter in the M33 galaxy, we have performed numerical simulations of the rotation curve in M33 assuming a disk-shaped mass distribution of the visible matter, different magnitudes of A1/2 ranging from 0 to 0.12, and without any contribution from the dark-matter halo. Results of these simulations are shown in Figure 3. Numerical simulations performed using A1/2 = 0.10 and A1/2 = 0.12 show a considerably improved agreement with the observational data (these results compared with Figure 1: the huge difference between the observed and the calculated rotational velocities is almost eliminated). While such simplified model calculations cannot produce a perfect match with the observational data, this improved agreement is nevertheless quite remarkable. It is noteworthy that these particular magnitudes of A1/2 were suggested by the “cosmological-clock” results shown in Figure 2. Our results strongly indicate that the typically assumed amounts of dark matter in disk galaxies must be carefully re-examined.
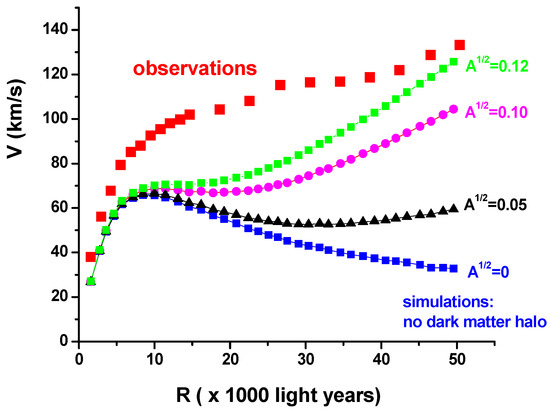
Figure 3.
Numerical simulations of the rotation curve in M33, which were performed for different magnitudes of A1/2 between 0 and 0.12 assuming a disk-shape mass distribution of the visible matter and no dark-matter halo. The different magnitudes of A1/2 used in this figure and in Figure 1 and Figure 2 are meant to give a plausible range of this constant. Calculations performed using A1/2 = 0.10 and A1/2 = 0.12 show a considerably improved agreement with the astronomical data (these results compared with Figure 1: the huge difference between the observed and the calculated rotational velocities is almost eliminated).
An important question to ask would be if the mechanism described above could considerably alter the observed dynamics of the Solar System. Based on Equation (22) it appears that any such correction would be beyond the accuracy of current observations. Indeed, within the Solar System we may approximate Equation (22) as
where M is the solar mass, rg is the solar gravitational radius, r0 is a radius of a planet orbit, and a0 is the current cosmological scale factor. Assuming r0 to be the radius of Pluto’s orbit, Equation (25) gives rise to corrections of the order of 5 × 10−20 to Pluto’s orbital velocity.
To summarize, according to the approach developed by Wang et al. [12,13] the true value of the cosmological constant is very large. It equals the magnitude predicted by quantum field theory. Wang et al. started with this very large value of the cosmological constant at the microscopic (Planck) scale, and by solving the nonlinear equations of general relativity, they have managed to reproduce the currently observed slow cosmological expansion of our universe (see Equation (75) from [12]). The side product of this theory is the prediction of fast oscillations of the cosmological scale factor.
The question that is addressed in this paper is what would happen within the scope of this model at galactic scales. By taking the Newtonian limit of the theory developed by Wang et al. we demonstrated that the fast oscillations of the cosmological scale factor would lead to an additional attractive force acting on distant stars rotating around a galaxy center. The end result of this consideration is that we managed to reproduce the "cosmological-clock" effect. Distant stars must rotate around the centers of their respective galaxies with about the same periodicity of about one billion years per rotation.
We should also note that it does not make sense to ask what would happen if we take this Newtonian limit of the original theory by Wang et al. and extrapolate it back to the cosmological scales. First of all, the Newtonian limit cannot be extrapolated to cosmological scales, because it assumes slow velocities. On the other hand, such an extrapolation (if somehow done properly) would come back to the original consideration of Wang et al., which successfully recovers the slow cosmological expansion of our universe.
Another important note that should be made here is that the scale-dependent effective cosmological constant appears generically in many other situations (so that the results of [12,13] are not unique in this respect). For example, a somewhat similar scale-dependent effective cosmological constant also appears in [22], where graviton fluctuations induce strong nonperturbative infrared renormalization effects for the cosmological constant.
4. Discussion and Conclusions
Based on the potential solution to the cosmological constant problem recently suggested in [12,13], which assumes Lorentz violation due to fast quantum-mechanical oscillations of the cosmological scale parameter, we have re-examined the sign and the magnitude of the cosmological force which modifies Newtonian dynamics around a central gravitating body in an expanding universe. The cosmological force in this model appears to be attractive, which means that it can mimic the effects of a spherical dark-matter halo around a galaxy center. Therefore, the total amount of dark matter (if any) in a typical galaxy needs to be carefully re-examined by taking into account the effect of the cosmological force. The obtained results have strong implications for astroparticle physics since they demonstrate that typical galaxy rotation curves may be obtained without (or almost without) dark-matter particles. The developed approach may be characterized as phenomenological, since it takes the Newtonian limit of general relativity described by the metric (1), and assumes that the cosmological scale factor in this metric exhibits fast fluctuations (based on results of [12,13]). In principle, this approach may be developed further by calculating the effective energy density and pressure based on Equations (41) and (42) of [12]. However, the main result of [12,13] involves the possibility of hiding very large energy densities by fast scale factor fluctuations, which may occur due to the nonlinear character of general relativity. Therefore, the value of the introduction of such an effective energy density and pressure may be debatable.
Since the long-distance behavior of the cosmological force is expected to be universal, this mechanism provides a simple and natural explanation of the “cosmic-clock” behavior [7] observed in the low-redshift disk galaxies. If confirmed by further observations, this effect may turn out to become very important observational evidence of macroscopic quantum gravity.
Finally, since the sign of the cosmological force due to scale factor fluctuations appears to be always attractive, the popular Big Rip scenarios [8] will also need to be re-examined.
Funding
This research received no external funding.
Conflicts of Interest
The author declares no conflict of interests.
References
- Zwicky, F. Die Rotverschiebung von extragalaktischen Nebeln. Helv. Phys. Acta 1933, 6, 110–127. [Google Scholar]
- Corbelli, E.; Salucci, P. The extended rotation curve and the dark matter halo of M33. Mon. Not. R. Astron. Soc. 2000, 311, 441–447. [Google Scholar] [CrossRef]
- Milgrom, M. A modification of the Newtonian dynamics as a possible alternative to the hidden mass hypothesis. Astrophys. J. 1983, 270, 365–370. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Relativistic gravitation theory for the MOND paradigm. Phys. Rev. D 2004, 70, 83509. [Google Scholar] [CrossRef]
- Smolyaninov, I.I. Galactic optical cloaking of visible baryonic matter. Phys. Rev. D 2018, 97, 104008. [Google Scholar] [CrossRef]
- Hossenfelder, S.; McGaugh, S. Is dark matter real? Sci. Am. 2018, 319, 36–43. [Google Scholar] [CrossRef] [PubMed]
- Meurer, G.R.; Obreschkow, D.; Wong, O.I.; Zheng, Z.; Audcent-Ross, F.M.; Hanish, D.J. Cosmic clocks: A tight radius-velocity relationship for HI-selected galaxies. Mon. Not. R. Astron. Soc. 2018, 476, 1624–1636. [Google Scholar] [CrossRef]
- Nesseris, S.; Perivolaropoulos, L. The fate of bound systems in phantom and quintessence cosmologies. Phys. Rev. D 2004, 70, 123529. [Google Scholar] [CrossRef]
- Nandra, R.; Lasenby, A.N.; Hobson, M.P. The effect of a massive object on an expanding universe. Mon. Not. R. Astron. Soc. 2012, 422, 2931–2944. [Google Scholar] [CrossRef]
- Einstein, A.; Straus, E.G. The influence of the expansion of space on the gravitation fields surrounding the individual stars. Rev. Mod. Phys. 1945, 17, 120. [Google Scholar] [CrossRef]
- Planck Collaboration Planck 2013 results. XXXII. The updated Planck catalogue of Sunyaev-Zeldovich sources. Astron. Astrophys. 2014, 571, A16.
- Wang, Q.; Zhu, Z.; Unruh, W.G. How the huge energy of quantum vacuum gravitates to drive the slow accelerating expansion of the Universe. Phys. Rev. D 2017, 95, 103504. [Google Scholar] [CrossRef]
- Cree, S.S.; Davis, T.M.; Ralph, T.C.; Wang, Q.; Zhu, Z.; Unruh, W.G. Can the fluctuations of the quantum vacuum solve the cosmological constant problem? Phys. Rev. D 2018, 98, 063506. [Google Scholar] [CrossRef]
- Matsui, H.; Watamura, N. Quantum spacetime instability and breakdown of semiclassical gravity. arXiv 2020, arXiv:1910.02186. [Google Scholar] [CrossRef]
- Pace, F.; Fedeli, C.; Moscardini, L.; Bartelmann, M. Structure formation in cosmologies with oscillating dark energy. Mon. Not. R. Astron. Soc. 2012, 422, 1186–1202. [Google Scholar] [CrossRef]
- Zaripov, F. Oscillating cosmological solutions in the modified theory of induced gravity. Adv. Astron. 2019, 2019, 1502453. [Google Scholar] [CrossRef]
- Lozanov, K.D. Lectures on reheating after inflation. arXiv 2019, arXiv:1907.04402. [Google Scholar]
- Ringermacher, H.I.; Mead, L.R. Observation of discrete oscillations in a model-independent plot of cosmological scale factor versus lookback time and scalar field model. Astron. J. 2015, 149, 137. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Mechanics, 3rd ed.; Butterworth-Heinemann: Oxford, UK, 1976; p. 131. [Google Scholar]
- Bennett, J.O.; Donahue, M.O.; Schneider, N.; Voit, M. The Essential Cosmic Perspective, 8th ed.; Pearson: Irving, TX, USA, 2018. [Google Scholar]
- Mo, H.J.; Mao, S.; White, S.D.M. The formation of galactic disks. Mon. Not. R. Astron. Soc. 1998, 295, 319. [Google Scholar] [CrossRef]
- Wetterich, C. Graviton fluctuations erase the cosmological constant. Phys. Let. B 2017, 773, 6–19. [Google Scholar] [CrossRef]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).