Parameters of the Supernova-Driven Interstellar Turbulence
Abstract
1. Introduction
2. Estimation of Interstellar Turbulence Parameters
2.1. Similarity Solutions
2.1.1. SNRs
2.1.2. SBs
2.2. Energy Injection Scales
2.2.1. SNRs
2.2.2. SBs
2.3. Energy Conversion Efficiency
2.4. Energy Input Into an Outflow
2.5. Relative Contribution from Isolated SNe and SBs
2.6. Turbulent Correlation Scale
2.7. RMS Turbulent Velocity
2.8. Correlation Time
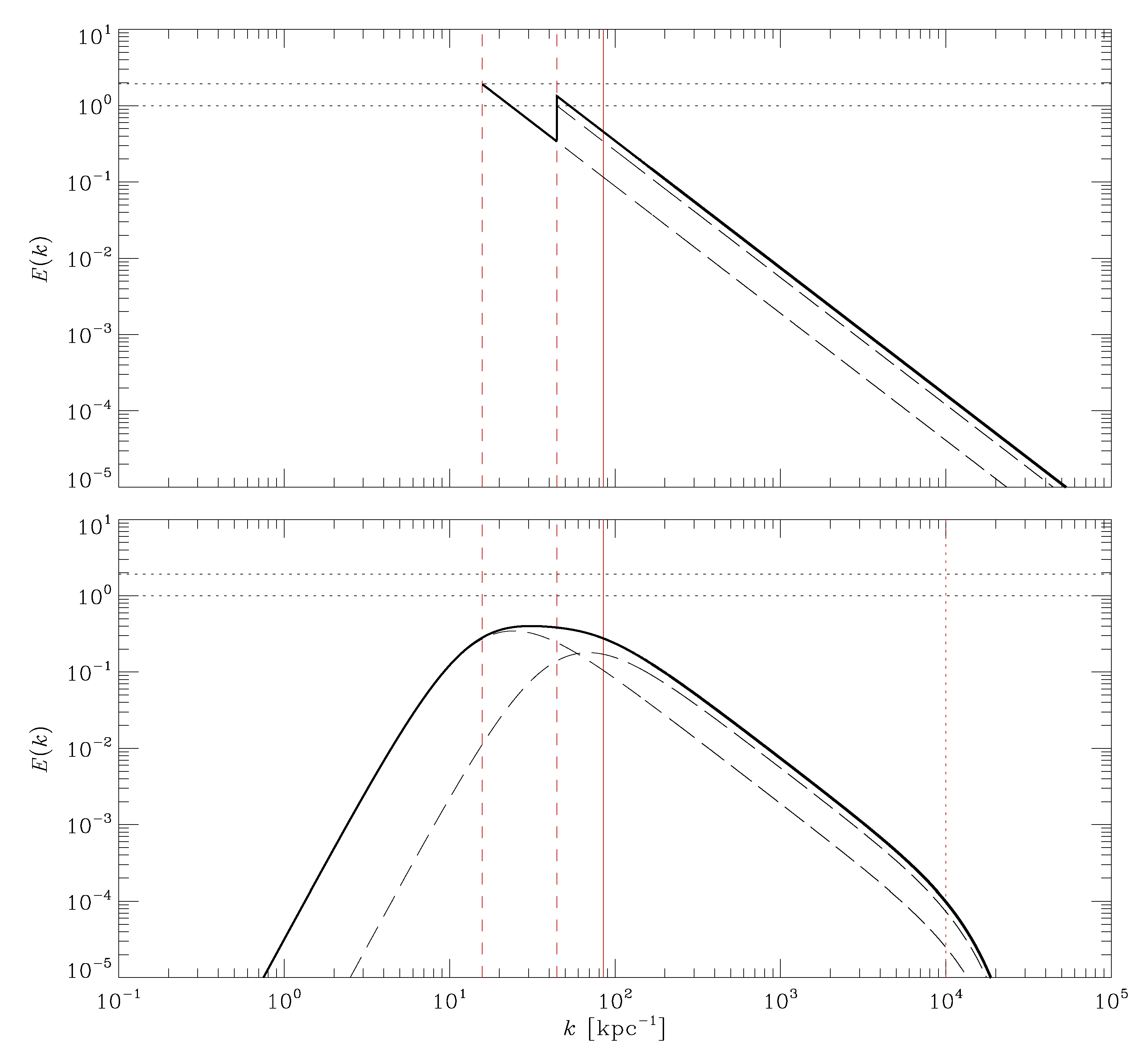
2.9. Graphical Example
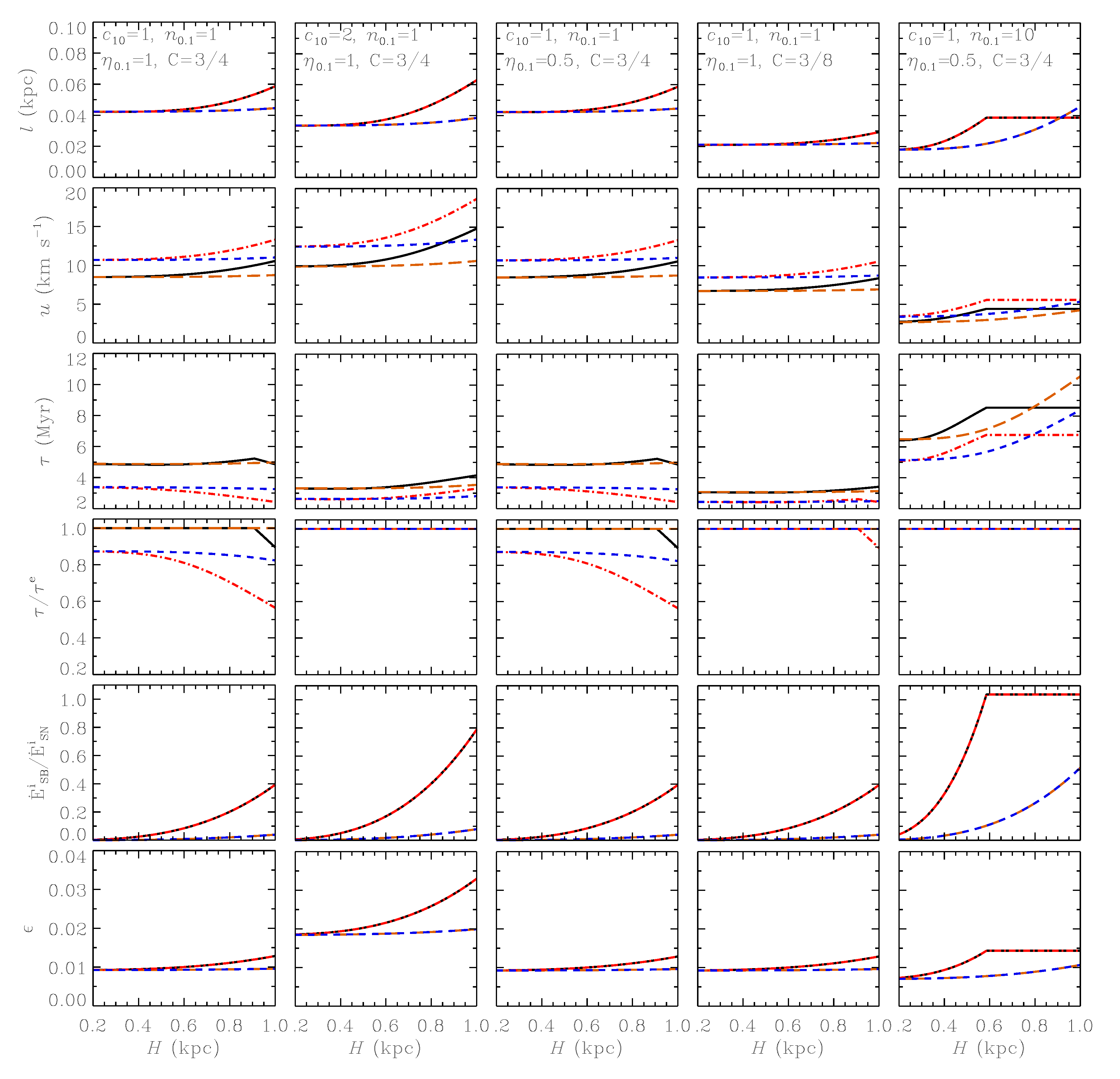
3. Exploration of the Parameter Space
4. Relative Importance of Isolated SNe and SBs and Effect of SN Clustering
5. Varying the Parameter
5.1. Motivation for Reducing
5.2. Results
5.3. Two-Layer Model
6. Limitations and Opportunities for Extending the Model
7. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Armstrong, J.W.; Rickett, B.J.; Spangler, S.R. Electron density power spectrum in the local interstellar medium. Astrophys J. 1995, 443, 209–221. [Google Scholar] [CrossRef]
- Chepurnov, A.; Lazarian, A. Extending the Big Power Law in the Sky with Turbulence Spectra from Wisconsin Hα Mapper Data. Astrophys J. 2010, 710, 853–858. [Google Scholar] [CrossRef]
- Ruzmaikin, A.A.; Shukurov, A.M.; Sokoloff, D.D. Magnetic Fields of Galaxies; Kluwer: Dordrecht, The Netherlands, 1988. [Google Scholar]
- Beck, R.; Brandenburg, A.; Moss, D.; Shukurov, A.; Sokoloff, D. Galactic Magnetism: Recent Developments and Perspectives. Ann. Rev. Astron. Astrophys. 1996, 34, 155–206. [Google Scholar] [CrossRef]
- Brandenburg, A.; Subramanian, K. Astrophysical magnetic fields and nonlinear dynamo theory. Phys. Rep. 2005, 417, 1–209. [Google Scholar] [CrossRef]
- Shukurov, A. Galactic dynamos. In Mathematical Aspects of Natural Dynamos; Dormy, E., Soward, A.M., Eds.; Chapman & Hall/CRC: Boca Raton, FL, USA, 2007; pp. 313–359. [Google Scholar]
- Beck, R.; Chamandy, L.; Elson, E.; Blackman, E.G. Synthesizing Observations and Theory to Understand Galactic Magnetic Fields: Progress and Challenges. Galaxies 2019, 8, 4. [Google Scholar] [CrossRef]
- Klessen, R.S.; Glover, S.C.O. Physical Processes in the Interstellar Medium. arXiv 2014, arXiv:1412.5182. [Google Scholar]
- Krumholz, M.R.; Burkhart, B.; Forbes, J.C.; Crocker, R.M. A unified model for galactic discs: Star formation, turbulence driving, and mass transport. Mon. Not. R. Astron. Soc. 2018, 477, 2716–2740. [Google Scholar] [CrossRef]
- Bacchini, C.; Fraternali, F.; Iorio, G.; Pezzulli, G.; Marasco, A.; Nipoti, C. Evidence for supernova feedback sustaining gas turbulence in nearby star-forming galaxies. arXiv 2020, arXiv:2006.10764. [Google Scholar]
- Leitherer, C.; Schaerer, D.; Goldader, J.D.; Delgado, R.M.G.; Robert, C.; Kune, D.F.; de Mello, D.F.; Devost, D.; Heckman, T.M. Starburst99: Synthesis Models for Galaxies with Active Star Formation. Astrophys. J. Suppl. Ser. 1999, 123, 3–40. [Google Scholar] [CrossRef]
- El-Badry, K.; Ostriker, E.C.; Kim, C.G.; Quataert, E.; Weisz, D.R. Evolution of supernovae-driven superbubbles with conduction and cooling. Mon. Not. R. Astron. Soc. 2019, 490, 1961–1990. [Google Scholar] [CrossRef]
- Kim, J.G.; Kim, W.T.; Ostriker, E.C. Modeling UV Radiation Feedback from Massive Stars. II. Dispersal of Star-forming Giant Molecular Clouds by Photoionization and Radiation Pressure. Astrophys J. 2018, 859, 68. [Google Scholar] [CrossRef]
- Mac Low, M.M.; Klessen, R.S. Control of star formation by supersonic turbulence. Rev. Mod. Phys. 2004, 76, 125–194. [Google Scholar] [CrossRef]
- Elmegreen, B.G.; Scalo, J. Interstellar Turbulence I: Observations and Processes. Ann. Rev. Astron. Astrophys. 2004, 42, 211–273. [Google Scholar] [CrossRef]
- Falceta-Gonçalves, D.; Kowal, G.; Falgarone, E.; Chian, A.C.L. Turbulence in the interstellar medium. Nonlinear Process. Geophys. 2014, 21, 587–604. [Google Scholar] [CrossRef]
- Falceta-Gonçalves, D.; Bonnell, I.; Kowal, G.; Lépine, J.R.D.; Braga, C.A.S. The onset of large-scale turbulence in the interstellar medium of spiral galaxies. Mon. Not. R. Astron. Soc. 2015, 446, 973–989. [Google Scholar] [CrossRef]
- Vázquez-Semadeni, E. Interstellar MHD Turbulence and Star Formation. In Magnetic Fields in Diffuse Media; Lazarian, A., de Gouveia Dal Pino, E.M., Melioli, C., Eds.; Springer: Berlin, Germany, 2015; Volume 407, p. 401. [Google Scholar] [CrossRef]
- Schmidt, T.M.; Bigiel, F.; Klessen, R.S.; de Blok, W.J.G. Radial gas motions in The HI Nearby Galaxy Survey (THINGS). arXiv 2016, arXiv:1601.01689. [Google Scholar]
- Sellwood, J.A.; Balbus, S.A. Differential Rotation and Turbulence in Extended H I Disks. Astrophys J. 1999, 511, 660–665. [Google Scholar] [CrossRef]
- Norman, C.A.; Ferrara, A. The Turbulent Interstellar Medium: Generalizing to a Scale-dependent Phase Continuum. Astrophys J. 1996, 467, 280. [Google Scholar] [CrossRef]
- Elmegreen, B.G.; Kim, S.; Staveley-Smith, L. A Fractal Analysis of the H I Emission from the Large Magellanic Cloud. Astrophys J. 2001, 548, 749–769. [Google Scholar] [CrossRef]
- Stanimirović, S.; Lazarian, A. Velocity and Density Spectra of the Small Magellanic Cloud. Astrophys J. Lett. 2001, 551, L53–L56. [Google Scholar] [CrossRef]
- Haverkorn, M.; Gaensler, B.M.; McClure-Griffiths, N.M.; Dickey, J.M.; Green, A.J. Magnetic Fields and Ionized Gas in the Inner Galaxy: An Outer Scale for Turbulence and the Possible Role of H II Regions. Astrophys J. 2004, 609, 776–784. [Google Scholar] [CrossRef]
- Dib, S.; Burkert, A. On the Origin of the H I Holes in the Interstellar Medium of Dwarf Irregular Galaxies. Astrophys J. 2005, 630, 238–249. [Google Scholar] [CrossRef][Green Version]
- Chepurnov, A.; Lazarian, A.; Stanimirović, S.; Heiles, C.; Peek, J.E.G. Velocity Spectrum for H I at High Latitudes. Astrophys J. 2010, 714, 1398–1406. [Google Scholar] [CrossRef]
- Dutta, P.; Begum, A.; Bharadwaj, S.; Chengalur, J.N. Probing interstellar turbulence in spiral galaxies using H I power spectrum analysis. New Astron. 2013, 19, 89–98. [Google Scholar] [CrossRef]
- Schober, J.; Schleicher, D.R.G.; Klessen, R.S. Galactic Synchrotron Emission and the Far-infrared-Radio Correlation at High Redshift. Astrophys J. 2016, 827, 109. [Google Scholar] [CrossRef]
- Elstner, D.; Gressel, O. The role of star formation for the galactic dynamo. arXiv 2012, arXiv:1206.5097, p. 151. [Google Scholar]
- Kulkarni, S.R.; Fich, M. The fraction of high velocity dispersion HI in the Galaxy. Astrophys J. 1985, 289, 792–802. [Google Scholar] [CrossRef]
- Chemin, L.; Carignan, C.; Foster, T. H I Kinematics and Dynamics of Messier 31. Astrophys J. 2009, 705, 1395–1415. [Google Scholar] [CrossRef]
- Tamburro, D.; Rix, H.W.; Leroy, A.K.; Mac Low, M.M.; Walter, F.; Kennicutt, R.C.; Brinks, E.; de Blok, W.J.G. What is Driving the H I Velocity Dispersion? Astron. J. 2009, 137, 4424–4435. [Google Scholar] [CrossRef]
- Mogotsi, K.M.; de Blok, W.J.G.; Caldú-Primo, A.; Walter, F.; Ianjamasimanana, R.; Leroy, A.K. Hi and CO Velocity Dispersions in Nearby Galaxies. Astron. J. 2016, 151, 15. [Google Scholar] [CrossRef]
- De Avillez, M.A.; Breitschwerdt, D. The Generation and Dissipation of Interstellar Turbulence: Results from Large-Scale High-Resolution Simulations. Astrophys J. Lett. 2007, 665, L35–L38. [Google Scholar] [CrossRef]
- Gressel, O.; Ziegler, U.; Elstner, D.; Rüdiger, G. Dynamo coefficients from local simulations of the turbulent ISM. Astronomische Nachrichten 2008, 329, 619. [Google Scholar] [CrossRef]
- Gent, F.A.; Shukurov, A.; Fletcher, A.; Sarson, G.R.; Mantere, M.J. The supernova-regulated ISM - I. The multiphase structure. Mon. Not. R. Astron. Soc. 2013, 432, 1396–1423. [Google Scholar] [CrossRef]
- Hollins, J.F.; Sarson, G.R.; Shukurov, A.; Fletcher, A.; Gent, F.A. Supernova-regulated ISM. V. Space and Time Correlations. Astrophys J. 2017, 850, 4. [Google Scholar] [CrossRef]
- Cox, D.P. The diffuse interstellar medium. The Interstellar Medium in Galaxies. In Astrophysics and Space Science Library; Thronson, H.A., Jr., Shull, J.M., Eds.; SPringer: Berlin, Germany, 1990; Volume 161, pp. 181–200. [Google Scholar]
- Breitschwerdt, D.; de Avillez, M.A.; Freyberg, M.J. Keynote Lecture: Galactic and Extragalactic Bubbles. arXiv 2005, arXiv:astro-ph/0501586. [Google Scholar]
- Ferrière, K.M. The interstellar environment of our galaxy. Rev. Mod. Phys. 2001, 73, 1031–1066. [Google Scholar] [CrossRef]
- Woltjer, L. Supernova Remnants. Ann. Rev. Astron. Astrophys. 1972, 10, 129. [Google Scholar] [CrossRef]
- Cox, D.P. Cooling and Evolution of a Supernova Remnant. Astrophys J. 1972, 178, 159–168. [Google Scholar] [CrossRef]
- Dyson, J.E.; Williams, D.A. The Physics of the Interstellar Medium; CRC Press: Boca Raton, FL, USA, 1997. [Google Scholar]
- Cioffi, D.F.; McKee, C.F.; Bertschinger, E. Dynamics of radiative supernova remnants. Astrophys J. 1988, 334, 252–265. [Google Scholar] [CrossRef]
- Kim, C.G.; Ostriker, E.C. Momentum Injection by Supernovae in the Interstellar Medium. Astrophys J. 2015, 802, 99. [Google Scholar] [CrossRef]
- Martizzi, D.; Faucher-Giguère, C.A.; Quataert, E. Supernova feedback in an inhomogeneous interstellar medium. Mon. Not. R. Astron. Soc. 2015, 450, 504–522. [Google Scholar] [CrossRef]
- Mac Low, M.M.; McCray, R. Superbubbles in disk galaxies. Astrophys J. 1988, 324, 776–785. [Google Scholar] [CrossRef]
- Weaver, R.; McCray, R.; Castor, J.; Shapiro, P.; Moore, R. Interstellar bubbles. II - Structure and evolution. Astrophys J. 1977, 218, 377–395. [Google Scholar] [CrossRef]
- Weaver, R.; McCray, R.; Castor, J.; Shapiro, P.; Moore, R. Errata: Interstellar Bubbles. II. Structure and Evolution. Astrophys J. 1978, 220, 742. [Google Scholar] [CrossRef]
- Yadav, N.; Mukherjee, D.; Sharma, P.; Nath, B.B. How multiple supernovae overlap to form superbubbles. Mon. Not. R. Astron. Soc. 2017, 465, 1720–1740. [Google Scholar] [CrossRef]
- Fierlinger, K.M.; Burkert, A.; Ntormousi, E.; Fierlinger, P.; Schartmann, M.; Ballone, A.; Krause, M.G.H.; Diehl, R. Stellar feedback efficiencies: Supernovae versus stellar winds. Mon. Not. R. Astron. Soc. 2016, 456, 710–730. [Google Scholar] [CrossRef]
- Stil, J.; Wityk, N.; Ouyed, R.; Taylor, A.R. Three-dimensional Simulations of Magnetized Superbubbles: New Insights into the Importance of MHD Effects on Observed Quantities. Astrophys J. 2009, 701, 330–347. [Google Scholar] [CrossRef]
- Ntormousi, E.; Dawson, J.R.; Hennebelle, P.; Fierlinger, K. The role of magnetic fields in the structure and interaction of supershells. Astron. Astrophys. 2017, 599, A94. [Google Scholar] [CrossRef]
- Lockman, F.J.; Hobbs, L.M.; Shull, J.M. The extent of the local H I halo. Astrophys J. 1986, 301, 380–394. [Google Scholar] [CrossRef]
- Mac Low, M.M.; McCray, R.; Norman, M.L. Superbubble blowout dynamics. Astrophys J. 1989, 337, 141–154. [Google Scholar] [CrossRef]
- Mac Low, M.M.; Ferrara, A. Starburst-driven Mass Loss from Dwarf Galaxies: Efficiency and Metal Ejection. Astrophys J. 1999, 513, 142–155. [Google Scholar] [CrossRef]
- Higdon, J.C.; Lingenfelter, R.E. OB Associations, Supernova-generated Superbubbles, and the Source of Cosmic Rays. Astrophys J. 2005, 628, 738–749. [Google Scholar] [CrossRef]
- Thornton, K.; Gaudlitz, M.; Janka, H.T.; Steinmetz, M. Energy Input and Mass Redistribution by Supernovae in the Interstellar Medium. Astrophys J. 1998, 500, 95–119. [Google Scholar] [CrossRef]
- Hill, A.S.; Benjamin, R.A.; Kowal, G.; Reynolds, R.J.; Haffner, L.M.; Lazarian, A. The Turbulent Warm Ionized Medium: Emission Measure Distribution and MHD Simulations. Astrophys J. 2008, 686, 363–378. [Google Scholar] [CrossRef]
- Iacobelli, M.; Burkhart, B.; Haverkorn, M.; Lazarian, A.; Carretti, E.; Staveley-Smith, L.; Gaensler, B.M.; Bernardi, G.; Kesteven, M.J.; Poppi, S. Galactic interstellar turbulence across the southern sky seen through spatial gradients of the polarization vector. Astron. Astrophys. 2014, 566, A5. [Google Scholar] [CrossRef]
- Kim, C.G.; Ostriker, E.C. Vertical Equilibrium, Energetics, and Star Formation Rates in Magnetized Galactic Disks Regulated by Momentum Feedback from Supernovae. Astrophys J. 2015, 815, 67. [Google Scholar] [CrossRef]
- Monin, A.S.; Yaglom, A.M. Statistical Fluid Mechanics: Mechanics of Turbulence; The MIT Press: Cambridge, MA, USA, 1975; Volume 2. [Google Scholar]
- Brandenburg, A.; Nordlund, Å. Astrophysical turbulence modeling. Rep. Prog. Phys. 2011, 74, 046901. [Google Scholar] [CrossRef]
- Schober, J.; Schleicher, D.R.G.; Federrath, C.; Bovino, S.; Klessen, R.S. Saturation of the turbulent dynamo. Phys. Rev. E 2015, 92, 023010. [Google Scholar] [CrossRef]
- Fouxon, I.; Mond, M. The role of the sonic scale in the growth of magnetic field in compressible turbulence. Mon. Not. R. Astron. Soc. 2020, 493, 4400–4408. [Google Scholar] [CrossRef]
- Wilkin, S.L.; Barenghi, C.F.; Shukurov, A. Magnetic Structures Produced by the Small-Scale Dynamo. Phys. Rev. Lett. 2007, 99, 134501. [Google Scholar] [CrossRef]
- McKee, C.F.; Cowie, L.L. The evaporation of spherical clouds in a hot gas. II. Effects of radiation. Astrophys J. 1977, 215, 213–225. [Google Scholar] [CrossRef]
- Kim, C.G.; Ostriker, E.C.; Raileanu, R. Superbubbles in the Multiphase ISM and the Loading of Galactic Winds. Astrophys J. 2017, 834, 25. [Google Scholar] [CrossRef]
- Dickey, J.M.; Lockman, F.J. H I in the Galaxy. Ann. Rev. Astron. Astrophys. 1990, 28, 215–261. [Google Scholar] [CrossRef]
- De Avillez, M.A.; Breitschwerdt, D. Volume filling factors of the ISM phases in star forming galaxies. I. The role of the disk-halo interaction. Astron. Astrophys. 2004, 425, 899–911. [Google Scholar] [CrossRef]
- Spitzer, L., Jr. Acoustic waves in supernova remnants. Astrophys J. 1982, 262, 315–321. [Google Scholar] [CrossRef]
- Bykov, A.M.; Toptygin, I.N. Effect of shocks on interstellar turbulence and cosmic-ray dynamics. Astrophys. Space Sci. 1987, 138, 341–354. [Google Scholar] [CrossRef]
- Zhou, H.; Blackman, E.G. Some consequences of shear on galactic dynamos with helicity fluxes. arXiv 2017, arXiv:1702.03560. [Google Scholar] [CrossRef]
- Oey, M.S.; Clarke, C.J. The superbubble size distribution in the interstellar medium of galaxies. Mon. Not. R. Astron. Soc. 1997, 289. [Google Scholar] [CrossRef]
- Ferriere, K. Alpha-tensor and diffusivity tensor due to supernovae and superbubbles in the Galactic disk. Astron. Astrophys. 1998, 335, 488–499. [Google Scholar]
- Nath, B.B.; Das, P.; Oey, M.S. Size distribution of superbubbles. Mon. Not. R. Astron. Soc. 2020, 493, 1034–1043. [Google Scholar] [CrossRef]
- Evirgen, C.C.; Gent, F.A.; Shukurov, A.; Fletcher, A.; Bushby, P.J. The supernova-regulated ISM - VI. Magnetic effects on the structure of the interstellar medium. Mon. Not. R. Astron. Soc. 2019, 488, 5065–5074. [Google Scholar] [CrossRef]
- Chamandy, L.; Shukurov, A.; Subramanian, K. Magnetic spiral arms and galactic outflows. Mon. Not. R. Astron. Soc. 2015, 446, L6–L10. [Google Scholar] [CrossRef]
- Chamandy, L. An analytical dynamo solution for large-scale magnetic fields of galaxies. Mon. Not. R. Astron. Soc. 2016, 462, 4402–4415. [Google Scholar] [CrossRef]
- Chamandy, L.; Shukurov, A.; Taylor, A.R. Statistical Tests of Galactic Dynamo Theory. Astrophys J. 2016, 833, 43. [Google Scholar] [CrossRef]
- Rodrigues, L.F.S.; Chamandy, L.; Shukurov, A.; Baugh, C.M.; Taylor, A.R. Evolution of galactic magnetic fields. Mon. Not. R. Astron. Soc. 2019, 483, 2424–2440. [Google Scholar] [CrossRef]
- Gressel, O.; Elstner, D. On the spatial and temporal non-locality of dynamo mean-field effects in supersonic interstellar turbulence. Mon. Not. R. Astron. Soc. 2020, 494, 1180–1188. [Google Scholar] [CrossRef]
- Yoo, H.; Cho, J. Effects of Multiple-scale Driving on Turbulence Statistics. Astrophys J. 2014, 780, 99. [Google Scholar] [CrossRef][Green Version]
| 1 | Elstner and Gressel [29] used MHD simulations of the local ISM to obtain empirical scaling relations for certain turbulent transport coefficients, with independent parameters being the star formation rate surface density, midplane gas density, and angular velocity of gas about the galactic centre. These could potentially be combined with standard analytic expressions for the turbulent transport coefficients to obtain scaling relations for and u. |
| 2 | Fierlinger et al. [51] performed 1D simulations of SN explosions of massive single stars in a dense ambient medium ∼, and found that the preceding wind-blown bubble phase leads to a strong overall reduction in radiative cooling losses. Consistent with the works mentioned above, they find that the importance of cooling depends on resolution, and argue that numerical diffusive mixing in their simulations approximates mixing by turbulent diffusion in nature. |
| 3 | Alternatively, we could have assumed that SNRs and SBs break up when their expansion velocity reduces to u. This would complicate the model by introducing an additional feedback, and is not expected to lead to important differences, since is of order unity (Section 3). As such, we leave this idea for future work. |
| 4 | The arguments can be adapted to other spectra. One possibility is to model the spectrum as a broken power law with a different spectral index, say , for scales larger than the sonic scale , and for scales smaller than [64,65]. However, the effect on the estimates provided would be rather negligible, particularly considering the myriad of other uncertainties and assumptions on which our model relies. |
| 5 | An extra factor greater than 1 and could be included in the numerator to account for the expectation that some of the injected energy is converted to magnetic energy via dynamo action. Given that we have so far neglected magnetic fields, we neglect this factor here; it would have the mild effect of reducing u by at most about 10%. |
| 6 | The proportionality constant would depend on the stellar mass function and contain the scale height of the SN distribution. |
| 7 | Note that we ignore possible correlations between the underlying parameters of the model. |
| 8 | Yoo and Cho [83] study MHD simulations with forcing on two scales and find that even a relatively small amount of energy injection on the larger scale can have important effects on the properties of the turbulence. |



| Usage | Symbol | Unit | Range | Fiducial | |
|---|---|---|---|---|---|
| Ambient sound speed | SN & SB | 10–20 | 10 | ||
| Ambient gas number density | SN & SB | n | –1 | ||
| SN rate per unit volume | SN & SB | 25–100 | 50 | ||
| Initial SN energy | SN & SB | – | |||
| Factor used in estimate of integral scale | SN & SB | C | – | –1 | |
| Fraction of SNe clustered into OB associations | SN & SB | – | – | ||
| Disk scale height | SB | H | –1 | ||
| Number of SNe residing in an SB | SB | – | – | ||
| Fraction of the SB energy that is mechanical | SB | – | – | ||
| SB horiz. radius at blowout, as fraction of H | SB | – | –1 | 1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chamandy, L.; Shukurov, A. Parameters of the Supernova-Driven Interstellar Turbulence. Galaxies 2020, 8, 56. https://doi.org/10.3390/galaxies8030056
Chamandy L, Shukurov A. Parameters of the Supernova-Driven Interstellar Turbulence. Galaxies. 2020; 8(3):56. https://doi.org/10.3390/galaxies8030056
Chicago/Turabian StyleChamandy, Luke, and Anvar Shukurov. 2020. "Parameters of the Supernova-Driven Interstellar Turbulence" Galaxies 8, no. 3: 56. https://doi.org/10.3390/galaxies8030056
APA StyleChamandy, L., & Shukurov, A. (2020). Parameters of the Supernova-Driven Interstellar Turbulence. Galaxies, 8(3), 56. https://doi.org/10.3390/galaxies8030056





