Magnetism Science with the Square Kilometre Array
Abstract
1. Introduction
2. SKA Magnetism Science Cases
2.1. Large-Scale Structure and Cosmology
2.1.1. The Cosmic Web
2.1.2. Early Universe and the Epoch of Reionization
2.1.3. Galaxy Clusters
2.1.4. Dark Matter
2.1.5. FRBs
2.2. Individual Galaxies
2.2.1. Normal and Star-Forming Galaxies
2.2.2. Active Galactic Nuclei
2.3. Galactic and Sub-Galactic Scale Fields
2.3.1. The Milky Way
2.3.2. The Interstellar Medium and Star Formation
3. Pathfinder Progress
3.1. Science Capability from New Technology
3.1.1. Phased Array Feeds
3.1.2. Wideband Single Pixel Feeds
3.1.3. Aperture Arrays
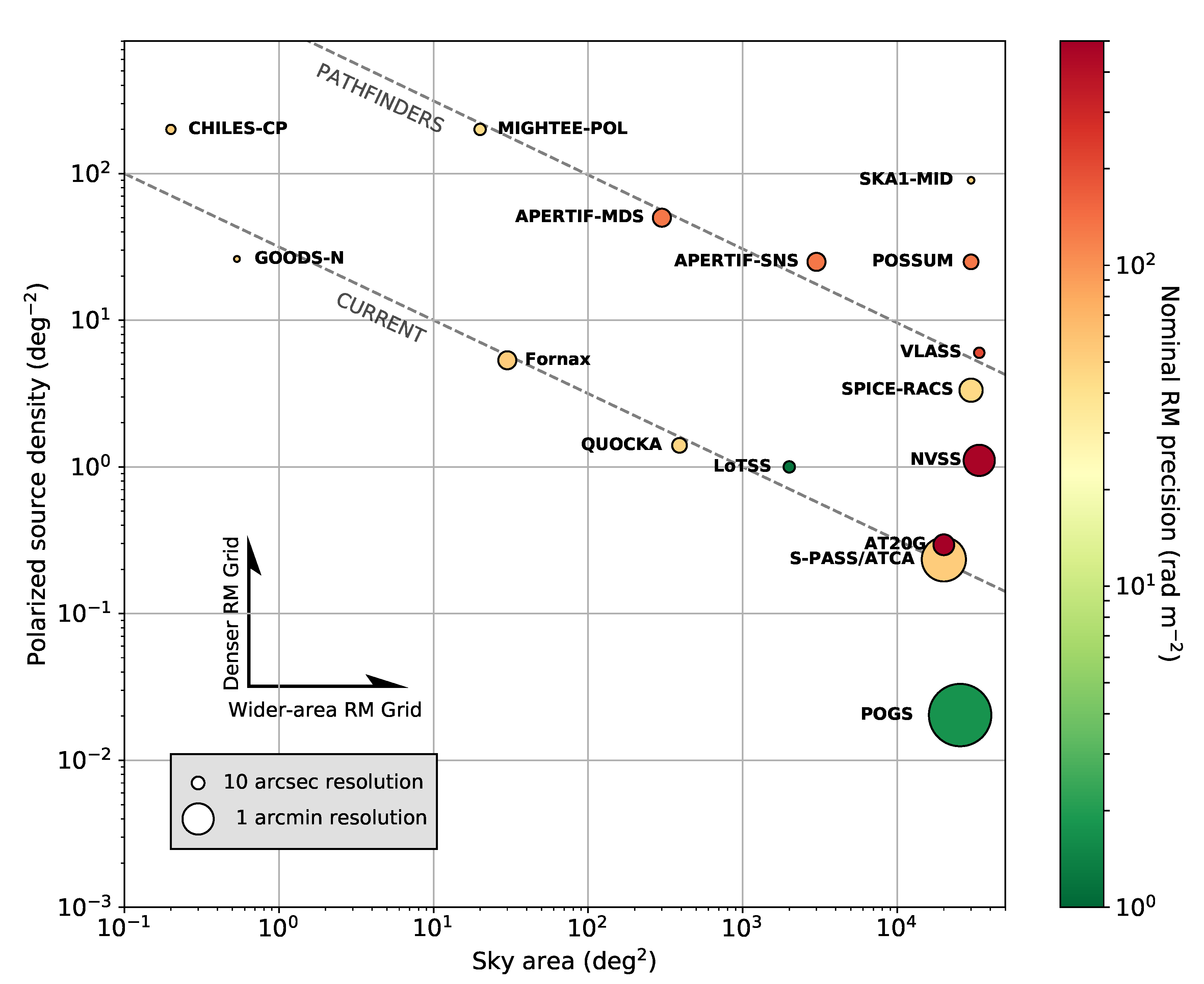
3.2. Upcoming Magnetism Projects
4. Technical Considerations
4.1. Calibration and Widefield Imaging
4.2. Polarization-Specific Processing
4.3. Getting to the Science: Analysis Tools
5. Survey Specifications
5.1. An SKA1-MID RM Grid Survey
5.2. Additional Considerations
6. Looking Forward
6.1. SKA Data Challenges
6.2. SKA Regional Centres
- A catalogue of polarisation and Faraday rotation properties for each detected polarised component, using a standard format 14;
- A cross-listing of detected polarised components matched to their component or source counterparts from total intensity;
- “Coarse” image cubes of , covering the entire survey area at modest (∼1 MHz) spectral resolution;
- Possible “fine” image cubes of , covering some subset of the sky at high spectral resolution (up to the maximum spectral resolution that will be available over the full bandwidth, 13.4 kHz [251]);
- Cubes of Faraday depth, either cut-outs around detected sources or covering the entire sky;
- Images of the peak Faraday depth and associated polarized intensity.
7. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gaensler, B.M.; Beck, R.; Feretti, L. The origin and evolution of cosmic magnetism. New Astron. Rev. 2004, 48, 1003–1012. [Google Scholar] [CrossRef]
- Feretti, L.; Burigana, C.; Enßlin, T.A. Diffuse radio emission from the intracluster medium. New Astron. Rev. 2004, 48, 1137–1144. [Google Scholar] [CrossRef]
- Feretti, L.; Johnston-Hollitt, M. Magnetic fields in clusters of galaxies. New Astron. Rev. 2004, 48, 1145–1150. [Google Scholar] [CrossRef]
- Beck, R.; Gaensler, B.M. Observations of magnetic fields in the Milky Way and in nearby galaxies with a Square Kilometre Array. New Astron. Rev. 2004, 48, 1289–1304. [Google Scholar] [CrossRef]
- Johnston-Hollitt, M.; Govoni, F.; Beck, R.; Dehghan, S.; Pratley, L.; Akahori, T.; Heald, G.; Agudo, I.; Bonafede, A.; Carretti, E.; et al. Using SKA Rotation Measures to Reveal the Mysteries of the Magnetised Universe. In Advancing Astrophysics with the Square Kilometre Array (AASKA14); Sissa Medialab: Trieste, Italy, 2015; p. 92. [Google Scholar]
- Agudo, I.; Boettcher, M.; Falcke, H.D.E.; Georganopoulos, M.; Ghisellini, G.; Giovannini, G.; Giroletti, M.; Gurvits, L.; Gómez, J.L.; Laing, R.; et al. Studies of Relativistic Jets in Active Galactic Nuclei with SKA. In Advancing Astrophysics with the Square Kilometre Array (AASKA14); Sissa Medialab: Trieste, Italy, 2015; p. 93. [Google Scholar]
- Gaensler, B.; Agudo, I.; Akahori, T.; Banfield, J.; Beck, R.; Carretti, E.; Farnes, J.; Haverkorn, M.; Heald, G.; Jones, D.; et al. Broadband Polarimetry with the Square Kilometre Array: A Unique Astrophysical Probe. In Advancing Astrophysics with the Square Kilometre Array (AASKA14); Sissa Medialab: Trieste, Italy, 2015; p. 103. [Google Scholar]
- Laing, R. Kinematics and Dynamics of kiloparsec-scale Jets in Radio Galaxies with SKA. In Advancing Astrophysics with the Square Kilometre Array (AASKA14); Sissa Medialab: Trieste, Italy, 2015; p. 107. [Google Scholar]
- Peng, B.; Chen, R.R.; Strom, R. Giant radio galaxies as probes of the ambient WHIM in the era of the SKA. In Advancing Astrophysics with the Square Kilometre Array (AASKA14); Sissa Medialab: Trieste, Italy, 2015; p. 109. [Google Scholar]
- Beck, R.; Bomans, D.; Colafrancesco, S.; Dettmar, R.J.; Ferrière, K.; Fletcher, A.; Heald, G.; Heesen, V.; Horellou, C.; Krause, M.; et al. Structure, dynamical impact and origin of magnetic fields in nearby galaxies in the SKA era. In Advancing Astrophysics with the Square Kilometre Array (AASKA14); Sissa Medialab: Trieste, Italy, 2015; p. 94. [Google Scholar]
- Heald, G.; Beck, R.; de Blok, W.J.G.; Dettmar, R.J.; Fletcher, A.; Gaensler, B.; Haverkorn, M.; Heesen, V.; Horellou, C.; Krause, M.; et al. Magnetic Field Tomography in Nearby Galaxies with the Square Kilometre Array. In Advancing Astrophysics with the Square Kilometre Array (AASKA14); Sissa Medialab: Trieste, Italy, 2015; p. 106. [Google Scholar]
- Bonafede, A.; Vazza, F.; Brüggen, M.; Akahori, T.; Carretti, E.; Colafrancesco, S.; Feretti, L.; Ferrari, C.; Giovannini, G.; Govoni, F.; et al. Unravelling the origin of large-scale magnetic fields in galaxy clusters and beyond through Faraday Rotation Measures with the SKA. In Advancing Astrophysics with the Square Kilometre Array (AASKA14); Sissa Medialab: Trieste, Italy, 2015; p. 95. [Google Scholar]
- Johnston-Hollitt, M.; Dehghan, S.; Pratley, L. Using Tailed Radio Galaxies to Probe the Environment and Magnetic Field of Galaxy Clusters in the SKA Era. In Advancing Astrophysics with the Square Kilometre Array (AASKA14); Sissa Medialab: Trieste, Italy, 2015; p. 101. [Google Scholar]
- Govoni, F.; Murgia, M.; Xu, H.; Li, H.; Norman, M.; Feretti, L.; Giovannini, G.; Vacca, V.; Bernardi, G.; Bonafede, A.; et al. Cluster magnetic fields through the study of polarized radio halos in the SKA era. In Advancing Astrophysics with the Square Kilometre Array (AASKA14); Sissa Medialab: Trieste, Italy, 2015; p. 105. [Google Scholar]
- Haverkorn, M.; Akahori, T.; Carretti, E.; Ferrière, K.; Frick, P.; Gaensler, B.; Heald, G.; Johnston-Hollitt, M.; Jones, D.; Landecker, T.; et al. Measuring magnetism in the Milky Way with the Square Kilometre Array. In Advancing Astrophysics with the Square Kilometre Array (AASKA14); Sissa Medialab: Trieste, Italy, 2015; p. 96. [Google Scholar]
- Han, J.L.; van Straten, W.; Lazio, T.J.W.; Deller, A.; Sobey, C.; Xu, J.; Schnitzeler, D.; Imai, H.; Chatterjee, S.; Macquart, J.P.; et al. Three-dimensional Tomography of the Galactic and Extragalactic Magnetoionic Medium with the SKA. In Advancing Astrophysics with the Square Kilometre Array (AASKA14); Sissa Medialab: Trieste, Italy, 2015; p. 41. [Google Scholar]
- Dickinson, C.; Beck, R.; Crocker, R.; Crutcher, R.M.; Davies, R.D.; Ferrière, K.; Fuller, G.; Jaffe, T.R.; Jones, D.; Leahy, P.; et al. SKA studies of in situ synchrotron radiation from molecular clouds. In Advancing Astrophysics with the Square Kilometre Array (AASKA14); Sissa Medialab: Trieste, Italy, 2015; p. 102. [Google Scholar]
- Robishaw, T.; Green, J.; Surcis, G.; Vlemmings, W.H.T.; Richards, A.M.S.; Etoka, S.; Bourke, T.; Fish, V.; Gray, M.D.; Imai, H.; et al. Measuring Magnetic Fields Near and Far with the SKA via the Zeeman Effect. In Advancing Astrophysics with the Square Kilometre Array (AASKA14); Sissa Medialab: Trieste, Italy, 2015; p. 110. [Google Scholar]
- Vazza, F.; Ferrari, C.; Bonafede, A.; Brüggen, M.; Gheller, C.; Braun, R.; Brown, S. Filaments of the radio cosmic web: Opportunities and challenges for SKA. In Advancing Astrophysics with the Square Kilometre Array (AASKA14); Sissa Medialab: Trieste, Italy, 2015; p. 97. [Google Scholar]
- Giovannini, G.; Bonafede, A.; Brown, S.; Feretti, L.; Ferrari, C.; Gitti, M.; Govoni, F.; Murgia, M.; Vacca, V. Mega-parsec scale magnetic fields in low density regions in the SKA era: Filaments connecting galaxy clusters and groups. In Advancing Astrophysics with the Square Kilometre Array (AASKA14); Sissa Medialab: Trieste, Italy, 2015; p. 104. [Google Scholar]
- Colafrancesco, S.; Regis, M.; Marchegiani, P.; Beck, G.; Beck, R.; Zechlin, H.; Lobanov, A.; Horns, D. Probing the nature of Dark Matter with the SKA. In Advancing Astrophysics with the Square Kilometre Array (AASKA14); Sissa Medialab: Trieste, Italy, 2015; p. 100. [Google Scholar]
- Stil, J.; Keller, B. Stacking for Cosmic Magnetism with SKA Surveys. In Advancing Astrophysics with the Square Kilometre Array (AASKA14); Sissa Medialab: Trieste, Italy, 2015; p. 112. [Google Scholar]
- Taylor, R.; Agudo, I.; Akahori, T.; Beck, R.; Gaensler, B.; Heald, G.; Johnston-Hollitt, M.; Langer, M.; Rudnick, L.; Scaife, A.; et al. SKA Deep Polarization and Cosmic Magnetism. In Advancing Astrophysics with the Square Kilometre Array (AASKA14); Sissa Medialab: Trieste, Italy, 2015; p. 113. [Google Scholar]
- Vacca, V.; Oppermann, N.; Ensslin, T.A.; Selig, M.; Junklewitz, H.; Greiner, M.; Jasche, J.; Hales, C.A.; Reneicke, M.; Carretti, E.; et al. Statistical methods for the analysis of rotation measure grids in large scale structures in the SKA era. In Advancing Astrophysics with the Square Kilometre Array (AASKA14); Sissa Medialab: Trieste, Italy, 2015; p. 114. [Google Scholar]
- Han, J.L. Observing Interstellar and Intergalactic Magnetic Fields. Aunn. Rew. 2017, 55, 111–157. [Google Scholar] [CrossRef]
- Akahori, T.; Nakanishi, H.; Sofue, Y.; Fujita, Y.; Ichiki, K.; Ideguchi, S.; Kameya, O.; Kudoh, T.; Kudoh, Y.; Machida, M.; et al. Cosmic magnetism in centimetre- and meter-wavelength radio astronomy. Publ. Astron. Soc. Jpn. 2018, 70, R2. [Google Scholar] [CrossRef]
- Heald, G. Synchrotron Radiation and Faraday Rotation. In Magnetic Fields in Diffuse Media; Lazarian, A., de Gouveia Dal Pino, E.M., Melioli, C., Eds.; Astrophysics and Space Science Library; Springer: Basel, Switzerland, 2015; Volume 407, p. 41. [Google Scholar] [CrossRef]
- Crutcher, R.M.; Kemball, A.J. Review of Zeeman Effect Observations of Regions of Star Formation K Zeeman Effect, Magnetic Fields, Star formation, Masers, Molecular clouds. Front. Astron. Space Sci. 2019. [Google Scholar] [CrossRef]
- Robishaw, T. Zeeman Splitting. Galaxies 2020, 8. in preparation. [Google Scholar]
- Carilli, C.L.; Rawlings, S. Motivation, key science projects, standards and assumptions. New Astron. Rev. 2004, 48, 979–984. [Google Scholar] [CrossRef]
- O’Sullivan, S.P.; McClure-Griffiths, N.M.; Feain, I.J.; Gaensler, B.M.; Sault, R.J. Broad-band radio circular polarization spectrum of the relativistic jet in PKS B2126-158. Mon. Not. R. Astron. Soc. 2013, 435, 311–319. [Google Scholar] [CrossRef]
- Gruzinov, A.; Levin, Y. Conversion Measure of Faraday Rotation-Conversion with Application to Fast Radio Bursts. Astrophys. J. 2019, 876, 74. [Google Scholar] [CrossRef]
- Burn, B.J. On the depolarization of discrete radio sources by Faraday dispersion. Mon. Not. R. Astron. Soc. 1966, 133, 67. [Google Scholar] [CrossRef]
- Brentjens, M.A.; de Bruyn, A.G. Faraday rotation measure synthesis. Astron. Astrophys. 2005, 441, 1217–1228. [Google Scholar] [CrossRef]
- Haverkorn, M.; Machida, M.; Akahori, T. Workshop Summary “The Power of Faraday Tomography”. Galaxies 2019, 7, 26. [Google Scholar] [CrossRef]
- Han, J.L.; Manchester, R.N.; van Straten, W.; Demorest, P. Pulsar Rotation Measures and Large-scale Magnetic Field Reversals in the Galactic Disk. Astrophys. J. Suppl. Ser. 2018, 234, 11. [Google Scholar] [CrossRef]
- Cen, R.; Ostriker, J.P. Where Are the Baryons? Astrophys. J. 1999, 514, 1–6. [Google Scholar] [CrossRef]
- Davé, R.; Cen, R.; Ostriker, J.P.; Bryan, G.L.; Hernquist, L.; Katz, N.; Weinberg, D.H.; Norman, M.L.; O’Shea, B. Baryons in the Warm-Hot Intergalactic Medium. Astrophys. J. 2001, 552, 473–483. [Google Scholar] [CrossRef]
- Brown, S.; Vernstrom, T.; Carretti, E.; Dolag, K.; Gaensler, B.M.; Staveley-Smith, L.; Bernardi, G.; Haverkorn, M.; Kesteven, M.; Poppi, S. Limiting magnetic fields in the cosmic web with diffuse radio emission. Mon. Not. R. Astron. Soc. 2017, 468, 4246–4253. [Google Scholar] [CrossRef]
- Vernstrom, T.; Gaensler, B.M.; Brown, S.; Lenc, E.; Norris, R.P. Low-frequency radio constraints on the synchrotron cosmic web. Mon. Not. R. Astron. Soc. 2017, 467, 4914–4936. [Google Scholar] [CrossRef]
- Vacca, V.; Murgia, M.; Govoni, F.; Loi, F.; Vazza, F.; Finoguenov, A.; Carretti, E.; Feretti, L.; Giovannini, G.; Concu, R.; et al. Observations of a nearby filament of galaxy clusters with the Sardinia Radio Telescope. Mon. Not. R. Astron. Soc. 2018, 479, 776–806. [Google Scholar] [CrossRef]
- Vernstrom, T.; Gaensler, B.M.; Rudnick, L.; Andernach, H. Differences in Faraday Rotation between Adjacent Extragalactic Radio Sources as a Probe of Cosmic Magnetic Fields. Astrophys. J. 2019, 878, 92. [Google Scholar] [CrossRef]
- Govoni, F.; Orrù, E.; Bonafede, A.; Iacobelli, M.; Paladino, R.; Vazza, F.; Murgia, M.; Vacca, V.; Giovannini, G.; Feretti, L.; et al. A radio ridge connecting two galaxy clusters in a filament of the cosmic web. Science 2019, 364, 981–984. [Google Scholar] [CrossRef] [PubMed]
- Pshirkov, M.S.; Tinyakov, P.G.; Urban, F.R. New Limits on Extragalactic Magnetic Fields from Rotation Measures. Phys. Rev. Lett. 2016, 116, 191302. [Google Scholar] [CrossRef] [PubMed]
- Ravi, V.; Shannon, R.M.; Bailes, M.; Bannister, K.; Bhandari, S.; Bhat, N.D.R.; Burke-Spolaor, S.; Caleb, M.; Flynn, C.; Jameson, A.; et al. The magnetic field and turbulence of the cosmic web measured using a brilliant fast radio burst. Science 2016, 354, 1249–1252. [Google Scholar] [CrossRef]
- Hackstein, S.; Brüggen, M.; Vazza, F.; Gaensler, B.M.; Heesen, V. Fast radio burst dispersion measures and rotation measures and the origin of intergalactic magnetic fields. Mon. Not. R. Astron. Soc. 2019, 488, 4220–4238. [Google Scholar] [CrossRef]
- O’Sullivan, S.P.; Machalski, J.; Van Eck, C.L.; Heald, G.; Brüggen, M.; Fynbo, J.P.U.; Heintz, K.E.; Lara-Lopez, M.A.; Vacca, V.; Hardcastle, M.J.; et al. The intergalactic magnetic field probed by a giant radio galaxy. Astron. Astrophys. 2019, 622, A16. [Google Scholar] [CrossRef]
- O’Sullivan, S.P.; Brüggen, M.; Vazza, F.; Carretti, E.; Locatelli, N.; Stuardi, C.; Vacca, V.; Vernstrom, T.; Heald, G.; Horellou, C.; et al. New constraints on the magnetization of the cosmic web using LOFAR Faraday rotation observations. arXiv 2020, arXiv:astro-ph.CO/2002.06924. [Google Scholar]
- Akahori, T.; Gaensler, B.M.; Ryu, D. Statistical Techniques for Detecting the Intergalactic Magnetic Field from Large Samples of Extragalactic Faraday Rotation Data. Astrophys. J. 2014, 790, 123. [Google Scholar] [CrossRef]
- Akahori, T.; Ryu, D.; Gaensler, B.M. Fast Radio Bursts as Probes of Magnetic Fields in the Intergalactic Medium. Astrophys. J. 2016, 824, 105. [Google Scholar] [CrossRef]
- Vazza, F.; Brüggen, M.; Gheller, C.; Hackstein, S.; Wittor, D.; Hinz, P.M. Simulations of extragalactic magnetic fields and of their observables. Class. Quantum Gravity 2017, 34, 234001. [Google Scholar] [CrossRef]
- Locatelli, N.; Vazza, F.; Domínguez-Fernández, P. The Challenge of Detecting Intracluster Filaments with Faraday Rotation. Galaxies 2018, 6, 128. [Google Scholar] [CrossRef]
- Vazza, F.; Brüggen, M.; Hinz, P.M.; Wittor, D.; Locatelli, N.; Gheller, C. Probing the origin of extragalactic magnetic fields with Fast Radio Bursts. Mon. Not. R. Astron. Soc. 2018, 480, 3907–3915. [Google Scholar] [CrossRef]
- Macquart, J.P.; Keane, E.; Grainge, K.; McQuinn, M.; Fender, R.; Hessels, J.; Deller, A.; Bhat, R.; Breton, R.; Chatterjee, S.; et al. Fast Transients at Cosmological Distances with the SKA. In Advancing Astrophysics with the Square Kilometre Array (AASKA14); Sissa Medialab: Trieste, Italy, 2015; p. 55. [Google Scholar]
- Subramanian, K. The origin, evolution and signatures of primordial magnetic fields. Rep. Prog. Phys. 2016, 79, 076901. [Google Scholar] [CrossRef] [PubMed]
- Schleicher, D.R.G.; Miniati, F. Primordial magnetic field constraints from the end of reionization. Mon. Not. R. Astron. Soc. 2011, 418, L143–L147. [Google Scholar] [CrossRef]
- Widrow, L.M.; Ryu, D.; Schleicher, D.R.G.; Subramanian, K.; Tsagas, C.G.; Treumann, R.A. The First Magnetic Fields. Space Sci. Rev. 2012, 166, 37–70. [Google Scholar] [CrossRef]
- Langer, M.; Durrive, J.B. Magnetizing the Cosmic Web during Reionization. Galaxies 2018, 6, 124. [Google Scholar] [CrossRef]
- Koopmans, L.; Pritchard, J.; Mellema, G.; Aguirre, J.; Ahn, K.; Barkana, R.; van Bemmel, I.; Bernardi, G.; Bonaldi, A.; Briggs, F.; et al. The Cosmic Dawn and Epoch of Reionisation with SKA. In Advancing Astrophysics with the Square Kilometre Array (AASKA14); Sissa Medialab: Trieste, Italy, 2015; p. 1. [Google Scholar]
- Minoda, T.; Hasegawa, K.; Tashiro, H.; Ichiki, K.; Sugiyama, N. Thermal Sunyaev-Zel’dovich Effect in the IGM due to Primordial Magnetic Fields. Galaxies 2018, 6, 143. [Google Scholar] [CrossRef]
- van Weeren, R.J.; de Gasperin, F.; Akamatsu, H.; Brüggen, M.; Feretti, L.; Kang, H.; Stroe, A.; Zandanel, F. Diffuse Radio Emission from Galaxy Clusters. Space Sci. Rev. 2019, 215, 16. [Google Scholar] [CrossRef]
- Govoni, F.; Murgia, M.; Xu, H.; Li, H.; Norman, M.L.; Feretti, L.; Giovannini, G.; Vacca, V. Polarization of cluster radio halos with upcoming radio interferometers. Astron. Astrophys. 2013, 554, A102. [Google Scholar] [CrossRef]
- Kang, H.; Ryu, D. Diffusive Shock Acceleration at Cosmological Shock Waves. Astrophys. J. 2013, 764, 95. [Google Scholar] [CrossRef]
- Brunetti, G.; Lazarian, A. Stochastic reacceleration of relativistic electrons by turbulent reconnection: A mechanism for cluster-scale radio emission? Mon. Not. R. Astron. Soc. 2016, 458, 2584–2595. [Google Scholar] [CrossRef]
- Dolag, K. Properties of Simulated Magnetized Galaxy Clusters. Constructing the Universe with Clusters of Galaxies. arXiv 2000, arXiv:astro-ph/astro-ph/0010149. [Google Scholar]
- Vazza, F.; Brunetti, G.; Brüggen, M.; Bonafede, A. Resolved magnetic dynamo action in the simulated intracluster medium. Mon. Not. R. Astron. Soc. 2018, 474, 1672–1687. [Google Scholar] [CrossRef]
- Vacca, V.; Murgia, M.; Govoni, F.; Enßlin, T.; Oppermann, N.; Feretti, L.; Giovannini, G.; Loi, F. Magnetic Fields in Galaxy Clusters and in the Large-Scale Structure of the Universe. Galaxies 2018, 6, 142. [Google Scholar] [CrossRef]
- Govoni, F.; Murgia, M.; Vacca, V.; Loi, F.; Girardi, M.; Gastaldello, F.; Giovannini, G.; Feretti, L.; Paladino, R.; Carretti, E.; et al. Sardinia Radio Telescope observations of Abell 194. The intra-cluster magnetic field power spectrum. Astron. Astrophys. 2017, 603, A122. [Google Scholar] [CrossRef]
- Loi, F.; Murgia, M.; Govoni, F.; Vacca, V.; Bonafede, A.; Ferrari, C.; Prandoni, I.; Feretti, L.; Giovannini, G.; Li, H. Rotation measure synthesis applied to synthetic SKA images of galaxy clusters. Mon. Not. R. Astron. Soc. 2019, 490, 4841–4857. [Google Scholar] [CrossRef]
- Markevitch, M.; Gonzalez, A.H.; Clowe, D.; Vikhlinin, A.; Forman, W.; Jones, C.; Murray, S.; Tucker, W. Direct Constraints on the Dark Matter Self-Interaction Cross Section from the Merging Galaxy Cluster 1E 0657-56. Astrophys. J. 2004, 606, 819–824. [Google Scholar] [CrossRef]
- Spekkens, K.; Mason, B.S.; Aguirre, J.E.; Nhan, B. A Deep Search for Extended Radio Continuum Emission from Dwarf Spheroidal Galaxies: Implications for Particle Dark Matter. Astrophys. J. 2013, 773, 61. [Google Scholar] [CrossRef]
- Regis, M.; Colafrancesco, S.; Profumo, S.; de Blok, W.; Massardi, M.; Richter, L. Local Group dSph radio survey with ATCA (III): Constraints on Particle Dark Matter. J. Cosmol. Astropart. Phys. 2014, 10, 016. [Google Scholar] [CrossRef]
- Regis, M.; Richter, L.; Colafrancesco, S. Dark matter in the Reticulum II dSph: A radio search. J. Cosmol. Astropart. Phys. 2017, 2017, 025. [Google Scholar] [CrossRef]
- Vollmann, M.; Heesen, V.; Shimwell, T.; Hardcastle, M.J.; Brüggen, M.; Sigl, G.; Röttgering, H. Radio constraints on dark matter annihilation in Canes Venatici I with LOFAR. arXiv 2019, arXiv:1909.12355. [Google Scholar] [CrossRef]
- Cook, R.H.W.; Seymour, N.; Spekkens, K.; Hurley-Walker, N.; Hancock, P.J.; Bell, M.E.; Callingham, J.R.; For, B.Q.; Franzen, T.M.O.; Gaensler, B.M.; et al. Searching for dark matter signals from local dwarf spheroidal galaxies at low radio frequencies in the GLEAM survey. Mon. Not. R. Astron. Soc. 2020, 494, 135–145. [Google Scholar] [CrossRef]
- Lorimer, D.R. A decade of fast radio bursts. Nat. Astron. 2018, 2, 860–864. [Google Scholar] [CrossRef]
- Lorimer, D.R.; Bailes, M.; McLaughlin, M.A.; Narkevic, D.J.; Crawford, F. A Bright Millisecond Radio Burst of Extragalactic Origin. Science 2007, 318, 777. [Google Scholar] [CrossRef]
- Chatterjee, S.; Law, C.J.; Wharton, R.S.; Burke-Spolaor, S.; Hessels, J.W.T.; Bower, G.C.; Cordes, J.M.; Tendulkar, S.P.; Bassa, C.G.; Demorest, P.; et al. A direct localization of a fast radio burst and its host. Nature 2017, 541, 58–61. [Google Scholar] [CrossRef] [PubMed]
- Bannister, K.W.; Deller, A.T.; Phillips, C.; Macquart, J.P.; Prochaska, J.X.; Tejos, N.; Ryder, S.D.; Sadler, E.M.; Shannon, R.M.; Simha, S.; et al. A single fast radio burst localized to a massive galaxy at cosmological distance. Science 2019, 365, 565–570. [Google Scholar] [CrossRef]
- Michilli, D.; Seymour, A.; Hessels, J.W.T.; Spitler, L.G.; Gajjar, V.; Archibald, A.M.; Bower, G.C.; Chatterjee, S.; Cordes, J.M.; Gourdji, K.; et al. An extreme magneto-ionic environment associated with the fast radio burst source FRB 121102. Nature 2018, 553, 182–185. [Google Scholar] [CrossRef]
- Wilkinson, P. The SKA and the Unknown Unknowns. In Advancing Astrophysics with the Square Kilometre Array (AASKA14); Sissa Medialab: Trieste, Italy, 2015; p. 65. [Google Scholar]
- Krumholz, M.R.; Federrath, C. The Role of Magnetic Fields in Setting the Star Formation Rate and the Initial Mass Function. Front. Astron. Space Sci. 2019, 6, 7. [Google Scholar] [CrossRef]
- Beck, R. Magnetic fields in spiral galaxies. Astron. Astrophys. Rev. 2015, 24, 4. [Google Scholar] [CrossRef]
- Arshakian, T.G.; Beck, R.; Krause, M.; Sokoloff, D. Evolution of magnetic fields in galaxies and future observational tests with the Square Kilometre Array. Astron. Astrophys. 2009, 494, 21–32. [Google Scholar] [CrossRef]
- Beck, A.M.; Lesch, H.; Dolag, K.; Kotarba, H.; Geng, A.; Stasyszyn, F.A. Origin of strong magnetic fields in Milky Way-like galactic haloes. Mon. Not. R. Astron. Soc. 2012, 422, 2152–2163. [Google Scholar] [CrossRef]
- Martin-Alvarez, S.; Devriendt, J.; Slyz, A.; Teyssier, R. A three-phase amplification of the cosmic magnetic field in galaxies. Mon. Not. R. Astron. Soc. 2018, 479, 3343–3365. [Google Scholar] [CrossRef]
- Rodrigues, L.F.S.; Chamandy, L.; Shukurov, A.; Baugh, C.M.; Taylor, A.R. Evolution of galactic magnetic fields. Mon. Not. R. Astron. Soc. 2019, 483, 2424–2440. [Google Scholar] [CrossRef]
- Bernet, M.L.; Miniati, F.; Lilly, S.J.; Kronberg, P.P.; Dessauges-Zavadsky, M. Strong magnetic fields in normal galaxies at high redshift. Nature 2008, 454, 302–304. [Google Scholar] [CrossRef] [PubMed]
- Farnes, J.S.; O’Sullivan, S.P.; Corrigan, M.E.; Gaensler, B.M. Faraday Rotation from Magnesium II Absorbers toward Polarized Background Radio Sources. Astrophys. J. 2014, 795, 63. [Google Scholar] [CrossRef]
- Mao, S.A.; Carilli, C.; Gaensler, B.M.; Wucknitz, O.; Keeton, C.; Basu, A.; Beck, R.; Kronberg, P.P.; Zweibel, E. Detection of microgauss coherent magnetic fields in a galaxy five billion years ago. Nat. Astron. 2017, 1, 621–626. [Google Scholar] [CrossRef]
- Sur, S.; Bhat, P.; Subramanian, K. Faraday rotation signatures of fluctuation dynamos in young galaxies. Mon. Not. R. Astron. Soc. 2018, 475, L72–L76. [Google Scholar] [CrossRef]
- Beck, R.; Chamandy, L.; Elson, E.; Blackman, E.G. Synthesizing Observations and Theory to Understand Galactic Magnetic Fields: Progress and Challenges. Galaxies 2019, 8, 4. [Google Scholar] [CrossRef]
- Heald, G.; Braun, R.; Edmonds, R. The Westerbork SINGS survey. II Polarization, Faraday rotation, and magnetic fields. Astron. Astrophys. 2009, 503, 409–435. [Google Scholar] [CrossRef]
- Irwin, J.; Beck, R.; Benjamin, R.A.; Dettmar, R.J.; English, J.; Heald, G.; Henriksen, R.N.; Johnson, M.; Krause, M.; Li, J.T.; et al. Continuum Halos in Nearby Galaxies: An EVLA Survey (CHANG-ES). I. Introduction to the Survey. Astrophys. J. 2012, 144, 43. [Google Scholar] [CrossRef]
- Mulcahy, D.D.; Beck, R.; Heald, G.H. Resolved magnetic structures in the disk-halo interface of NGC 628. Astron. Astrophys. 2017, 600, A6. [Google Scholar] [CrossRef]
- Mulcahy, D.D.; Horneffer, A.; Beck, R.; Krause, M.; Schmidt, P.; Basu, A.; Chyży, K.T.; Dettmar, R.J.; Haverkorn, M.; Heald, G.; et al. Investigation of the cosmic ray population and magnetic field strength in the halo of NGC 891. Astron. Astrophys. 2018, 615, A98. [Google Scholar] [CrossRef]
- Irwin, J.; Damas-Segovia, A.; Krause, M.; Miskolczi, A.; Li, J.; Stein, Y.; English, J.; Henriksen, R.; Beck, R.; Wiegert, T.; et al. CHANG-ES: XVIII—The CHANG-ES Survey and Selected Results. Galaxies 2019, 7, 42. [Google Scholar] [CrossRef]
- Heesen, V.; Buie, E.I.; Huff, C.J.; Perez, L.A.; Woolsey, J.G.; Rafferty, D.A.; Basu, A.; Beck, R.; Brinks, E.; Horellou, C.; et al. Calibrating the relation of low-frequency radio continuum to star formation rate at 1 kpc scale with LOFAR. Astron. Astrophys. 2019, 622, A8. [Google Scholar] [CrossRef]
- Krause, M.; Irwin, J.; Wiegert, T.; Miskolczi, A.; Damas-Segovia, A.; Beck, R.; Li, J.T.; Heald, G.; Müller, P.; Stein, Y.; et al. CHANG-ES. IX. Radio scale heights and scale lengths of a consistent sample of 13 spiral galaxies seen edge-on and their correlations. Astron. Astrophys. 2018, 611, A72. [Google Scholar] [CrossRef]
- Heesen, V.; Krause, M.; Beck, R.; Adebahr, B.; Bomans, D.J.; Carretti, E.; Dumke, M.; Heald, G.; Irwin, J.; Koribalski, B.S.; et al. Radio haloes in nearby galaxies modelled with 1D cosmic ray transport using SPINNAKER. Mon. Not. R. Astron. Soc. 2018, 476, 158–183. [Google Scholar] [CrossRef]
- Bertone, S.; Vogt, C.; Enßlin, T. Magnetic field seeding by galactic winds. Mon. Not. R. Astron. Soc. 2006, 370, 319–330. [Google Scholar] [CrossRef]
- Pakmor, R.; van de Voort, F.; Bieri, R.; Gomez, F.A.; Grand, R.J.J.; Guillet, T.; Marinacci, F.; Pfrommer, C.; Simpson, C.M.; Springel, V. Magnetising the circumgalactic medium of disk galaxies. arXiv 2019, arXiv:1911.11163. [Google Scholar]
- Berlok, T.; Pfrommer, C. The impact of magnetic fields on cold streams feeding galaxies. Mon. Not. R. Astron. Soc. 2019, 489, 3368–3384. [Google Scholar] [CrossRef]
- Vogelsberger, M.; Marinacci, F.; Torrey, P.; Puchwein, E. Cosmological simulations of galaxy formation. Nat. Rev. Phys. 2020, 2, 42–66. [Google Scholar] [CrossRef]
- Mulcahy, D.D.; Horneffer, A.; Beck, R.; Heald, G.; Fletcher, A.; Scaife, A.; Adebahr, B.; Anderson, J.M.; Bonafede, A.; Brüggen, M.; et al. The nature of the low-frequency emission of M 51. First observations of a nearby galaxy with LOFAR. Astron. Astrophys. 2014, 568, A74. [Google Scholar] [CrossRef]
- Neld, A.; Horellou, C.; Mulcahy, D.D.; Beck, R.; Bourke, S.; Carozzi, T.D.; Chyży, K.T.; Conway, J.E.; Farnes, J.S.; Fletcher, A.; et al. Reliable detection and characterization of low-frequency polarized sources in the LOFAR M51 field. Astron. Astrophys. 2018, 617, A136. [Google Scholar] [CrossRef]
- Nikiel-Wroczyński, B.; Berger, A.; Herrera Ruiz, N.; Bomans, D.J.; Blex, S.; Horellou, C.; Paladino, R.; Becker, A.; Miskolczi, A.; Beck, R.; et al. Exploring the properties of low-frequency radio emission and magnetic fields in a sample of compact galaxy groups using the LOFAR Two-Metre Sky Survey (LoTSS). Astron. Astrophys. 2019, 622, A23. [Google Scholar] [CrossRef]
- Kaczmarek, J.F.; Purcell, C.R.; Gaensler, B.M.; McClure-Griffiths, N.M.; Stevens, J. Detection of a Coherent Magnetic Field in the Magellanic Bridge through Faraday Rotation. Mon. Not. R. Astron. Soc. 2017, 467, 1776–1794. [Google Scholar] [CrossRef]
- Basu, A.; Mao, S.A.; Kepley, A.A.; Robishaw, T.; Zweibel, E.G.; Gallagher, J.S., III. Detection of an ∼20 kpc coherent magnetic field in the outskirt of merging spirals: The Antennae galaxies. Mon. Not. R. Astron. Soc. 2017, 464, 1003–1017. [Google Scholar] [CrossRef]
- Ulrich, M.H.; Maraschi, L.; Urry, C.M. Variability of Active Galactic Nuclei. Annu. Rev. 1997, 35, 445–502. [Google Scholar] [CrossRef]
- Balbus, S.A.; Hawley, J.F. A Powerful Local Shear Instability in Weakly Magnetized Disks. I. Linear Analysis. Astrophys. J. 1991, 376, 214. [Google Scholar] [CrossRef]
- Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; Baloković, M.; Barrett, J.; Event Horizon Telescope Collaboration; et al. First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole. Astrophys. J. 2019, 875, L1. [Google Scholar] [CrossRef]
- Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; Baloković, M.; Barrett, J.; Event Horizon Telescope Collaboration; et al. First M87 Event Horizon Telescope Results. VI. The Shadow and Mass of the Central Black Hole. Astrophys. J. 2019, 875, L6. [Google Scholar] [CrossRef]
- Gabuzda, D.C.; Nagle, M.; Roche, N. The jets of AGN as giant coaxial cables. Astron. Astrophys. 2018, 612, A67. [Google Scholar] [CrossRef]
- Furlanetto, S.R.; Loeb, A. Intergalactic Magnetic Fields from Quasar Outflows. Astrophys. J. 2001, 556, 619–634. [Google Scholar] [CrossRef]
- Calzadilla, M.S.; McDonald, M.; Bayliss, M.; Benson, B.A.; Bleem, L.E.; Brodwin, M.; Edge, A.C.; Floyd, B.; Gupta, N.; Hlavacek-Larrondo, J.; et al. Discovery of a Powerful <1061 erg AGN Outburst in the Distant Galaxy Cluster SPT-CLJ0528-5300. Astrophys. J. 2019, 887, L17. [Google Scholar] [CrossRef]
- Giacintucci, S.; Markevitch, M.; Johnston-Hollitt, M.; Wik, D.R.; Wang, Q.H.S.; Clarke, T.E. Discovery of a Giant Radio Fossil in the Ophiuchus Galaxy Cluster. Astrophys. J. 2020, 891, 1. [Google Scholar] [CrossRef]
- Roy, S.; Pramesh Rao, A.; Subrahmanyan, R. Magnetic field near the central region of the Galaxy: Rotation measure of extragalactic sources. Astron. Astrophys. 2008, 478, 435–442. [Google Scholar] [CrossRef][Green Version]
- Xu, J.; Han, J.L. Magnetic fields in the solar vicinity and in the Galactic halo. Mon. Not. R. Astron. Soc. 2019, 486, 4275–4289. [Google Scholar] [CrossRef]
- Sobey, C.; Bilous, A.V.; Grießmeier, J.M.; Hessels, J.W.T.; Karastergiou, A.; Keane, E.F.; Kondratiev, V.I.; Kramer, M.; Michilli, D.; Noutsos, A.; et al. Low-frequency Faraday rotation measures towards pulsars using LOFAR: Probing the 3D Galactic halo magnetic field. Mon. Not. R. Astron. Soc. 2019, 484, 3646–3664. [Google Scholar] [CrossRef]
- Rodrigues, L.F.S.; Sarson, G.R.; Shukurov, A.; Bushby, P.J.; Fletcher, A. The Parker Instability in Disk Galaxies. Astrophys. J. 2016, 816, 2. [Google Scholar] [CrossRef]
- Pakmor, R.; Springel, V. Simulations of magnetic fields in isolated disc galaxies. Mon. Not. R. Astron. Soc. 2013, 432, 176–193. [Google Scholar] [CrossRef]
- Chamandy, L.; Shukurov, A.; Taylor, A.R. New Insights on Galactic Dynamos. arXiv 2018, arXiv:1810.07246. [Google Scholar]
- Brandenburg, A.; Brüggen, M. Hemispheric handedness in the Galactic synchrotron polarization foreground. arXiv 2020, arXiv:2003.14178. [Google Scholar]
- Gaensler, B.M.; Haverkorn, M.; Burkhart, B.; Newton-McGee, K.J.; Ekers, R.D.; Lazarian, A.; McClure-Griffiths, N.M.; Robishaw, T.; Dickey, J.M.; Green, A.J. Low-Mach-number turbulence in interstellar gas revealed by radio polarization gradients. Nature 2011, 478, 214–217. [Google Scholar] [CrossRef] [PubMed]
- Basu, A.; Fletcher, A.; Mao, S.A.; Burkhart, B.; Beck, R.; Schnitzeler, D. An In-depth Investigation of Faraday Depth Spectrum Using Synthetic Observations of Turbulent MHD Simulations. Galaxies 2019, 7, 89. [Google Scholar] [CrossRef]
- Costa, A.H.; Spangler, S.R.; Sink, J.R.; Brown, S.; Mao, S.A. Denser Sampling of the Rosette Nebula with Faraday Rotation Measurements: Improved Estimates of Magnetic Fields in H II Regions. Astrophys. J. 2016, 821, 92. [Google Scholar] [CrossRef]
- West, J.L.; Safi-Harb, S.; Ferrand, G. The connection between supernova remnants and the Galactic magnetic field: An analysis of quasi-parallel and quasi-perpendicular cosmic-ray acceleration for the axisymmetric sample. Astron. Astrophys. 2017, 597, A121. [Google Scholar] [CrossRef]
- Costa, A.H.; Spangler, S.R. A Faraday Rotation Study of the Stellar Bubble and H II Region Associated with the W4 Complex. Astrophys. J. 2018, 865, 65. [Google Scholar] [CrossRef]
- Abbate, F.; Possenti, A.; Tiburzi, C.; Barr, E.; van Straten, W.; Ridolfi, A.; Freire, P. Constraints on the magnetic field in the Galactic halo from globular cluster pulsars. Nat. Astron. 2020. [Google Scholar] [CrossRef]
- Betti, S.K.; Hill, A.S.; Mao, S.A.; Gaensler, B.M.; Lockman, F.J.; McClure-Griffiths, N.M.; Benjamin, R.A. Constraining the Magnetic Field of the Smith High-velocity Cloud Using Faraday Rotation. Astrophys. J. 2019, 871, 215. [Google Scholar] [CrossRef]
- Wolleben, M.; Landecker, T.L.; Carretti, E.; Dickey, J.M.; Fletcher, A.; McClure-Griffiths, N.M.; McConnell, D.; Thomson, A.J.M.; Hill, A.S.; Gaensler, B.M.; et al. The Global Magneto-Ionic Medium Survey: Polarimetry of the Southern Sky from 300 to 480 MHz. Astrophys. J. 2019, 158, 44. [Google Scholar] [CrossRef]
- Carretti, E.; Haverkorn, M.; Staveley-Smith, L.; Bernardi, G.; Gaensler, B.M.; Kesteven, M.J.; Poppi, S.; Brown, S.; Crocker, R.M.; Purcell, C.; et al. S-band Polarization All-Sky Survey (S-PASS): Survey description and maps. Mon. Not. R. Astron. Soc. 2019, 489, 2330–2354. [Google Scholar] [CrossRef]
- Dickey, J.M.; Landecker, T.L.; Thomson, A.J.M.; Wolleben, M.; Sun, X.; Carretti, E.; Douglas, K.; Fletcher, A.; Gaensler, B.M.; Gray, A.; et al. The Galactic Magneto-ionic Medium Survey: Moments of the Faraday Spectra. Astrophys. J. 2019, 871, 106. [Google Scholar] [CrossRef]
- Thomson, A.J.M.; Landecker, T.L.; Dickey, J.M.; McClure-Griffiths, N.M.; Wolleben, M.; Carretti, E.; Fletcher, A.; Federrath, C.; Hill, A.S.; Mao, S.A.; et al. Through thick or thin: Multiple components of the magneto-ionic medium towards the nearby H II region Sharpless 2-27 revealed by Faraday tomography. Mon. Not. R. Astron. Soc. 2019, 487, 4751–4767. [Google Scholar] [CrossRef]
- Farrar, G.R.; Jansson, R.; Feain, I.J.; Gaensler, B.M. Galactic magnetic deflections and Centaurus A as a UHECR source. J. Cosmol. Astropart. Phys. 2013, 2013, 023. [Google Scholar] [CrossRef]
- Boulanger, F.; Enßlin, T.; Fletcher, A.; Girichides, P.; Hackstein, S.; Haverkorn, M.; Hörandel, J.R.; Jaffe, T.; Jasche, J.; Kachelrieß, M.; et al. IMAGINE: A comprehensive view of the interstellar medium, Galactic magnetic fields and cosmic rays. J. Cosmol. Astropart. Phys. 2018, 2018, 049. [Google Scholar] [CrossRef]
- Poidevin, F.; Rubino-Martin, J.A.; Genova-Santos, R.; Rebolo, R.; Aguiar, M.; Gomez-Renasco, F.; Guidi, F.; Gutierrez, C.; Hoyland, R.J.; Lopez-Caraballo, C.; et al. The QUIJOTE Experiment: Prospects for CMB B-MODE polarization detection and foregrounds characterization. arXiv 2018, arXiv:1802.04594. [Google Scholar]
- Krachmalnicoff, N.; Carretti, E.; Baccigalupi, C.; Bernardi, G.; Brown, S.; Gaensler, B.M.; Haverkorn, M.; Kesteven, M.; Perrotta, F.; Poppi, S.; et al. S-PASS view of polarized Galactic synchrotron at 2.3 GHz as a contaminant to CMB observations. Astron. Astrophys. 2018, 618, A166. [Google Scholar] [CrossRef]
- Basu, A.; Schwarz, D.J.; Klöckner, H.R.; von Hausegger, S.; Kramer, M.; Wieching, G.; Burkhart, B. CMB foreground measurements through broad-band radio spectro-polarimetry: Prospects of the SKA-MPG telescope. Mon. Not. R. Astron. Soc. 2019, 488, 1618–1634. [Google Scholar] [CrossRef]
- de la Hoz, E.; Vielva, P.; Barreiro, R.B.; Martínez-González, E. On the Detection of CMB B-modes from Ground at Low Frequency. arXiv 2020, arXiv:2002.12206. [Google Scholar]
- Hutschenreuter, S.; Enßlin, T.A. The Galactic Faraday depth sky revisited. Astron. Astrophys. 2020, 633, A150. [Google Scholar] [CrossRef]
- Sun, X.H.; Landecker, T.L.; Gaensler, B.M.; Carretti, E.; Reich, W.; Leahy, J.P.; McClure-Griffiths, N.M.; Crocker, R.M.; Wolleben, M.; Haverkorn, M.; et al. Faraday Tomography of the North Polar Spur: Constraints on the Distance to the Spur and on the Magnetic Field of the Galaxy. Astrophys. J. 2015, 811, 40. [Google Scholar] [CrossRef]
- Crutcher, R.M. Magnetic Fields in Molecular Clouds. Annu. Rev. 2012, 50, 29–63. [Google Scholar] [CrossRef]
- Li, H.B.; Goodman, A.; Sridharan, T.K.; Houde, M.; Li, Z.Y.; Novak, G.; Tang, K.S. The Link Between Magnetic Fields and Cloud/Star Formation. In Protostars and Planets VI; Beuther, H., Klessen, R.S., Dullemond, C.P., Henning, T., Eds.; University of Arizona Press: Tucson, AZ, USA, 2014; p. 101. [Google Scholar] [CrossRef]
- Hennebelle, P.; Inutsuka, S.i. The role of magnetic field in molecular cloud formation and evolution. Front. Astron. Space Sci. 2019, 6, 5. [Google Scholar] [CrossRef]
- Federrath, C.; Klessen, R.S. The Star Formation Rate of Turbulent Magnetized Clouds: Comparing Theory, Simulations, and Observations. Astrophys. J. 2012, 761, 156. [Google Scholar] [CrossRef]
- Federrath, C. Inefficient star formation through turbulence, magnetic fields and feedback. Mon. Not. R. Astron. Soc. 2015, 450, 4035–4042. [Google Scholar] [CrossRef]
- Pudritz, R.E.; Ray, T.P. The Role of Magnetic Fields in Protostellar Outflows and Star Formation. Front. Astron. Space Sci. 2019, 6, 54. [Google Scholar] [CrossRef]
- Wurster, J.; Li, Z.Y. The role of magnetic fields in the formation of protostellar discs. Front. Astron. Space Sci. 2018, 5, 39. [Google Scholar] [CrossRef]
- Soler, J.D. Using Herschel and Planck observations to delineate the role of magnetic fields in molecular cloud structure. Astron. Astrophys. 2019, 629, A96. [Google Scholar] [CrossRef]
- Brandenburg, A.; Subramanian, K. Astrophysical magnetic fields and nonlinear dynamo theory. Phys. Rep. 2005, 417, 1–209. [Google Scholar] [CrossRef]
- Houde, M.; Rao, R.; Vaillancourt, J.E.; Hildebrand, R.H. Dispersion of Magnetic Fields in Molecular Clouds. III. Astrophys. J. 2011, 733, 109. [Google Scholar] [CrossRef]
- Burkhart, B.; Lazarian, A.; Gaensler, B.M. Properties of Interstellar Turbulence from Gradients of Linear Polarization Maps. Astrophys. J. 2012, 749, 145. [Google Scholar] [CrossRef]
- Falgarone, E.; Momferratos, G.; Lesaffre, P. The Intermittency of ISM Turbulence: What Do the Observations Tell Us? In Magnetic Fields in Diffuse Media; Lazarian, A., de Gouveia Dal Pino, E.M., Melioli, C., Eds.; Astrophysics and Space Science Library, Springer: Basel, Switzerland, 2015; Volume 407. [Google Scholar] [CrossRef]
- Federrath, C. The role of turbulence, magnetic fields and feedback for star formation. J. Phys. Conf. Ser. 2016, 719, 12002. [Google Scholar] [CrossRef]
- Padovani, M.; Galli, D. Synchrotron emission in molecular cloud cores: The SKA view. Astron. Astrophys. 2018, 620, L4. [Google Scholar] [CrossRef]
- André, P.; Di Francesco, J.; Ward-Thompson, D.; Inutsuka, S.I.; Pudritz, R.E.; Pineda, J.E. From Filamentary Networks to Dense Cores in Molecular Clouds: Toward a New Paradigm for Star Formation. In Protostars and Planets VI; Beuther, H., Klessen, R.S., Dullemond, C.P., Henning, T., Eds.; University of Arizona Press: Tucson, AZ, USA, 2014; p. 27. [Google Scholar] [CrossRef]
- Poidevin, F. Analysis of Galactic molecular cloud polarization maps: A review of the methods. Eur. Phys. J. Web Conf. 2020, 228, 19. [Google Scholar] [CrossRef]
- Green, J.A.; McClure-Griffiths, N.M.; Caswell, J.L.; Robishaw, T.; Harvey-Smith, L. MAGMO: Coherent magnetic fields in the star-forming regions of the Carina-Sagittarius spiral arm tangent. Mon. Not. R. Astron. Soc. 2012, 425, 2530–2547. [Google Scholar] [CrossRef]
- Ogbodo, C.S.; Green, J.A.; Dawson, J.R.; Breen, S.L.; Mao, S.A.; McClure-Griffiths, N.M.; Robishaw, T.; Harvey-Smith, L. MAGMO: Polarimetry of 1720-MHz OH masers towards southern star-forming regions. Mon. Not. R. Astron. Soc. 2020, 493, 199–233. [Google Scholar] [CrossRef]
- Tahani, M.; Plume, R.; Brown, J.C.; Kainulainen, J. Helical magnetic fields in molecular clouds?. A new method to determine the line-of-sight magnetic field structure in molecular clouds. Astron. Astrophys. 2018, 614, A100. [Google Scholar] [CrossRef]
- Tahani, M.; Plume, R.; Brown, J.C.; Soler, J.D.; Kainulainen, J. Could bow-shaped magnetic morphologies surround filamentary molecular clouds?. The 3D magnetic field structure of Orion-A. Astron. Astrophys. 2019, 632, A68. [Google Scholar] [CrossRef]
- Shang, H.; Allen, A.; Li, Z.Y.; Liu, C.F.; Chou, M.Y.; Anderson, J. A Unified Model for Bipolar Outflows from Young Stars. Astrophys. J. 2006, 649, 845–855. [Google Scholar] [CrossRef]
- Gerrard, I.A.; Federrath, C.; Kuruwita, R. The role of initial magnetic field structure in the launching of protostellar jets. Mon. Not. R. Astron. Soc. 2019, 485, 5532–5542. [Google Scholar] [CrossRef]
- Hu, X.; Zhu, Z.; Okuzumi, S.; Bai, X.N.; Wang, L.; Tomida, K.; Stone, J.M. Nonideal MHD Simulation of HL Tau Disk: Formation of Rings. Astrophys. J. 2019, 885, 36. [Google Scholar] [CrossRef]
- Mori, S.; Bai, X.N.; Okuzumi, S. Temperature Structure in the Inner Regions of Protoplanetary Disks: Inefficient Accretion Heating Controlled by Nonideal Magnetohydrodynamics. Astrophys. J. 2019, 872, 98. [Google Scholar] [CrossRef]
- Hull, C.L.H.; Carrasco-González, C.; Williams, P.K.G.; Girart, J.M.; Robishaw, T.; Galván-Madrid, R.; Bourke, T. Magnetic Fields in Forming Stars with the ngVLA. In Science with a Next Generation Very Large Array; Murphy, E., Ed.; Astronomical Society of the Pacific Conference Series; Astronomical Society of the Pacific: San Francisco, CA, USA, 2018; Volume 517, p. 357. [Google Scholar]
- Guillet, V.; Girart, J.M.; Maury, A.J.; Alves, F.O. Polarized emission by aligned grains in the Mie regime: Application to protoplanetary disks observed by ALMA. Astron. Astrophys. 2020, 634, L15. [Google Scholar] [CrossRef]
- Stil, J.; Wityk, N.; Ouyed, R.; Taylor, A.R. Three-dimensional Simulations of Magnetized Superbubbles: New Insights into the Importance of MHD Effects on Observed Quantities. Astrophys. J. 2009, 701, 330–347. [Google Scholar] [CrossRef]
- Padovani, M.; Marcowith, A.; Sánchez-Monge, Á.; Meng, F.; Schilke, P. Non-thermal emission from cosmic rays accelerated in H II regions. Astron. Astrophys. 2019, 630, A72. [Google Scholar] [CrossRef]
- Meng, F.; Sánchez-Monge, Á.; Schilke, P.; Padovani, M.; Marcowith, A.; Ginsburg, A.; Schmiedeke, A.; Schwörer, A.; DePree, C.; Veena, V.S.; et al. The physical and chemical structure of Sagittarius B2. V. Non-thermal emission in the envelope of Sgr B2. Astron. Astrophys. 2019, 630, A73. [Google Scholar] [CrossRef]
- Kothes, R.; Brown, J.A. Probing interstellar magnetic fields with Supernova remnants. In Cosmic Magnetic Fields: From Planets, to Stars and Galaxies; Strassmeier, K.G., Kosovichev, A.G., Beckman, J.E., Eds.; IAU Symposium, Cambridge University Press: Cambridge, UK, 2009; Volume 259, pp. 75–80. [Google Scholar] [CrossRef]
- West, J.L.; Safi-Harb, S.; Jaffe, T.; Kothes, R.; Landecker, T.L.; Foster, T. The connection between supernova remnants and the Galactic magnetic field: A global radio study of the axisymmetric sample. Astron. Astrophys. 2016, 587, A148. [Google Scholar] [CrossRef]
- Howard, T.A.; Stovall, K.; Dowell, J.; Taylor, G.B.; White, S.M. Measuring the Magnetic Field of Coronal Mass Ejections Near the Sun Using Pulsars. Astrophys. J. 2016, 831, 208. [Google Scholar] [CrossRef]
- Kooi, J.E.; Fischer, P.D.; Buffo, J.J.; Spangler, S.R. VLA Measurements of Faraday Rotation through Coronal Mass Ejections. Sol. Phys. 2017, 292, 56. [Google Scholar] [CrossRef]
- Hurley-Walker, N.; Hancock, P.J. De-distorting ionospheric effects in the image plane. Astron. Comput. 2018, 25, 94–102. [Google Scholar] [CrossRef]
- Sotomayor-Beltran, C.; Sobey, C.; Hessels, J.W.T.; de Bruyn, G.; Noutsos, A.; Alexov, A.; Anderson, J.; Asgekar, A.; Avruch, I.M.; Beck, R.; et al. Calibrating high-precision Faraday rotation measurements for LOFAR and the next generation of low-frequency radio telescopes. Astron. Astrophys. 2013, 552, A58. [Google Scholar] [CrossRef]
- Porayko, N.K.; Noutsos, A.; Tiburzi, C.; Verbiest, J.P.W.; Horneffer, A.; Künsemöller, J.; Osłowski, S.; Kramer, M.; Schnitzeler, D.H.F.M.; Anderson, J.M.; et al. Testing the accuracy of the ionospheric Faraday rotation corrections through LOFAR observations of bright northern pulsars. Mon. Not. R. Astron. Soc. 2019, 483, 4100–4113. [Google Scholar] [CrossRef]
- Oosterloo, T.; Verheijen, M.; van Cappellen, W. The latest on Apertif. In Proceedings of the ISKAF2010 Science Meeting, Assen, The Netherlands, 10–14 June 2010; p. 43. [Google Scholar]
- Johnston, S.; Taylor, R.; Bailes, M.; Bartel, N.; Baugh, C.; Bietenholz, M.; Blake, C.; Braun, R.; Brown, J.; Chatterjee, S.; et al. Science with ASKAP. The Australian square-kilometre-array pathfinder. Exp. Astron. 2008, 22, 151–273. [Google Scholar] [CrossRef]
- Anderson, C.; Heald, G.; O’Sullivan, S.; Bunton, J.; Carretti, E.; Chippendale, A.; Collier, J.; Farnes, J.; Gaensler, B.; Harvey-Smith, L.; et al. The Extraordinary Linear Polarisation Structure of the Southern Centaurus A Lobe Revealed by ASKAP. Galaxies 2018, 6, 127. [Google Scholar] [CrossRef]
- Jonas, J.; MeerKAT Team. The MeerKAT Radio Telescope. In MeerKAT Science: On the Pathway to the SKA; Sissa Medialab: Trieste, Italy, 2016; p. 1. [Google Scholar]
- Camilo, F. African star joins the radio astronomy firmament. Nat. Astron. 2018, 2, 594. [Google Scholar] [CrossRef]
- Lacy, M.; Baum, S.A.; Chandler, C.J.; Chatterjee, S.; Clarke, T.E.; Deustua, S.; English, J.; Farnes, J.; Gaensler, B.M.; Gugliucci, N.; et al. The Karl G. Jansky Very Large Array Sky Survey (VLASS). Science Case and Survey Design. Publ. Astron. Soc. Pac. 2020, 132, 035001. [Google Scholar] [CrossRef]
- Hobbs, G.; Manchester, R.N.; Dunning, A.; Jameson, A.; Roberts, P.; George, D.; Green, J.A.; Tuthill, J.; Toomey, L.; Kaczmarek, J.F.; et al. An ultra-wide bandwidth (704 to 4 032 MHz) receiver for the Parkes radio telescope. Publ. Astron. Soc. Aust. 2020, 37, e012. [Google Scholar] [CrossRef]
- Shanahan, R.; Lemmer, S.J.; Stil, J.M.; Beuther, H.; Wang, Y.; Soler, J.; Anderson, L.D.; Bigiel, F.; Glover, S.C.O.; Goldsmith, P.; et al. Strong Excess Faraday Rotation on the Inside of the Sagittarius Spiral Arm. Astrophys. J. 2019, 887, L7. [Google Scholar] [CrossRef]
- Zhang, L.; Hobbs, G.; Manchester, R.N.; Li, D.; Wang, P.; Dai, S.; Wang, J.; Kaczmarek, J.F.; Cameron, A.D.; Toomey, L.; et al. Wide Bandwidth Observations of Pulsars C, D, and J in 47 Tucanae. Astrophys. J. 2019, 885, L37. [Google Scholar] [CrossRef]
- Dai, S.; Johnston, S.; Kerr, M.; Camilo, F.O.; Cameron, A.; Toomey, L.; Kumamoto, H. Discovery of Millisecond Pulsars in the Globular Cluster Omega Centauri. Astrophys. J. 2020, 888, L18. [Google Scholar] [CrossRef]
- van Haarlem, M.P.; Wise, M.W.; Gunst, A.W.; Heald, G.; McKean, J.P.; Hessels, J.W.T.; de Bruyn, A.G.; Nijboer, R.; Swinbank, J.; Fallows, R.; et al. LOFAR: The LOw-Frequency ARray. Astron. Astrophys. 2013, 556, A2. [Google Scholar] [CrossRef]
- Tingay, S.J.; Goeke, R.; Bowman, J.D.; Emrich, D.; Ord, S.M.; Mitchell, D.A.; Morales, M.F.; Booler, T.; Crosse, B.; Wayth, R.B.; et al. The Murchison Widefield Array: The Square Kilometre Array Precursor at Low Radio Frequencies. Publ. Astron. Soc. Aust. 2013, 30, e007. [Google Scholar] [CrossRef]
- Wayth, R.B.; Tingay, S.J.; Trott, C.M.; Emrich, D.; Johnston-Hollitt, M.; McKinley, B.; Gaensler, B.M.; Beardsley, A.P.; Booler, T.; Crosse, B.; et al. The Phase II Murchison Widefield Array: Design overview. Publ. Astron. Soc. Aust. 2018, 35, 33. [Google Scholar] [CrossRef]
- Lenc, E.; Gaensler, B.M.; Sun, X.H.; Sadler, E.M.; Willis, A.G.; Barry, N.; Beardsley, A.P.; Bell, M.E.; Bernardi, G.; Bowman, J.D.; et al. Low-frequency Observations of Linearly Polarized Structures in the Interstellar Medium near the South Galactic Pole. Astrophys. J. 2016, 830, 38. [Google Scholar] [CrossRef]
- Lenc, E.; Anderson, C.S.; Barry, N.; Bowman, J.D.; Cairns, I.H.; Farnes, J.S.; Gaensler, B.M.; Heald, G.; Johnston-Hollitt, M.; Kaplan, D.L.; et al. The Challenges of Low-Frequency Radio Polarimetry: Lessons from the Murchison Widefield Array. Publ. Astron. Soc. Aust. 2017, 34, e040. [Google Scholar] [CrossRef]
- Riseley, C.J.; Lenc, E.; Van Eck, C.L.; Heald, G.; Gaensler, B.M.; Anderson, C.S.; Hancock, P.J.; Hurley-Walker, N.; Sridhar, S.S.; White, S.V. The POlarised GLEAM Survey (POGS) I: First results from a low-frequency radio linear polarisation survey of the southern sky. Publ. Astron. Soc. Aust. 2018, 35, 43. [Google Scholar] [CrossRef]
- Van Eck, C.L.; Haverkorn, M.; Alves, M.I.R.; Beck, R.; Best, P.; Carretti, E.; Chyży, K.T.; Farnes, J.S.; Ferrière, K.; Hardcastle, M.J.; et al. Polarized point sources in the LOFAR Two-meter Sky Survey: A preliminary catalogue. Astron. Astrophys. 2018, 613, A58. [Google Scholar] [CrossRef]
- Condon, J.J.; Cotton, W.D.; Greisen, E.W.; Yin, Q.F.; Perley, R.A.; Taylor, G.B.; Broderick, J.J. The NRAO VLA Sky Survey. Astrophys. J. 1998, 115, 1693–1716. [Google Scholar] [CrossRef]
- Bock, D.C.J.; Large, M.I.; Sadler, E.M. SUMSS: A Wide-Field Radio Imaging Survey of the Southern Sky. I. Science Goals, Survey Design, and Instrumentation. Astrophys. J. 1999, 117, 1578–1593. [Google Scholar] [CrossRef]
- Gaensler, B.M.; Landecker, T.L.; Taylor, A.R.; POSSUM Collaboration. Survey Science with ASKAP: Polarization Sky Survey of the Universe’s Magnetism (POSSUM). In American Astronomical Society Meeting Abstracts #215; American Astronomical Society: Washington, DC, USA, 2010; Volume 215, p. 470.13. [Google Scholar]
- Norris, R.P.; Hopkins, A.M.; Afonso, J.; Brown, S.; Condon, J.J.; Dunne, L.; Feain, I.; Hollow, R.; Jarvis, M.; Johnston-Hollitt, M.; et al. EMU: Evolutionary Map of the Universe. Publ. Astron. Soc. Aust. 2011, 28, 215–248. [Google Scholar] [CrossRef]
- Jarvis, M.; Taylor, R.; Agudo, I.; Allison, J.R.; Deane, R.P.; Frank, B.; Gupta, N.; Heywood, I.; Maddox, N.; McAlpine, K.; et al. The MeerKAT International GHz Tiered Extragalactic Exploration (MIGHTEE) Survey. In MeerKAT Science: On the Pathway to the SKA; Sissa Medialab: Trieste, Italy, 2016; p. 6. [Google Scholar]
- Blyth, S.; Baker, A.J.; Holwerda, B.; Bouchard, A.; Catinella, B.; Chemin, L.; Cunnama, D.; Davé, R.; Faltenbacher, A.; February, S.; et al. LADUMA: Looking at the Distant Universe with the MeerKAT Array. In MeerKAT Science: On the Pathway to the SKA; Sissa Medialab: Trieste, Italy, 2016; p. 4. [Google Scholar]
- de Blok, W.J.G.; Adams, E.A.K.; Amram, P.; Athanassoula, E.; Bagetakos, I.; Balkowski, C.; Bershady, M.A.; Beswick, R.J.; Bigiel, F.; Blyth, S.L.; et al. An Overview of the MHONGOOSE Survey: Observing Nearby Galaxies with MeerKAT. In MeerKAT Science: On the Pathway to the SKA; Sissa Medialab: Trieste, Italy, 2016; p. 7. [Google Scholar]
- Bailes, M.; Barr, E.; Bhat, N.D.R.; Brink, J.; Buchner, S.; Burgay, M.; Camilo, F.; Champion, D.J.; Hessels, J.; Janssen, G.H.; et al. MeerTime - the MeerKAT Key Science Program on Pulsar Timing. arXiv 2018, arXiv:1803.07424. [Google Scholar]
- Johnston, S.; Karastergiou, A.; Keith, M.J.; Song, X.; Weltevrede, P.; Abbate, F.; Bailes, M.; Buchner, S.; Camilo, F.; Geyer, M.; et al. The Thousand-Pulsar-Array programme on MeerKAT - I. Science objectives and first results. Mon. Not. R. Astron. Soc. 2020, 493, 3608–3615. [Google Scholar] [CrossRef]
- Wolleben, M.; Landecker, T.L.; Carretti, E.; Dickey, J.M.; Fletcher, A.; Gaensler, B.M.; Han, J.L.; Haverkorn, M.; Leahy, J.P.; McClure-Griffiths, N.M.; et al. GMIMS: The Global Magneto-Ionic Medium Survey. In Cosmic Magnetic Fields: From Planets, to Stars and Galaxies; Strassmeier, K.G., Kosovichev, A.G., Beckman, J.E., Eds.; IAU Symposium; Cambridge University Press: Cambridge, UK, 2009; Volume 259, pp. 89–90. [Google Scholar] [CrossRef]
- Amiri, M.; Bandura, K.; Berger, P.; Bhardwaj, M.; Boyce, M.M.; Boyle, P.J.; Brar, C.; Burhanpurkar, M.; Chawla, P.; CHIME/FRB Collaboration; et al. The LOFAR Two-metre Sky Survey. I. Survey description and preliminary data release. Astrophys. J. 2018, 863, 48. [Google Scholar] [CrossRef]
- Shimwell, T.W.; Röttgering, H.J.A.; Best, P.N.; Williams, W.L.; Dijkema, T.J.; de Gasperin, F.; Hardcastle, M.J.; Heald, G.H.; Hoang, D.N.; Horneffer, A.; et al. The LOFAR Two-metre Sky Survey. I. Survey description and preliminary data release. Astron. Astrophys. 2017, 598, A104. [Google Scholar] [CrossRef]
- Shimwell, T.W.; Tasse, C.; Hardcastle, M.J.; Mechev, A.P.; Williams, W.L.; Best, P.N.; Röttgering, H.J.A.; Callingham, J.R.; Dijkema, T.J.; de Gasperin, F.; et al. The LOFAR Two-metre Sky Survey. II. First data release. Astron. Astrophys. 2019, 622, A1. [Google Scholar] [CrossRef]
- Stuardi, C.; O’Sullivan, S.P.; Bonafede, A.; Brüggen, M.; Dabhade, P.; Horellou, C.; Morganti, R.; Carretti, E.; Heald, G.; Iacobelli, M.; et al. The LOFAR view of intergalactic magnetic fields with giant radio galaxies. arXiv 2020, arXiv:2004.05169. [Google Scholar] [CrossRef]
- Smith, D.J.B.; Best, P.N.; Duncan, K.J.; Hatch, N.A.; Jarvis, M.J.; Röttgering, H.J.A.; Simpson, C.J.; Stott, J.P.; Cochrane, R.K.; Coppin, K.E.; et al. The WEAVE-LOFAR Survey. In Proceedings of the SF2A-2016: Annual Meeting of the French Society of Astronomy and Astrophysics, Lyon, France, 14–17 June 2016; Reylé, C., Richard, J., Cambrésy, L., Deleuil, M., Pécontal, E., Tresse, L., Vauglin, I., Eds.; French Society of Astronomy and Astrophysics: Paris, France, 2016; pp. 271–280. [Google Scholar]
- Wayth, R.B.; Lenc, E.; Bell, M.E.; Callingham, J.R.; Dwarakanath, K.S.; Franzen, T.M.O.; For, B.Q.; Gaensler, B.; Hancock, P.; Hindson, L.; et al. GLEAM: The GaLactic and Extragalactic All-Sky MWA Survey. Publ. Astron. Soc. Aust. 2015, 32, e025. [Google Scholar] [CrossRef]
- Hurley-Walker, N.; Callingham, J.R.; Hancock, P.J.; Franzen, T.M.O.; Hindson, L.; Kapińska, A.D.; Morgan, J.; Offringa, A.R.; Wayth, R.B.; Wu, C.; et al. GaLactic and Extragalactic All-sky Murchison Widefield Array (GLEAM) survey - I. A low-frequency extragalactic catalogue. Mon. Not. R. Astron. Soc. 2017, 464, 1146–1167. [Google Scholar] [CrossRef]
- Hurley-Walker, N.; Hancock, P.J.; Franzen, T.M.O.; Callingham, J.R.; Offringa, A.R.; Hindson, L.; Wu, C.; Bell, M.E.; For, B.Q.; Gaensler, B.M.; et al. GaLactic and Extragalactic All-sky Murchison Widefield Array (GLEAM) survey II: Galactic plane 345° < l < 67°, 180° < l < 240°. Publ. Astron. Soc. Aust. 2019, 36, e047. [Google Scholar] [CrossRef]
- Riseley, C.J.; Galvin, T.J.; Sobey, C.; Vernstrom, T.; White, S.V.; Zhang, X.; Gaensler, B.M.; Heald, G.; Anderson, C.S.; Franzen, T.M.O.; et al. The POlarised GLEAM Survey (POGS) II: Results from an All-Sky Rotation Measure Synthesis Survey at Long Wavelengths. arXiv 2020, arXiv:2005.09266. [Google Scholar]
- Beardsley, A.P.; Johnston-Hollitt, M.; Trott, C.M.; Pober, J.C.; Morgan, J.; Oberoi, D.; Kaplan, D.L.; Lynch, C.R.; Anderson, G.E.; McCauley, P.I.; et al. Science with the Murchison Widefield Array: Phase I results and Phase II opportunities. Publ. Astron. Soc. Aust. 2019, 36, e050. [Google Scholar] [CrossRef]
- Ferrière, K.M. The interstellar environment of our galaxy. Rev. Mod. Phys. 2001, 73, 1031–1066. [Google Scholar] [CrossRef]
- Heiles, C.; Haverkorn, M. Magnetic Fields in the Multiphase Interstellar Medium. Space Sci. Rev. 2012, 166, 293–305. [Google Scholar] [CrossRef]
- Hales, C.A. Calibration Errors in Interferometric Radio Polarimetry. Astrophys. J. 2017, 154, 54. [Google Scholar] [CrossRef]
- Eyles, R.A.J.; Birkinshaw, M.; Smolčić, V.; Horellou, C.; Huynh, M.; Butler, A.; Delhaize, J.; Vignali, C.; Pierre, M. The XXL Survey. XXXIX. Polarised radio sources in the XXL-South field. Astron. Astrophys. 2020, 633, A6. [Google Scholar] [CrossRef]
- Asad, K.M.B.; Koopmans, L.V.E.; Jelić, V.; de Bruyn, A.G.; Pandey, V.N.; Gehlot, B.K. Polarization leakage in epoch of reionization windows - III. Wide-field effects of narrow-field arrays. Mon. Not. R. Astron. Soc. 2018, 476, 3051–3062. [Google Scholar] [CrossRef]
- Smirnov, O.M. Revisiting the radio interferometer measurement equation. I. A full-sky Jones formalism. Astron. Astrophys. 2011, 527, A106. [Google Scholar] [CrossRef]
- Bhatnagar, S.; Rau, U.; Golap, K. Wide-field wide-band Interferometric Imaging: The WB A-Projection and Hybrid Algorithms. Astrophys. J. 2013, 770, 91. [Google Scholar] [CrossRef]
- Mevius, M.; van der Tol, S.; Pandey, V.N.; Vedantham, H.K.; Brentjens, M.A.; de Bruyn, A.G.; Abdalla, F.B.; Asad, K.M.B.; Bregman, J.D.; Brouw, W.N.; et al. Probing ionospheric structures using the LOFAR radio telescope. Radio Sci. 2016, 51, 927–941. [Google Scholar] [CrossRef]
- Loi, S.T.; Trott, C.M.; Murphy, T.; Cairns, I.H.; Bell, M.; Hurley-Walker, N.; Morgan, J.; Lenc, E.; Offringa, A.R.; Feng, L.; et al. Power spectrum analysis of ionospheric fluctuations with the Murchison Widefield Array. Radio Science 2015, 50, 574–597. [Google Scholar] [CrossRef]
- Mannucci, A.J.; Wilson, B.D.; Yuan, D.N.; Ho, C.H.; Lindqwister, U.J.; Runge, T.F. A global mapping technique for GPS-derived ionospheric total electron content measurements. Radio Sci. 1998, 33, 565–582. [Google Scholar] [CrossRef]
- Orús, R.; Hernández-Pajares, M.; Juan, J.M.; Sanz, J. Improvement of global ionospheric VTEC maps by using kriging interpolation technique. J.f Atmos. Sol. Terr. Phys. 2005, 67, 1598–1609. [Google Scholar] [CrossRef]
- Malins, J.B.; White, S.M.; Taylor, G.B.; Stovall, K.; Dowell, J. Modeling the Ionosphere with GPS and Rotation Measure Observations. Radio Sci. 2018, 53, 724–738. [Google Scholar] [CrossRef]
- Brentjens, M.A. Polarization Imaging with LOFAR; Astrophysics and Space Science Library, Springer: Basel, Switzerland, 2018; Volume 426, p. 159. [Google Scholar] [CrossRef]
- Farnsworth, D.; Rudnick, L.; Brown, S. Integrated Polarization of Sources at λ ~1 m and New Rotation Measure Ambiguities. Astrophys. J. 2011, 141, 191. [Google Scholar] [CrossRef]
- O’Sullivan, S.P.; Brown, S.; Robishaw, T.; Schnitzeler, D.H.F.M.; McClure-Griffiths, N.M.; Feain, I.J.; Taylor, A.R.; Gaensler, B.M.; Land ecker, T.L.; Harvey-Smith, L.; et al. Complex Faraday depth structure of active galactic nuclei as revealed by broad-band radio polarimetry. Mon. Not. R. Astron. Soc. 2012, 421, 3300–3315. [Google Scholar] [CrossRef]
- Hales, C.A.; Gaensler, B.M.; Norris, R.P.; Middelberg, E. Analytic detection thresholds for measurements of linearly polarized intensity using rotation measure synthesis. Mon. Not. R. Astron. Soc. 2012, 424, 2160–2172. [Google Scholar] [CrossRef]
- Hales, C.A.; Murphy, T.; Curran, J.R.; Middelberg, E.; Gaensler, B.M.; Norris, R.P. BLOBCAT: Software to catalogue flood-filled blobs in radio images of total intensity and linear polarization. Mon. Not. R. Astron. Soc. 2012, 425, 979–996. [Google Scholar] [CrossRef]
- Farnes, J.S.; Heald, G.; Junklewitz, H.; Mulcahy, D.D.; Haverkorn, M.; Van Eck, C.L.; Riseley, C.J.; Brentjens, M.; Horellou, C.; Vacca, V.; et al. Source finding in linear polarization for LOFAR, and SKA predecessor surveys, using Faraday moments. Mon. Not. R. Astron. Soc. 2018, 474, 3280–3296. [Google Scholar] [CrossRef]
- Bell, M.R.; Enßlin, T.A. Faraday synthesis. The synergy of aperture and rotation measure synthesis. Astron. Astrophys. 2012, 540, A80. [Google Scholar] [CrossRef]
- Sridhar, S.S.; Heald, G.; van der Hulst, J.M. cuFFS: A GPU-accelerated code for Fast Faraday rotation measure Synthesis. Astron. Comput. 2018, 25, 205–212. [Google Scholar] [CrossRef]
- Bell, M.R.; Oppermann, N.; Crai, A.; Enßlin, T.A. Improved CLEAN reconstructions for rotation measure synthesis with maximum likelihood estimation. Astron. Astrophys. 2013, 551, L7. [Google Scholar] [CrossRef]
- Schnitzeler, D.H.F.M. Finding a complex polarized signal in wide-band radio data. Mon. Not. R. Astron. Soc. 2018, 474, 300–312. [Google Scholar] [CrossRef]
- Brown, S.; Bergerud, B.; Costa, A.; Gaensler, B.M.; Isbell, J.; LaRocca, D.; Norris, R.; Purcell, C.; Rudnick, L.; Sun, X. Classifying complex Faraday spectra with convolutional neural networks. Mon. Not. R. Astron. Soc. 2019, 483, 964–970. [Google Scholar] [CrossRef]
- Pratley, L.; Johnston-Hollitt, M. Wide-band Rotation Measure Synthesis. arXiv 2019, arXiv:1906.00866. [Google Scholar] [CrossRef]
- Enßlin, T.A.; Frommert, M.; Kitaura, F.S. Information field theory for cosmological perturbation reconstruction and nonlinear signal analysis. Phys. Rev. D 2009, 80, 105005. [Google Scholar] [CrossRef]
- Oppermann, N.; Junklewitz, H.; Robbers, G.; Bell, M.R.; Enßlin, T.A.; Bonafede, A.; Braun, R.; Brown, J.C.; Clarke, T.E.; Feain, I.J.; et al. An improved map of the Galactic Faraday sky. Astron. Astrophys. 2012, 542, A93. [Google Scholar] [CrossRef]
- Oppermann, N.; Junklewitz, H.; Greiner, M.; Enßlin, T.A.; Akahori, T.; Carretti, E.; Gaensler, B.M.; Goobar, A.; Harvey-Smith, L.; Johnston-Hollitt, M.; et al. Estimating extragalactic Faraday rotation. Astron. Astrophys. 2015, 575, A118. [Google Scholar] [CrossRef]
- Vacca, V.; Oppermann, N.; Enßlin, T.; Jasche, J.; Selig, M.; Greiner, M.; Junklewitz, H.; Reinecke, M.; Brüggen, M.; Carretti, E.; et al. Using rotation measure grids to detect cosmological magnetic fields: A Bayesian approach. Astron. Astrophys. 2016, 591, A13. [Google Scholar] [CrossRef]
- Taylor, A.R.; Stil, J.M.; Sunstrum, C. A Rotation Measure Image of the Sky. Astrophys. J. 2009, 702, 1230–1236. [Google Scholar] [CrossRef]
- Jelić, V.; Prelogović, D.; Haverkorn, M.; Remeijn, J.; Klindžić, D. Magnetically aligned straight depolarization canals and the rolling Hough transform. Astron. Astrophys. 2018, 615, L3. [Google Scholar] [CrossRef]
- Clark, S.E.; Hensley, B.S. Mapping the Magnetic Interstellar Medium in Three Dimensions over the Full Sky with Neutral Hydrogen. Astrophys. J. 2019, 887, 136. [Google Scholar] [CrossRef]
- Pratley, L.; Johnston-Hollitt, M. An improved method for polarimetric image restoration in interferometry. Mon. Not. R. Astron. Soc. 2016, 462, 3483–3501. [Google Scholar] [CrossRef]
- Stil, J.M.; Keller, B.W.; George, S.J.; Taylor, A.R. Degree of Polarization and Source Counts of Faint Radio Sources from Stacking Polarized Intensity. Astrophys. J. 2014, 787, 99. [Google Scholar] [CrossRef]
- Rudnick, L.; Owen, F.N. The Distribution of Polarized Radio Sources >15 μJy in GOODS-N. Astrophys. J. 2014, 785, 45. [Google Scholar] [CrossRef]
- Braun, R.; Bonaldi, A.; Bourke, T.; Keane, E.; Wagg, J. Anticipated Performance of the Square Kilometre Array – Phase 1 (SKA1). arXiv 2019, arXiv:1912.12699. [Google Scholar]
- Prandoni, I.; Seymour, N. Revealing the Physics and Evolution of Galaxies and Galaxy Clusters with SKA Continuum Surveys. In Advancing Astrophysics with the Square Kilometre Array (AASKA14); Sissa Medialab: Trieste, Italy, 2015; p. 67. [Google Scholar]
- Rudnick, L. Optimizing Faraday Background Grids. arXiv 2019, arXiv:1901.09074. [Google Scholar]
- Loi, F.; Murgia, M.; Govoni, F.; Vacca, V.; Prand oni, I.; Bonafede, A.; Feretti, L. Simulations of the polarized radio sky and predictions on the confusion limit in polarization for future radio surveys. Mon. Not. R. Astron. Soc. 2019, 485, 5285–5293. [Google Scholar] [CrossRef]
- SKAO Science Team. SKA1 Level 0 Science Requirements. 2015. Available online: https://astronomers.skatelescope.org/wp-content/uploads/2015/11/SKA-TEL-SKO-0000007_SKA1_Level_0_Science_RequirementsRev02-part-1-signed.pdf (accessed on 4 June 2020).
- Cantwell, T.M.; Bray, J.D.; Croston, J.H.; Scaife, A.M.M.; Mulcahy, D.D.; Best, P.N.; Bruggen, M.; Brunetti, G.; Callingham, J.R.; Clarke, A.O.; et al. Low-frequency observations of the Giant Radio Galaxy NGC 6251. arXiv 2020, arXiv:2004.11104. [Google Scholar]
- Bonaldi, A.; Robert Braun for the SKAO Science Team. Square Kilometre Array Science Data Challenge 1. arXiv 2018, arXiv:1811.10454. [Google Scholar]
- Sun, X.H.; Rudnick, L.; Akahori, T.; Anderson, C.S.; Bell, M.R.; Bray, J.D.; Farnes, J.S.; Ideguchi, S.; Kumazaki, K.; O’Brien, T.; et al. Comparison of Algorithms for Determination of Rotation Measure and Faraday Structure. I. 1100–1400 MHz. Astrophys. J. 2015, 149, 60. [Google Scholar] [CrossRef]
- Van Eck, C.L.; Haverkorn, M.; Alves, M.I.R.; Beck, R.; de Bruyn, A.G.; Enßlin, T.; Farnes, J.S.; Ferrière, K.; Heald, G.; Horellou, C.; et al. Faraday tomography of the local interstellar medium with LOFAR: Galactic foregrounds towards IC 342. Astron. Astrophys. 2017, 597, A98. [Google Scholar] [CrossRef]
- Van Eck, C.L.; Haverkorn, M.; Alves, M.I.R.; Beck, R.; Best, P.; Carretti, E.; Chyży, K.T.; Enßlin, T.; Farnes, J.S.; Ferrière, K.; et al. Diffuse polarized emission in the LOFAR Two-meter Sky Survey. Astron. Astrophys. 2019, 623, A71. [Google Scholar] [CrossRef]
- Bolton, R.C.; SRCCG. SKA Regional Centre Requirements. 2017. Available online: https://astronomers.skatelescope.org/wp-content/uploads/2017/10/SKA-TEL-SKO-0000735_01-SKA_Regional_Centre_Requirements.pdf (accessed on 4 June 2020).
- An, T.; Wu, X.P.; Hong, X. SKA data take centre stage in China. Nat. Astron. 2019, 3, 1030. [Google Scholar] [CrossRef]
| 1 | |
| 2 | |
| 3 | |
| 4 | In this paper, we focus primarily on the frequency range intended to be covered by the SKA: . |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | See, for example: https://science.nrao.edu/facilities/vla/docs/manuals/obsguide/rfi |
| 14 | See https://github.com/Cameron-Van-Eck/RMTable for a proposed format. |
| 15 | |
| 16 | |
| 17 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Heald, G.; Mao, S.A.; Vacca, V.; Akahori, T.; Damas-Segovia, A.; Gaensler, B.M.; Hoeft, M.; Agudo, I.; Basu, A.; Beck, R.; et al. Magnetism Science with the Square Kilometre Array. Galaxies 2020, 8, 53. https://doi.org/10.3390/galaxies8030053
Heald G, Mao SA, Vacca V, Akahori T, Damas-Segovia A, Gaensler BM, Hoeft M, Agudo I, Basu A, Beck R, et al. Magnetism Science with the Square Kilometre Array. Galaxies. 2020; 8(3):53. https://doi.org/10.3390/galaxies8030053
Chicago/Turabian StyleHeald, George, Sui Ann Mao, Valentina Vacca, Takuya Akahori, Ancor Damas-Segovia, B. M. Gaensler, Matthias Hoeft, Ivan Agudo, Aritra Basu, Rainer Beck, and et al. 2020. "Magnetism Science with the Square Kilometre Array" Galaxies 8, no. 3: 53. https://doi.org/10.3390/galaxies8030053
APA StyleHeald, G., Mao, S. A., Vacca, V., Akahori, T., Damas-Segovia, A., Gaensler, B. M., Hoeft, M., Agudo, I., Basu, A., Beck, R., Birkinshaw, M., Bonafede, A., Bourke, T. L., Bracco, A., Carretti, E., Feretti, L., Girart, J. M., Govoni, F., Green, J. A., ... the SKA Magnetism Science Working Group. (2020). Magnetism Science with the Square Kilometre Array. Galaxies, 8(3), 53. https://doi.org/10.3390/galaxies8030053






