Entropy and Mass Distribution in Disc Galaxies
Abstract
1. Introduction
2. Entropy Changes within an Evolving Galaxy
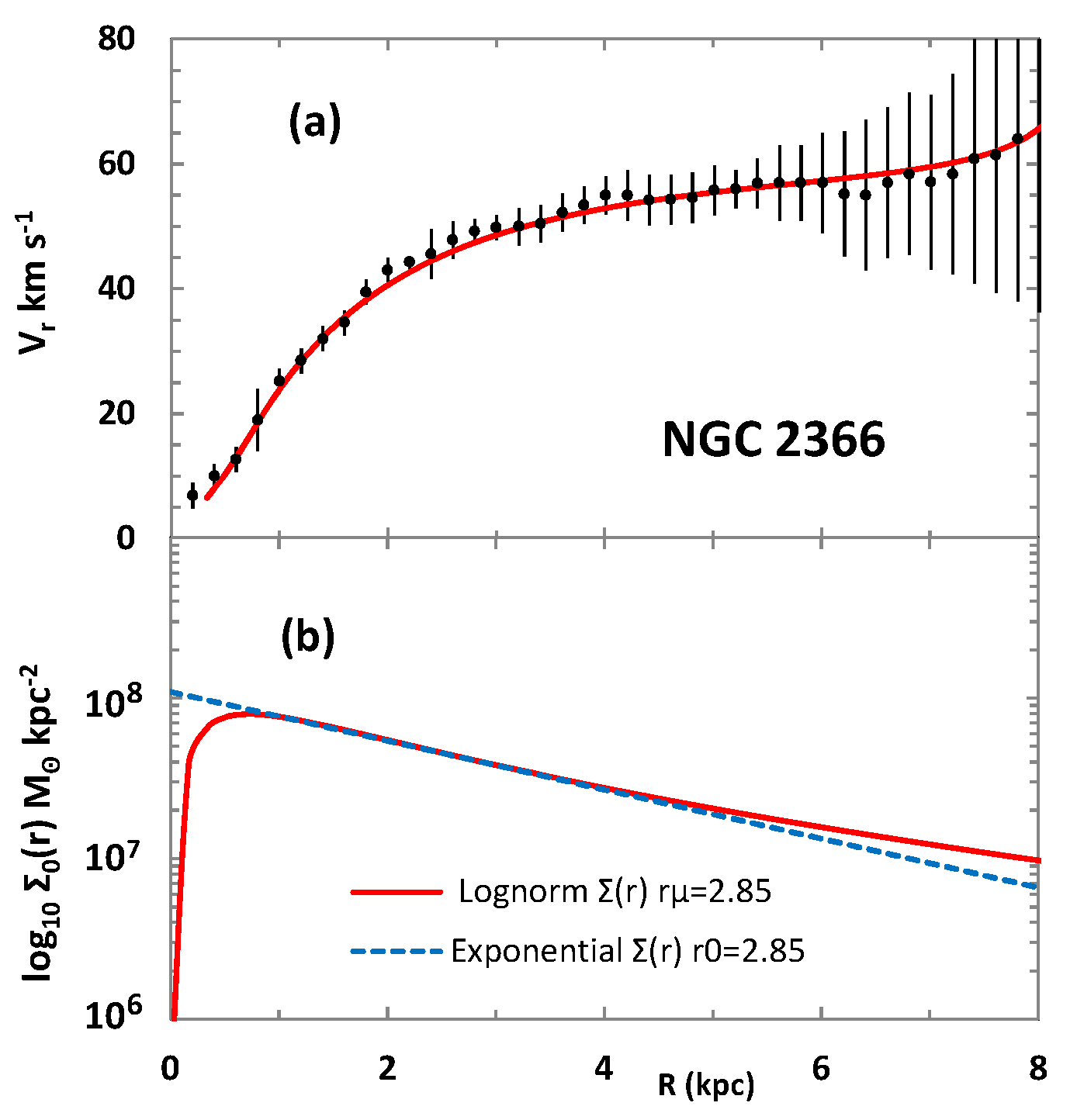
Rationale for a Lognormal Density Distribution
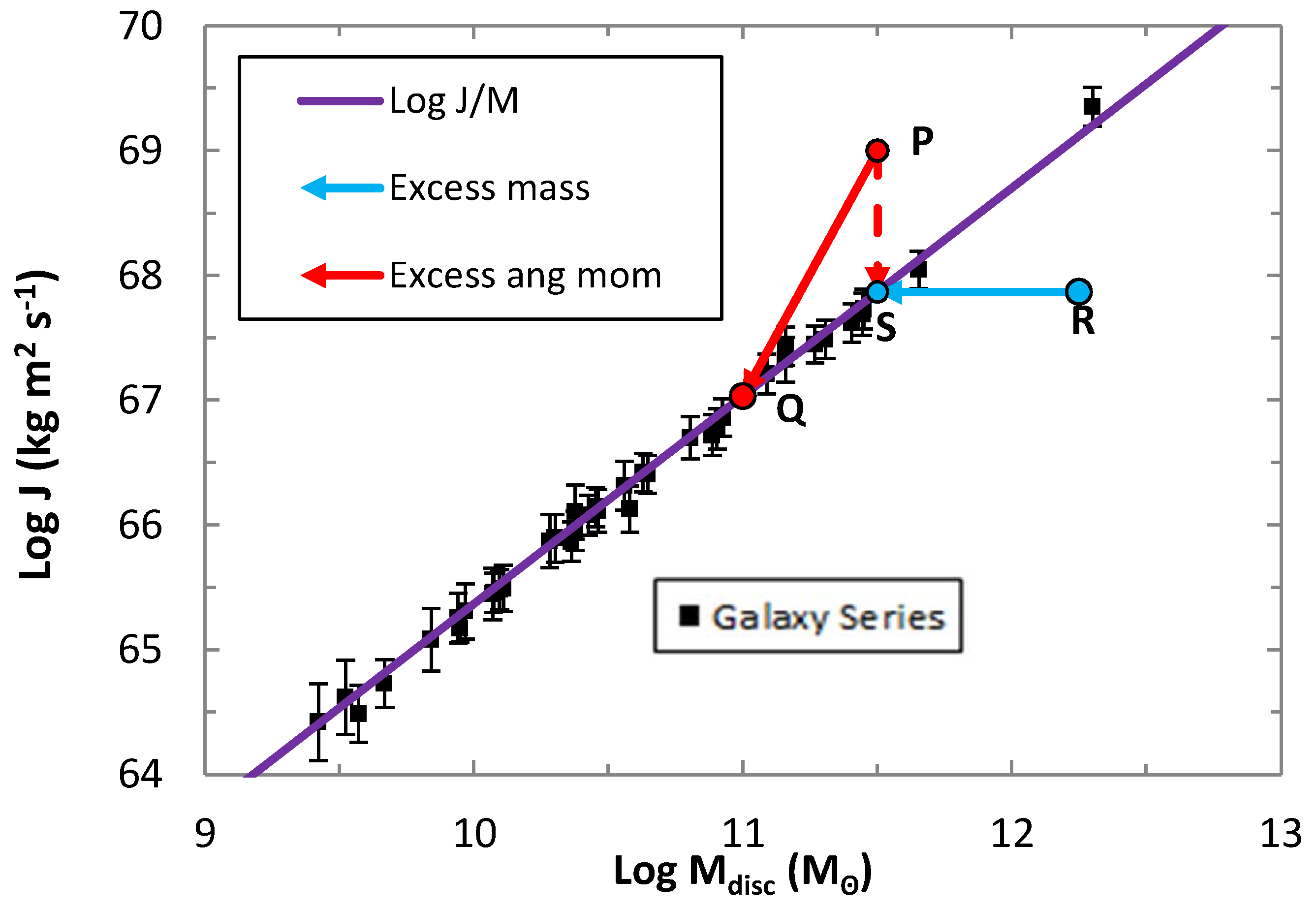
3. Generating the Spin Parameter and Virial Mass Estimator
Changes in Mass and Angular Momentum to Reach Equilibrium
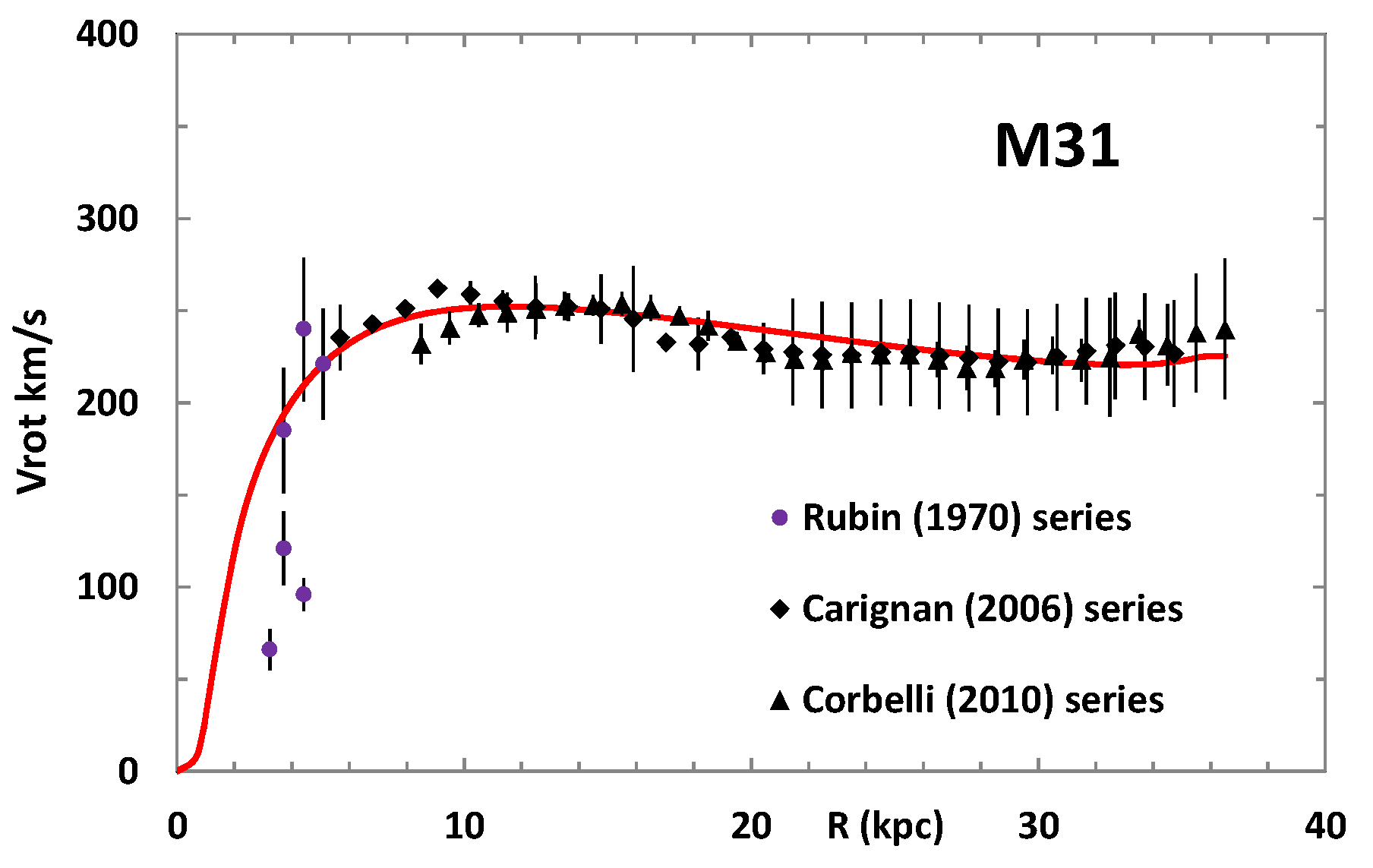
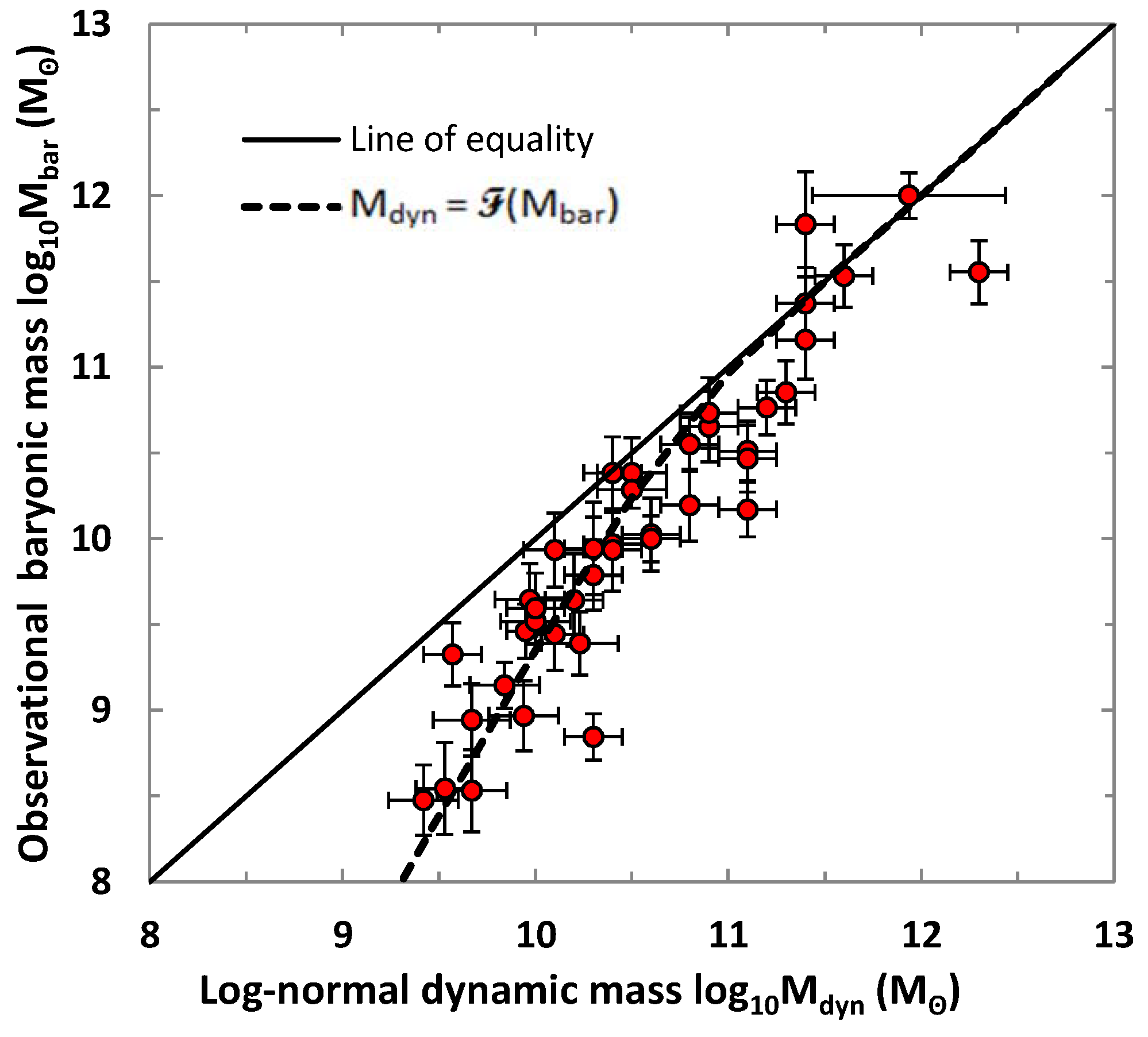
4. The Mass Discrepancy Relation
5. Discussion
Funding
Acknowledgments
Conflicts of Interest
References
- Peebles, P.J.E. Origin of the Angular Momentum of Galaxies. Astrophys. J. 1969, 155, 393. [Google Scholar] [CrossRef]
- Herpich, J.; Tremaine, S.; Rix, H.W. Galactic disc profiles and a universal angular momentum distribution from statistical physics. Mon. Not. R. Astron. Soc. 2017, 467, 5022–5032. [Google Scholar] [CrossRef][Green Version]
- Sellwood, J.A.; Binney, J.J. Radial mixing in galactic discs. Mon. Not. R. Astron. Soc. 2002, 336, 785–796. [Google Scholar] [CrossRef]
- De Simone, R.; Wu, X.; Tremaine, S. The stellar velocity distribution in the solar neighbourhood. Mon. Not. R. Astron. Soc. 2004, 350, 627–643. [Google Scholar] [CrossRef]
- Chakrabarty, D. Local Phase Space—Shaped by Chaos? Astrophys. Space Sci. Proc. 2009, 8, 151. [Google Scholar] [CrossRef]
- Tutukov, A.V.; Shustov, B.M.; Wiebe, D.S. The Stellar Epoch in the Evolution of the Galaxy. Astron. Rep. 2000, 44, 711–718. [Google Scholar] [CrossRef]
- Gurovich, S.; Freeman, K.; Jerjen, H.; Staveley-Smith, L.; Puerari, I. The Slope of the Baryonic Tully-Fisher Relation. Astron. J. 2010, 140, 663–676. [Google Scholar] [CrossRef]
- Papovich, C.; Labbé, I.; Glazebrook, K.; Quadri, R.; Bekiaris, G.; Dickinson, M.; Finkelstein, S.L.; Fisher, D.; Inami, H.; Livermore, R.C.; et al. Large molecular gas reservoirs in ancestors of Milky Way-mass galaxies nine billion years ago. Nat. Astron. 2016, 1, 0003. [Google Scholar] [CrossRef]
- Bellstedt, S.; Lidman, C.; Muzzin, A. The evolution in the stellar mass of brightest cluster galaxies over the past 10 billion years. Mon. Not. R. Astron. Soc. 2016, 460, 2862–2874. [Google Scholar] [CrossRef]
- Padmanabhan, T. Statistical mechanics of gravitating systems. Phys. Rep. 1990, 188, 285–362. [Google Scholar] [CrossRef]
- Marr, J.H. Galaxy rotation curves with lognormal density distribution. Mon. Not. R. Astron. Soc. 2015, 448, 3229–3241. [Google Scholar] [CrossRef]
- Marr, J.H. Angular momentum of disc galaxies with a lognormal density distribution. Mon. Not. R. Astron. Soc. 2015, 453, 2214–2219. [Google Scholar] [CrossRef]
- Binney, J.; Tremaine, S. Galactic Dynamics, 2nd ed.; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Alcobé, S.; Cubarsi, R. Disk populations from HIPPARCOS kinematic data. Discontinuities in the local velocity distribution. Astron. Astrophys. 2005, 442, 929–946. [Google Scholar] [CrossRef][Green Version]
- Cubarsi, R. Large and small-scale structures of the local Galactic disc. A maximum entropy approach to the stellar velocity distribution. Astron. Astrophys. 2010, 510, A103. [Google Scholar] [CrossRef]
- Beck, R. Galactic magnetic fields. Scholarpedia 2007, 2, 2411. [Google Scholar] [CrossRef]
- Ntormousi, E. Magnetic fields in massive spirals: The role of feedback and initial conditions. Astron. Astrophys. 2018, 619, L5. [Google Scholar] [CrossRef]
- Reif, F. Fundamentals of Statistical and Thermal Physics; Waveland Press: Long Grove, IL, USA, 1965. [Google Scholar]
- Sieniutycz, S. Thermodynamic Approaches in Engineering Systems; Elsevier: Amsterdam, The Netherlands, 2016; pp. 260–261. [Google Scholar]
- Anand, V.; Nelanti, K. Second Law Analysis of Laminar Flow in a Circular Pipe Immersed in an Isothermal Fluid. J. Thermodyn. 2013, 2013, 234–264. [Google Scholar] [CrossRef]
- Jaynes, E. Probability Theory: The Logic of Science; Cambridge University Press: Cambridge, UK, 2003; pp. 351–355. [Google Scholar]
- Limpert, E.; Stahel, W.A.; Abbt, M. Log-normal Distributions across the Sciences: Keys and Clues. BioScience 2001, 51, 341–352. [Google Scholar] [CrossRef]
- Park, S.Y.; Bera, A.K. Maximum entropy autoregressive conditional heteroskedasticity model. J. Econometr. 2009, 150, 219–230. [Google Scholar] [CrossRef]
- Stinson, G.S.; Brook, C.; Macciò, A.V.; Wadsley, J.; Quinn, T.R.; Couchman, H.M.P. Making Galaxies In a Cosmological Context: The need for early stellar feedback. Mon. Not. R. Astron. Soc. 2013, 428, 129–140. [Google Scholar] [CrossRef]
- Kapur, J.N.; Kesavan, H.K. Entropy Optimization Principles with Applications; Academic Press: Boston, MA, USA, 1992. [Google Scholar]
- Passot, T.; Vázquez-Semadeni, E. Density probability distribution in one-dimensional polytropic gas dynamics. Phys. Rev. E 1998, 58, 4501–4510. [Google Scholar] [CrossRef]
- Ostriker, E.C.; Stone, J.M.; Gammie, C.F. Density, Velocity, and Magnetic Field Structure in Turbulent Molecular Cloud Models. Astrophys. J. 2001, 546, 980–1005. [Google Scholar] [CrossRef]
- Kainulainen, J.; Beuther, H.; Henning, T.; Plume, R. Probing the evolution of molecular cloud structure. From quiescence to birth. Astron. Astrophys. 2009, 508, L35–L38. [Google Scholar] [CrossRef]
- Brunt, C.M.; Federrath, C.; Price, D.J. A method for reconstructing the PDF of a 3D turbulent density field from 2D observations. Mon. Not. R. Astron. Soc. 2010, 405, L56–L60. [Google Scholar] [CrossRef]
- Fischera, J. On the probability distribution function of the mass surface density of molecular clouds. II. Astron. Astrophys. 2014, 571, A95. [Google Scholar] [CrossRef]
- Pratt, G.W.; Arnaud, M.; Piffaretti, R.; Böhringer, H.; Ponman, T.J.; Croston, J.H.; Voit, G.M.; Borgani, S.; Bower, R.G. Gas entropy in a representative sample of nearby X-ray galaxy clusters (REXCESS): relationship to gas mass fraction. Astron. Astrophys. 2010, 511, A85. [Google Scholar] [CrossRef]
- Pichon, C. Dynamics of Self-Gravitating Disks. Ph.D. Thesis, University of Cambridge, Clare College and Institute of Astronomy, Cambridge, UK, 1994. [Google Scholar]
- Verheijen, M.A.W. The Ursa Major Cluster of Galaxies. V. H I Rotation Curve Shapes and the Tully-Fisher Relations. Astrophys. J. 2001, 563, 694–715. [Google Scholar] [CrossRef]
- Criss, R.; Hofmeister, A. Galactic Density and Evolution Based on the Virial Theorem, Energy Minimization, and Conservation of Angular Momentum. Galaxies 2018, 6, 115. [Google Scholar] [CrossRef]
- Feigelson, E.D.; Babu, G.J. Modern Statistical Methods for Astronomy; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Erwin, P.; Pohlen, M.; Beckman, J.E. The Outer Disks of Early-Type Galaxies. I. Surface-Brightness Profiles of Barred Galaxies. Astron. J. 2008, 135, 20–54. [Google Scholar] [CrossRef]
- Herrmann, K.A.; Hunter, D.A.; Elmegreen, B.G. Surface Brightness Profiles of Dwarf Galaxies. I. Profiles and Statistics. Astron. J. 2013, 146, 104. [Google Scholar] [CrossRef]
- De Blok, W.J.G.; Walter, F.; Brinks, E.; Trachternach, C.; Oh, S.H.; Kennicutt, R.C., Jr. High-Resolution Rotation Curves and Galaxy Mass Models from THINGS. Astron. J. 2008, 136, 2648–2719. [Google Scholar] [CrossRef]
- Rubin, V.C.; Ford, W.K., Jr. Rotation of the Andromeda Nebula from a Spectroscopic Survey of Emission Regions. Astrophys. J. 1970, 159, 379. [Google Scholar] [CrossRef]
- Carignan, C.; Chemin, L.; Huchtmeier, W.K.; Lockman, F.J. The Extended H I Rotation Curve and Mass Distribution of M31. Astrophys. J. Lett. 2006, 641, L109–L112. [Google Scholar] [CrossRef]
- Corbelli, E.; Lorenzoni, S.; Walterbos, R.; Braun, R.; Thilker, D. A wide-field H I mosaic of Messier 31. II. The disk warp, rotation, and the dark matter halo. Astron. Astrophys. 2010, 511, A89. [Google Scholar] [CrossRef]
- Oh, S.H.; de Blok, W.J.G.; Walter, F.; Brinks, E.; Kennicutt, R.C., Jr. High-Resolution Dark Matter Density Profiles of THINGS Dwarf Galaxies: Correcting for Noncircular Motions. Astron. J. 2008, 136, 2761–2781. [Google Scholar] [CrossRef]
- Navarro, J.F.; Steinmetz, M. Dark Halo and Disk Galaxy Scaling Laws in Hierarchical Universes. Astrophys. J. 2000, 538, 477–488. [Google Scholar] [CrossRef]
- Van den Bosch, F.C. The impact of cooling and feedback on disc galaxies. Mon. Not. R. Astron. Soc. 2002, 332, 456–472. [Google Scholar] [CrossRef][Green Version]
- Teklu, A.F.; Remus, R.S.; Dolag, K.; Beck, A.M.; Burkert, A.; Schmidt, A.S.; Schulze, F.; Steinborn, L.K. Connecting Angular Momentum and Galactic Dynamics: The Complex Interplay between Spin, Mass, and Morphology. Astrophys. J. 2015, 812, 29. [Google Scholar] [CrossRef]
- Vettolani, G.; Bergamini, R.; Marano, B.; Zamorani, G. The mass-angular momentum density relation for spiral galaxies. Mon. Not. R. Astron. Soc. 1980, 193, 269–276. [Google Scholar] [CrossRef][Green Version]
- Walter, F.; Brinks, E.; de Blok, W.J.G.; Bigiel, F.; Kennicutt, R.C., Jr.; Thornley, M.D.; Leroy, A. THINGS: The H I Nearby Galaxy Survey. Astron. J. 2008, 136, 2563–2647. [Google Scholar] [CrossRef]
- Gnedin, O.Y.; Brown, W.R.; Geller, M.J.; Kenyon, S.J. The Mass Profile of the Galaxy to 80 kpc. Astrophys. J. Lett. 2010, 720, L108–L112. [Google Scholar] [CrossRef]
- Bhattacharjee, P.; Chaudhury, S.; Kundu, S. Rotation Curve of the Milky Way out to ∼200 kpc. Astrophys. J. 2014, 785, 63. [Google Scholar] [CrossRef]
- McGaugh, S.S. The Baryonic Tully-Fisher Relation of Gas-rich Galaxies as a Test of ΛCDM and MOND. Astron. J. 2012, 143, 40. [Google Scholar] [CrossRef]
- Carignan, C.; Purton, C. The “Total” Mass of DDO 154. Astrophys. J. 1998, 506, 125–134. [Google Scholar] [CrossRef]
- Swaters, R.A.; Madore, B.F.; Trewhella, M. High-Resolution Rotation Curves of Low Surface Brightness Galaxies. Astrophys. J. Lett. 2000, 531, L107–L110. [Google Scholar] [CrossRef] [PubMed]
- McGaugh, S.S. The Baryonic Tully-Fisher Relation of Galaxies with Extended Rotation Curves and the Stellar Mass of Rotating Galaxies. Astrophys. J. 2005, 632, 859–871. [Google Scholar] [CrossRef]
- O’Brien, J.G.; Mannheim, P.D. Fitting dwarf galaxy rotation curves with conformal gravity. Mon. Not. R. Astron. Soc. 2012, 421, 1273–1282. [Google Scholar] [CrossRef]
- Lelli, F.; Fraternali, F.; Sancisi, R. Structure and dynamics of giant low surface brightness galaxies. Astron. Astrophys. 2010, 516, A11. [Google Scholar] [CrossRef]
- Barth, A.J. A Normal Stellar Disk in the Galaxy Malin 1. Bull. Am. Astron. Soc. 2007, 39, 272. [Google Scholar] [CrossRef]
- Elson, E.C.; de Blok, W.J.G.; Kraan-Korteweg, R.C. Star Formation Models for the Dwarf Galaxies NGC 2915 and NGC 1705. Astron. J. 2012, 143, 1. [Google Scholar] [CrossRef]
- Romano, D.; Tosi, M.; Matteucci, F. Formation and evolution of late-type dwarf galaxies—I. NGC1705 and NGC1569. Mon. Not. R. Astron. Soc. 2006, 365, 759–778. [Google Scholar] [CrossRef]
- Tully, R.B.; Courtois, H.M.; Dolphin, A.E.; Fisher, J.R.; Héraudeau, P.; Jacobs, B.A.; Karachentsev, I.D.; Makarov, D.; Makarova, L.; Mitronova, S.; et al. Cosmicflows-2: The Data. Astron. J. 2013, 146, 86. [Google Scholar] [CrossRef]
- Smith, B.J.; Struck, C.; Hancock, M.; Appleton, P.N.; Charmandaris, V.; Reach, W.T. The Spitzer Spirals, Bridges, and Tails Interacting Galaxy Survey: Interaction-Induced Star Formation in the Mid-Infrared. Astron. J. 2007, 133, 791–817. [Google Scholar] [CrossRef]
- Sanders, R.H.; Verheijen, M.A.W. Rotation Curves of Ursa Major Galaxies in the Context of Modified Newtonian Dynamics. Astrophys. J. 1998, 503, 97–108. [Google Scholar] [CrossRef]
- Zavala, J.; Avila-Reese, V.; Hernández-Toledo, H.; Firmani, C. The luminous and dark matter content of disk galaxies. Astron. Astrophys. 2003, 412, 633–650. [Google Scholar] [CrossRef][Green Version]
- Bottema, R. Dark and luminous matter in the NGC 3992 group of galaxies. II. The dwarf companions UGC 6923, UGC 6940, UGC 6969, and the Tully-Fisher relation. Astron. Astrophys. 2002, 388, 809–825. [Google Scholar] [CrossRef]
- Cappellari, M.; Emsellem, E.; Krajnović, D. The ATLAS3D project—I. A volume-limited sample of 260 nearby early-type galaxies: science goals and selection criteria. Mon. Not. R. Astron. Soc. 2011, 413, 813–836. [Google Scholar] [CrossRef]
- Stark, D.V.; McGaugh, S.S.; Swaters, R.A. A First Attempt to Calibrate the Baryonic Tully-Fisher Relation with Gas-Dominated Galaxies. Astron. J. 2009, 138, 392–401. [Google Scholar] [CrossRef]
- Van Albada, T.S.; Sancisi, R. Dark Matter in Spiral Galaxies. Phil. Trans. R. Soc. Lond. A 1986, 320, 447–464. [Google Scholar]
- Janz, J.; Cappellari, M.; Romanowsky, A.J.; Ciotti, L.; Alabi, A.; Forbes, D.A. The mass discrepancy acceleration relation in early-type galaxies: Extended mass profiles and the phantom menace to MOND. Mon. Not. R. Astron. Soc. 2016, 461, 2367–2373. [Google Scholar] [CrossRef][Green Version]
- McGaugh, S.S.; Lelli, F.; Schombert, J.M. Radial Acceleration Relation in Rotationally Supported Galaxies. Phys. Rev. Lett. 2016, 117, 201101. [Google Scholar] [CrossRef] [PubMed]
- Casertano, S.; van Gorkom, J.H. Declining rotation curves—The end of a conspiracy? Astron. J. 1991, 101, 1231–1241. [Google Scholar] [CrossRef]
- Milgrom, M. A modification of the Newtonian dynamics as a possible alternative to the hidden mass hypothesis. Astrophys. J. 1983, 270, 365–370. [Google Scholar] [CrossRef]
- Sanders, R.H. The Published Extended Rotation Curves of Spiral Galaxies: Confrontation with Modified Dynamics. Astrophys. J. 1996, 473, 117. [Google Scholar] [CrossRef]
- De Blok, W.J.G.; McGaugh, S.S. Testing Modified Newtonian Dynamics with Low Surface Brightness Galaxies: Rotation Curve FITS. Astrophys. J. 1998, 508, 132–140. [Google Scholar] [CrossRef]
- Sanders, R.H.; McGaugh, S.S. Modified Newtonian Dynamics as an Alternative to Dark Matter. Annu. Rev. Astron. Astrophys. 2002, 40, 263–317. [Google Scholar] [CrossRef]
- Swaters, R.A.; Sanders, R.H.; McGaugh, S.S. Testing Modified Newtonian Dynamics with Rotation Curves of Dwarf and Low Surface Brightness Galaxies. Astrophys. J. 2010, 718, 380–391. [Google Scholar] [CrossRef]
- Christodoulou, D.M.; Kazanas, D. The Case against Dark Matter and Modified Gravity: Flat Rotation Curves Are a Rigorous Requirement in Rotating Self-Gravitating Newtonian Gaseous Discs. J. Mod. Phys. 2016, 7, 680–698. [Google Scholar] [CrossRef][Green Version]
- Hofmeister, A.M.; Criss, R.E.; Criss, E.M. Verified solutions for the gravitational attraction to an oblate spheroid: Implications for planet mass and satellite orbits. Planet. Space Sci. 2018, 152, 68–81. [Google Scholar] [CrossRef]
- Feng, J.; Gallo, C. Mass Distribution in Rotating Thin-Disk Galaxies According to Newtonian Dynamics. Galaxies 2014, 2, 199–222. [Google Scholar] [CrossRef]
- Pavlovich, K.; Pavlovich, A.; Sipols, A. Newtonian explanation of galaxy rotation curves based on distribution of baryonic matter. arXiv 2014, arXiv:1406.2401. [Google Scholar]
- Kronawitter, A.; Saglia, R.P.; Gerhard, O.; Bender, R. Orbital structure and mass distribution in elliptical galaxies. Astron. Astrophys. Suppl. Ser. 2000, 144, 53–84. [Google Scholar] [CrossRef]
- Bosma, A. Dark Matter in Galaxies: Observational overview. Symp.-Int. Astron. Union 2004, 220, 39. [Google Scholar] [CrossRef][Green Version]
- Danieli, S.; van Dokkum, P.; Conroy, C.; Abraham, R.; Romanowsky, A.J. Still Missing Dark Matter: KCWI High-resolution Stellar Kinematics of NGC1052-DF2. Astrophys. J. Lett. 2019, 874, L12. [Google Scholar] [CrossRef]
- Van Dokkum, P.; Danieli, S.; Abraham, R.; Conroy, C.; Romanowsky, A.J. A Second Galaxy Missing Dark Matter in the NGC 1052 Group. Astrophys. J. Lett. 2019, 874, L5. [Google Scholar] [CrossRef]
- Trujillo, I.; Beasley, M.A.; Borlaff, A.; Carrasco, E.R.; Di Cintio, A.; Filho, M.; Monelli, M.; Montes, M.; Román, J.; Ruiz-Lara, T.; et al. A distance of 13 Mpc resolves the claimed anomalies of the galaxy lacking dark matter. Mon. Not. R. Astron. Soc. 2019, 486, 1192–1219. [Google Scholar] [CrossRef]
- Navarro, J.F.; Benítez-Llambay, A.; Fattahi, A.; Frenk, C.S.; Ludlow, A.D.; Oman, K.A.; Schaller, M.; Theuns, T. The origin of the mass discrepancy-acceleration relation in ΛCDM. Mon. Not. R. Astron. Soc. 2017, 471, 1841–1848. [Google Scholar] [CrossRef]
- Di Cintio, A.; Lelli, F. The mass discrepancy acceleration relation in a ΛCDM context. Mon. Not. R. Astron. Soc. 2016, 456, L127–L131. [Google Scholar] [CrossRef]
- Salem, M.; Besla, G.; Bryan, G.; Putman, M.; van der Marel, R.P.; Tonnesen, S. Ram pressure stripping of the large magellanic cloud’s disk as a probe of the milky way’s circumgalactic medium. Astrophys. J. 2015, 815, 77. [Google Scholar] [CrossRef]
- Gupta, A.; Mathur, S.; Krongold, Y.; Nicastro, F.; Galeazzi, M. A Huge Reservoir of Ionized Gas around the Milky Way: Accounting for the Missing Mass? Astrophys. J. Lett. 2012, 756, L8. [Google Scholar] [CrossRef]
- Draine, B.T.; Dale, D.A.; Bendo, G. Dust Masses, PAH Abundances, and Starlight Intensities in the SINGS Galaxy Sample. Astrophys. J. 2007, 663, 866–894. [Google Scholar] [CrossRef]
- Mendis, D.A.; Marconi, M.L. A note on the total mass of comets in the solar system. Earth Moon Planets 1986, 36, 187–190. [Google Scholar] [CrossRef]
- Moro-Martín, A. Origin of ’Oumuamua. I. An Ejected Protoplanetary Disk Object? Astrophys. J. 2018, 866, 131. [Google Scholar] [CrossRef]
| Name | D | M | M | Total Mass | LN Mass | Refs. |
|---|---|---|---|---|---|---|
| Mpc | (log) | (log) | (log) | (log) | [D][] | |
| DDO 154 | 4.04 | 8.40 | 8.00 | 8.54 ± 0.27 | 9.53 ± 0.15 | [50,51] |
| F563-V2 | 61.0 | 9.51 | 9.74 | 9.94 ± 0.18 | 10.30 ± 0.15 | [52,53] |
| F568-1 | 85.0 | 9.87 | 9.50 | 10.02 ± 0.21 | 10.60 ± 0.15 | [52,53] |
| F568-3 | 77.0 | 9.71 | 9.62 | 9.97 ± 0.18 | 10.40 ± 0.15 | [52,53] |
| F568-V1 | 84.8 | 9.53 | 9.82 | 10.00 ± 0.13 | 10.60 ± 0.15 | [50,53] |
| F574-1 | 96.0 | 10.32 | 9.52 | 10.38 ± 0.21 | 10.40 ± 0.15 | [52,54] |
| IC 2574 | 3.91 | 9.20 | 8.94 | 9.39 ± 0.18 | 10.23 ± 0.20 | [50,53] |
| M31 | 0.78 | 9.70 | 11.36 | 11.37 ± 0.21 | 11.40 ± 0.15 | [40,40] |
| Malin 1 | 366.0 | 10.97 | - - - | 12.00 ± 0.13 | 11.94 ± 0.50 | [55,56] |
| Milky Way | - - - | - - - | - - - | 11.83 ± 0.31 | 11.40 ± 0.15 | [–][49] |
| NGC 1705 | 5.10 | 8.23 | 8.23 | 8.53 ± 0.24 | 9.67 ± 0.18 | [57,58] |
| NGC 2366 | 3.27 | 8.79 | 8.41 | 8.94 ± 0.21 | 9.67 ± 0.20 | [38,50] |
| NGC 2403 | 3.16 | 9.67 | 10.04 | 10.20 ± 0.21 | 10.80 ± 0.15 | [50,53] |
| NGC 2683 | 8.59 | 8.70 | 10.54 | 10.55 ± 0.16 | 10.80 ± 0.15 | [53,59] |
| NGC 2841 | 14.10 | 10.23 | 11.51 | 11.53 ± 0.18 | 11.60 ± 0.15 | [50,53] |
| NGC 2903 | 8.90 | 9.49 | 10.74 | 10.76 ± 0.16 | 11.20 ± 0.15 | [50,53] |
| NGC 2915 | 3.78 | 8.78 | 7.99 | 8.85 ± 0.13 | 10.30 ± 0.15 | [53,53] |
| NGC 2976 | 3.58 | 8.53 | 9.25 | 9.33 ± 0.18 | 9.57 ± 0.15 | [38,50] |
| NGC 3198 | 13.80 | 9.80 | 10.36 | 10.47 ± 0.19 | 11.10 ± 0.15 | [50,53] |
| NGC 3521 | 8.00 | 9.80 | 10.81 | 10.85 ± 0.18 | 11.30 ± 0.15 | [50,53] |
| NGC 3726 | 13.37 | 9.79 | 10.42 | 10.51 ± 0.17 | 11.10 ± 0.15 | [53,59] |
| NGC 3741 | 3.0 | 8.45 | 7.24 | 8.48 ± 0.21 | 9.42 ± 0.18 | [53,53] |
| NGC 4217 | 20.14 | 9.40 | 10.63 | 10.65 ± 0.21 | 10.90 ± 0.15 | [53,59] |
| NGC 4389 | 9.42 | 8.75 | 9.37 | 9.46 ± 0.16 | 9.95 ± 0.10 | [53,59] |
| NGC 6946 | 5.5 | 10.43 | 10.43 | 10.73 ± 0.21 | 10.90 ± 0.15 | [53,60] |
| NGC 7331 | 13.87 | 10.04 | 11.12 | 11.16 ± 0.23 | 11.40 ± 0.15 | [53,59] |
| NGC 7793 | 3.38 | 9.46 | 9.76 | 9.93 ± 0.22 | 10.10 ± 0.16 | [53,59] |
| NGC 925 | 8.91 | 10.15 | 10.01 | 10.38 ± 0.21 | 10.50 ± 0.18 | [38,59] |
| UGC 128 | 58.5 | 9.96 | 9.76 | 10.17 ± 0.16 | 11.10 ± 0.15 | [50,53] |
| UGC 2885 | 75.9 | 10.70 | 11.49 | 11.55 ± 0.18 | 12.30 ± 0.15 | [50,53] |
| UGC 5750 | 56.1 | 9.71 | 9.00 | 9.79 ± 0.21 | 10.30 ± 0.15 | [54,54] |
| UGC 6399 | 15.5 | 8.85 | 9.32 | 9.44 ± 0.21 | 10.10 ± 0.15 | [61,61] |
| UGC 6446 | 15.5 | 9.51 | 9.07 | 9.64 ± 0.27 | 10.20 ± 0.15 | [61,61] |
| UGC 6667 | 18.2 | 8.90 | 9.40 | 9.52 ± 0.13 | 10.00 ± 0.18 | [53,59] |
| UGC 6818 | 19.5 | 9.00 | 8.60 | 9.15 ± 0.13 | 9.84 ± 0.18 | [53,59] |
| UGC 6917 | 15.5 | 9.53 | 9.73 | 9.94 ± 0.27 | 10.30 ± 0.15 | [53,61] |
| UGC 6923 | 18.67 | 9.07 | 9.44 | 9.59 ± 0.21 | 10.00 ± 0.15 | [59,62] |
| UGC 6969 | 18.6 | 8.79 | 8.49 | 8.97 ± 0.21 | 9.94 ± 0.18 | [63,63] |
| UGC 6973 | 36.8 | 9.38 | 10.23 | 10.29 ± 0.02 | 10.50 ± 0.18 | [61,64] |
| UGC 6983 | 18.6 | 9.46 | 9.76 | 9.93 ± 0.24 | 10.40 ± 0.15 | [53,65] |
| UGC 7089 | 15.5 | 9.40 | 9.28 | 9.65 ± 0.21 | 9.97 ± 0.18 | [61,62] |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marr, J.H. Entropy and Mass Distribution in Disc Galaxies. Galaxies 2020, 8, 12. https://doi.org/10.3390/galaxies8010012
Marr JH. Entropy and Mass Distribution in Disc Galaxies. Galaxies. 2020; 8(1):12. https://doi.org/10.3390/galaxies8010012
Chicago/Turabian StyleMarr, John Herbert. 2020. "Entropy and Mass Distribution in Disc Galaxies" Galaxies 8, no. 1: 12. https://doi.org/10.3390/galaxies8010012
APA StyleMarr, J. H. (2020). Entropy and Mass Distribution in Disc Galaxies. Galaxies, 8(1), 12. https://doi.org/10.3390/galaxies8010012





