Rotating Disk Galaxies without Dark Matter Based on Scientific Reasoning

Abstract

The most cited evidence for (non-baryonic) dark matter has been an apparent lack of visible mass to gravitationally support the observed orbital velocity of matter in rotating disk galaxies, yet measurement of the mass of celestial objects cannot be straightforward, requiring theories derived from the known physical laws along with some empirically established semi-quantitative relationship. The most reliable means for determining the mass distribution in rotating disk galaxies is to solve a force balance equation according to Newton’s laws from measured rotation curves, similar to calculating the Sun’s mass from the Earth’s orbital velocity. Another common method to estimate galactic mass distribution is to convert measured brightness from surface photometry based on empirically established mass-to-light ratio. For convenience, most astronomers commonly assumed a constant mass-to-light ratio for estimation of the so-called “luminous” or “visible” mass, which would not likely be accurate. The mass determined from a rotation curve typically exhibits an exponential-like decline with galactrocentric distance, qualitatively consistent with observed surface brightness but often with a larger disk radial scale length. This fact scientifically suggests variable mass-to-light ratio of baryonic matter in galaxies without the need for dark matter.

1. Introduction

Based on scientific observations, many galaxies (including the Milky Way) appear to have a common visible shape of thin disk as shown in Figure 1. Known as a stellar system of an ensemble of stars and other masses, a disk galaxy (such as the Milky Way) usually contains 10⁵ to 10¹² stars distributed in a flattened, roughly axisymmetric structure, rotating around a common axis in nearly circular orbits. Besides stars, the galactic “disk” is also known to contain an interstellar medium such as gases (mostly atomic and molecular hydrogen) as well as relatively small solid “dust particles”. The general behavior of stellar systems, including disk galaxies, has been believed to follow Newton’s laws of motion and Newton’s law of universal gravitation [1].

Since their discovery in the 17th century, Newton’s laws of motion have been used to successfully determine the relationship between a body of mass and the forces acting upon it, and its motion in response to those forces, for a great variety of situations and phenomena. When combined with his law of gravitation, Newton [2] could show (in terms of mathematical expressions) that Kepler’s mysterious laws are actually consequences of his laws of motion. To date, there is no direct evidence suggesting a failure of Newtonian dynamics in describing motions of celestial objects in stellar systems, although some relativistic effects may be present at the centers of galaxies [1]. According to Newtonian dynamics, the mass of an object can be determined from its motion such as acceleration in a gravitational field. If the mass distribution in a galaxy cannot be measured directly, it can be derived from the measured rotation curve, expressed in terms of distribution of objects’ orbital velocity as a function of galactocentric distance, which may require some mathematical efforts but should be a theoretically rather straightforward exercise. Such a derived mass distribution (from rotation curve according to Newtonian dynamics) should be considered reasonable as long as the value of mass does not appear against any physical laws, e.g., having a negative value or infinity, etc.

However, in recent decades we have been told that about 83% mass of our universe is made up by some type of mysterious “dark matter”, which cannot be detected by electromagnetic radiation or reaction, in contrast to any known substances of properties determined by available scientific method. The reason for the belief of existence of the dark matter with its mysterious properties is due to inference from its gravitational effects on “visible” matter, radiation, and large-scale structure of the universe [3]. Numerous articles have been published to investigate the elusive dark matter, with many books also written to describe such efforts [3,4,5,6,7,8], yet very few attempted to examine the validity and certainty of the claimed evidence for existence of the so-called dark matter, based on scientific reasoning with rigorous logic [9].

To understand the natural world, scientists acquire knowledge using the scientific method which involves observation, formulating hypotheses via induction, experimental testing with quantitative measurements, and refinement or elimination of the hypotheses based on the experimental findings. If well supported by experimental measurements, a particular hypothesis may be further developed to a general theory. By scientific reasoning we should inquire whether or not evidence is consistent with a claim or theory, or whether the evidence that render a claim could be invalid. Therefore, the claimed existence of the (mysterious) dark matter should have been put under rigorous scientific scrutiny, before making it sound like being well supported by observational evidence. Actually, deficient reasoning for dark matter in galaxies has been pointed out by examining the claimed evidence in the literature [9], though nonmainstream.

It is understandable that as human beings, scientists can be tempted to tell the mystery of dark matter for being much more effective to attract press attention than simply describing the observed astronomical phenomena in terms of the well-known Newtonian dynamics. When discussing the subject of dark matter, few authors bother to question whether the reasoning for dark matter might be invalid, whereas majority would rather present strange models assuming the presence of dark matter. Nowadays, the dark matter is so firmly believed to be present that the finding of “a galaxy lacking dark matter” can become quite a news-making story in the scientific community [10,11]. Yet scientists are expected to have the genuine passion in truth seeking.

In what follows, we first examine the nature of astronomical measurements, and technical challenges as well as certainty or uncertainty associated with them. The methods for determining mass of celestial objects are briefly reviewed next. Then, mass distribution in a rotating disk galaxy, determined with the available measurements, is discussed with explanations based on scientific reasoning without dark matter. Concluding remarks are provided in the final section.

2. Astronomical Measurements

The behavior of celestial objects, such as stars and galaxies, cannot be described without mentioning their mass, distance and velocity of movement. It turns out that the distance between objects becomes the key for determining the mass and velocity of an object. Once the distance of an object is measured, its variation within a given time interval determines the object’s velocity, and its relative position with respect to other objects can be determined, but the measurements of astronomical distance have been quite challenging with considerable uncertainties [9,12]. In fact, a recent analysis has shown a significant difference between a previously indicated distance of 20 Mpc and presently determined 13 Mpc [13] (1 pc = 3.26 light-years = 3.08 × 10¹⁶ m).

Space is actually huge. Astronomical objects are typically scattered in a vast space, separated by distances often measured in units of light-years (1 light-year = 9.46 × 10¹⁵ m, the distance for light to travel in 1 year in vacuum). For example, the nearest star to our solar system is about 4.22 light-years away. The distance between the Sun and Earth is ~1.5 × 10¹¹ m, taking about 8.3 minutes for light from the Sun to reach us. Even our next-door neighbor, the Moon, is about 3.8 × 10⁸ m away, a lot farther than most people would think. Only objects within our own solar system can our present spacecraft reach. For the most part, the cosmos is out of our reach, except light that travels throughout the universe can bring information about distant objects to us on the Earth.

In astronomy, measurements are carried out almost exclusively by studying and analyzing the “light”, or more generally the electromagnetic radiation, emitted or absorbed or reflected or scattered or transmitted by remote objects such as stars, galaxies, and so forth [14,15]. The emission and absorption line spectra can be used to determine the material composition, while the continuous thermal radiation spectrum can tell us the temperature of a remote object. The speed of a celestial object moving toward or away from us can be determined by the Doppler shift in the light spectral lines, which actually became the basis for measuring the rotation curve of galaxies.

For stars, their (surface) temperature, luminosity, and mass are among the most important properties. A star’s surface temperature can be obtained fairly easily from its thermal radiation spectrum or even simply its color, which is not influenced by its distance (theoretically). But measurements of a star’s luminosity (the total amount of power it emits into space) from the apparent brightness (the brightness of a star as it appear to our eyes, or to a detector like a CCD) relies on the inverse square law for light which directly uses its distance from us. Thus, to determine the distance of a star becomes the key to determine its luminosity.

The most direct way to measure a star’s distance is by stellar parallax, which uses the angle due to annual shift of its position relative to distant background stars, as Earth moves from one side of its orbit to the other, to determine its distance. This is why the parsec or pc (corresponding to PARallax of one arcSECond”)—a measure of tiny angles in the stellar sphere—becomes the preferred distance unit for astronomers in professional literature. Parallaxes may provide us distances to stars up to a few thousand light years away, i.e., in the solar neighborhood. But even the nearest galaxies and galaxy clusters are millions of light-years away, too far for measurements by just using parallax. So, a system called the cosmic distance ladder has been created based on overlapping methods to calculate successively farther distances [12].

Larger distances rely on the so-called standard candle as well as a technique known as the main-sequence fitting to estimate, based on assumptions over assumptions [12,14,15], yet no astronomical object is a perfect standard candle; the challenge of finding the objects that can serve as the standard candles leads to the challenge of measuring large astronomical distances. In short, uncertainties in astronomical distances can be significant [9], as may not even be easily quantified due to multiple steps of overlapping, each brings in its own uncertainties.

The distance of an astronomical object seems to be difficult to determine, yet it plays the key role in calculating the object’s mass from the known physical laws. In other words, masses of astronomical objects cannot be determined without knowing the relative distances among them.

3. Mass Determined by Newtonian Dynamics—“Gravitational Mass”

Once the relative distance and velocity of motion of objects are known from measurements, each object’s mass may be determined from Newton’s laws. If we believe the forces among celestial objects are of gravitational nature (according to Newton’s universal law of gravitation), the gravitational field of an object (which is proportional to its mass) can be determined by measuring the acceleration of a small nearby “test object”. Then the object’s mass can be determined from its gravitational field. For example, the Sun’s mass can be determined using the Earth as a test object (which has a negligible mass comparing to that of the Sun) by applying the formula of Newton’s version of Kepler’s third law, with the measured average distance between the Earth and the Sun, a (≈ 1.5 × 10¹¹ m) and the Earth’s orbital period, p ((≈ 3.15 × 10⁷ s, i.e., 1 year) [14,15]. In other words, having centripetal acceleration of the Earth:

$$\frac{{\left(2 \pi \right)}^2 a}{p^2}=\frac{V^2}{a}$$

(1)

equal to the gravitational field of the Sun:

$$\frac{G M_{sun}}{a^2}$$

(2)

where G (= 6.67 × 10⁻¹¹ m³ kg⁻¹ s⁻²) is the gravitational constant and M_sun the Sun’s mass, yields the value of M_sun ≈ 2.0 × 10³⁰ kg (= 1 solar mass M_⊙). Here V denotes the Earth’s (or the test object’s) orbital velocity.

By the same token, stellar masses in a binary star system—consisting of two gravitationally bound stars orbiting around a common center of mass—can, in principle, also be determined with known separation a or orbital velocity V and orbital period p based on the theory of Newtonian dynamics for a two-body problem. It has been shown that the two-body problem can be treated as an equivalent one-body problem in which the reduced mass m = m₁ m₂ / (m₁ + m₂) is orbiting about a fixed mass M = m₁ + m₂ at a distance a = a₁ + a₂ where the subscripts “1” and “2” denotes the masses and radii of the star “1” and star “2” [16]. In fact, the value of M_sun determined from an equation of (1) = (2) is actually reduced from the solution for two-body Kepler’s problem to an extreme case when m₁ >> m₂ such that m $\to$ 0, a₁ $\to$ 0, and M $\to$ m₁ (= M_sun or 1.0 M_⊙). Thus, the value of M (= m₁ + m₂) in a binary star systems can be determined. With the known M, the values of m₁ and m₂ can be determined from the relationship of m₂ / m₁ = a₁ / a₂ = v₁ / v₂ (where v₁ and v₂ are the orbital velocities of the two stars) derived from the two-body problem. In reality, the distances a₁ and a₂ are not easy to determine accurately. Instead, the values of v₁ and v₂ can be measured much more reliably based on the measured Doppler shifts, especially for the so-called “eclipsing binaries” with their orbit planes lying very close in the line of sight [14,15].

In a galaxy, a large number (10⁵–10¹²) of stars, with an interstellar medium of gas and cosmic dust, among others, are distributed in an extensive space such as a thin disk of radius about 10 kpc (or 3.09 × 10²⁰ m). Simply adding the “point mass” fields of such a distributed stellar system with ~10¹¹ stars is impractical to compute the gravitational field in a typical galaxy, so it becomes a common practice, for most purposes, to model the gravitational field or potential “by smoothing the mass density in stars on a scale that is small compared to the size of the galaxy, but large compared to the mean distance between stars” [1], i.e., to treat the distributed mass system as a continuum, as a reasonable approximation.

Observations have shown that many astronomical systems, such as planetary systems, planetary rings, accretion disks, spiral galaxies, etc., appear flat (cf. Figure 1) for a basic reason of the state with lowest energy in a flat disk perpendicular to an axis along which a distribution of angular momentum is given for a system of constant mass [1]. Therefore, it may not be unreasonable to approximately consider a galaxy as an axisymmetric rotating thin disk, shown in Figure 2, consisting of distributed self-gravitating mass (as a function of the galactocentric distance r) in balance with distributed centrifugal force due to distributed circular orbital velocity (as a function of r). Over years, various mathematical methods have been developed for deducing the mass distribution from the measured rotation curve with the axisymmetric thin-disk model at mechanical equilibrium [1,17], each with its own pros and cons. Here a numerical method by Gallo and Feng [18,19,20,21] is briefly described, without loss of generality.

At any point in a rotating axisymmetric disk galaxy with negligible disk thickness effect, the centripetal acceleration of (related to the centrifugal force on) a test object:

$$\frac{V_0^2}{R_g} \frac{V{\left(r\right)}^2}{r}$$

(3)

is expected to be equal to the gravitational field from the distributed mass in the entire disk:

$$\frac{G M_g}{R_g^2}{\int }_0^1\left[{\int }_0^{2 \pi }\frac{\left(r-\widehat{r}\cos \theta \right) d\theta }{{\left({\widehat{r}}^2+r^2-2 \widehat{r} r\cos \theta \right)}^{3/2}}\right]\rho \left(\widehat{r}\right)h\widehat{r}d\widehat{r}$$

(4)

where R_g denotes the galactic radius (or the galactocentric distance of the galaxy edge, taken as the cut-off radius in rotation curve beyond which the detectable signal diminishes), M_g the total mass of the galaxy, and V₀ the characteristic rotation velocity as a representative value of the flat part of rotation curve. All the variables in (3) and (4) are made dimensionless by measuring length r, h in units of the galactic radius R_g, mass density ρ in units of M_g / R_g³, and rotation velocity V in units of V₀, with the disk thickness h assumed to be constant.

It is noteworthy that equating (3) and (4) has the exactly same physical meaning as equating (1) and (2), as the force balance equation for determining the rotation velocity from a known gravitational field source—the amount of mass or mass distribution, or vice versa. For example, the Sun’s mass can be determined from the known Earth’s orbital velocity as shown with equating (1) and (2). Similarly, when the galactic rotation curve V(r) is available from measurements, the mass distribution ρ(r) can be determined by solving the force balance equation from equating (3) and (4), which will involve some mathematical manipulations.

Among many different approaches to solution of the force balance equation (3) = (4), Gallo and Feng [18,19,20,21] showed that with slight algebraic arrangements an equation can be obtained of the form:

$${\int }_0^1\left[\frac{E\left(m\right)}{\widehat{r}-r}-\frac{K\left(m\right)}{\widehat{r}+r}\right]\rho \left(\widehat{r}\right)h\widehat{r}d\widehat{r}+\frac{A}{2} \frac{V{\left(r\right)}^2}{r}=0$$

(5)

where K(m) and E(m) denote the complete elliptic integrals of the first kind and second kind, with:

$$m\equiv \frac{4 \widehat{r} r}{{\left(\widehat{r}+r\right)}^2}.$$

The dimensionless parameter A in (5), called the galactic rotation parameter, is defined as:

$$A\equiv \frac{V_0^2 R_g}{G M_g}$$

(6)

which can be determined by introducing a constraint equation for mass conservation,

$$2 \pi {\int }_0^1\rho \left(\widehat{r}\right)h\widehat{r}d\widehat{r}=1$$

(7)

Equations (5) and (7) can be discretized by dividing the problem domain 0 ≤ r ≤ 1 into a large number, e.g., N − 1, of small line segments called (linear) elements, leading to a linear algebraic problem in the matrix-vector form, for solving N nodal values of ρ plus A in (6) with N equations for individual nodes from (5) and an equation based on (7), with known V(r) [18,19,20,21]. Conversely, the same matrix-vector equation can also be used for calculating the rotation curve V(r) if the mass distribution ρ(r) is known or assumed given. The matrix-vector approach described here as well as the implemented computational code was validated by producing the same results as the known analytical solutions for the Mestel disk and Freeman disk [20]. It also yielded mass distribution for NGC 4736 based on measured rotation curves, comparable to that obtained using an iterative spectral method with Bessel functions by other authors [21]. Similar results from the equation of (3) = (4) were also shown with a model using lognormal mass distribution function [22]. By adding a spherical core at the galactic center, as can easily be implemented with this matrix-vector approach, mass distribution can be computed without central singular mass density for rotation curves with nonzero velocity at r = 0 [21]. Thus, the mass distribution ρ(r) (actually the surface mass distribution [ρ(r) h]) can be determined for any galaxy from its measured rotation curve V(r), according to Newtonian dynamics.

Since the rotation curve in a spiral galaxy can be measured with reasonable certainty [23], it has been accepted to provide the most reliable means for determining the distribution of gravitating matter therein [17]. However, a rotation curve of V(r) implies axisymmetry and negligible variation across the thickness and is at best a piece of approximate information about the behavior of a rotating thin-disk galaxy, which is usually not exactly axisymmetric with detailed asymmetric structures such as spiral arms. Hence, the mass distribution ρ(r) determined from a rotation curve V(r) with a thin-disk model provides the value only in a sense of averaging over the ring of radius r which may not be the same as the local mass density at a specific position on this very ring. The galaxies, though appearing like a thin disk, also have “vertical” structures across the visible thickness. Therefore, taking the predicted mass density with an axisymmetric thin-disk model out of context to compare some measured value at a specific location inside a galaxy (e.g., the solar neighborhood in the Milky Way) could naturally lead to substantial discrepancy. If splitting hairs with such an expected discrepancy to discredit the thin-disk model, the outcomes can be confusing with technically immature arguments. Only with a thorough understanding of the assumptions and approximate nature in using the rotation curve to determine mass distribution in a disk galaxy, can the model results be interpreted correctly for enhancing scientific knowledge.

The computational results based on measured rotation curves for many galaxies of various types had shown more or less exponential decrease of (surface) mass density with galactocentric distance such as ρ(r) = ρ(0) exp(−r / R_d), i.e., the computed ρ verses r in a log-linear plots appear to be nearly straight lines with negative slopes, for the most part when the abruptly varying ends at r = 0 and 1 are trimmed out [18,19,20,21]. Hence, the “gravitational mass”—determined from rotation curves--distributions in disk galaxies qualitatively agree with the measured radial distributions of surface brightness for a large number of disk galaxies [24,25,26], but the disk radial scale length, R_d, determined from rotation curve based thin-disk model appears to be larger than that from fitting the brightness data (e.g., 4.5 kpc versus 2.5 kpc for Milky Way [20]). A straightforward interpretation of such a discrepancy would be an indication of increasing mass-to-light ratio with galactocentric distance, namely the (baryonic) matter becomes less luminous in regions further away from the galactic center. This is consistent with typical edge-on views of disk galaxies that often revealing a dark edge against a bright background central bulge (cf. the image of NGC 891 in Figure 1).

4. Mass Determined by Mass-to-Light Ratio—“Luminous Mass”

Astronomical measurements rely on the analysis of signals carried by electromagnetic waves, or the “light”. Considerably efforts have been made in correlating the light signal to characteristic physical properties of stars and galaxies. Anything that may be derived from the light signal are taken seriously and used for describing the behavior of celestial objects.

For example, the stellar (gravitational) mass M determined from binary stars has become the key component for establishing the so-called “mass-to-light” ratio M/L, by correlating the luminosity L of stars to their masses. As the apparent brightness of a star is measured from a detector, it is expected to relate to the star’s luminosity and distance based on the inverse square law. With the given luminosity L and (surface) temperature T determined from its thermal radiation spectrum (based on Stefan-Boltzmann law and Wien’s displacement law), the surface area and size (i.e., the radius R) of a star may be calculated from the relationship [1,14,15]:

$$L=4 \pi R^2\times \sigma T^4$$

(8)

where σ = 5.67 × 10⁻⁸ W m⁻² K⁻⁴ is the Stefan-Boltzmann constant for black-body radiation. However, it should be kept in mind that the emissions of galaxies may not exactly follow that of a blackbody with emissivity equal to 1, in the presence of dust and gases.

With the measured stellar properties (from nearby stars in the solar neighborhood), Hertzsprung and Russelll independently developed a stellar classification system by plotting luminosities versus surface temperatures—now called Hertzsprung-Russell (H-R) diagram or the color-magnitude diagram. This kind of diagram has become “the primary point of contact between observations and the theory of stellar structure and evolution” [1]. Most stars, including our Sun, fall somewhere along the streak from the upper left (high luminosity and temperature corner) to the lower right (low luminosity and temperature corner) on the H-R diagram; they are called the main-sequence stars. There are also larger and brighter stars located above those of the main sequence, called giants and supergiants, whereas smaller high temperature stars, located below those of the main sequence, are called white dwarfs, because they appear white in color. All stars along the main sequence are fusing hydrogen into helium in their cores, like the Sun. However, the main sequence stars differ in surface temperature and luminosity because the rate of hydrogen fusion depends strongly on the stellar mass, i.e., a star with more massive outer layer must sustain a higher nuclear fusion rate in order to maintain gravitational equilibrium. When astronomers measured the masses of main-sequence stars in binary star systems, they found that a star’s position along the main sequence is very closely related to its mass [14,15]. For stars with both mass and luminosity determined, the values of their stellar mass-to-light ratio M / L become known, which may be used for estimating the masses of similar stars either not belonging to the binary systems or being too remote to measure directly.

Surface photometry—a technique to measure the surface brightness distribution of extended objects, such as galaxies—has shown that galaxies typically have luminosity profiles decreasing approximately as an exponential function of the galactocentric distance r [24,25,26]. Many authors simply assumed the same exponential function for the surface mass density distribution, implying an assumption of constant M / L [24] for deriving the “luminous mass”.

But among all the observable galaxies, individual stars can only be observed in the few closest ones. A galaxy is a composite of millions and millions of stars of differing ages and masses over a wide spectrum. To evaluate the overall mass-to-light ratio of a galaxy involves, its stellar population must be studied with stellar population synthesis modeling, etc. Such a challenging sophisticated endeavor with severely limited means of direct observation and measurements is expected to lead to results of questionable certainties, which might be only useful for order-of-magnitude rough estimate of the amount of mass. Nonetheless, luminous masses from observed brightness based on estimated mass-to-light ratios have been taken so seriously with overwhelming confidence that their apparent difference from the gravitational masses (determined from rotation curves) became a primary evidence for dark matter in galaxies [3,4,5,6,7,8].

5. Galaxy Rotation Curves Described without Dark Matter

Celestial objects cannot be brought to the Earth and weighed on a balance to measure their masses. But their motion can be observed with movement velocity measured from the Doppler shift of their light spectral lines. The motions of astronomical objects are believed as their responses to the gravitational interactions, according to Newtonian dynamics [1,14,15] (as had been tested and confirmed numerous times over hundreds of years).

Newton’s laws of motion describe the relationship among force, acceleration and mass. Newton’s law of universal gravitation relates the gravitational force to the distribution of masses and relative positions of interacting objects. Once the masses and relative positions of interacting celestial objects are known, the gravitational force on each of them and their motions (in terms of velocity, acceleration) can be determined. Conversely, their masses can be determined from their relative positions and motions, if made available by measurements.

For example, the mathematical form of Newtonian dynamics for a rotating thin disk galaxy of gravitationally bound objects, e.g., stars, gases, dust, etc., can be expressed (approximately by assuming the axisymmetry) as (3) equal to (4), relating the mass distribution ρ(r) to measured rotation curve V(r). Thus, the rotation curve V(r) can be determined if mass distribution ρ(r) is known, by calculating the integral in (4); conversely, ρ(r) in (4) can be determined from the known V(r) in (3), which usually takes more mathematical effort though. As a matter of fact, various methods for solving ρ(r) or [ρ(r) h] from the known V(r) have been developed by different authors, with pros and cons pointed out and discussed from various perspectives [1,17,18,19,20,21,22]. Despite the apparent differences in calculation procedures among different authors, the end results should be the same theoretically because the solution to equation (3) = (4) is unique due to its linear nature.

With available modern technologies, the rotation curves have been measured for many (disk) galaxies [23]. Using a measured rotation curve V(r), the calculated surface mass density [ρ(r) h], e.g., by solving the linear algebra matrix problem based on (5) and (7), appears to decrease linearly in the log-linear plot excluding the small regions around the galactic center and disk edge (where the measured rotation curve terminates), for various galaxies [20,21]. This indicates that the surface mass density in a thin-disk galaxy declines exponentially with the galactocentric distance, in general, as consistent with what have been measured by surface photometry for surface brightness profiles of many galaxies [24,25,26], qualitatively at least. Because the galactic rotation parameter A, defined in (6), is also determined as part of the solution to the linear algebra problem based on (5) and (7), the total mass of M_g can be calculated from the predicted value of A as M_g = V₀² R_g / (G A). For example, the Milky Way total mass is determined as 1.41 × 10¹¹ M_⊙ from predicted A = 1.6365 with V₀ = 220 km/s and R_g = 20.55 kpc [21], very close to the Milky Way star counts of about 100 billion [1,27]. The numerical approach for solving (5) and (7) can also account for the effect of a spherical bulge at galactic center with slight mathematical manipulation [21], with results illustrated in Figure 3 for the Milky Way. It has been shown that even for a bulge of mass as large as 7.57 × 10¹⁰ M_⊙, the Milky Way total mass would only change to 1.52 × 10¹¹ M_⊙ (i.e., a less than 8% increase [21]). The total mass of the Andromeda (NGC 224) can also be calculated as 2.76 × 10¹¹ M_⊙ from A = 1.6450 with V₀ = 250 km/s and R_g = 31.25 kpc [21], about twice that of the Milky Way, as commonly being anticipated.

Interestingly, the value of A defined in (6) seems to be around 1.70 for various rotation curves, when the characteristic velocity V₀ is taken as a representative value of the flat part of rotation curve [18,19,20,21]. For Mestel’s disk of constant rotation velocity with available analytical solution, the value of A is determined as π/2 = 1.5707063 [20]. A proportionality constant from a lognormal density distribution model results of 38 galaxies for M_g versus V_max ² R_g [28] indicates a value of A equal to 1.57063 if V_max and V₀ happen to be the same as with Mestel’s disk. Comparing with the scalar virial theorem, M_g = <V²> r_g / G with <V²> and r_g denoting the mean-square speed of the system’s stars and the gravitational radius [1], this suggests that <V²> r_g = V₀ ² R_g / A, i.e., r_g ~ 0.59 R_g if <V²> = V₀ ² is assumed. Given the fact that <V²> also includes the velocity dispersion in addition to the rotational orbital part, it seems that r_g = 0.5 R_g (corresponding to <V²> ~ 1.18 V₀ ²) could be a reasonable approximation for rough estimate of the total mass in a disk galaxy from the measured rotational velocity based on the virial theorem.

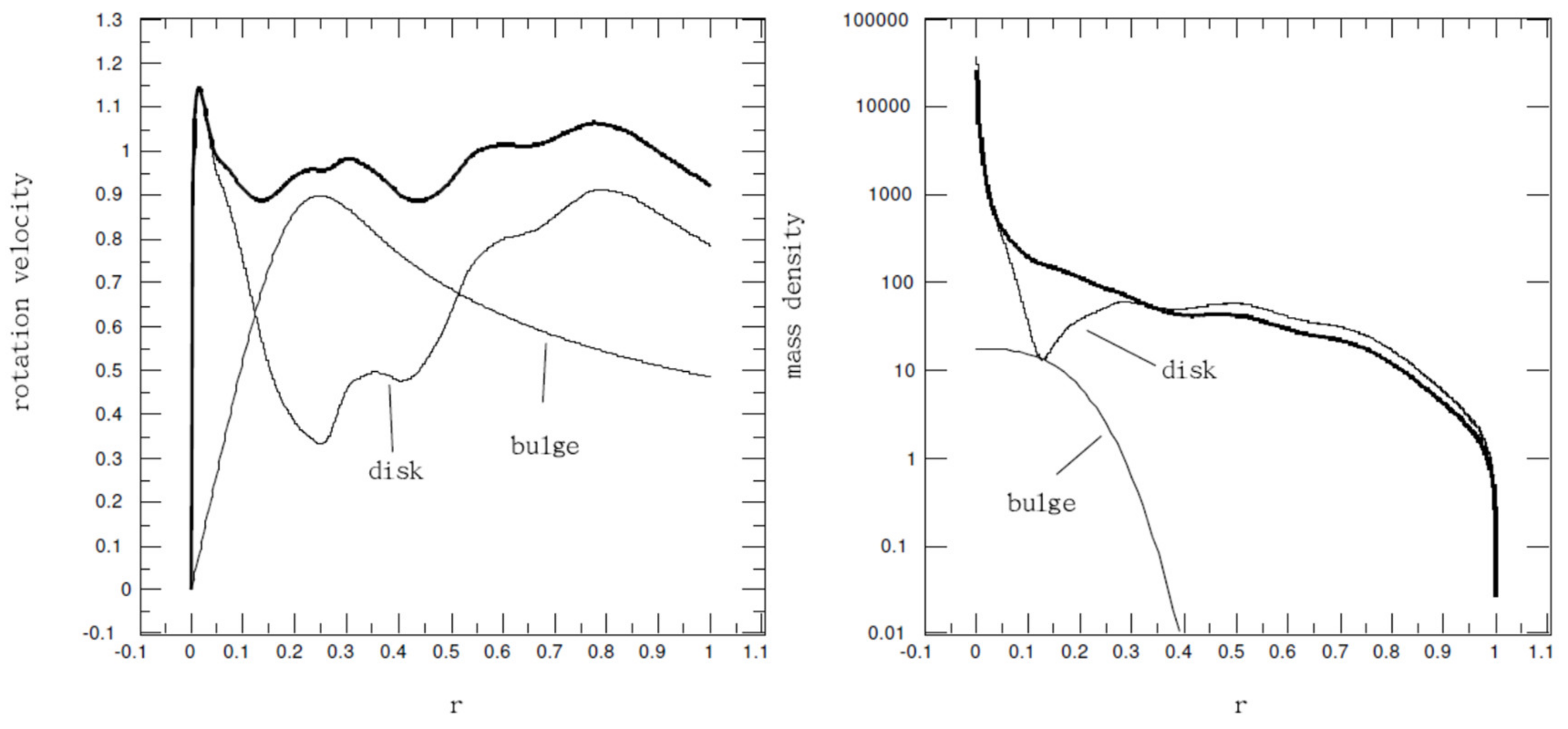
Besides the region of 0.1 < r < 0.9 for near-exponential decline of mass distribution, Figure 3 also shows a much sharper increase of mass density toward the galactic center for r < 0.1, which seems to be fairly typical for many galaxies [21]. Rapid increasing luminosity toward the galactic center has also been commonly shown in the surface brightness profiles which some authors would categorize as the “bulge”region [26]. To seriously include the bulge effect in the disk model may introduce more variables to the result, unless the bulge mass distribution is known a priori for uniquely determined mass in disk with a given rotation curve [21].

However, if the mass distribution is assumed to follow exactly that of surface luminosity by a constant mass-to-light ratio, the surface mass density [ρ(r) h] becomes known and the predicted rotation curve V(r) determined from the equation of (3) = (4) might not match the measured one. The mass converted from the mass-to-light ratio is usually found to decrease at a higher rate with galactocentric distance (corresponding to a smaller disk radial scale length) than that determined from rotation curve [20]. Such an apparent discrepancy has been called the “galactic rotation problem”, as a subject for various scientific interpretations. Most astronomers and astrophysicists would take this as a “compelling evidence” for (nonbaryonic) dark matter in galaxies [3,4,5,6,7,8]. Only a few authors would want to consider uncertainties in mass-to-light ratio as well as generally questionable accuracy in astronomical measurements, as the root cause [9]. Recently, the notion of nonbaryonic dark matter has also been challenged from the perspective of dynamical evolution of galaxies [29].

First of all, the values of stellar mass-to-light ratio, as determined from measurements, can vary substantially depending upon the nature of light emitting objects (as shown by the H-R diagram for stars [14,15]). For galaxies, Tully and Fisher [30] proposed an empirical relation between (intrinsic) luminosity and (maximum) rotation velocity (inferred from the “hydrogen profile width”), which might be used for estimating galaxy (total) mass from measured rotation velocity with a mass-to-light ratio. However, the luminosity was subsequently shown not to be a perfect predictor of mass, as the stellar mass-to-light ratio can vary with galaxy type and the Tully-Fisher relation can have different slopes depending on the luminosity bandpass [31,32,33,34].

Galaxies are known to contain matter other than stars. For example, the rotation curves measured with the 21 cm wavelength signals emitted from atomic hydrogen (H I) extends far beyond the starlight in galaxies, indicating certain amount of H I exists at least as far as where the rotation curve can be measured. Actually, H I may not be considered as totally dark; it is luminous at the 21 cm wavelength (in a different photometric bandpass from that of stars), which could be detected for estimating its mass. In fact, the “column” mass density of atomic hydrogen had been estimated using emission in the 21-cm line in terms of integral of the brightness temperature over the velocity width of the line, suggesting an atomic hydrogen number density of order 1 cm⁻³ in the galactic plane [35,36], but apparently without an independent method to validate. There are also hydrogen molecules (as molecular hydrogen) found in molecular clouds and in the Interstellar Medium (ISM), which appear to be literally dark when cold as majority of them are (e.g., around 10-20K [37,38]). The amount of “dark” hydrogen molecules could only be estimated by assuming a constant ratio from the luminosity of carbon monoxide, with unknown uncertainties, of course. Furthermore, condensed baryonic matter in the form of dust and debris is expected to have minimal effect on optical extinction and can easily avoid detection due to the small optical cross section [39]. The presence of those optically undetectable components (with Μ / L approaching to infinity) makes it certain that there must be more baryonic matter than what can be represented in terms of mass-to-light ratio. Indeed, the baryonic Tully-Fisher relation was shown to be optimally improved when the HI mass is multiplied by a factor of about 3 [40]. Therefore, estimating mass in a galaxy simply based on a constant mass-to-light ratio can be seriously flawed, though convenient. Its usage may provide some order-of-magnitude rough idea about the amount of mass, but should not be considered for serious comparison and verification in scientific analysis. In view of the technical difficulties in detecting astronomical matter and evaluating celestial mass, the existence of invisible baryonic matter that cannot be accounted for by a simple M/L is naturally expected following scientific logic.

Some authors would like to use multicomponent models, composed of a bulge, a disk, and a (dark matter) halo extending to a very large virial radius, for estimate of galaxy mass [41,42]. While the central bulge and circular disk are commonly observed, visible in photographic images of galaxies [1], whether there should be a dark matter halo has been a debatable subject [9]. Even to this day, “the shape of dark matter halos remains a mystery” [7]. The reason for having a massive invisible (spherical) dark matter halo came from an argument that it offers a plausible way to stabilize the Galaxy against the bar instability [43], but some galaxies have been shown to have rotation curves that do not satisfy the so-called sphericity condition (based on the fact that mass cannot have negative value), indicating a significantly massive spherical halo cannot be present at large galactocentric distance beyond the central bulge [44,45]. There are also N-body simulations showing that a disk galaxy with flat rotation curve can be stabilized by dense central bulge without the dark matter halo [46]. Actually, there has not been clear scientific justification for having a massive dark matter halo around the disk galaxies.

It was stated in a recent report that the Milky Way “mass estimates can vary markedly based on the types of data used, the techniques used, and the assumptions that go into the mass estimate …” [42]. Nevertheless, a value of the Milky Way mass could be derived as ~1.5 × 10¹² M_⊙ from an assumed composition of a nucleus, bulge, disk, and a halo of a virial radius over 200 kpc [42]. Interestingly, the mass within 21.5 kpc (where the Gaia rotation curve terminates) was estimated about 2.1 × 10¹¹ M_⊙ [42], quite comparable to 1.52 × 10¹¹ M_⊙ or 1.41 × 10¹¹ M_⊙ with or without a central bulge as numerically determined from a measured rotation curve up to 20.55 kpc [21].

In fact, the mass in a galaxy determined from measured rotation curve, according to Newtonian dynamics, seems to be fairly consistent regardless of the sources of rotation curve measurement data, which could vary somewhat. Further calculation shows that the predicted surface mass density in the solar neighborhood around 8 kpc should be ~144 M_⊙/pc² using a pure disk model or ~74 M_⊙/pc² when a sizable bulge is included in the computation [21]. As a reference, the current textbook value of surface mass density for solar neighborhood is ~49 M_⊙/pc² based on estimates from observations [1]. In view the fact that an axisymmetric disk model describes a surface mass density only meaningful in terms of averaging over the entire circular ring of radius ~8 kpc, while the local mass density may actually vary significantly along the ring (as shown in the photographic images), shouldn’t we consider the Newtonian dynamic model to be reasonably accurate? Moreover, a surface mass density of 100 M_⊙/pc² in the Milky Way model [21] corresponds to equivalently ~20 hydrogen atoms or ~10 hydrogen molecules per cm³ for an assumed disk thickness of 200 pc [9], extremely tenuous by the terrestrial standards and well within the reported range of estimated gas density in the Interstellar Medium [1,47]. If the typical density of cold molecular clouds to enable star formation ranges from 10² to 10⁶ molecules per cm³ [47], it is not difficult to realize the possible magnitude of variations in mass density just within a ring containing the solar neighborhood.

Thus, the measured galactic rotation curves generally coincide with exponentially declining mass density (distributed in thin disk) with increasing galactocentric distance, according to Newtonian dynamics. The assumption of mass distribution mostly in a circular thin disk comes from the optical images of disk shaped galaxies, based on a belief that luminosity correlates to mass, somewhat roughly if not exactly. The total mass in a rotating disk galaxy, determined from measured rotation curve according to Newtonian dynamics, appears to match the star counts reasonably well (at least for the Milky Way). Adding a spherical central bulge with substantial amount of mass to the thin-disk model may only change the total mass by a few percent, but can have noticeable effect on local mass density in the solar neighborhood [21]. A recent examination of a large number of galaxies yielded a universal fitting formula with one fit parameter—the “acceleration scale”—to relate observed radial (centripetal) acceleration (as determined from rotation curves) to that from the “baryons” (i.e., that determined from measured luminosity profile with an assumed constant mass-to-light ratio) [48]. While a popular interpretation of this finding had attributed the difference between the observed radial acceleration and that due to the baryons to the non-baryonic dark matter [48], it could also be much more straightforwardly explained by having a non-constant, variable (e.g., increasing) mass-to-light ratio as a function of galactocentric distance [9], possibly with one fit parameter. By virtue of scientific understanding about distributed matter, it is actually natural to expect the mass-to-light ratio, if meaningful at all, to be a non-constant variable in different regions of a galaxy, considering the fact that certain forms of baryonic matter in the universe can exist with very small optical cross section and become invisible to detection except by gravitational effects [39]. Then, the value of total mass associated with the mass distribution corresponding to measured rotation curve, with or without a central bulge being accounted for, seems also to be consistent with astronomical observations and well-established Newtonian dynamics. In other words, galaxy rotation curves can be supported with reasonable amount of mass (consistent with star counts) according to Newtonian dynamics, without involving mysterious non-baryonic dark matter or modification of the known laws of Newtonian dynamics (e.g., MOND).

6. Conclusions

The scientific method involves observation, formulating hypotheses via induction, experimental testing with quantitative measurements, and refinement or elimination of the hypotheses based on the experimental findings. Numerous astronomical observations have shown spiral galaxies exhibiting the common configuration of a bright circular disk with a relatively small central bulge (cf. Figure 1), suggesting that mass therein would likely distribute in a similar configuration. Further measurements have indicated that matter in those disk galaxies is generally moving in circular orbits in the disk, with quantified description known as the rotation curves (with the circular orbital velocity given as a function of galactrocentric distance). From well-established Newtonian dynamics, matters moving in circular orbits are expected to have their centripetal acceleration balanced by the gravitational force of distributed mass. Then a logically induced model for theoretical understanding could consist of an approximate axisymmetric disk, with or without a central bulge, wherein the mass distribution and measured rotation curve are consistent with Newtonian dynamics, as that determined by solving the (3) = (4) equation.

Astronomical measurements are generally challenging for accuracy due to limited means with obvious technical difficulties. Most quantities cannot be measured directly, but must be inferred via assumptions over assumptions with raw data presented in graphs often scattering over orders of magnitude for an anticipated point. Although the efforts in searching for independent test of theory should not be discouraged, findings of quantitative discrepancies between observational data and theoretical prediction ought to stimulate serious interrogations of the measurement accuracy as well as simplifying assumptions in theoretical calculations.

In the case of galactic rotation, the surface mass density determined from measured rotation curve exhibits an exponential-like decline with the galactocentric distance (for the most part) similar to that based on observed luminosity in a qualitative sense. The overall amount of mass consistent with the rotation curve matches the known star counts. An apparent discrepancy (e.g., in regard to local mass density in the solar neighborhood) appears to be within a factor of two to three, while in general the uncertainties in astronomical measurements have not been clearly quantified and could become well over an order of magnitude. The estimated mass using an assumed constant mass-to-light ratio is scientifically expected to be flawed, because it cannot adequately account for the optically undetectable baryonic “dark” components that can exist in the universe such as molecular hydrogen, dust, etc. On the other hand, the rotation curve itself is not error free, with an implication of axisymmetry in the galactic disk which can only be an approximation at best. Therefore, the predicted mass distribution based on Newtonian dynamics using measured rotation curve cannot be an exact prediction, especially for the asymmetric features such as bars and spiral arms, not because of any fundamental shortcomings in Newtonian dynamics but rather due to limited means for accurate, comprehensive measurements. By examining the historical evidence with scientific logic, the so-called “galactic rotation problem” becomes very likely a consequence of misinterpreted measurement data with poorly examined, underestimated intrinsic uncertainties and misunderstood theoretical model description, rather than an indication of mysterious nonbaryonic dark matter.

The lack of means for accurate evaluation of amount of matter at different astronomical scales leaves plenty of room and freedom for theoretical speculations; “there is always the possibility that one or all of the estimates could be wrong” [7]. Inability of directly and reliably measuring the amount of all baryonic matter in the observable universe with the available technology is scientifically expected and should not be regarded as a mystery. For disk galaxies, the measured rotation curves provide the most reliable information for deriving the mass distribution base on Newtonian dynamics [17,23]. When the Newtonian dynamics model suggests more mass than that indicated by luminosity based on some value of mass-to-light ratio, there is likely to exist some “invisible” baryonic matter that is “dark” and undetectable to the available instrument. If the mass obtained by other (less reliable) methods, such as that from a mass-to-light ratio, does not match that determined from rotation curve, it should be naturally understandable as a consequence of inevitable uncertainties of an inaccurate estimate, instead of being considered as primary evidence for mysterious dark matter. The validity of indirect observational evidence for (nonbaryonic) dark matter remains generally questionable, because of decades-long efforts with again and again failed direct detection. Yet numerous research papers published in scientific literature rather faithfully presumed the existence of nonbaryonic dark matter (for the convenience of obtaining seemingly “self-consistent” results), without serious consideration alternative possibilities. This appears to be a common “snowball” effect in modern astronomy and cosmology for scientists to conform to the mainstream ideas so as to obtain research funds and observing time on major telescopes [49,50]. But the progress of science generally relies on truth-seeking people who look critically at the contemporary schemes, and continuously point out flaws in the established, especially unsubstantiated, views based on more reliable evidence. Without inquisitive doubt and skepticism, science cannot thrive and will stagnate.