Blazar Optical Polarimetry: Current Progress in Observations and Theories
Abstract
1. Introduction
2. Progress in Observations
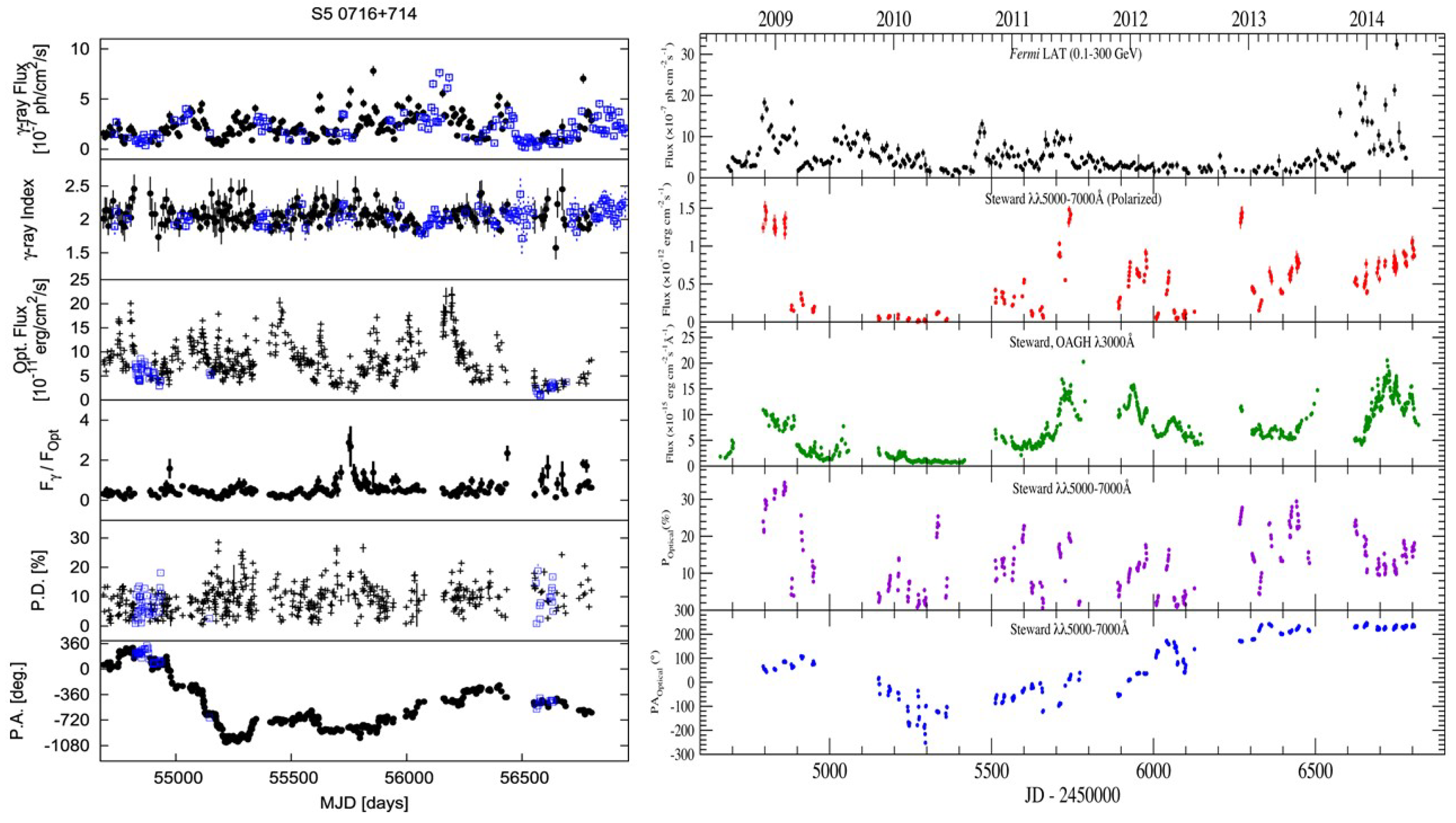
2.1. Overview
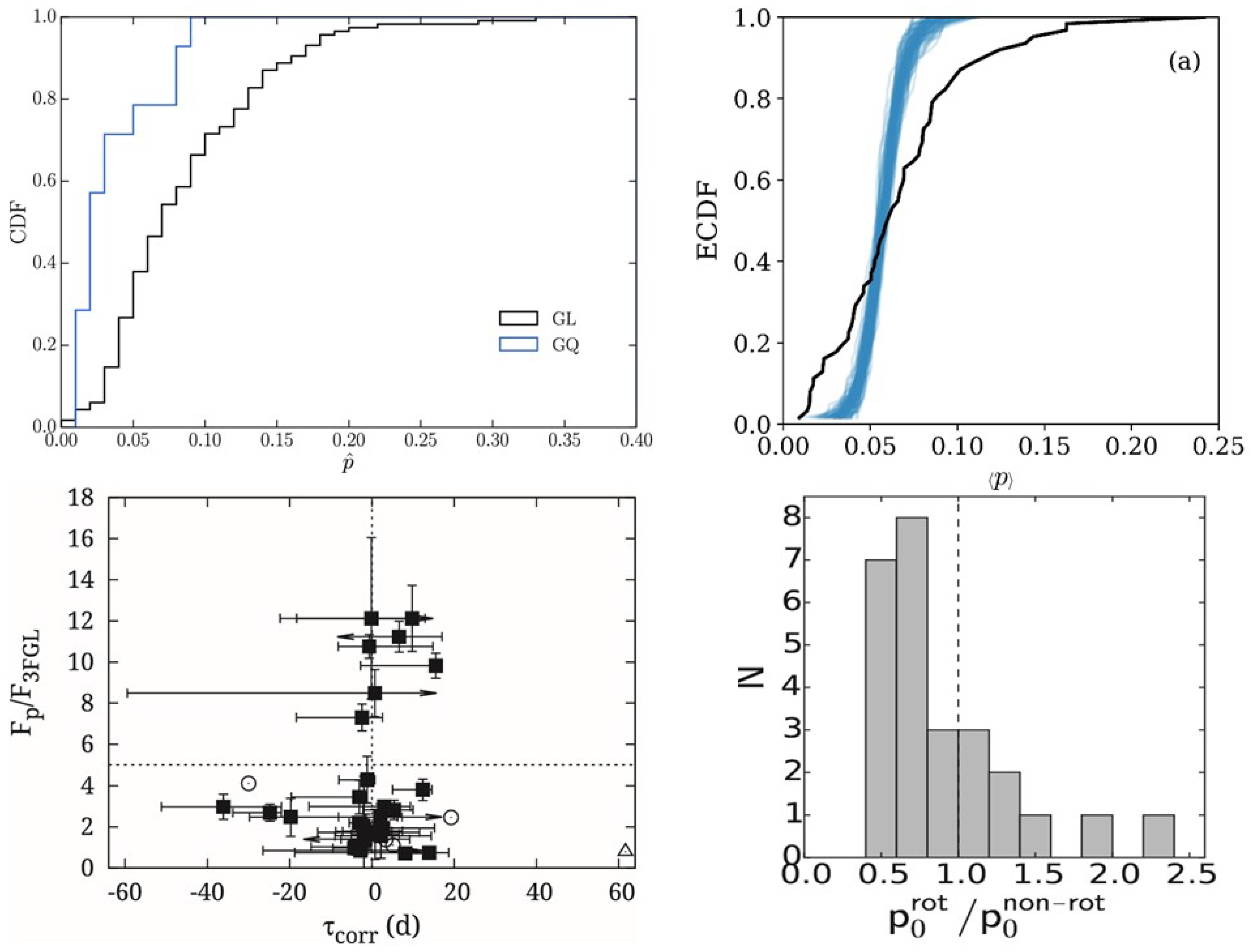
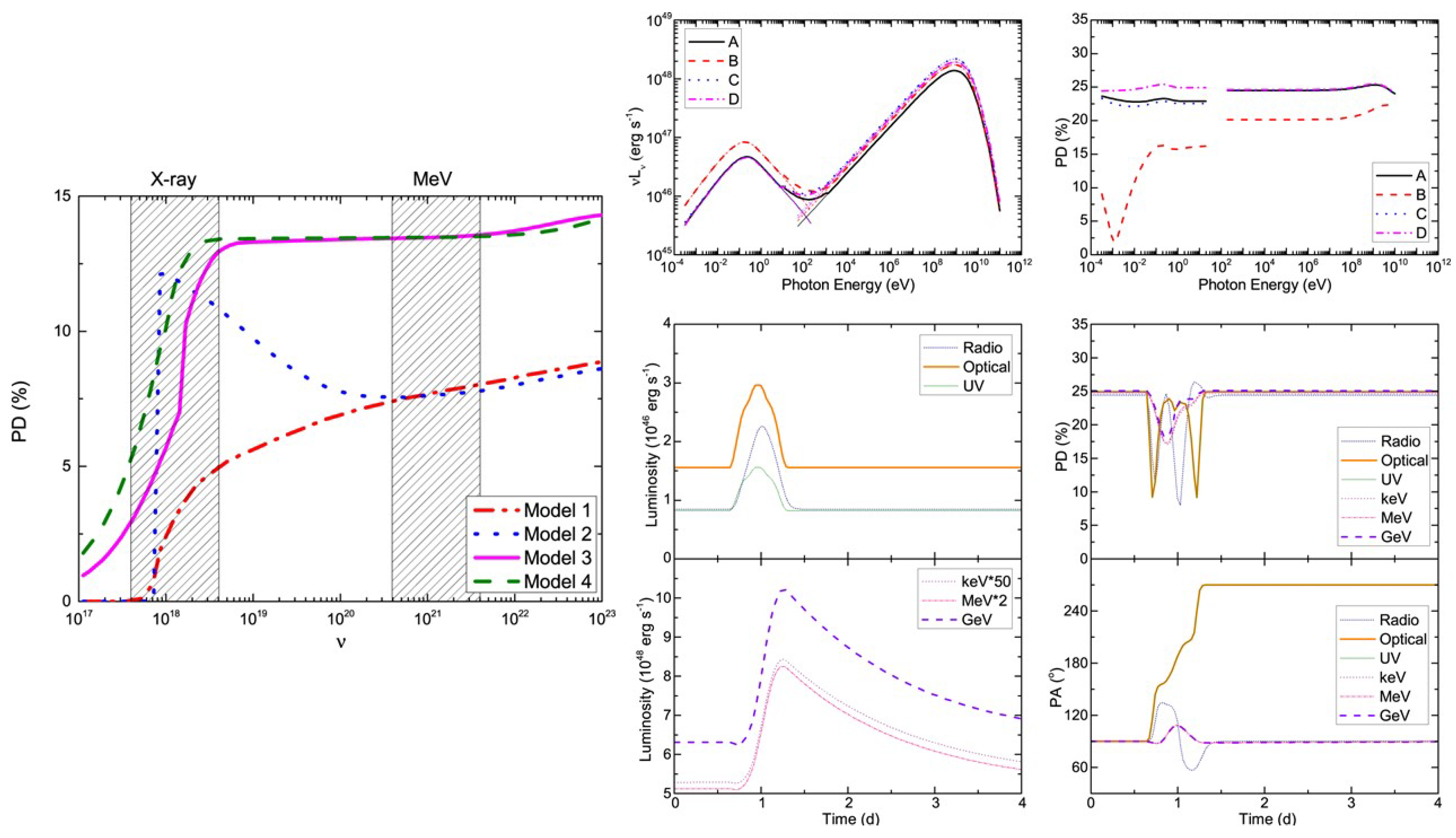
- The average polarization degree of -ray-loud blazars appears systematically higher than -ray-quiet ones [74].
- The overall polarization temporal behaviors are similar regardless of whether the blazar is detected in the TeV band [75].
- The polarization degree variability cannot be completely reproduced by random walk simulations [78].
2.2. Polarization Angle Rotation
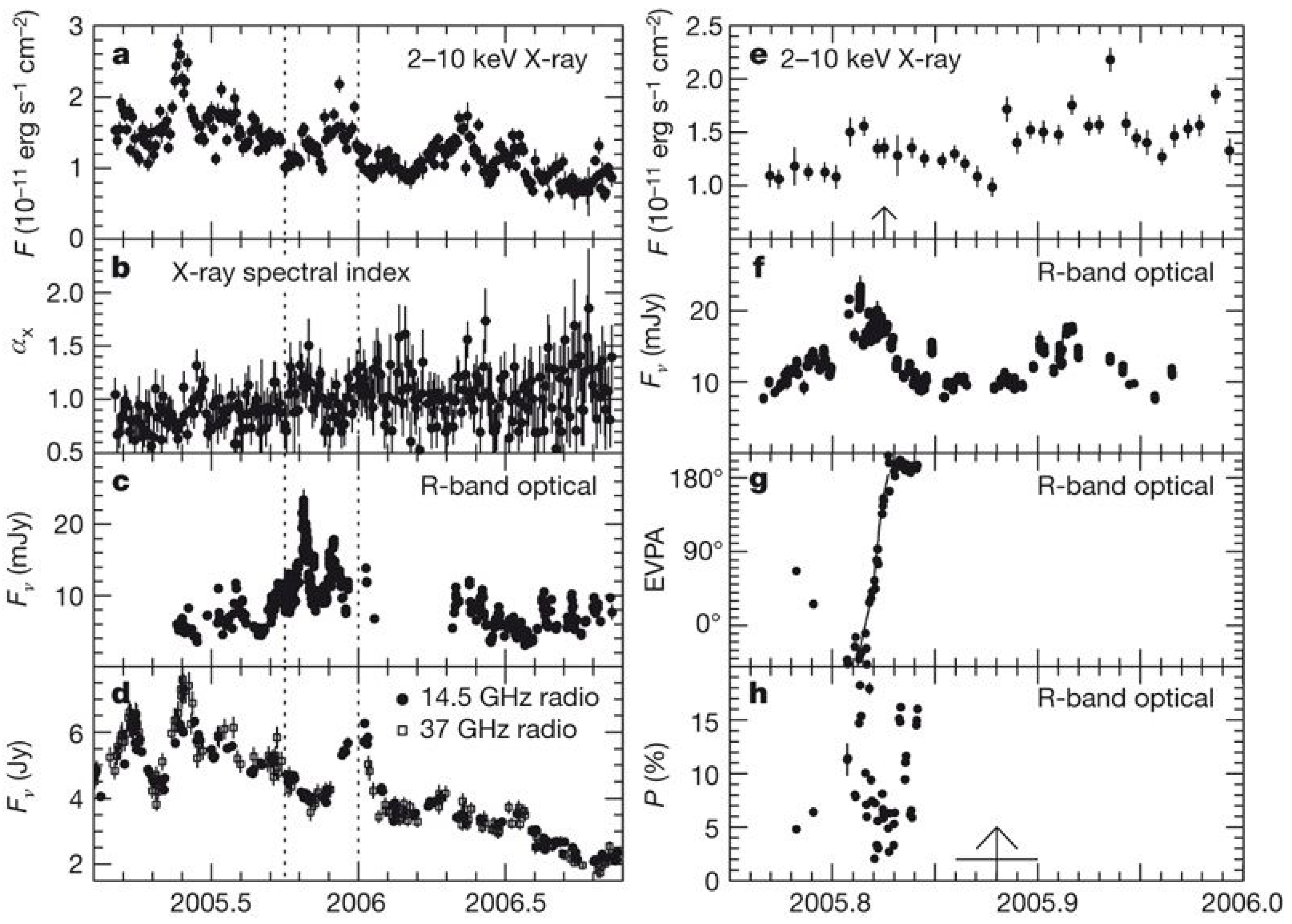
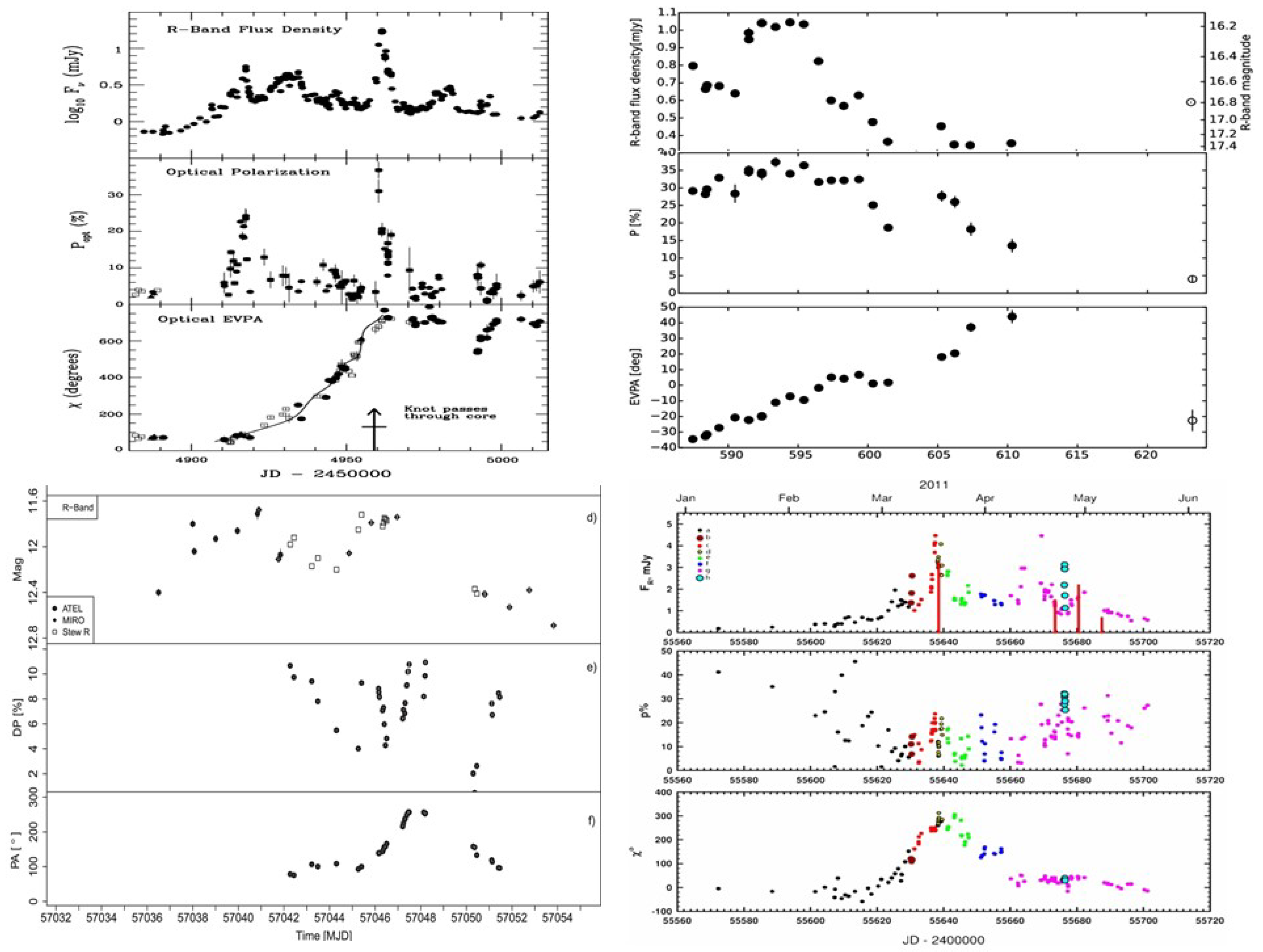
- Polarization angle swings are associated with -ray flares, with little time lag [73].
- Polarization angle swings do not happen in all blazars, but they can happen in both FSRQs and BL Lacs [80].
- Blazars that have shown rotations generally have brighter and more variable -ray emission [80].
- The polarization degree generally decreases during angle rotations [80].
- It is unlikely that all rotations are consistent with random walks [78].
3. Theoretical Models
3.1. Geometrical Models
3.2. Physical Models
4. Future Prospects
4.1. Polarization Variability
4.2. Multi-Wavelength Polarimetry
5. Summary
Acknowledgments
Conflicts of Interest
References
- Leahy, J.P.; Williams, A.G. The bridges of classical double radio sources. Mon. Not. R. Astron. Soc. 1984, 210, 929–951. [Google Scholar] [CrossRef]
- Carilli, C.L.; Barthel, P.D. Cygnus A. T Astron. Astrophys. Rev. 1996, 7, 1–54. [Google Scholar] [CrossRef]
- MAGIC Collaboration; Albert, J.; Aliu, E.; Anderhub, H.; Antonelli, L.A.; Antoranz, P.; Backes, M.; Baixeras, C.; Barrio, J.A.; Bartko, H.; et al. Very-High-Energy gamma rays from a Distant Quasar: How Transparent Is the Universe? Science 2008, 320, 1752. [Google Scholar] [CrossRef] [PubMed]
- Aharonian, F.; Akhperjanian, A.G.; Anton, G.; de Almeida, U.B.; Bazer-Bachi, A.R.; Becherini, Y.; Behera, B.; Benbow, W.; Bernlöhr, K.; Boisson, C.; et al. Discovery of Very High Energy γ-Ray Emission from Centaurus a with H.E.S.S. Astrophys. J. Lett. 2009, 695, L40–L44. [Google Scholar] [CrossRef]
- Abramowski, A.; Acero, F.; Aharonian, F.; Akhperjanian, A.G.; Anton, G.; Balzer, A.; Barnacka, A.; Barres de Almeida, U.; Becherini, Y.; Becker, J.; et al. The 2010 Very High Energy γ-Ray Flare and 10 Years of Multi-wavelength Observations of M 87. Astrophys. J. 2012, 746, 151. [Google Scholar] [CrossRef]
- Ahnen, M.L.; Ansoldi, S.; Antonelli, L.A.; Antoranz, P.; Babic, A.; Banerjee, B.; Bangale, P.; Barres de Almeida, U.; Barrio, J.A.; Becerra González, J.; et al. Long-term multi-wavelength variability and correlation study of Markarian 421 from 2007 to 2009. Astron. Astrophys. 2016, 593, A91. [Google Scholar] [CrossRef]
- Acero, F.; Ackermann, M.; Ajello, M.; Albert, A.; Atwood, W.B.; Axelsson, M.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; et al. Fermi Large Area Telescope Third Source Catalog. Astrophys. J. Suppl. Ser. 2015, 218, 23. [Google Scholar] [CrossRef]
- The Fermi-LAT Collaboration. Fermi Large Area Telescope Fourth Source Catalog. arXiv 2019, arXiv:1902.10045. [Google Scholar]
- Romero, G.E.; Boettcher, M.; Markoff, S.; Tavecchio, F. Relativistic Jets in Active Galactic Nuclei and Microquasars. Space Sci. Rev. 2017, 207, 5–61. [Google Scholar] [CrossRef]
- Böttcher, M. Progress in Multi-wavelength and Multi-Messenger Observations of Blazars and Theoretical Challenges. Galaxies 2019, 7, 20. [Google Scholar] [CrossRef]
- Scarpa, R.; Falomo, R. Are high polarization quasars and BL Lacertae objects really different? A study of the optical spectral properties. Astron. Astrophys. 1997, 325, 109–123. [Google Scholar]
- Lister, M.L.; Aller, M.F.; Aller, H.D.; Hodge, M.A.; Homan, D.C.; Kovalev, Y.Y.; Pushkarev, A.B.; Savolainen, T. MOJAVE. XV. VLBA 15 GHz Total Intensity and Polarization Maps of 437 Parsec-scale AGN Jets from 1996 to 2017. Astrophys. J. Suppl. Ser. 2018, 234, 12. [Google Scholar] [CrossRef]
- Marscher, A.P.; Gear, W.K. Models for high-frequency radio outbursts in extragalactic sources, with application to the early 1983 millimeter-to-infrared flare of 3C 273. Astrophys. J. 1985, 298, 114–127. [Google Scholar] [CrossRef]
- Maraschi, L.; Ghisellini, G.; Celotti, A. A jet model for the gamma-ray emitting blazar 3C 279. Astrophys. J. Lett. 1992, 397, L5–L9. [Google Scholar] [CrossRef]
- Dermer, C.D.; Schlickeiser, R.; Mastichiadis, A. High-energy gamma radiation from extragalactic radio sources. Astron. Astrophys. 1992, 256, L27–L30. [Google Scholar]
- Sikora, M.; Begelman, M.C.; Rees, M.J. Comptonization of diffuse ambient radiation by a relativistic jet: The source of gamma rays from blazars? Astrophys. J. 1994, 421, 153–162. [Google Scholar] [CrossRef]
- Ghisellini, G.; Madau, P. On the origin of the gamma-ray emission in blazars. Mon. Not. R. Astron. Soc. 1996, 280, 67–76. [Google Scholar] [CrossRef]
- Böttcher, M.; Reimer, A.; Sweeney, K.; Prakash, A. Leptonic and Hadronic Modeling of Fermi-detected Blazars. Astrophys. J. 2013, 768, 54. [Google Scholar] [CrossRef]
- Celotti, A.; Ghisellini, G. The power of blazar jets. Mon. Not. R. Astron. Soc. 2008, 385, 283–300. [Google Scholar] [CrossRef]
- Mannheim, K. The proton blazar. Astron. Astrophys. 1993, 269, 67–76. [Google Scholar]
- Aharonian, F.A. TeV gamma rays from BL Lac objects due to synchrotron radiation of extremely high energy protons. New Astron. 2000, 5, 377–395. [Google Scholar] [CrossRef]
- Mücke, A.; Protheroe, R.J.; Engel, R.; Rachen, J.P.; Stanev, T. BL Lac objects in the synchrotron proton blazar model. Astropart. Phys. 2003, 18, 593–613. [Google Scholar] [CrossRef]
- Cerruti, M.; Zech, A.; Boisson, C.; Inoue, S. A hadronic origin for ultra-high-frequency-peaked BL Lac objects. Mon. Not. R. Astron. Soc. 2015, 448, 910–927. [Google Scholar] [CrossRef]
- Li, H.; Kusunose, M. Temporal and Spectral Variabilities of High-Energy Emission from Blazars Using Synchrotron Self-Compton Models. Astrophys. J. 2000, 536, 729–741. [Google Scholar] [CrossRef]
- Chen, X.; Fossati, G.; Liang, E.P.; Böttcher, M. Time-dependent simulations of multiwavelength variability of the blazar Mrk 421 with a Monte Carlo multizone code. Mon. Not. R. Astron. Soc. 2011, 416, 2368–2387. [Google Scholar] [CrossRef]
- Sahu, S.; Oliveros, A.F.O.; Sanabria, J.C. Hadronic-origin orphan TeV flare from 1ES 1959+650. Phys. Rev. D 2013, 87, 103015. [Google Scholar] [CrossRef]
- Petropoulou, M.; Dimitrakoudis, S.; Padovani, P.; Mastichiadis, A.; Resconi, E. Photohadronic origin of γ-ray BL Lac emission: implications for IceCube neutrinos. Mon. Not. R. Astron. Soc. 2015, 448, 2412–2429. [Google Scholar] [CrossRef]
- Diltz, C.; Böttcher, M.; Fossati, G. Time Dependent Hadronic Modeling of Flat Spectrum Radio Quasars. Astrophys. J. 2015, 802, 133. [Google Scholar] [CrossRef]
- IceCube Collaboration; Aartsen, M.G.; Ackermann, M.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Ahrens, M.; Al Samarai, I.; Altmann, D.; Andeen, K.; et al. Multimessenger observations of a flaring blazar coincident with high-energy neutrino IceCube-170922A. Science 2018, 361, eaat1378. [Google Scholar] [CrossRef]
- IceCube Collaboration; Aartsen, M.G.; Ackermann, M.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Ahrens, M.; Samarai, I.A.; Altmann, D.; Andeen, K.; et al. Neutrino emission from the direction of the blazar TXS 0506+056 prior to the IceCube-170922A alert. Science 2018, 361, 147–151. [Google Scholar] [CrossRef]
- Ansoldi, S.; Antonelli, L.A.; Arcaro, C.; Baack, D.; Babić, A.; Banerjee, B.; Bangale, P.; Barres de Almeida, U.; Barrio, J.A.; Becerra González, J.; et al. The Blazar TXS 0506+056 Associated with a High-energy Neutrino: Insights into Extragalactic Jets and Cosmic-Ray Acceleration. Astrophys. J. Lett. 2018, 863, L10. [Google Scholar] [CrossRef]
- Keivani, A.; Murase, K.; Petropoulou, M.; Fox, D.B.; Cenko, S.B.; Chaty, S.; Coleiro, A.; DeLaunay, J.J.; Dimitrakoudis, S.; Evans, P.A.; et al. A Multimessenger Picture of the Flaring Blazar TXS 0506+056: Implications for High-energy Neutrino Emission and Cosmic-Ray Acceleration. Astrophys. J. 2018, 864, 84. [Google Scholar] [CrossRef]
- Cerruti, M.; Zech, A.; Boisson, C.; Emery, G.; Inoue, S.; Lenain, J.P. Leptohadronic single-zone models for the electromagnetic and neutrino emission of TXS 0506+056. Mon. Not. R. Astron. Soc. 2019, 483, L12–L16. [Google Scholar] [CrossRef]
- Gao, S.; Fedynitch, A.; Winter, W.; Pohl, M. Modelling the coincident observation of a high-energy neutrino and a bright blazar flare. Nat. Astron. 2019, 3, 88–92. [Google Scholar] [CrossRef]
- Reimer, A.; Böttcher, M.; Buson, S. Cascading Constraints from Neutrino-emitting Blazars: The Case of TXS 0506+056. Astrophys. J. 2019, 881, 46. [Google Scholar] [CrossRef]
- Wills, B.J.; Wills, D.; Breger, M.; Antonucci, R.R.J.; Barvainis, R. A Survey for High Optical Polarization in Quasars with Core-dominant Radio Structure: Is There a Beamed Optical Continuum? Astrophys. J. 1992, 398, 454–475. [Google Scholar] [CrossRef]
- Gabuzda, D.C.; Sitko, M.L. Nearly Simultaneous Very Long Baseline Interferometry and Optical Polarimetry of Blazars. Astron. J. 1994, 107, 884–991. [Google Scholar] [CrossRef]
- Aller, M.F.; Aller, H.D.; Hughes, P.A.; Latimer, G.E. Centimeter-Wavelength Total Flux and Linear Polarization Properties of Radio-loud BL Lacertae Objects. Astrophys. J. 1999, 512, 601–622. [Google Scholar] [CrossRef]
- Lister, M.L.; Smith, P.S. Intrinsic Differences in the Inner Jets of High and Low Optically Polarized Radio Quasars. Astrophys. J. 2000, 541, 66–87. [Google Scholar] [CrossRef]
- Smith, P.S.; Montiel, E.; Rightley, S.; Turner, J.; Schmidt, G.D.; Jannuzi, B.T. Coordinated Fermi/Optical Monitoring of Blazars and the Great 2009 September Gamma-ray Flare of 3C 454.3. arXiv 2009, arXiv:0912.3621. [Google Scholar]
- D’Ammando, F.; Raiteri, C.M.; Villata, M.; Romano, P.; Pucella, G.; Krimm, H.A.; Covino, S.; Orienti, M.; Giovannini, G.; Vercellone, S.; et al. AGILE detection of extreme γ-ray activity from the blazar PKS 1510-089 during March 2009. Multifrequency analysis. Astron. Astrophys. 2011, 529, A145. [Google Scholar] [CrossRef]
- Ikejiri, Y.; Uemura, M.; Sasada, M.; Ito, R.; Yamanaka, M.; Sakimoto, K.; Arai, A.; Fukazawa, Y.; Ohsugi, T.; Kawabata, K.S.; et al. Photopolarimetric Monitoring of Blazars in the Optical and Near-Infrared Bands with the Kanata Telescope. I. Correlations between Flux, Color, and Polarization. Publ. Astron. Soc. Jpn. 2011, 63, 639–675. [Google Scholar] [CrossRef]
- Aleksić, J.; Ansoldi, S.; Antonelli, L.A.; Antoranz, P.; Babic, A.; Bangale, P.; Barres de Almeida, U.; Barrio, J.A.; Becerra González, J.; Bednarek, W.; et al. MAGIC gamma-ray and multi-frequency observations of flat spectrum radio quasar PKS 1510-089 in early 2012. Astron. Astrophys. 2014, 569, A46. [Google Scholar] [CrossRef]
- Marscher, A.P.; Jorstad, S.G.; D’Arcangelo, F.D.; Smith, P.S.; Williams, G.G.; Larionov, V.M.; Oh, H.; Olmstead, A.R.; Aller, M.F.; Aller, H.D.; et al. The inner jet of an active galactic nucleus as revealed by a radio-to-γ-ray outburst. Nature 2008, 452, 966–969. [Google Scholar] [CrossRef] [PubMed]
- Larionov, V.M.; Jorstad, S.G.; Marscher, A.P.; Morozova, D.A.; Blinov, D.A.; Hagen-Thorn, V.A.; Konstantinova, T.S.; Kopatskaya, E.N.; Larionova, L.V.; Larionova, E.G.; et al. The Outburst of the Blazar S5 0716+71 in 2011 October: Shock in a Helical Jet. Astrophys. J. 2013, 768, 40. [Google Scholar] [CrossRef]
- Blinov, D.; Pavlidou, V.; Papadakis, I.; Kiehlmann, S.; Panopoulou, G.; Liodakis, I.; King, O.G.; Angelakis, E.; Baloković, M.; Das, H.; et al. RoboPol: First season rotations of optical polarization plane in blazars. Mon. Not. R. Astron. Soc. 2015, 453, 1669–1683. [Google Scholar] [CrossRef]
- Summerlin, E.J.; Baring, M.G. Diffusive Acceleration of Particles at Oblique, Relativistic, Magnetohydrodynamic Shocks. Astrophys. J. 2012, 745, 63. [Google Scholar] [CrossRef]
- O’Neill, S.M.; Beckwith, K.; Begelman, M.C. Local simulations of instabilities in relativistic jets—I. Morphology and energetics of the current-driven instability. Mon. Not. R. Astron. Soc. 2012, 422, 1436–1452. [Google Scholar] [CrossRef]
- Sironi, L.; Spitkovsky, A. Relativistic Reconnection: An Efficient Source of Non-thermal Particles. Astrophys. J. Lett. 2014, 783, L21. [Google Scholar] [CrossRef]
- Guo, F.; Li, H.; Daughton, W.; Liu, Y.H. Formation of Hard Power Laws in the Energetic Particle Spectra Resulting from Relativistic Magnetic Reconnection. Phys. Rev. Lett. 2014, 113, 155005. [Google Scholar] [CrossRef]
- Zhang, H.; Böttcher, M. X-Ray and Gamma-Ray Polarization in Leptonic and Hadronic Jet Models of Blazars. Astrophys. J. 2013, 774, 18. [Google Scholar] [CrossRef]
- Paliya, V.S.; Zhang, H.; Böttcher, M.; Ajello, M.; Domínguez, A.; Joshi, M.; Hartmann, D.; Stalin, C.S. Leptonic and Hadronic Modeling of Fermi-LAT Hard Spectrum Quasars and Predictions for High-energy Polarization. Astrophys. J. 2018, 863, 98. [Google Scholar] [CrossRef]
- Morozova, D.A.; Larionov, V.M.; Troitsky, I.S.; Jorstad, S.G.; Marscher, A.P.; Gómez, J.L.; Blinov, D.A.; Efimova, N.V.; Hagen-Thorn, V.A.; Hagen-Thorn, E.I.; et al. The Outburst of the Blazar S4 0954+658 in 2011 March-April. Astron. J. 2014, 148, 42. [Google Scholar] [CrossRef]
- Smith, P.S. Extremely High Optical Polarization Observed in the Blazar PKS1502+106. Astron. Telegr. 2017, 11047, 1. [Google Scholar]
- Hutsemékers, D.; Borguet, B.; Sluse, D.; Cabanac, R.; Lamy, H. Optical circular polarization in quasars. Astron. Astrophys. 2010, 520, L7. [Google Scholar] [CrossRef]
- Itoh, R.; Fukazawa, Y.; Tanaka, Y.T.; Abe, Y.; Akitaya, H.; Arai, A.; Hayashi, M.; Hori, T.; Isogai, M.; Izumiura, H.; et al. Dense Optical and Near-infrared Monitoring of CTA 102 during High State in 2012 with OISTER: Detection of Intra-night “Orphan Polarized Flux Flare”. Astrophys. J. Lett. 2013, 768, L24. [Google Scholar] [CrossRef]
- Marscher, A.P.; Jorstad, S.G.; Larionov, V.M.; Aller, M.F.; Aller, H.D.; Lähteenmäki, A.; Agudo, I.; Smith, P.S.; Gurwell, M.; Hagen-Thorn, V.A.; et al. Probing the Inner Jet of the Quasar PKS 1510-089 with Multi-Waveband Monitoring During Strong Gamma-Ray Activity. Astrophys. J. Lett. 2010, 710, L126–L131. [Google Scholar] [CrossRef]
- Itoh, R.; Nalewajko, K.; Fukazawa, Y.; Uemura, M.; Tanaka, Y.T.; Kawabata, K.S.; Madejski, G.M.; Schinzel, F.K.; Kanda, Y.; Shiki, K.; et al. Systematic Study of Gamma-ray-bright Blazars with Optical Polarization and Gamma-Ray Variability. Astrophys. J. 2016, 833, 77. [Google Scholar] [CrossRef]
- Pekeur, N.W.; Taylor, A.R.; Potter, S.B.; Kraan-Korteweg, R.C. Evidence for quasi-periodic oscillations in the optical polarization of the blazar PKS 2155-304. Mon. Not. R. Astron. Soc. 2016, 462, L80–L83. [Google Scholar] [CrossRef]
- Böttcher, M.; van Soelen, B.; Britto, R.; Buckley, D.; Marais, J.; Schutte, H. SALT Spectropolarimetry and Self-Consistent SED and Polarization Modeling of Blazars. Galaxies 2017, 5, 52. [Google Scholar] [CrossRef]
- Aliu, E.; Archambault, S.; Archer, A.; Arlen, T.; Aune, T.; Barnacka, A.; Behera, B.; Beilicke, M.; Benbow, W.; Berger, K.; et al. Very high energy outburst of Markarian 501 in May 2009. Astron. Astrophys. 2016, 594, A76. [Google Scholar] [CrossRef]
- Jorstad, S.G.; Marscher, A.P.; Smith, P.S.; Larionov, V.M.; Agudo, I.; Gurwell, M.; Wehrle, A.E.; Lähteenmäki, A.; Nikolashvili, M.G.; Schmidt, G.D.; et al. A Tight Connection between Gamma-Ray Outbursts and Parsec-scale Jet Activity in the Quasar 3C 454.3. Astrophys. J. 2013, 773, 147. [Google Scholar] [CrossRef]
- Rani, B.; Jorstad, S.G.; Marscher, A.P.; Agudo, I.; Sokolovsky, K.V.; Larionov, V.M.; Smith, P.; Mosunova, D.A.; Borman, G.A.; Grishina, T.S.; et al. Exploring the Connection between Parsec-scale Jet Activity and Broadband Outbursts in 3C 279. Astrophys. J. 2018, 858, 80. [Google Scholar] [CrossRef]
- Patiño-Álvarez, V.M.; Fernandes, S.; Chavushyan, V.; López-Rodríguez, E.; León-Tavares, J.; Schlegel, E.M.; Carrasco, L.; Valdés, J.; Carramiñana, A. Multiwavelength photometric and spectropolarimetric analysis of the FSRQ 3C 279. Mon. Not. R. Astron. Soc. 2018, 479, 2037–2064. [Google Scholar] [CrossRef]
- Jermak, H.; Steele, I.A.; Lindfors, E.; Hovatta, T.; Nilsson, K.; Lamb, G.P.; Mundell, C.; Barres de Almeida, U.; Berdyugin, A.; Kadenius, V.; et al. The RINGO2 and DIPOL optical polarization catalogue of blazars. Mon. Not. R. Astron. Soc. 2016, 462, 4267–4299. [Google Scholar] [CrossRef]
- Andruchow, I.; Cellone, S.A.; Romero, G.E.; Dominici, T.P.; Abraham, Z. Microvariability in the optical polarization of 3C 279. Astron. Astrophys. 2003, 409, 857–865. [Google Scholar] [CrossRef]
- Covino, S.; Baglio, M.C.; Foschini, L.; Sandrinelli, A.; Tavecchio, F.; Treves, A.; Zhang, H.; Barres de Almeida, U.; Bonnoli, G.; Böttcher, M.; et al. Short timescale photometric and polarimetric behavior of two BL Lacertae type objects. Astron. Astrophys. 2015, 578, A68. [Google Scholar] [CrossRef]
- Cellone, S.A.; Romero, G.E.; Combi, J.A.; Martí, J. Extreme photopolarimetric behaviour of the blazar AO0235+164. Mon. Not. R. Astron. Soc. 2007, 381, L60–L64. [Google Scholar] [CrossRef]
- Hagen-Thorn, V.A.; Larionov, V.M.; Jorstad, S.G.; Arkharov, A.A.; Hagen-Thorn, E.I.; Efimova, N.V.; Larionova, L.V.; Marscher, A.P. The Outburst of the Blazar AO 0235+164 in 2006 December: Shock-in-Jet Interpretation. Astrophys. J. 2008, 672, 40–47. [Google Scholar] [CrossRef]
- Laing, R.A. A model for the magnetic-field structure in extended radio sources. Mon. Not. R. Astron. Soc. 1980, 193, 439–449. [Google Scholar] [CrossRef]
- Marscher, A.P. Turbulent, Extreme Multi-zone Model for Simulating Flux and Polarization Variability in Blazars. Astrophys. J. 2014, 780, 87. [Google Scholar] [CrossRef]
- Chandra, S.; Zhang, H.; Kushwaha, P.; Singh, K.P.; Bottcher, M.; Kaur, N.; Baliyan, K.S. Multi-wavelength Study of Flaring Activity in BL Lac Object S5 0716+714 during the 2015 Outburst. Astrophys. J. 2015, 809, 130. [Google Scholar] [CrossRef]
- Blinov, D.; Pavlidou, V.; Papadakis, I.; Kiehlmann, S.; Liodakis, I.; Panopoulou, G.V.; Angelakis, E.; Baloković, M.; Hovatta, T.; King, O.G.; et al. RoboPol: Connection between optical polarization plane rotations and gamma-ray flares in blazars. Mon. Not. R. Astron. Soc. 2018, 474, 1296–1306. [Google Scholar] [CrossRef]
- Angelakis, E.; Hovatta, T.; Blinov, D.; Pavlidou, V.; Kiehlmann, S.; Myserlis, I.; Böttcher, M.; Mao, P.; Panopoulou, G.V.; Liodakis, I.; et al. RoboPol: The optical polarization of gamma-ray-loud and gamma-ray-quiet blazars. Mon. Not. R. Astron. Soc. 2016, 463, 3365–3380. [Google Scholar] [CrossRef]
- Hovatta, T.; Lindfors, E.; Blinov, D.; Pavlidou, V.; Nilsson, K.; Kiehlmann, S.; Angelakis, E.; Fallah Ramazani, V.; Liodakis, I.; Myserlis, I.; et al. Optical polarization of high-energy BL Lacertae objects. Astron. Astrophys. 2016, 596, A78. [Google Scholar] [CrossRef]
- Jannuzi, B.T.; Smith, P.S.; Elston, R. The Optical Polarization Properties of X-ray—Selected BL Lacertae Objects. Astrophys. J. 1994, 428, 130. [Google Scholar] [CrossRef]
- Smith, P.S.; Williams, G.G.; Schmidt, G.D.; Diamond-Stanic, A.M.; Means, D.L. Highly Polarized Optically Selected BL Lacertae Objects. Astrophys. J. 2007, 663, 118–124. [Google Scholar] [CrossRef]
- Kiehlmann, S.; Blinov, D.; Pearson, T.J.; Liodakis, I. Optical EVPA rotations in blazars: Testing a stochastic variability model with RoboPol data. Mon. Not. R. Astron. Soc. 2017, 472, 3589–3604. [Google Scholar] [CrossRef]
- Fossati, G.; Maraschi, L.; Celotti, A.; Comastri, A.; Ghisellini, G. A unifying view of the spectral energy distributions of blazars. Mon. Not. R. Astron. Soc. 1998, 299, 433–448. [Google Scholar] [CrossRef]
- Blinov, D.; Pavlidou, V.; Papadakis, I.E.; Hovatta, T.; Pearson, T.J.; Liodakis, I.; Panopoulou, G.V.; Angelakis, E.; Baloković, M.; Das, H.; et al. RoboPol: Optical polarization-plane rotations and flaring activity in blazars. Mon. Not. R. Astron. Soc. 2016, 457, 2252–2262. [Google Scholar] [CrossRef]
- Abdo, A.A.; Ackermann, M.; Ajello, M.; Axelsson, M.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Baughman, B.M.; Bechtol, K.; et al. A change in the optical polarization associated with a γ-ray flare in the blazar 3C279. Nature 2010, 463, 919–923. [Google Scholar] [CrossRef]
- Lyutikov, M.; Pariev, V.I.; Gabuzda, D.C. Polarization and structure of relativistic parsec-scale AGN jets. Mon. Not. R. Astron. Soc. 2005, 360, 869–891. [Google Scholar] [CrossRef]
- Pushkarev, A.B.; Gabuzda, D.C.; Vetukhnovskaya, Y.N.; Yakimov, V.E. Spine-sheath polarization structures in four active galactic nuclei jets. Mon. Not. R. Astron. Soc. 2005, 356, 859–871. [Google Scholar] [CrossRef]
- Homan, D.C.; Wardle, J.F.C.; Cheung, C.C.; Roberts, D.H.; Attridge, J.M. PKS 1510-089: A Head-on View of a Relativistic Jet. Astrophys. J. 2002, 580, 742–748. [Google Scholar] [CrossRef]
- Lister, M.L.; Aller, M.F.; Aller, H.D.; Homan, D.C.; Kellermann, K.I.; Kovalev, Y.Y.; Pushkarev, A.B.; Richards, J.L.; Ros, E.; Savolainen, T. MOJAVE. X. Parsec-scale Jet Orientation Variations and Superluminal Motion in Active Galactic Nuclei. Astron. J. 2013, 146, 120. [Google Scholar] [CrossRef]
- Lyutikov, M.; Kravchenko, E.V. Polarization swings in blazars. Mon. Not. R. Astron. Soc. 2017, 467, 3876–3886. [Google Scholar] [CrossRef]
- Peirson, A.L.; Romani, R.W. The Polarization Behavior of Relativistic Synchrotron Jets. Astrophys. J. 2018, 864, 140. [Google Scholar] [CrossRef]
- Yuan, Y.; Nalewajko, K.; Zrake, J.; East, W.E.; Blandford, R.D. Kinetic Study of Radiation-reaction-limited Particle Acceleration During the Relaxation of Unstable Force-free Equilibria. Astrophys. J. 2016, 828, 92. [Google Scholar] [CrossRef]
- Marscher, A.; Jorstad, S.; Williamson, K. Modeling the Time-Dependent Polarization of Blazars. Galaxies 2017, 5, 63. [Google Scholar] [CrossRef]
- Achterberg, A.; Gallant, Y.A.; Kirk, J.G.; Guthmann, A.W. Particle acceleration by ultrarelativistic shocks: Theory and simulations. Mon. Not. R. Astron. Soc. 2001, 328, 393–408. [Google Scholar] [CrossRef]
- Spitkovsky, A. Particle Acceleration in Relativistic Collisionless Shocks: Fermi Process at Last? Astrophys. J. Lett. 2008, 682, L5. [Google Scholar] [CrossRef]
- Mizuno, Y.; Lyubarsky, Y.; Nishikawa, K.I.; Hardee, P.E. Three-Dimensional Relativistic Magnetohydrodynamic Simulations of Current-Driven Instability. I. Instability of a Static Column. Astrophys. J. 2009, 700, 684–693. [Google Scholar] [CrossRef]
- Alves, E.P.; Zrake, J.; Fiuza, F. Efficient Nonthermal Particle Acceleration by the Kink Instability in Relativistic Jets. PRL 2018, 121, 245101. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Chen, X.; Böttcher, M. Synchrotron Polarization in Blazars. Astrophys. J. 2014, 789, 66. [Google Scholar] [CrossRef]
- Chen, X.; Chatterjee, R.; Zhang, H.; Pohl, M.; Fossati, G.; Böttcher, M.; Bailyn, C.D.; Bonning, E.W.; Buxton, M.; Coppi, P.; et al. Magnetic field amplification and flat spectrum radio quasars. Mon. Not. R. Astron. Soc. 2014, 441, 2188–2199. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, X.; Böttcher, M.; Guo, F.; Li, H. Polarization Swings Reveal Magnetic Energy Dissipation in Blazars. Astrophys. J. 2015, 804, 58. [Google Scholar] [CrossRef]
- Zhang, H.; Li, H.; Guo, F.; Taylor, G. Polarization Signatures of Kink Instabilities in the Blazar Emission Region from Relativistic Magnetohydrodynamic Simulations. Astrophys. J. 2017, 835, 125. [Google Scholar] [CrossRef]
- Zhang, H.; Deng, W.; Li, H.; Böttcher, M. Polarization Signatures of Relativistic Magnetohydrodynamic Shocks in the Blazar Emission Region. I. Force-free Helical Magnetic Fields. Astrophys. J. 2016, 817, 63. [Google Scholar] [CrossRef]
- Deng, W.; Zhang, H.; Zhang, B.; Li, H. Collision-induced Magnetic Reconnection and a Unified Interpretation of Polarization Properties of GRBs and Blazars. Astrophys. J. Lett. 2016, 821, L12. [Google Scholar] [CrossRef]
- Nalewajko, K. A Model of Polarisation Rotations in Blazars from Kink Instabilities in Relativistic Jets. Galaxies 2017, 5, 64. [Google Scholar] [CrossRef]
- Giannios, D.; Uzdensky, D.A.; Begelman, M.C. Fast TeV variability in blazars: Jets in a jet. Mon. Not. R. Astron. Soc. 2009, 395, L29–L33. [Google Scholar] [CrossRef]
- Sironi, L.; Petropoulou, M.; Giannios, D. Relativistic jets shine through shocks or magnetic reconnection? Mon. Not. R. Astron. Soc. 2015, 450, 183–191. [Google Scholar] [CrossRef]
- Guo, F.; Li, X.; Li, H.; Daughton, W.; Zhang, B.; Lloyd-Ronning, N.; Liu, Y.H.; Zhang, H.; Deng, W. Efficient Production of High-energy Nonthermal Particles during Magnetic Reconnection in a Magnetically Dominated Ion-Electron Plasma. Astrophys. J. Lett. 2016, 818, L9. [Google Scholar] [CrossRef]
- Petropoulou, M.; Giannios, D.; Sironi, L. Blazar flares powered by plasmoids in relativistic reconnection. Mon. Not. R. Astron. Soc. 2016, 462, 3325–3343. [Google Scholar] [CrossRef]
- Christie, I.M.; Petropoulou, M.; Sironi, L.; Giannios, D. Radiative signatures of plasmoid-dominated reconnection in blazar jets. Mon. Not. R. Astron. Soc. 2019, 482, 65–82. [Google Scholar] [CrossRef]
- Zhang, H.; Li, X.; Guo, F.; Giannios, D. Large-amplitude Blazar Polarization Angle Swing as a Signature of Magnetic Reconnection. Astrophys. J. Lett. 2018, 862, L25. [Google Scholar] [CrossRef]
- Zhang, H.; Fang, K.; Li, H.; Giannios, D.; Böttcher, M.; Buson, S. Probing the Emission Mechanism and Magnetic Field of Neutrino Blazars with Multiwavelength Polarization Signatures. Astrophys. J. 2019, 876, 109. [Google Scholar] [CrossRef]
- Krawczynski, H. The Polarization Properties of Inverse Compton Emission and Implications for Blazar Observations with the GEMS X-Ray Polarimeter. Astrophys. J. 2012, 744, 30. [Google Scholar] [CrossRef]
- Zhang, H.; Diltz, C.; Böttcher, M. Radiation and Polarization Signatures of the 3D Multizone Time-dependent Hadronic Blazar Model. Astrophys. J. 2016, 829, 69. [Google Scholar] [CrossRef]
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H. Blazar Optical Polarimetry: Current Progress in Observations and Theories. Galaxies 2019, 7, 85. https://doi.org/10.3390/galaxies7040085
Zhang H. Blazar Optical Polarimetry: Current Progress in Observations and Theories. Galaxies. 2019; 7(4):85. https://doi.org/10.3390/galaxies7040085
Chicago/Turabian StyleZhang, Haocheng. 2019. "Blazar Optical Polarimetry: Current Progress in Observations and Theories" Galaxies 7, no. 4: 85. https://doi.org/10.3390/galaxies7040085
APA StyleZhang, H. (2019). Blazar Optical Polarimetry: Current Progress in Observations and Theories. Galaxies, 7(4), 85. https://doi.org/10.3390/galaxies7040085




