Abstract
Binary systems are very common among field stars, yet the vast majority of known exoplanets have been detected around single stars. While this relatively small number of planets in binaries is probably partly due to strong observational biases, there is, however, statistical evidence that planets are indeed less frequent in binaries with separations smaller than 100 au, strongly suggesting that the presence of a close-in companion star has an adverse effect on planet formation. It is indeed possible for the gravitational pull of the second star to affect all the different stages of planet formation, from proto-planetary disk formation to dust accumulation into planetesimals, to the accretion of these planetesimals into large planetary embryos and, eventually, the final growth of these embryos into planets. For the crucial planetesimal-accretion phase, the complex coupling between dynamical perturbations from the binary and friction due to gas in the proto-planetary disk suggests that planetesimal accretion might be hampered due to increased, accretion-hostile impact velocities. Likewise, the interplay between the binary’s secular perturbations and mean motion resonances lead to unstable regions, where not only planet formation is inhibited, but where a massive body would be ejected from the system on a hyperbolic orbit. The amplitude of these two main effects is different for S- and P-type planets, so that a comparison between the two populations might outline the influence of the companion star on the planet formation process. Unfortunately, at present the two populations (circumstellar or circumbinary) are not known equally well and different biases and uncertainties prevent a quantitative comparison. We also highlight the long-term dynamical evolution of both S and P-type systems and focus on how these different evolutions influence the final architecture of planetary systems in binaries.
1. Introduction
In a binary star system, the gravity of the companion star may strongly influence both the formation of planets and their subsequent dynamical evolution. The final architecture of a system strongly depends on how the efficiency of the accretion process is affected by the presence of a close massive body and on how the subsequent evolution due to migration by interaction with the circumstellar disk, tidal interaction with the star, planet–planet scattering or Kozai mechanism, is altered by the second star. The differences in planet growth and dynamics in binaries, with respect to single stars, should show up in the fraction of binary systems harboring planets and in their present dynamical configurations. However, to interpret properly what the data tell us, we need to develop models that can explain the specificities of these planetary systems compared to those around single stars.
We will focus here on the main characteristics of planets in both S and P–type orbital configurations which significantly differ in terms of perturbations by the companion star. In the S-type configuration, where planets orbit one of the star of the system, the most critical regions for planet formation are the outer ones where the gravity of the second star may excite large eccentricities, potentially leading to instability via resonance superposition and, in case of orbital misalignment, may also be involved in fast Kozai cycles with large eccentricity/inclination variations. The inner regions of the circumstellar disk appears then most promising for a ’regular’ core–accretion growth of planets and for subsequent stable orbital behavior. In the case of P–type configurations, where the planets orbit around both stars, perturbations are the strongest in the inner regions close to the central binary. In this configuration, instability is expected close to the center of the system, while planet formation should safely occur in the outer regions of the circumbinary disk. In this case, planet migration may play a major role in bringing outer planets close to the binary.
We expect that these diversities in the dynamics of S and P–type trajectories lead to distinct populations of planets, differing both from a physical and dynamical point of view. The diversity would be a consequence of the different effect the companion star has on the formation of planets and on their subsequent dynamical evolution. Unfortunately, modeling the formation and evolution of planets in binaries is a very complex task due to the wide parameter space to explore, which include the binary mass ratio and the semi-major axis, eccentricity and inclination of the binary orbit. A change in these parameters may increase/decrease the dynamical perturbation at different locations in the planet forming disk affecting all the stages of the evolution of the system, from proto-planetary disk formation to the final dynamical evolution of the system. Due to this variety of binary configurations it is an impossible task to outline a ’standard model’ of planet formation in binaries as opposed to that around single stars. In some configurations of the binary the growth of planets may follow a path similar to that around single stars, while in others, due to the companion star stronger influence, the evolution may be completely different, either favoring the formation of more/less massive planets or inhibiting the presence of stable planets at given radial distances from the primary star or from the baricenter of the pair, or leading to planets which are more eccentric or more inclined with respect to those around single stars. In addition, the two populations of planets, either circumstellar or circumbinary, are not equally well known since more than 120 planets on S-type orbits are known, as compared to only a dozen of P-type planets. In addition, the majority of confirmed S-type planets were detected by radial velocities, whereas circumbinary planets were mostly detected by transits.
In this paper we summarize the properties and peculiarities of planets in binaries and relate them to the formation process and the subsequent complex dynamics caused by the companion star.
2. Planets in S–Type Orbits
2.1. Observational Constraints
2.1.1. Adverse Biases
As of July 2019, 122 exoplanet host stars, out of 3055, are known to be part of binary or multiple systems. In an ideal world, the effect of binarity on exoplanet presence could be directly inferred from this raw data, by simply estimating the binarity rate among exoplanet hosts, as well as the distribution of separations for these planet-bearing binaries, and compare it to the corresponding statistics for field stars. Unfortunately, such a simple comparison is almost certainly misleading.
Taken at face value, 122 out of 3055 exoplanet-host stars would indeed yield a very low binary fraction of ∼4%, as compared to approximately 50% for solar type field stars [1,2], which would imply that binarity has a very strong adverse effect on the presence of exoplanets. However, this fraction should be taken with great caution because it suffers from very strong biases. The first issue is that radial velocity (RV) surveys, which account for roughly half of the discovered S-type exoplanets, are in general strongly biased against binaries, and often discard any binaries with separation ≤2 that can fall to within the spectrograph slit [3,4]. An additional problem is that these biases are never well characterized and might differ from one survey to the other. One of the few attempts at investigating the effect of binarity on exoplanet occurrence within one coherent RV survey is that of Eggenberger and her team [3,5,6], which compared the binarity fraction of a sample of exoplanet host stars to a control sample of stars with no RV planets, and found these fraction to be ∼5.5% and ∼13.7%, respectively [3], thus confirming the global adverse effect of binarity on exoplanet presence. Note, however, that, despite these adverse selection effects, the vast majority of exoplanets in tight binaries (of separation ≤50 au) were detected by radial velocity surveys (Figure 1).
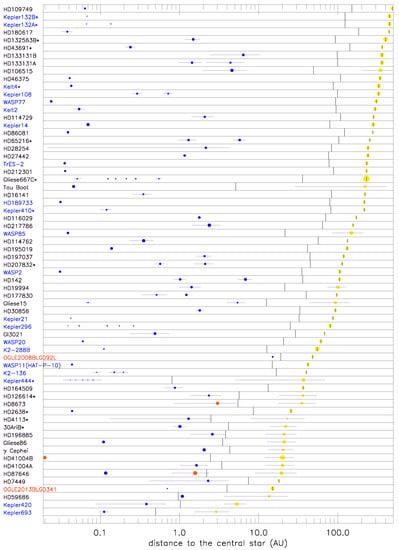
Figure 1.
All circumstellar (S-type orbits, as opposed to circumbinary P-type orbits) planet-hosting binaries with separation ≤500 au (as of July 2019). Companion stars are displayed as yellow circles, whose radius is proportional to . Planets are marked as blue circles whose radius is proportional to . The horizontal lines represent the radial excursion of the planet and star orbits (when they are known). When the binary orbit is known, the displayed distance is the semi-major axis, otherwise it is the projected current separation. The short vertical lines correspond to the outer limit of the orbital stability region around the primary estimated by Holman and Wiegert [7] assuming prograde orbits and coplanarity (for the seemingly “unstable” planet HD59686Ab, a retrograde orbit was suggested as a possible stable solution [8]. Planets detected by the radial velocity method are written in black, planets detected by transit are in blue, and planets detected by other methods are in red.
Transit surveys, which account for ∼40% of S-type exoplanets, do not suffer from these adverse selection effects. However, the stars they are targeting, in particular those of the NASA Kepler telescope, are generally more distant and have often not been vetted for binarity yet, so that a significant fraction might be wrongly labelled as singles. To alleviate this problem, several adaptive optic (AO) surveys were carried out in recent years, which detected a large number of companion stars to known transit-planet hosts [4,9,10,11]1. Note, however, that most of these surveys were targeting non-confirmed Kepler Objects of Interest (KOIs), so that the actual binarity fraction among confirmed exoplanets stays relatively low. This is why, even if transit detections represent more than 70% of known exoplanets, they only account for ∼40% of confirmed exoplanets in binaries.
However, despite their respective shortcomings and limitations, RV and transit detections have uncovered some general and relatively robust trends regarding exoplanets in binaries.
2.1.2. Characteristics of Exoplanets in Binaries
An investigation that is in principle not sensitive to target selection biases is the comparison between the exoplanet populations in single and multiple systems.
A trend that was identified early on, albeit on a relatively limited sample of RV-detected systems, is the high fraction of massive close-in planets (“hot Jupiters”) in tight ( au) binaries as compared to their fraction in wide binaries or single stars [5,15,16]. More recent studies, considering larger samples of exoplanet systems, confirmed that there is indeed a clear difference regarding the populations of hot Jupiters in multiple and single stars, but the picture that emerges is different from the one envisaged early on. On the one hand, contrary to early estimates, the tendency towards more frequent hot-Jupiters in tight binaries is no longer found. Indeed, reference [17] find that, for separations ≤50 au, the stellar multiplicity rate for hot-Jupiters is in fact 4 times lower than that of field stars, which is approximately the same ratio as the one derived, for the same separation range, for the general population of exoplanet hosts [18]. On the other hand, there is a clear tendency towards a very high fraction of hot-Jupiter in moderate-to-wide binaries. For the au separation range, reference [17] indeed find a multiplicity fraction that is 2.9 times higher for hot-Jupiter hosts than for field stars, a result which was confirmed by [19] for close-in companions up to the brown dwarf regime.
Regarding the population of exoplanets with semi-major axis au, however, there does not seem to be any statistical difference between single and multiple stellar systems [4], neither regarding planet masses nor their orbital parameters.
2.1.3. Multiplicity Rate of Exoplanet Hosts
One of the most obvious trends that shows up on the global raw distribution of separations of exoplanet-hosting binaries is a depletion of close-in companions ( au) as compared to the distribution of binary separations for solar-type field stars, which peaks around 30–50 au (see Figure 2). This trend did already show up in the results of AO surveys looking for companions to RV-exoplanet hosts [16,20], but the complexity of selection biases in RV targets prevented an undisputed confirmation as to its reality. It is the large-scale surveys looking for companions to transit exoplanet hosts that allowed to confirm this trend. The Doppler and AO–based search of [9] and the AO survey of [18] showed that, while the multiplicity fraction is statistically indistinguishable between planet and non-planet hosts for binary separations ≥100 au, there is a very strong depletion of tighter companions for exoplanet hosts, comprised between a factor ∼4 and ∼15. Reference [18] estimated that the distributions of close-in companions to exoplanet-hosting primary stars can be fitted by considering that the separation distribution for field stars is diminished by a factor ∼3 below a limiting separation au. In the absence of selection biases, this is equivalent to saying that the planet occurrence rate is 3 times smaller in au binaries than for single stars. Note, however, that this issue is not fully settled yet. As an example, while [10] confirm a strong drop of planet occurrences in close-in binaries, they also found that this lower occurrence rate extends, albeit less pronounced, up to separations of ∼1500 au. On the contrary, the recent AO survey by [21] did not find any depletion of au binaries in K2 exoplanet host stars. These conflicting results might be due to the fact that, for Kepler targets, the au separation domain is at the limit of what is feasible with AO companion searches. Note also that these statistics about multiplicity rates in planet-hosts are only valid for the type of exoplanets that are detectable by given observing facilities. As an example, the planet occurrence suppression rate for tight binaries found by [10] or [18] apply to the short period (typically less than 100 days) planets investigated by Kepler, while the results regarding companions to RV-exoplanet hosts found by [16,20] are less biased in orbital-periods but strongly biased towards large mass planets.
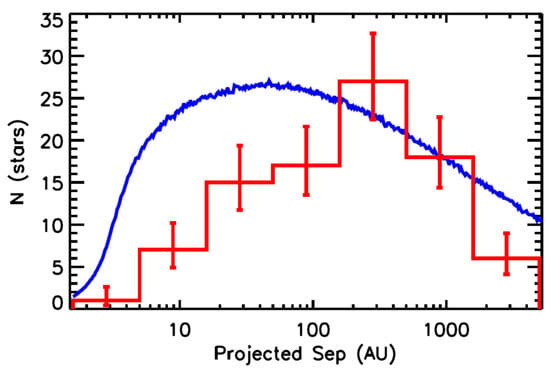
Figure 2.
Red histogram: Marginalized distribution of projected separations for all stellar companions to S-type exoplanet-host stars found by [18] for a large sample of Kepler Objects of Interest (KOIs). The blue line represents the predicted distribution if binaries were drawn from the distribution reported by [2]. Taken from [18], courtesy of the Astrophysical Journal.
There remains one potentially significant feature that shows up on the raw distribution of binary separations of exoplanet-hosts that has not been investigated yet, which is the apparent accumulation of exoplanet-host binaries around a au separation (Figure 3). Given the still limited number (9) of systems concerned it is still difficult to assess the reality of this feature, but should it be confirmed then it would put very strong constraints on the formation and evolution of planets in multiple systems. At any rate, the very presence of planets in such “extreme” systems, where a stellar companion is located at the same position as Uranus in the solar system, is a challenge to the standard model of planet formation, especially when considering that some of these planets (HD196885b, Cephei b, HD41004Ab) are both very massive and beyond 1.5 au from their central star.
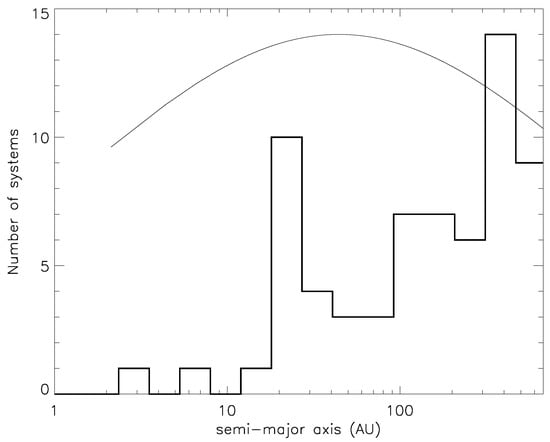
Figure 3.
Distribution of the semi-major axis of all S-type exoplanet-hosting binaries with a projected separation up to 500 au. When the semi-major axis is not known and only the projected separation is available, is estimated through the statistical relation [1,2]. The solid-line curve represents the normalized distribution for field stars derived by [2].
2.2. Planet Formation in Binaries
As shown in the previous section, there seems to be reliable observational evidence that a close-in stellar companion (≤50 au) has a detrimental effect on the presence of an exoplanet around a host star. In addition, for the few exoplanets that have been found to inhabit “extreme” systems with binary separation of the order of 20 au or less, it is very unlikely that their formation process could have proceeded without being strongly affected by the perturbations of the companion star. At any rate, studying planet formation in binaries can be used as a test bench for planet formation models, by confronting them to an unusual and sometimes “extreme” environment where some crucial parameters might be pushed to extreme values.
For a detailed discussion on the issue of planet formation in binaries, we refer the reader to the review by [22]. We shall here highlight the main aspects of this very complex issue.
2.2.1. Early Stages
The presence of a close-in stellar companion can have an effect early on in the planet formation, by tidally truncating the circumstellar proto-planetary disk. This truncation radius is typically located at 1/3 to 1/4 of the binary’s separation [23,24], which means that, if we assume that the dense parts of a proto-planetary disk have a typical size of ∼50–100 au, then this truncation effect should affect all binaries with separation ≤150–200 au. Observations show that disks are indeed less frequent in tight binaries, even though this trend is clearly confirmed only for separations of less than 40 au, with a disc frequency of only ∼30–40% as compared to ∼80% for single stars (Figure 4). Observational surveys also show that, even when present, disks are on average less massive in tight binaries [25].
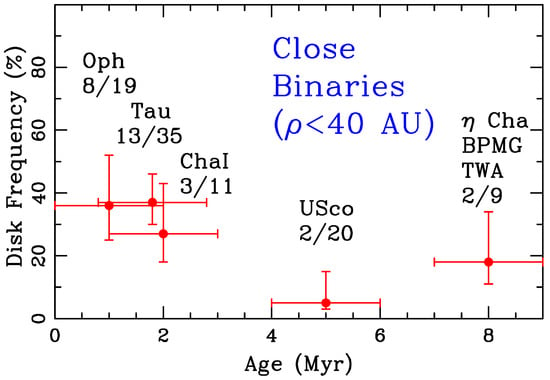
Figure 4.
Frequency of disk–bearing tight binaries (with projected separation au) as a function of age in several young stellar associations (from [23], courtesy of the Astrophysical Journal).
This can have two major consequences on the planet-formation process. The first one is that a truncated disk has a faster viscous evolution and should be more short-lived, leaving less time for planet formation [26]. This could be especially troublesome for giant gaseous planets that need to accrete vast amount of gas before the primordial disk’s dispersal, and numerical studies have shown for example that the giant planet in the Cephei binary (of separation ∼20 au) would not have enough time to form in situ by the canonical core-accretion scenario. There is observational backing to this shorter lifetime of disks-in-binaries, with [23] showing that the the typical lifetime of disks in ≤40 au binaries is less than 1Myr, as compared to the 5–10 Myrs typical of single stars. The other potential consequence of disk truncation is that there might not be enough mass left to form jovian planets in close-in binaries. Studies focusing on the specific case of Cephei found that a truncated proto-planetary disk might contain just enough mass to form the observed planet [26,27], but recent re-evaluations of this planet’s mass to 9 M might challenge these optimistic results [28].
2.2.2. Planetesimal Accretion
The planet-formation stage that has been, by far, the most studied in the context of binaries is the intermediate stage leading from kilometer-sized planetesimals to Lunar-sized planetary embryos. This is probably because planetesimal accretion, controlled by their mutual gravity, requires very low encounter velocities, of the order of a few m s for km-sized bodies, in order to successfully proceed (e.g., [29]), and is thus very sensitive to dynamical perturbations such as those coming from a stellar companion. Various studies performed by the authors of this review showed that a crucial mechanism is in this case the coupling between the gravitational pull of the companion and the drag from the still-present primordial gas disk on the planetesimals. This coupling induces a strong size-dependent phasing of planetesimal orbits which reduces impact velocities among same-sized objects [30,31] but strongly increases those between non-equally sized bodies, leading to collision velocities far above the threshold allowing mutual accretion [32,33]. For any realistic distribution of planetesimal sizes, the latter effect dominates the former, leading to a globally adverse consequence of the companion star on the accretion process. Assuming a small inclination between the binary and the circumstellar planetesimal disks tend to mitigate this effect, but at the costly price of a drastic slowing down of the growth rate [34,35]. All in all, for close-in binaries with separation ∼20 au, models show that planetesimal accretion is prevented beyond ∼0.5–1 au from each star [36,37]. This makes the in situ formation of the HD196885b, Cephei b or HD41004Ab planets problematic [31,38], and also raises issues as to the potential formation of planets in the habitable zones within the Centauri system (Figure 5).
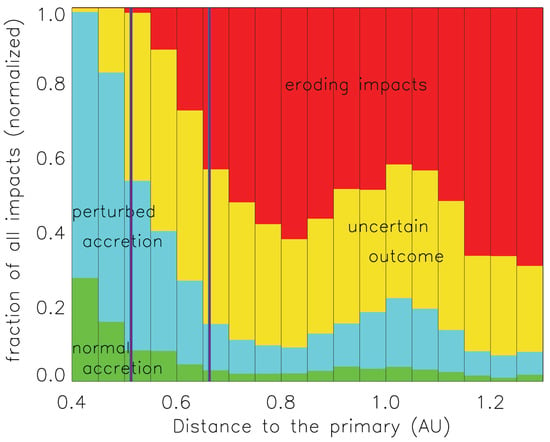
Figure 5.
The accretion behavior in a planetesimal disk around Cen B, estimated with numerical simulations taking into account gas drag. The relative importance of different types of collisional outcomes is displayed as a function of radial distance. Red: impacts for which the impact velocity , where is the threshold velocity beyond which an impact between two objects of sizes and always results in net mass loss. Yellow: Uncertain outcome. The erosion vs. accretion net balance depends on the physical composition of the planetesimals. Green: , where is the escape velocity of the () pair. Accretion can here proceed unimpeded, in a “runaway growth” way, as around a single star. Light blue: . Collisions result in net accretion, but are high enough to switch off the fast-runaway growth mode. The two thick blue lines denote the location of the inner limit of the “optimistic” and “conservative” habitable zone around the star. The planetesimal size distribution is assumed to be a Maxwellian centered on 5 km (modified from [36]).
Recent analytical investigations showed that, if the gas disk is massive () and nearly axisymmetric (), then the disk’s self-gravity could reduce encounter velocities among planetesimals to values low enough to allow their mutual accretion [39,40,41]. However, numerical studies of gas disk dynamics in binaries showed that is probably never low enough (with ) for this mechanism to be effective [26,42,43,44,45]. Moreover, the only preliminary numerical study that has, to this day, investigated planetesimal dynamics taking into account gas disk self gravity has found that disk gravity tends to increase impact velocities instead of reducing them [46]. More detailed investigations are required to quantitatively assess this issue.
2.2.3. Late Stages
The prospects for the last stages of planet formation, leading from lunar-sized embryos to fully formed planets, look much more promising. This mainly comes down to the fact that it is much more difficult to hinder the accretion of ∼1000 km objects than that of kilometer-sized ones. The companion star perturbations would indeed have to induce impact velocities exceeding ∼1 km s instead of a few m s. This was confirmed by several numerical studies (see Figure 6) which showed that the mutual growth of large embryos is possible in mostly all the regions of orbital stability around each star [32,47,48,49,50,51]. The one caveat is that, of course, this last stage can proceed only if the preceding stage of planetesimal accretion has been successful in forming lunar-sized embryos.
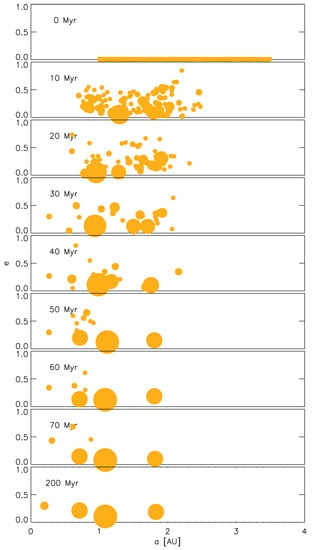
Figure 6.
Numerical simulation of the mutual accretion within an initial disk of lunar-sized embryos around Centauri B. At the end of the simulation, four terrestrial planets were formed. (Taken from [47], courtesy of the Astrophysical Journal)
2.2.4. Alternative Scenarios?
Given the potential concerns regarding some stages of the canonical planet-formation scenario, several authors considered alternative explanations for the paradoxical presence of exoplanets in close-in binaries. One possibility is that these planets formed closer to their host star, in regions more protected from the adverse influence of the stellar companion, and later migrated outward. However, it seems that this migration is not large enough, limited to a radial displacement of ∼30%, to explain the HD196885 or Cephei planets [52]. In the same family of scenarios, there is the possibility that these planets were injected in their current orbit after dynamical scattering with another planet [53]. However, this would require the presence of another, more massive but yet undetected planet closer to the central star, which might be difficult to explain given that this second planet should in principle be easier to detect than the first one. On a related note, reference [54] showed that such planet-planet scattering followed by tidal capture might transfer a planet from a circumbinary orbit (P-type) to a circumstellar one (S-type), effectively creating a tight planet-hosting binary. However, this process might only work for binary separations of less than ∼3 au.
Another possibility is that planet formation follows a different channel in a binary environment. References [55,56] for example showed that planetesimal growth might still be possible, but in a different form, in a high impact velocities environment. The basic idea is that, while mutual planetesimal collisions are destructive and produce small fragments, these produced fragments might be easily re-accreted by other planetesimals that were not destroyed by mutual impacts. These “lucky seeds” will then continue to sweep up such small dust-sized debris until they reach sizes big enough to be protected against destructive impacts with other planetesimals. However, these two studies remain very qualitative and this sweeping growth mode should be quantitatively investigated by more detailed models. Reference [57] considers a more radical alternative, which is that most planets in ≤100 au binaries are not formed by “classical” core accretion but by the concurrent gravitational instability scenario. The main argument is that binary-truncated proto-planetary disks are more compact and thus more gravitationally unstable, and also that companion perturbations could act as an additional trigger to start these instabilities. This explanation would also explain why planets in tight binaries tend to be larger than around single stars. However, this scenario does not seem to be backed by numerical models, which show that, on the contrary, the development of instabilities is hindered by the presence of a close-in companion [58,59], so that the presence of larger planets in tight binaries is probably not due to this alternative formation channel.
The last family of solutions to the planets-in-tight-binaries paradox invokes stellar interactions that could have modified the dynamical environment around the host star after the formation of the planet. Reference [60] showed that some tight planet-hosting binaries can be formed from unstable hierarchical triple systems, after the ejection of the third star shrinks the central binary, which was thus initially wider and less disruptive for planet formation. Similarly, reference [61] showed that early stellar encounters in stellar clusters also lead, on average, to a shrinking of binary separations, so that the accretion-hostile binary configuration could come about after the formation of the planet (Figure 7). More recently, reference [62] estimated that there is a limited but non-zero possibility for a planet-hosting star to be injected into a pre-existing binary after an encounter with it, ejecting the former companion star and replacing it in the binary, at a separation that is, on average, smaller than that of the initial binary.
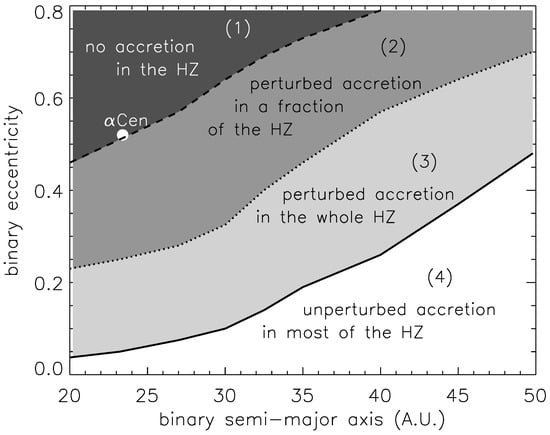
Figure 7.
Accretion vs. Erosion behavior of a population of kilometer-sized planetesimals in the habitable zone around Centauri B when varying the binary’s separation and eccentricity. The white circle marks the current orbit of the binary. This shows that planetesimal accretion is possible if the binary has suffered a stellar encounter that shrank its initial wider orbit to its current value (taken from [36], courtesy of the MNRAS).
3. Planets in P–Type Orbits: Circumbinary Planets
The number of known exoplanets on P–type orbits (circumbinary) is smaller compared to those in S-type orbits, leaving their dynamical and physical properties less constrained. Most of them (at present 10) were discovered by Kepler with the transit method while the more massive ones () were found either by eclipsing binary timing [63] around evolved stars or direct imaging. The most interesting among transiting circumbinary planets is Kepler–47, the only multi–planet system that has 3 exoplanets with masses ranging from 2 to about 43 Earth masses moving in almost circular orbits, coplanar to the binary orbital plane, stable at least over 100 Myr and with the inner and less massive planet right next to the dynamical stability limit [64]. Almost all Kepler circumbinary planets found so far orbit their stars very close to the plane of the binary in a prograde direction. This coplanarity seems to be suggested also by the statistical analysis of [65] showing that if planetary orbital inclinations were randomly distributed with respect to the binary orbital plane, then the inferred frequency of planets in circumbinary orbits should be exceptionally high compared to that around single stars. On the other hand, if coplanarity is the preferred orbital architecture, then the rate of occurrence of circumbinary planets appears to be consistent with that of single stars.
The three main features that seem to pop up from the current known population of circumbinary transiting planets are:
- (1)
- A lack of planets around tight binaries ( days) [66]
- (2)
- A pile–up close to the inner dynamical stability limit
- (3)
- Masses smaller than that of Jupiter
The last two items face the exception of Kepler-1647 [67], which is both the most massive (∼1.5 ) P-type planet and the one with the widest orbit, with a semi-major axis of 27 au well beyond the inner stability limit of the system.
The reason no P-type planet has been found around tight binaries is possibly due to the formation path of such tight binaries, which might be the outcome of the evolution of a triple system via the Kozai–Lidov mechanism followed by dynamical instability that ejected the third star (see [68] for recent modeling). As for the pile-up of planets smaller than Jupiter, it is possibly due to the formation mechanism and subsequent evolution of planets in the circumbinary disk.
3.1. Formation and Evolution of Circumbinary Planets
Several theoretical works have shown that the binary perturbations may create a hostile environment for forming a planet close to the stellar pair. Reference [69] modeled the planetesimal accretion phase in Kepler 16, the first circumbinary planet detected with Kepler, with an N-body code including the aerodynamic drag induced by an axisymmetric gaseous disk. He found that, although the size-dependent pericenter phasing of the orbits might allow planetesimal accumulation in a narrow region in between 1 and 1.8 au, the most likely region for the growth of planetary embryos lies beyond 4 au. Reference [70] improved this calculation by including, in their model, dust accretion onto planetesimals and extending the computations to the cases of Kepler-34 and Kepler-35. Their simulations confirm that planetesimal accumulation close to the central stars is strongly inhibited by the binary perturbations. An additional refinement to these N-body models was done by [71], which included the effect of the planetesimal disk self-gravity and considered an improved collisional model. Their results confirm that, in the case of Kepler-34, the inner region of the circumbinary disk is a hostile environment for planetesimal accretion even for planetesimals as large as 120 km. According to [72], the region where planetesimal accumulation is forbidden may be reduced if we consider the effects of the gravity field of the gaseous disk on the secular evolution of the planetesimals. The precession rates of the pericenters of the planetesimals are indeed faster once perturbed by a massive circumbinary disk and a strong damping of the planetesimal eccentricity is expected beyond 2–3 au from the stars, shifting inwards the location of the accretion friendly zone, even if not enough to encompass the region where the planets are currently located.
In all the previous models the effects of gas drag on planetesimals were computed assuming a fixed axisymmetric gas disk. References [73,74] relaxed this assumption and used an hybrid algorithm solving at the same time the evolution of the gaseous disk with the FARGO model [75] and the N-body equations for the planetesimals including gas drag and the gravitational pull of the disk. They find that density waves and a significant disk eccentricity strongly affect the planetesimal orbital evolution, both via a non-axisymmetric gas drag force and direct gravitational pull, leading to a higher dephasing of the pericenters and to higher mutual encounter velocities causing erosive impacts. Figure 8 shows that, for Kepler-16, the whole region within 10 au from the central binary is very hostile to planetesimal accretion due to the gravity from the eccentric gas disk. All these studies rule out the formation of a planet by core-accretion close to its present location (near the binary inner stability limit), strongly suggesting a scenario in which the planet forms further out in the disk and subsequently moves with traditional migration processes to its current orbit.
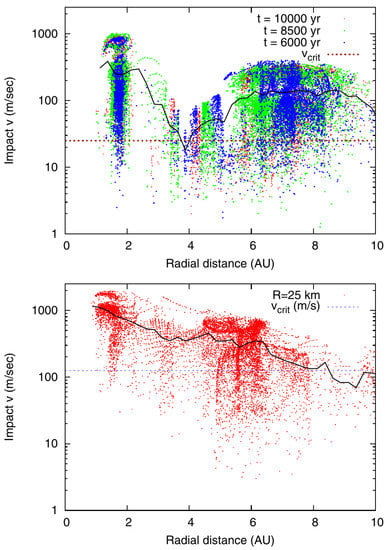
Figure 8.
Figure from [74] showing at different evolutionary times the relative impact velocities for a putative planetesimal population in Kepler-16. In the upper panel the impact velocities between equal size R = 5 km planetesimals, computed at different radial distances from the baricenter of the binary, are compared with the critical erosion velocity (black dashed line). The continuous black line shows the average impact velocity for the population. In the lower panel the impact speeds are computed for larger planetesimals R = 25 km in size.
3.2. Migration Towards the Inner Hole
The pile-up of most circumbinary planets just outside the inner stability limit despite the difficulty of forming them in these highly perturbed regions suggests that they formed further out and later migrated inward by interaction with the circumbinary disk. Indeed, if a massive Jupiter-like planet forms in a circumbinary disk, it carves a gap and it drifts inward in the regime of Type II migration. At some stage of its inward drift, the planet-carved gap will reach the outer edge of the large cavity formed by tidal pull around the central binary, merging with it to form a single wide gap in which both the stellar pair and the planet are embedded [76]. The planet will then continue to migrate until it reaches the 4:1 MMR with the binary’s orbit and, at that point, either it stalls close to the MMR or it may follow different unstable paths [76]. According to [77], in most cases the planet is ejected out of the system on a hyperbolic orbit, filling the population of free floating planets, or it may impact either the secondary star (more frequently) or the primary contributing to develop a difference in star metallicity between the two due to their different amount of planet pollution. More complex is the evolution in the case of less massive planets not opening a gap in the disk. Type I migration drives them close to the stellar pair, but when they get close to the inner border of the disk hole, their final location is determined by a balance between the gravitational pull of the stars and the interaction with the disk in which they are still embedded. According to the modeling of [78,79] the main relevant parameter is then the thermal profile of the disk, which may significantly influence the last stages of evolution of these lower-mass planets as they approach the 4:1 or 5:1 MMRs. In addition, they find that, to prevent the scattering of the planet out of the system, a low density disk is required and, possibly, the present of a second planet in the system.
4. Dynamics and Stability in S-Type Orbits
The main players determining the dynamical evolution of planets orbiting in the S-type configuration are:
- The interaction with the circumstellar disk. In the early phases of evolution of the system it may significantly change the architecture of the planetary system [80].
- Mean Motion Resonances (hereinafter MMR) between the planets and between the planets and the binary companion.
- Secular perturbations and secular resonances, linear and non-linear [81,82], with the main frequencies of the system.
- The Kozai dynamics when significant mutual inclinations are present among the bodies [83].
- Planet–planet or planet–star scattering if the system becomes temporarily unstable [53].
All these mechanism may act, together or at different times, to determine the evolution of a system of planets in binaries. In particular, to determine the outer limit of stability of a planet orbit [7,84], secular and mean motion resonances are the most active players. Superposition of resonances may determine large areas of instability where planets cannot survive for a long enough time [85,86]. Secular perturbations, by increasing the average eccentricity of the planet(s) orbit, may drive them into these chaotic region caused by resonance overlap.
4.1. Secular Evolution
A simple model for the secular perturbations of the binary companion on the orbit of a circumstellar planet is given by [87] which derived an averaged disturbing function in the orbital elements of the planet and binary star which leads to the solution for the planet non-singular orbital elements of the form:
where , the frequency of circulation of the pericenter longitude of the planet, is given by:
The forced eccentricity is computed as:
with the semi-major axis and mean motion of the planet, the semi-major axis and eccentricity of the binary companion, the mass of the central star, that of the secondary and their ratio. From Equation (3) it follows that is proportional to and it increases while approaching the outer stability limit of the planet while the frequency also depends on the mass ratio .
Higher order theories are needed when either the ratio or , or both, are not small. Reference [88] has shown that, under these circumstances, second order theories are more accurate in computing both and close to the outer border of stability. As illustrated in Figure 9, the model of [87] in general predicts too high values of and slower oscillation frequencies respect to the outcome of a direct numerical integration while the second order analytical model follows more closely the numerical solution.
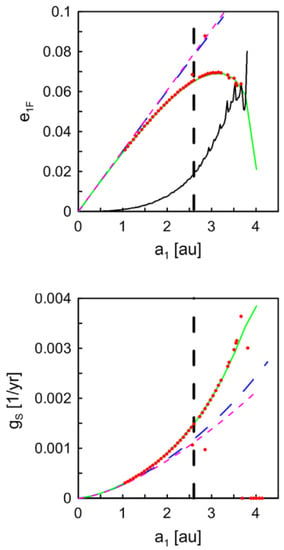
Figure 9.
Figure taken from [88]. The values of (top panel) and (bottom panel) are computed for the planet in HD 196885 (the vertical dashed line shows its location). The red dots are reference outcomes of numerical simulations [7], the magenta curve is derived from [87], the blue curve from the first order model of [88] while the green curve is the second order model of [88]. The black curve shows the amplitude of the short period variations of the eccentricity.
4.2. Stability Limit for One Planet
A planet in a binary system is affected both by secular and resonant perturbations which may interact and lead to instability beyond a given value of . The threshold value of , for a given value of , is called the critical semi-major axis and it has been estimated for different values of , and mass ratio by [7,89] via a large number of numerical simulations. The more accurate semi-empirical formula for , given by [7], is:
where the mass ratio is defined as . The source of instability beyond is related to the growth of the forced eccentricity due to the secular perturbations which becomes higher for larger values of (Equation (3)). This drives the planet into the region where mean motion resonances (MMRs) overlap leading to chaos [85]. The critical semi-major axis estimated by [7] is, however, a lower estimate. A more accurate numerical approach based on the FMA (Frequency Map Analisys, referneces [90,91,92]) by [84] has shown that:
- The value of computed by [7] underestimates the real stability limit and stable planetary orbits can be found beyond .
- Some planets may be trapped in low order resonance (3:1, 5:2) with the companion star, far beyond , and be stable over a long timescale.
- For large values of , large unstable regions can be found within due to non-linear secular resonances with the binary companion.
In Figure 10 this behavior is illustrated for a circular and eccentric () binary with a semi-major axis au. The FMA diffusion index is plotted for different values of the planet semi-major axis. Low values mean stability, high values suggest chaotic behavior. In both cases the stability limit exceeds that derived from [7] while unstable cases can be found within it, in particular in the eccentric case. In addition, in the circular case, some putative planets are trapped in stable mean motion resonances with the companion star well beyond the stability limit.
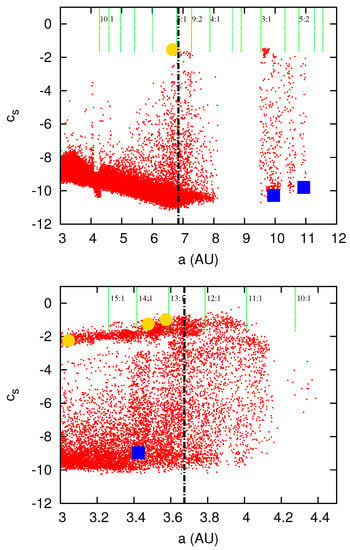
Figure 10.
Figure taken from [84]. The FMA analysis is performed on a Jupiter-size single planet orbiting in a binary system with AU and (top panel) and (bottom panel). The diffusion index of the main secular frequency of the planet is drawn vs. its semi-major axis. Small values of means low diffusion, while large values connote chaotic orbits. The black dash-dotted line marks the critical semi-major axis computed from the empirical formula of [7]. The green dashed lines show the location of mean motion resonances between the planet and the companion star. The blue squares show stable cases whose orbits were numerically integrated over 4 Gyr, the yellow circles unstable ones.
4.3. Stability of Multiple Planet Systems
When two or more planets are present in the system, the situation is more complex since, in addition to the resonances with the binary, mean motion and secular resonances develop among the planets that may overlap with those due to the companion star. As a consequence, we do not expect that a system of two planets in binaries to be necessarily stable if both planets orbit within . Reference [93] studied the location of secular resonances and chaos in a system with two planets, focusing their investigation on the system HD 41004. They consider different binary configurations and test the stability of a putative inner planet perturbed also by the giant planet detected in the system. The stability of the inner planet is studied with the maximum eccentricity criterion and a semi-analytical method is outlined to determine the location of secular resonances within with a reduced computational load. Reference [84] has instead applied the FMA method to test the influence of a binary companion on the Hill stability limit for two giant planets orbiting within . They found that the minimum separation between the two planets for stability is still marked by the 3:2 mean motion resonance between them but that the level of chaoticity close to this threshold is higher in a binary system. In addition, they derived a semi-empirical equation giving the minimum semi-major axis of a binary orbit compatible with a stable two-planet system orbiting the main star. This computation is different from the calculation of the critical for a single planet [7] since it requires that two planets are present in the system. The value of is given by:
where and is the semi-major axis of the inner planet. This equation has a limited range of validity i.e., , au, and au but it can be exploited to predict the presence of an additional planet when one has been already detected. It is an approximated formula based on a large number of numerical tests but it does not have an accuracy estimate due to the complexity of the numerical interpretation.
4.4. Kozai Evolution in Presence of Inclined Binaries
Planets in binaries may have their orbital plane tilted with respect to that of the binary. This may occur either because the rotation axes of the stars in the binary are misaligned at the moment of their formation [94,95,96,97] or because a dynamical mechanism like planet-planet scattering [53] has lead to large inclinations of the planets with respect to their original orbital plane (possibly the equator of the central star). In either cases, the misalignment has important dynamical consequences on the long term evolution of the planetary orbits related to the Kozai mechanism. The classical Kozai evolution is usually described by the quadrupole approximation of the Hamiltonian that, neglecting the Keplerian terms, is:
where are the orbital elements of the planet in a reference frame attached to the binary orbit. Since does not depend on the node , the component of the angular momentum along z is constant and this leads to the classical conservation law:
If the initial mutual inclination between the planet and the binary companion is higher than approximately 39 the oscillations in eccentricity, always in anti-phase with those in inclination, may become wide even if the initial eccentricity of the orbit was small. This behavior was invoked to explain the high eccentricity of the giant planet orbiting the star 16 Cygn B [98]. If the planet formed in a circular orbit but on a plane misaligned by more than 39 with respect to that of the binary, its orbit would switch between low-eccentricity and high-eccentricity orbits. During the high eccentricity phase, a strong tidal interaction with the central star may cause an inward migration of the planet, the so-called ‘Kozai migration’ [99].
The classical formulation of the Kozai mechanism assumes that the planet is handled as a massless test particle. If the planet is massive, than the expression for changes but the main properties of the evolution are similar. However, if the coefficient:
is not negligible, in particular when the eccentricity of the binary is high, then the quadrupole approximation is not accurate and the octupole term must be considered [83,100]. Interesting behaviors appear when the octupole term is considered, in particular the planet (either as a test particle or as a massive body) may undergo flips from prograde to retrograde orbits and the large oscillations in both eccentricity and inclinations may become chaotic. The large eccentricity achieved during the oscillations may also lead the planet to impact the star, unless some mechanisms like the General Relativity periastron precession and tides suppress the eccentricity excitations.
5. Dynamics and Stability in P-Type Orbits
Circumbinary orbits are perturbed by the tidal gravity field of the stellar couple which establishes a web of MMRs close to them. This web is responsible for:
- The unstable region surrounding the two stars due to resonance overlap,
- Halting the planet migration in the early phases of the evolution of the system by trapping the planet in a stable resonance.
5.1. A Secular Theory
Reference [101] developed a secular theory for bodies orbiting around a stellar binary which leads to equations similar to those derived for S-type orbits. The non-singular variables are solution of the following differential equations:
where
and . The forced eccentricity is given by:
The frequency of oscillation of the free eccentricity is equal to A. Contrary to the case of S-type orbits, both and increase while approaching the baricenter of the stars since both quantities are inversely proportional to the semi-major axis of the body. The increase of for smaller radial distances facilitates the entry into the chaotic region surrounding the two stars and due to resonance overlap.
In the initial stages of a circumbinary system, when the gaseous disk is still present, the secular evolution of the system has to include the gravity of the disk. As shown in [72], the term A in Equation (11) becomes where the additional term is given by:
assuming an initial superficial density profile for the disk:
with mass of the disk, the binary mass equal to the sum of the masses of the two stars and a reference radial distance. In addition, the term is no longer constant because changes with time. The precession of the binary orbit forced by the disk potential is given by:
where is approximately equal to , i.e., twice the binary semi-major axis. The forced eccentricity in this scenario assumes a value given by:
and its value depends on both and while the precession frequency becomes , faster than in the case without the disk potential. While this correction to the secular theory is expected to be important for the planetesimal evolution, it is probably less relevant when dealing with fully formed planets since, at that evolutionary stage, the disk is significantly less massive.
5.2. The Inner Unstable Hole
Bodies orbiting a stellar pair are influenced by its tidal time-periodic gravitational potential. References [7,89,102] explored the effects of these potential on putative planets orbiting the binary proving the existence of an unstable chaotic region surrounding the two stars. Planets ending up in this region have their eccentricity pumped up and they have a close encounter with the binary. This gap surrounding the stars has been shown to form also for circumbinary disk by [103]. Following the same procedure adopted to outline the stability region for S-type orbits, [7] calculated a critical semi-major axis beyond which orbits are dynamically stable. It can be computed as:
As stated above, the mechanism responsible for the dynamical instability within is the resonance overlap of MMRs with the binary while the forced eccentricity (Equation (12)) favors the entry into the chaotic region. If multiple planets are present in the system, the behavior is also influenced by mutual secular perturbations, in addition to those with the binary, and mutual MMRs. In this scenario General Relativity is not expected to be relevant since the planets orbit always far enough from the star. Beyond the critical value of there may be islands of instability, in particular for high value of , due to mean motion resonances [77].
Reference [104] has shown that the Kozai evolution is not important in this scenario, at least for planets with masses smaller than 5 and a binary mass ratio . The stellar binary system is not significantly affected by the perturbations of the outer body in this case.
6. Perspectives
An important step towards a better understanding of the formation and evolution of planets in binaries is to enrich the sample of known planets, in particular for the circumbinary ones. At present, only a dozen of them are known and it is still not clear if some of their properties, like the pile-up at the inner edge of the stable region or the overall low mass, are real characteristics due to the perturbations of the binary or if they are due to under-sampling and bias. As for planets on S-type orbits, what is crucially needed is a large-scale survey that is both unbiased against binaries and target stars that are close enough for their potential multiplicity to be well established beforehand. Another potentially interesting survey would be one specifically targeting a statistically significant sample of all the nearest binaries.
Another important issue that requires a significant observational effort concerns the orientation of the binary orbit with respect to the equator of the main star and the potential misalignment of the planetary orbit. The early study by [94] pointed toward a transition from alignment to misalignment around 30–40 au of separation, but updated observational investigations, as well as theoretical works, are now clearly needed. Locating the transition from alignment to misalignment may help the interpretation of the dynamical features of planets in binaries and, in particular, give an estimate of the importance of the Kozai mechanism in sculpting planetary systems in binaries.
From a theoretical point of view, additional work is needed on one important stage of the planet-formation scenario that has so far barely been investigated in the context of binaries, that is the coagulation of the first condensed grains into to kilometer-sized planetesimals. The pioneering work by [58] has for instance shown that the heat generated by spiral shock waves might inhibit dust coagulation in au binaries. In addition, 3-D simulations by [105] showed that strong hydraulic jumps occur at the shock front of spiral waves which are expected to affect the vertical distribution of dust particles and their accretion process by different merging mechanisms (collisional or instability driven accumulation, dust traps etc., see [106] for a review). The presence of spirals will not only affect the timescale and initial size distribution of planetesimals but also the following stages of the core-accretion process like the fast pebble accumulation of planetary cores [107] which is expected to accelerate the growth of giant planets.
Regarding the stage that has so far proven to be the most sensitive to binary perturbations, i.e., the mutual accretion of planetesimals into Lunar-sized embryos, a crucial step forward would be the development of a numerical model coupling the dynamics of planetesimals and of the gas disk, and taking into account both the gas drag and the effect of the disk’s self gravity. This would allow quantitatively assessing the respective importance of the concurring accretion-favoring and accretion-inhibiting effects triggered by the response of the gas disk to binary perturbations.
Author Contributions
The authors have equally contributed to the writing of the paper.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Duquennoy, A.; Mayor, M. Multiplicity among solar-type stars in the solar neighbourhood. II - Distribution of the orbital elements in an unbiased sample. Astron. Astrophys. 1991, 248, 485–524. [Google Scholar]
- Raghavan, D.; McAlister, H.A.; Henry, T.J.; Latham, D.W.; Marcy, G.W.; Mason, B.D.; Gies, D.R.; White, R.J.; ten Brummelaar, T.A. A Survey of Stellar Families: Multiplicity of Solar-type Stars. Astrophys. J. Suppl. 2010, 190, 1–42. [Google Scholar] [CrossRef]
- Eggenberger, A.; Udry, S. Detection and Characterization of Extrasolar Planets through Doppler Spectroscopy; EAS Publications, Series; Montmerle, T., Ehrenreich, D., Lagrange, A.M., Eds.; Cambridge University Press: Cambridge, UK, 2010; Volume 41, pp. 27–75. [Google Scholar]
- Ngo, H.; Knutson, H.A.; Bryan, M.L.; Blunt, S.; Nielsen, E.L.; Batygin, K.; Bowler, B.P.; Crepp, J.R.; Hinkley, S.; Howard, A.W.; et al. No Difference in Orbital Parameters of RV-detected Giant Planets between 0.1 and 5 au in Single versus Multi-stellar Systems. Astron. J. 2017, 153, 242. [Google Scholar] [CrossRef]
- Eggenberger, A.; Udry, S.; Mayor, M. Statistical properties of exoplanets. III. Planet properties and stellar multiplicity. Astron. Astrophys. 2004, 417, 353–360. [Google Scholar] [CrossRef]
- Eggenberger, A.; Udry, S.; Chauvin, G.; Beuzit, J.L.; Lagrange, A.M.; Ségransan, D.; Mayor, M. The impact of stellar duplicity on planet occurrence and properties. I. Observational results of a VLT/NACO search for stellar companions to 130 nearby stars with and without planets. Astron. Astrophys. 2007, 474, 273–291. [Google Scholar] [CrossRef]
- Holman, M.J.; Wiegert, P.A. Long-Term Stability of Planets in Binary Systems. Astron. J. 1999, 117, 621–628. [Google Scholar] [CrossRef]
- Trifonov, T.; Lee, M.H.; Reffert, S.; Quirrenbach, A. Dynamical Analysis of the Circumprimary Planet in the Eccentric Binary System HD 59686. Astron. J. 2018, 155, 174. [Google Scholar] [CrossRef]
- Wang, J.; Xie, J.W.; Barclay, T.; Fischer, D.A. Influence of Stellar Multiplicity on Planet Formation. I. Evidence of Suppressed Planet Formation due to Stellar Companions within 20 AU and Validation of Four Planets from the Kepler Multiple Planet Candidates. Astrophys. J. 2014, 783, 4. [Google Scholar] [CrossRef]
- Wang, J.; Fischer, D.A.; Xie, J.W.; Ciardi, D.R. Influence of Stellar Multiplicity on Planet Formation. II. Planets are Less Common in Multiple-star Systems with Separations Smaller than 1500 AU. Astrophys. J. 2014, 791, 111. [Google Scholar] [CrossRef]
- Ziegler, C.; Law, N.M.; Morton, T.; Baranec, C.; Riddle, R.; Atkinson, D.; Baker, A.; Roberts, S.; Ciardi, D.R. Robo-AO Kepler Planetary Candidate Survey. III. Adaptive Optics Imaging of 1629 Kepler Exoplanet Candidate Host Stars. Astron. J. 2017, 153, 66. [Google Scholar] [CrossRef]
- Mugrauer, M.; Ginski, C. High-contrast imaging search for stellar and substellar companions of exoplanet host stars. Mon. Not. RAS 2015, 450, 3127–3136. [Google Scholar] [CrossRef]
- Ginski, C.; Mugrauer, M.; Seeliger, M.; Eisenbeiss, T. A lucky imaging multiplicity study of exoplanet host stars. Mon. Not. RAS 2012, 421, 2498–2509. [Google Scholar] [CrossRef][Green Version]
- Ginski, C.; Mugrauer, M.; Seeliger, M.; Buder, S.; Errmann, R.; Avenhaus, H.; Mouillet, D.; Maire, A.L.; Raetz, S. A lucky imaging multiplicity study of exoplanet host stars—II. Mon. Not. RAS 2016, 457, 2173–2191. [Google Scholar] [CrossRef]
- Zucker, S.; Mazeh, T. On the Mass-Period Correlation of the Extrasolar Planets. Astrophys. J. 2002, 568, L113–L116. [Google Scholar] [CrossRef]
- Desidera, S.; Barbieri, M. Properties of planets in binary systems. The role of binary separation. Astron. Astrophys. 2007, 462, 345–353. [Google Scholar] [CrossRef]
- Ngo, H.; Knutson, H.A.; Hinkley, S.; Bryan, M.; Crepp, J.R.; Batygin, K.; Crossfield, I.; Hansen, B.; Howard, A.W.; Johnson, J.A.; et al. Friends of Hot Jupiters. IV. Stellar Companions Beyond 50 au Might Facilitate Giant Planet Formation, but Most are Unlikely to Cause Kozai-Lidov Migration. Astrophys. J. 2016, 827, 8. [Google Scholar] [CrossRef]
- Kraus, A.L.; Ireland, M.J.; Huber, D.; Mann, A.W.; Dupuy, T.J. The Impact of Stellar Multiplicity on Planetary Systems. I. The Ruinous Influence of Close Binary Companions. Astron. J. 2016, 152, 8. [Google Scholar] [CrossRef]
- Fontanive, C.; Rice, K.; Bonavita, M.; Lopez, E.; Mužić, K.; Biller, B. A high binary fraction for the most massive close-in giant planets and brown dwarf desert members. Mon. Not. RAS 2019, 485, 4967–4996. [Google Scholar] [CrossRef]
- Eggenberger, A.; Udry, S.; Chauvin, G.; Forveille, T.; Beuzit, J.L.; Lagrange, A.M.; Mayor, M. Probing the impact of stellar duplicity on the frequency of giant planets: Final results of our VLT/NACO survey. In The Astrophysics of Planetary Systems: Formation, Structure, and Dynamical Evolution; Sozzetti, A., Lattanzi, M.G., Boss, A.P., Eds.; Cambridge University Press: Cambridge, UK, 2011; Volume 276, pp. 409–410. [Google Scholar]
- Matson, R.A.; Howell, S.B.; Horch, E.P.; Everett, M.E. Stellar Companions of Exoplanet Host Stars in K2. Astron. J. 2018, 156, 31. [Google Scholar] [CrossRef]
- Thebault, P.; Haghighipour, N. Planet Formation in Binaries. In Planetary Exploration and Science: Recent Results and Advances, Edited by Shuanggen Jin, Nader Haghighipour, and Wing-Huen Ip. Springer Geophysics; Springer: Berlin, Germany, 2015; pp. 309–340. ISBN 978-3-662-45051-2. [Google Scholar]
- Kraus, A.L.; Ireland, M.J.; Hillenbrand, L.A.; Martinache, F. The Role of Multiplicity in Disk Evolution and Planet Formation. Astrophys. J. 2012, 745, 19. [Google Scholar] [CrossRef]
- Savonije, G.J.; Papaloizou, J.C.B.; Lin, D.N.C. On Tidally Induced Shocks in Accretion Discs in Close Binary Systems. Mon. Not. RAS 1994, 268, 13. [Google Scholar] [CrossRef]
- Harris, R.J.; Andrews, S.M.; Wilner, D.J.; Kraus, A.L. A Resolved Census of Millimeter Emission from Taurus Multiple Star Systems. Astrophys. J. 2012, 751, 115. [Google Scholar] [CrossRef]
- Müller, T.W.A.; Kley, W. Circumstellar disks in binary star systems. Models for γ Cephei and α Centauri. Astron. Astrophys. 2012, 539, A18. [Google Scholar] [CrossRef]
- Jang-Condell, H.; Mugrauer, M.; Schmidt, T. Disk Truncation and Planet Formation in γ Cephei. Astrophys. J. 2008, 683, L191. [Google Scholar] [CrossRef]
- Benedict, G.F.; Harrison, T.E.; Endl, M.; Torres, G. A Mass for γ Cep Ab. Res. Notes Am. Astron. Soc. 2018, 2, 7. [Google Scholar] [CrossRef]
- Lissauer, J.J. Planet formation. Ann. Rev. Astron. Astrophys. 1993, 31, 129–174. [Google Scholar] [CrossRef]
- Marzari, F.; Scholl, H. Planetesimal Accretion in Binary Star Systems. Astrophys. J. 2000, 543, 328–339. [Google Scholar] [CrossRef]
- Paardekooper, S.J.; Thébault, P.; Mellema, G. Planetesimal and gas dynamics in binaries. Mon. Not. RAS 2008, 386, 973–988. [Google Scholar] [CrossRef][Green Version]
- Thébault, P.; Marzari, F.; Scholl, H.; Turrini, D.; Barbieri, M. Planetary formation in the γ Cephei system. Astron. Astrophys. 2004, 427, 1097–1104. [Google Scholar] [CrossRef]
- Thébault, P.; Marzari, F.; Scholl, H. Relative velocities among accreting planetesimals in binary systems: The circumprimary case. Icarus 2006, 183, 193–206. [Google Scholar] [CrossRef][Green Version]
- Xie, J.W.; Zhou, J.L. Planetesimal Accretion in Binary Systems: Role of the Companion’s Orbital Inclination. Astrophys. J. 2009, 698, 2066–2074. [Google Scholar] [CrossRef]
- Xie, J.W.; Zhou, J.L.; Ge, J. Planetesimal Accretion in Binary Systems: Could Planets Form Around α Centauri B? Astrophys. J. 2010, 708, 1566–1578. [Google Scholar] [CrossRef]
- Thébault, P.; Marzari, F.; Scholl, H. Planet formation in the habitable zone of α Centauri B. Mon. Not. RAS 2009, 393, L21–L25. [Google Scholar] [CrossRef]
- Thébault, P.; Marzari, F.; Scholl, H. Planet formation in α Centauri A revisited: Not so accretion friendly after all. Mon. Not. RAS 2008, 388, 1528–1536. [Google Scholar] [CrossRef][Green Version]
- Thebault, P. Against all odds? Forming the planet of the HD 196885 binary. Celest. Mech. Dyn. Astron. 2011, 111, 29–49. [Google Scholar] [CrossRef][Green Version]
- Rafikov, R.R. Planet Formation in Small Separation Binaries: Not so Secularly Excited by the Companion. Astrophys. J. 2013, 765, L8. [Google Scholar] [CrossRef]
- Rafikov, R.R.; Silsbee, K. Planet Formation in Stellar Binaries. II. Overcoming the Fragmentation Barrier in α Centauri and γ Cephei-like Systems. Astrophys. J. 2015, 798, 70. [Google Scholar] [CrossRef]
- Silsbee, K.; Rafikov, R.R. Planet Formation in Binaries: Dynamics of Planetesimals Perturbed by the Eccentric Protoplanetary Disk and the Secondary. Astrophys. J. 2015, 798, 71. [Google Scholar] [CrossRef]
- Kley, W.; Nelson, R. On the Formation and Dynamical Evolution of Planets in Binaries. arXiv 2007, arXiv:0705.3421. [Google Scholar]
- Marzari, F.; Scholl, H.; Thébault, P.; Baruteau, C. On the eccentricity of self-gravitating circumstellar disks in eccentric binary systems. Astron. Astrophys. 2009, 508, 1493–1502. [Google Scholar] [CrossRef][Green Version]
- Marzari, F.; Baruteau, C.; Scholl, H.; Thebault, P. Eccentricity of radiative disks in close binary-star systems. Astron. Astrophys. 2012, 539, A98. [Google Scholar] [CrossRef]
- Zsom, A.; Sándor, Z.; Dullemond, C.P. The first stages of planet formation in binary systems: How far can dust coagulation proceed? Astron. Astrophys. 2011, 527, A10. [Google Scholar] [CrossRef]
- Fragner, M.M.; Nelson, R.P.; Kley, W. On the dynamics and collisional growth of planetesimals in misaligned binary systems. Astron. Astrophys. 2011, 528, A40. [Google Scholar] [CrossRef]
- Guedes, J.M.; Rivera, E.J.; Davis, E.; Laughlin, G.; Quintana, E.V.; Fischer, D.A. Formation and Detectability of Terrestrial Planets around α Centauri B. Astrophys. J. 2008, 679, 1582–1587. [Google Scholar] [CrossRef][Green Version]
- Barbieri, M.; Marzari, F.; Scholl, H. Formation of terrestrial planets in close binary systems: The case of alpha Centauri A. Astron. Astrophys. 2002, 396, 219–224. [Google Scholar] [CrossRef]
- Quintana, E.V.; Lissauer, J.J.; Chambers, J.E.; Duncan, M.J. Terrestrial Planet Formation in the α Centauri System. Astrophys. J. 2002, 576, 982–996. [Google Scholar] [CrossRef]
- Quintana, E.V.; Adams, F.C.; Lissauer, J.J.; Chambers, J.E. Terrestrial Planet Formation around Individual Stars within Binary Star Systems. Astrophys. J. 2007, 660, 807–822. [Google Scholar] [CrossRef]
- Haghighipour, N.; Raymond, S.N. Habitable Planet Formation in Binary Planetary Systems. Astrophys. J. 2007, 666, 436–446. [Google Scholar] [CrossRef]
- Payne, M.J.; Wyatt, M.C.; Thébault, P. Outward migration of terrestrial embryos in binary systems. Mon. Not. RAS 2009, 400, 1936–1944. [Google Scholar] [CrossRef]
- Marzari, F.; Weidenschilling, S.J.; Barbieri, M.; Granata, V. Jumping Jupiters in Binary Star Systems. Astrophys. J. 2005, 618, 502–511. [Google Scholar] [CrossRef]
- Gong, Y.X.; Ji, J. Formation of S-type planets in close binaries: Scattering-induced tidal capture of circumbinary planets. Mon. Not. RAS 2018, 478, 4565–4574. [Google Scholar] [CrossRef]
- Xie, J.W.; Payne, M.J.; Thébault, P.; Zhou, J.L.; Ge, J. From Dust to Planetesimal: The Snowball Phase? Astrophys. J. 2010, 724, 1153–1164. [Google Scholar] [CrossRef]
- Paardekooper, S.J.; Leinhardt, Z.M. Planetesimal collisions in binary systems. Mon. Not. RAS 2010, 403, L64–L68. [Google Scholar] [CrossRef]
- Duchêne, G. Planet Formation in Binary Systems: A Separation-Dependent Mechanism? Astrophys. J. 2010, 709, L114–L118. [Google Scholar] [CrossRef]
- Nelson, A.F. Planet Formation is Unlikely in Equal-Mass Binary Systems with A ~50 AU. Astrophys. J. 2000, 537, L65–L68. [Google Scholar] [CrossRef]
- Mayer, L.; Boss, A.; Nelson, A.F. Gravitational Instability in Binary Protoplanetary Disks. In Planets in Binary Star Systems; Haghighipour, N., Ed.; Astrophysics and Space Science Library-Springer: Basel, Switzerland, 2010; Volume 366, p. 195. [Google Scholar]
- Marzari, F.; Barbieri, M. Planets in binary systems: Is the present configuration indicative of the formation process? Astron. Astrophys. 2007, 467, 347–351. [Google Scholar] [CrossRef][Green Version]
- Malmberg, D.; de Angeli, F.; Davies, M.B.; Church, R.P.; Mackey, D.; Wilkinson, M.I. Close encounters in young stellar clusters: Implications for planetary systems in the solar neighbourhood. Mon. Not. RAS 2007, 378, 1207–1216. [Google Scholar] [CrossRef]
- Fragione, G. Dynamical origin of S-type planets in close binary stars. Mon. Not. RAS 2019, 483, 3465–3471. [Google Scholar] [CrossRef]
- Schwarz, R.; Haghighipour, N.; Eggl, S.; Pilat-Lohinger, E.; Funk, B. Prospects of the detection of circumbinary planets with Kepler and CoRoT using the variations of eclipse timing. Mon. Not. RAS 2011, 414, 2763–2770. [Google Scholar] [CrossRef]
- Orosz, J.A.; Welsh, W.F.; Haghighipour, N.; Quarles, B.; Short, D.R.; Mills, S.M.; Satyal, S.; Torres, G.; Agol, E.; Fabrycky, D.C. Discovery of a Third Transiting Planet in the Kepler-47 Circumbinary System. Astron. J. 2019, 157, 174. [Google Scholar] [CrossRef]
- Armstrong, D.J.; Osborn, H.P.; Brown, D.J.A.; Faedi, F.; Gómez Maqueo Chew, Y.; Martin, D.V.; Pollacco, D.; Udry, S. On the abundance of circumbinary planets. Mon. Not. RAS 2014, 444, 1873–1883. [Google Scholar] [CrossRef]
- Martin, D.V. Populations of Planets in Multiple Star Systems. In Handbook of Exoplanets; Springer: Berlin, Germany, 2018; p. 156. ISBN 978-3-319-55332-0. [Google Scholar]
- Kostov, V.B.; Orosz, J.A.; Welsh, W.F.; Doyle, L.R.; Fabrycky, D.C.; Haghighipour, N.; Quarles, B.; Short, D.R.; Cochran, W.D.; Endl, M. Kepler-1647b: The Largest and Longest-period Kepler Transiting Circumbinary Planet. Astrophys. J. 2016, 827, 86. [Google Scholar] [CrossRef]
- Moe, M.; Kratter, K.M. Dynamical Formation of Close Binaries during the Pre-main-sequence Phase. Astrophys. J. 2018, 854, 44. [Google Scholar] [CrossRef]
- Meschiari, S. Circumbinary Planet Formation in the Kepler-16 System. I. N-body Simulations. Astrophys. J. 2012, 752, 71. [Google Scholar] [CrossRef]
- Paardekooper, S.J.; Leinhardt, Z.M.; Thébault, P.; Baruteau, C. How Not to Build Tatooine: The Difficulty of In Situ Formation of Circumbinary Planets Kepler 16b, Kepler 34b, and Kepler 35b. Astrophys. J. 2012, 754, L16. [Google Scholar] [CrossRef]
- Lines, S.; Leinhardt, Z.M.; Paardekooper, S.; Baruteau, C.; Thebault, P. Forming Circumbinary Planets: N-body Simulations of Kepler-34. Astrophys. J. 2014, 782, L11. [Google Scholar] [CrossRef]
- Rafikov, R.R. Building Tatooine: Suppression of the Direct Secular Excitation in Kepler Circumbinary Planet Formation. Astrophys. J. 2013, 764, L16. [Google Scholar] [CrossRef]
- Marzari, F.; Thébault, P.; Scholl, H. Planetesimal Evolution in Circumbinary Gaseous Disks: A Hybrid Model. Astrophys. J. 2008, 681, 1599–1608. [Google Scholar] [CrossRef]
- Marzari, F.; Thebault, P.; Scholl, H.; Picogna, G.; Baruteau, C. Influence of the circumbinary disk gravity on planetesimal accumulation in the Kepler-16 system. Astron. Astrophys. 2013, 553, A71. [Google Scholar] [CrossRef][Green Version]
- Masset, F. FARGO: A fast eulerian transport algorithm for differentially rotating disks. Astron. Astrophys. 2000, 141, 165–173. [Google Scholar] [CrossRef]
- Nelson, R.P. On the evolution of giant protoplanets forming in circumbinary discs. Mon. Not. RAS 2003, 345, 233–242. [Google Scholar] [CrossRef][Green Version]
- Sutherland, A.P.; Fabrycky, D.C. On the Fate of Unstable Circumbinary Planets: Tatooine’s Close Encounters with a Death Star. Astrophys. J. 2016, 818, 6. [Google Scholar] [CrossRef]
- Kley, W.; Haghighipour, N. Modeling circumbinary planets: The case of Kepler-38. Astron. Astrophys. 2014, 564, A72. [Google Scholar] [CrossRef][Green Version]
- Kley, W.; Haghighipour, N. Evolution of circumbinary planets around eccentric binaries: The case of Kepler-34. Astron. Astrophys. 2015, 581, A20. [Google Scholar] [CrossRef]
- Kley, W.; Nelson, R.P. Early Evolution of Planets in Binaries: Planet-Disk Interaction. In Planets in Binary Star Systems; Haghighipour, N., Ed.; Astrophysics and Space Science Library-Springer: Basel, Switzerland, 2010; Volume 366, p. 135. [Google Scholar]
- Michtchenko, T.A.; Malhotra, R. Secular dynamics of the three-body problem: Application to the upsilon Andromedae planetary system. Icarus 2004, 168, 237–248. [Google Scholar] [CrossRef]
- Libert, A.S.; Henrard, J. Analytical Approach to the Secular Behaviour of Exoplanetary Systems. Celest. Mech. Dyn. Astron. 2005, 93, 187–200. [Google Scholar] [CrossRef]
- Naoz, S. The Eccentric Kozai-Lidov Effect and Its Applications. Ann. Rev. Astron. Astrophys. 2016, 54, 441–489. [Google Scholar] [CrossRef]
- Marzari, F.; Gallina, G. Stability of multiplanet systems in binaries. Astron. Astrophys. 2016, 594, A89. [Google Scholar] [CrossRef]
- Mudryk, L.R.; Wu, Y. Resonance Overlap Is Responsible for Ejecting Planets in Binary Systems. Astrophys. J. 2006, 639, 423–431. [Google Scholar] [CrossRef][Green Version]
- Deck, K.M.; Payne, M.; Holman, M.J. First-order Resonance Overlap and the Stability of Close Two-planet Systems. Astrophys. J. 2013, 774, 129. [Google Scholar] [CrossRef]
- Heppenheimer, T.A. On the formation of planets in binary star systems. Astron. Astrophys. 1978, 65, 421–426. [Google Scholar]
- Andrade-Ines, E.; Beaugé, C.; Michtchenko, T.; Robutel, P. Secular dynamics of S-type planetary orbits in binary star systems: Applicability domains of first- and second-order theories. Celest. Mech. Dyn. Astron. 2016, 124, 405–432. [Google Scholar] [CrossRef]
- Rabl, G.; Dvorak, R. Satellite-type planetary orbits in double stars - A numerical approach. Astron. Astrophys. 1988, 191, 385–391. [Google Scholar]
- Laskar, J. Frequency analysis for multi-dimensional systems. Global dynamics and diffusion. Physics D 1993, 67, 257–281. [Google Scholar] [CrossRef]
- Šidlichovský, M.; Nesvorný, D. Frequency modified Fourier transform and its applications to asteroids. Celest. Mech. Dyn. Astron. 1996, 65, 137–148. [Google Scholar] [CrossRef]
- Marzari, F.; Tricarico, P.; Scholl, H. Stability of Jupiter Trojans investigated using frequency map analysis: The MATROS project. MNRAS 2003, 345, 1091–1100. [Google Scholar] [CrossRef]
- Pilat-Lohinger, E.; Bazsó, A.; Funk, B. A Quick Method to Identify Secular Resonances in Multi-planet Systems with a Binary Companion. Astron. J. 2016, 152, 139. [Google Scholar] [CrossRef]
- Hale, A. Orbital CoPlanetary in Solar-Type Binary Systems: Implications for Planetary System Formation and Detection. Astron. J. 1994, 107, 306. [Google Scholar] [CrossRef]
- Chen, X.; Bourke, T.L.; Launhardt, R.; Henning, T. SMA CO (2-1) Observations of CG 30: A Protostellar Binary System with a High-Velocity Quadrupolar Molecular Outflow. Astrophys. J. 2008, 686, L107. [Google Scholar] [CrossRef]
- Ratzka, T.; Schegerer, A.A.; Leinert, C.; Ábrahám, P.; Henning, T.; Herbst, T.M.; Köhler, R.; Wolf, S.; Zinnecker, H. Spatially resolved mid-infrared observations of the triple system T Tauri. Astron. Astrophys. 2009, 502, 623–646. [Google Scholar] [CrossRef]
- Jensen, E.L.N.; Akeson, R. Misaligned protoplanetary disks in a young binary star system. Nature 2014, 511, 567–569. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Holman, M.; Touma, J.; Tremaine, S. Chaotic variations in the eccentricity of the planet orbiting 16 Cygni B. Nature 1997, 386, 254–256. [Google Scholar] [CrossRef]
- Wu, Y.; Murray, N. Planet Migration and Binary Companions: The Case of HD 80606b. Astrophys. J. 2003, 589, 605–614. [Google Scholar] [CrossRef]
- Lithwick, Y.; Naoz, S. The Eccentric Kozai Mechanism for a Test Particle. Astrophys. J. 2011, 742, 94. [Google Scholar] [CrossRef]
- Moriwaki, K.; Nakagawa, Y. A Planetesimal Accretion Zone in a Circumbinary Disk. Astrophys. J. 2004, 609, 1065–1070. [Google Scholar] [CrossRef]
- Moriwaki, K.; Nakagawa, Y. Stability of a Planet in a Binary System: MACHO 97-BLG-41. Astron. J. 2002, 124, 3364–3369. [Google Scholar] [CrossRef]
- Artymowicz, P.; Lubow, S.H. Dynamics of binary-disk interaction. 1: Resonances and disk gap sizes. Astrophys. J. 1994, 421, 651–667. [Google Scholar] [CrossRef]
- Martin, D.V.; Triaud, A.H.M.J. Kozai-Lidov cycles towards the limit of circumbinary planets. Mon. Not. RAS 2016, 455, L46–L50. [Google Scholar] [CrossRef]
- Picogna, G.; Marzari, F. Three-dimensional modeling of radiative disks in binaries. Astron. Astrophys. 2013, 556, A148. [Google Scholar] [CrossRef][Green Version]
- Johansen, A.; Blum, J.; Tanaka, H.; Ormel, C.; Bizzarro, M.; Rickman, H. The Multifaceted Planetesimal Formation Process. In Protostars and Planets VI; Beuther, H., Klessen, R.S., Dullemond, C.P., Henning, T., Eds.; University of Arizona Press: Tucson, AZ, USA, 2014; p. 547. [Google Scholar]
- Ormel, C.W.; Klahr, H.H. The effect of gas drag on the growth of protoplanets. Analytical expressions for the accretion of small bodies in laminar disks. Astron. Astrophys. 2010, 520, A43. [Google Scholar] [CrossRef]
| 1 | Such AO searches for stellar companions have also been performed for RV-planet hosts, and have increased the binary fraction among them, but not by a factor as large as for transit exoplanet hosts [6,12,13,14]. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).