Planets in Binaries: Formation and Dynamical Evolution
Abstract
1. Introduction
2. Planets in S–Type Orbits
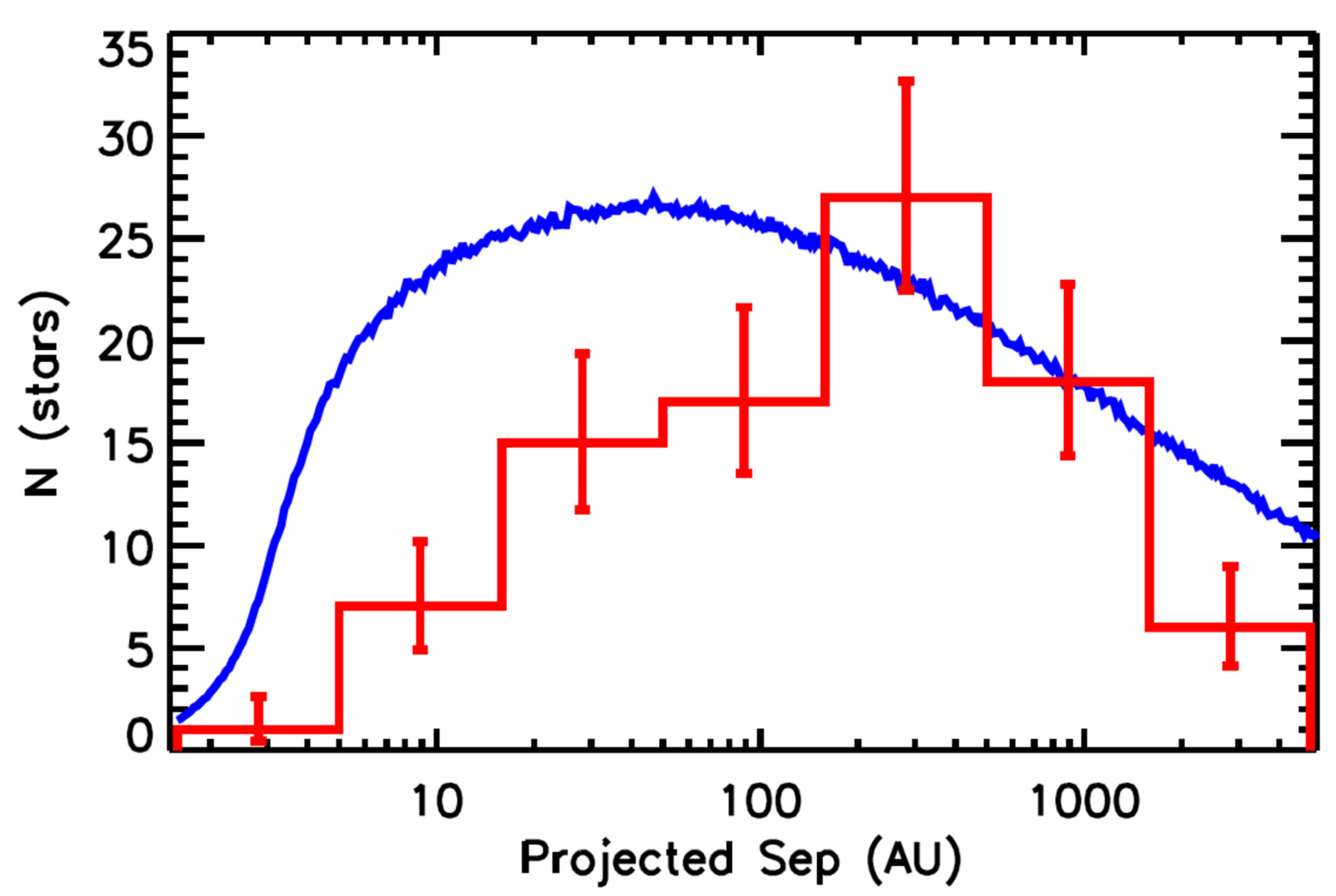
2.1. Observational Constraints
2.1.1. Adverse Biases
2.1.2. Characteristics of Exoplanets in Binaries
2.1.3. Multiplicity Rate of Exoplanet Hosts
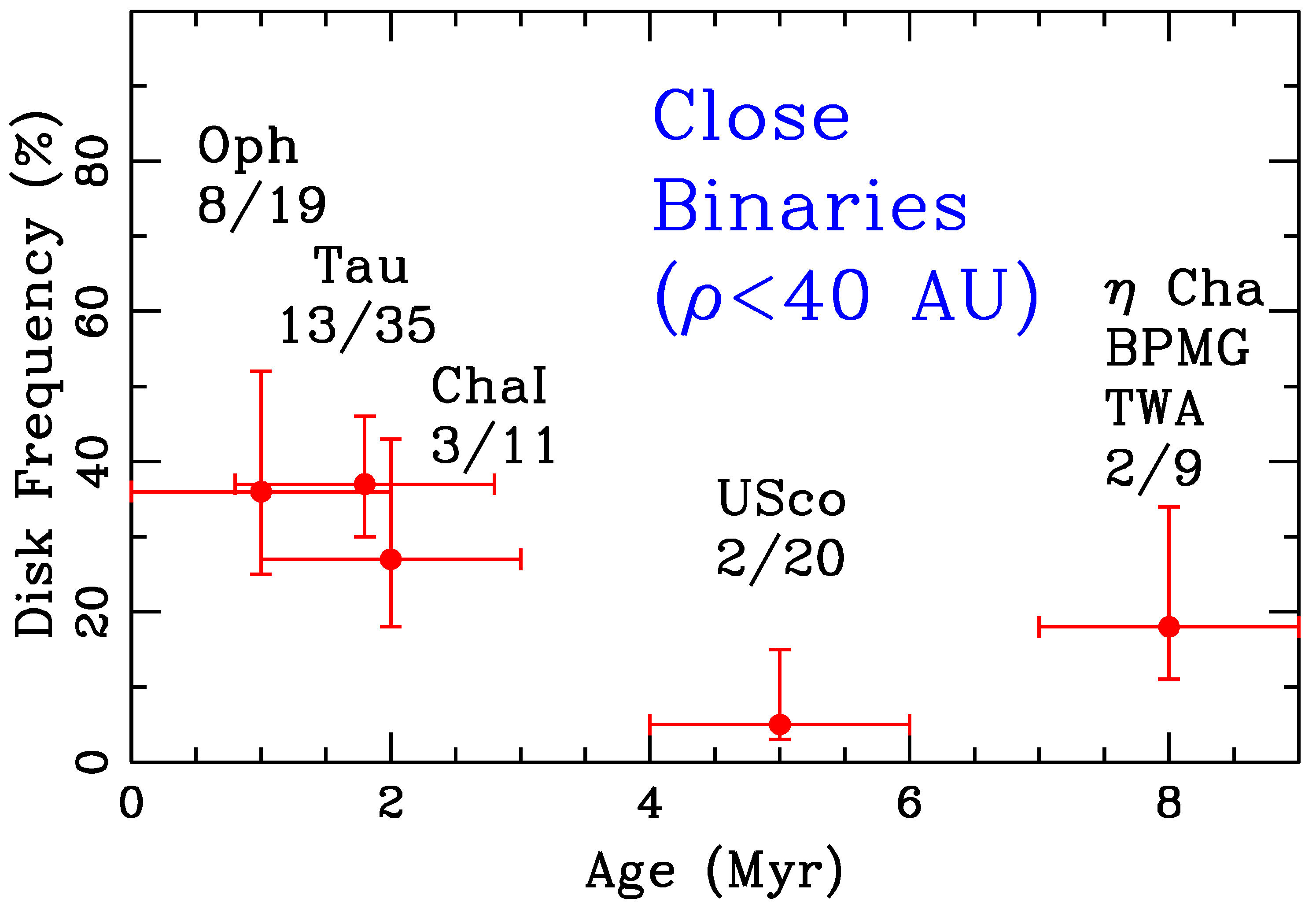
2.2. Planet Formation in Binaries
2.2.1. Early Stages
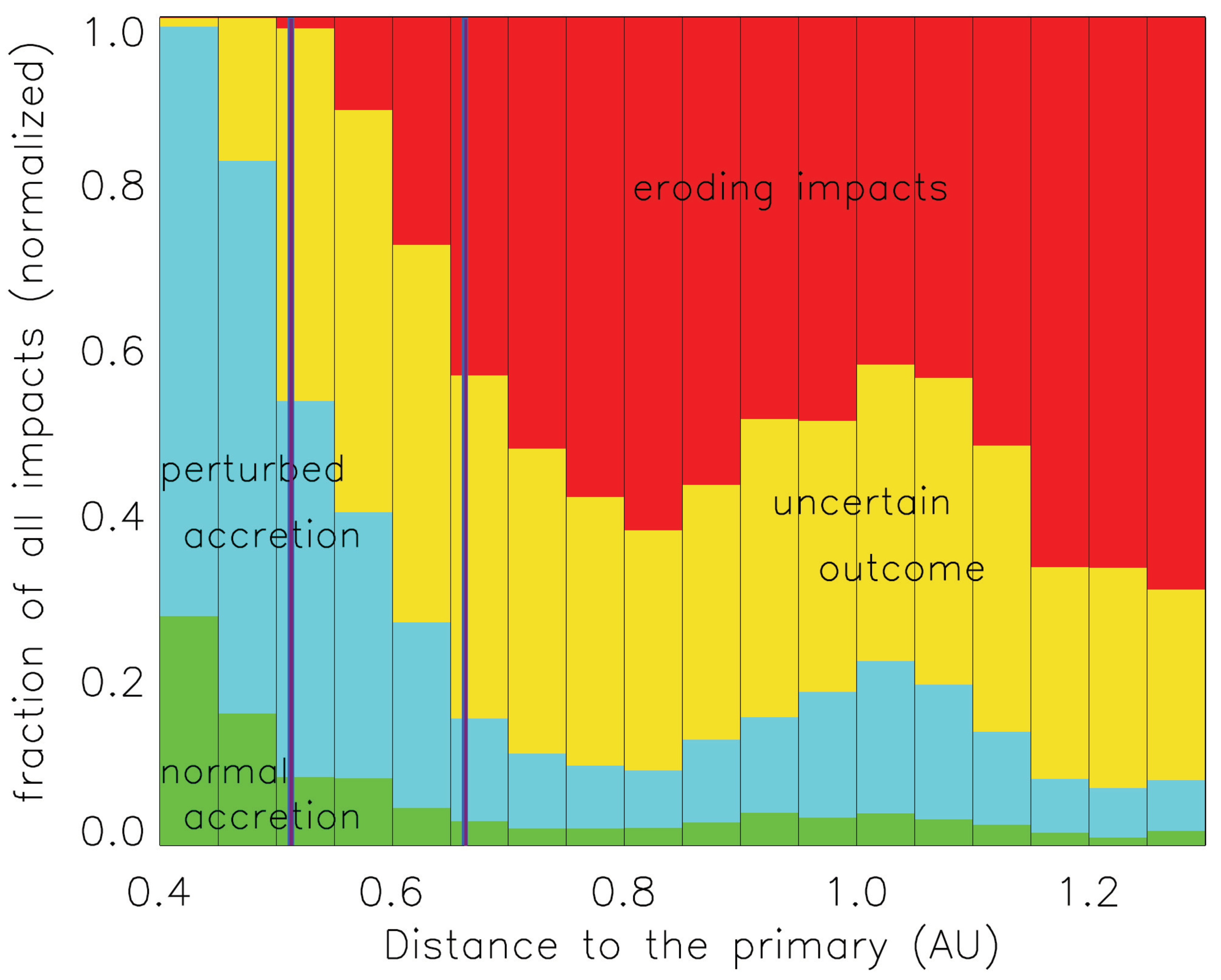
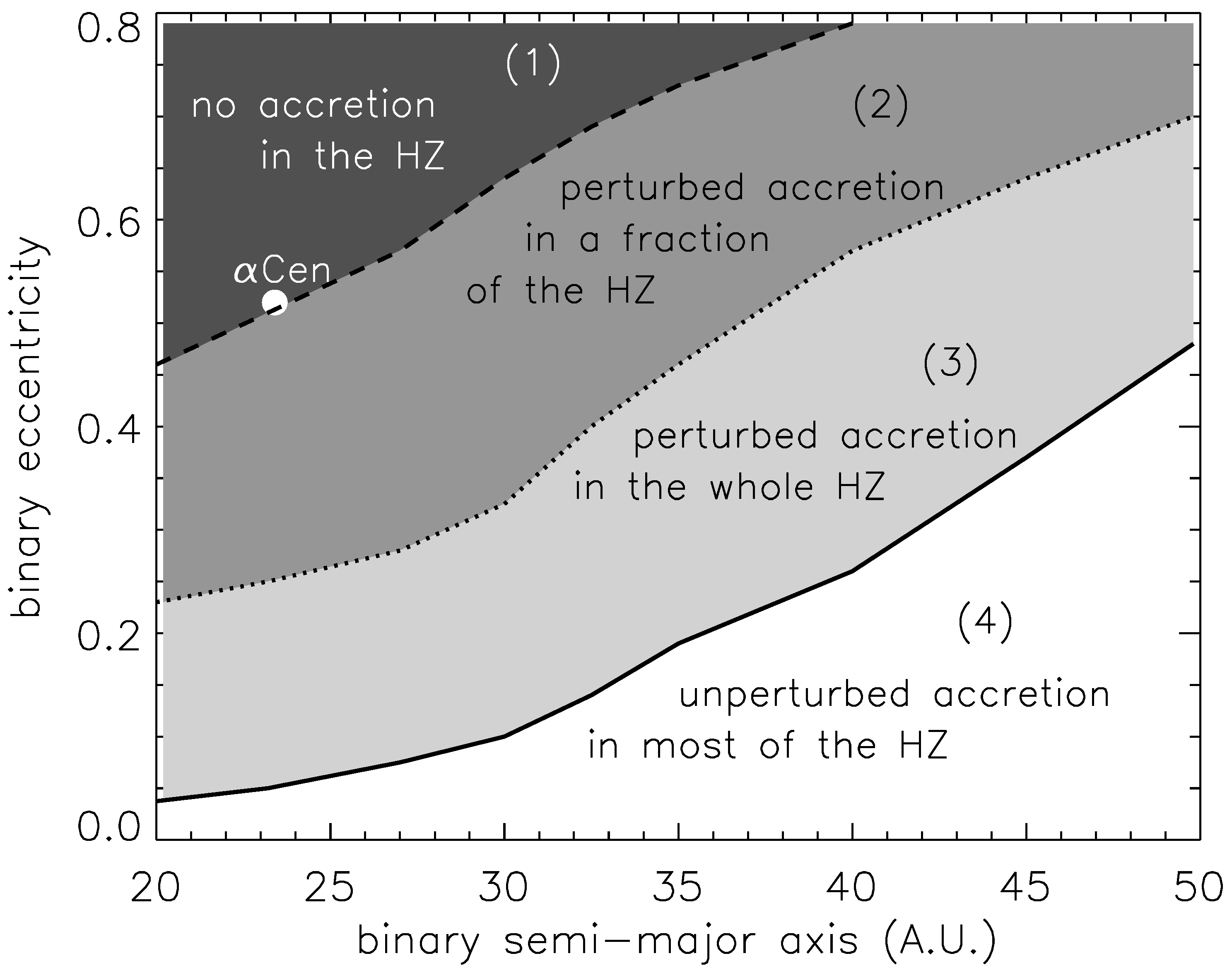
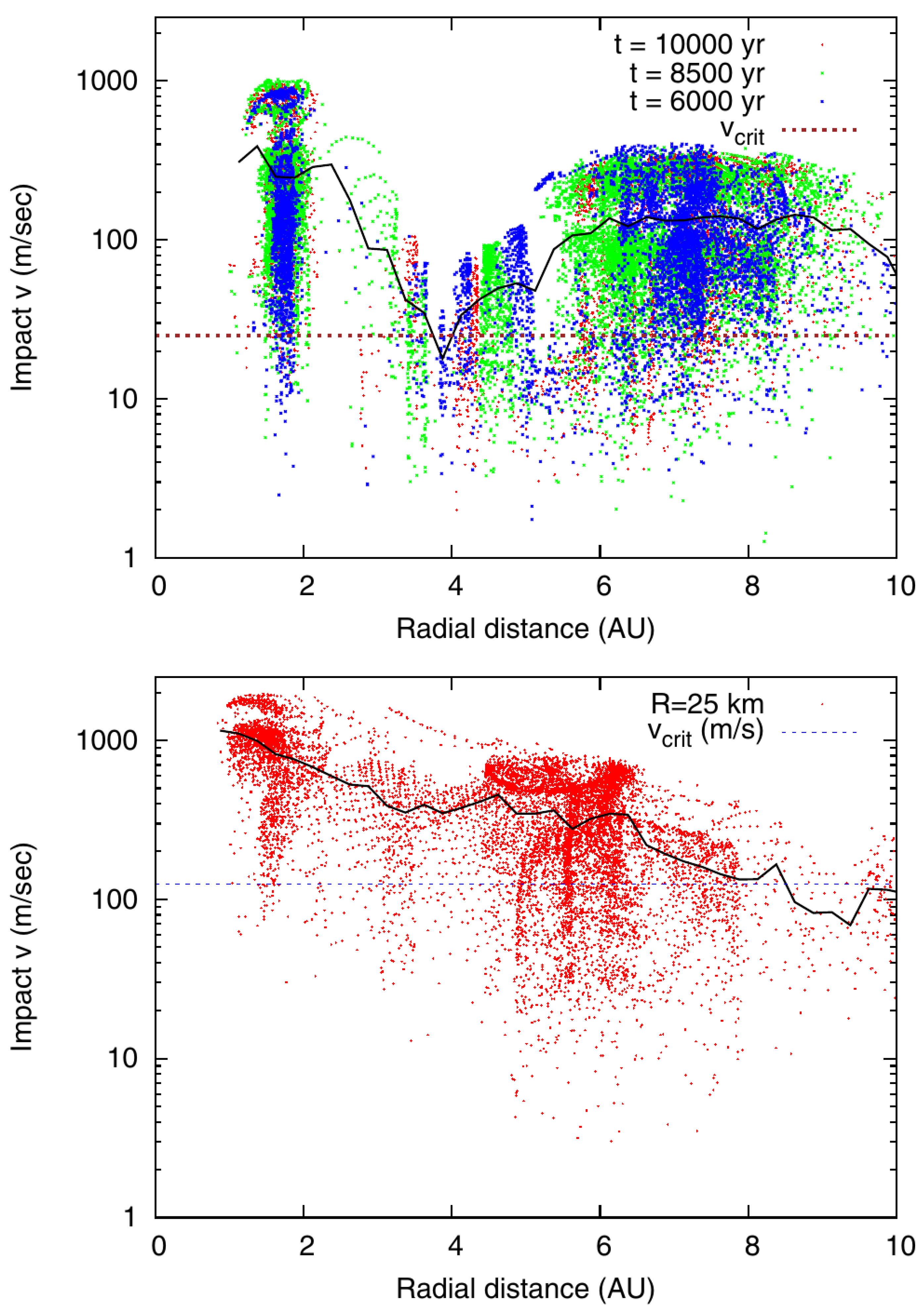
2.2.2. Planetesimal Accretion
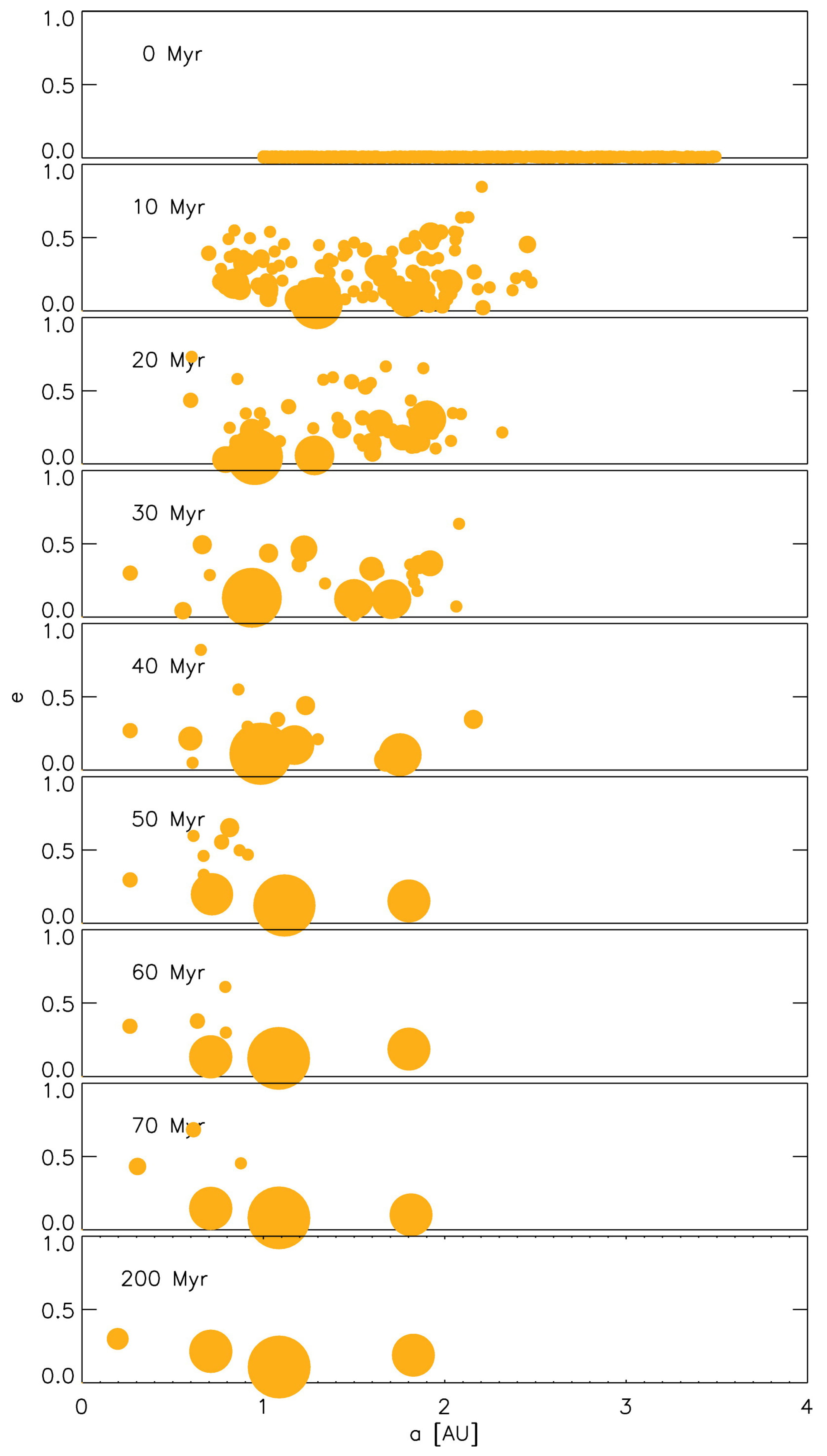
2.2.3. Late Stages
2.2.4. Alternative Scenarios?
3. Planets in P–Type Orbits: Circumbinary Planets
- (1)
- A lack of planets around tight binaries ( days) [66]
- (2)
- A pile–up close to the inner dynamical stability limit
- (3)
- Masses smaller than that of Jupiter
3.1. Formation and Evolution of Circumbinary Planets
3.2. Migration Towards the Inner Hole
4. Dynamics and Stability in S-Type Orbits
- The interaction with the circumstellar disk. In the early phases of evolution of the system it may significantly change the architecture of the planetary system [80].
- Mean Motion Resonances (hereinafter MMR) between the planets and between the planets and the binary companion.
- The Kozai dynamics when significant mutual inclinations are present among the bodies [83].
- Planet–planet or planet–star scattering if the system becomes temporarily unstable [53].
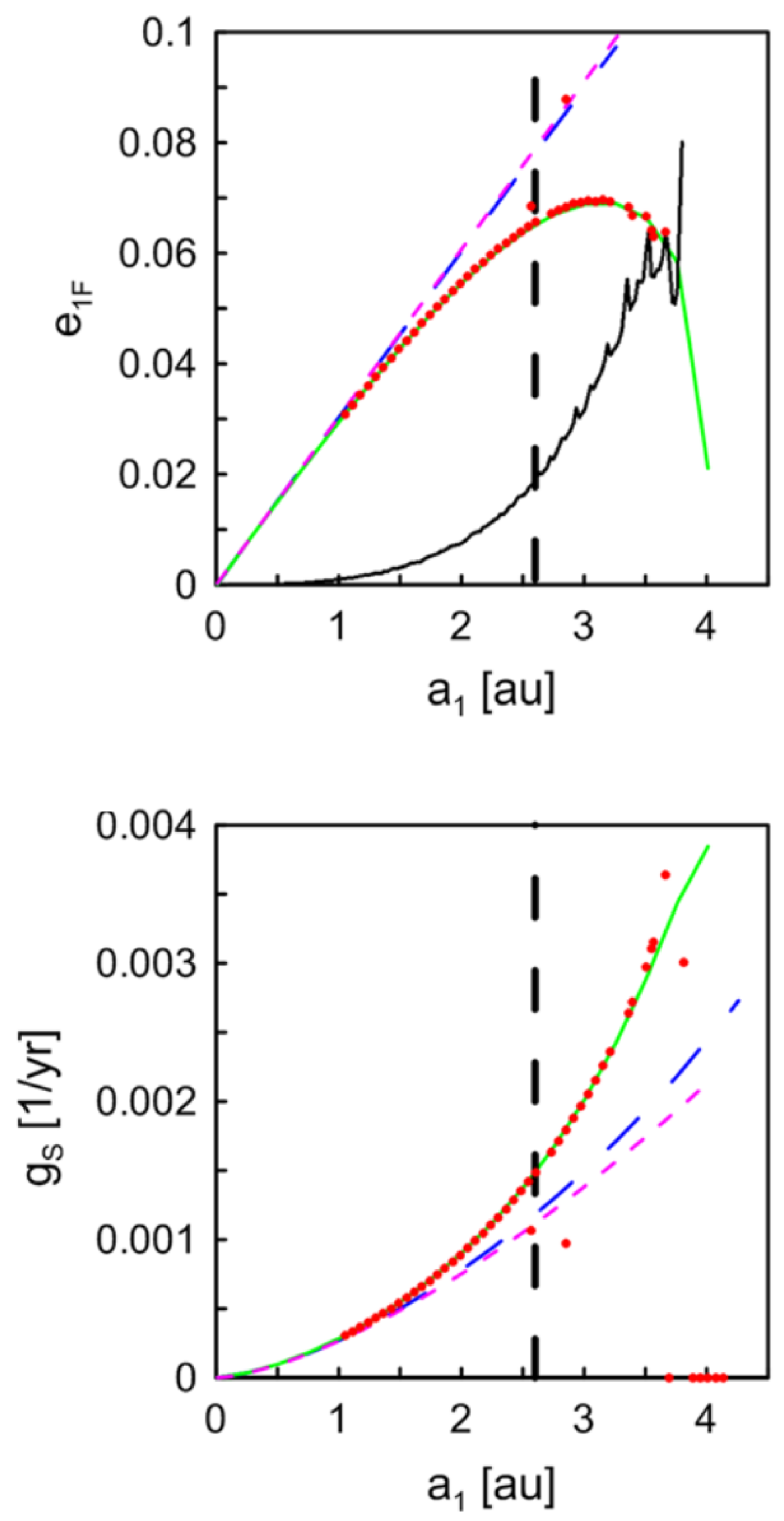
4.1. Secular Evolution
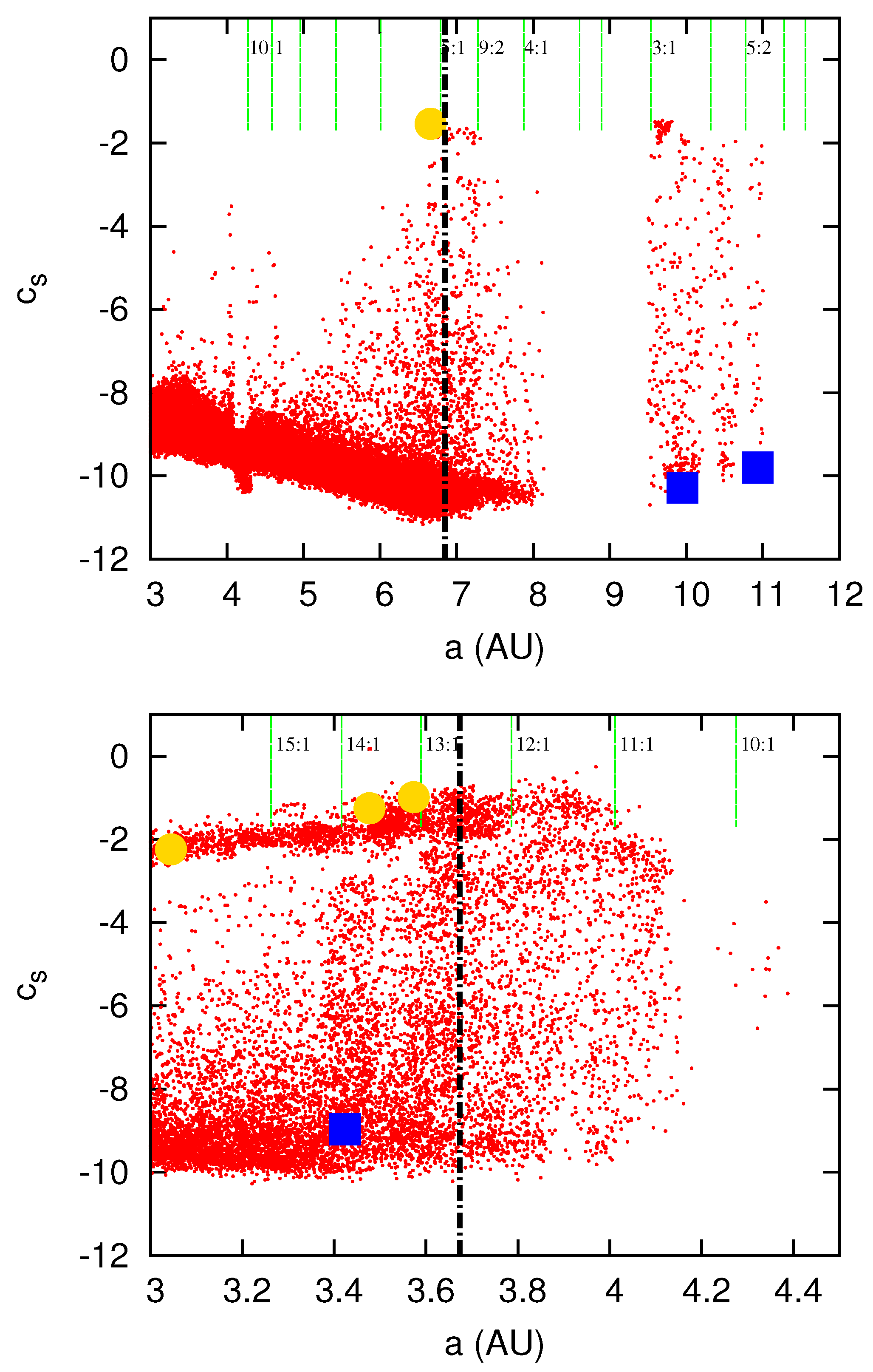
4.2. Stability Limit for One Planet
- The value of computed by [7] underestimates the real stability limit and stable planetary orbits can be found beyond .
- Some planets may be trapped in low order resonance (3:1, 5:2) with the companion star, far beyond , and be stable over a long timescale.
- For large values of , large unstable regions can be found within due to non-linear secular resonances with the binary companion.
4.3. Stability of Multiple Planet Systems
4.4. Kozai Evolution in Presence of Inclined Binaries
5. Dynamics and Stability in P-Type Orbits
- The unstable region surrounding the two stars due to resonance overlap,
- Halting the planet migration in the early phases of the evolution of the system by trapping the planet in a stable resonance.
5.1. A Secular Theory
5.2. The Inner Unstable Hole
6. Perspectives
Author Contributions
Funding
Conflicts of Interest
References
- Duquennoy, A.; Mayor, M. Multiplicity among solar-type stars in the solar neighbourhood. II - Distribution of the orbital elements in an unbiased sample. Astron. Astrophys. 1991, 248, 485–524. [Google Scholar]
- Raghavan, D.; McAlister, H.A.; Henry, T.J.; Latham, D.W.; Marcy, G.W.; Mason, B.D.; Gies, D.R.; White, R.J.; ten Brummelaar, T.A. A Survey of Stellar Families: Multiplicity of Solar-type Stars. Astrophys. J. Suppl. 2010, 190, 1–42. [Google Scholar] [CrossRef]
- Eggenberger, A.; Udry, S. Detection and Characterization of Extrasolar Planets through Doppler Spectroscopy; EAS Publications, Series; Montmerle, T., Ehrenreich, D., Lagrange, A.M., Eds.; Cambridge University Press: Cambridge, UK, 2010; Volume 41, pp. 27–75. [Google Scholar]
- Ngo, H.; Knutson, H.A.; Bryan, M.L.; Blunt, S.; Nielsen, E.L.; Batygin, K.; Bowler, B.P.; Crepp, J.R.; Hinkley, S.; Howard, A.W.; et al. No Difference in Orbital Parameters of RV-detected Giant Planets between 0.1 and 5 au in Single versus Multi-stellar Systems. Astron. J. 2017, 153, 242. [Google Scholar] [CrossRef]
- Eggenberger, A.; Udry, S.; Mayor, M. Statistical properties of exoplanets. III. Planet properties and stellar multiplicity. Astron. Astrophys. 2004, 417, 353–360. [Google Scholar] [CrossRef]
- Eggenberger, A.; Udry, S.; Chauvin, G.; Beuzit, J.L.; Lagrange, A.M.; Ségransan, D.; Mayor, M. The impact of stellar duplicity on planet occurrence and properties. I. Observational results of a VLT/NACO search for stellar companions to 130 nearby stars with and without planets. Astron. Astrophys. 2007, 474, 273–291. [Google Scholar] [CrossRef]
- Holman, M.J.; Wiegert, P.A. Long-Term Stability of Planets in Binary Systems. Astron. J. 1999, 117, 621–628. [Google Scholar] [CrossRef]
- Trifonov, T.; Lee, M.H.; Reffert, S.; Quirrenbach, A. Dynamical Analysis of the Circumprimary Planet in the Eccentric Binary System HD 59686. Astron. J. 2018, 155, 174. [Google Scholar] [CrossRef]
- Wang, J.; Xie, J.W.; Barclay, T.; Fischer, D.A. Influence of Stellar Multiplicity on Planet Formation. I. Evidence of Suppressed Planet Formation due to Stellar Companions within 20 AU and Validation of Four Planets from the Kepler Multiple Planet Candidates. Astrophys. J. 2014, 783, 4. [Google Scholar] [CrossRef]
- Wang, J.; Fischer, D.A.; Xie, J.W.; Ciardi, D.R. Influence of Stellar Multiplicity on Planet Formation. II. Planets are Less Common in Multiple-star Systems with Separations Smaller than 1500 AU. Astrophys. J. 2014, 791, 111. [Google Scholar] [CrossRef]
- Ziegler, C.; Law, N.M.; Morton, T.; Baranec, C.; Riddle, R.; Atkinson, D.; Baker, A.; Roberts, S.; Ciardi, D.R. Robo-AO Kepler Planetary Candidate Survey. III. Adaptive Optics Imaging of 1629 Kepler Exoplanet Candidate Host Stars. Astron. J. 2017, 153, 66. [Google Scholar] [CrossRef]
- Mugrauer, M.; Ginski, C. High-contrast imaging search for stellar and substellar companions of exoplanet host stars. Mon. Not. RAS 2015, 450, 3127–3136. [Google Scholar] [CrossRef]
- Ginski, C.; Mugrauer, M.; Seeliger, M.; Eisenbeiss, T. A lucky imaging multiplicity study of exoplanet host stars. Mon. Not. RAS 2012, 421, 2498–2509. [Google Scholar] [CrossRef][Green Version]
- Ginski, C.; Mugrauer, M.; Seeliger, M.; Buder, S.; Errmann, R.; Avenhaus, H.; Mouillet, D.; Maire, A.L.; Raetz, S. A lucky imaging multiplicity study of exoplanet host stars—II. Mon. Not. RAS 2016, 457, 2173–2191. [Google Scholar] [CrossRef]
- Zucker, S.; Mazeh, T. On the Mass-Period Correlation of the Extrasolar Planets. Astrophys. J. 2002, 568, L113–L116. [Google Scholar] [CrossRef]
- Desidera, S.; Barbieri, M. Properties of planets in binary systems. The role of binary separation. Astron. Astrophys. 2007, 462, 345–353. [Google Scholar] [CrossRef]
- Ngo, H.; Knutson, H.A.; Hinkley, S.; Bryan, M.; Crepp, J.R.; Batygin, K.; Crossfield, I.; Hansen, B.; Howard, A.W.; Johnson, J.A.; et al. Friends of Hot Jupiters. IV. Stellar Companions Beyond 50 au Might Facilitate Giant Planet Formation, but Most are Unlikely to Cause Kozai-Lidov Migration. Astrophys. J. 2016, 827, 8. [Google Scholar] [CrossRef]
- Kraus, A.L.; Ireland, M.J.; Huber, D.; Mann, A.W.; Dupuy, T.J. The Impact of Stellar Multiplicity on Planetary Systems. I. The Ruinous Influence of Close Binary Companions. Astron. J. 2016, 152, 8. [Google Scholar] [CrossRef]
- Fontanive, C.; Rice, K.; Bonavita, M.; Lopez, E.; Mužić, K.; Biller, B. A high binary fraction for the most massive close-in giant planets and brown dwarf desert members. Mon. Not. RAS 2019, 485, 4967–4996. [Google Scholar] [CrossRef]
- Eggenberger, A.; Udry, S.; Chauvin, G.; Forveille, T.; Beuzit, J.L.; Lagrange, A.M.; Mayor, M. Probing the impact of stellar duplicity on the frequency of giant planets: Final results of our VLT/NACO survey. In The Astrophysics of Planetary Systems: Formation, Structure, and Dynamical Evolution; Sozzetti, A., Lattanzi, M.G., Boss, A.P., Eds.; Cambridge University Press: Cambridge, UK, 2011; Volume 276, pp. 409–410. [Google Scholar]
- Matson, R.A.; Howell, S.B.; Horch, E.P.; Everett, M.E. Stellar Companions of Exoplanet Host Stars in K2. Astron. J. 2018, 156, 31. [Google Scholar] [CrossRef]
- Thebault, P.; Haghighipour, N. Planet Formation in Binaries. In Planetary Exploration and Science: Recent Results and Advances, Edited by Shuanggen Jin, Nader Haghighipour, and Wing-Huen Ip. Springer Geophysics; Springer: Berlin, Germany, 2015; pp. 309–340. ISBN 978-3-662-45051-2. [Google Scholar]
- Kraus, A.L.; Ireland, M.J.; Hillenbrand, L.A.; Martinache, F. The Role of Multiplicity in Disk Evolution and Planet Formation. Astrophys. J. 2012, 745, 19. [Google Scholar] [CrossRef]
- Savonije, G.J.; Papaloizou, J.C.B.; Lin, D.N.C. On Tidally Induced Shocks in Accretion Discs in Close Binary Systems. Mon. Not. RAS 1994, 268, 13. [Google Scholar] [CrossRef]
- Harris, R.J.; Andrews, S.M.; Wilner, D.J.; Kraus, A.L. A Resolved Census of Millimeter Emission from Taurus Multiple Star Systems. Astrophys. J. 2012, 751, 115. [Google Scholar] [CrossRef]
- Müller, T.W.A.; Kley, W. Circumstellar disks in binary star systems. Models for γ Cephei and α Centauri. Astron. Astrophys. 2012, 539, A18. [Google Scholar] [CrossRef]
- Jang-Condell, H.; Mugrauer, M.; Schmidt, T. Disk Truncation and Planet Formation in γ Cephei. Astrophys. J. 2008, 683, L191. [Google Scholar] [CrossRef]
- Benedict, G.F.; Harrison, T.E.; Endl, M.; Torres, G. A Mass for γ Cep Ab. Res. Notes Am. Astron. Soc. 2018, 2, 7. [Google Scholar] [CrossRef]
- Lissauer, J.J. Planet formation. Ann. Rev. Astron. Astrophys. 1993, 31, 129–174. [Google Scholar] [CrossRef]
- Marzari, F.; Scholl, H. Planetesimal Accretion in Binary Star Systems. Astrophys. J. 2000, 543, 328–339. [Google Scholar] [CrossRef]
- Paardekooper, S.J.; Thébault, P.; Mellema, G. Planetesimal and gas dynamics in binaries. Mon. Not. RAS 2008, 386, 973–988. [Google Scholar] [CrossRef][Green Version]
- Thébault, P.; Marzari, F.; Scholl, H.; Turrini, D.; Barbieri, M. Planetary formation in the γ Cephei system. Astron. Astrophys. 2004, 427, 1097–1104. [Google Scholar] [CrossRef]
- Thébault, P.; Marzari, F.; Scholl, H. Relative velocities among accreting planetesimals in binary systems: The circumprimary case. Icarus 2006, 183, 193–206. [Google Scholar] [CrossRef][Green Version]
- Xie, J.W.; Zhou, J.L. Planetesimal Accretion in Binary Systems: Role of the Companion’s Orbital Inclination. Astrophys. J. 2009, 698, 2066–2074. [Google Scholar] [CrossRef]
- Xie, J.W.; Zhou, J.L.; Ge, J. Planetesimal Accretion in Binary Systems: Could Planets Form Around α Centauri B? Astrophys. J. 2010, 708, 1566–1578. [Google Scholar] [CrossRef]
- Thébault, P.; Marzari, F.; Scholl, H. Planet formation in the habitable zone of α Centauri B. Mon. Not. RAS 2009, 393, L21–L25. [Google Scholar] [CrossRef]
- Thébault, P.; Marzari, F.; Scholl, H. Planet formation in α Centauri A revisited: Not so accretion friendly after all. Mon. Not. RAS 2008, 388, 1528–1536. [Google Scholar] [CrossRef][Green Version]
- Thebault, P. Against all odds? Forming the planet of the HD 196885 binary. Celest. Mech. Dyn. Astron. 2011, 111, 29–49. [Google Scholar] [CrossRef][Green Version]
- Rafikov, R.R. Planet Formation in Small Separation Binaries: Not so Secularly Excited by the Companion. Astrophys. J. 2013, 765, L8. [Google Scholar] [CrossRef]
- Rafikov, R.R.; Silsbee, K. Planet Formation in Stellar Binaries. II. Overcoming the Fragmentation Barrier in α Centauri and γ Cephei-like Systems. Astrophys. J. 2015, 798, 70. [Google Scholar] [CrossRef]
- Silsbee, K.; Rafikov, R.R. Planet Formation in Binaries: Dynamics of Planetesimals Perturbed by the Eccentric Protoplanetary Disk and the Secondary. Astrophys. J. 2015, 798, 71. [Google Scholar] [CrossRef]
- Kley, W.; Nelson, R. On the Formation and Dynamical Evolution of Planets in Binaries. arXiv 2007, arXiv:0705.3421. [Google Scholar]
- Marzari, F.; Scholl, H.; Thébault, P.; Baruteau, C. On the eccentricity of self-gravitating circumstellar disks in eccentric binary systems. Astron. Astrophys. 2009, 508, 1493–1502. [Google Scholar] [CrossRef][Green Version]
- Marzari, F.; Baruteau, C.; Scholl, H.; Thebault, P. Eccentricity of radiative disks in close binary-star systems. Astron. Astrophys. 2012, 539, A98. [Google Scholar] [CrossRef]
- Zsom, A.; Sándor, Z.; Dullemond, C.P. The first stages of planet formation in binary systems: How far can dust coagulation proceed? Astron. Astrophys. 2011, 527, A10. [Google Scholar] [CrossRef]
- Fragner, M.M.; Nelson, R.P.; Kley, W. On the dynamics and collisional growth of planetesimals in misaligned binary systems. Astron. Astrophys. 2011, 528, A40. [Google Scholar] [CrossRef]
- Guedes, J.M.; Rivera, E.J.; Davis, E.; Laughlin, G.; Quintana, E.V.; Fischer, D.A. Formation and Detectability of Terrestrial Planets around α Centauri B. Astrophys. J. 2008, 679, 1582–1587. [Google Scholar] [CrossRef][Green Version]
- Barbieri, M.; Marzari, F.; Scholl, H. Formation of terrestrial planets in close binary systems: The case of alpha Centauri A. Astron. Astrophys. 2002, 396, 219–224. [Google Scholar] [CrossRef]
- Quintana, E.V.; Lissauer, J.J.; Chambers, J.E.; Duncan, M.J. Terrestrial Planet Formation in the α Centauri System. Astrophys. J. 2002, 576, 982–996. [Google Scholar] [CrossRef]
- Quintana, E.V.; Adams, F.C.; Lissauer, J.J.; Chambers, J.E. Terrestrial Planet Formation around Individual Stars within Binary Star Systems. Astrophys. J. 2007, 660, 807–822. [Google Scholar] [CrossRef]
- Haghighipour, N.; Raymond, S.N. Habitable Planet Formation in Binary Planetary Systems. Astrophys. J. 2007, 666, 436–446. [Google Scholar] [CrossRef]
- Payne, M.J.; Wyatt, M.C.; Thébault, P. Outward migration of terrestrial embryos in binary systems. Mon. Not. RAS 2009, 400, 1936–1944. [Google Scholar] [CrossRef]
- Marzari, F.; Weidenschilling, S.J.; Barbieri, M.; Granata, V. Jumping Jupiters in Binary Star Systems. Astrophys. J. 2005, 618, 502–511. [Google Scholar] [CrossRef]
- Gong, Y.X.; Ji, J. Formation of S-type planets in close binaries: Scattering-induced tidal capture of circumbinary planets. Mon. Not. RAS 2018, 478, 4565–4574. [Google Scholar] [CrossRef]
- Xie, J.W.; Payne, M.J.; Thébault, P.; Zhou, J.L.; Ge, J. From Dust to Planetesimal: The Snowball Phase? Astrophys. J. 2010, 724, 1153–1164. [Google Scholar] [CrossRef]
- Paardekooper, S.J.; Leinhardt, Z.M. Planetesimal collisions in binary systems. Mon. Not. RAS 2010, 403, L64–L68. [Google Scholar] [CrossRef]
- Duchêne, G. Planet Formation in Binary Systems: A Separation-Dependent Mechanism? Astrophys. J. 2010, 709, L114–L118. [Google Scholar] [CrossRef]
- Nelson, A.F. Planet Formation is Unlikely in Equal-Mass Binary Systems with A ~50 AU. Astrophys. J. 2000, 537, L65–L68. [Google Scholar] [CrossRef]
- Mayer, L.; Boss, A.; Nelson, A.F. Gravitational Instability in Binary Protoplanetary Disks. In Planets in Binary Star Systems; Haghighipour, N., Ed.; Astrophysics and Space Science Library-Springer: Basel, Switzerland, 2010; Volume 366, p. 195. [Google Scholar]
- Marzari, F.; Barbieri, M. Planets in binary systems: Is the present configuration indicative of the formation process? Astron. Astrophys. 2007, 467, 347–351. [Google Scholar] [CrossRef][Green Version]
- Malmberg, D.; de Angeli, F.; Davies, M.B.; Church, R.P.; Mackey, D.; Wilkinson, M.I. Close encounters in young stellar clusters: Implications for planetary systems in the solar neighbourhood. Mon. Not. RAS 2007, 378, 1207–1216. [Google Scholar] [CrossRef]
- Fragione, G. Dynamical origin of S-type planets in close binary stars. Mon. Not. RAS 2019, 483, 3465–3471. [Google Scholar] [CrossRef]
- Schwarz, R.; Haghighipour, N.; Eggl, S.; Pilat-Lohinger, E.; Funk, B. Prospects of the detection of circumbinary planets with Kepler and CoRoT using the variations of eclipse timing. Mon. Not. RAS 2011, 414, 2763–2770. [Google Scholar] [CrossRef]
- Orosz, J.A.; Welsh, W.F.; Haghighipour, N.; Quarles, B.; Short, D.R.; Mills, S.M.; Satyal, S.; Torres, G.; Agol, E.; Fabrycky, D.C. Discovery of a Third Transiting Planet in the Kepler-47 Circumbinary System. Astron. J. 2019, 157, 174. [Google Scholar] [CrossRef]
- Armstrong, D.J.; Osborn, H.P.; Brown, D.J.A.; Faedi, F.; Gómez Maqueo Chew, Y.; Martin, D.V.; Pollacco, D.; Udry, S. On the abundance of circumbinary planets. Mon. Not. RAS 2014, 444, 1873–1883. [Google Scholar] [CrossRef]
- Martin, D.V. Populations of Planets in Multiple Star Systems. In Handbook of Exoplanets; Springer: Berlin, Germany, 2018; p. 156. ISBN 978-3-319-55332-0. [Google Scholar]
- Kostov, V.B.; Orosz, J.A.; Welsh, W.F.; Doyle, L.R.; Fabrycky, D.C.; Haghighipour, N.; Quarles, B.; Short, D.R.; Cochran, W.D.; Endl, M. Kepler-1647b: The Largest and Longest-period Kepler Transiting Circumbinary Planet. Astrophys. J. 2016, 827, 86. [Google Scholar] [CrossRef]
- Moe, M.; Kratter, K.M. Dynamical Formation of Close Binaries during the Pre-main-sequence Phase. Astrophys. J. 2018, 854, 44. [Google Scholar] [CrossRef]
- Meschiari, S. Circumbinary Planet Formation in the Kepler-16 System. I. N-body Simulations. Astrophys. J. 2012, 752, 71. [Google Scholar] [CrossRef]
- Paardekooper, S.J.; Leinhardt, Z.M.; Thébault, P.; Baruteau, C. How Not to Build Tatooine: The Difficulty of In Situ Formation of Circumbinary Planets Kepler 16b, Kepler 34b, and Kepler 35b. Astrophys. J. 2012, 754, L16. [Google Scholar] [CrossRef]
- Lines, S.; Leinhardt, Z.M.; Paardekooper, S.; Baruteau, C.; Thebault, P. Forming Circumbinary Planets: N-body Simulations of Kepler-34. Astrophys. J. 2014, 782, L11. [Google Scholar] [CrossRef]
- Rafikov, R.R. Building Tatooine: Suppression of the Direct Secular Excitation in Kepler Circumbinary Planet Formation. Astrophys. J. 2013, 764, L16. [Google Scholar] [CrossRef]
- Marzari, F.; Thébault, P.; Scholl, H. Planetesimal Evolution in Circumbinary Gaseous Disks: A Hybrid Model. Astrophys. J. 2008, 681, 1599–1608. [Google Scholar] [CrossRef]
- Marzari, F.; Thebault, P.; Scholl, H.; Picogna, G.; Baruteau, C. Influence of the circumbinary disk gravity on planetesimal accumulation in the Kepler-16 system. Astron. Astrophys. 2013, 553, A71. [Google Scholar] [CrossRef][Green Version]
- Masset, F. FARGO: A fast eulerian transport algorithm for differentially rotating disks. Astron. Astrophys. 2000, 141, 165–173. [Google Scholar] [CrossRef]
- Nelson, R.P. On the evolution of giant protoplanets forming in circumbinary discs. Mon. Not. RAS 2003, 345, 233–242. [Google Scholar] [CrossRef][Green Version]
- Sutherland, A.P.; Fabrycky, D.C. On the Fate of Unstable Circumbinary Planets: Tatooine’s Close Encounters with a Death Star. Astrophys. J. 2016, 818, 6. [Google Scholar] [CrossRef]
- Kley, W.; Haghighipour, N. Modeling circumbinary planets: The case of Kepler-38. Astron. Astrophys. 2014, 564, A72. [Google Scholar] [CrossRef][Green Version]
- Kley, W.; Haghighipour, N. Evolution of circumbinary planets around eccentric binaries: The case of Kepler-34. Astron. Astrophys. 2015, 581, A20. [Google Scholar] [CrossRef]
- Kley, W.; Nelson, R.P. Early Evolution of Planets in Binaries: Planet-Disk Interaction. In Planets in Binary Star Systems; Haghighipour, N., Ed.; Astrophysics and Space Science Library-Springer: Basel, Switzerland, 2010; Volume 366, p. 135. [Google Scholar]
- Michtchenko, T.A.; Malhotra, R. Secular dynamics of the three-body problem: Application to the upsilon Andromedae planetary system. Icarus 2004, 168, 237–248. [Google Scholar] [CrossRef]
- Libert, A.S.; Henrard, J. Analytical Approach to the Secular Behaviour of Exoplanetary Systems. Celest. Mech. Dyn. Astron. 2005, 93, 187–200. [Google Scholar] [CrossRef]
- Naoz, S. The Eccentric Kozai-Lidov Effect and Its Applications. Ann. Rev. Astron. Astrophys. 2016, 54, 441–489. [Google Scholar] [CrossRef]
- Marzari, F.; Gallina, G. Stability of multiplanet systems in binaries. Astron. Astrophys. 2016, 594, A89. [Google Scholar] [CrossRef]
- Mudryk, L.R.; Wu, Y. Resonance Overlap Is Responsible for Ejecting Planets in Binary Systems. Astrophys. J. 2006, 639, 423–431. [Google Scholar] [CrossRef][Green Version]
- Deck, K.M.; Payne, M.; Holman, M.J. First-order Resonance Overlap and the Stability of Close Two-planet Systems. Astrophys. J. 2013, 774, 129. [Google Scholar] [CrossRef]
- Heppenheimer, T.A. On the formation of planets in binary star systems. Astron. Astrophys. 1978, 65, 421–426. [Google Scholar]
- Andrade-Ines, E.; Beaugé, C.; Michtchenko, T.; Robutel, P. Secular dynamics of S-type planetary orbits in binary star systems: Applicability domains of first- and second-order theories. Celest. Mech. Dyn. Astron. 2016, 124, 405–432. [Google Scholar] [CrossRef]
- Rabl, G.; Dvorak, R. Satellite-type planetary orbits in double stars - A numerical approach. Astron. Astrophys. 1988, 191, 385–391. [Google Scholar]
- Laskar, J. Frequency analysis for multi-dimensional systems. Global dynamics and diffusion. Physics D 1993, 67, 257–281. [Google Scholar] [CrossRef]
- Šidlichovský, M.; Nesvorný, D. Frequency modified Fourier transform and its applications to asteroids. Celest. Mech. Dyn. Astron. 1996, 65, 137–148. [Google Scholar] [CrossRef]
- Marzari, F.; Tricarico, P.; Scholl, H. Stability of Jupiter Trojans investigated using frequency map analysis: The MATROS project. MNRAS 2003, 345, 1091–1100. [Google Scholar] [CrossRef]
- Pilat-Lohinger, E.; Bazsó, A.; Funk, B. A Quick Method to Identify Secular Resonances in Multi-planet Systems with a Binary Companion. Astron. J. 2016, 152, 139. [Google Scholar] [CrossRef]
- Hale, A. Orbital CoPlanetary in Solar-Type Binary Systems: Implications for Planetary System Formation and Detection. Astron. J. 1994, 107, 306. [Google Scholar] [CrossRef]
- Chen, X.; Bourke, T.L.; Launhardt, R.; Henning, T. SMA CO (2-1) Observations of CG 30: A Protostellar Binary System with a High-Velocity Quadrupolar Molecular Outflow. Astrophys. J. 2008, 686, L107. [Google Scholar] [CrossRef]
- Ratzka, T.; Schegerer, A.A.; Leinert, C.; Ábrahám, P.; Henning, T.; Herbst, T.M.; Köhler, R.; Wolf, S.; Zinnecker, H. Spatially resolved mid-infrared observations of the triple system T Tauri. Astron. Astrophys. 2009, 502, 623–646. [Google Scholar] [CrossRef]
- Jensen, E.L.N.; Akeson, R. Misaligned protoplanetary disks in a young binary star system. Nature 2014, 511, 567–569. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Holman, M.; Touma, J.; Tremaine, S. Chaotic variations in the eccentricity of the planet orbiting 16 Cygni B. Nature 1997, 386, 254–256. [Google Scholar] [CrossRef]
- Wu, Y.; Murray, N. Planet Migration and Binary Companions: The Case of HD 80606b. Astrophys. J. 2003, 589, 605–614. [Google Scholar] [CrossRef]
- Lithwick, Y.; Naoz, S. The Eccentric Kozai Mechanism for a Test Particle. Astrophys. J. 2011, 742, 94. [Google Scholar] [CrossRef]
- Moriwaki, K.; Nakagawa, Y. A Planetesimal Accretion Zone in a Circumbinary Disk. Astrophys. J. 2004, 609, 1065–1070. [Google Scholar] [CrossRef]
- Moriwaki, K.; Nakagawa, Y. Stability of a Planet in a Binary System: MACHO 97-BLG-41. Astron. J. 2002, 124, 3364–3369. [Google Scholar] [CrossRef]
- Artymowicz, P.; Lubow, S.H. Dynamics of binary-disk interaction. 1: Resonances and disk gap sizes. Astrophys. J. 1994, 421, 651–667. [Google Scholar] [CrossRef]
- Martin, D.V.; Triaud, A.H.M.J. Kozai-Lidov cycles towards the limit of circumbinary planets. Mon. Not. RAS 2016, 455, L46–L50. [Google Scholar] [CrossRef]
- Picogna, G.; Marzari, F. Three-dimensional modeling of radiative disks in binaries. Astron. Astrophys. 2013, 556, A148. [Google Scholar] [CrossRef][Green Version]
- Johansen, A.; Blum, J.; Tanaka, H.; Ormel, C.; Bizzarro, M.; Rickman, H. The Multifaceted Planetesimal Formation Process. In Protostars and Planets VI; Beuther, H., Klessen, R.S., Dullemond, C.P., Henning, T., Eds.; University of Arizona Press: Tucson, AZ, USA, 2014; p. 547. [Google Scholar]
- Ormel, C.W.; Klahr, H.H. The effect of gas drag on the growth of protoplanets. Analytical expressions for the accretion of small bodies in laminar disks. Astron. Astrophys. 2010, 520, A43. [Google Scholar] [CrossRef]
| 1 |


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marzari, F.; Thebault, P. Planets in Binaries: Formation and Dynamical Evolution. Galaxies 2019, 7, 84. https://doi.org/10.3390/galaxies7040084
Marzari F, Thebault P. Planets in Binaries: Formation and Dynamical Evolution. Galaxies. 2019; 7(4):84. https://doi.org/10.3390/galaxies7040084
Chicago/Turabian StyleMarzari, Francesco, and Philippe Thebault. 2019. "Planets in Binaries: Formation and Dynamical Evolution" Galaxies 7, no. 4: 84. https://doi.org/10.3390/galaxies7040084
APA StyleMarzari, F., & Thebault, P. (2019). Planets in Binaries: Formation and Dynamical Evolution. Galaxies, 7(4), 84. https://doi.org/10.3390/galaxies7040084




