An Introduction to Particle Acceleration in Shearing Flows
Abstract
1. Introduction
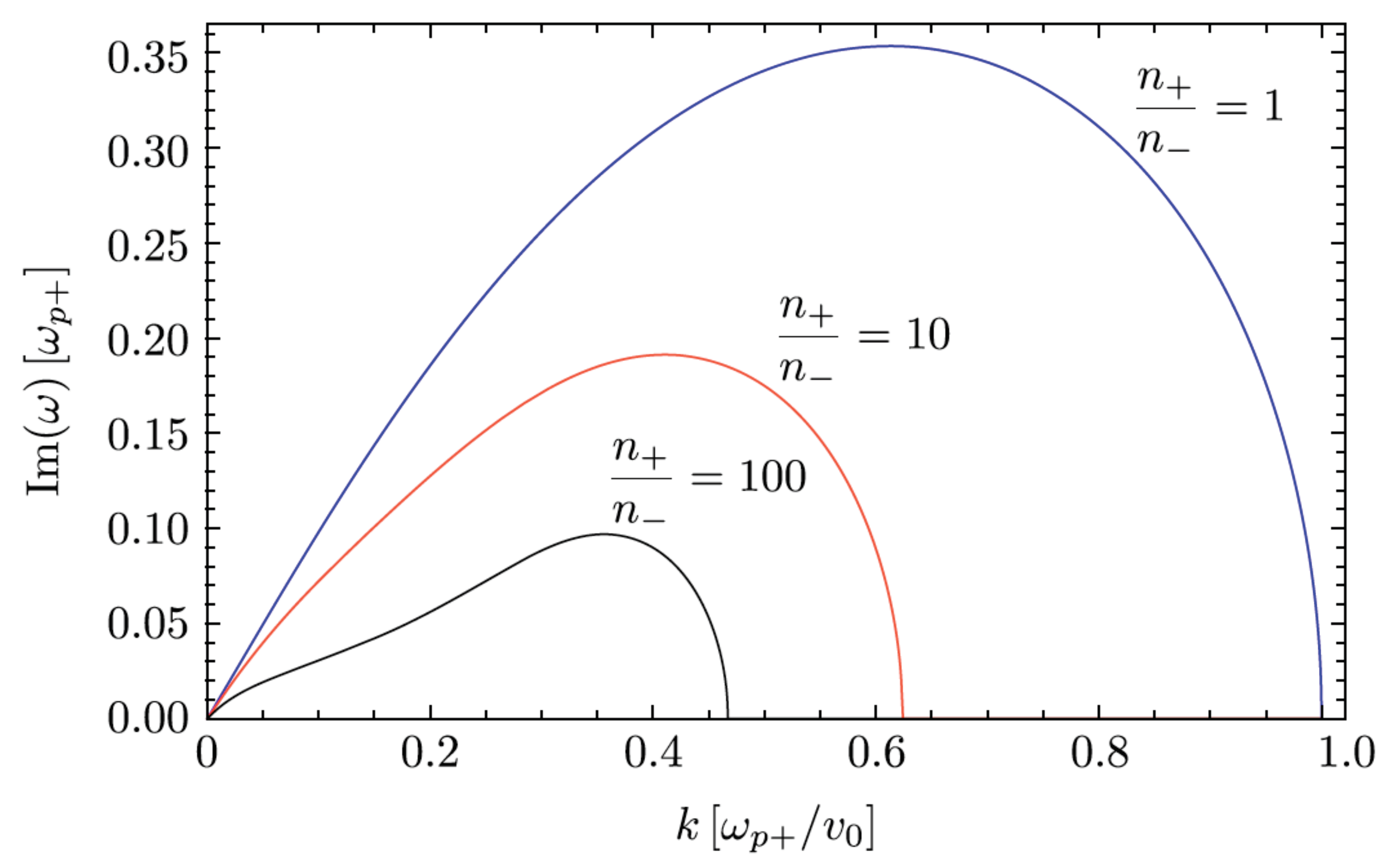
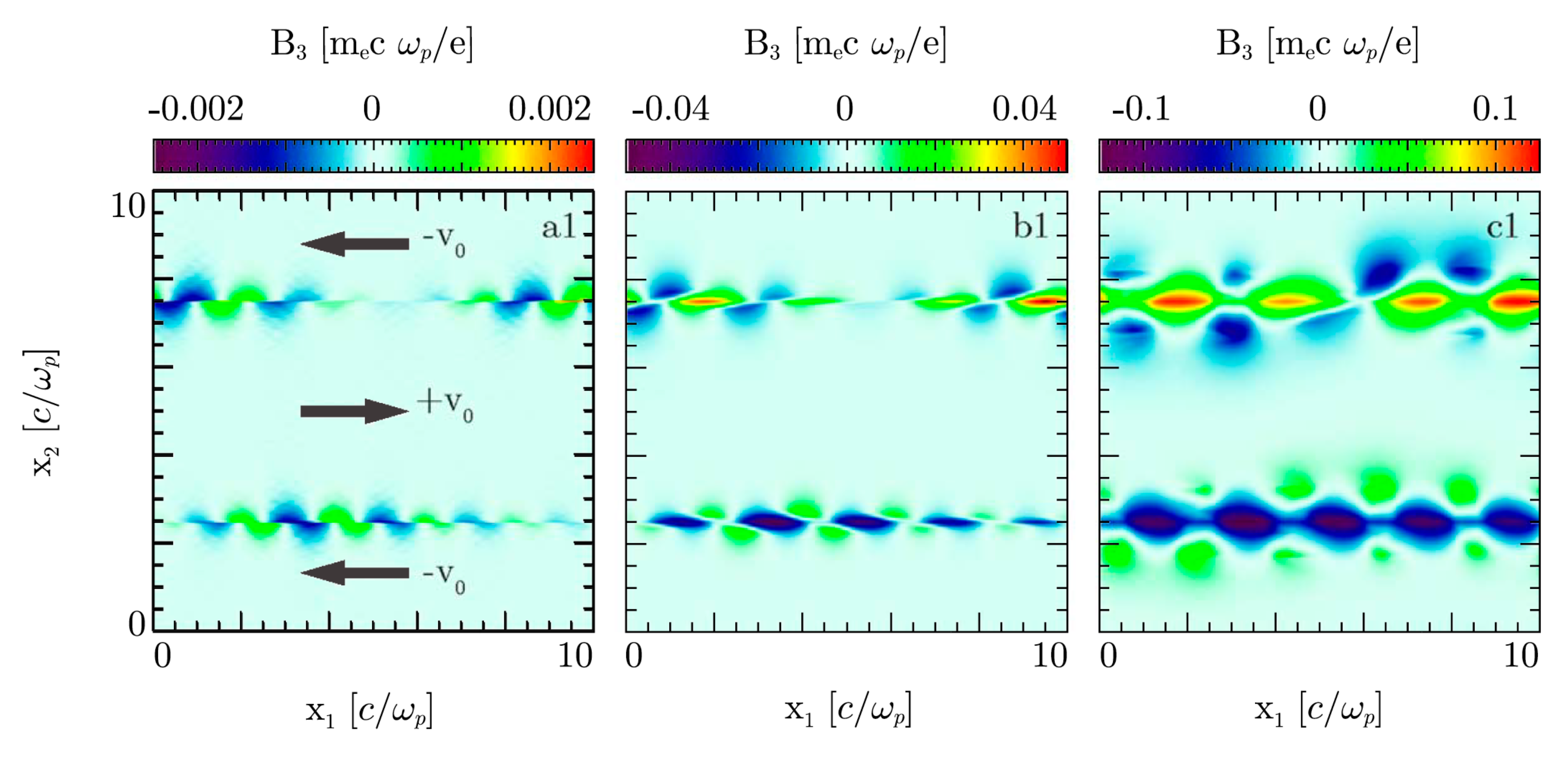
2. Supra-Thermal Particle Acceleration in Microscopic Shear Flows
3. Fermi-Type Particle Acceleration in Macroscopic Shear Flows
3.1. Gradual Shear Flows
3.1.1. A Microscopic Approach—Momentum Space Diffusion
3.1.2. Propagation and Acceleration in Non-Relativistic Shear Flows
3.1.3. Generalization of the Particle Transport to Relativistic Shear Flows
3.1.4. Recent Applications of Gradual Shear Acceleration
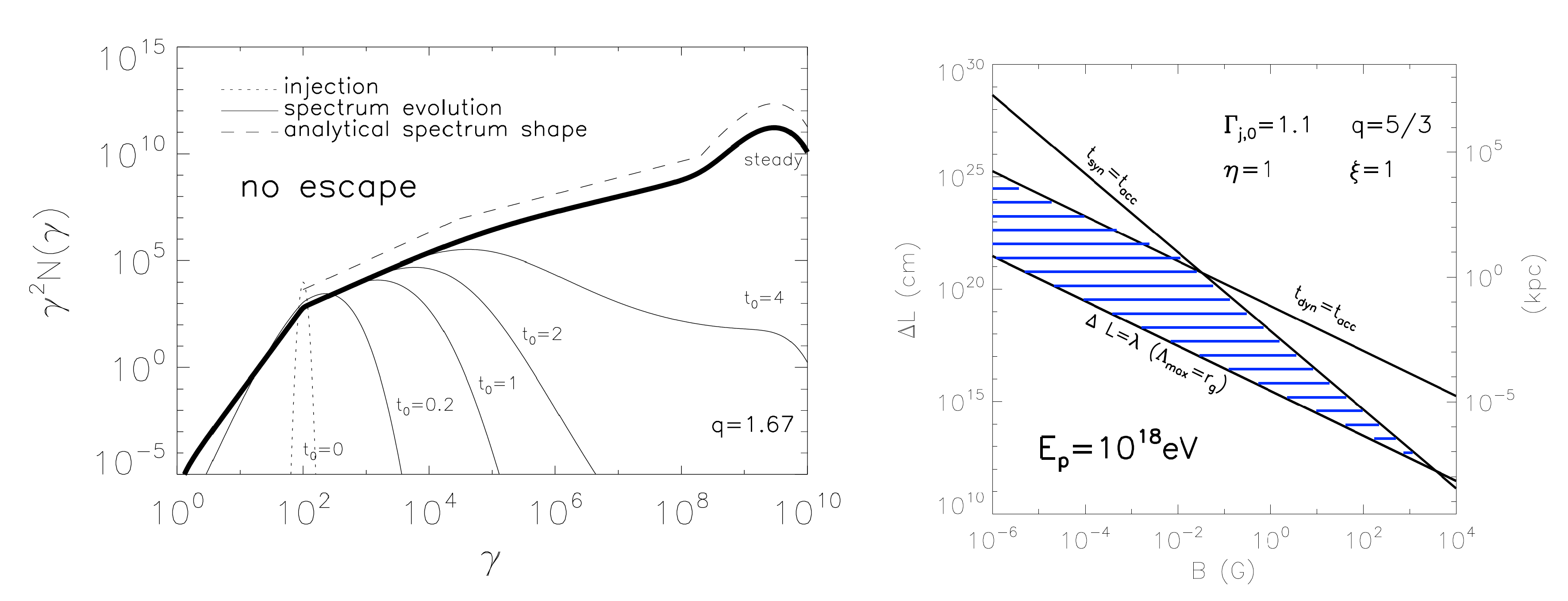
- (i) Shear Particle Acceleration in Expanding Relativistic Outflows:The jetted outflows from AGN and GRBs can exhibit highly relativistic speeds, regions of (quasi-conical) expansion and flow Lorentz factors varying with polar angle (e.g., [83,84,85,86]). This makes them possible sites where gradual shear particle acceleration could occur [28,59]. An application to AGN-type outflows has been presented recently, considering the case of a radial velocity shear profile , where denotes the polar angle, r the radial coordinate, and the bulk flow Lorentz factor [28]. When the impact of different functional dependencies for such as a power-law-, Gaussian- or Fermi-Dirac-type profile is explored (see Figure 6), the characteristic (co-moving) acceleration timescale is found to be a strong function of . This could facilitate the generation of some prominent, non-axis (e.g., ’ridge line’) emission features in AGN jets [28].In order to overcome adiabatic losses () and allow for efficient acceleration, relativistic outflow speeds and sufficient energetic seed particles ( for the example shown in Figure 6) would be needed. When put in GRB context, particle acceleration in expanding shear flows might result in a weak and long-duration leptonic emission component in GRBs, as well as be conducive to UHE cosmic-ray production [59].
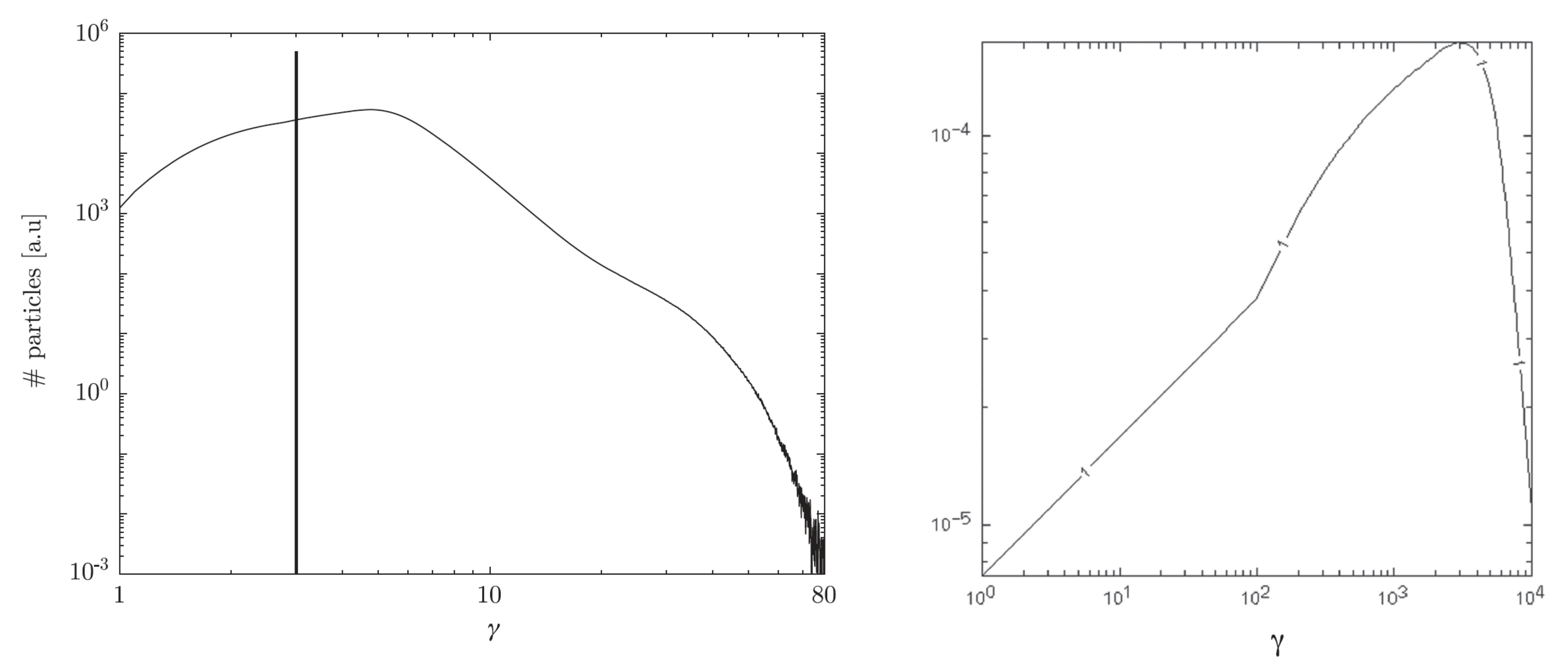
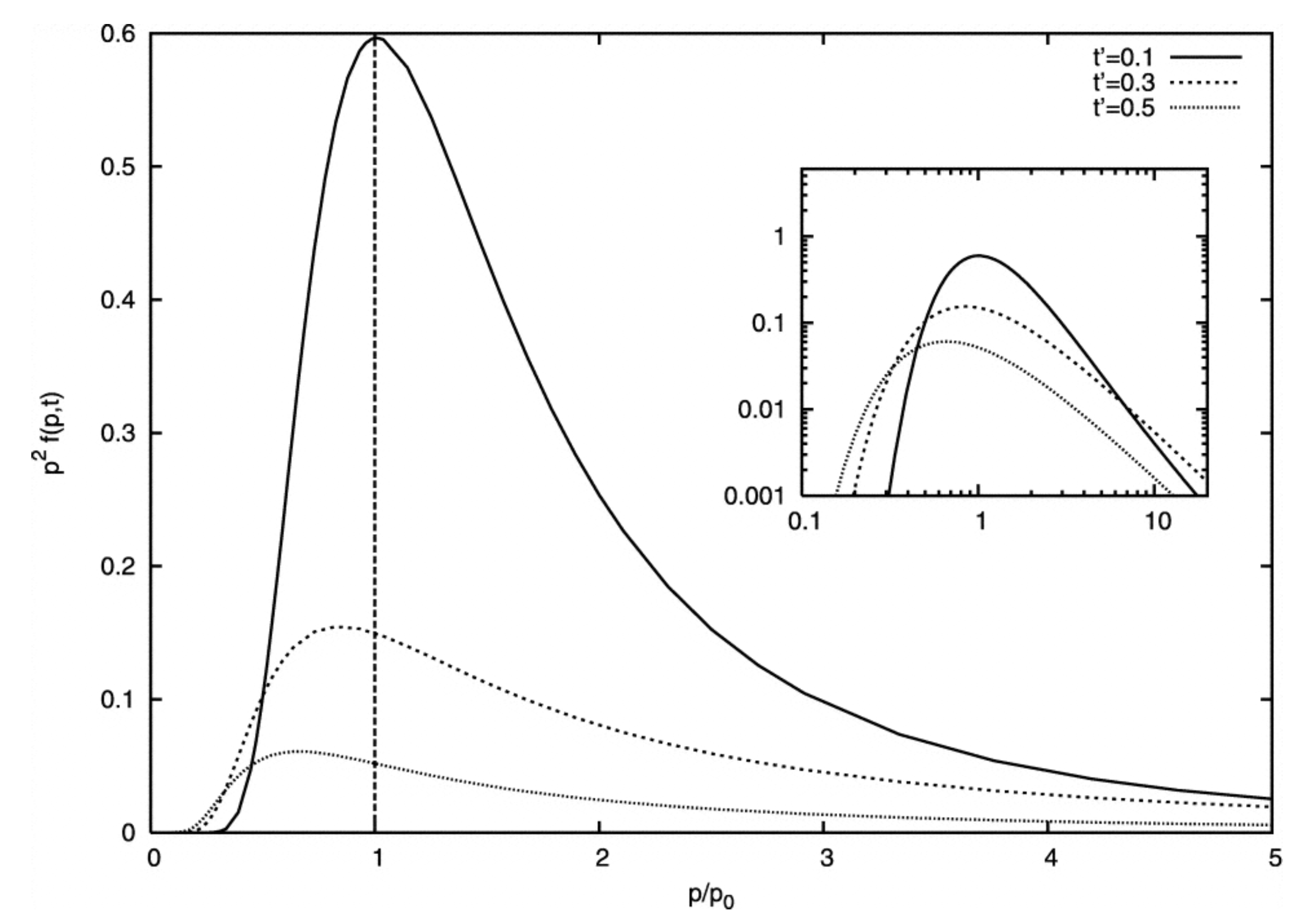
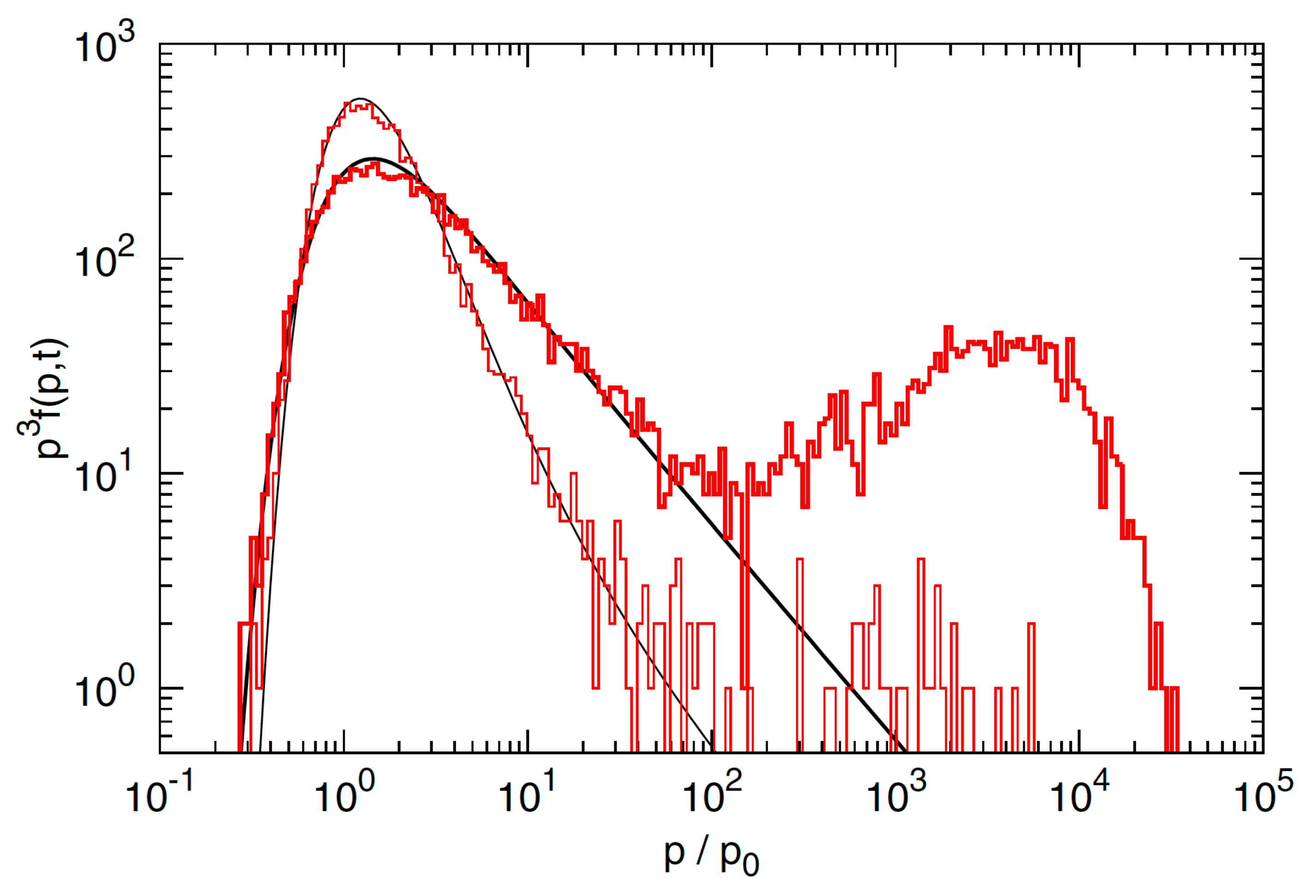
- (ii) Multi-Component Particle Distributions and Extended Emission:Since (Equation (13)), gradual shear particle acceleration will begin to dominate over conventional first- and second-order Fermi acceleration () above a certain energy threshold. This could naturally result in the formation of multi-component particle distributions. A basic example assuming radiative-loss-limited acceleration in a cylindrical, mildly relativistic shearing flow is shown in Figure 7 [31]. The figure is based on a time-dependent solution of the Fokker-Planck equation for , or equivalently , including the effects of classical second-order Fermi and gradual shear particle acceleration as well as synchrotron losses. Employing a Kolmogorov-type () scaling for the particle mean free path, , and using parameters applicable to mildly relativistic large-scale jets in AGN, electron acceleration up to Lorentz factors of seems feasible (cf. Figure 7 (left)). In the example given, stochastic second-order Fermi acceleration dominates particle energization up to , while above this threshold shear acceleration becomes operative leading to a somewhat flatter spectral slope (with a change by in the example shown). Synchrotron radiation eventually introduces a spectral cut-off at high energies.As shearing conditions are likely to prevail along astrophysical jets, stochastic-shear particle acceleration is expected to be of relevance for understanding the extended X-ray emission in the large-scale jets of AGN (cf. Section 1) [31]. In reality, the anticipated change in spectral slope will also depend on the spatial transport and escape properties (see below). As a consequence, higher speeds would be needed to achieve comparable, moderate breaks. When put in UHE cosmic-ray context, gradual shear acceleration of protons up to eV seems feasible in the large-scale jets of AGN [31,33,82], cf. also Figure 7 (right). Higher energies might be achieved for faster flows and for heavier particles.
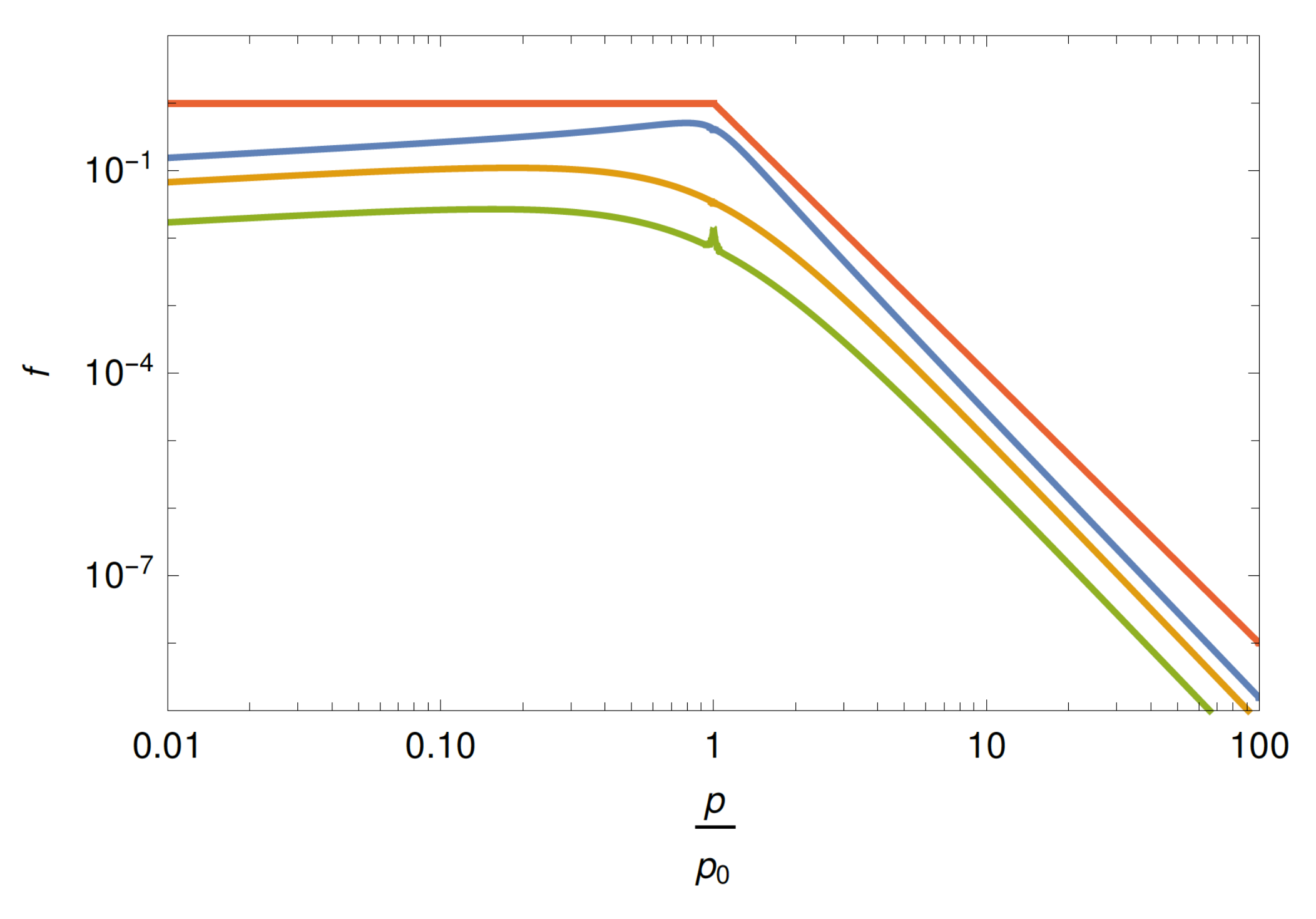
- (iii) Incorporating Spatial Transport and Diffusive Escape:In the previous Fokker-Planck approach details of the spatial transport, and possible modifications introduced by the diffusive escape of particles from the system, have not been incorporated. Implications of the spatial transport could in principle be studied by using the full relativistic particle transport Equation (23). Analytical examples in this regard have been recently presented by Webb et al. [33,82]. Focusing on steady-state solutions for a cylindrical jet with longitudinal shear and allowing for a specific radial dependence of the scattering time, , they showed that diffusive escape can counter-act efficient acceleration. In particular, while the local particle distribution still follows a power law , its momentum index becomes dependent on the maximum flow speed on the jet axis, and significantly steepens with decreasing (approaching for ) [33,82]. Though possible limitations due to the chosen -dependence may deserve some further studies, these results imply that efficient gradual shear particle acceleration requires relativistic flow speeds. The analytical solutions [33] can be used to explore the full radial evolution of the particle transport. Figure 8 represents an example for a hyperbolic, relativistic shear flow profile with a maximum Lorentz factor on the jet axis [72].As can be seen, away from injection at the known power-law momentum dependence, Equation (18), is approximately recovered at high flow speeds (). Clearly, advancing our understanding of the (radial) diffusion properties in astrophysical jets will be important to further improve our understanding of the particle acceleration in gradual shear flows.
3.2. Non-Gradual Shear Flows
4. Particle Acceleration by Large-Scale Velocity Turbulence
5. Concluding Remarks
Funding
Acknowledgments
Conflicts of Interest
References
- Rieger, F.M.; Duffy, P. Shear Acceleration in Relativistic Astrophysical Jets. Astrophys. J. 2004, 617, 155–161. [Google Scholar] [CrossRef]
- Martí, J.M. Numerical Simulations of Jets from Active Galactic Nuclei. Galaxies 2019, 7, 24. [Google Scholar] [CrossRef]
- Fendt, C. Approaching the Black Hole by Numerical Simulations. Universe 2019, 5, 99. [Google Scholar] [CrossRef]
- Perucho, M. Dissipative processes and their role in the evolution of radio galaxies. Galaxies 2019, 7, 70. [Google Scholar] [CrossRef]
- Giroletti, M.; Giovannini, G.; Feretti, L.; Cotton, W.D.; Edwards, P.G.; Lara, L.; Marscher, A.P.; Mattox, J.R.; Piner, B.G.; Venturi, T. Parsec-Scale Properties of Markarian 501. Astrophys. J. 2004, 600, 127–140. [Google Scholar] [CrossRef]
- Pushkarev, A.B.; Gabuzda, D.C.; Vetukhnovskaya, Y.N.; Yakimov, V.E. Spine-sheath polarization structures in four active galactic nuclei jets. Mon. Not. R. Astron. Soc. 2005, 356, 859–871. [Google Scholar] [CrossRef]
- Giroletti, M.; Giovannini, G.; Cotton, W.D.; Taylor, G.B.; Pérez-Torres, M.A.; Chiaberge, M.; Edwards, P.G. The jet of Markarian 501 from millions of Schwarzschild radii down to a few hundreds. Astron. Astrophys. 2008, 488, 905–914. [Google Scholar] [CrossRef]
- Blasi, M.G.; Lico, R.; Giroletti, M.; Orienti, M.; Giovannini, G.; Cotton, W.; Edwards, P.G.; Fuhrmann, L.; Krichbaum, T.P.; Kovalev, Y.Y.; et al. The TeV blazar Markarian 421 at the highest spatial resolution. Astron. Astrophys. 2013, 559, A75. [Google Scholar] [CrossRef]
- Piner, B.G.; Edwards, P.G. First-epoch VLBA Imaging of 20 New TeV Blazars. Astrophys. J. 2014, 797, 25. [Google Scholar] [CrossRef]
- Nagai, H.; Haga, T.; Giovannini, G.; Doi, A.; Orienti, M.; D’Ammando, F.; Kino, M.; Nakamura, M.; Asada, K.; Hada, K.; et al. Limb-brightened Jet of 3C 84 Revealed by the 43 GHz Very-Long-Baseline-Array Observation. Astrophys. J. 2014, 785, 53. [Google Scholar] [CrossRef]
- Gabuzda, D.C.; Reichstein, A.R.; O’Neill, E.L. Are spine-sheath polarization structures in the jets of active galactic nuclei associated with helical magnetic fields? Mon. Not. R. Astron. Soc. 2014, 444, 172–184. [Google Scholar] [CrossRef]
- Boccardi, B.; Krichbaum, T.P.; Bach, U.; Mertens, F.; Ros, E.; Alef, W.; Zensus, J.A. The stratified two-sided jet of Cygnus A. Acceleration and collimation. Astron. Astrophys. 2016, 585, A33. [Google Scholar] [CrossRef]
- Hardee, P.E.; Hughes, P.A. The Effect of External Winds on Relativistic Jets. Astrophys. J. 2003, 583, 116–123. [Google Scholar] [CrossRef]
- Meliani, Z.; Keppens, R. Transverse stability of relativistic two-component jets. Astron. Astrophys. 2007, 475, 785–789. [Google Scholar] [CrossRef]
- Meliani, Z.; Keppens, R. Decelerating Relativistic Two-Component Jets. Astrophys. J. 2009, 705, 1594–1606. [Google Scholar] [CrossRef]
- Hardee, P.; Mizuno, Y.; Nishikawa, K.I. GRMHD/RMHD simulations & stability of magnetized spine-sheath relativistic jets. Astrophys. Space Sci. 2007, 311, 281–286. [Google Scholar] [CrossRef]
- Mizuno, Y.; Hardee, P.; Nishikawa, K.I. Three-dimensional Relativistic Magnetohydrodynamic Simulations of Magnetized Spine-Sheath Relativistic Jets. Astrophys. J. 2007, 662, 835–850. [Google Scholar] [CrossRef]
- Mizuno, Y.; Lyubarsky, Y.; Nishikawa, K.I.; Hardee, P.E. Three-dimensional Relativistic Magnetohydrodynamic Simulations of Current-driven Instability. III. Rotating Relativistic Jets. Astrophys. J. 2012, 757, 16. [Google Scholar] [CrossRef]
- Millas, D.; Keppens, R.; Meliani, Z. Rotation and toroidal magnetic field effects on the stability of two-component jets. Mon. Not. R. Astron. Soc. 2017, 470, 592–605. [Google Scholar] [CrossRef]
- Aloy, M.A.; Mimica, P. Observational Effects of Anomalous Boundary Layers in Relativistic Jets. Astrophys. J. 2008, 681, 84–95. [Google Scholar] [CrossRef][Green Version]
- Rieger, F.M.; Aharonian, F.A. Centaurus A as TeV γ-ray and possible UHE cosmic-ray source. Astron. Astrophys. 2009, 506, L41–L44. [Google Scholar] [CrossRef]
- Sahayanathan, S. Boundary shear acceleration in the jet of MKN501. Mon. Not. R. Astron. Soc. 2009, 398, L49–L53. [Google Scholar] [CrossRef]
- Tammi, J.; Duffy, P. Particle-acceleration time-scales in TeV blazar flares. Mon. Not. R. Astron. Soc. 2009, 393, 1063–1069. [Google Scholar] [CrossRef]
- Liang, E.; Boettcher, M.; Smith, I. Magnetic Field Generation and Particle Energization at Relativistic Shear Boundaries in Collisionless Electron-Positron Plasmas. Astrophys. J. Lett. 2013, 766, L19. [Google Scholar] [CrossRef]
- Laing, R.A.; Bridle, A.H. Systematic properties of decelerating relativistic jets in low-luminosity radio galaxies. Mon. Not. R. Astron. Soc. 2014, 437, 3405–3441. [Google Scholar] [CrossRef]
- Tavecchio, F.; Ghisellini, G. On the spine-layer scenario for the very high-energy emission of NGC 1275. Mon. Not. R. Astron. Soc. 2014, 443, 1224–1230. [Google Scholar] [CrossRef]
- Tavecchio, F.; Ghisellini, G. High-energy cosmic neutrinos from spine-sheath BL Lac jets. Mon. Not. R. Astron. Soc. 2015, 451, 1502–1510. [Google Scholar] [CrossRef]
- Rieger, F.M.; Duffy, P. Shear Acceleration in Expanding Flows. Astrophys. J. 2016, 833, 34. [Google Scholar] [CrossRef]
- Liang, E.; Fu, W.; Böttcher, M. Relativistic Shear Flow between Electron-Ion and Electron-Positron Plasmas and Astrophysical Applications. Astrophys. J. 2017, 847, 90. [Google Scholar] [CrossRef]
- Chhotray, A.; Nappo, F.; Ghisellini, G.; Salafia, O.S.; Tavecchio, F.; Lazzati, D. On radiative acceleration in spine-sheath structured blazar jets. Mon. Not. R. Astron. Soc. 2017, 466, 3544–3557. [Google Scholar] [CrossRef][Green Version]
- Liu, R.Y.; Rieger, F.M.; Aharonian, F.A. Particle Acceleration in Mildly Relativistic Shearing Flows: The Interplay of Systematic and Stochastic Effects, and the Origin of the Extended High-energy Emission in AGN Jets. Astrophys. J. 2017, 842, 39. [Google Scholar] [CrossRef]
- Kimura, S.S.; Murase, K.; Zhang, B.T. Ultrahigh-energy cosmic-ray nuclei from black hole jets: Recycling galactic cosmic rays through shear acceleration. Phys. Rev. D 2018, 97, 023026. [Google Scholar] [CrossRef]
- Webb, G.M.; Barghouty, A.F.; Hu, Q.; le Roux, J.A. Particle Acceleration Due to Cosmic-ray Viscosity and Fluid Shear in Astrophysical Jets. Astrophys. J. 2018, 855, 31. [Google Scholar] [CrossRef]
- Worrall, D.M.; Birkinshaw, M. Multiwavelength Evidence of the Physical Processes in Radio Jets. In Physics of Active Galactic Nuclei at all Scales; Alloin, D., Ed.; Lecture Notes in Physics; Springer: Berlin, Germany, 2006; Volume 693, p. 39. [Google Scholar] [CrossRef]
- Harris, D.E.; Krawczynski, H. X-Ray Emission from Extragalactic Jets. Annu. Rev. Astron. Astrophys. 2006, 44, 463–506. [Google Scholar] [CrossRef]
- Rieger, F.M.; Bosch-Ramon, V.; Duffy, P. Fermi acceleration in astrophysical jets. Astrophys. Space Sci. 2007, 309, 119–125. [Google Scholar] [CrossRef]
- Georganopoulos, M.; Meyer, E.; Perlman, E. Recent Progress in Understanding the Large Scale Jets of Powerful Quasars. Galaxies 2016, 4, 65. [Google Scholar] [CrossRef]
- Sun, X.N.; Yang, R.Z.; Rieger, F.M.; Liu, R.Y.; Aharonian, F. Energy distribution of relativistic electrons in the kiloparsec scale jet of M 87 with Chandra. Astron. Astrophys. 2018, 612, A106. [Google Scholar] [CrossRef]
- Ostrowski, M. Acceleration of ultra-high energy cosmic ray particles in relativistic jets in extragalactic radio sources. Astron. Astrophys. 1998, 335, 134–144. [Google Scholar]
- Aharonian, F.A.; Belyanin, A.A.; Derishev, E.V.; Kocharovsky, V.V.; Kocharovsky, V.V. Constraints on the extremely high-energy cosmic ray accelerators from classical electrodynamics. Phys. Rev. D 2002, 66, 023005. [Google Scholar] [CrossRef]
- Kotera, K.; Olinto, A.V. The Astrophysics of Ultrahigh-Energy Cosmic Rays. Annu. Rev. Astron. Astrophys. 2011, 49, 119–153. [Google Scholar] [CrossRef]
- Perucho, M.; Martí, J.M. A numerical simulation of the evolution and fate of a Fanaroff-Riley type I jet. The case of 3C 31. Mon. Not. R. Astron. Soc. 2007, 382, 526–542. [Google Scholar] [CrossRef]
- Rossi, P.; Mignone, A.; Bodo, G.; Massaglia, S.; Ferrari, A. Formation of dynamical structures in relativistic jets: the FRI case. Astron. Astrophys. 2008, 488, 795–806. [Google Scholar] [CrossRef]
- Matthews, J.H.; Bell, A.R.; Blundell, K.M.; Araudo, A.T. Ultrahigh energy cosmic rays from shocks in the lobes of powerful radio galaxies. Mon. Not. R. Astron. Soc. 2019, 482, 4303–4321. [Google Scholar] [CrossRef]
- Perucho, M.; Martí, J.M.; Quilis, V. Long-term FRII jet evolution: clues from three-dimensional simulations. Mon. Not. R. Astron. Soc. 2019, 482, 3718–3735. [Google Scholar] [CrossRef]
- Alves, E.P.; Grismayer, T.; Martins, S.F.; Fiúza, F.; Fonseca, R.A.; Silva, L.O. Large-scale Magnetic Field Generation via the Kinetic Kelvin-Helmholtz Instability in Unmagnetized Scenarios. Astrophys. J. Lett. 2012, 746, L14. [Google Scholar] [CrossRef]
- Liang, E.; Fu, W.; Boettcher, M.; Smith, I.; Roustazadeh, P. Relativistic Positron-Electron-Ion Shear Flows and Application to Gamma-Ray Bursts. Astrophys. J. Lett. 2013, 779, L27. [Google Scholar] [CrossRef]
- Berezhko, E.G.; Krymskii, G.F. A Kinetic Analysis of the Charged Particle Acceleration Process in Collisionless Plasma Shear Flows. Sov. Astron. Lett. 1981, 7, 352. [Google Scholar]
- Earl, J.A.; Jokipii, J.R.; Morfill, G. Cosmic-ray viscosity. Astrophys. J. 1988, 331, L91–L94. [Google Scholar] [CrossRef]
- Ohira, Y. Turbulent Shear Acceleration. Astrophys. J. Lett. 2013, 767, L16. [Google Scholar] [CrossRef]
- Lemoine, M. Generalized Fermi acceleration. Phys. Rev. D 2019, 99, 083006. [Google Scholar] [CrossRef]
- Berezhko, E.G. On Acceleration Possibility of Charged Particles Under Cosmic Plasma Shearing Flows. Int. Cosm. Ray Conf. 1981, 3, 506. [Google Scholar]
- Berezhko, E.G. The Friction Mechanism for Accelerating Particles in Interplanetary Space. Sov. Astron. Lett. 1982, 8, 403–405. [Google Scholar]
- Webb, G.M. The diffusion approximation and transport theory for cosmic rays in relativistic flows. Astrophys. J. 1989, 340, 1112–1123. [Google Scholar] [CrossRef]
- Jokipii, J.R.; Morfill, G.E. Particle acceleration in step function shear flows—A microscopic analysis. Astrophys. J. 1990, 356, 255–258. [Google Scholar] [CrossRef]
- Ostrowski, M. Diffusive acceleration of cosmic ray particles at tangential discontinuity of velocity field. Astron. Astrophys. 1990, 238, 435–438. [Google Scholar]
- Webb, G.M.; Jokipii, J.R.; Morfill, G.E. Green’s formula and variational principles for cosmic-ray transport with application to rotating and shearing flows. Astrophys. J. 1994, 424, 158–180. [Google Scholar] [CrossRef]
- Rieger, F.M.; Mannheim, K. Particle acceleration in rotating and shearing jets from AGN. Astron. Astrophys. 2002, 396, 833–846. [Google Scholar] [CrossRef]
- Rieger, F.M.; Duffy, P. Particle Acceleration in Gamma-Ray Burst Jets. Astrophys. J. Lett. 2005, 632, L21–L24. [Google Scholar] [CrossRef]
- Rieger, F.M.; Duffy, P. A Microscopic Analysis of Shear Acceleration. Astrophys. J. 2006, 652, 1044–1049. [Google Scholar] [CrossRef]
- Dempsey, P.; Rieger, F.M. On Particle Acceleration in Rotating AGN Flows. Int. J. Mod. Phys. D 2009, 18, 1651–1654. [Google Scholar] [CrossRef]
- Alves, E.P.; Grismayer, T.; Fonseca, R.A.; Silva, L.O. Electron-scale shear instabilities: magnetic field generation and particle acceleration in astrophysical jets. New J. Phys. 2014, 16, 035007. [Google Scholar] [CrossRef]
- Alves, E.P.; Grismayer, T.; Fonseca, R.A.; Silva, L.O. Transverse electron-scale instability in relativistic shear flows. Phys. Rev. E 2015, 92, 021101. [Google Scholar] [CrossRef] [PubMed]
- Grismayer, T.; Alves, E.P.; Fonseca, R.A.; Silva, L.O. dc-Magnetic-Field Generation in Unmagnetized Shear Flows. Phys. Rev. Lett. 2013, 111, 015005. [Google Scholar] [CrossRef] [PubMed]
- Liang, E.; Fu, W.; Böttcher, M.; Roustazadeh, P. Scaling of Relativistic Shear Flows with the Bulk Lorentz Factor. Astrophys. J. 2018, 854, 129. [Google Scholar] [CrossRef]
- Nishikawa, K.I.; Hardee, P.E.; Duţan, I.; Niemiec, J.; Medvedev, M.; Mizuno, Y.; Meli, A.; Sol, H.; Zhang, B.; Pohl, M.; et al. Magnetic Field Generation in Core-sheath Jets via the Kinetic Kelvin-Helmholtz Instability. Astrophys. J. 2014, 793, 60. [Google Scholar] [CrossRef]
- Grismayer, T.; Alves, E.P.; Fonseca, R.A.; Silva, L.O. Theory of multidimensional electron-scale instabilities in unmagnetized shear flows. Plasma Phys. Controll. Fusion 2013, 55, 124031. [Google Scholar] [CrossRef]
- Nakamura, T.K.M.; Daughton, W.; Karimabadi, H.; Eriksson, S. Three-dimensional dynamics of vortex-induced reconnection and comparison with THEMIS observations. J. Geophys. Res. (Space Phys.) 2013, 118, 5742–5757. [Google Scholar] [CrossRef]
- Daughton, W.; Nakamura, T.K.M.; Karimabadi, H.; Roytershteyn, V.; Loring, B. Computing the reconnection rate in turbulent kinetic layers by using electron mixing to identify topology. Phys. Plasmas 2014, 21, 052307. [Google Scholar] [CrossRef]
- Nakamura, T.K.M.; Hasegawa, H.; Daughton, W.; Eriksson, S.; Li, W.Y.; Nakamura, R. Turbulent mass transfer caused by vortex induced reconnection in collisionless magnetospheric plasmas. Nat. Commun. 2017, 8, 1582. [Google Scholar] [CrossRef]
- Fermi, E. On the Origin of the Cosmic Radiation. Phys. Rev. 1949, 75, 1169–1174. [Google Scholar] [CrossRef]
- Rieger, F.M. Energetic Particle Acceleration in Shearing Flows. In Proceedings of the 18th International Astrophysics Conference, Pasadena, CA, USA, 18–22 February 2019. IOP Conference Series, to appear. [Google Scholar]
- Sironi, L.; Spitkovsky, A. Relativistic Reconnection: An Efficient Source of Non-thermal Particles. Astrophys. J. Lett. 2014, 783, L21. [Google Scholar] [CrossRef]
- Guo, F.; Liu, Y.H.; Daughton, W.; Li, H. Particle Acceleration and Plasma Dynamics during Magnetic Reconnection in the Magnetically Dominated Regime. Astrophys. J. 2015, 806, 167. [Google Scholar] [CrossRef]
- Zhdankin, V.; Werner, G.R.; Uzdensky, D.A.; Begelman, M.C. Kinetic Turbulence in Relativistic Plasma: From Thermal Bath to Nonthermal Continuum. Phys. Rev. Lett. 2017, 118, 055103. [Google Scholar] [CrossRef] [PubMed]
- Parker, E.N. The passage of energetic charged particles through interplanetary space. Planet. Space Sci. 1965, 13, 9–49. [Google Scholar] [CrossRef]
- Williams, L.L.; Jokipii, J.R. Viscosity and inertia in cosmic-ray transport - Effects of an average magnetic field. Astrophys. J. 1991, 371, 639–647. [Google Scholar] [CrossRef]
- Williams, L.L.; Schwadron, N.; Jokipii, J.R.; Gombosi, T.I. A Unified Transport Equation for Both Cosmic Rays and Thermal Particles. Astrophys. J. Lett. 1993, 405, L79. [Google Scholar] [CrossRef]
- le Roux, J.A.; Zank, G.P.; Webb, G.M.; Khabarova, O. A Kinetic Transport Theory for Particle Acceleration and Transport in Regions of Multiple Contracting and Reconnecting Inertial-scale Flux Ropes. Astrophys. J. 2015, 801, 112. [Google Scholar] [CrossRef]
- le Roux, J.A.; Zank, G.P.; Khabarova, O.V. Self-consistent Energetic Particle Acceleration by Contracting and Reconnecting Small-scale Flux Ropes: The Governing Equations. Astrophys. J. 2018, 864, 158. [Google Scholar] [CrossRef]
- Li, X.; Guo, F.; Li, H.; Birn, J. The Roles of Fluid Compression and Shear in Electron Energization during Magnetic Reconnection. Astrophys. J. 2018, 855, 80. [Google Scholar] [CrossRef]
- Webb, G.M.; Al-Nussirat, S.; Mostafavi, P.; Barghouty, A.F.; Li, G.; le Roux, J.A.; Zank, G.P. Particle Acceleration by Cosmic Ray Viscosity in Radio-jet Shear Flows. Astrophys. J. 2019, 881, 123. [Google Scholar] [CrossRef]
- Pushkarev, A.B.; Kovalev, Y.Y.; Lister, M.L.; Savolainen, T. MOJAVE - XIV. Shapes and opening angles of AGN jets. Mon. Not. R. Astron. Soc. 2017, 468, 4992–5003. [Google Scholar] [CrossRef]
- Kovalev, Y.Y.; Pushkarev, A.B.; Nokhrina, E.E.; Plavin, A.V.; Beskin, V.S.; Chernoglazov, A.; Lister, M.L.; Savolainen, T. Discovery of geometry transition in nearby AGN jets. arXiv 2019, arXiv:1907.01485. [Google Scholar]
- Salafia, O.S.; Ghisellini, G.; Pescalli, A.; Ghirlanda, G.; Nappo, F. Structure of gamma-ray burst jets: intrinsic versus apparent properties. Mon. Not. R. Astron. Soc. 2015, 450, 3549–3558. [Google Scholar] [CrossRef]
- Zhang, B. The Physics of Gamma-Ray Bursts; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar] [CrossRef]
- Ostrowski, M. On possible ‘cosmic ray cocoons’ of relativistic jets. Mon. Not. R. Astron. Soc. 2000, 312, 579–584. [Google Scholar] [CrossRef][Green Version]
- Stawarz, Ł.; Ostrowski, M. Radiation from the Relativistic Jet: A Role of the Shear Boundary Layer. Astrophys. J. 2002, 578, 763–774. [Google Scholar] [CrossRef]
- Caprioli, D. “Espresso” Acceleration of Ultra-high-energy Cosmic Rays. Astrophys. J. Lett. 2015, 811, L38. [Google Scholar] [CrossRef]
- Mbarek, R.; Caprioli, D. Bottom-up Acceleration of Ultra-High-Energy Cosmic Rays in the Jets of Active Galactic Nuclei. arXiv 2019, arXiv:1904.02720. [Google Scholar]
- Bykov, A.M.; Toptygin, I.N. The theory of particle acceleration in astrophysical objects containing shock waves and turbulent plasma motions. J. Geophys. Z. Geophys. 1982, 50, 221–226. [Google Scholar]
- Bykov, A.M.; Toptygin, I.N. Cosmic Rays Acceleration by Large Scale Compressible and Incompressible Motions of Plasma. Int. Cosm. Ray Conf. 1983, 9, 313. [Google Scholar]
- Ptuskin, V.S. The acceleration of cosmic rays by long-wave turbulence. Pisma v Astronomicheskii Zhurnal 1988, 14, 599–605. [Google Scholar]
- Fisk, L.A.; Gloeckler, G. Acceleration of Suprathermal Tails in the Solar Wind. Astrophys. J. 2008, 686, 1466–1473. [Google Scholar] [CrossRef]
- Jokipii, J.R.; Lee, M.A. Compression Acceleration in Astrophysical Plasmas and the Production of f(v) ∝ v−5 Spectra in the Heliosphere. Astrophys. J. 2010, 713, 475–483. [Google Scholar] [CrossRef]

© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rieger, F.M. An Introduction to Particle Acceleration in Shearing Flows. Galaxies 2019, 7, 78. https://doi.org/10.3390/galaxies7030078
Rieger FM. An Introduction to Particle Acceleration in Shearing Flows. Galaxies. 2019; 7(3):78. https://doi.org/10.3390/galaxies7030078
Chicago/Turabian StyleRieger, Frank M. 2019. "An Introduction to Particle Acceleration in Shearing Flows" Galaxies 7, no. 3: 78. https://doi.org/10.3390/galaxies7030078
APA StyleRieger, F. M. (2019). An Introduction to Particle Acceleration in Shearing Flows. Galaxies, 7(3), 78. https://doi.org/10.3390/galaxies7030078




