Abstract
Shear flows are ubiquitously present in space and astrophysical plasmas. This paper highlights the central idea of the non-thermal acceleration of charged particles in shearing flows and reviews some of the recent developments. Topics include the acceleration of charged particles by microscopic instabilities in collisionless relativistic shear flows, Fermi-type particle acceleration in macroscopic, gradual and non-gradual shear flows, as well as shear particle acceleration by large-scale velocity turbulence. When put in the context of jetted astrophysical sources such as Active Galactic Nuclei, the results illustrate a variety of means beyond conventional diffusive shock acceleration by which power-law like particle distributions might be generated. This suggests that relativistic shear flows can account for efficient in-situ acceleration of energetic electrons and be of relevance for the production of extreme cosmic rays.
1. Introduction
Shear flows are naturally expected in a variety of astrophysical environments. Prominent examples include the rotating accretion flows around compact objects and the relativistic outflows (jets) in gamma-ray bursts (GRBs) or Active Galactic Nuclei (AGN) [1]. On conceptual grounds the jets in AGN are expected to exhibit some internal velocity stratification from the very beginning, with a black hole ergo-spheric driven, highly relativistic (electron-positron) flow surrounded by a slower moving (electron-proton dominated) wind from the inner parts of the disk (e.g., see Refs. [2,3] for recent overviews). In addition, as these jets continue to propagate, interactions with the ambient medium are likely to excite instabilities and induce mass loading, resulting in a velocity-sheared structure (cf. Ref. [4] for a recent review). Radio observations of parcec-scale AGN jets indeed provide evidence for some shear layer morphology, such as a boundary layer with parallel magnetic fields or a limb-brightened structure (e.g., [5,6,7,8,9,10,11,12]). In connection with this, various relativistic hydrodynamic and magneto-hydrodynamic simulations of two-component (spine-sheath/layer) and rotating AGN-type jets have been carried out to study their stability properties (e.g., [13,14,15,16,17,18,19]), indicating for example that the presence of a sheath has a stabilising effect on the jet (e.g., [13,14,15,16,17,18,19]). All this suggests that a transversal velocity stratification is a generic feature of AGN-type jets. Given the challenges and complexity of observed emission properties, this has lead to a renewed interest in multi-zone/spine-shear layer acceleration and emission models (e.g., [20,21,22,23,24,25,26,27,28,29,30,31,32,33]).
One particularly interesting example concerns the emission properties of large-scale AGN jets. Spatially, the fast jets of powerful AGN are observed to extend over several hundreds of kilo-parsec (kpc), with bright hot spots being formed and significant backflows induced when these jets eventually terminate in the intergalactic medium. Though these jets are associated with large fluid Reynolds numbers, they often appear laminar (see e.g., Ref. [34] for general orientation). The detection of extended (i.e., kpc-scale), non-thermal X-ray emission along several of them indicates that they must contain highly energetic particles [35,36,37]. The favoured electron synchrotron explanation in fact implies the presence of ultra-relativistic electrons with particle Lorentz factors up to (e.g., [38]). Since the typical cooling length of these electrons is very short (≪1 kpc), a distributed or continuous (re-)acceleration mechanism is required to keep them energized throughout the jet. Stochastic-shear particle acceleration in a stratified jet has been proposed as possible candidate for this (e.g., [31]). It seems in principle conceivable that particle acceleration in transversal shear flows could also facilitate the acceleration of cosmic rays (CRs) to extreme energies (e.g., [1,32,33,39]), supporting the idea that large-scale AGN jets are potential ultra-high-energy (UHE)CR acceleration sites (e.g., [40,41]). Since the backflow speeds in AGN can be substantial (e.g., [42,43,44,45]), this could becomes particularly interesting for cosmic-ray particles that are able to sample the velocity contrast between the main jet and its backflow [33].
The present paper focuses on the potential of fast shearing flows to facilitate efficient particle acceleration. As shown below, the transport and acceleration of charged particles in shearing flows can be described and explored on different scales, from the plasma skin depth (electron inertial-scale) (e.g., [46,47]) (see Section 2) via the relativistic gyro-scale (e.g., [36,48,49]) (see Section 3) to large turbulent length scales [50,51] (see Section 4). This paper aims at an accessible introduction to them, reviewing some of the key findings along with some recent developments. A particular attention is given to the second one in order to recapture early ideas and developments over the years [1,28,31,32,33,36,39,48,49,52,53,54,55,56,57,58,59,60,61]. When viewed in context, this review shows that a variety of processes beyond conventional diffusive shock acceleration could contribute to the efficient energization of particles in jetted astrophysical sources.
2. Supra-Thermal Particle Acceleration in Microscopic Shear Flows
Within recent years, Particle-in-Cell (PIC) simulations have been used to explore the kinetic physics of collisionless, un-magnetized, strong (on scales of the electron plasma skin depth) shear flows for different plasma compositions (i.e., pure electron-proton, pure electron-positron and some hybrid version) (e.g., [24,29,46,47,62,63,64,65,66]). In these simulations a variety of microscopic instabilities near the shear surface are encountered that can generate microscopic turbulence (i.e., scatterings sites for particle acceleration) as well as lead to the emergence of ordered steady (DC) electromagnetic fields and the production of non-thermal particle distributions.
One well-studied case relates to the excitation of the kinetic (electron-scale) Kelvin-Helmholtz instability (kKHI) in an un-magnetized electron-proton shear flow which has been explored by means of theory and simulations (e.g., [46,62,64,67]). The theoretical analysis of the longitudinal kKHI dispersion relation relies on the relativistic fluid formalism of un-magnetized plasmas (in the cold plasma limit) coupled with Maxwell’s equations, i.e., in cgs units
where Equations (1)–(4) refer to the continuity equation and the conservation of momentum equation, respectively, as well as Faraday’s and Ampere’s law. Here, with n the plasma number density, and denote the current density, the electric field vector and the magnetic field vector, respectively. and are the linear momentum and velocity of the flow, with its Lorentz factor. The protons are considered to be free streaming in this approximation. In order to gain insights into the system one can then specify a simple two-dimensional velocity shear profile,
characterizing a flow that propagates in the y-direction with a speed that depends on the x-coordinate, and prescribe a related (not necessarily constant) density profile . To study the response of the system to perturbations, each of the quantities () are further written as following the usual perturbation analysis (first-order approximation), and these expressions then substituted in Equations (1)–(4). The resultant equations are then linearized assuming that the perturbed quantities scale as
with parallel to the flow direction. Assuming that external fields are absent (), one can in this way derive a wave equation describing the linear eigenmodes of the system (see [62,67]), e.g.,
for the perturbations of the electric field, where are functions depending on the wave frequency , the wave number k, the flow velocity and Lorentz factor as well as on the relativistic plasma frequency , where denotes the usual electron plasma frequency
Solutions of Equation (7) for which becomes imaginary describe unstable modes that grow with time, cf. Equation (6). Figure 1 provides exemplary solutions for the growth rate of the resultant kinetic (electron-scale) Kelvin-Helmholtz instability in the case of a simple tangential shear flow profile (i.e., for , and for ) with different density contrast.
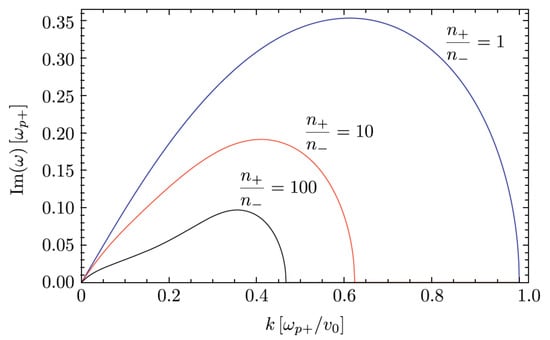
Figure 1.
Growth rate of unstable kinetic Kelvin-Helmholtz modes in an electron-proton plasma following linear theory for a microscopic tangential shear flow with step-functional velocity jump across the plane, corresponding to two counter-propagating flows with speed and different densities (for the flow in the upper region ) and (for the flow in the lower region ). The curves shown are for a density contrast , respectively. The growth rates display a cut-off at (in units of , where ), and take on a maximum value somewhat below. The three curves qualitatively resemble each other, but with a growth rate that is lowered for . Note, however, that the results of linear fluid theory do not predict a growth of a DC () mode as found in PIC simulations (see below). From Ref. [62].
The highest growth rate of is achieved for at . Note that these modes are obtained in the cold plasma limit, i.e., when the effects of thermal motion are negligible compared with . Comparing theory and simulation, PIC simulations provide general confirmation to this picture, but at late time also reveal the formation of a sub-equipartition (), large-scale DC () magnetic field component along the shear surface with transverse width and strength exceeding the one at by a factor of some few, that is not predicted in linear fluid theory, see Figure 2. The growth of this DC field cannot be really captured in a fluid description, but seems to be of intrinsically kinetic nature. It can be attributed to an effective current density associated with electron transport (mixing) across the shear interface.
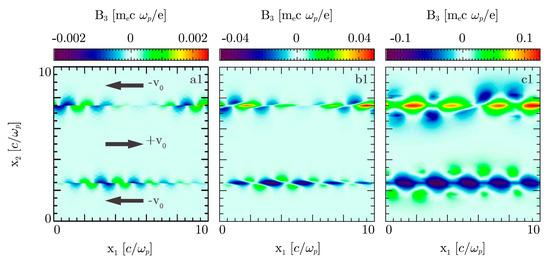
Figure 2.
Results of two-dimensional PIC simulations of counter-propagating flows of equal density () and with c, showing the emergence of a dominant DC () magnetic field component along the shear on top of the harmonic structure inferred from the linear fluid regime at times (a1), 45 (b1) and 55 (c1). From Ref. [62].
As the DC magnetic field grows, the Larmor radius of electrons crossing the shear decreases, until they eventually become trapped, imposing an upper limit on the current. In the absence of a large-scale magnetic field the inferred saturation level of the emergent DC electric and magnetic fields are typically of the order [64]
and seemingly persistent beyond the electron time scale (up to ). On much longer time scales (>), the emergent magnetic fields in two-dimensional PIC simulations start to affect the protons more due to their larger gyro-radii, leading to charge separation and the formation of a double-layered structure [47].
The emergence of organized, self-generated electric and magnetic fields in the shear region could in principle lead to efficient particle acceleration. Figure 3 (left) shows an exemplary outcome of a two-dimensional PIC simulation of two counter-propagating flows in which electrons experience acceleration in the self-generated electric fields along the shear. According to this simulation, electrons might be accelerated up to times their rest mass energy, possibly with some power-type behaviour in between [62].
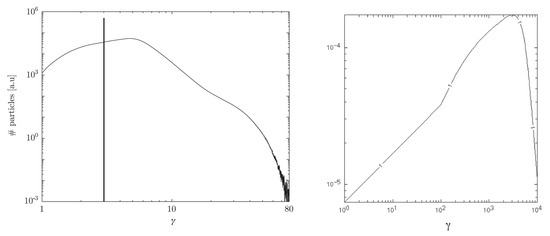
Figure 3.
Left: Resultant electron energy distribution for a relativistic, cold electron-proton shear flow with at time . At low energies () the distributions resembles a thermal one, while in the intermediate range it exhibits some smooth (power-law-type ) evolution. After some hardening, a tail is seen extending up to . From Ref. [62]. Right: Electron energy distribution in the case of a relativistic shear flow with at late times . The distribution peaks around , but shows little evidence for a conventional power-law behaviour. Both distributions refer to the center-of-momentum frame. From Ref. [65].
Other two-dimensional simulations find however, that at late time the electron distribution (at least for higher ) reveals a rather narrow peak around the decelerated proton kinetic energy, , with a relatively sharp cutoff and little evidence for some power-law extension [65]. It has been conjecture that in hybrid positron-electron-ion (instead of a pure electron-proton) plasmas a power-law tail could develop due to the presence of non-linear electromagnetic waves facilitating stochastic acceleration of electrons [47], though the slopes are expected to be sensitive to the composition and the shear flow Lorentz factor [65]. As things are, the situation appears inconclusive and the possible formation of a persistent, long-range power-law electron distribution in microscopic shear flows still remains to be demonstrated.
While conceptually highly interesting, the generalisation of these simulation results to realistic astrophysical sources is not yet straightforward. The outflows in AGN are likely to be magnetized from the onset, affecting its plasma dynamics and instability conditions. It appears conceivable, for example, that magnetic trapping of electrons could suppress the growth of a DC field along the shear. While we also know from 3D PIC simulations of non-relativistic, magnetized plasmas that turbulence can be generated at shear boundary layers (e.g., [68,69,70]), extension to the relativistic regime still remains to be carried out. In addition, the simulation setups rely on the existence of an idealized (relativistic) velocity jump (shear) on scales of the electron skin depth . For large-scale AGN jets, for example, one typically estimates ls ≲ 1011 cm, which would be minute compared to the jet width. Increasing the shear gradient length in the noted PIC simulations, however, decreases the growth rate of the kKHI instability (e.g., [62]), so that it appears uncertain to which extent the noted effects should be expected. Nevertheless, the simulations mentioned above clearly demonstrate that given suitable conditions microscopic instabilities in collisionless relativistic shear flows can efficiently generate electron-scale electromagnetic turbulence, allowing for the dissipation of kinetic energy of the flow and the production of supra-thermal particles.
3. Fermi-Type Particle Acceleration in Macroscopic Shear Flows
In a seminal paper, E. Fermi [71] has proposed a mechanisms for the acceleration of energetic charged particles in astrophysical plasma that has become a benchmark for acceleration theory. Fermi-type particle acceleration essentially relies on repeated interactions with moving scattering centers, and typically considers this process to be mediated by resonant wave-particle interactions (where the particle mean free path is comparable to the wavelength of the electromagnetic turbulence). In principle, the acceleration of energetic particles (of velocity ) in macroscopic shear flows can be understood as such a stochastic process in which particle energization occurs as a results of elastically scattering off differently moving (magnetic) inhomogeneities [36,51]. In macroscopic shear particle acceleration the scattering centers are taken to be frozen into a background flow whose velocity varies with transversal coordinate. Their velocities are thus essentially characterized by the general bulk flow profile. Depending on the characteristics of the velocity shear, a gradual (continuous) and a non-gradual or discontinuous ( characteristic length scale of the velocity shear) case might be distinguished, see Section 3.1 and Section 3.2 below.
The basic concept might be understood with reference to the energy change in an elastic scattering event (cf. [72]). Transforming into the scattering frame and again back to the laboratory frame, a simple analysis shows this energy change to be given by
where is the characteristic scattering center speed (u its magnitude, the corresponding Lorentz factor). and are the initial particle energy and momentum, respectively. According to Equation (10) an energetic particle (for which ) will gain energy in a head-on (for which ) collision, and lose energy in a following (for which ) collision. If one averages over an isotropic particle distribution, however, a net energy gain (i.e., stochastic acceleration) is obtained due to the fact that the interaction probability for head-on collisions is higher than the one for following collisions. This leads to a second order dependence on , such that
3.1. Gradual Shear Flows
For a particle moving across a continuous non-relativistic shear flow, the flow velocity (and hence the scattering center speed) changes by an amount given by the gradient in flow speed, , multiplied by the particle free path, . Hence, in the context of Fermi-type acceleration, gradual shear particle acceleration can be understood as a stochastic acceleration process, in which the conventional scattering center speed is replaced by an effective velocity determined by the shear flow profile [36] (cf. also Ref. [72] for a related review of gradual shear). In the case of a continuous velocity shear , for example (cf. Figure 4), this effective velocity is approximately given by .
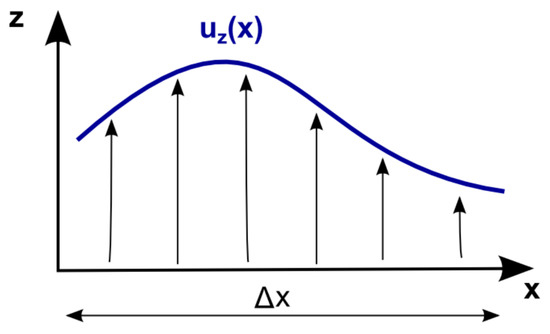
Figure 4.
Schematic illustration of a simple two-dimensional velocity shear profile, in which a flow, directed along the z-axis, is characterized by a velocity whose magnitude smoothly varies with the x-coordinate. denotes the shear width.
Accordingly, the fractional energy changes becomes (cf. Equation (11))
This suggests a scaling of the characteristic acceleration timescale
which, in contrast to classical first and second-order Fermi acceleration, is inversely depending on the particle mean free path [60]. The principal reason for this seemingly unusual behaviour is related to the fact that as a particle increases its energy (), and thereby its mean free path (), a higher effective velocity is experienced. This scaling has interesting implications, but also implies that for an efficient acceleration of electrons an injection of some pre-accelerated seed particles, either from acceleration at shocks or via classical second-order Fermi processes is required [31]. Alternatively, reconnection or plasma turbulence might facilitate electron seed injection (e.g., [73,74,75]). On the other hand, given their larger mean free paths, efficient shear acceleration of protons or ions is typically much more easily achieved.
3.1.1. A Microscopic Approach—Momentum Space Diffusion
As a stochastic process, gradual shear particle acceleration is accompanied not only by a momentum change (energy gain), but also by momentum dispersion (broadening) term. This can be shown in a microscopic picture by evaluating the average rate of momentum change and dispersion, i.e., by calculating the respective Fokker-Planck coefficients. For simplicity, consider again a non-relativistic shear flow with . While travelling for one scattering time across such a flow, the momentum of a particle relative to it changes by , where and , with the x-component of the particle velocity, and m the relativistic particle mass. In general, the timescale for collisions (mean scattering time) is expected to be an increasing function of momentum, i.e., . By expanding to second order in and averaging over an isotropic particle distribution, the Fokker-Planck coefficients become [55,60]
One can show that these coefficients are related by the equation
i.e., that they satisfy the principle of detailed balance (scattering being reversible). Here, the symbol on the right hand side of Equation (15) denotes the shear flow coefficient, which for the employed flow profile is simply given by .
Under the condition of detailed balance, the associated Fokker-Planck equation is known to reduce to a diffusion equation in momentum space. Hence in the absence of radiative losses and escape, the momentum-space particle distribution experiencing gradual shear acceleration obeys a simple Fokker-Planck type diffusion equation [55,60]
where denotes the momentum space (shear) diffusion coefficient. For the considered application
with . Figure 5 shows an exemplary solution of Equation (16) for the case [60].
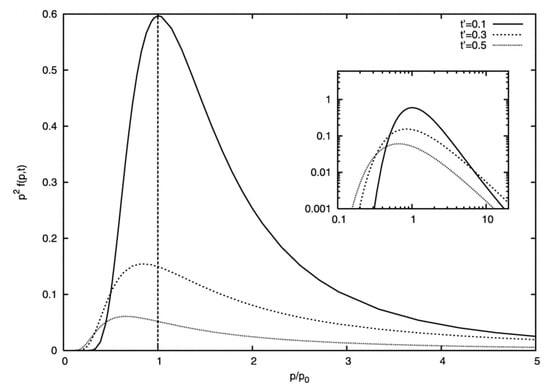
Figure 5.
Time-dependent solution of the Fokker-Planck diffusion equation for non-relativistic gradual shear acceleration assuming an impulsive, mono-energetic injection with at . A linear momentum-dependence () has been used for the scattering time The distribution broadens with time due to momentum dispersion. The (double logarithmic) inlet illustrates the formation of a power law like distribution above for . From Ref. [60].
At sufficiently large times, the particle distribution above injection approaches a power law shape
for , with power law index depending on the momentum scaling of the particle mean free path () [48,53,60]. In particular, for a gyro-dependence, , one has , which is comparable to the index for first-order Fermi acceleration at non-relativistic (high Mach number) shocks. The quasi steady-state (time-integrated) particle distribution for continuous injection then becomes constant below , and takes on the noted power-law shape above it.
3.1.2. Propagation and Acceleration in Non-Relativistic Shear Flows
In order to take spatial transport into account, a suitable particle transport equation has to be derived. For general shear flows this requires an extension of the original Parker transport equation [76], describing the propagation and acceleration of energetic particles scattered by turbulent inhomogeneities embedded in a background plasma. In the limit of non-relativistic flow speeds this has been done by Earl, Jokipii & Morfill [49], starting from the non-relativistic Boltzmann equation for the phase-space distribution and assuming a simple BKG-type collision term, (. The approach utilises a mixed system of phase-space coordinates such that quantities which are operated upon the scattering operator, i.e., the momentum, are evaluated in the co-moving flow frame (allowing for a convenient treatment of the scattering physics), while time and space coordinates are still measured in the laboratory frame. Given non-relativistic flow speeds, the particle momentum components are then related by a Galilean transformation , where denotes the background flow speed and the co-moving particle momentum. The analysis subsequently only requires that scattering is strong enough to guarantee the diffusion approximation, i.e., to ensure that departures of the particle distribution from isotropy are small, hence that the particle distribution function is well approximated by , with and . The full non-relativistic particle transport equation for eventually takes the form [49]
(). Here, denotes the isotropic spatial diffusion coefficient, , is the total acceleration vector
and is the viscous shear flow coefficient given by
The second, third and fourth term in Equation (19) describe the well-known effects of convection, adiabatic energy change and spatial diffusion [76], while the terms involving describe the effects of inertial drifts (cf. also [77,78] for incorporation of a mean magnetic field). The additional term involving characterizes energy changes due to flow shear and divergence.
When a steady (non-relativistic) shear flow of the form is considered, the adiabatic and inertial terms vanish ( and ), while becomes . The space-independent part of Equation (19) then reduces to
which coincides with Equation (16). For completeness, let us mention, that a significant velocity shear could also occur during magnetic reconnection, suggesting that shear acceleration in outflowing regions can contribute to particle energization if the particle distribution is sufficiently anisotropic (e.g., [79,80,81]).
3.1.3. Generalization of the Particle Transport to Relativistic Shear Flows
In order to compete with the diffusive escape of particles, efficient shear particle acceleration generally requires relativistic flow speeds (see also below). This then demands a suitable extension of the particle transport equation to the relativistic regime as has been obtained by Webb et al. [54,57], utilising as before a mixed-frame approach (with the momentum being evaluated in the co-moving flow frame). Assuming isotropic diffusion with and denoting the (covariant) metric tensor by , the zero component of the (comoving) particle momentum four vector by , the fluid four velocity by and the fluid four acceleration by , where denotes covariant derivation, the full particle transport equation for the isotopic distribution function with takes the form [54]
where Q denotes the source term and Greek indices () run from 0 to 3. denotes the (generalized) relativistic shear coefficient, which in the strong scattering limit is given by
where is the (covariant) fluid shear tensor given by
In the case of a cylindrical jet with a steady (relativistic) shear flow profile , the fluid four acceleration () and divergence () vanish, retaining only the shear term with
with , in the second line of Equation (23). The characteristic co-moving acceleration timescale then becomes [1,33]
where is the mean scattering time.
Full z-independent, steady-state solutions of Equation (23) for such a flow profile and specific forms of the radial dependence of have been recently presented by Webb et al. [33,82] and discussed in connection with extragalactic radio jets. In principle, Equation (23) also allows to treat particle acceleration in relativistic outflows where intrinsic jet rotation introduce a velocity shear. In such a case a complex interplay between shear and centrifugal effects can occur [58,61]. This could be of particular relevance in the context of AGN-type jets where some internal jet rotation is expected (e.g., [14,15,19]).
Note that when the generalized relativistic transport Equation (23) is reduced to its non-relativistic limit, also an additional term quadratic in the acceleration vector is recovered, which as such does not appear in the previous version of the non-relativistic transport Equation (19) [49,54,78]. This is due to the fact that in the derivation of Equation (19), focusing on cosmic-ray transport, the relevant terms have been neglected as they are typically of order smaller than the viscous term.
3.1.4. Recent Applications of Gradual Shear Acceleration
A variety of topics and applications have been discussed in the context of gradual shear acceleration (e.g., [21,22,31,33,36]). In the following three recent results are briefly mentioned:
- (i) Shear Particle Acceleration in Expanding Relativistic Outflows:The jetted outflows from AGN and GRBs can exhibit highly relativistic speeds, regions of (quasi-conical) expansion and flow Lorentz factors varying with polar angle (e.g., [83,84,85,86]). This makes them possible sites where gradual shear particle acceleration could occur [28,59]. An application to AGN-type outflows has been presented recently, considering the case of a radial velocity shear profile , where denotes the polar angle, r the radial coordinate, and the bulk flow Lorentz factor [28]. When the impact of different functional dependencies for such as a power-law-, Gaussian- or Fermi-Dirac-type profile is explored (see Figure 6), the characteristic (co-moving) acceleration timescale is found to be a strong function of . This could facilitate the generation of some prominent, non-axis (e.g., ’ridge line’) emission features in AGN jets [28].
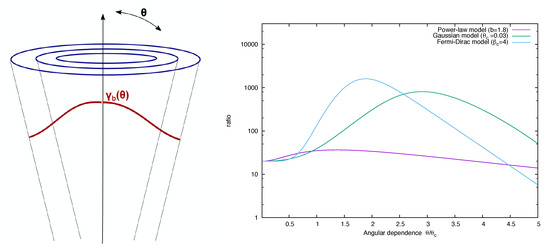 Figure 6. Left: Illustration of a simple conical flow whose radial outflow speeds varies with polar angle . Right: Ratio of viscous shear gain versus adiabatic losses multiplied by (), illustrated assuming a core angle rad and an on-axis flow Lorentz factor . A non-axis preference becomes particularly evident for a Gaussian or Fermi-Dirac shaped flow profile. From Ref. [28].In order to overcome adiabatic losses () and allow for efficient acceleration, relativistic outflow speeds and sufficient energetic seed particles ( for the example shown in Figure 6) would be needed. When put in GRB context, particle acceleration in expanding shear flows might result in a weak and long-duration leptonic emission component in GRBs, as well as be conducive to UHE cosmic-ray production [59].
Figure 6. Left: Illustration of a simple conical flow whose radial outflow speeds varies with polar angle . Right: Ratio of viscous shear gain versus adiabatic losses multiplied by (), illustrated assuming a core angle rad and an on-axis flow Lorentz factor . A non-axis preference becomes particularly evident for a Gaussian or Fermi-Dirac shaped flow profile. From Ref. [28].In order to overcome adiabatic losses () and allow for efficient acceleration, relativistic outflow speeds and sufficient energetic seed particles ( for the example shown in Figure 6) would be needed. When put in GRB context, particle acceleration in expanding shear flows might result in a weak and long-duration leptonic emission component in GRBs, as well as be conducive to UHE cosmic-ray production [59]. - (ii) Multi-Component Particle Distributions and Extended Emission:Since (Equation (13)), gradual shear particle acceleration will begin to dominate over conventional first- and second-order Fermi acceleration () above a certain energy threshold. This could naturally result in the formation of multi-component particle distributions. A basic example assuming radiative-loss-limited acceleration in a cylindrical, mildly relativistic shearing flow is shown in Figure 7 [31]. The figure is based on a time-dependent solution of the Fokker-Planck equation for , or equivalently , including the effects of classical second-order Fermi and gradual shear particle acceleration as well as synchrotron losses. Employing a Kolmogorov-type () scaling for the particle mean free path, , and using parameters applicable to mildly relativistic large-scale jets in AGN, electron acceleration up to Lorentz factors of seems feasible (cf. Figure 7 (left)). In the example given, stochastic second-order Fermi acceleration dominates particle energization up to , while above this threshold shear acceleration becomes operative leading to a somewhat flatter spectral slope (with a change by in the example shown). Synchrotron radiation eventually introduces a spectral cut-off at high energies.
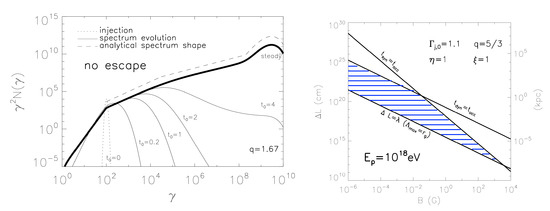 Figure 7. Left: Time-evolution of the electron spectrum, , in the presence of stochastic-shear particle acceleration, where represents a solution of the corresponding Fokker-Planck equation for a linearly decreasing (trans-relativistic) velocity shear of width , and an Alfven speed . Above particle Lorentz factors of a few times the spectrum is shaped by shear acceleration, with a high-energy spectral cut-off around being introduced by synchrotron losses. The successive operation of different acceleration processes here naturally results in a broken-power law distribution. Right: Required (blue-hatched) range of parameters (magnetic field strength B, shear layer width ) to allow shear acceleration of protons to eV given confinement and loss constraints for the noted conditions. The required conditions might be met in large-scale AGN jets. From Ref. [31].As shearing conditions are likely to prevail along astrophysical jets, stochastic-shear particle acceleration is expected to be of relevance for understanding the extended X-ray emission in the large-scale jets of AGN (cf. Section 1) [31]. In reality, the anticipated change in spectral slope will also depend on the spatial transport and escape properties (see below). As a consequence, higher speeds would be needed to achieve comparable, moderate breaks. When put in UHE cosmic-ray context, gradual shear acceleration of protons up to eV seems feasible in the large-scale jets of AGN [31,33,82], cf. also Figure 7 (right). Higher energies might be achieved for faster flows and for heavier particles.
Figure 7. Left: Time-evolution of the electron spectrum, , in the presence of stochastic-shear particle acceleration, where represents a solution of the corresponding Fokker-Planck equation for a linearly decreasing (trans-relativistic) velocity shear of width , and an Alfven speed . Above particle Lorentz factors of a few times the spectrum is shaped by shear acceleration, with a high-energy spectral cut-off around being introduced by synchrotron losses. The successive operation of different acceleration processes here naturally results in a broken-power law distribution. Right: Required (blue-hatched) range of parameters (magnetic field strength B, shear layer width ) to allow shear acceleration of protons to eV given confinement and loss constraints for the noted conditions. The required conditions might be met in large-scale AGN jets. From Ref. [31].As shearing conditions are likely to prevail along astrophysical jets, stochastic-shear particle acceleration is expected to be of relevance for understanding the extended X-ray emission in the large-scale jets of AGN (cf. Section 1) [31]. In reality, the anticipated change in spectral slope will also depend on the spatial transport and escape properties (see below). As a consequence, higher speeds would be needed to achieve comparable, moderate breaks. When put in UHE cosmic-ray context, gradual shear acceleration of protons up to eV seems feasible in the large-scale jets of AGN [31,33,82], cf. also Figure 7 (right). Higher energies might be achieved for faster flows and for heavier particles. - (iii) Incorporating Spatial Transport and Diffusive Escape:In the previous Fokker-Planck approach details of the spatial transport, and possible modifications introduced by the diffusive escape of particles from the system, have not been incorporated. Implications of the spatial transport could in principle be studied by using the full relativistic particle transport Equation (23). Analytical examples in this regard have been recently presented by Webb et al. [33,82]. Focusing on steady-state solutions for a cylindrical jet with longitudinal shear and allowing for a specific radial dependence of the scattering time, , they showed that diffusive escape can counter-act efficient acceleration. In particular, while the local particle distribution still follows a power law , its momentum index becomes dependent on the maximum flow speed on the jet axis, and significantly steepens with decreasing (approaching for ) [33,82]. Though possible limitations due to the chosen -dependence may deserve some further studies, these results imply that efficient gradual shear particle acceleration requires relativistic flow speeds. The analytical solutions [33] can be used to explore the full radial evolution of the particle transport. Figure 8 represents an example for a hyperbolic, relativistic shear flow profile with a maximum Lorentz factor on the jet axis [72].
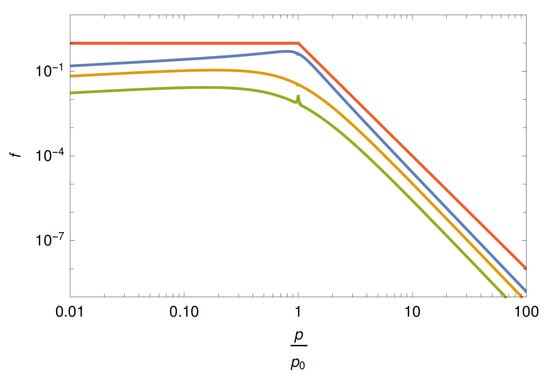 Figure 8. Normalized steady-state particle distribution function in the presence of a gradual, hyperbolic relativistic shear flow as a function of momentum , shown for three different spatial locations, (blue), (orange), (green). Mono-energetic particle injection with at and an outer (escape) boundary at have been assumed. A linear momentum-dependence has been used for the scattering time. The red curve (top) shows the expected power-law dependence above , as inferred from the Fokker-Planck approach in Equation (18).As can be seen, away from injection at the known power-law momentum dependence, Equation (18), is approximately recovered at high flow speeds (). Clearly, advancing our understanding of the (radial) diffusion properties in astrophysical jets will be important to further improve our understanding of the particle acceleration in gradual shear flows.
Figure 8. Normalized steady-state particle distribution function in the presence of a gradual, hyperbolic relativistic shear flow as a function of momentum , shown for three different spatial locations, (blue), (orange), (green). Mono-energetic particle injection with at and an outer (escape) boundary at have been assumed. A linear momentum-dependence has been used for the scattering time. The red curve (top) shows the expected power-law dependence above , as inferred from the Fokker-Planck approach in Equation (18).As can be seen, away from injection at the known power-law momentum dependence, Equation (18), is approximately recovered at high flow speeds (). Clearly, advancing our understanding of the (radial) diffusion properties in astrophysical jets will be important to further improve our understanding of the particle acceleration in gradual shear flows.
3.2. Non-Gradual Shear Flows
Once the particle mean free path becomes larger than the characteristic scale () of the shear transition layer, acceleration essentially becomes non-gradual. A particle may then be viewed as passing almost unaffected through the layer and experiencing a strong, quasi-discontinuous jump in velocity. Such a situation could arise, for example, at the interface between the ambient medium and the interior of powerful (FR II-type) large-scale AGN jets [1,39,56,87]. If a particle is able to repeatedly cross the transition layer, efficient particle acceleration to high energy may occur. This may allow to boost pre-accelerated cosmic rays further to ultra-high energies (UHECR) (e.g., [39]), or to enhance the electron synchrotron emission of large-scale AGN jets (e.g., [88]). In case of ultra-relativistic jet flow velocities () a “one-shot boost” by might occur (crossing and re-crossing the layer), cf. Equation (10). It has been argued that this could be sufficient to boost seed galactic cosmic rays of energy ≲ 1017 eV in blazar-type AGN to ultra-high energies > 1018 e [89,90]
If the particle distribution would remain nearly isotropic near the shear discontinuity, the mean energy for a single crossing is approximately given by (e.g., [1]). This would suggest that the increase in particle energy could be substantial provided the velocity shear is sufficiently relativistic. For non-relativistic velocities (), on the other hand, only the usual energy gain of second order in is obtained. To properly treat relativistic flow speeds () the non-negligible anisotropy of the particle distribution needs to be taken into account. The principal effects of this is a reduction in efficiency. Accordingly, the mean energy gain may be expressed as
where . Monte Carlo particle simulations within the strong scattering limit (i.e., assuming ) suggest that may still be a substantial fraction of unity [56]. One can then define an acceleration timescale , where is the mean time for boundary crossing and , with the particle mean free path ( the gyro-radius) cf. [1]. In the laboratory (ambient medium) rest frame one thus obtains [39,87]
Simulations suggest that for suitable choices (high , small ) might be as small as ∼(1−10) assuming that particles are allowed to escape once they have crossed a boundary at some lateral distance . In general, however, is a sensitive function of , increasing quasi-linearly with increasing [56]. Nevertheless, provided particles with and ( denoting the jet radius) are present, acceleration may proceed fairly quickly.
Observations of pc-scale AGN jets with evidence for a shear layer morphology (e.g., a boundary layer with parallel magnetic fields or limb-brightened structure (e.g., [5,6,7,8,9])) suggest that . Taking pc and G for a semi-quantitative estimate, the condition would require very energetic seed electrons of Lorentz factor and protons of Lorentz factors , respectively. The associated acceleration timescale would be of the order of yrs. Hence, unless the transition layer would be much narrower, the considered mechanism may not work efficiently for electrons given their rapid synchrotron losses. The mechanism is, however, much more favourable for protons (or cosmic rays). Given suitable seed injection (e.g., by gradual shear) cosmic rays may be further accelerated until their gyro-radius rg becomes larger than the width of the jet rj. Note that for non-gradual shear one has tacc ∝ λ, while for gradual shear tacc ∝ 1/λ (Equation (13)).
An application of mildly relativistic (), non-gradual shear acceleration to the possible energization of UHE cosmic rays in the kiloparsec-scale jets of FR I type objects has been recently presented by Kimura et al. [32]. In the considered setup (Figure 9) galactic cosmic rays are swept up by the jet and reaccelerated to UHE energies. Monte Carlo simulations suggests that cosmic rays escaping through the cocoon exhibit a very hard, power-law like spectrum and a cut-off around the maximum energy that is much slower than exponential [32]. The results are somewhat sensitive to the turbulence description in the cocoon (e.g., coherence scale, cocoon size) and the assumed thickness of the transition layer (defining the injection energy threshold of galactic cosmic rays).
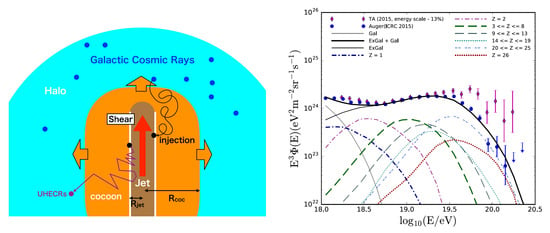
Figure 9.
Left: Cartoon of the considered scenario assuming a recycling of galactic cosmic rays by non-gradual shear acceleration in a jet - (turbulent) cocoon system. Some fraction of galactic cosmic rays are considered to be swept up by the kiloparsec-scale jet and reaccelerated to high energies. The return probability of a particle here is dominated by the scattering (turbulence) properties (i.e., particle mean free path) in the cocoon and not in the jet. Right: Reconstruction of the observed UHECR spectrum assuming mildly relativistic (), non-gradual shear acceleration in an extragalactic jet-cocoon system with a thin transition layer pc ( mG, kpc). The composition at the highest end is dominated by intermediate and heavy nuclei. From Ref. [32].
Enlarging and considering a strongly turbulent layer (see above), for example, is likely to affect the results. Nevertheless, these simulations show that non-gradual shear acceleration in large-scale AGN jets (not necessarily of the FR II type) could in principle play an important role in the (re)acceleration of UHE cosmic rays.
4. Particle Acceleration by Large-Scale Velocity Turbulence
If the turbulence scale of the flow is much larger than the particle mean free path, i.e., , stochastic (non-resonant) particle acceleration could in principle occur due to random compression and rarefaction/decompression of the medium, or due to incompressible large-scale motions. Particle acceleration by large-scale (long-wavelength) compressible velocity turbulence has been studied some time ago (e.g., [91,92,93]), and more recently discussed with respect to the production of supra-thermal ions in the solar wind [94,95]. Interestingly however, particle acceleration may also occur in incompressible (divergence-free, ) velocity turbulence, i.e., by scattering centers (small-scale inhomogeneities) carried by a plasma flow with large-scale velocity fluctuations [92], resulting in what has been referred to as “turbulent shear acceleration” (TSA) [50]. The total energy change for an ensemble of particles will obviously be sensitive to the presumed turbulent velocity field, with different descriptions yielding different efficiencies.
For non-relativistic turbulence (cf. also Ref. [51] for a discussion of relativistic turbulence), one can draw on Equation (19) to describe the ensemble-averaged particle transport. Its space-independent part, or respectively the equation for the spatially and ensemble averaged distribution function f, then reduces to a diffusion equation in momentum space (cf. also Equation (16))
where is the momentum space (TSA) diffusion coefficient. Using Equation (21) and assuming a pure static, homogeneous and isotropic, incompressible velocity turbulence, , , this coefficient can be written as [50]
Here, again denotes the mean scattering time, and k and are the wavenumber and spectrum of the incompressible velocity turbulence. Equation (31) implies that is dominated by small-scale (large k) turbulence whenever is an increasing function of k. Hence for a (3D) Kolmogorov-type spectrum [50], , i.e.,
in the range , turbulent shear acceleration would become relevant towards the smaller scales. The upper limit of the k-integration in Equation (31) should not exceed and hence approximately be given by , where is the maximum wave number of the turbulence, and ( being the turbulence injection scale). For the diffusion coefficient for the noted spectrum thus scales as
while for , or for a mono-chromatic spectrum , one instead obtains . Analytical solutions of Equation (30) for general momentum indices of can be found in, e.g., Ref. [60]. Monte Carlo simulations of the acceleration of particles in static, homogeneous and isotropic incompressible turbulence have been presented by Ohira [50], confirming the general picture. Figure 10 provides an illustration for turbulent shear particle acceleration in mono-chromatic turbulence.
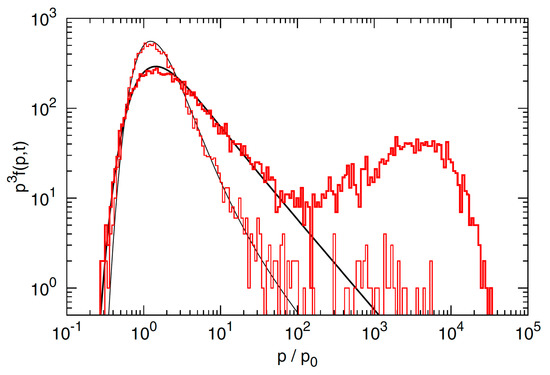
Figure 10.
Particle distribution function for turbulent shear acceleration at two different times assuming static incompressible velocity turbulence with mean amplitude . Red histograms show results of Monte Carlo simulations for a mono-chromatic wave spectrum with , where (i.e., ) has been employed. Thin and thick lines show analytical solutions at times and , respectively. The formation of a power-law tail above injection and below becomes apparent with time. Deviations with regard to the analytical solutions are seen towards higher momenta () where the particle mean free path starts exceeding the turbulence scale . From Ref. [50].
The simulation results are in good agreement with analytical expectations up to , where in the chosen setup the particle mean free path starts to exceed the turbulence scale () and approximations for the analytical treatment no longer apply.
The characteristic acceleration timescale for non-relativistic turbulent shear for the case of (Equation (33)) is of the order of (cf. [50])
Comparing shear particle acceleration in (purely) turbulent flows to the one in non-relativistic laminar flows, i.e., (Equation (17)) and (Equation (33)), roughly yields and suggests that for non-relativistic (!) flow velocities, shear acceleration in large-scale turbulent flows (assumed to be Kolmogorov-type) could be more effective than in laminar shear flows if the relevant shear transition region () is not sufficiently narrow. Note, however, that in reality the situation is more complex as many astrophysical flows exhibit some directionality (i.e., are composed of an underlying bulk velocity plus some turbulent fluctuations), so that an interplay between both effects may occur. An extension to relativistic turbulence still remains to be explored.
5. Concluding Remarks
As described in this review, a variety of (not mutually exclusive) processes may be operative in astrophysical shear flows and facilitate particle transport and energization. Key results include the self-consistent generation of electromagnetic micro-turbulence and supra-thermal particle distributions as well as efficient Fermi-type particle acceleration in relativistic shearing flows. In particular, given sufficient turbulence, the latter processes can lead to a continued acceleration of charged particles, capable of producing power-law particle momentum distributions as long as the velocity shear persists. This offers an interesting explanation for the extended high-energy emission observed in large-scale AGN jets. Similar processes can contribute to the energization of extreme cosmic rays. In general, injection of energetic seed particles (in particular with respect to electrons) and relativistic flow speeds are required for these processes to operate efficiently. In the case of AGN and GRBs the former condition can be met by first-order shock and/or classical second-order Fermi processes. For non-relativistic speeds, on the other hand, turbulent shear acceleration can be more efficient than shear acceleration in quasi laminar flows.
Open issues concerning our understanding of shear particle acceleration include extensions of PIC simulations to 3D and magnetized shear flows, a detailed characterization of the diffusive transport in fast shearing flows along with the reaction effects of accelerated particles, as well as a generalization of turbulent shear to relativistic velocity turbulences. It is hard to see, however, how velocity shear could not play a role in the energization of charged particles. High-resolution studies of astrophysical jets can offer complementary information concerning their internal structure and provide relevant constraints for more detailed applications.
Funding
Funding by a DFG Heisenberg Fellowship RI 1187/6-1 is gratefully acknowledged.
Acknowledgments
It is a pleasure to thank Peter Duffy and Felix Aharonian for collaboration over the years, and Martin Lemoine and Gary Webb for recent discussions on the topic. I also would like to thank Paulo Alves, Edison Liang, Kohta Murase and Yutaka Ohira for permission to use figures from their papers. Useful comments by the anonymous referees are gratefully acknowledged.
Conflicts of Interest
The author declares no conflict of interest.
References
- Rieger, F.M.; Duffy, P. Shear Acceleration in Relativistic Astrophysical Jets. Astrophys. J. 2004, 617, 155–161. [Google Scholar] [CrossRef]
- Martí, J.M. Numerical Simulations of Jets from Active Galactic Nuclei. Galaxies 2019, 7, 24. [Google Scholar] [CrossRef]
- Fendt, C. Approaching the Black Hole by Numerical Simulations. Universe 2019, 5, 99. [Google Scholar] [CrossRef]
- Perucho, M. Dissipative processes and their role in the evolution of radio galaxies. Galaxies 2019, 7, 70. [Google Scholar] [CrossRef]
- Giroletti, M.; Giovannini, G.; Feretti, L.; Cotton, W.D.; Edwards, P.G.; Lara, L.; Marscher, A.P.; Mattox, J.R.; Piner, B.G.; Venturi, T. Parsec-Scale Properties of Markarian 501. Astrophys. J. 2004, 600, 127–140. [Google Scholar] [CrossRef]
- Pushkarev, A.B.; Gabuzda, D.C.; Vetukhnovskaya, Y.N.; Yakimov, V.E. Spine-sheath polarization structures in four active galactic nuclei jets. Mon. Not. R. Astron. Soc. 2005, 356, 859–871. [Google Scholar] [CrossRef]
- Giroletti, M.; Giovannini, G.; Cotton, W.D.; Taylor, G.B.; Pérez-Torres, M.A.; Chiaberge, M.; Edwards, P.G. The jet of Markarian 501 from millions of Schwarzschild radii down to a few hundreds. Astron. Astrophys. 2008, 488, 905–914. [Google Scholar] [CrossRef]
- Blasi, M.G.; Lico, R.; Giroletti, M.; Orienti, M.; Giovannini, G.; Cotton, W.; Edwards, P.G.; Fuhrmann, L.; Krichbaum, T.P.; Kovalev, Y.Y.; et al. The TeV blazar Markarian 421 at the highest spatial resolution. Astron. Astrophys. 2013, 559, A75. [Google Scholar] [CrossRef]
- Piner, B.G.; Edwards, P.G. First-epoch VLBA Imaging of 20 New TeV Blazars. Astrophys. J. 2014, 797, 25. [Google Scholar] [CrossRef]
- Nagai, H.; Haga, T.; Giovannini, G.; Doi, A.; Orienti, M.; D’Ammando, F.; Kino, M.; Nakamura, M.; Asada, K.; Hada, K.; et al. Limb-brightened Jet of 3C 84 Revealed by the 43 GHz Very-Long-Baseline-Array Observation. Astrophys. J. 2014, 785, 53. [Google Scholar] [CrossRef]
- Gabuzda, D.C.; Reichstein, A.R.; O’Neill, E.L. Are spine-sheath polarization structures in the jets of active galactic nuclei associated with helical magnetic fields? Mon. Not. R. Astron. Soc. 2014, 444, 172–184. [Google Scholar] [CrossRef]
- Boccardi, B.; Krichbaum, T.P.; Bach, U.; Mertens, F.; Ros, E.; Alef, W.; Zensus, J.A. The stratified two-sided jet of Cygnus A. Acceleration and collimation. Astron. Astrophys. 2016, 585, A33. [Google Scholar] [CrossRef]
- Hardee, P.E.; Hughes, P.A. The Effect of External Winds on Relativistic Jets. Astrophys. J. 2003, 583, 116–123. [Google Scholar] [CrossRef]
- Meliani, Z.; Keppens, R. Transverse stability of relativistic two-component jets. Astron. Astrophys. 2007, 475, 785–789. [Google Scholar] [CrossRef]
- Meliani, Z.; Keppens, R. Decelerating Relativistic Two-Component Jets. Astrophys. J. 2009, 705, 1594–1606. [Google Scholar] [CrossRef]
- Hardee, P.; Mizuno, Y.; Nishikawa, K.I. GRMHD/RMHD simulations & stability of magnetized spine-sheath relativistic jets. Astrophys. Space Sci. 2007, 311, 281–286. [Google Scholar] [CrossRef]
- Mizuno, Y.; Hardee, P.; Nishikawa, K.I. Three-dimensional Relativistic Magnetohydrodynamic Simulations of Magnetized Spine-Sheath Relativistic Jets. Astrophys. J. 2007, 662, 835–850. [Google Scholar] [CrossRef]
- Mizuno, Y.; Lyubarsky, Y.; Nishikawa, K.I.; Hardee, P.E. Three-dimensional Relativistic Magnetohydrodynamic Simulations of Current-driven Instability. III. Rotating Relativistic Jets. Astrophys. J. 2012, 757, 16. [Google Scholar] [CrossRef]
- Millas, D.; Keppens, R.; Meliani, Z. Rotation and toroidal magnetic field effects on the stability of two-component jets. Mon. Not. R. Astron. Soc. 2017, 470, 592–605. [Google Scholar] [CrossRef]
- Aloy, M.A.; Mimica, P. Observational Effects of Anomalous Boundary Layers in Relativistic Jets. Astrophys. J. 2008, 681, 84–95. [Google Scholar] [CrossRef][Green Version]
- Rieger, F.M.; Aharonian, F.A. Centaurus A as TeV γ-ray and possible UHE cosmic-ray source. Astron. Astrophys. 2009, 506, L41–L44. [Google Scholar] [CrossRef]
- Sahayanathan, S. Boundary shear acceleration in the jet of MKN501. Mon. Not. R. Astron. Soc. 2009, 398, L49–L53. [Google Scholar] [CrossRef]
- Tammi, J.; Duffy, P. Particle-acceleration time-scales in TeV blazar flares. Mon. Not. R. Astron. Soc. 2009, 393, 1063–1069. [Google Scholar] [CrossRef]
- Liang, E.; Boettcher, M.; Smith, I. Magnetic Field Generation and Particle Energization at Relativistic Shear Boundaries in Collisionless Electron-Positron Plasmas. Astrophys. J. Lett. 2013, 766, L19. [Google Scholar] [CrossRef]
- Laing, R.A.; Bridle, A.H. Systematic properties of decelerating relativistic jets in low-luminosity radio galaxies. Mon. Not. R. Astron. Soc. 2014, 437, 3405–3441. [Google Scholar] [CrossRef]
- Tavecchio, F.; Ghisellini, G. On the spine-layer scenario for the very high-energy emission of NGC 1275. Mon. Not. R. Astron. Soc. 2014, 443, 1224–1230. [Google Scholar] [CrossRef]
- Tavecchio, F.; Ghisellini, G. High-energy cosmic neutrinos from spine-sheath BL Lac jets. Mon. Not. R. Astron. Soc. 2015, 451, 1502–1510. [Google Scholar] [CrossRef]
- Rieger, F.M.; Duffy, P. Shear Acceleration in Expanding Flows. Astrophys. J. 2016, 833, 34. [Google Scholar] [CrossRef]
- Liang, E.; Fu, W.; Böttcher, M. Relativistic Shear Flow between Electron-Ion and Electron-Positron Plasmas and Astrophysical Applications. Astrophys. J. 2017, 847, 90. [Google Scholar] [CrossRef]
- Chhotray, A.; Nappo, F.; Ghisellini, G.; Salafia, O.S.; Tavecchio, F.; Lazzati, D. On radiative acceleration in spine-sheath structured blazar jets. Mon. Not. R. Astron. Soc. 2017, 466, 3544–3557. [Google Scholar] [CrossRef][Green Version]
- Liu, R.Y.; Rieger, F.M.; Aharonian, F.A. Particle Acceleration in Mildly Relativistic Shearing Flows: The Interplay of Systematic and Stochastic Effects, and the Origin of the Extended High-energy Emission in AGN Jets. Astrophys. J. 2017, 842, 39. [Google Scholar] [CrossRef]
- Kimura, S.S.; Murase, K.; Zhang, B.T. Ultrahigh-energy cosmic-ray nuclei from black hole jets: Recycling galactic cosmic rays through shear acceleration. Phys. Rev. D 2018, 97, 023026. [Google Scholar] [CrossRef]
- Webb, G.M.; Barghouty, A.F.; Hu, Q.; le Roux, J.A. Particle Acceleration Due to Cosmic-ray Viscosity and Fluid Shear in Astrophysical Jets. Astrophys. J. 2018, 855, 31. [Google Scholar] [CrossRef]
- Worrall, D.M.; Birkinshaw, M. Multiwavelength Evidence of the Physical Processes in Radio Jets. In Physics of Active Galactic Nuclei at all Scales; Alloin, D., Ed.; Lecture Notes in Physics; Springer: Berlin, Germany, 2006; Volume 693, p. 39. [Google Scholar] [CrossRef]
- Harris, D.E.; Krawczynski, H. X-Ray Emission from Extragalactic Jets. Annu. Rev. Astron. Astrophys. 2006, 44, 463–506. [Google Scholar] [CrossRef]
- Rieger, F.M.; Bosch-Ramon, V.; Duffy, P. Fermi acceleration in astrophysical jets. Astrophys. Space Sci. 2007, 309, 119–125. [Google Scholar] [CrossRef]
- Georganopoulos, M.; Meyer, E.; Perlman, E. Recent Progress in Understanding the Large Scale Jets of Powerful Quasars. Galaxies 2016, 4, 65. [Google Scholar] [CrossRef]
- Sun, X.N.; Yang, R.Z.; Rieger, F.M.; Liu, R.Y.; Aharonian, F. Energy distribution of relativistic electrons in the kiloparsec scale jet of M 87 with Chandra. Astron. Astrophys. 2018, 612, A106. [Google Scholar] [CrossRef]
- Ostrowski, M. Acceleration of ultra-high energy cosmic ray particles in relativistic jets in extragalactic radio sources. Astron. Astrophys. 1998, 335, 134–144. [Google Scholar]
- Aharonian, F.A.; Belyanin, A.A.; Derishev, E.V.; Kocharovsky, V.V.; Kocharovsky, V.V. Constraints on the extremely high-energy cosmic ray accelerators from classical electrodynamics. Phys. Rev. D 2002, 66, 023005. [Google Scholar] [CrossRef]
- Kotera, K.; Olinto, A.V. The Astrophysics of Ultrahigh-Energy Cosmic Rays. Annu. Rev. Astron. Astrophys. 2011, 49, 119–153. [Google Scholar] [CrossRef]
- Perucho, M.; Martí, J.M. A numerical simulation of the evolution and fate of a Fanaroff-Riley type I jet. The case of 3C 31. Mon. Not. R. Astron. Soc. 2007, 382, 526–542. [Google Scholar] [CrossRef]
- Rossi, P.; Mignone, A.; Bodo, G.; Massaglia, S.; Ferrari, A. Formation of dynamical structures in relativistic jets: the FRI case. Astron. Astrophys. 2008, 488, 795–806. [Google Scholar] [CrossRef]
- Matthews, J.H.; Bell, A.R.; Blundell, K.M.; Araudo, A.T. Ultrahigh energy cosmic rays from shocks in the lobes of powerful radio galaxies. Mon. Not. R. Astron. Soc. 2019, 482, 4303–4321. [Google Scholar] [CrossRef]
- Perucho, M.; Martí, J.M.; Quilis, V. Long-term FRII jet evolution: clues from three-dimensional simulations. Mon. Not. R. Astron. Soc. 2019, 482, 3718–3735. [Google Scholar] [CrossRef]
- Alves, E.P.; Grismayer, T.; Martins, S.F.; Fiúza, F.; Fonseca, R.A.; Silva, L.O. Large-scale Magnetic Field Generation via the Kinetic Kelvin-Helmholtz Instability in Unmagnetized Scenarios. Astrophys. J. Lett. 2012, 746, L14. [Google Scholar] [CrossRef]
- Liang, E.; Fu, W.; Boettcher, M.; Smith, I.; Roustazadeh, P. Relativistic Positron-Electron-Ion Shear Flows and Application to Gamma-Ray Bursts. Astrophys. J. Lett. 2013, 779, L27. [Google Scholar] [CrossRef]
- Berezhko, E.G.; Krymskii, G.F. A Kinetic Analysis of the Charged Particle Acceleration Process in Collisionless Plasma Shear Flows. Sov. Astron. Lett. 1981, 7, 352. [Google Scholar]
- Earl, J.A.; Jokipii, J.R.; Morfill, G. Cosmic-ray viscosity. Astrophys. J. 1988, 331, L91–L94. [Google Scholar] [CrossRef]
- Ohira, Y. Turbulent Shear Acceleration. Astrophys. J. Lett. 2013, 767, L16. [Google Scholar] [CrossRef]
- Lemoine, M. Generalized Fermi acceleration. Phys. Rev. D 2019, 99, 083006. [Google Scholar] [CrossRef]
- Berezhko, E.G. On Acceleration Possibility of Charged Particles Under Cosmic Plasma Shearing Flows. Int. Cosm. Ray Conf. 1981, 3, 506. [Google Scholar]
- Berezhko, E.G. The Friction Mechanism for Accelerating Particles in Interplanetary Space. Sov. Astron. Lett. 1982, 8, 403–405. [Google Scholar]
- Webb, G.M. The diffusion approximation and transport theory for cosmic rays in relativistic flows. Astrophys. J. 1989, 340, 1112–1123. [Google Scholar] [CrossRef]
- Jokipii, J.R.; Morfill, G.E. Particle acceleration in step function shear flows—A microscopic analysis. Astrophys. J. 1990, 356, 255–258. [Google Scholar] [CrossRef]
- Ostrowski, M. Diffusive acceleration of cosmic ray particles at tangential discontinuity of velocity field. Astron. Astrophys. 1990, 238, 435–438. [Google Scholar]
- Webb, G.M.; Jokipii, J.R.; Morfill, G.E. Green’s formula and variational principles for cosmic-ray transport with application to rotating and shearing flows. Astrophys. J. 1994, 424, 158–180. [Google Scholar] [CrossRef]
- Rieger, F.M.; Mannheim, K. Particle acceleration in rotating and shearing jets from AGN. Astron. Astrophys. 2002, 396, 833–846. [Google Scholar] [CrossRef]
- Rieger, F.M.; Duffy, P. Particle Acceleration in Gamma-Ray Burst Jets. Astrophys. J. Lett. 2005, 632, L21–L24. [Google Scholar] [CrossRef]
- Rieger, F.M.; Duffy, P. A Microscopic Analysis of Shear Acceleration. Astrophys. J. 2006, 652, 1044–1049. [Google Scholar] [CrossRef]
- Dempsey, P.; Rieger, F.M. On Particle Acceleration in Rotating AGN Flows. Int. J. Mod. Phys. D 2009, 18, 1651–1654. [Google Scholar] [CrossRef]
- Alves, E.P.; Grismayer, T.; Fonseca, R.A.; Silva, L.O. Electron-scale shear instabilities: magnetic field generation and particle acceleration in astrophysical jets. New J. Phys. 2014, 16, 035007. [Google Scholar] [CrossRef]
- Alves, E.P.; Grismayer, T.; Fonseca, R.A.; Silva, L.O. Transverse electron-scale instability in relativistic shear flows. Phys. Rev. E 2015, 92, 021101. [Google Scholar] [CrossRef] [PubMed]
- Grismayer, T.; Alves, E.P.; Fonseca, R.A.; Silva, L.O. dc-Magnetic-Field Generation in Unmagnetized Shear Flows. Phys. Rev. Lett. 2013, 111, 015005. [Google Scholar] [CrossRef] [PubMed]
- Liang, E.; Fu, W.; Böttcher, M.; Roustazadeh, P. Scaling of Relativistic Shear Flows with the Bulk Lorentz Factor. Astrophys. J. 2018, 854, 129. [Google Scholar] [CrossRef]
- Nishikawa, K.I.; Hardee, P.E.; Duţan, I.; Niemiec, J.; Medvedev, M.; Mizuno, Y.; Meli, A.; Sol, H.; Zhang, B.; Pohl, M.; et al. Magnetic Field Generation in Core-sheath Jets via the Kinetic Kelvin-Helmholtz Instability. Astrophys. J. 2014, 793, 60. [Google Scholar] [CrossRef]
- Grismayer, T.; Alves, E.P.; Fonseca, R.A.; Silva, L.O. Theory of multidimensional electron-scale instabilities in unmagnetized shear flows. Plasma Phys. Controll. Fusion 2013, 55, 124031. [Google Scholar] [CrossRef]
- Nakamura, T.K.M.; Daughton, W.; Karimabadi, H.; Eriksson, S. Three-dimensional dynamics of vortex-induced reconnection and comparison with THEMIS observations. J. Geophys. Res. (Space Phys.) 2013, 118, 5742–5757. [Google Scholar] [CrossRef]
- Daughton, W.; Nakamura, T.K.M.; Karimabadi, H.; Roytershteyn, V.; Loring, B. Computing the reconnection rate in turbulent kinetic layers by using electron mixing to identify topology. Phys. Plasmas 2014, 21, 052307. [Google Scholar] [CrossRef]
- Nakamura, T.K.M.; Hasegawa, H.; Daughton, W.; Eriksson, S.; Li, W.Y.; Nakamura, R. Turbulent mass transfer caused by vortex induced reconnection in collisionless magnetospheric plasmas. Nat. Commun. 2017, 8, 1582. [Google Scholar] [CrossRef]
- Fermi, E. On the Origin of the Cosmic Radiation. Phys. Rev. 1949, 75, 1169–1174. [Google Scholar] [CrossRef]
- Rieger, F.M. Energetic Particle Acceleration in Shearing Flows. In Proceedings of the 18th International Astrophysics Conference, Pasadena, CA, USA, 18–22 February 2019. IOP Conference Series, to appear. [Google Scholar]
- Sironi, L.; Spitkovsky, A. Relativistic Reconnection: An Efficient Source of Non-thermal Particles. Astrophys. J. Lett. 2014, 783, L21. [Google Scholar] [CrossRef]
- Guo, F.; Liu, Y.H.; Daughton, W.; Li, H. Particle Acceleration and Plasma Dynamics during Magnetic Reconnection in the Magnetically Dominated Regime. Astrophys. J. 2015, 806, 167. [Google Scholar] [CrossRef]
- Zhdankin, V.; Werner, G.R.; Uzdensky, D.A.; Begelman, M.C. Kinetic Turbulence in Relativistic Plasma: From Thermal Bath to Nonthermal Continuum. Phys. Rev. Lett. 2017, 118, 055103. [Google Scholar] [CrossRef] [PubMed]
- Parker, E.N. The passage of energetic charged particles through interplanetary space. Planet. Space Sci. 1965, 13, 9–49. [Google Scholar] [CrossRef]
- Williams, L.L.; Jokipii, J.R. Viscosity and inertia in cosmic-ray transport - Effects of an average magnetic field. Astrophys. J. 1991, 371, 639–647. [Google Scholar] [CrossRef]
- Williams, L.L.; Schwadron, N.; Jokipii, J.R.; Gombosi, T.I. A Unified Transport Equation for Both Cosmic Rays and Thermal Particles. Astrophys. J. Lett. 1993, 405, L79. [Google Scholar] [CrossRef]
- le Roux, J.A.; Zank, G.P.; Webb, G.M.; Khabarova, O. A Kinetic Transport Theory for Particle Acceleration and Transport in Regions of Multiple Contracting and Reconnecting Inertial-scale Flux Ropes. Astrophys. J. 2015, 801, 112. [Google Scholar] [CrossRef]
- le Roux, J.A.; Zank, G.P.; Khabarova, O.V. Self-consistent Energetic Particle Acceleration by Contracting and Reconnecting Small-scale Flux Ropes: The Governing Equations. Astrophys. J. 2018, 864, 158. [Google Scholar] [CrossRef]
- Li, X.; Guo, F.; Li, H.; Birn, J. The Roles of Fluid Compression and Shear in Electron Energization during Magnetic Reconnection. Astrophys. J. 2018, 855, 80. [Google Scholar] [CrossRef]
- Webb, G.M.; Al-Nussirat, S.; Mostafavi, P.; Barghouty, A.F.; Li, G.; le Roux, J.A.; Zank, G.P. Particle Acceleration by Cosmic Ray Viscosity in Radio-jet Shear Flows. Astrophys. J. 2019, 881, 123. [Google Scholar] [CrossRef]
- Pushkarev, A.B.; Kovalev, Y.Y.; Lister, M.L.; Savolainen, T. MOJAVE - XIV. Shapes and opening angles of AGN jets. Mon. Not. R. Astron. Soc. 2017, 468, 4992–5003. [Google Scholar] [CrossRef]
- Kovalev, Y.Y.; Pushkarev, A.B.; Nokhrina, E.E.; Plavin, A.V.; Beskin, V.S.; Chernoglazov, A.; Lister, M.L.; Savolainen, T. Discovery of geometry transition in nearby AGN jets. arXiv 2019, arXiv:1907.01485. [Google Scholar]
- Salafia, O.S.; Ghisellini, G.; Pescalli, A.; Ghirlanda, G.; Nappo, F. Structure of gamma-ray burst jets: intrinsic versus apparent properties. Mon. Not. R. Astron. Soc. 2015, 450, 3549–3558. [Google Scholar] [CrossRef]
- Zhang, B. The Physics of Gamma-Ray Bursts; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar] [CrossRef]
- Ostrowski, M. On possible ‘cosmic ray cocoons’ of relativistic jets. Mon. Not. R. Astron. Soc. 2000, 312, 579–584. [Google Scholar] [CrossRef][Green Version]
- Stawarz, Ł.; Ostrowski, M. Radiation from the Relativistic Jet: A Role of the Shear Boundary Layer. Astrophys. J. 2002, 578, 763–774. [Google Scholar] [CrossRef]
- Caprioli, D. “Espresso” Acceleration of Ultra-high-energy Cosmic Rays. Astrophys. J. Lett. 2015, 811, L38. [Google Scholar] [CrossRef]
- Mbarek, R.; Caprioli, D. Bottom-up Acceleration of Ultra-High-Energy Cosmic Rays in the Jets of Active Galactic Nuclei. arXiv 2019, arXiv:1904.02720. [Google Scholar]
- Bykov, A.M.; Toptygin, I.N. The theory of particle acceleration in astrophysical objects containing shock waves and turbulent plasma motions. J. Geophys. Z. Geophys. 1982, 50, 221–226. [Google Scholar]
- Bykov, A.M.; Toptygin, I.N. Cosmic Rays Acceleration by Large Scale Compressible and Incompressible Motions of Plasma. Int. Cosm. Ray Conf. 1983, 9, 313. [Google Scholar]
- Ptuskin, V.S. The acceleration of cosmic rays by long-wave turbulence. Pisma v Astronomicheskii Zhurnal 1988, 14, 599–605. [Google Scholar]
- Fisk, L.A.; Gloeckler, G. Acceleration of Suprathermal Tails in the Solar Wind. Astrophys. J. 2008, 686, 1466–1473. [Google Scholar] [CrossRef]
- Jokipii, J.R.; Lee, M.A. Compression Acceleration in Astrophysical Plasmas and the Production of f(v) ∝ v−5 Spectra in the Heliosphere. Astrophys. J. 2010, 713, 475–483. [Google Scholar] [CrossRef]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).