Remnants of Galactic Subhalos and Their Impact on Indirect Dark-Matter Searches
Abstract
1. Introduction
2. Semianalytical Model of Galactic Subhalos
2.1. Review of the Stref and Lavalle Model
2.2. Subhalo Disruption?
2.3. Calibration Procedure
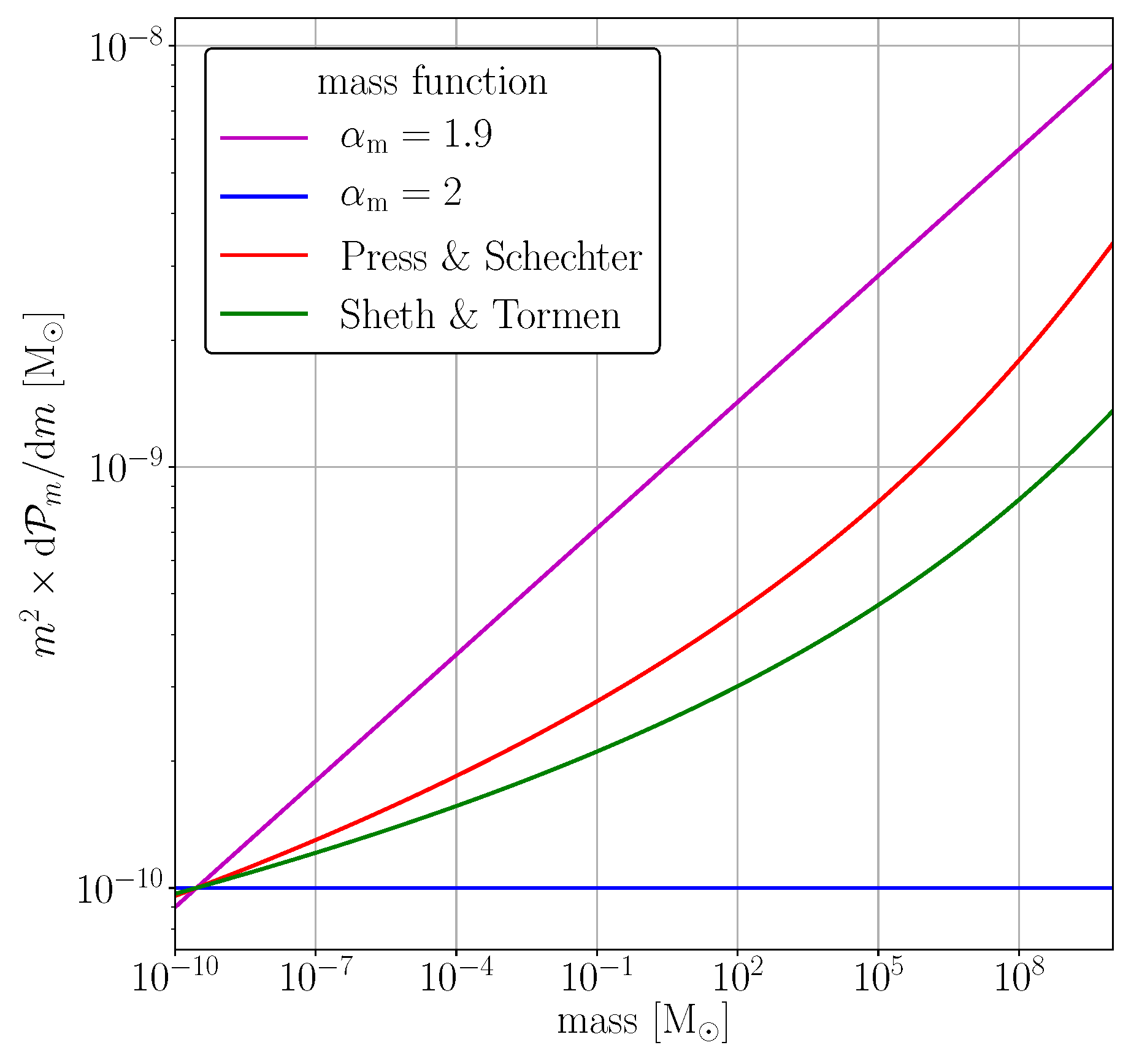
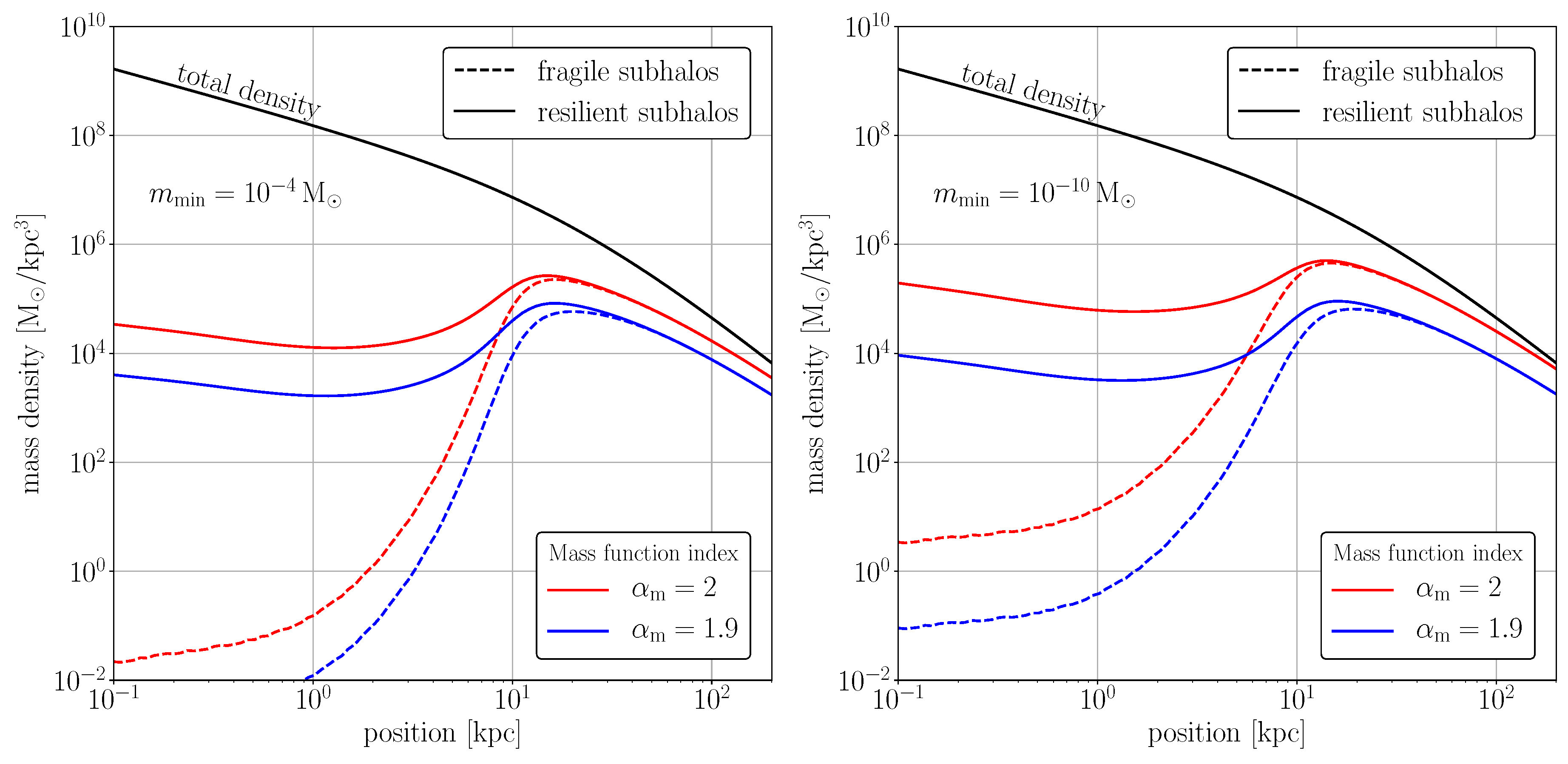
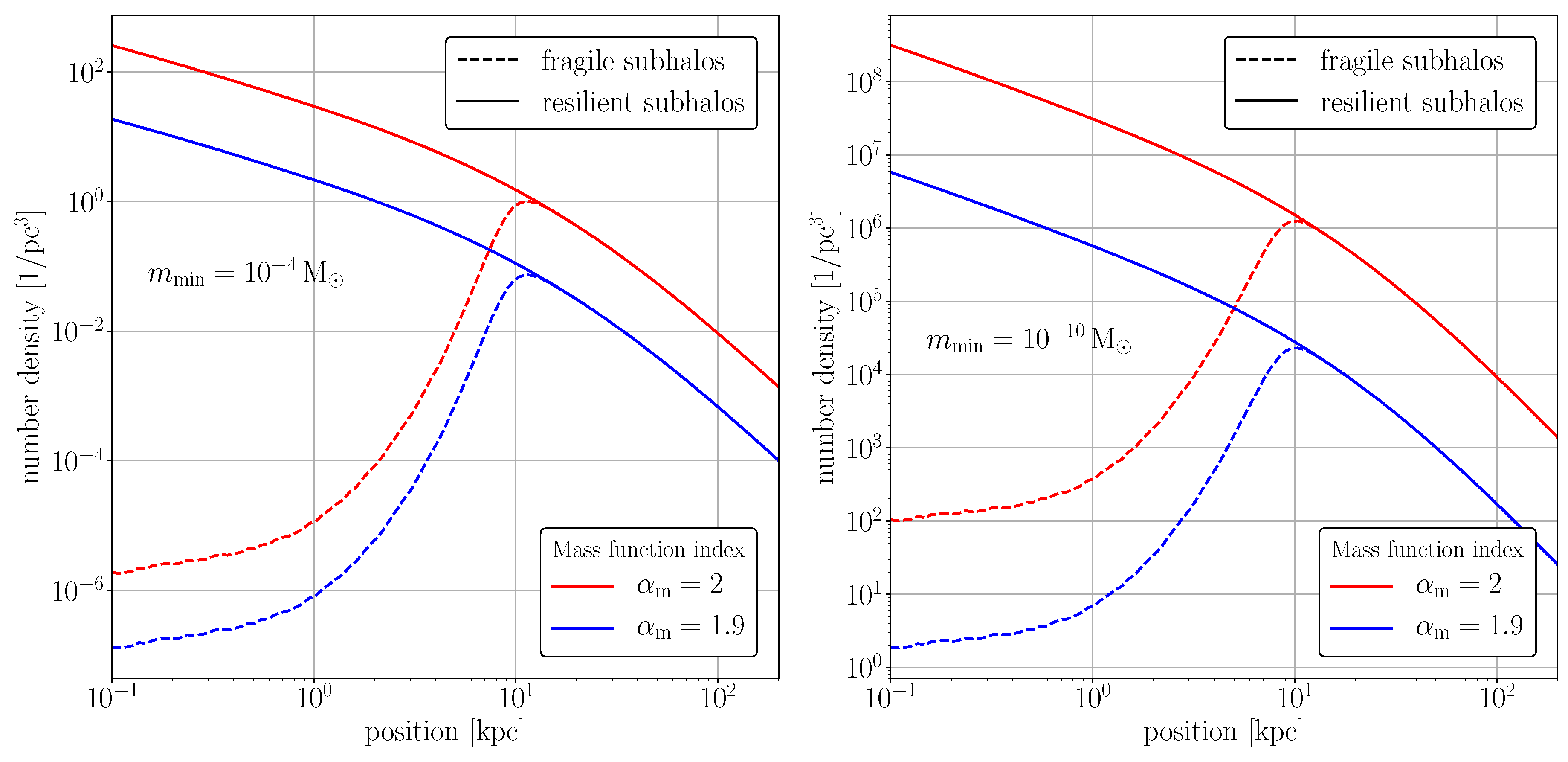
3. Mass and Number Densities of Subhalos
4. Impact on Indirect Searches for Annihilating Dark Matter
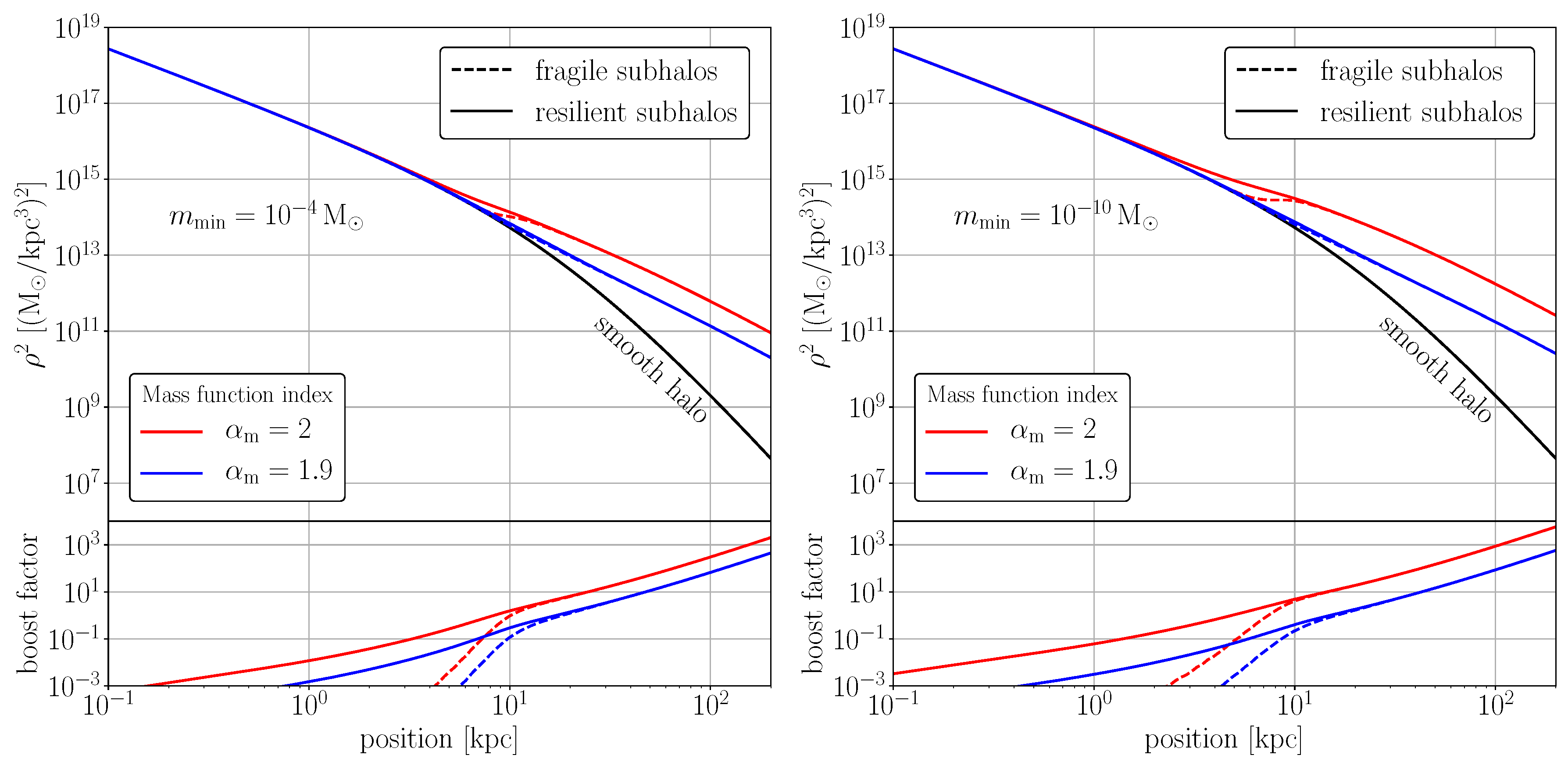
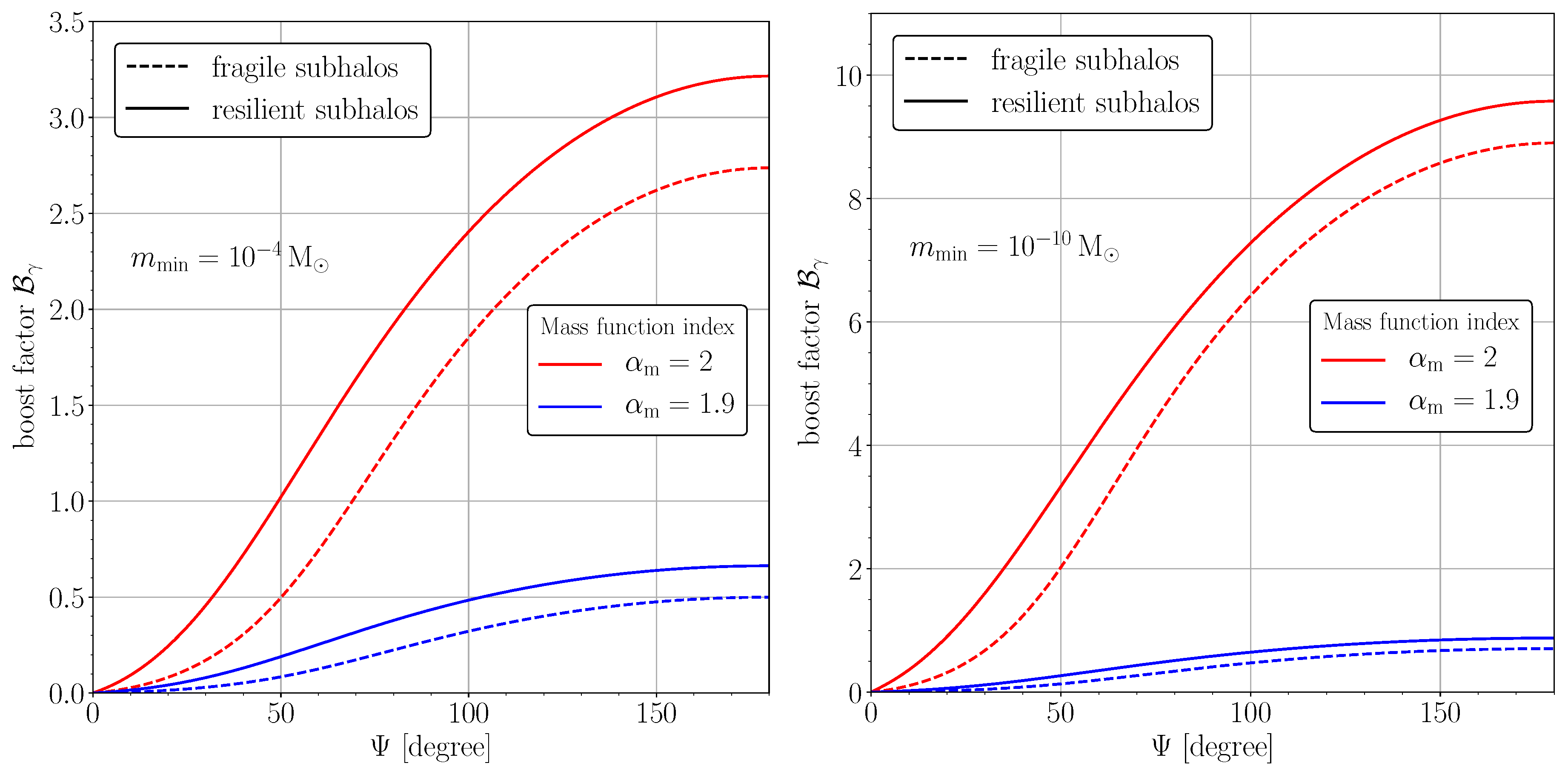
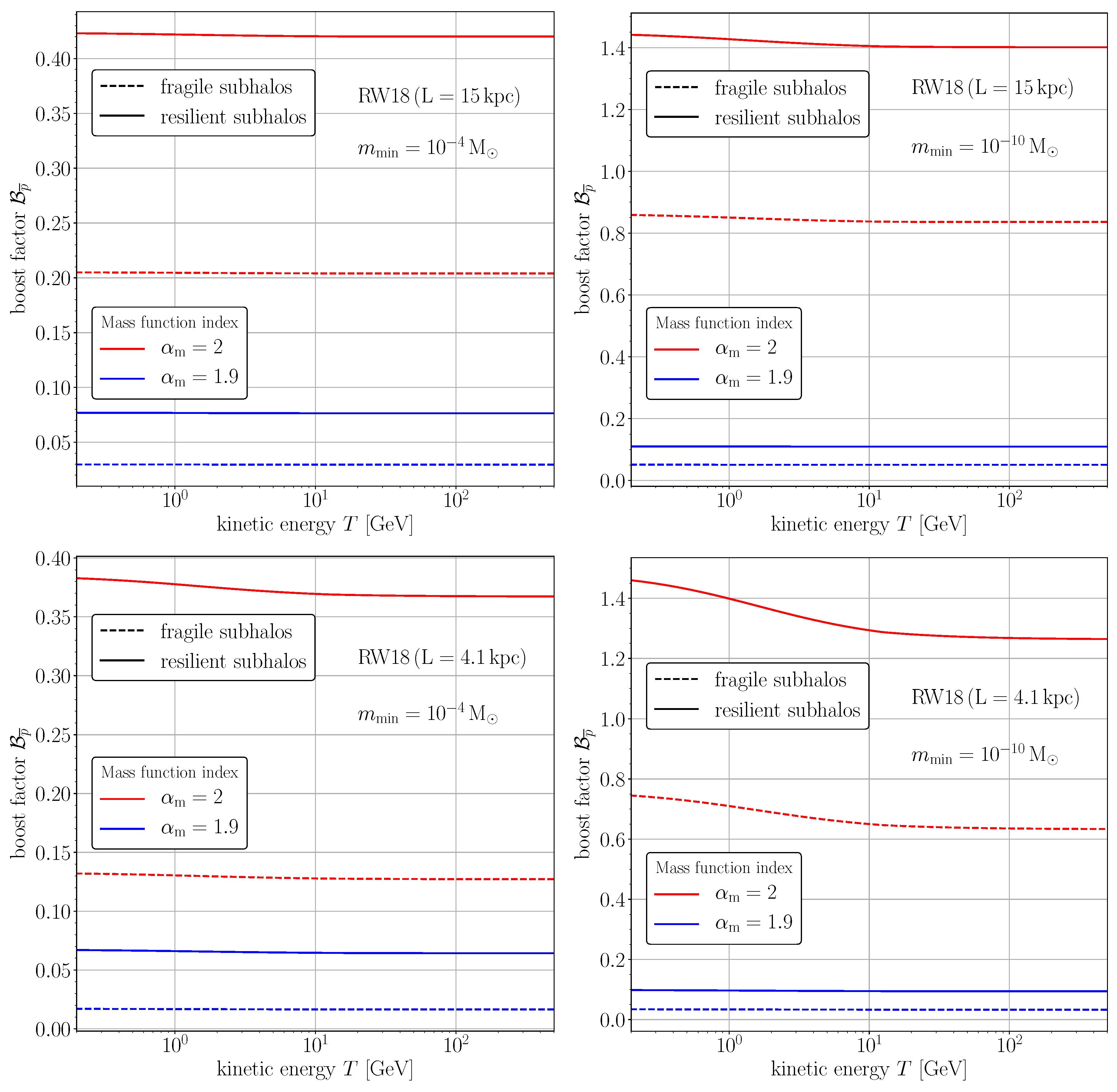
4.1. Annihilation Profiles and Local Boost Factors
4.2. Application to Gamma Rays
4.3. Application to Cosmic-Ray Antiprotons
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. VI. Cosmological parameters. arXiv 2018, arXiv:1807.06209. [Google Scholar]
- Bertone, G.; Hooper, D.; Silk, J. Particle dark matter: Evidence, candidates and constraints. Phys. Rep. 2005, 405, 279–390. [Google Scholar] [CrossRef]
- Feng, J.L. Dark Matter Candidates from Particle Physics and Methods of Detection. Annu. Rev. Astron. Astrophys. 2010, 48, 495–545. [Google Scholar] [CrossRef]
- Fairbairn, M.; Kraan, A.C.; Milstead, D.A.; Sjöstrand, T.; Skands, P.; Sloan, T. Stable massive particles at colliders. Phys. Rep. 2007, 438, 1–63. [Google Scholar] [CrossRef]
- Goodman, J.; Ibe, M.; Rajaraman, A.; Shepherd, W.; Tait, T.M.P.; Yu, H.B. Constraints on Dark Matter from Colliders. Phys. Rev. 2010, D82, 116010. [Google Scholar] [CrossRef]
- Kahlhoefer, F. Review of LHC Dark Matter Searches. Int. J. Mod. Phys. 2017, A32, 1730006. [Google Scholar] [CrossRef]
- Cerdeno, D.G.; Green, A.M. Direct detection of WIMPs. In Particle Dark Matter: Observations, Models and Searches; Cambridge University Press: Cambridge, UK, 2010; pp. 347–369. [Google Scholar]
- Baudis, L. Direct dark matter detection: The next decade. Phys. Dark Univ. 2012, 1, 94–108. [Google Scholar] [CrossRef]
- Freese, K.; Lisanti, M.; Savage, C. Colloquium: Annual modulation of dark matter. Rev. Mod. Phys. 2013, 85, 1561–1581. [Google Scholar] [CrossRef]
- Lavalle, J.; Salati, P. Dark matter indirect signatures. C. R. Phys. 2012, 13, 740–782. [Google Scholar] [CrossRef]
- Gaskins, J.M. A review of indirect searches for particle dark matter. Contemp. Phys. 2016, 57, 496–525. [Google Scholar] [CrossRef]
- Jungman, G.; Kamionkowski, M.; Griest, K. Supersymmetric dark matter. Phys. Rep. 1996, 267, 195–373. [Google Scholar] [CrossRef]
- Servant, G.; Tait, T.M.P. Is the lightest Kaluza-Klein particle a viable dark matter candidate? Nucl. Phys. B 2003, 650, 391–419. [Google Scholar] [CrossRef]
- Agashe, K.; Servant, G. Warped Unification, Proton Stability, and Dark Matter. Phys. Rev. Lett. 2004, 93, 231805. [Google Scholar] [CrossRef]
- Leane, R.K.; Slatyer, T.R.; Beacom, J.F.; Ng, K.C.Y. GeV-scale thermal WIMPs: Not even slightly ruled out. Phys. Rev. 2018, D98, 023016. [Google Scholar] [CrossRef]
- Marsh, D.J.E. Axion Cosmology. Phys. Rep. 2016, 643, 1–79. [Google Scholar] [CrossRef]
- Boyarsky, A.; Ruchayskiy, O.; Shaposhnikov, M. The Role of sterile neutrinos in cosmology and astrophysics. Annu. Rev. Nucl. Part. Sci. 2009, 59, 191–214. [Google Scholar] [CrossRef]
- Carr, B.; Kuhnel, F.; Sandstad, M. Primordial Black Holes as Dark Matter. Phys. Rev. 2016, D94, 083504. [Google Scholar] [CrossRef]
- Alexander, J.; Battaglieri, M.; Echenard, B.; Essig, R.; Graham, M.; Izaguirre, G.; Jaros, J.; Krnjaic, G.; Mardon, J.; Morrissey, D.; et al. Dark Sectors 2016 Workshop: Community Report. arXiv 2016, arXiv:1608.08632. [Google Scholar]
- Blumenthal, G.R.; Faber, S.M.; Primack, J.R.; Rees, M.J. Formation of galaxies and large-scale structure with cold dark matter. Nature 1984, 311, 517–525. [Google Scholar] [CrossRef]
- Davis, M.; Efstathiou, G.; Frenk, C.S.; White, S.D.M. The evolution of large-scale structure in a universe dominated by cold dark matter. Astrophys. J. 1985, 292, 371–394. [Google Scholar] [CrossRef]
- Bullock, J.S.; Boylan-Kolchin, M. Small-Scale Challenges to the ΛCDM Paradigm. Annu. Rev. Astron. Astrophys. 2017, 55, 343–387. [Google Scholar] [CrossRef]
- Tulin, S.; Yu, H.B. Dark Matter Self-interactions and Small Scale Structure. Phys. Rep. 2018, 730, 1–57. [Google Scholar] [CrossRef]
- Pontzen, A.; Governato, F. How supernova feedback turns dark matter cusps into cores. Mon. Not. R. Astron. Soc. 2012, 421, 3464. [Google Scholar] [CrossRef]
- Moore, B.; Ghigna, S.; Governato, F.; Lake, G.; Quinn, T.R.; Stadel, J.; Tozzi, P. Dark matter substructure within galactic halos. Astrophys. J. 1999, 524, L19–L22. [Google Scholar] [CrossRef]
- Diemand, J.; Kuhlen, M.; Madau, P.; Zemp, M.; Moore, B.; Potter, D.; Stadel, J. Clumps and streams in the local dark matter distribution. Nature 2008, 454, 735–738. [Google Scholar] [CrossRef]
- Springel, V.; Wang, J.; Vogelsberger, M.; Ludlow, A.; Jenkins, A.; Helmi, A.; Navarro, J.F.; Frenk, C.S.; White, S.D.M. The Aquarius Project: The subhalos of galactic halos. Mon. Not. R. Astron. Soc. 2008, 391, 1685–1711. [Google Scholar] [CrossRef]
- Springel, V.; White, S.D.M.; Frenk, C.S.; Navarro, J.F.; Jenkins, A.; Vogelsberger, M.; Wang, J.; Ludlow, A.; Helmi, A. Prospects for detecting supersymmetric dark matter in the Galactic halo. Nature 2008, 456, 73–76. [Google Scholar] [CrossRef]
- Berezinsky, V.; Dokuchaev, V.; Eroshenko, Y. Small-scale clumps in the galactic halo and dark matter annihilation. Phys. Rev. 2003, D68, 103003. [Google Scholar] [CrossRef]
- Penarrubia, J.; Benson, A.J. Effects of dynamical evolution on the distribution of substructures. Mon. Not. R. Astron. Soc. 2005, 364, 977–989. [Google Scholar] [CrossRef]
- Lavalle, J.; Yuan, Q.; Maurin, D.; Bi, X.J. Full calculation of clumpiness boost factors for antimatter cosmic rays in the light of ΛCDM N-body simulation results. Abandoning hope in clumpiness enhancement? Astron. Astrophys. 2008, 479, 427–452. [Google Scholar] [CrossRef]
- Bartels, R.; Ando, S. Boosting the annihilation boost: Tidal effects on dark matter subhalos and consistent luminosity modeling. Phys. Rev. 2015, D92, 123508. [Google Scholar] [CrossRef]
- van den Bosch, F.C.; Ogiya, G.; Hahn, O.; Burkert, A. Disruption of Dark Matter Substructure: Fact or Fiction? Mon. Not. R. Astron. Soc. 2018, 474, 3043–3066. [Google Scholar] [CrossRef]
- van den Bosch, F.C.; Ogiya, G. Dark Matter Substructure in Numerical Simulations: A Tale of Discreteness Noise, Runaway Instabilities, and Artificial Disruption. Mon. Not. R. Astron. Soc. 2018, 475, 4066–4087. [Google Scholar] [CrossRef]
- Stref, M.; Lavalle, J. Modeling dark matter subhalos in a constrained galaxy: Global mass and boosted annihilation profiles. Phys. Rev. 2017, D95, 063003. [Google Scholar] [CrossRef]
- McMillan, P.J. The mass distribution and gravitational potential of the Milky Way. Mon. Not. R. Astron. Soc. 2017, 465, 76–94. [Google Scholar] [CrossRef]
- Press, W.H.; Schechter, P. Formation of Galaxies and Clusters of Galaxies by Self-Similar Gravitational Condensation. Astrophys. J. 1974, 187, 425–438. [Google Scholar] [CrossRef]
- Sheth, R.K.; Tormen, G. Large-scale bias and the peak background split. Mon. Not. R. Astron. Soc. 1999, 308, 119–126. [Google Scholar] [CrossRef]
- Bond, J.R.; Cole, S.; Efstathiou, G.; Kaiser, N. Excursion set mass functions for hierarchical Gaussian fluctuations. Astrophys. J. 1991, 379, 440–460. [Google Scholar] [CrossRef]
- Hofmann, S.; Schwarz, D.J.; Stoecker, H. Damping scales of neutralino cold dark matter. Phys. Rev. 2001, D64, 083507. [Google Scholar] [CrossRef]
- Loeb, A.; Zaldarriaga, M. The Small-scale power spectrum of cold dark matter. Phys. Rev. 2005, D71, 103520. [Google Scholar] [CrossRef]
- Green, A.M.; Hofmann, S.; Schwarz, D.J. The First wimpy halos. J. Cosmol. Astropart. Phys. 2005, 0508, 003. [Google Scholar] [CrossRef]
- Bertschinger, E. The Effects of Cold Dark Matter Decoupling and Pair Annihilation on Cosmological Perturbations. Phys. Rev. 2006, D74, 063509. [Google Scholar] [CrossRef]
- Bringmann, T.; Hofmann, S. Thermal decoupling of WIMPs from first principles. J. Cosmol. Astropart. Phys. 2007, 0704, 016. [Google Scholar] [CrossRef]
- Bringmann, T. Particle Models and the Small-Scale Structure of Dark Matter. New J. Phys. 2009, 11, 105027. [Google Scholar] [CrossRef]
- Bullock, J.S.; Kolatt, T.S.; Sigad, Y.; Somerville, R.S.; Kravtsov, A.V.; Klypin, A.A.; Primack, J.R.; Dekel, A. Profiles of dark haloes: Evolution, scatter and environment. Mon. Not. R. Astron. Soc. 2001, 321, 559–575. [Google Scholar] [CrossRef]
- Macciò, A.V.; Dutton, A.A.; van den Bosch, F.C. Concentration, spin and shape of dark matter haloes as a function of the cosmological model: WMAP1, WMAP3 and WMAP5 results. Mon. Not. R. Astron. Soc. 2008, 391, 1940–1954. [Google Scholar] [CrossRef]
- Sánchez-Conde, M.A.; Prada, F. The flattening of the concentration mass relation towards low halo masses and its implications for the annihilation signal boost. Mon. Not. R. Astron. Soc. 2014, 442, 2271–2277. [Google Scholar] [CrossRef]
- Navarro, J.F.; Frenk, C.S.; White, S.D.M. A Universal Density Profile from Hierarchical Clustering. Astrophys. J. 1997, 490, 493–508. [Google Scholar] [CrossRef]
- Einasto, J. On the Construction of a Composite Model for the Galaxy and on the Determination of the System of Galactic Parameters. Trudy Astrofizicheskogo Instituta Alma-Ata 1965, 5, 87–100. [Google Scholar]
- Eisenstein, D.J.; Hu, W. Baryonic features in the matter transfer function. Astrophys. J. 1998, 496, 605. [Google Scholar] [CrossRef]
- Binney, J.; Tremaine, S. Galactic Dynamics; Princeton University Press: Princeton, NJ, USA, 1987. [Google Scholar]
- Drakos, N.E.; Taylor, J.E.; Benson, A.J. The phase-space structure of tidally stripped haloes. Mon. Not. R. Astron. Soc. 2017, 468, 2345–2358. [Google Scholar] [CrossRef]
- Ostriker, J.P.; Spitzer, L., Jr.; Chevalier, R.A. On the Evolution of Globular Clusters. Astrophys. J. Lett. 1972, 176, L51. [Google Scholar] [CrossRef]
- Gnedin, O.Y.; Ostriker, J.P. On the selfconsistent response of stellar systems to gravitational shocks. Astrophys. J. 1999, 513, 626. [Google Scholar] [CrossRef]
- D’Onghia, E.; Springel, V.; Hernquist, L.; Keres, D. Substructure Depletion in the Milky Way Halo by the Disk. Astrophys. J. 2010, 709, 1138–1147. [Google Scholar] [CrossRef]
- Errani, R.; Peñarrubia, J.; Laporte, C.F.P.; Gómez, F.A. The effect of a disc on the population of cuspy and cored dark matter substructures in Milky Way-like galaxies. Mon. Not. R. Astron. Soc. 2017, 465, L59–L63. [Google Scholar] [CrossRef]
- Kelley, T.; Bullock, J.S.; Garrison-Kimmel, S.; Boylan-Kolchin, M.; Pawlowski, M.S.; Graus, A.S. Phat ELVIS: The inevitable effect of the Milky Way’s disk on its dark matter subhaloes. arXiv 2018, arXiv:1811.12413. [Google Scholar]
- Hayashi, E.; Navarro, J.F.; Taylor, J.E.; Stadel, J.; Quinn, T.R. The Structural evolution of substructure. Astrophys. J. 2003, 584, 541–558. [Google Scholar] [CrossRef]
- Goerdt, T.; Gnedin, O.Y.; Moore, B.; Diemand, J.; Stadel, J. The survival and disruption of CDM micro-haloes: Implications for direct and indirect detection experiments. Mon. Not. R. Astron. Soc. 2007, 375, 191–198. [Google Scholar] [CrossRef]
- Berezinsky, V.; Dokuchaev, V.; Eroshenko, Y. Remnants of dark matter clumps. Phys. Rev. 2008, D77, 083519. [Google Scholar] [CrossRef]
- Peñarrubia, J.; Benson, A.J.; Walker, M.G.; Gilmore, G.; McConnachie, A.W.; Mayer, L. The impact of dark matter cusps and cores on the satellite galaxy population around spiral galaxies. Mon. Not. R. Astron. Soc. 2010, 406, 1290–1305. [Google Scholar] [CrossRef]
- van den Bosch, F.C. Dissecting the Evolution of Dark Matter Subhaloes in the Bolshoi Simulation. Mon. Not. R. Astron. Soc. 2017, 468, 885–909. [Google Scholar] [CrossRef]
- Berezinsky, V.; Dokuchaev, V.; Eroshenko, Y. Destruction of small-scale dark matter clumps in the hierarchical structures and galaxies. Phys. Rev. 2006, D73, 063504. [Google Scholar] [CrossRef]
- Zhao, H.; Taylor, J.E.; Silk, J.; Hooper, D. Tidal Disruption of the First Dark Microhalos. Astrophys. J. 2007, 654, 697–701. [Google Scholar] [CrossRef]
- Angus, G.W.; Zhao, H. Analysis of galactic tides and stars on CDM microhalos. Mon. Not. R. Astron. Soc. 2007, 375, 1146–1156. [Google Scholar] [CrossRef][Green Version]
- Green, A.M.; Goodwin, S.P. On mini-halo encounters with stars. Mon. Not. R. Astron. Soc. 2007, 375, 1111–1120. [Google Scholar] [CrossRef]
- Schneider, A.; Krauss, L.; Moore, B. Impact of Dark Matter Microhalos on Signatures for Direct and Indirect Detection. Phys. Rev. 2010, D82, 063525. [Google Scholar] [CrossRef]
- Silk, J.; Stebbins, A. Clumpy cold dark matter. Astrophys. J. 1993, 411, 439–449. [Google Scholar] [CrossRef]
- Bergstrom, L.; Edsjo, J.; Gondolo, P.; Ullio, P. Clumpy neutralino dark matter. Phys. Rev. 1999, D59, 043506. [Google Scholar] [CrossRef]
- Diemand, J.; Kuhlen, M.; Madau, P. Dark matter substructure and gamma-ray annihilation in the Milky Way halo. Astrophys. J. 2007, 657, 262–270. [Google Scholar] [CrossRef]
- Strigari, L.E.; Koushiappas, S.M.; Bullock, J.S.; Kaplinghat, M. Precise constraints on the dark matter content of Milky Way dwarf galaxies for gamma-ray experiments. Phys. Rev. 2007, D75, 083526. [Google Scholar] [CrossRef]
- Pieri, L.; Bertone, G.; Branchini, E. Dark Matter Annihilation in Substructures Revised. Mon. Not. R. Astron. Soc. 2008, 384, 1627. [Google Scholar] [CrossRef]
- Pieri, L.; Lavalle, J.; Bertone, G.; Branchini, E. Implications of high-resolution simulations on indirect dark matter searches. Phys. Rev. D 2011, 83, 023518. [Google Scholar] [CrossRef]
- Blanchet, S.; Lavalle, J. Diffuse gamma-ray constraints on dark matter revisited. I: The impact of subhalos. J. Cosmol. Astropart. Phys. 2012, 1211, 021. [Google Scholar] [CrossRef]
- Ishiyama, T. Hierarchical Formation of Dark Matter Halos and the Free Streaming Scale. Astrophys. J. 2014, 788, 27. [Google Scholar] [CrossRef]
- Moliné, A.; Sánchez-Conde, M.A.; Palomares-Ruiz, S.; Prada, F. Characterization of subhalo structural properties and implications for dark matter annihilation signals. Mon. Not. R. Astron. Soc. 2017, 466, 4974–4990. [Google Scholar] [CrossRef]
- Hiroshima, N.; Ando, S.; Ishiyama, T. Modeling evolution of dark matter substructure and annihilation boost. Phys. Rev. 2018, D97, 123002. [Google Scholar] [CrossRef]
- Chang, L.J.; Lisanti, M.; Mishra-Sharma, S. Search for dark matter annihilation in the Milky Way halo. Phys. Rev. 2018, D98, 123004. [Google Scholar] [CrossRef]
- Maurin, D.; Taillet, R.; Donato, F.; Salati, P.; Barrau, A.; Boudoul, G. Galactic cosmic ray nuclei as a tool for astroparticle physics. arXiv 2002, arXiv:astro-ph/0212111. [Google Scholar]
- Silk, J.; Srednicki, M. Cosmic-ray antiprotons as a probe of a photino-dominated universe. Phys. Rev. Lett. 1984, 53, 624–627. [Google Scholar] [CrossRef]
- Bergström, L.; Edsjö, J.; Ullio, P. Cosmic Antiprotons as a Probe for Supersymmetric Dark Matter? Astrophys. J. 1999, 526, 215–235. [Google Scholar] [CrossRef]
- Donato, F.; Fornengo, N.; Maurin, D.; Salati, P. Antiprotons in cosmic rays from neutralino annihilation. Phys. Rev. 2004, D69, 063501. [Google Scholar] [CrossRef]
- Barrau, A.; Salati, P.; Servant, G.; Donato, F.; Grain, J.; Maurin, D.; Taillet, R. Kaluza-Klein dark matter and Galactic antiprotons. Phys. Rev. 2005, D72, 063507. [Google Scholar] [CrossRef]
- Bringmann, T.; Salati, P. The galactic antiproton spectrum at high energies: Background expectation vs. exotic contributions. Phys. Rev. 2007, D75, 083006. [Google Scholar] [CrossRef]
- Cirelli, M.; Kadastik, M.; Raidal, M.; Strumia, A. Model-independent implications of the e+-, anti-proton cosmic ray spectra on properties of Dark Matter. Nucl. Phys. 2009, B813, 1–21. [Google Scholar] [CrossRef]
- Boudaud, M.; Cirelli, M.; Giesen, G.; Salati, P. A fussy revisitation of antiprotons as a tool for Dark Matter searches. J. Cosmol. Astropart. Phys. 2015, 5, 13. [Google Scholar] [CrossRef]
- Giesen, G.; Boudaud, M.; Génolini, Y.; Poulin, V.; Cirelli, M.; Salati, P.; Serpico, P.D. AMS-02 antiprotons, at last! Secondary astrophysical component and immediate implications for Dark Matter. J. Cosmol. Astropart. Phys. 2015, 1509, 023. [Google Scholar] [CrossRef][Green Version]
- Aguilar, M.; Ali Cavasonza, L.; Alpat, B.; Ambrosi, G.; Arruda, L.; Attig, N.; Aupetit, S.; Azzarello, P.; Bachlechner, A.; Barao, F.; et al. Antiproton Flux, Antiproton-to-Proton Flux Ratio, and Properties of Elementary Particle Fluxes in Primary Cosmic Rays Measured with the Alpha Magnetic Spectrometer on the International Space Station. Phys. Rev. Lett. 2016, 117, 091103. [Google Scholar] [CrossRef]
- Cuoco, A.; Krämer, M.; Korsmeier, M. Novel Dark Matter Constraints from Antiprotons in Light of AMS-02. Phys. Rev. Lett. 2017, 118, 191102. [Google Scholar] [CrossRef]
- Cui, M.Y.; Yuan, Q.; Tsai, Y.L.S.; Fan, Y.Z. Possible dark matter annihilation signal in the AMS-02 antiproton data. Phys. Rev. Lett. 2017, 118, 191101. [Google Scholar] [CrossRef]
- Reinert, A.; Winkler, M.W. A Precision Search for WIMPs with Charged Cosmic Rays. J. Cosmol. Astropart. Phys. 2018, 1801, 055. [Google Scholar] [CrossRef]
- Cui, M.Y.; Pan, X.; Yuan, Q.; Fan, Y.Z.; Zong, H.S. Revisit of cosmic ray antiprotons from dark matter annihilation with updated constraints on the background model from AMS-02 and collider data. J. Cosmol. Astropart. Phys. 2018, 1806, 024. [Google Scholar] [CrossRef]
- Cuoco, A.; Heisig, J.; Klamt, L.; Korsmeier, M.; Krämer, M. Scrutinizing the evidence for dark matter in cosmic-ray antiprotons. arXiv 2019, arXiv:1903.01472. [Google Scholar] [CrossRef]
- Cholis, I.; Linden, T.; Hooper, D. A Robust Excess in the Cosmic-Ray Antiproton Spectrum: Implications for Annihilating Dark Matter. arXiv 2019, arXiv:1903.02549. [Google Scholar] [CrossRef]
- Lavalle, J.; Pochon, J.; Salati, P.; Taillet, R. Clumpiness of dark matter and positron annihilation signal: Computing the odds of the galactic lottery. Astron. Astrophys. 2007, 462, 827–848. [Google Scholar] [CrossRef][Green Version]
- Strong, A.W.; Moskalenko, I.V. Propagation of cosmic-ray nucleons in the galaxy. Astrophys. J. 1998, 509, 212–228. [Google Scholar] [CrossRef]
- Lavalle, J.; Maurin, D.; Putze, A. Direct constraints on diffusion models from cosmic-ray positron data: Excluding the minimal model for dark matter searches. Phys. Rev. 2014, D90, 081301. [Google Scholar] [CrossRef]
- Hütten, M.; Stref, M.; Combet, C.; Lavalle, J.; Maurin, D. γ-ray and ν searches for dark matter subhalos in the Milky Way with a baryonic potential. arXiv 2019, arXiv:1904.10935. [Google Scholar] [CrossRef]
| 1. | We refer to this model as semianalytical because it involves integrals that must be computed numerically. The model does not rely on numerical simulations except at the level of a calibration described in Section 2.3. |
| 2. | This differs by one unit from the definition used in Reference [35]. |
| 3. | The expression of should be multiplied by if the DM particle is not its own antiparticle. |
| 4. | If DM is not its own antiparticle, Q should be divided by 2. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stref, M.; Lacroix, T.; Lavalle, J. Remnants of Galactic Subhalos and Their Impact on Indirect Dark-Matter Searches. Galaxies 2019, 7, 65. https://doi.org/10.3390/galaxies7020065
Stref M, Lacroix T, Lavalle J. Remnants of Galactic Subhalos and Their Impact on Indirect Dark-Matter Searches. Galaxies. 2019; 7(2):65. https://doi.org/10.3390/galaxies7020065
Chicago/Turabian StyleStref, Martin, Thomas Lacroix, and Julien Lavalle. 2019. "Remnants of Galactic Subhalos and Their Impact on Indirect Dark-Matter Searches" Galaxies 7, no. 2: 65. https://doi.org/10.3390/galaxies7020065
APA StyleStref, M., Lacroix, T., & Lavalle, J. (2019). Remnants of Galactic Subhalos and Their Impact on Indirect Dark-Matter Searches. Galaxies, 7(2), 65. https://doi.org/10.3390/galaxies7020065





