γ-ray and ν Searches for Dark-Matter Subhalos in the Milky Way with a Baryonic Potential
Abstract
1. Introduction
2. Important Quantities and Methodology
2.1. -ray and Fluxes from Dark Matter
2.2. Generating Skymaps with CLUMPY v3.0
- CLUMPYand the particle physics term: Equation (1) shows that the particle physics term and the astrophysical terms are decoupled.4 As the flux depends on the specific DM candidate chosen, we provide results in terms of J- and D-factors only; CLUMPY can easily be used to transform those into -ray or fluxes for any user-defined DM candidate (see CLUMPY’s online documentation5).
- CLUMPYand the astrophysics term: to calculate skymaps of , one should rely in principle on Equation (2). However, this is impractical in terms of computing time, as ∼ subhalos are expected in a Milky Way-sized DM halo. This problem can be overcome by formally separating Equation (2) in an average and “resolved” component,With this ansatz, only a limited number of subhalos need to have their J-factor profiles calculated individually, while an average description is sought for the remaining “unresolved” DM. The criterion to discriminate between resolved and unresolved components often relies on a simple subhalo mass threshold, e.g., as done in works directly relying on numerical simulations [57] or their subhalo catalogs [58]. CLUMPY has been developed to treat this problem in a more efficient way, acknowledging the fact that rather light, but close-by subhalos may show J-factors comparable to heavier, more distant objects. The CLUMPY approach relies on the notion that the overall DM signal fluctuates around an average description, , and we refer to [4] for a detailed description of our criterion to accordingly discriminate between unresolved and resolved halos. For the purpose of this work (and also the previous [1]), this approach allows us to preselect halos likely to shine bright at Earth and to consider all decades down to the smallest subhalo masses in the calculation.
3. Modeling the Galactic Subhalo Distribution
3.1. Fixed Subhalo-Related Quantities
- Index of the power-law subhalo mass PDF and subhalo mass range: We choose , , and . The maximum clump mass for all models is set to of the NFW halo from Section 3.2.3. This is motivated by the fact that we do not consider the possibility of any subhalos heavier than the Magellanic clouds, the heaviest satellites of our galaxy. The minimal clump mass and mostly affect the diffuse emission boost from unresolved halos. For a fixed normalization , a steeper mass function () decreases the number of bright halos () by not more than ∼30%.
- Subhalo density profile: We model all subhalos with a spherically symmetric NFW profile [65]. Using an Einasto profile [65,66] instead amounts to a global increase ∼2 of the number of subhalos per flux decade within the considered integration regions . Please note that micro-halos with may show steeper inner slopes [67,68,69]; however, we have found that these micro-halos do not provide new bright, resolved subhalo candidates [1].
- Level of sub-substructures: We do not consider an emission boost from substructure within subhalos. Such a boost from additional levels of substructure8 increases the number of subhalos per flux decade, with the largest increase of almost a factor 2 for the largest luminosities. Sub-substructures actually increase the signal in the outskirts of halos (see Figure 4 of [1]), the impact of which depends on the instrument angular resolution or containment angle used in the analysis. For instance, in [1], no impact was found for dark clumps within the angular resolution of CTA.
3.2. The Spatial Distribution of Subhalos
3.2.1. Model #1: DM only (as Implemented in Hütten et al., 2016)
3.2.2. Model #2: DM + Galactic Disk Potential (Numerical, Phat-ELVIS)
3.2.3. Models #3 and #4: DM + Disk Potential (Semi-Analytical, SL17)
3.2.4. Model Comparison
4. Results
4.1. Subhalo Source Count Distributions
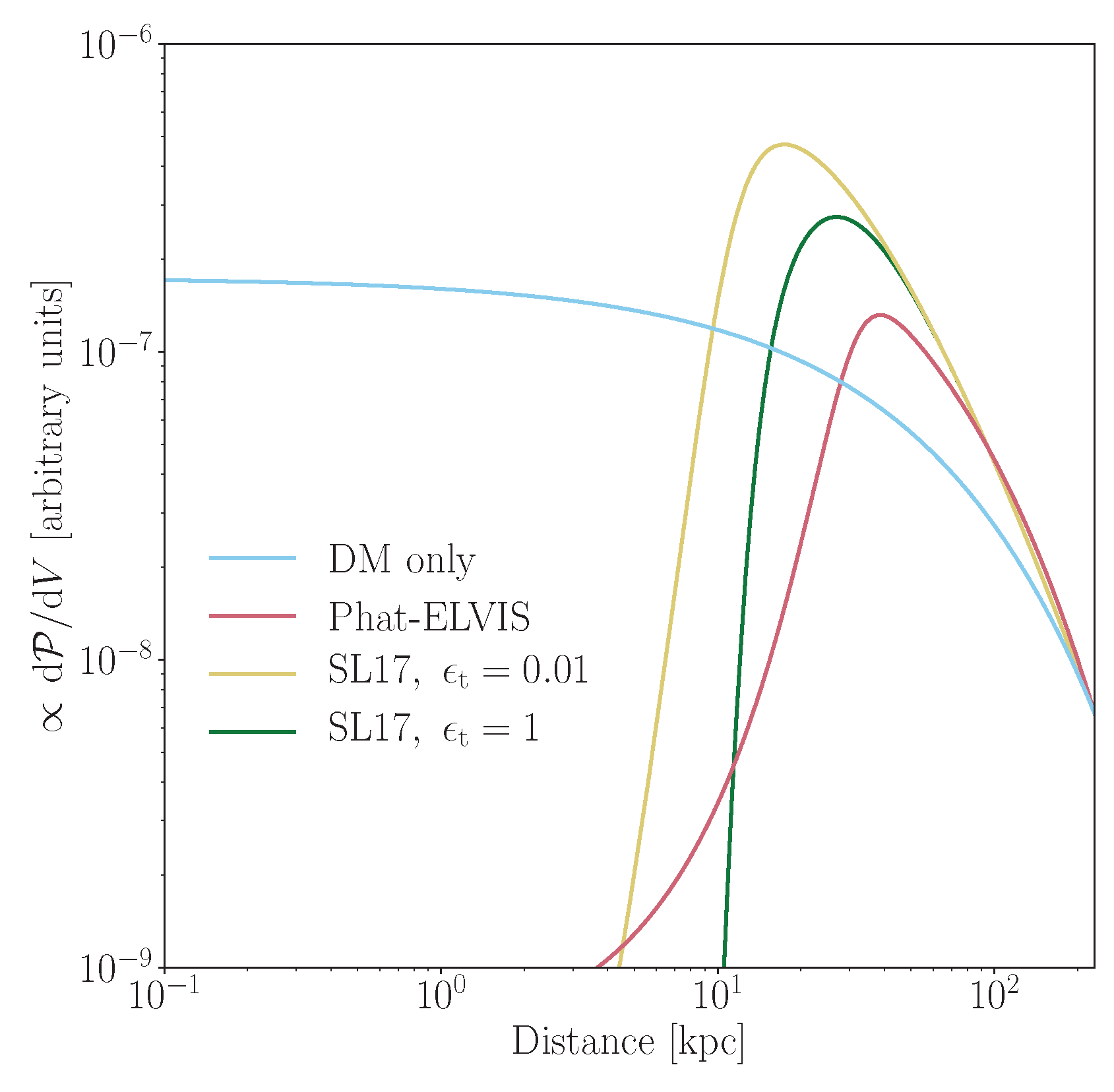
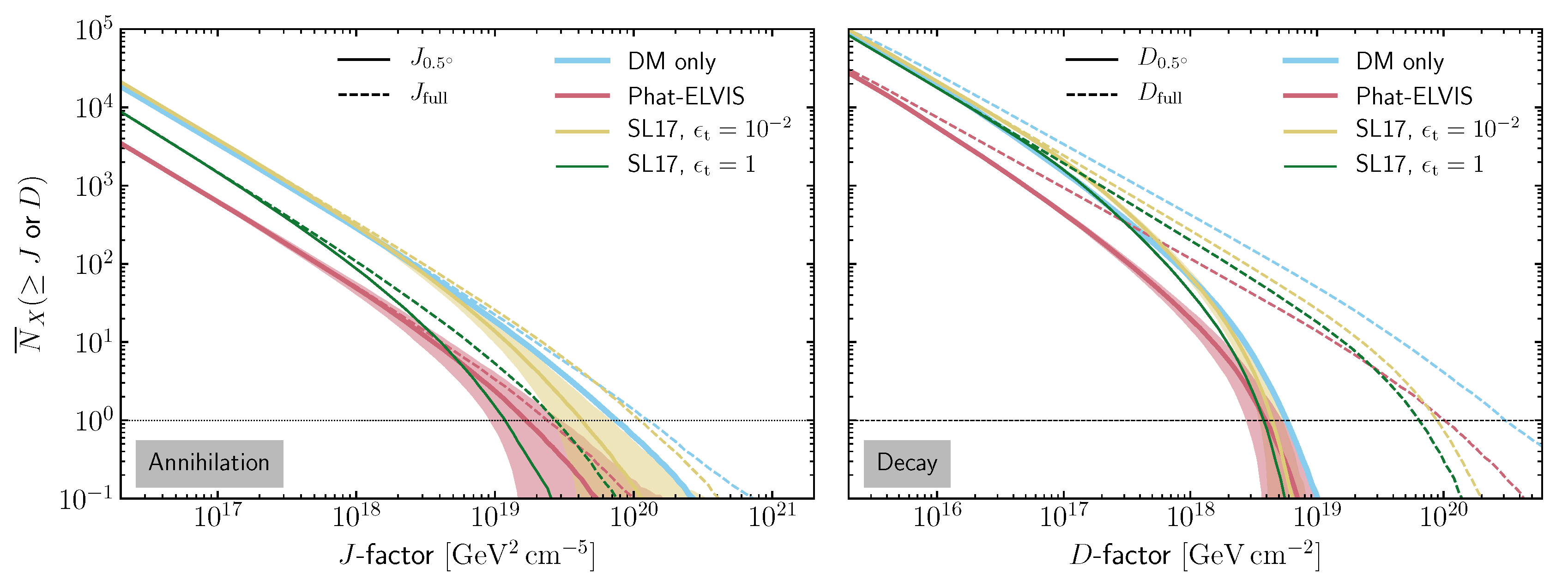
- Model #2 (Phat-ELVIS, red lines) predicts about a factor 5 less halos per flux decade than the Aquarius-like DM-only reference model #1. The average brightest halo (within ) is about a factor 4 fainter than expected for the DM-only case. This drastic decrease of bright objects is both attributed to the fact that the Phat-ELVIS simulations [10] find (i) overall less subhalos in Milky Way-like galactic halos ( vs. ) and (ii), no subhalos are found close to Earth in the innermost 30 kpc of the galactic halo.
- Model #3 (SL17, yellow lines) predicts almost the same abundance of bright halos as the DM-only model #1. Model #3 starts from an initial subhalo distribution biased towards the Galactic center following the overall DM distribution, and accounts for tidal subhalo disruption and stripping afterwards according to the semi-analytical model of [15]. With few subhalos are affected. In turn, the DM-only model #1 already includes a subhalo distribution anti-biased towards the Galactic center in an evolved galactic halo according to the Aquarius simulations (although the considered fitting to the Aquarius simulations [74] does not account for a mass dependence of the halo depletion).
- Model #4 (SL17, green lines) applies a much stronger condition on tidal stripping and total depletion than the model #3 configuration within the semi-analytical approach of [15]. Illustratively, we calculate a total of initial subhalos (in the full range between and ) for the subhalo models #3 and #4, out of which 20,000 are completely disrupted for the model #3 (). In contrast, 530,000 halos are disrupted for in the model #4.13 In result, a factor 2 less halos are present above the lower end of the displayed brightness distributions, the ratio increasing for the brightest decades. Recall that surviving halos are truncated at the same tidal radius in models #3 and #4.
- Changing the signal integration region drastically impacts the collected signal, as the emission shows a much broader profile than for annihilation. This loss is most drastic for the brightest halos.
- For an integration angle of , all models are in remarkable agreement at the brightest end. For fainter flux decades and considering the signal over the full halos extent, models differ by a factor ∼5 (however, with a rather large spread in the D-factor PDF of the brightest halo in the individual models, see the later Figure 5). This suggests that predictions for the largest subhalo flux from decaying DM should be rather model-independent.
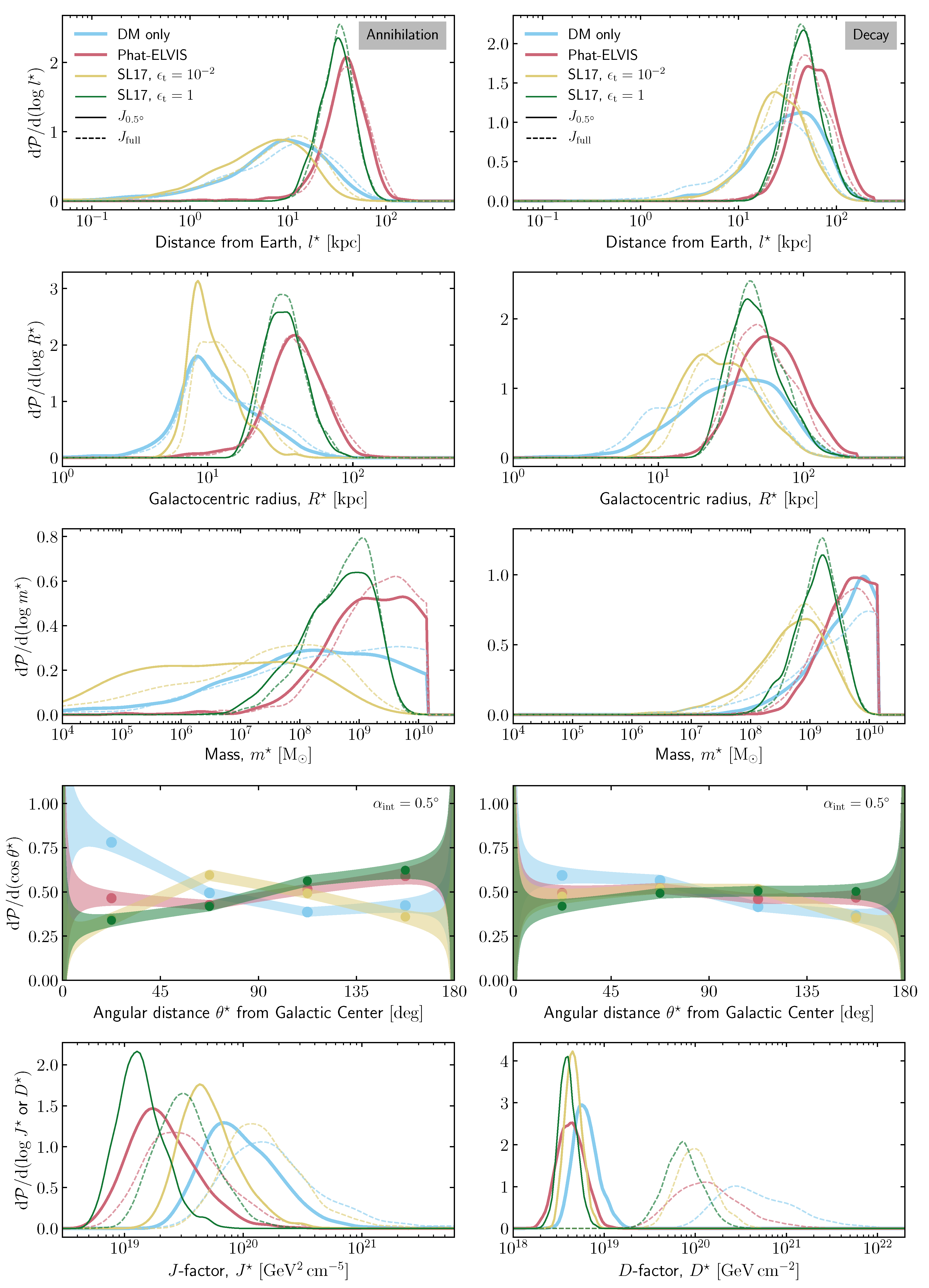
4.2. Statistical Properties of the Brightest Halo
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Properties of the Brightest Subhalos in the Example Maps
| Position in Map | Distance | Mass | |||||
|---|---|---|---|---|---|---|---|
| DM only | |||||||
| Phat-ELVIS | |||||||
| SL17, | |||||||
| SL17, | |||||||
References
- Hütten, M.; Combet, C.; Maier, G.; Maurin, D. Dark matter substructure modelling and sensitivity of the Cherenkov Telescope Array to Galactic dark halos. J. Cosmol. Astropart. Phys. 2016, 9, 047. [Google Scholar] [CrossRef]
- Profumo, S.; Sigurdson, K.; Kamionkowski, M. What Mass Are the Smallest Protohalos? Phys. Rev. Lett. 2006, 97, 031301. [Google Scholar] [CrossRef] [PubMed]
- Bringmann, T. Particle models and the small-scale structure of dark matter. New J. Phys. 2009, 11, 105027. [Google Scholar] [CrossRef]
- Charbonnier, A.; Combet, C.; Maurin, D. CLUMPY: A code for γ-ray signals from dark matter structures. Comput. Phys. Commun. 2012, 183, 656–668. [Google Scholar] [CrossRef]
- Bonnivard, V.; Hütten, M.; Nezri, E.; Charbonnier, A.; Combet, C.; Maurin, D. CLUMPY: Jeans analysis, γ-ray and ν fluxes from dark matter (sub-)structures. Comput. Phys. Commun. 2016, 200, 336–349. [Google Scholar] [CrossRef]
- Hütten, M.; Combet, C.; Maurin, D. CLUMPY v3: γ-ray and ν signals from dark matter at all scales. Comput. Phys. Commun. 2019, 235, 336–345. [Google Scholar] [CrossRef]
- Acharya, B.S.; Actis, M.; Aghajani, T.; Agnetta, G.; Aguilar, J.; Aharonian, F.; Ajello, M.; Akhperjanian, A.; Alcubierre, M.; Aleksić, J.; et al. Introducing the CTA concept. Astropart. Phys. 2013, 43, 3–18. [Google Scholar] [CrossRef]
- D’Onghia, E.; Springel, V.; Hernquist, L.; Keres, D. Substructure Depletion in the Milky Way Halo by the Disk. Astrophys. J. 2010, 709, 1138–1147. [Google Scholar] [CrossRef]
- Zhu, Q.; Marinacci, F.; Maji, M.; Li, Y.; Springel, V.; Hernquist, L. Baryonic impact on the dark matter distribution in Milky Way-sized galaxies and their satellites. Mon. Not. R. Astron. Soc. 2016, 458, 1559–1580. [Google Scholar] [CrossRef]
- Kelley, T.; Bullock, J.S.; Garrison-Kimmel, S.; Boylan-Kolchin, M.; Pawlowski, M.S.; Graus, A.S. Phat ELVIS: The inevitable effect of the Milky Way’s disk on its dark matter subhaloes. arXiv 2018, arXiv:1811.12413. [Google Scholar] [CrossRef]
- Green, A.M.; Goodwin, S.P. On mini-halo encounters with stars. Mon. Not. R. Astron. Soc. 2007, 375, 1111–1120. [Google Scholar] [CrossRef]
- Goerdt, T.; Gnedin, O.Y.; Moore, B.; Diemand, J.; Stadel, J. The survival and disruption of cold dark matter microhaloes: Implications for direct and indirect detection experiments. Mon. Not. R. Astron. Soc. 2007, 375, 191–198. [Google Scholar] [CrossRef]
- Berezinsky, V.; Dokuchaev, V.; Eroshenko, Y. Remnants of dark matter clumps. Phys. Rev. D 2008, 77, 083519. [Google Scholar] [CrossRef]
- Berezinsky, V.S.; Dokuchaev, V.I.; Eroshenko, Y.N. Small-scale clumps of dark matter. Phys. Uspekhi 2014, 57, 1–36. [Google Scholar] [CrossRef]
- Stref, M.; Lavalle, J. Modeling dark matter subhalos in a constrained galaxy: Global mass and boosted annihilation profiles. Phys. Rev. D 2017, 95, 063003. [Google Scholar] [CrossRef]
- Berlin, A.; Hooper, D. Stringent constraints on the dark matter annihilation cross section from subhalo searches with the Fermi Gamma-Ray Space Telescope. Phys. Rev. D 2014, 89, 016014. [Google Scholar] [CrossRef]
- Bertoni, B.; Hooper, D.; Linden, T. Examining The Fermi-LAT Third Source Catalog in search of dark matter subhalos. J. Cosmol. Astropart. Phys. 2015, 12, 035. [Google Scholar] [CrossRef]
- Schoonenberg, D.; Gaskins, J.; Bertone, G.; Diemand, J. Dark matter subhalos and unidentified sources in the Fermi 3FGL source catalog. J. Cosmol. Astropart. Phys. 2016, 5, 028. [Google Scholar] [CrossRef]
- Mirabal, N.; Charles, E.; Ferrara, E.C.; Gonthier, P.L.; Harding, A.K.; Sánchez-Conde, M.A.; Thompson, D.J. 3FGL Demographics Outside the Galactic Plane using Supervised Machine Learning: Pulsar and Dark Matter Subhalo Interpretations. Astrophys. J. 2016, 825, 69. [Google Scholar] [CrossRef]
- Bertoni, B.; Hooper, D.; Linden, T. Is the gamma-ray source 3FGL J2212.5+0703 a dark matter subhalo? J. Cosmol. Astropart. Phys. 2016, 5, 049. [Google Scholar] [CrossRef]
- Wang, Y.P.; Duan, K.K.; Ma, P.X.; Liang, Y.F.; Shen, Z.Q.; Li, S.; Yue, C.; Yuan, Q.; Zang, J.J.; Fan, Y.Z.; et al. Testing the dark matter subhalo hypothesis of the gamma-ray source 3FGL J 2212.5 +0703. Phys. Rev. D 2016, 94, 123002. [Google Scholar] [CrossRef]
- Liang, Y.F.; Xia, Z.Q.; Duan, K.K.; Shen, Z.Q.; Li, X.; Fan, Y.Z. Limits on dark matter annihilation cross sections to gamma-ray lines with subhalo distributions in N-body simulations and Fermi LAT data. Phys. Rev. D 2017, 95, 063531. [Google Scholar] [CrossRef]
- Calore, F.; De Romeri, V.; Di Mauro, M.; Donato, F.; Marinacci, F. Realistic estimation for the detectability of dark matter subhalos using Fermi-LAT catalogs. Phys. Rev. D 2017, 96, 063009. [Google Scholar] [CrossRef]
- Hooper, D.; Witte, S.J. Gamma rays from dark matter subhalos revisited: Refining the predictions and constraints. J. Cosmol. Astropart. Phys. 2017, 4, 018. [Google Scholar] [CrossRef]
- Charles, E.; Sánchez-Conde, M.; Anderson, B.; Caputo, R.; Cuoco, A.; Di Mauro, M.; Drlica-Wagner, A.; Gomez-Vargas, G.A.; Meyer, M.; Tibaldo, L.; et al. Sensitivity projections for dark matter searches with the Fermi large area telescope. Phys. Rep. 2016, 636, 1–46. [Google Scholar] [CrossRef]
- Harding, J.P.; Dingus, B. Dark Matter Annihilation and Decay Searches with the High Altitude Water Cherenkov (HAWC) Observatory. In Proceedings of the 34th International Cosmic Ray Conference (ICRC2015), The Hague, The Netherlands, 30 July–6 August 2015; Volume 34, p. 1227. [Google Scholar]
- Abeysekara, A.U.; Albert, A.; Alfaro, R.; Alvarez, C.; Arceo, R.; Arteaga-Velázquez, J.C.; Rojas, D.A.; Solares, H.A.; Belmont-Moreno, E.; BenZvi, S.Y.; et al. Searching for Dark Matter Sub-structure with HAWC. arXiv 2018, arXiv:1811.11732. [Google Scholar]
- Egorov, A.E.; Galper, A.M.; Topchiev, N.P.; Leonov, A.A.; Suchkov, S.I.; Kheymits, M.D.; Yurkin, Y.T. Detactability of Dark Matter Subhalos by Means of the GAMMA-400 Telescope. Phys. Atom. Nuclei 2018, 81, 373–378. [Google Scholar] [CrossRef]
- Brun, P.; Moulin, E.; Diemand, J.; Glicenstein, J.F. Searches for dark matter subhaloes with wide-field Cherenkov telescope surveys. Phys. Rev. D 2011, 83, 015003. [Google Scholar] [CrossRef]
- Gunn, J.E.; Lee, B.W.; Lerche, I.; Schramm, D.N.; Steigman, G. Some astrophysical consequences of the existence of a heavy stable neutral lepton. Astrophys. J. 1978, 223, 1015–1031. [Google Scholar] [CrossRef]
- Lake, G. Detectability of gamma-rays from clumps of dark matter. Nature 1990, 346, 39–40. [Google Scholar] [CrossRef]
- Silk, J.; Stebbins, A. Clumpy cold dark matter. Astrophys. J. 1993, 411, 439–449. [Google Scholar] [CrossRef]
- Berezinsky, V.; Masiero, A.; Valle, J.W.F. Cosmological signatures of supersymmetry with spontaneously broken R parity. Phys. Lett. B 1991, 266, 382–388. [Google Scholar] [CrossRef]
- Bertone, G.; Buchmüller, W.; Covi, L.; Ibarra, A. Gamma-rays from decaying dark matter. J. Cosmol. Astropart. Phys. 2007, 11, 3. [Google Scholar] [CrossRef]
- Bergström, L.; Ullio, P.; Buckley, J.H. Observability of γ rays from dark matter neutralino annihilations in the Milky Way halo. Astropart. Phys. 1998, 9, 137–162. [Google Scholar] [CrossRef]
- Press, W.H.; Schechter, P. Formation of Galaxies and Clusters of Galaxies by Self-Similar Gravitational Condensation. Astrophys. J. 1974, 187, 425–438. [Google Scholar] [CrossRef]
- Walker, M.G.; Combet, C.; Hinton, J.A.; Maurin, D.; Wilkinson, M.I. Dark Matter in the Classical Dwarf Spheroidal Galaxies: A Robust Constraint on the Astrophysical Factor for γ-Ray Flux Calculations. Astrophys. J. Lett. 2011, 733, L46. [Google Scholar] [CrossRef]
- Charbonnier, A.; Combet, C.; Daniel, M.; Funk, S.; Hinton, J.A.; Maurin, D.; Power, C.; Read, J.I.; Sarkar, S.; Walker, M.G.; et al. Dark matter profiles and annihilation in dwarf spheroidal galaxies: Prospectives for present and future γ-ray observatories—I. The classical dwarf spheroidal galaxies. Mon. Not. R. Astron. Soc. 2011, 418, 1526–1556. [Google Scholar] [CrossRef]
- Bonnivard, V.; Combet, C.; Maurin, D.; Walker, M.G. Spherical Jeans analysis for dark matter indirect detection in dwarf spheroidal galaxies—Impact of physical parameters and triaxiality. Mon. Not. R. Astron. Soc. 2015, 446, 3002–3021. [Google Scholar] [CrossRef]
- Bonnivard, V.; Combet, C.; Daniel, M.; Funk, S.; Geringer-Sameth, A.; Hinton, J.A.; Maurin, D.; Read, J.I.; Sarkar, S.; Walker, M.G.; et al. Dark matter annihilation and decay in dwarf spheroidal galaxies: The classical and ultrafaint dSphs. Mon. Not. R. Astron. Soc. 2015, 453, 849–867. [Google Scholar] [CrossRef]
- Bonnivard, V.; Combet, C.; Maurin, D.; Geringer-Sameth, A.; Koushiappas, S.M.; Walker, M.G.; Mateo, M.; Olszewski, E.W.; Bailey, J.I., III. Dark Matter Annihilation and Decay Profiles for the Reticulum II Dwarf Spheroidal Galaxy. Astrophys. J. Lett. 2015, 808, L36. [Google Scholar] [CrossRef]
- Bonnivard, V.; Maurin, D.; Walker, M.G. Contamination of stellar-kinematic samples and uncertainty about dark matter annihilation profiles in ultrafaint dwarf galaxies: The example of Segue I. Mon. Not. R. Astron. Soc. 2016, 462, 223–234. [Google Scholar] [CrossRef]
- Genina, A.; Fairbairn, M. The potential of the dwarf galaxy Triangulum II for dark matter indirect detection. Mon. Not. R. Astron. Soc. 2016, 463, 3630–3636. [Google Scholar] [CrossRef]
- Walker, M.G.; Mateo, M.; Olszewski, E.W.; Koposov, S.; Belokurov, V.; Jethwa, P.; Nidever, D.L.; Bonnivard, V.; Bailey, J.I., III; Bell, E.F.; et al. Magellan/M2FS Spectroscopy of Tucana 2 and Grus 1. Astrophys. J. 2016, 819, 53. [Google Scholar] [CrossRef]
- Campos, M.D.; Queiroz, F.S.; Yaguna, C.E.; Weniger, C. Search for right-handed neutrinos from dark matter annihilation with gamma-rays. J. Cosmol. Astropart. Phys. 2017, 7, 016. [Google Scholar] [CrossRef]
- Albert, A.; Alfaro, R.; Alvarez, C.; Álvarez, J.D.; Arceo, R.; Arteaga-Velázquez, J.C.; Rojas, D.A.; Solares, H.A.; Bautista-Elivar, N.; Becerril, A.; et al. Dark Matter Limits from Dwarf Spheroidal Galaxies with the HAWC Gamma-Ray Observatory. Astrophys. J. 2018, 853, 154. [Google Scholar] [CrossRef]
- The ANTARES Collaboration. Search of dark matter annihilation in the galactic centre using the ANTARES neutrino telescope. J. Cosmol. Astropart. Phys. 2015, 10, 068. [Google Scholar]
- Albert, A.; André, M.; Anghinolfi, M.; Anton, G.; Ardid, M.; Aubert, J.J.; Avgitas, T.; Baret, B.; Barrios-Martí, J.; Basa, S.; et al. Results from the search for dark matter in the Milky Way with 9 years of data of the ANTARES neutrino telescope. Phys. Lett. B 2017, 769, 249–254. [Google Scholar] [CrossRef]
- Balázs, C.; Conrad, J.; Farmer, B.; Jacques, T.; Li, T.; Meyer, M.; Queiroz, F.S.; Sánchez-Conde, M.A. Sensitivity of the Cherenkov Telescope Array to the detection of a dark matter signal in comparison to direct detection and collider experiments. Phys. Rev. D 2017, 96, 083002. [Google Scholar] [CrossRef]
- Nichols, M.; Mirabal, N.; Agertz, O.; Lockman, F.J.; Bland-Hawthorn, J. The Smith Cloud and its dark matter halo: Survival of a Galactic disc passage. Mon. Not. R. Astron. Soc. 2014, 442, 2883–2891. [Google Scholar] [CrossRef][Green Version]
- Albert, A.; Alfaro, R.; Alvarez, C.; Álvarez, J.D.; Arceo, R.; Arteaga-Velázquez, J.C.; Rojas, D.A.; Solares, H.A.; Becerril, A.; Belmont-Moreno, E.; et al. Search for dark matter gamma-ray emission from the Andromeda Galaxy with the High-Altitude Water Cherenkov Observatory. J. Cosmol. Astropart. Phys. 2018, 6, 043. [Google Scholar] [CrossRef]
- Combet, C.; Maurin, D.; Nezri, E.; Pointecouteau, E.; Hinton, J.A.; White, R. Decaying dark matter: Stacking analysis of galaxy clusters to improve on current limits. Phys. Rev. D 2012, 85, 063517. [Google Scholar] [CrossRef]
- Nezri, E.; White, R.; Combet, C.; Hinton, J.A.; Maurin, D.; Pointecouteau, E. γ-rays from annihilating dark matter in galaxy clusters: Stacking versus single source analysis. Mon. Not. R. Astron. Soc. 2012, 425, 477–489. [Google Scholar] [CrossRef][Green Version]
- Maurin, D.; Combet, C.; Nezri, E.; Pointecouteau, E. Disentangling cosmic-ray and dark-matter induced γ-rays in galaxy clusters. Astron. Astrophys. 2012, 547, A16. [Google Scholar] [CrossRef]
- Hütten, M.; Combet, C.; Maurin, D. Extragalactic diffuse γ-rays from dark matter annihilation: Revised prediction and full modelling uncertainties. J. Cosmol. Astropart. Phys. 2018, 2, 005. [Google Scholar] [CrossRef]
- Bryan, G.L.; Norman, M.L. Statistical Properties of X-Ray Clusters: Analytic and Numerical Comparisons. Astrophys. J. 1998, 495, 80–99. [Google Scholar] [CrossRef]
- Springel, V.; White, S.D.M.; Frenk, C.S.; Navarro, J.F.; Jenkins, A.; Vogelsberger, M.; Wang, J.; Ludlow, A.; Helmi, A. Prospects for detecting supersymmetric dark matter in the Galactic halo. Nature 2008, 456, 73–76. [Google Scholar] [CrossRef] [PubMed]
- Lange, J.U.; Chu, M.C. Can galactic dark matter substructure contribute to the cosmic gamma-ray anisotropy? Mon. Not. R. Astron. Soc. 2015, 447, 939–947. [Google Scholar] [CrossRef][Green Version]
- Kim, S.Y.; Peter, A.H.G.; Hargis, J.R. Missing Satellites Problem: Completeness Corrections to the Number of Satellite Galaxies in the Milky Way are Consistent with Cold Dark Matter Predictions. Phys. Rev. Lett. 2018, 121, 211302. [Google Scholar] [CrossRef]
- Klypin, A.; Kravtsov, A.V.; Valenzuela, O.; Prada, F. Where Are the Missing Galactic Satellites? Astrophys. J. 1999, 522, 82–92. [Google Scholar] [CrossRef]
- Strigari, L.E.; Bullock, J.S.; Kaplinghat, M.; Diemand, J.; Kuhlen, M.; Madau, P. Redefining the Missing Satellites Problem. Astrophys. J. 2007, 669, 676–683. [Google Scholar] [CrossRef]
- Han, J.; Cole, S.; Frenk, C.S.; Jing, Y. A unified model for the spatial and mass distribution of subhaloes. Mon. Not. R. Astron. Soc. 2016, 457, 1208–1223. [Google Scholar] [CrossRef]
- Sánchez-Conde, M.A.; Prada, F. The flattening of the concentration-mass relation towards low halo masses and its implications for the annihilation signal boost. Mon. Not. R. Astron. Soc. 2014, 442, 2271–2277. [Google Scholar] [CrossRef]
- Bullock, J.S.; Kolatt, T.S.; Sigad, Y.; Somerville, R.S.; Kravtsov, A.V.; Klypin, A.A.; Primack, J.R.; Dekel, A. Profiles of dark haloes: Evolution, scatter and environment. Mon. Not. R. Astron. Soc. 2001, 321, 559–575. [Google Scholar] [CrossRef]
- Navarro, J.F.; Frenk, C.S.; White, S.D.M. The Structure of Cold Dark Matter Halos. Astrophys. J. 1996, 462, 563. [Google Scholar] [CrossRef]
- Einasto, J.; Haud, U. Galactic models with massive corona. I—Method. II—Galaxy. Astron. Astrophys. 1989, 223, 89–106. [Google Scholar]
- Ishiyama, T.; Makino, J.; Ebisuzaki, T. Gamma-ray Signal from Earth-mass Dark Matter Microhalos. Astrophys. J. Lett. 2010, 723, L195–L200. [Google Scholar] [CrossRef]
- Ishiyama, T. Hierarchical Formation of Dark Matter Halos and the Free Streaming Scale. Astrophys. J. 2014, 788, 27. [Google Scholar] [CrossRef]
- Angulo, R.E.; Hahn, O.; Ludlow, A.D.; Bonoli, S. Earth-mass haloes and the emergence of NFW density profiles. Mon. Not. R. Astron. Soc. 2017, 471, 4687–4701. [Google Scholar] [CrossRef]
- Piffl, T.; Binney, J.; McMillan, P.J.; Steinmetz, M.; Helmi, A.; Wyse, R.F.G.; Bienayme, O.; Bland-Hawthorn, J.; Freeman, K.; Gibson, B.; et al. Constraining the Galaxy’s dark halo with RAVE stars. Mon. Not. R. Astron. Soc. 2014, 445, 3133–3151. [Google Scholar] [CrossRef]
- McMillan, P.J. The mass distribution and gravitational potential of the Milky Way. Mon. Not. R. Astron. Soc. 2017, 465, 76–94. [Google Scholar] [CrossRef]
- Binney, J. Self-consistent modelling of our Galaxy with Gaia data. arXiv 2017, arXiv:1706.01374. [Google Scholar]
- Brown, A.G.A.; Vallenari, A.; Prusti, T.; de Bruijne, J.H.J.; Babusiaux, C.; Bailer-Jones, C.A.L.; Biermann, M.; Evans, D.W.; Eyer, L.; Jansen, F.; et al. Gaia Data Release 2. Summary of the contents and survey properties. Astron. Astrophys. 2018, 616, A1. [Google Scholar]
- Springel, V.; Wang, J.; Vogelsberger, M.; Ludlow, A.; Jenkins, A.; Helmi, A.; Navarro, J.F.; Frenk, C.S.; White, S.D. The Aquarius Project: The subhaloes of galactic haloes. Mon. Not. R. Astron. Soc. 2008, 391, 1685–1711. [Google Scholar] [CrossRef]
- Moliné, Á.; Sánchez-Conde, M.A.; Palomares-Ruiz, S.; Prada, F. Characterization of subhalo structural properties and implications for dark matter annihilation signals. Mon. Not. R. Astron. Soc. 2017, 466, 4974–4990. [Google Scholar] [CrossRef]
- Diemand, J.; Kuhlen, M.; Madau, P.; Zemp, M.; Moore, B.; Potter, D.; Stadel, J. Clumps and streams in the local dark matter distribution. Nature 2008, 454, 735–738. [Google Scholar] [CrossRef]
- Garrison-Kimmel, S.; Boylan-Kolchin, M.; Bullock, J.S.; Lee, K. ELVIS: Exploring the Local Volume in Simulations. Mon. Not. R. Astron. Soc. 2014, 438, 2578–2596. [Google Scholar] [CrossRef]
- Zhao, H. Analytical models for galactic nuclei. Mon. Not. R. Astron. Soc. 1996, 278, 488–496. [Google Scholar] [CrossRef]
- Hayashi, E.; Navarro, J.F.; Taylor, J.E.; Stadel, J.; Quinn, T.R. The Structural evolution of substructure. Astrophys. J. 2003, 584, 541–558. [Google Scholar] [CrossRef]
- van den Bosch, F.C.; Ogiya, G.; Hahn, O.; Burkert, A. Disruption of dark matter substructure: Fact or fiction? Mon. Not. R. Astron. Soc. 2018, 474, 3043–3066. [Google Scholar] [CrossRef]
- van den Bosch, F.C.; Ogiya, G. Dark matter substructure in numerical simulations: A tale of discreteness noise, runaway instabilities, and artificial disruption. Mon. Not. R. Astron. Soc. 2018, 475, 4066–4087. [Google Scholar] [CrossRef]
- Weinberg, M.D. Adiabatic invariants in stellar dynamics. 1: Basic concepts. Astrophys. J. 1994, 108, 1398–1402. [Google Scholar] [CrossRef]
- Gnedin, O.Y.; Lee, H.M.; Ostriker, J.P. Effects of Tidal Shocks on the Evolution of Globular Clusters. Astrophys. J. 1999, 522, 935–949. [Google Scholar] [CrossRef]
- Peñarrubia, J.; Benson, A.J.; Walker, M.G.; Gilmore, G.; McConnachie, A.W.; Mayer, L. The impact of dark matter cusps and cores on the satellite galaxy population around spiral galaxies. Mon. Not. R. Astron. Soc. 2010, 406, 1290–1305. [Google Scholar] [CrossRef]
- Ackermann, M.; Ajello, M.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Bellazzini, R.; Bissaldi, E.; Blandford, R.D.; Bloom, E.D.; et al. The Search for Spatial Extension in High-latitude Sources Detected by the Fermi Large Area Telescope. Astrophys. J. Suppl. Ser. 2018, 237, 32. [Google Scholar] [CrossRef]
- The Fermi-LAT collaboration. Fermi Large Area Telescope Fourth Source Catalog. arXiv 2019, arXiv:1902.10045. [Google Scholar]
- Scott, D.W. Multivariate Density Estimation: Theory, Practice, and Visualization; John Wiley and Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Strigari, L.E. Dark matter in dwarf spheroidal galaxies and indirect detection: A review. Rep. Prog. Phys. 2018, 81, 056901. [Google Scholar] [CrossRef] [PubMed]
- Hiroshima, N.; Ando, S.; Ishiyama, T. Modeling evolution of dark matter substructure and annihilation boost. Phys. Rev. D 2018, 97, 123002. [Google Scholar] [CrossRef]
- Ando, S.; Ishiyama, T.; Hiroshima, N. Halo substructure boosts to the signatures of dark matter annihilation. arXiv 2019, arXiv:1903.11427. [Google Scholar]
- Peñarrubia, J.; Navarro, J.F.; McConnachie, A.W. The Tidal Evolution of Local Group Dwarf Spheroidals. Astrophys. J. 2008, 673, 226–240. [Google Scholar] [CrossRef]
- Drakos, N.E.; Taylor, J.E.; Benson, A.J. The phase-space structure of tidally stripped haloes. Mon. Not. R. Astron. Soc. 2017, 468, 2345–2358. [Google Scholar] [CrossRef]
| 1. | We assume here the DM particle to be a Majorana particle, so that (for a Dirac, ). |
| 2. | |
| 3. | When releasing CLUMPY v3.0, we corrected a misprint that was present in v2.0, related to our implementation of the virial overdensity from [56]. This issue was responsible for obtaining in [1] about a factor 3 more subhalos than expected per flux decade (see full details in the CLUMPY documentation). We recall that in [1], we found that galactic variance is responsible for a factor uncertainty on the value of the brightest subhalo, and that other subhalo properties were responsible for another factor ∼6. Given these very large uncertainties, the conclusions on DM limits set from dark clumps with CLUMPY v2.0 are not qualitatively changed, but we urge users to rely on CLUMPY v3.0 for future studies. |
| 4. | Strictly speaking, this factorization holds true only for DM candidates for which is independent of the velocity and consideration of small redshift cells, . |
| 5. | |
| 6. | The concentration is defined to be , with , taken to be the subhalo boundary, is the radius at which the mean subhalo density is times the critical density (see, e.g., [6]), and is the position in the subhalo for which the slope of the density is . We use in this work. |
| 7. | This range was recently shown to be in agreement with the observed number of dwarf spheroidal galaxies SDSS corrected by the detection efficiency [59], alleviating the tension caused by the so-called missing satellite problem in CDM scenarios [60,61]. Given the minimal mass of subhalos, , can be used to calculate the mass fraction, , of DM in subhalos. |
| 8. | As shown in [5] (see their Figure 1), only the first level of substructure significantly boosts the halo luminosity, the next levels bringing a few extra percent at most. |
| 9. | We still provide later the total DM profile for the semi-analytical configurations (model #3 and model #4) because it is one of the building blocks of the model. |
| 10. | The difference between using the space-dependent or field halo concentration was found to be a factor ∼2 larger on the brightest subhalo in [1]. |
| 11. | The Milky-Way-like halos in the Phat-ELVIS simulations have masses ranging from to , and virial radii from 235 kpc to 329 kpc respectively. The fit above was performed on the radial range common to all host halos, namely from 0 to 235 kpc. The value of the parameters remain compatible at the one-sigma level when increasing the radial range to 329 kpc, or when cutting on masses above . |
| 12. | We checked for convergence in order to obtain a complete ensemble of objects above these thresholds. |
| 13. | Please note that most drawn subhalos are disrupted at masses below a tidal mass of , the scale above which subhalos are shown in the later Figure 4. |
| 14. | Probability distributions were derived using a kernel density estimation (KDE) with an adaptive Gaussian kernel according to [87] (except , which was obtained from a histogram). To handle the boundary conditions of and , we use the PyQt-Fit KDE implementation by P. Barbier de Reuille, https://pyqt-fit.readthedocs.io (not anymore maintained as of submission of the manuscript), which accounts for a renormalization algorithm at the boundary. Please note that for a precise power-law source count distribution, the PDF of / follows a Fréchet distribution, see App. B of [1]. |

| Model #1 | Model #2 | Model #3 | Model #4 | |
|---|---|---|---|---|
| Aquarius [74] | Phat-ELVIS [10] | SL17 [15] with | SL 17 [15] with | |
| Einasto | Sigmoid-Einasto Equation (5) | |||
| NFW | NFW | |||
| kpc | kpc | kpc | kpc | |
| - | kpc | - | - | |
| - | kpc | - | - | |
| 300 | - | 276 | 276 | |
| - | 90 | |||
| Moliné et al. [75] | Moliné et al. [75] | Sánchez-Conde & Prada [63] | Sánchez-Conde & Prada [63] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hütten, M.; Stref, M.; Combet, C.; Lavalle, J.; Maurin, D. γ-ray and ν Searches for Dark-Matter Subhalos in the Milky Way with a Baryonic Potential. Galaxies 2019, 7, 60. https://doi.org/10.3390/galaxies7020060
Hütten M, Stref M, Combet C, Lavalle J, Maurin D. γ-ray and ν Searches for Dark-Matter Subhalos in the Milky Way with a Baryonic Potential. Galaxies. 2019; 7(2):60. https://doi.org/10.3390/galaxies7020060
Chicago/Turabian StyleHütten, Moritz, Martin Stref, Céline Combet, Julien Lavalle, and David Maurin. 2019. "γ-ray and ν Searches for Dark-Matter Subhalos in the Milky Way with a Baryonic Potential" Galaxies 7, no. 2: 60. https://doi.org/10.3390/galaxies7020060
APA StyleHütten, M., Stref, M., Combet, C., Lavalle, J., & Maurin, D. (2019). γ-ray and ν Searches for Dark-Matter Subhalos in the Milky Way with a Baryonic Potential. Galaxies, 7(2), 60. https://doi.org/10.3390/galaxies7020060






