Practical Modeling of Large-Scale Galactic Magnetic Fields: Status and Prospects
Abstract
1. Introduction
2. Observables
2.1. Polarized Starlight
2.2. Faraday Rotation Measures (RMs) of Point Sources
2.3. Diffuse Polarized Synchrotron Emission
2.4. Diffuse Polarized Thermal Dust Emission
2.5. Diffuse -ray Emission
2.6. Faraday Tomography/RM Synthesis
2.7. Supernova Remnants
3. Modeling Components
3.1. Magnetic Field
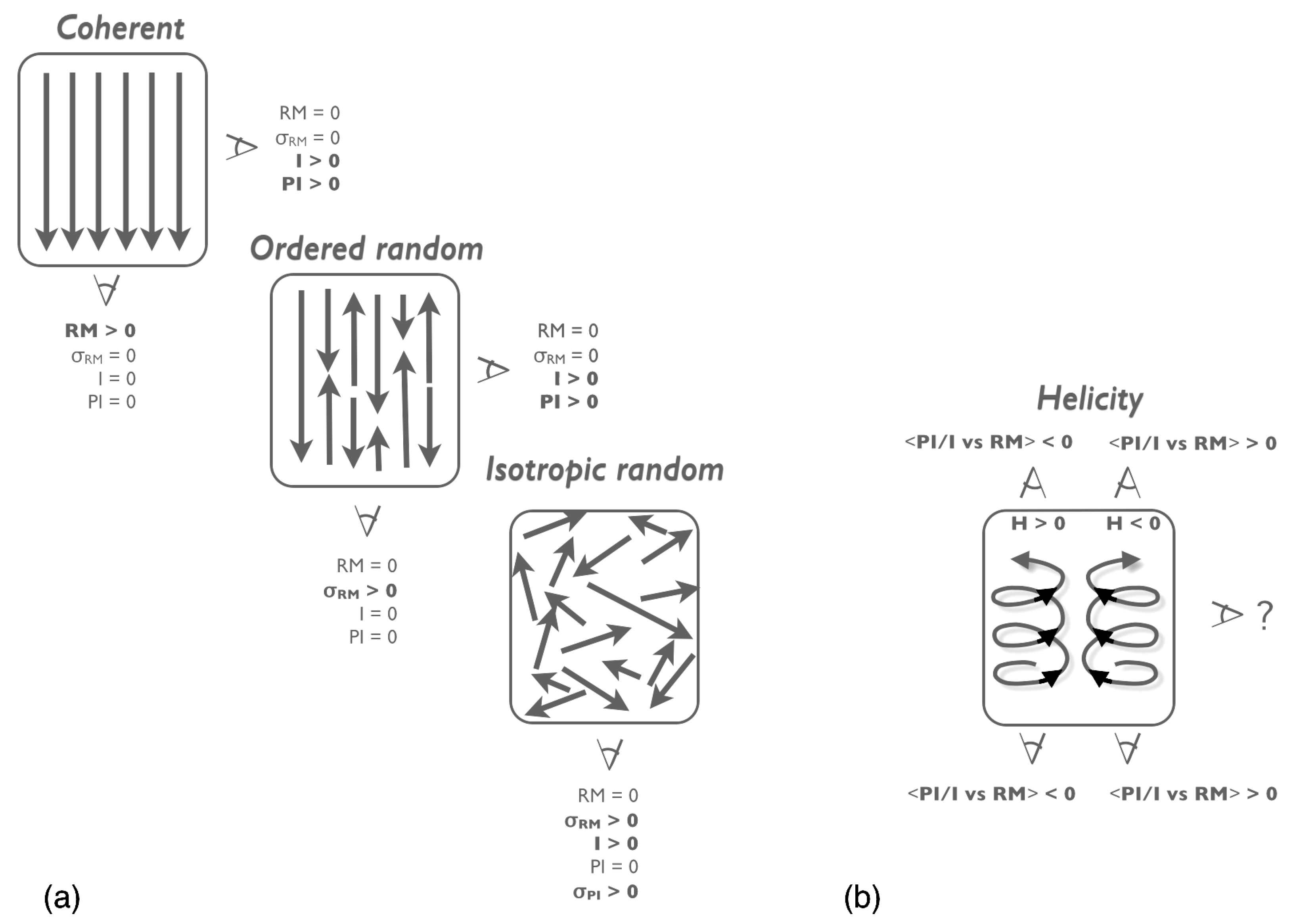
3.1.1. Definitions: “Random”, “Regular”, “Ordered”, “Striated”...?
- The coherent field is the component whose direction remains coherent over large regions. This is also referred to as the mean field. When observed from a perpendicular direction, the synchrotron polarization adds coherently, and when observed in parallel, the RM adds coherently. See left-most box in Figure 1a.
- The isotropic random component represents a zeroth-order simplification for the ISM turbulence, where local field fluctuations are equally likely to be in any direction. Such a component does not have to be single-scale (e.g., as in Sun et al. [42]); one can define an isotropic Gaussian random field (GRF) that encodes correlations as a function of distance but has equal power in all directions (e.g., as in Jaffe et al. [41]). This component contributes only to the total synchrotron intensity but does not add coherently to its polarization or to the RM; see the lower right box of Figure 1a.
- The third component can be thought of representing a first-order approximation of the ISM, where local field fluctuations are not isotropic but rather prefer certain orientations. Please note that it does not prefer certain directions; that would simply be part of the coherent component. The definition of this third component is that the RMs must still average to zero but that the polarized emission adds up. See the middle box of Figure 1a. This component has variously been called the “ordered random” (Jaffe et al. [41]), or the “striated” component (Jansson and Farrar [43]). The term “anisotropic random” used by Beck et al. [2] can be ambiguous in that it has sometimes been used to refer to the Figure 1a middle component only and sometimes to the total random component, the sum of the middle and right boxes, i.e., the ordered random plus isotropic random.
3.1.2. Coherent Field
3.1.3. Isotropic Random Field
3.1.4. Ordered Random Field
3.1.5. Helicity
3.2. Thermal Electrons—WHIM
3.3. Dust Grains
3.4. Galactic Cosmic Rays
4. Models and Analyses
4.1. Current Magnetic Field Model Fits
- Sun et al. [42] (refined in [64], “Sun10”) first used the combination of synchrotron total and polarized intensity (at 408 MHz and 23 GHz respectively) along with RMs to compare several 3D models of the GMF. They used the NE2001 model for thermal electrons and a simple exponential disk with a power law spectrum of index for the cosmic rays. This work included an analysis of the impact of the filling factor of the ionized gas in the ISM and examined several models from the literature, both axi-symmetric and bisymmetric spirals. The model they concluded was favored by the data was the “ASS+RING” based on an axisymmetric spiral disk with field reversals defined in several regions to match the data. The turbulence was modeled with a single-scale random field. This was the first such analysis, though it was not quantitative model fit, and it assumed a very high local cosmic-ray density to fit the data without an ordered random field component.
- Jaffe et al. [41] (refined in [29,60], “Jaffe13”) used these same synchrotron observables and the SGPS and CGPS extragalactic RMs to perform a systematic likelihood exploration in the plane of a 2D model based loosely on previous work by [65]. It used the NE2001 model for thermal electrons and a Galprop cosmic-ray model from [35]. It included an exponential disk to which is added four Gaussian-profiled spiral arms as well as a ring around the Galactic center. This analysis first included realizations of the random components, both isotropic and ordered, based on a Kolmogorov-like GRF in an MCMC likelihood space optimization, but only in 2D. The update in Jaffe et al. [29] simultaneously constrained the CR lepton break at low energies in one of the first attempts to model the CRs and GMF simultaneously. Then [60] added the polarized dust information and saw how the different distributions of particles means that the two observables can perhaps constrain the GMF in different regions of the ISM. These analyses, though, remain limited by the systematic uncertainties of the particle distributions.
- Jansson and Farrar [43] (refined in [59], “JF12”) used the synchrotron total and polarized intensity from WMAP 23 GHz as well as the 40k extragalactic RMs to perform a systematic likelihood exploration in 3D of a model with both thin and thick disk components, eight spiral arm or inter-arm segments, and an x-shaped halo field. It was based on the NE2001 thermal electron density model (with the scale height correction from [51]) and a CR model based on the “71Xvarh7S” from Galprop. It used an analytical method to treat the random field components, and the measured pixel variance was used in the likelihood. (See Section 4.2.6) This was the first 3D model optimization with an MCMC likelihood analysis, but the use of the WMAP synchrotron map at 23 GHz meant that the extra total intensity foregrounds biased their estimate of the random field component. See also Unger & Farrar below for updates.
- Han et al. [13] used both Galactic and extragalactic radio sources to model the RM reversals in the Galactic plane with a set of spiral arm and inter-arm segments. The analysis used the YMW16 model for thermal electrons. This is not a global GMF model for the Galaxy, but an analysis specifically focused on where the field reversals lie using the distance information from pulsars.
- Terral and Ferriere [66] (“TF17”) used the spiraling x-shaped field models derived in [67] to fit the RM data. They explore both axisymmetric and bisymmetric possibilities. This work represents the first quantitative fitting to models of spiraling x-shaped fields in theoretically derived forms (rather than ad hoc).
- Unger & Farrar [68] built on the JF12 work by replacing the ad hoc x-shaped halo field by the models of Ferriere and Terral [67]. They also compared the results of fits based on different datasets (WMAP synchrotron total intensity versus 408 MHz), different thermal electron models (NE2001 vs. YMW16), and CR distributions from the original work compared to those of [35,37].
- Shukurov et al. [69] derived eigenfunctions of the mean-field dynamo equation that can be used to construct any model consistent with those assumptions. Though this analysis does not present one model fit to the data, it provides a framework for fitting more physically realistic models in future with a publicly available software package.
4.2. Magnetic Field Morphological Features
4.2.1. Axisymmetric Spirals
4.2.2. Spiral Arms
4.2.3. Reversals
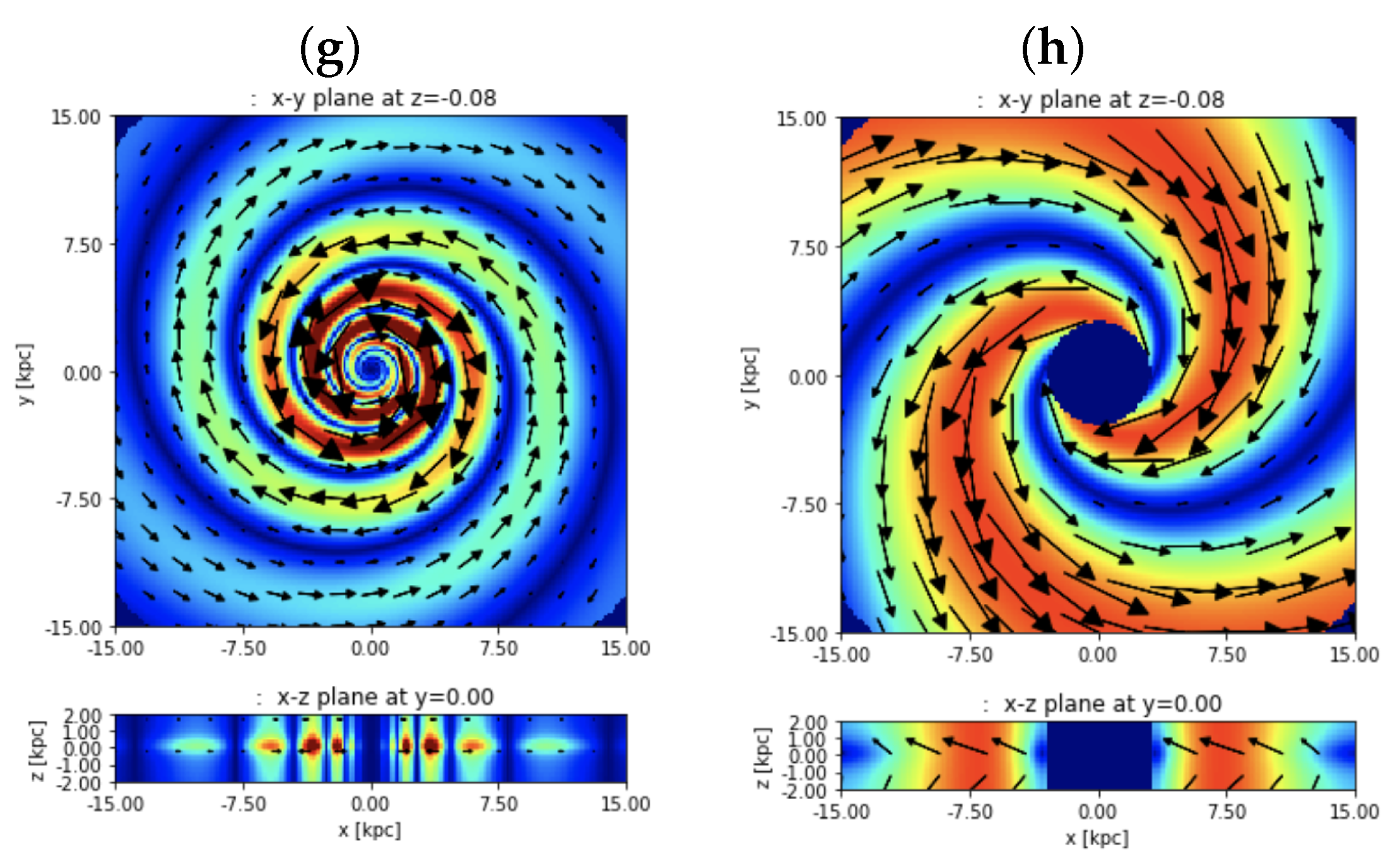
4.2.4. Vertical (Poloidal) Field
4.2.5. Beyond the Ad Hoc
4.2.6. Turbulent Field
5. Challenges
5.1. Synchrotron and CR spectra
5.2. Local Features
5.2.1. Loops and Spurs
5.2.2. Fan Region
5.2.3. Local Bubble
5.3. Galactic Center, Outflow, and Fermi Bubbles
5.4. Sub-Grid Modeling
6. Prospects
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| GMF | Galactic magnetic field |
| GRF | Gaussian random field |
| RM | Faraday rotation measure |
| CMB | cosmic microwave background |
| ISM | interstellar medium |
| MCMC | Markov chain Monte Carlo |
| MHD | magnetohydrodynamics |
| CR | cosmic ray |
| UHECR | ultra-high-energy cosmic ray |
References
- Haverkorn, M. Magnetic Fields in the Milky Way. In Magnetic Fields in Diffuse Media; de Gouveia Dal Pino, E.M., Lazarian, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 483–506. [Google Scholar]
- Beck, R.; Shukurov, A.; Sokoloff, D.; Wielebinski, R. Systematic bias in interstellar magnetic field estimates. Astron. Astrophys. 2003, 411, 99–107. [Google Scholar] [CrossRef]
- Zaroubi, S. The Epoch of Reionization. In The First Galaxies: Theoretical Predictions and Observational Clues; Springer: Basel, Switzerland, 2013. [Google Scholar]
- Fish, V.L.; Reid, M.J.; Argon, A.L.; Menten, K.M. Interstellar Hydroxyl Masers in the Galaxy. II. Zeeman Pairs and the Galactic Magnetic Field. Astrophys. J. 2003, 596, 328–343. [Google Scholar] [CrossRef][Green Version]
- Han, J.L.; Zhang, J.S. The Galactic distribution of magnetic fields in molecular clouds and HII regions. Astron. Astrophys. 2006, 464, 609–614. [Google Scholar] [CrossRef]
- Green, J.A.; McClure-Griffiths, N.M.; Caswell, J.L.; Robishaw, T.; Harvey-Smith, L. MAGMO: Coherent magnetic fields in the star forming regions of the Carina-Sagittarius spiral arm tangent. Mon. Notices R. Astron. Soc. 2012, 4, 2530–2547. [Google Scholar] [CrossRef]
- González-Casanova, D.F.; Lazarian, A. Velocity Gradients as a Tracer for Magnetic Fields. Astrophys. J. 2017, 835, 41. [Google Scholar] [CrossRef]
- Han, J.L. Observing Interstellar and Intergalactic Magnetic Fields. Annu. Rev. Astron. Astrophys. 2017, 55, 111–157. [Google Scholar] [CrossRef]
- Heiles, C. 9286 Stars: An Agglomeration of Stellar Polarization Catalogs. Astrophys. J. 2000, 119, 923–927. [Google Scholar] [CrossRef]
- Santos, F.P.; Corradi, W.; Reis, W. Optical Polarization Mapping Toward the Interface Between the Local Cavity and Loop I. Astrophys. J. 2011, 728, 104. [Google Scholar] [CrossRef]
- Pavel, M.D. Constraining Galactic Magnetic Field Models with Starlight Polarimetry. Astrophys. J. 2011, 740, 21. [Google Scholar] [CrossRef]
- Panopoulou, G.V.; Tassis, K.; Skalidis, R.; Blinov, D.; Liodakis, I.; Pavlidou, V.; Potter, S.B.; Ramaprakash, A.N.; Readhead, A.C.S.; Wehus, I.K. Demonstration of magnetic field tomography with starlight polarization towards a diffuse sightline of the ISM. Astrophys. J. 2019, 872, 56. [Google Scholar] [CrossRef]
- Han, J.L.; Manchester, R.N.; van Straten, W.; Demorest, P. Pulsar Rotation Measures and Large-scale Magnetic Field Reversals in the Galactic Disk. Astrophys. J. Suppl. 2018, 234, 11. [Google Scholar] [CrossRef]
- Taylor, A.R.; Stil, J.M.; Sunstrum, C. A Rotation Measure Image of the Sky. Astrophys. J. 2009, 702, 1230. [Google Scholar] [CrossRef]
- Xu, J.; Han, J.L. A compiled catalog of rotation measures of radio point sources. Res. Astron. Astrophys. 2014, 14, 942–958. [Google Scholar] [CrossRef]
- Schnitzeler, D.H.F.M.; Carretti, E.; Wieringa, M.H.; Gaensler, B.M.; Haverkorn, M.; Poppi, S. S-PASS/ATCA: A window on the magnetic universe in the southern hemisphere. Mon. Notices R. Astron. Soc. 2019, 485, 1293–1309. [Google Scholar] [CrossRef]
- Brown, J.C.; Taylor, A.R.; Jackel, B.J. Rotation Measures of Compact Sources in the Canadian Galactic Plane Survey. Astrophys. J. 2003, 145, 213–223. [Google Scholar] [CrossRef]
- Brown, J.C.; Haverkorn, M.; Gaensler, B.M.; Taylor, A.R.; Bizunok, N.S.; McClure-Griffiths, N.M.; Dickey, J.M.; Green, A.J. Rotation Measures of Extragalactic Sources behind the Southern Galactic Plane: New Insights into the Large-Scale Magnetic Field of the Inner Milky Way. Astrophys. J. 2007, 663, 258–266. [Google Scholar] [CrossRef]
- Oppermann, N.; Junklewitz, H.; Robbers, G.; Bell, M.R.; Enßlin, T.A.; Bonafede, A.; Braun, R.; Brown, J.C.; Clarke, T.E.; Feain, I.J.; et al. An improved map of the Galactic Faraday sky. Astron. Astrophys. 2012, 542, 93. [Google Scholar] [CrossRef]
- Haslam, C.G.T.; Salter, C.J.; Stoffel, H.; Wilson, W.E. A 408 MHz all-sky continuum survey. II - The atlas of contour maps. Astron. Astrophys. Suppl. 1982, 47, 1. [Google Scholar]
- Remazeilles, M.; Dickinson, C.; Banday, A.J.; Bigot-Sazy, M.A.; Ghosh, T. An improved source-subtracted and destriped 408 MHz all-sky map. Astron. Astrophys. 2015, 451, 4311–4327. [Google Scholar] [CrossRef]
- Reich, P.; Testori, J.C.; Reich, W. A radio continuum survey of the southern sky at 1420 MHz. The atlas of contour maps. Astron. Astrophys. 2001, 376, 861–877. [Google Scholar] [CrossRef]
- Testori, J.C.; Reich, P.; Reich, W. A fully sampled λ21 cm linear polarization survey of the southern sky. Astron. Astrophys. 2008, 484, 733–742. [Google Scholar] [CrossRef]
- Uyaniker, B.; Landecker, T.L.; Gray, A.D.; Kothes, R. Radio Polarization from the Galactic Plane in Cygnus. Astrophys. J. 2003, 585, 785–800. [Google Scholar] [CrossRef]
- Hill, A. Is There a Polarization Horizon? Galaxies 2018, 6, 129. [Google Scholar] [CrossRef]
- Bennett, C.L.; Larson, D.; Weiland, J.L.; Jarosik, N.; Hinshaw, G.; Odegard, N.; Smith, K.M.; Hill, R.S.; Gold, B.; Halpern, M.; et al. Nine-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Final Maps and Results. Astrophys. J. Suppl. 2012, 208, 20. [Google Scholar] [CrossRef]
- Planck Collaboration I. Planck 2018 results. I. Overview and the cosmological legacy of Planck. arXiv 2018, arXiv:1807.06205. [Google Scholar]
- Wehus, I.K.; Fuskeland, U.; Eriksen, H.K.; Banday, A.J.; Dickinson, C.; Ghosh, T.; Górski, K.M.; Lawrence, C.R.; Leahy, J.P.; Maino, D.; Reich, P.; Reich, W. Monopole and dipole estimation for multi-frequency sky maps by linear regression. arXiv 2014, arXiv:1411.7616. [Google Scholar] [CrossRef]
- Jaffe, T.R.; Banday, A.J.; Leahy, J.P.; Leach, S.; Strong, A.W. Connecting synchrotron, cosmic rays and magnetic fields in the plane of the Galaxy. Mon. Notices R. Astron. Soc. 2011, 416, 1152–1162. [Google Scholar] [CrossRef]
- King, O.G.; Jones, M.E.; Blackhurst, E.J.; Copley, C.; Davis, R.J.; Dickinson, C.; Holler, C.M.; Irfan, M.O.; John, J.J.; Leahy, J.P.; et al. The C-Band All-Sky Survey (C-BASS): Design and implementation of the northern receiver. Mon. Notices R. Astron. Soc. 2014, 438, 2426–2439. [Google Scholar] [CrossRef]
- Irfan, M.O.; Dickinson, C.; Davies, R.D.; Copley, C.; Davis, R.J.; Ferreira, P.G.; Holler, C.M.; Jonas, J.L.; Jones, M.E.; King, O.G.; et al. C-Band All-Sky Survey: A First Look at the Galaxy. Astron. Astrophys. 2015, 448, 3572–3586. [Google Scholar] [CrossRef]
- Benoît, A.E.A. First detection of polarization of the submillimetre diffuse galactic dust emission by Archeops. Astron. Astrophys. 2004, 424, 571. [Google Scholar] [CrossRef]
- Planck Collaboration XIX. Planck intermediate results. XIX. An overview of the polarized thermal emission from Galactic dust. Astron. Astrophys. 2015, 576, A104. [Google Scholar] [CrossRef]
- Lallement, R.; Capitanio, L.; Ruiz-Dern, L.; Danielski, C.; Babusiaux, C.; Vergely, L.; Elyajouri, M.; Arenou, F.; Leclerc, N. Three-dimensional maps of interstellar dust in the Local Arm: Using Gaia, 2MASS, and APOGEE-DR14. Astron. Astrophys. 2018, 616, A132. [Google Scholar] [CrossRef]
- Strong, A.; Porter, T.; Digel, S.; Jóhannesson, G.; Martin, P.; Moskalenko, I.; Murphy, E.; Orlando, E. Global Cosmic-ray-related Luminosity and Energy Budget of the Milky Way. Astrophys. J. 2010, 722, L58. [Google Scholar] [CrossRef]
- Strong, A.W.; Orlando, E.; Jaffe, T.R. The interstellar cosmic-ray electron spectrum from synchrotron radiation and direct measurements. Astron. Astrophys. 2011, 534, 54. [Google Scholar] [CrossRef]
- Orlando, E.; Strong, A. Galactic synchrotron emission with cosmic ray propagation models. Mon. Notices R. Astron. Soc. 2013, 436, 2127–2142. [Google Scholar] [CrossRef]
- Orlando, E. Implications on Spatial Models of Interstellar Gamma-Ray Inverse-Compton Emission from Synchrotron Emission Studies in Radio and Microwaves. Phys. Rev. 2019, 99, 043007. [Google Scholar]
- Ferriere, K. Faraday tomography: A new, three-dimensional probe of the interstellar magnetic field. J. Phys. Conf. Ser. 2016, 767, 012006. [Google Scholar] [CrossRef]
- West, J.L.; Safi-Harb, S.; Jaffe, T.; Kothes, R.; Landecker, T.L.; Foster, T. The connection between supernova remnants and the Galactic magnetic field: A global radio study of the axisymmetric sample. Astron. Astrophys. 2016, 587, A148. [Google Scholar] [CrossRef]
- Jaffe, T.R.; Leahy, J.P.; Banday, A.J.; Leach, S.M.; Lowe, S.R.; Wilkinson, A. Modelling the Galactic magnetic field on the plane in two dimensions. Mon. Notices R. Astron. Soc. 2010, 401, 1013–1028. [Google Scholar] [CrossRef]
- Sun, X.H.; Reich, W.; Waelkens, A.; Enßlin, T.A. Radio observational constraints on Galactic 3D-emission models. Astron. Astrophys. 2008, 477, 573–592. [Google Scholar] [CrossRef]
- Jansson, R.; Farrar, G.R. A New Model of the Galactic Magnetic Field. Astrophys. J. 2012, 757, 14. [Google Scholar] [CrossRef]
- Evirgen, C.C.; Armstrong Gent, F.; Shukurov, A.; Fletcher, A.; Bushby, P. The distribution of mean and fluctuating magnetic fields in the multi-phase ISM. Mon. Notices R. Astron. Soc. 2016, 464, L105–L109. [Google Scholar] [CrossRef]
- Haverkorn, M.; Gaensler, B.M.; McClure-Griffiths, N.M.; Dickey, J.M.; Green, A.J. Magnetic Fields and Ionized Gas in the Inner Galaxy: An Outer Scale for Turbulence and the Possible Role of H II Regions. Astrophys. J. 2004, 609, 776–784. [Google Scholar] [CrossRef]
- Brandenburg, A.; Subramanian, K. Astrophysical magnetic fields and nonlinear dynamo theory. Phys. Rep. 2004, 417, 1–209. [Google Scholar] [CrossRef]
- Volegova, A.A.; Stepanov, R.A. Helicity detection of astrophysical magnetic fields from radio emission statistics. J. Exp. Theor. Phys. Lett. 2010, 90, 637–641. [Google Scholar] [CrossRef]
- Brandenburg, A.; Stepanov, R. Faraday Signature of Magnetic Helicity from Reduced Depolarization. Astrophys. J. 2014, 786, 91. [Google Scholar] [CrossRef]
- Tashiro, H.; Chen, W.; Ferrer, F.; Vachaspati, T. Search for CP Violating Signature of Intergalactic Magnetic Helicity in the Gamma Ray Sky. Mon. Not. R. Astron. Soc. Lett. 2014, 445, L41–L45. [Google Scholar] [CrossRef]
- Cordes, J.M.; Lazio, T.J.W. NE2001.I. A New Model for the Galactic Distribution of Free Electrons and its Fluctuations. arXiv 2002, arXiv:astro-ph/0207156. [Google Scholar]
- Gaensler, B.M.; Madsen, G.J.; Chatterjee, S.; Mao, S.A. The Vertical Structure of Warm Ionised Gas in the Milky Way. Publ. Astron. Soc. Aust. 2008, 25, 184–200. [Google Scholar] [CrossRef]
- Yao, J.M.; Manchester, R.N.; Wang, N. A New Electron-density Model for Estimation of Pulsar and FRB Distances. Astrophys. J. 2017, 835, 29. [Google Scholar] [CrossRef]
- Di Bernardo, G.; Grasso, D.; Evoli, C.; Gaggero, D. Diffuse synchrotron emission from galactic cosmic ray electrons. Astrophys. Space. Sci. Trans. Proc. 2015, 2, 21–26. [Google Scholar] [CrossRef][Green Version]
- Orlando, E. Imprints of cosmic rays in multifrequency observations of the interstellar emission. Mon. Not. R. Astron. Soc. Lett. 2018, 475, 2724–2742. [Google Scholar] [CrossRef]
- Strong, A.W.; Moskalenko, I.V.; Porter, T.A.; Johannesson, G.; Orlando, E.; Digel, S.W. The GALPROP Cosmic-Ray Propagation Code. arXiv 2009, arXiv:0907.0559. [Google Scholar]
- Evoli, C.; Gaggero, D.; Grasso, D.; Maccione, L. Cosmic-Ray Nuclei, Antiprotons and Gamma-rays in the Galaxy: A New Diffusion Model. J. Cosmol. Astropart. Phys. 2008, 10, 018. [Google Scholar] [CrossRef]
- Kissmann, R. PICARD: A novel code for the Galactic Cosmic Ray propagation problem. Astropart. Phys. 2014, 55, 37–50. [Google Scholar] [CrossRef]
- Waelkens, A.; Jaffe, T.; Reinecke, M.; Kitaura, F.S.; Enßlin, T.A. Simulating polarized Galactic synchrotron emission at all frequencies. The Hammurabi code. Astron. Astrophys. 2009, 495, 697–706. [Google Scholar] [CrossRef]
- Jansson, R.; Farrar, G.R. The Galactic Magnetic Field. Astrophys. J. Lett. 2012, 761, L11. [Google Scholar] [CrossRef]
- Jaffe, T.R.; Ferrière, K.M.; Banday, A.J.; Strong, A.W.; Orlando, E.; Macias-Perez, J.F.; Fauvet, L.; Combet, C.; Falgarone, E. Comparing polarized synchrotron and thermal dust emission in the Galactic plane. Mon. Not. R. Astron. Soc. Lett. 2013, 431, 683–694. [Google Scholar] [CrossRef]
- Kachelrieß, M.; Serpico, P.; Teshima, M. The Galactic magnetic field as spectrograph for ultra-high energy cosmic rays. Astropart. Phys. 2007, 26, 378–386. [Google Scholar] [CrossRef]
- Fauvet, L.; Macías-Pérez, J.F.; Aumont, J.; Désert, F.X.; Jaffe, T.R.; Banday, A.J.; Tristram, M.; Waelkens, A.H.; Santos, D. Joint 3D modelling of the polarized Galactic synchrotron and thermal dust foreground diffuse emission. Astron. Astrophys. 2011, 526, 145. [Google Scholar] [CrossRef]
- Planck Collaboration XLII. Planck intermediate results. XLII. Large-scale Galactic magnetic fields. Astron. Astrophys. 2016, 596, A103. [Google Scholar] [CrossRef]
- Sun, X.H.; Reich, W. The Galactic halo magnetic field revisited. Res. Astron. Astrophys. 2010, 10, 1287–1297. [Google Scholar] [CrossRef]
- Broadbent, A.; Haslam, C.G.T.; Osborne, J.L. A Detailed Model of the Synchrotron Radiation in the Galactic Disk. In Proceedings of the 21st International Cosmic Ray Conference. Volume 3 (OG Sessions); University of Adelaide: Adelaide, Australia, 1990. [Google Scholar]
- Terral, P.; Ferriere, K. Constraints from Faraday rotation on the magnetic field structure in the Galactic halo. Astron. Astrophys. 2017, 600, A29. [Google Scholar] [CrossRef]
- Ferriere, K.; Terral, P. Analytical models of X-shape magnetic fields in galactic halos. Astron. Astrophys. 2013, 561, A100. [Google Scholar] [CrossRef]
- Unger, M.; Farrar, G.R. Uncertainties in the Magnetic Field of the Milky Way. arXiv 2017, arXiv:1707.02339. [Google Scholar]
- Shukurov, A.; Rodrigues, L.F.S.; Bushby, P.J.; Hollins, J.; Rachen, J.P. A physical model of the galactic large-scale magnetic field. arXiv 2018, arXiv:1809.03595. [Google Scholar]
- Page, L.; Hinshaw, G.; Komatsu, E.; Nolta, M.R.; Spergel, D.N.; Bennett, C.L.; Barnes, C.; Bean, R.; Doré, O.; Dunkley, J.; Halpern, M. Three-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Polarization Analysis. Astrophys. J. Suppl. 2007, 170, 335–376. [Google Scholar] [CrossRef]
- Sobey, C.; Bilous, A.V.; Grießmeier, J.M.; Hessels, J.W.T.; Karastergiou, A.; Keane, E.F.; Kondratiev, V.I.; Kramer, M.; Michilli, D.; Noutsos, A.; et al. Low-frequency Faraday rotation measures towards pulsars using LOFAR: Probing the 3-D Galactic halo magnetic field. Mon. Not. R. Astron. Soc. 2019, 484, 3646–3664. [Google Scholar] [CrossRef]
- Steininger, T.; Ensslin, T.A.; Greiner, M.; Jaffe, T.; van der Velden, E.; Wang, J.; Haverkorn, M.; Hörandel, J.R.; Jasche, J.; Rachen, J.P. Inferring Galactic magnetic field model parameters using IMAGINE - An Interstellar MAGnetic field INference Engine. arXiv 2018, arXiv:1801.04341. [Google Scholar]
- Beck, R.; Wielebinski, R. Magnetic Fields in Galaxies. In Planets, Stars and Stellar Systems; Oswalt , T.D., Gilmore, G., Eds.; Springer: Dordrecht, the Netherlands, 2013; p. 641. [Google Scholar]
- Moss, D.; Beck, R.; Sokoloff, D.; Stepanov, R.; Krause, M.; Arshakian, T.G. The relation between magnetic and material arms in models for spiral galaxies. Astron. Astrophys. 2013, 556. [Google Scholar] [CrossRef]
- Ordog, A.; Brown, J.C.; Kothes, R.; Landecker, T.L. Three-Dimensional Structure of the Magnetic Field in the Disk of the Milky Way. Astron. Astrophys. 2017, 603, A15. [Google Scholar] [CrossRef]
- O’Dea, D.T.; Clark, C.N.; Contaldi, C.R.; MacTavish, C.J. A model for polarized microwave foreground emission from interstellar dust. Mon. Not. R. Astron. Soc. 2011, 419, 1795–1803. [Google Scholar] [CrossRef]
- Herron, C.A.; Federrath, C.; Gaensler, B.M.; Lewis, G.F.; McClure-Griffiths, N.M.; Burkhart, B. Probes of turbulent driving mechanisms in molecular clouds from fluctuations in synchrotron intensity. Mon. Not. R. Astron. Soc. 2017, 466, 2272–2283. [Google Scholar] [CrossRef]
- Gaensler, B.M.; Haverkorn, M.; Burkhart, B.; Newton-McGee, K.J.; Ekers, R.D.; Lazarian, A.; McClure-Griffiths, N.M.; Robishaw, T.; Dickey, J.M.; Green, A.J. Low-Mach-number turbulence in interstellar gas revealed by radio polarization gradients. Nature 2011, 478, 214–217. [Google Scholar] [CrossRef]
- Burkhart, B.; Lazarian, A.; Gaensler, B.M. Properties of Interstellar Turbulence from Gradients of Linear Polarization Maps. Astrophys. J. 2012, 749, 145. [Google Scholar] [CrossRef]
- Herron, C.A.; Burkhart, B.; Gaensler, B.M.; Lewis, G.F.; McClure-Griffiths, N.M.; Bernardi, G.; Carretti, E.; Haverkorn, M.; Kesteven, M.; Poppi, S.; et al. Advanced Diagnostics for the Study of Linearly Polarized Emission. II. Application to Diffuse Interstellar Radio Synchrotron Emission. Astrophys. J. 2018, 855, 29. [Google Scholar] [CrossRef]
- Planck Collaboration XII. Planck 2018 results. XII. Galactic astrophysics using polarized dust emission. arXiv 2018, arXiv:1807.06212. [Google Scholar]
- Stepanov, R.; Shukurov, A.; Fletcher, A.; Beck, R.; La Porta, L.; Tabatabaei, F. An observational test for correlations between cosmic rays and magnetic fields. Mon. Not. R. Astron. Soc. 2013, 437, 2201–2216. [Google Scholar] [CrossRef]
- Planck Collaboration XX. Planck intermediate results. XX. Comparison of polarized thermal emission from Galactic dust with simulations of MHD turbulence. Astron. Astrophys. 2015, 576, A105. [Google Scholar] [CrossRef]
- Kandel, D.; Lazarian, A.; Pogosyan, D. Ratio of E to B Mode Power for Galactic Foreground. Mon. Not. R. Astron. Soc. Lett. 2017. [Google Scholar] [CrossRef]
- Kogut, A. Synchrotron Spectral Curvature from 22 MHz to 23 GHz. Astrophys. J. 2012, 753, 110. [Google Scholar] [CrossRef]
- Fuskeland, U.; Wehus, I.K.; Eriksen, H.K.; Næss, S.K. Spatial Variations in the Spectral Index of Polarized Synchrotron Emission in the 9 yr Wmapsky Maps. Astrophys. J. 2014, 790, 104. [Google Scholar] [CrossRef]
- Cummings, A.C.; Stone, E.C.; Heikkila, B.C.; Lal, N.; Webber, W.R.; Johannesson, G.; Moskalenko, I.V.; Orlando, E.; Porter, T.A. Galactic Cosmic Rays in the Local Interstellar Medium: Voyager 1 Observations and Model Results. Astrophys. J. 2016, 831, 18. [Google Scholar] [CrossRef]
- Liu, H.; Mertsch, P.; Sarkar, S. Fingerprints of Galactic Loop I on the Cosmic Microwave Background. Astrophys. J. 2014, 789. [Google Scholar] [CrossRef]
- Mertsch, P.; Sarkar, S. Loops and spurs: The angular power spectrum of the Galactic synchrotron background. J. Cosmol. Astropart. Phys. 2013, 2013, 041. [Google Scholar] [CrossRef]
- Vidal, M.; Dickinson, C.; Davies, R.D.; Leahy, J.P. Polarized radio filaments outside the Galactic plane. Mon. Not. R. Astron. Soc. 2015, 452, 656–675. [Google Scholar] [CrossRef]
- Han, J.L.; Manchester, R.N.; Berkhuijsen, E.M.; Beck, R. Antisymmetric rotation measures in our Galaxy: Evidence for an A0 dynamo. Astron. Astrophys. 1997, 322, 98–102. [Google Scholar]
- Wolleben, M.; Fletcher, A.; Landecker, T.L.; Carretti, E.; Dickey, J.M.; Gaensler, B.M.; Haverkorn, M.; McClure-Griffiths, N.; Reich, W.; Taylor, A.R. Antisymmetry in the Faraday Rotation Sky Caused by a Nearby Magnetized Bubble. Astrophys. J. 2010, 724, L48–L52. [Google Scholar] [CrossRef]
- Hill, A.S.; Landecker, T.L.; Carretti, E.; Douglas, K.; Schnitzeler, D.H.F.M. The Fan Region at 1.5 GHz. I: Polarized synchrotron emission extending beyond the Perseus Arm. Mon. Not. R. Astron. Soc. 2017, 467, 1–17. [Google Scholar] [CrossRef]
- Frisch, P.C.; Redfield, S.; Slavin, J.D. The Interstellar Medium Surrounding the Sun. Annu. Rev. Astron. Astrophys. 2011, 49, 237–279. [Google Scholar] [CrossRef]
- Alves, M.I.R.; Boulanger, F.; Ferriere, K.; Montier, L. The Local Bubble: A magnetic veil to our Galaxy. Astron. Astrophys. 2018, 611, L5. [Google Scholar] [CrossRef]
- Su, M.; Slatyer, T.R.; Finkbeiner, D.P. Giant Gamma-ray Bubbles from Fermi-LAT: AGN Activity or Bipolar Galactic Wind? Astrophys. J. 2010, 724, 1044–1082. [Google Scholar]
- Carretti, E.; Crocker, R.M.; Staveley-Smith, L.; Haverkorn, M.; Purcell, C.; Gaensler, B.M.; Bernardi, G.; Kesteven, M.J.; Poppi, S. Giant magnetized outflows from the centre of the Milky Way. Nature 2013, 493, 66–69. [Google Scholar] [CrossRef]
- Seta, A.; Shukurov, A.; Wood, T.S.; Bushby, P.J.; Snodin, A.P. Relative distribution of cosmic rays and magnetic fields. Mon. Not. R. Astron. Soc. 2017, 473, 4544–4557. [Google Scholar] [CrossRef]
- Fanciullo, L.; Guillet, V.; Boulanger, F.; Jones, A. Interplay of dust alignment, grain growth and magnetic fields in polarization: Lessons from the emission-to-extinction ratio. Astron. Astrophys. 2017, 602, A7. [Google Scholar] [CrossRef]
- Keane, E.F.; Bhattacharyya, B.; Kramer, M.; Stappers, B.W.; Bates, S.D.; Burgay, M.; Chatterjee, S.; Champion, D.J.; Eatough, R.P.; Hessels, J.W.T.; et al. A Cosmic Census of Radio Pulsars with the SKA. Proceedings of Advancing Astrophysics with the Square Kilometre Array (AASKA14), Giardini Naxos, Italy, 9–13 June 2015; p. 40. [Google Scholar]
- The HAWC Collaboration. All-Sky Measurement of the Anisotropy of Cosmic Rays at 10 TeV and Mapping of the Local Interstellar Magnetic Field. Astrophys. J. 2019, 871, 96. [Google Scholar] [CrossRef]
- Lazarian, A.; Yuen, K.H. Gradients of Synchrotron Polarization: Tracing 3D distribution of magnetic fields. Astrophys. J. 2018, 865, 59. [Google Scholar] [CrossRef]
- Ho, K.W.; Yuen, K.H.; Leung, P.K.; Lazarian, A. A comparison between Faraday Tomography and Synchrotron Polarization Gradients. arXiv 2019, arXiv:1901.07731. [Google Scholar]
- Green, J.A.; McClure-Griffiths, N.M.; Caswell, J.L.; Robishaw, T.; Harvey-Smith, L.; Mao, S.A. MAGMO: Mapping the Galactic Magnetic field through OH masers. Proc. Int. Astron. Union 2012, 10, 402. [Google Scholar] [CrossRef]
- Boulanger, F.; Ensslin, T.; Fletcher, A.; Girichides, P.; Hackstein, S.; Haverkorn, M.; Hörandel, J.R.; Jaffe, T.; Jasche, J.; Kachelriess, M.; et al. IMAGINE: A comprehensive view of the interstellar medium, Galactic magnetic fields and cosmic rays. J. Cosmol. Astropart. Phys. 2018, 8, 049. [Google Scholar] [CrossRef]
- Pakmor, R.; Gomez, F.A.; Grand, R.J.J.; Marinacci, F.; Simpson, C.M.; Springel, V.; Campbell, D.J.R.; Frenk, C.S.; Guillet, T.; Pfrommer, C.; White, S.D.M. Magnetic field formation in the Milky Way-like disk galaxies of the Auriga project. Mon. Not. R. Astron. Soc. 2017, 469, 3185–3199. [Google Scholar] [CrossRef]
| 1. | |
| 2. | |
| 3. | |
| 4. | |
| 5. | |
| 6. | |
| 7. | |
| 8. | |
| 9. |
| Observable | GMF Property Probed | Dependencies | Pros | Cons |
|---|---|---|---|---|
| Starlight polarization | orientation | dust grain properties and distribution | 3D information | sampling limited to a few kpc |
| Faraday rotation (extragalactic) | direction and strength | thermal electron density | good full-sky sampling (42k sources); full LOS through Galaxy | no 3D info along LOS |
| Faraday rotation (Galactic) | direction and strength | thermal electron density | 3D sampling along the LOS through the Galaxy | mostly in Galactic plane; currently insufficient sampling (1k) |
| Faraday tomography (extragalactic) | direction and strength | thermal electron density | probes variations along the LOS through the Galaxy | low physical resolution, not a probe of the Milky Way |
| Faraday tomography (Galactic) | direction and strength | thermal electron density | probes variations in 3D along the LOS | no physical distances associated with Faraday depth variations |
| Diffuse synchrotron emission (radio) | orientation and strength (squared) | cosmic-ray density; thermal electron density | goes as ; full-sky coverage; probes turbulent Faraday effects | no 3D info along LOS; polarization horizon of a few kpc due to Faraday depolarization effects |
| Diffuse synchrotron emission (microwave) | orientation and strength (squared) | cosmic-ray density | goes as ; full-sky coverage; full LOS through the Galaxy; no Faraday rotation | no 3D info along LOS; total intensity contaminated by Bremsstrahlung and AME. |
| Diffuse dust emission | orientation | dust grain density, properties, environment, and alignment | full-sky coverage; full LOS through the Galaxy; 3D information with extinction surveys (e.g., Gaia) no Faraday rotation | probes only close to Galactic plane pc |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jaffe, T. Practical Modeling of Large-Scale Galactic Magnetic Fields: Status and Prospects. Galaxies 2019, 7, 52. https://doi.org/10.3390/galaxies7020052
Jaffe T. Practical Modeling of Large-Scale Galactic Magnetic Fields: Status and Prospects. Galaxies. 2019; 7(2):52. https://doi.org/10.3390/galaxies7020052
Chicago/Turabian StyleJaffe, Tess R. 2019. "Practical Modeling of Large-Scale Galactic Magnetic Fields: Status and Prospects" Galaxies 7, no. 2: 52. https://doi.org/10.3390/galaxies7020052
APA StyleJaffe, T. (2019). Practical Modeling of Large-Scale Galactic Magnetic Fields: Status and Prospects. Galaxies, 7(2), 52. https://doi.org/10.3390/galaxies7020052





