Revisiting the Equipartition Assumption in Star-Forming Galaxies
Abstract
1. Introduction
2. Cosmic Rays and Magnetic Fields: Why Do We Expect Energy Equipartition?
3. The Equipartition Method
3.1. Basic Assumptions
3.2. Restrictions
4. Inferences from Observations
4.1. Definition of Magnetic Field Components
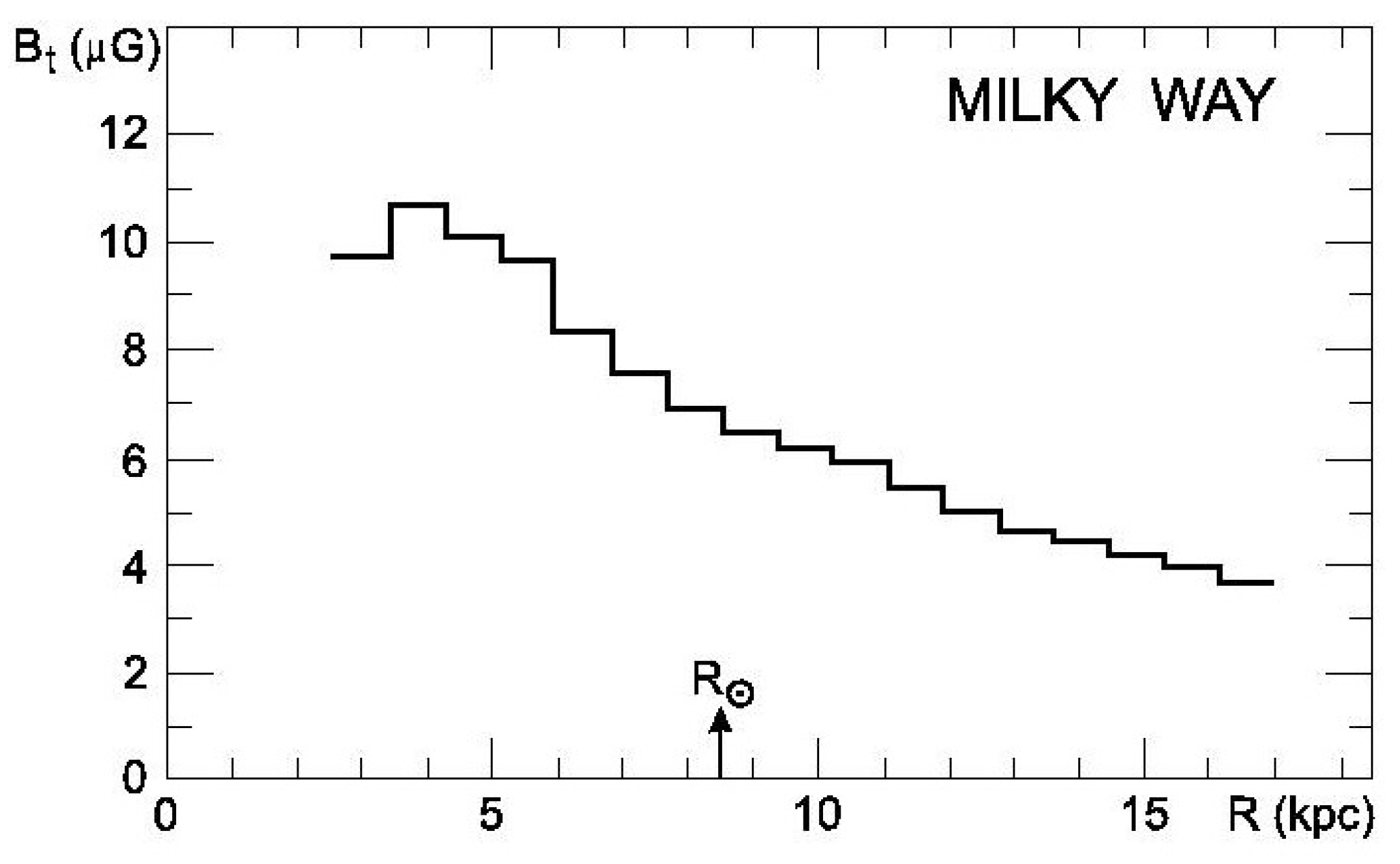
4.2. Equipartition Estimates in Galaxies
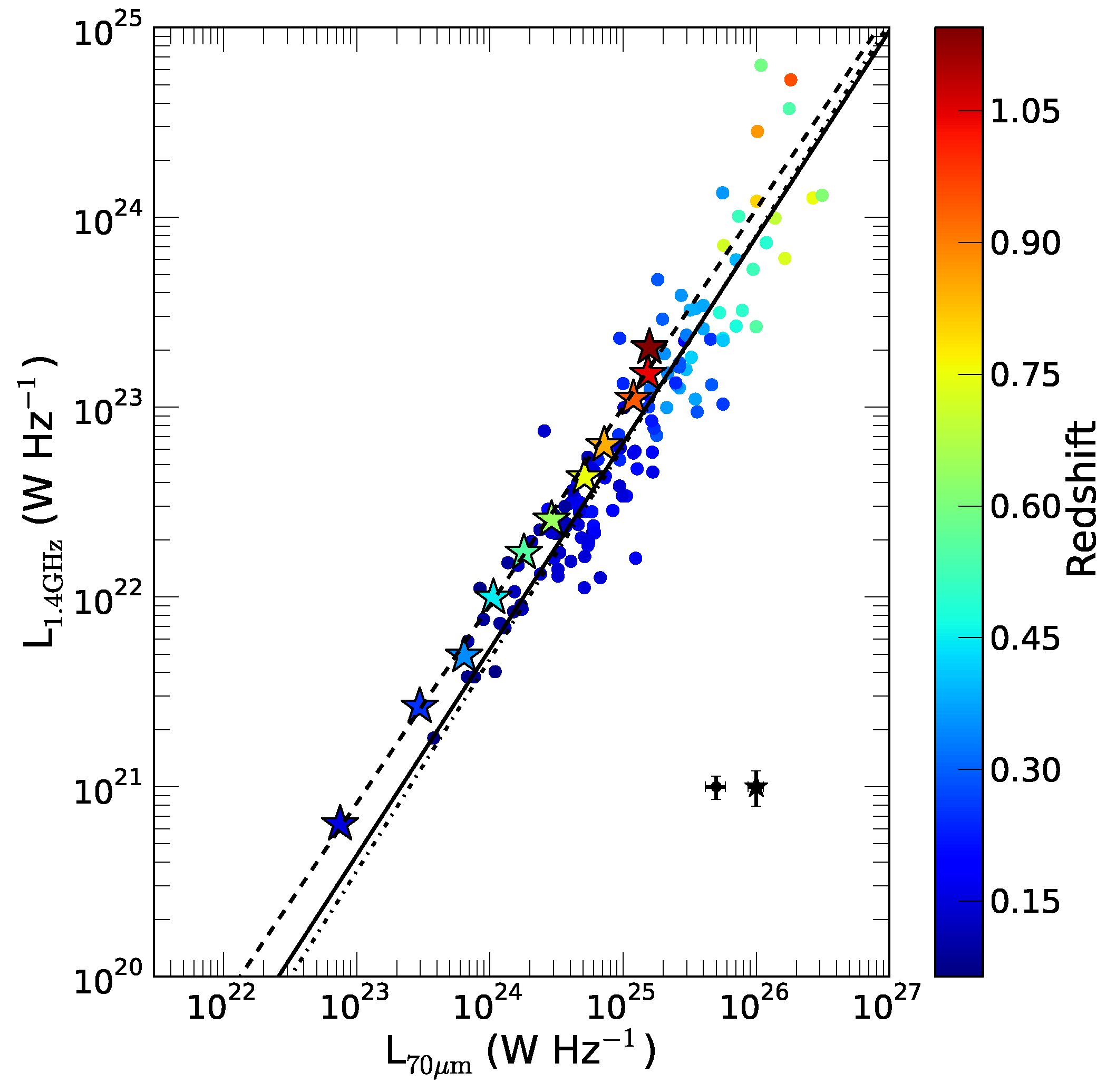
4.3. How Do Magnetic Field Strengths Derived from the Equipartition Assumption Compare with Those from Other Methods?
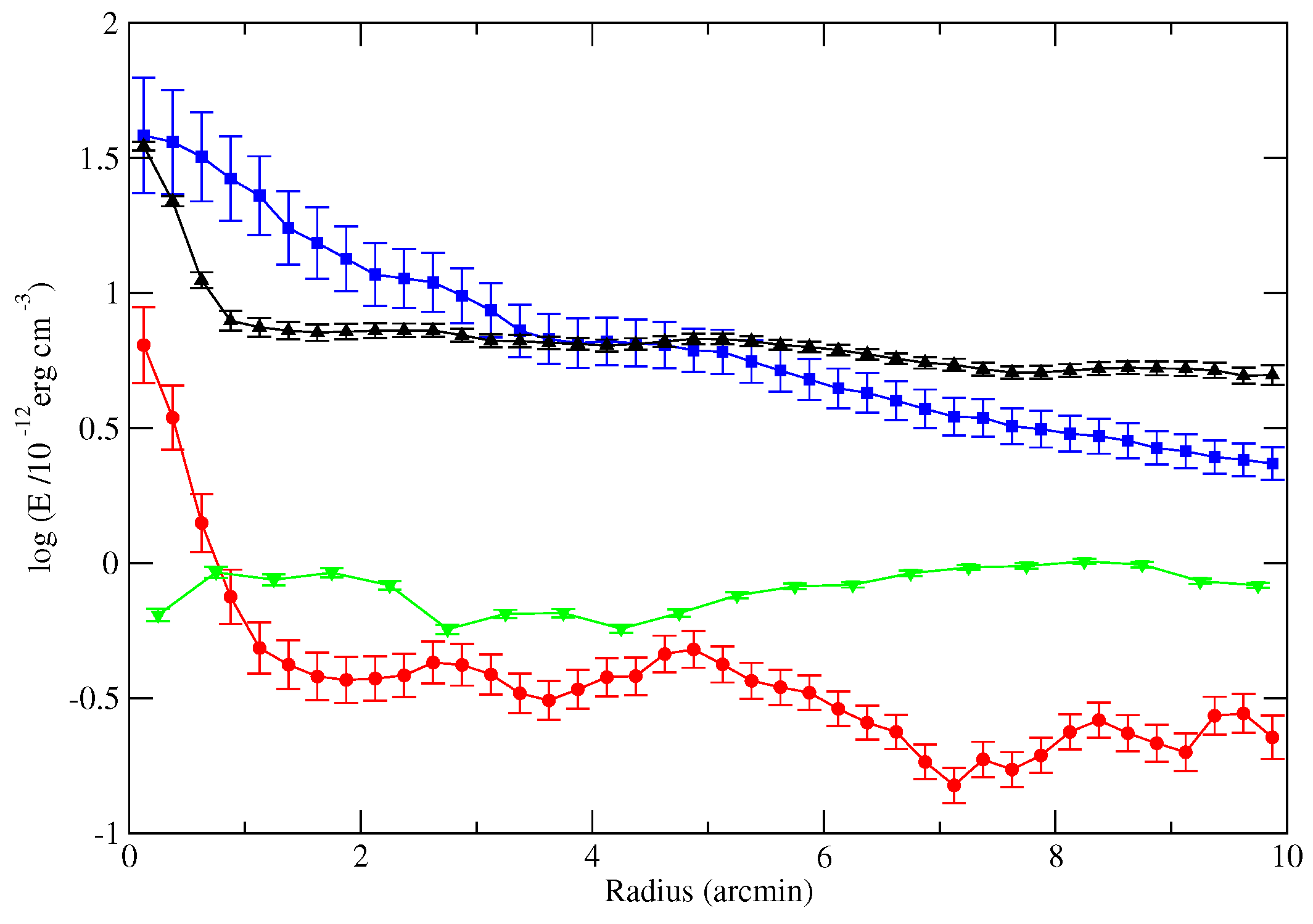
4.4. Observational Indications for Deviations from the Equipartition Assumption
5. Testing of the Equipartition Assumption at Small Scales from Direct Numerical Simulations
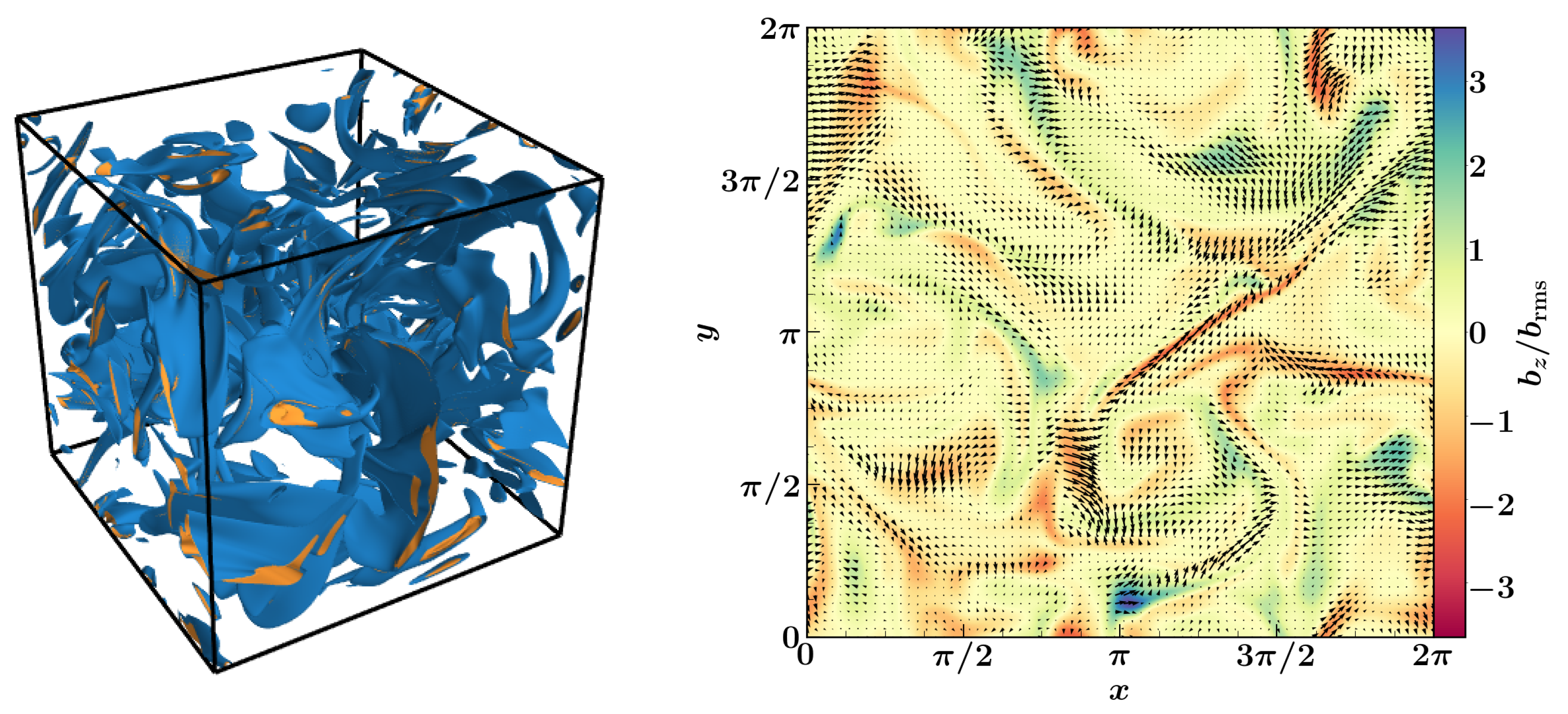
5.1. Cosmic Ray–Magnetic Field Interaction
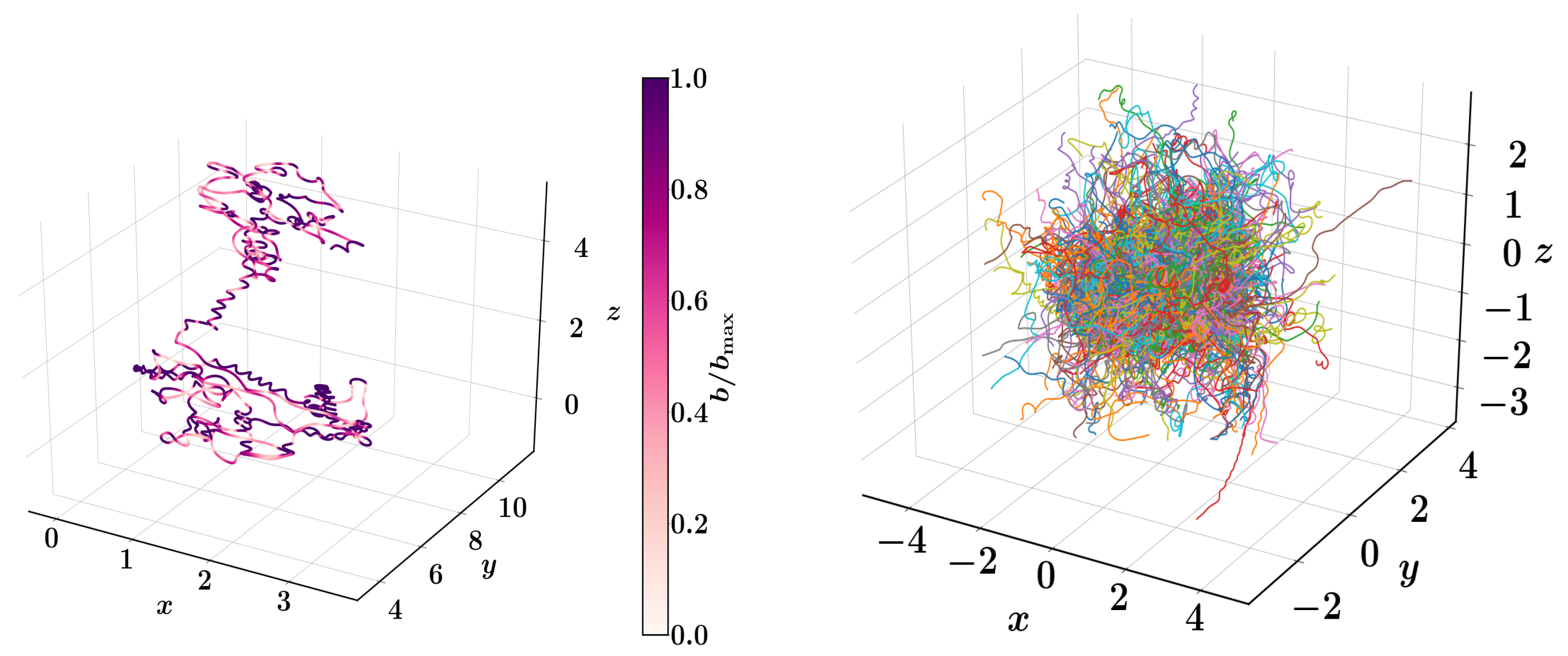
5.2. Cosmic Rays as Test-Particles
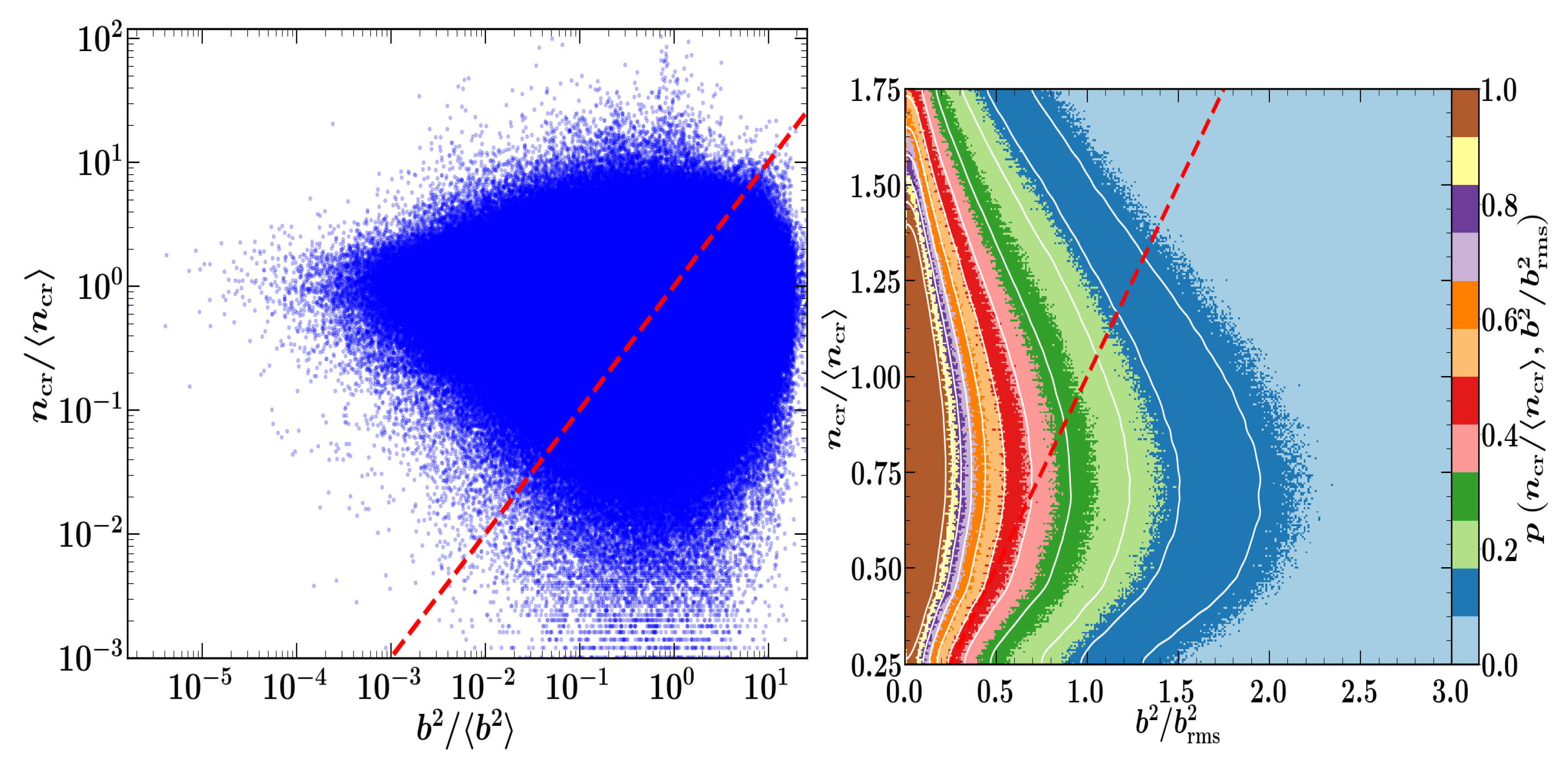
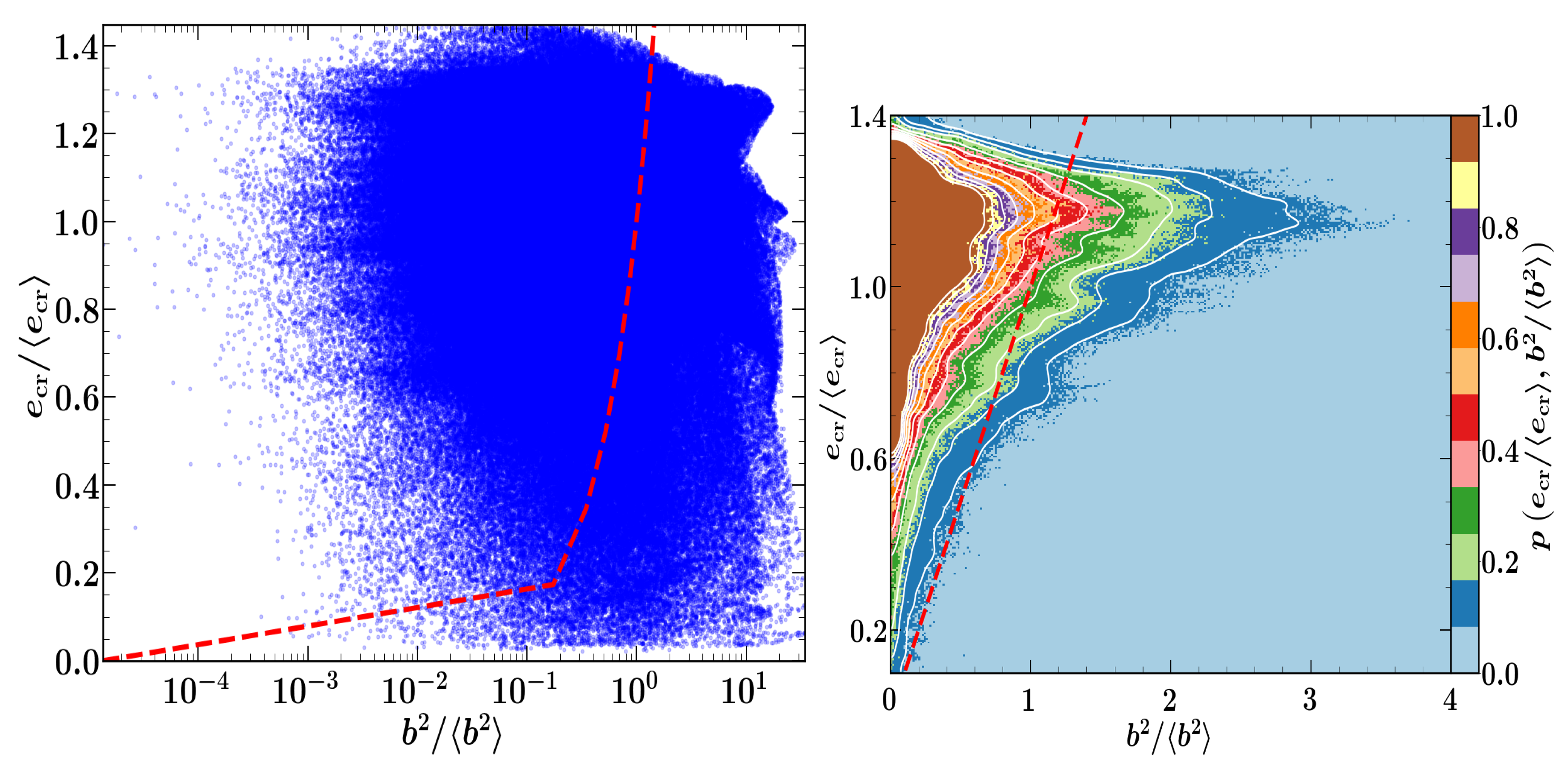
5.3. Cosmic Rays as a Diffusive Fluid in MHD Turbulence
6. Conclusions, Discussion and Future Directions of Research
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Boulares, A.; Cox, D.P. Galactic Hydrostatic Equilibrium with Magnetic Tension and Cosmic-Ray Diffusion. Astrophys. J. 1990, 365, 544. [Google Scholar] [CrossRef]
- Kulsrud, R.; Pearce, W.P. The Effect of Wave-Particle Interactions on the Propagation of Cosmic Rays. Astrophys. J. 1969, 156, 445. [Google Scholar] [CrossRef]
- Wentzel, D.G. Cosmic-ray propagation in the Galaxy—Collective effects. Annu. Rev. Astron. Astrophys. 1974, 12, 71–96. [Google Scholar] [CrossRef]
- Zweibel, E.G. The microphysics and macrophysics of cosmic raysa. Phys. Plasmas 2013, 20, 055501. [Google Scholar] [CrossRef]
- Shukurov, A.; Snodin, A.P.; Seta, A.; Bushby, P.J.; Wood, T.S. Cosmic Rays in Intermittent Magnetic Fields. Astrophys. J. Lett. 2017, 839, L16. [Google Scholar] [CrossRef]
- Birnboim, Y.; Balberg, S.; Teyssier, R. Galaxy evolution: Modelling the role of non-thermal pressure in the interstellar medium. Month. Not. R. Astron. Soc. 2015, 447, 3678–3692. [Google Scholar] [CrossRef][Green Version]
- Krumholz, M.R.; Federrath, C. The Role of Magnetic Fields in Setting the Star Formation Rate and the Initial Mass Function. arXiv 2019, arXiv:1902.02557. [Google Scholar] [CrossRef]
- Bendre, A.; Gressel, O.; Elstner, D. Dynamo saturation in direct simulations of the multi-phase turbulent interstellar medium. Astron. Nachr. 2015, 336, 991. [Google Scholar] [CrossRef]
- Shukurov, A.; Evirgen, C.C.; Fletcher, A.; Bushby, P.J.; Gent, F.A. Magnetic field effects on the ISM structure and galactic outflows. arXiv 2018, arXiv:1810.01202. [Google Scholar]
- Klein, U.; Fletcher, A. Galactic and Intergalactic Magnetic Fields; Springer Praxis Books, Springer International Publishing: Heidelberg, Germany, 2015. [Google Scholar]
- Beck, R.; Brandenburg, A.; Moss, D.; Shukurov, A.; Sokoloff, D. Galactic Magnetism: Recent Developments and Perspectives. Annu. Rev. Astron. Astrophys. 1996, 34, 155–206. [Google Scholar] [CrossRef]
- Brandenburg, A.; Subramanian, K. Astrophysical magnetic fields and nonlinear dynamo theory. Phys. Rep. 2005, 417, 1–209. [Google Scholar] [CrossRef]
- Minter, A.H.; Spangler, S.R. Observation of Turbulent Fluctuations in the Interstellar Plasma Density and Magnetic Field on Spatial Scales of 0.01 to 100 Parsecs. Astrophys. J. 1996, 458, 194. [Google Scholar] [CrossRef]
- Haverkorn, M.; Brown, J.C.; Gaensler, B.M.; McClure-Griffiths, N.M. The Outer Scale of Turbulence in the Magnetoionized Galactic Interstellar Medium. Astrophys. J. 2008, 680, 362–370. [Google Scholar] [CrossRef]
- Iacobelli, M.; Haverkorn, M.; Orrú, E.; Pizzo, R.F.; Anderson, J.; Beck, R.; Bell, M.R.; Bonafede, A.; Chyzy, K.; Dettmar, R.J.; et al. Studying Galactic interstellar turbulence through fluctuations in synchrotron emission. First LOFAR Galactic foreground detection. Astron. Astrophys. 2013, 558, A72. [Google Scholar] [CrossRef]
- Ohno, H.; Shibata, S. The random magnetic field in the Galaxy. Month. Not. R. Astron. Soc. 1993, 262, 953–962. [Google Scholar] [CrossRef]
- Gaensler, B.M.; Haverkorn, M.; Staveley-Smith, L.; Dickey, J.M.; McClure-Griffiths, N.M.; Dickel, J.R.; Wolleben, M. The Magnetic Field of the Large Magellanic Cloud Revealed Through Faraday Rotation. Science 2005, 307, 1610–1612. [Google Scholar] [CrossRef]
- Fletcher, A.; Beck, R.; Shukurov, A.; Berkhuijsen, E.M.; Horellou, C. Magnetic fields and spiral arms in the galaxy M51. Month. Not. R. Astron. Soc. 2011, 412, 2396–2416. [Google Scholar] [CrossRef]
- Houde, M.; Fletcher, A.; Beck, R.; Hildebrand, R.H.; Vaillancourt, J.E.; Stil, J.M. Characterizing Magnetized Turbulence in M51. Astrophys. J. 2013, 766, 49. [Google Scholar] [CrossRef]
- Longair, M.S. High Energy Astrophysics. Volume 2. Stars, the Galaxy and the Interstellar Medium; Cambridge University Press: Cambridge, UK, 1994. [Google Scholar]
- Bell, A.R. The acceleration of cosmic rays in shock fronts. I. Month. Not. R. Astron. Soc. 1978, 182, 147–156. [Google Scholar] [CrossRef]
- Bell, A.R. The acceleration of cosmic rays in shock fronts. II. Month. Not. R. Astron. Soc. 1978, 182, 443–455. [Google Scholar] [CrossRef]
- Blandford, R.D.; Ostriker, J.P. Particle acceleration by astrophysical shocks. Astrophys. J. Lett. 1978, 221, L29–L32. [Google Scholar] [CrossRef]
- Drury, L.O. An introduction to the theory of diffusive shock acceleration of energetic particles in tenuous plasmas. Rep. Prog. Phys. 1983, 46, 973. [Google Scholar] [CrossRef]
- Burbidge, G.R. On Synchrotron Radiation from Messier 87. Astrophys. J. 1956, 124, 416. [Google Scholar] [CrossRef]
- Stepanov, R.; Fletcher, A.; Shukurov, A.; Beck, R.; La Porta, L.; Tabatabaei, F.S. Relative distributions of cosmic ray electrons and magnetic fields in the ISM. In Cosmic Magnetic Fields: From Planets, to Stars and Galaxies; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Stepanov, R.; Shukurov, A.; Fletcher, A.; Beck, R.; La Porta, L.; Tabatabaei, F. An observational test for correlations between cosmic rays and magnetic fields. Month. Not. R. Astron. Soc. 2014, 437, 2201–2216. [Google Scholar] [CrossRef]
- Pohl, M. On the predictive power of the minimum energy condition. I—Isotropic steady-state configurations. Astron. Astrophys. 1993, 270, 91–101. [Google Scholar]
- Arbutina, B.; Urošević, D.; Andjelić, M.M.; Pavlović, M.Z.; Vukotić, B. Modified Equipartition Calculation for Supernova Remnants. Astrophys. J. 2012, 746, 79. [Google Scholar] [CrossRef]
- Caprioli, D. Understanding hadronic gamma-ray emission from supernova remnants. J. Cosmol. Astropart. Phys. 2011, 5, 026. [Google Scholar] [CrossRef]
- Morlino, G.; Caprioli, D. Strong evidence for hadron acceleration in Tycho’s supernova remnant. Astron. Astrophys. 2012, 538, A81. [Google Scholar] [CrossRef]
- Strong, A.W.; Moskalenko, I.V.; Reimer, O. Diffuse Galactic Continuum Gamma Rays: A Model Compatible with EGRET Data and Cosmic-Ray Measurements. Astrophys. J. 2004, 613, 962–976. [Google Scholar] [CrossRef]
- Picozza, P.; Marcelli, L.; Adriani, O.; Barbarino, G.C.; Bazilevskaya, G.A.; Bellotti, R.; Boezio, M.; Bogomolov, E.A.; Bongi, M.; Bonvicini, V.; et al. Cosmic Ray Study with the PAMELA Experiment. J. Phys. Conf. Ser. 2013, 409, 012003. [Google Scholar] [CrossRef]
- Beck, R.; Krause, M. Revised equipartition and minimum energy formula for magnetic field strength estimates from radio synchrotron observations. Astron. Nachr. 2005, 326, 414–427. [Google Scholar] [CrossRef]
- Fitt, A.J.; Alexander, P. Magnetic fields in late-type galaxies. Month. Not. R. Astron. Soc. 1993, 261, 445–452. [Google Scholar] [CrossRef][Green Version]
- Lacki, B.C.; Beck, R. The equipartition magnetic field formula in starburst galaxies: Accounting for pionic secondaries and strong energy losses. Month. Not. R. Astron. Soc. 2013, 430, 3171–3186. [Google Scholar] [CrossRef]
- Niklas, S. Eigenschaften von Spiralgalaxien im Hochfrequenten Radiokontinuum. Ph.D. Thesis, University of Bonn, Bonn, Germany, 1995. [Google Scholar]
- Beuermann, K.; Kanbach, G.; Berkhuijsen, E.M. Radio structure of the Galaxy—Thick disk and thin disk at 408 MHz. Astron. Astrophys. 1985, 153, 17–34. [Google Scholar]
- Beck, R. Magnetic fields in the nearby spiral galaxy IC 342: A multi-frequency radio polarization study. Astron. Astrophys. 2015, 578, A93. [Google Scholar] [CrossRef]
- Basu, A.; Roy, S. Magnetic fields in nearby normal galaxies: Energy equipartition. Month. Not. R. Astron. Soc. 2013, 433, 1675–1686. [Google Scholar] [CrossRef]
- Chamandy, L.; Singh, N.K. Non-linear galactic dynamos and the magnetic Rädler effect. Month. Not. R. Astron. Soc. 2018, 481, 1300–1319. [Google Scholar] [CrossRef]
- Bell, E.F. Estimating Star Formation Rates from Infrared and Radio Luminosities: The Origin of the Radio-Infrared Correlation. Astrophys. J. 2003, 586, 794–813. [Google Scholar] [CrossRef]
- Basu, A.; Wadadekar, Y.; Beelen, A.; Singh, V.; Archana, K.N.; Sirothia, S.; Ishwara-Chandra, C.H. Radio-Far-infrared Correlation in “Blue Cloud” Galaxies with 0 < z < 1.2. Astrophys. J. 2015, 803, 51. [Google Scholar] [CrossRef]
- Price, R.; Duric, N. New results on the radio-far-infrared relation for galaxies. Astrophys. J. 1992, 401, 81–86. [Google Scholar] [CrossRef]
- Niklas, S.; Beck, R. A new approach to the radio-far infrared correlation for non-calorimeter galaxies. Astron. Astrophys. 1997, 320, 54–64. [Google Scholar]
- Hoernes, P.; Berkhuijsen, E.M.; Xu, C. Radio-FIR correlations within M 31. Astron. Astrophys. 1998, 334, 57–70. [Google Scholar]
- Beck, R. Magnetism in the spiral galaxy NGC 6946: Magnetic arms, depolarization rings, dynamo modes, and helical fields. Astron. Astrophys. 2007, 470, 539–556. [Google Scholar] [CrossRef]
- Han, J.L.; Ferriere, K.; Manchester, R.N. The Spatial Energy Spectrum of Magnetic Fields in Our Galaxy. Astrophys. J. 2004, 610, 820–826. [Google Scholar] [CrossRef]
- Han, J.L.; Manchester, R.N.; Lyne, A.G.; Qiao, G.J.; van Straten, W. Pulsar Rotation Measures and the Large-Scale Structure of the Galactic Magnetic Field. Astrophys. J. 2006, 642, 868–881. [Google Scholar] [CrossRef]
- Crutcher, R.M.; Wandelt, B.; Heiles, C.; Falgarone, E.; Troland, T.H. Magnetic Fields in Interstellar Clouds from Zeeman Observations: Inference of Total Field Strengths by Bayesian Analysis. Astrophys. J. 2010, 725, 466–479. [Google Scholar] [CrossRef]
- Crutcher, R.M. Magnetic Fields in Molecular Clouds. Annu. Rev. Astron. Astrophys. 2012, 50, 29–63. [Google Scholar] [CrossRef]
- Burlaga, L.F.; Ness, N.F. Observations of the Interstellar Magnetic Field in the Outer Heliosheath: Voyager 1. Astrophys. J. 2016, 829, 134. [Google Scholar] [CrossRef]
- Zirnstein, E.J.; Heerikhuisen, J.; Funsten, H.O.; Livadiotis, G.; McComas, D.J.; Pogorelov, N.V. Local Interstellar Magnetic Field Determined from the Interstellar Boundary Explorer Ribbon. Astrophys. J. Lett. 2016, 818, L18. [Google Scholar] [CrossRef]
- Govoni, F.; Feretti, L. Magnetic Fields in Clusters of Galaxies. Int. J. Mod. Phys. D 2004, 13, 1549–1594. [Google Scholar] [CrossRef]
- Yoast-Hull, T.M.; Gallagher, J.S.; Zweibel, E.G. Equipartition and cosmic ray energy densities in central molecular zones of starbursts. Month. Not. R. Astron. Soc. 2016, 457, L29–L33. [Google Scholar] [CrossRef]
- Strong, A.W.; Moskalenko, I.V.; Reimer, O. Diffuse Continuum Gamma Rays from the Galaxy. Astrophys. J. 2000, 537, 763–784. [Google Scholar] [CrossRef]
- Orlando, E.; Strong, A. Galactic synchrotron emission with cosmic ray propagation models. Month. Not. R. Astron. Soc. 2013, 436, 2127–2142. [Google Scholar] [CrossRef]
- Berkhuijsen, E.M.; Beck, R.; Tabatabaei, F.S. How cosmic ray electron propagation affects radio-far-infrared correlations in M 31 and M 33. Month. Not. R. Astron. Soc. 2013, 435, 1598–1609. [Google Scholar] [CrossRef]
- Heesen, V.; Brinks, E.; Leroy, A.K.; Heald, G.; Braun, R.; Bigiel, F.; Beck, R. The Radio Continuum-Star Formation Rate Relation in WSRT SINGS Galaxies. Astron. J. 2014, 147, 103. [Google Scholar] [CrossRef]
- Schleicher, D.R.G.; Beck, R. Star-forming dwarf galaxies: The correlation between far-infrared and radio fluxes. Astron. Astrophys. 2016, 593, A77. [Google Scholar] [CrossRef]
- Filho, M.E.; Tabatabaei, F.S.; Sánchez Almeida, J.; Muñoz-Tuñón, C.; Elmegreen, B.G. Global correlations between the radio continuum, infrared, and CO emissions in dwarf galaxies. Month. Not. R. Astron. Soc. 2019, 484, 543–561. [Google Scholar] [CrossRef]
- Cesarsky, C.J. Cosmic-ray confinement in the galaxy. Annu. Rev. Astron. Astrophys. 1980, 18, 289–319. [Google Scholar] [CrossRef]
- Bhat, P.; Subramanian, K. Fluctuation dynamos and their Faraday rotation signatures. Month. Not. R. Astron. Soc. 2013, 429, 2469–2481. [Google Scholar] [CrossRef]
- Webber, W.R.; Simpson, G.A.; Cane, H.V. Radio emission, cosmic ray electrons, and the production of gamma-rays in the Galaxy. Astrophys. J. 1980, 236, 448–459. [Google Scholar] [CrossRef]
- Webber, W.R. A New Estimate of the Local Interstellar Energy Density and Ionization Rate of Galactic Cosmic Cosmic Rays. Astrophys. J. 1998, 506, 329–334. [Google Scholar] [CrossRef]
- Giacalone, J.; Jokipii, J.R. The Transport of Cosmic Rays across a Turbulent Magnetic Field. Astrophys. J. 1999, 520, 204–214. [Google Scholar] [CrossRef]
- Casse, F.; Lemoine, M.; Pelletier, G. Transport of cosmic rays in chaotic magnetic fields. Phys. Rev. D 2002, 65, 023002. [Google Scholar] [CrossRef]
- Desiati, P.; Zweibel, E.G. The Transport of Cosmic Rays Across Magnetic Fieldlines. Astrophys. J. 2014, 791, 51. [Google Scholar] [CrossRef]
- Snodin, A.P.; Shukurov, A.; Sarson, G.R.; Bushby, P.J.; Rodrigues, L.F.S. Global diffusion of cosmic rays in random magnetic fields. Month. Not. R. Astron. Soc. 2016, 457, 3975–3987. [Google Scholar] [CrossRef]
- Haugen, N.E.; Brandenburg, A.; Dobler, W. Simulations of nonhelical hydromagnetic turbulence. Phys. Rev. E 2004, 70, 016308. [Google Scholar] [CrossRef]
- Wilkin, S.L.; Barenghi, C.F.; Shukurov, A. Magnetic Structures Produced by the Small-Scale Dynamo. Phys. Rev. Lett. 2007, 99, 134501. [Google Scholar] [CrossRef]
- Seta, A.; Shukurov, A.; Wood, T.S.; Bushby, P.J.; Snodin, A.P. Relative distribution of cosmic rays and magnetic fields. Month. Not. R. Astron. Soc. 2018, 473, 4544–4557. [Google Scholar] [CrossRef]
- Snodin, A.P.; Brandenburg, A.; Mee, A.J.; Shukurov, A. Simulating field-aligned diffusion of a cosmic ray gas. Month. Not. R. Astron. Soc. 2006, 373, 643–652. [Google Scholar] [CrossRef]
- Rodrigues, L.F.S.; Snodin, A.P.; Sarson, G.R.; Shukurov, A. Fickian and non-Fickian diffusion of cosmic rays. arXiv 2018, arXiv:1809.07194. [Google Scholar]
- Berezinskii, V.S.; Bulanov, S.V.; Dogiel, V.A.; Ptuskin, V.S. Astrophysics of Cosmic Rays; North-Holland: Amsterdam, The Netherlands, 1990. [Google Scholar]
- Shukurov, A. Introduction to galactic dynamos. arXiv 2004, arXiv:astro-ph/0411739. [Google Scholar]
- Gaensler, B.M.; Haverkorn, M.; Burkhart, B.; Newton-McGee, K.J.; Ekers, R.D.; Lazarian, A.; McClure-Griffiths, N.M.; Robishaw, T.; Dickey, J.M.; Green, A.J. Low-Mach-number turbulence in interstellar gas revealed by radio polarization gradients. Nature 2011, 478, 214–217. [Google Scholar] [CrossRef]
- Beck, R.; Bomans, D.; Colafrancesco, S.; Dettmar, R.J.; Ferrière, K.; Fletcher, A.; Heald, G.; Heesen, V.; Horellou, C.; Krause, M.; et al. Structure, dynamical impact and origin of magnetic fields in nearby galaxies in the SKA era. Proc. Sci. 2015, 215. [Google Scholar] [CrossRef]
- de Angelis, A.; Tatischeff, V.; Grenier, I.A.; McEnery, J.; Mallamaci, M.; Tavani, M.; Oberlack, U.; Hanlon, L.; Walter, R.; Argan, A.; et al. Science with e-ASTROGAM. A space mission for MeV-GeV gamma-ray astrophysics. J. High Energy Astrophys. 2018, 19, 1–106. [Google Scholar] [CrossRef]
- Skilling, J. Cosmic Rays in the Galaxy: Convection or Diffusion? Astrophys. J. 1971, 170, 265. [Google Scholar] [CrossRef]
- Sharma, P.; Colella, P.; Martin, D. Numerical Implementation of Streaming Down the Gradient: Application to Fluid Modelling of Cosmic Rays and Saturated Conduction. SIAM J. Sci. Comput. 2010, 32, 3564–3583. [Google Scholar] [CrossRef][Green Version]
- Thomas, T.; Pfrommer, C. Cosmic-ray hydrodynamics: Alfvén-wave regulated transport of cosmic rays. Month. Not. R. Astron. Soc. 2019, 485. [Google Scholar] [CrossRef]
- Ruszkowski, M.; Yang, H.Y.K.; Zweibel, E. Global Simulations of Galactic Winds Including Cosmic-ray Streaming. Astrophys. J. 2017, 834, 208. [Google Scholar] [CrossRef]
- Zweibel, E.G. The basis for cosmic ray feedback: Written on the wind. Phys. Plasmas 2017, 24, 055402. [Google Scholar] [CrossRef]
- Heintz, E.; Zweibel, E.G. The Parker Instability with Cosmic-Ray Streaming. Astrophys. J. 2018, 860, 97. [Google Scholar] [CrossRef]
- Gent, F.A.; Shukurov, A.; Fletcher, A.; Sarson, G.R.; Mantere, M.J. The supernova-regulated ISM—I. The multiphase structure. Month. Not. R. Astron. Soc. 2013, 432, 1396–1423. [Google Scholar] [CrossRef]
- Li, M.; Ostriker, J.P.; Cen, R.; Bryan, G.L.; Naab, T. Supernova Feedback and the Hot Gas Filling Fraction of the Interstellar Medium. Astrophys. J. 2015, 814, 4. [Google Scholar] [CrossRef]
- Kim, C.G.; Ostriker, E.C. Three-phase Interstellar Medium in Galaxies Resolving Evolution with Star Formation and Supernova Feedback (TIGRESS): Algorithms, Fiducial Model, and Convergence. Astrophys. J. 2017, 846, 133. [Google Scholar] [CrossRef]
| 1. | |
| 2. | Arbutina et al. [29] argue that K is smaller if the injection energy is comparable to or larger than the electron’s rest mass energy. |
| 3. | If the IR emission emerges mostly from the cool dust that is heated by the general interstellar radiation field, the exponent of the correlation can be smaller than one [46]. |
| 4. | |
| 5. | In an ideal situation, a perfectly isotropic and homogeneous distribution would always remain isotropic and homogeneous in a static magnetic field due to Liouville’s theorem. |
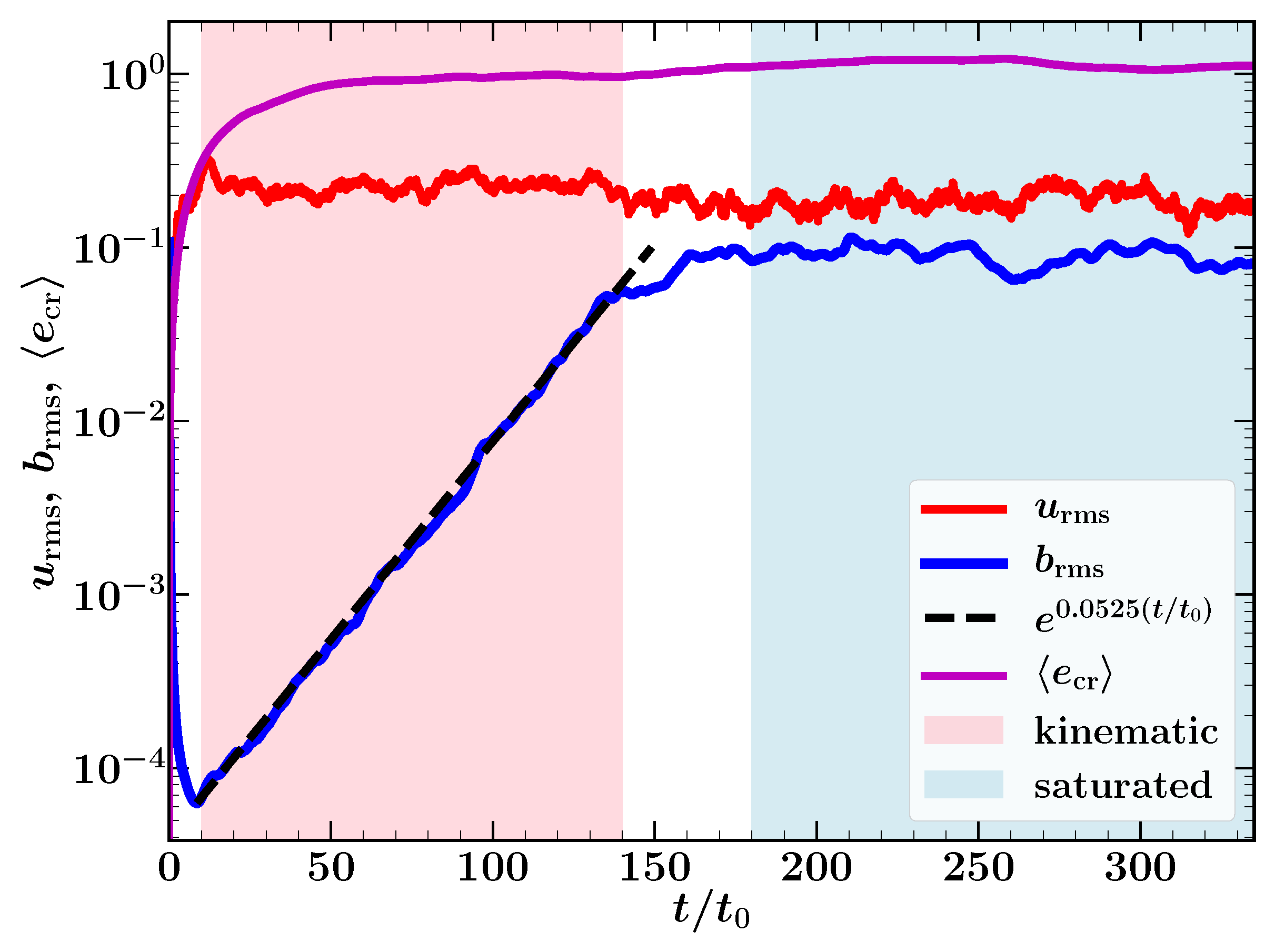
| 6. | For a GeV cosmic ray particle in a magnetic field, the parallel cosmic ray diffusivity in the ISM is approximately [75]. This number is not yet accessible in numerical simulations where the turbulence is driven at the box scale of a physical size 100 pc. Therefore, we also decrease the magnetic field diffusivity in our simulations. The magnetic field in the ISM mostly diffuses via turbulent diffusion with the diffusivity of the order of [76]. Thus, in our numerical simulations, we chose and such that the ratio of these two terms is . |
| 7. | The seed magnetic field is initialized to be a Gaussian random magnetic field, which is not a solution of the induction equation. Thus, the field decays initially as shown in Figure 7. |
| Parameter | Numerical Value | ISM Value |
|---|---|---|
| kF | 1 and 2 | 100 pc and 50 pc |
| 0 | 0 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seta, A.; Beck, R. Revisiting the Equipartition Assumption in Star-Forming Galaxies. Galaxies 2019, 7, 45. https://doi.org/10.3390/galaxies7020045
Seta A, Beck R. Revisiting the Equipartition Assumption in Star-Forming Galaxies. Galaxies. 2019; 7(2):45. https://doi.org/10.3390/galaxies7020045
Chicago/Turabian StyleSeta, Amit, and Rainer Beck. 2019. "Revisiting the Equipartition Assumption in Star-Forming Galaxies" Galaxies 7, no. 2: 45. https://doi.org/10.3390/galaxies7020045
APA StyleSeta, A., & Beck, R. (2019). Revisiting the Equipartition Assumption in Star-Forming Galaxies. Galaxies, 7(2), 45. https://doi.org/10.3390/galaxies7020045




