On the Connection of Radio and γ-Ray Emission in Blazars
Abstract
1. Introduction
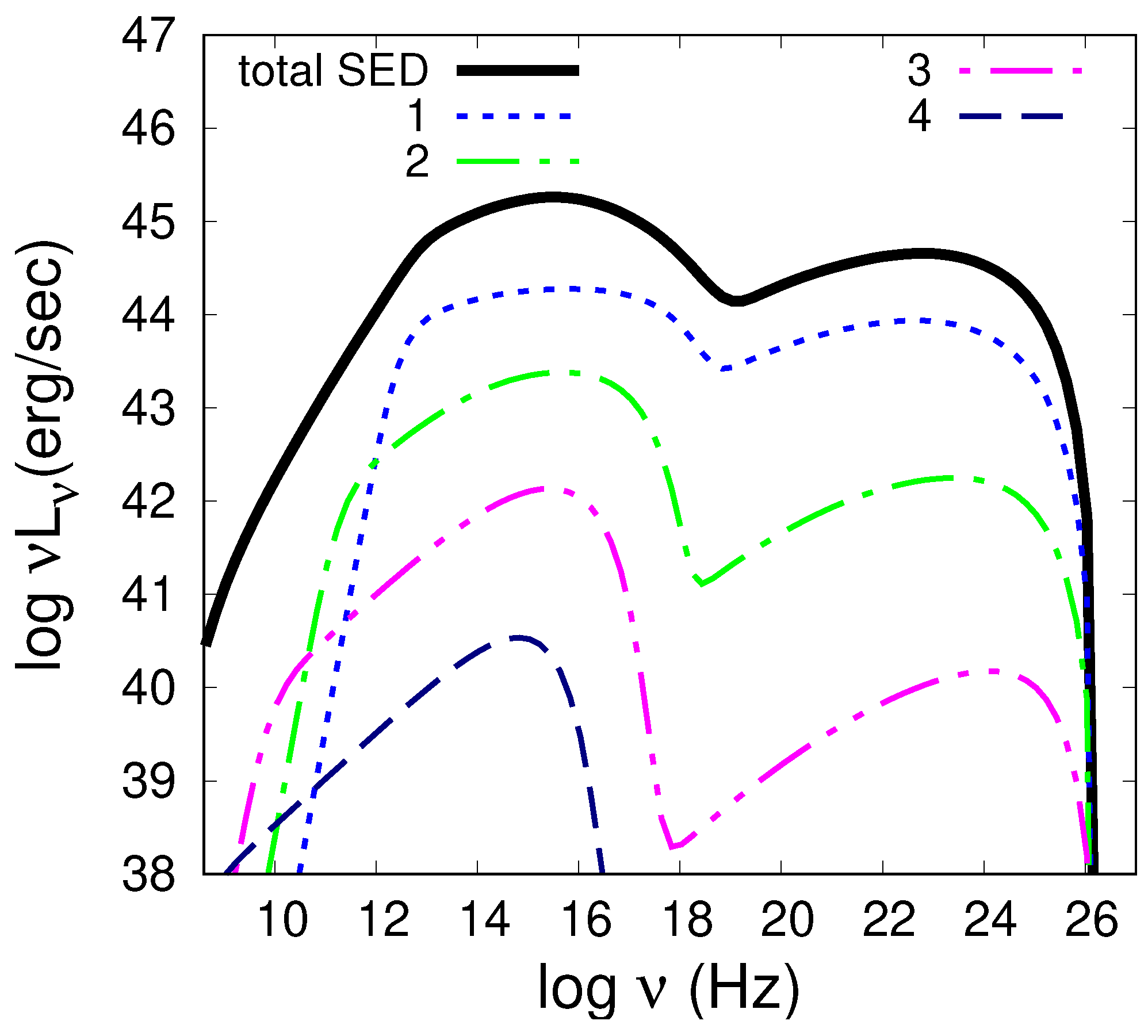
2. Model Description and Numerical Approach
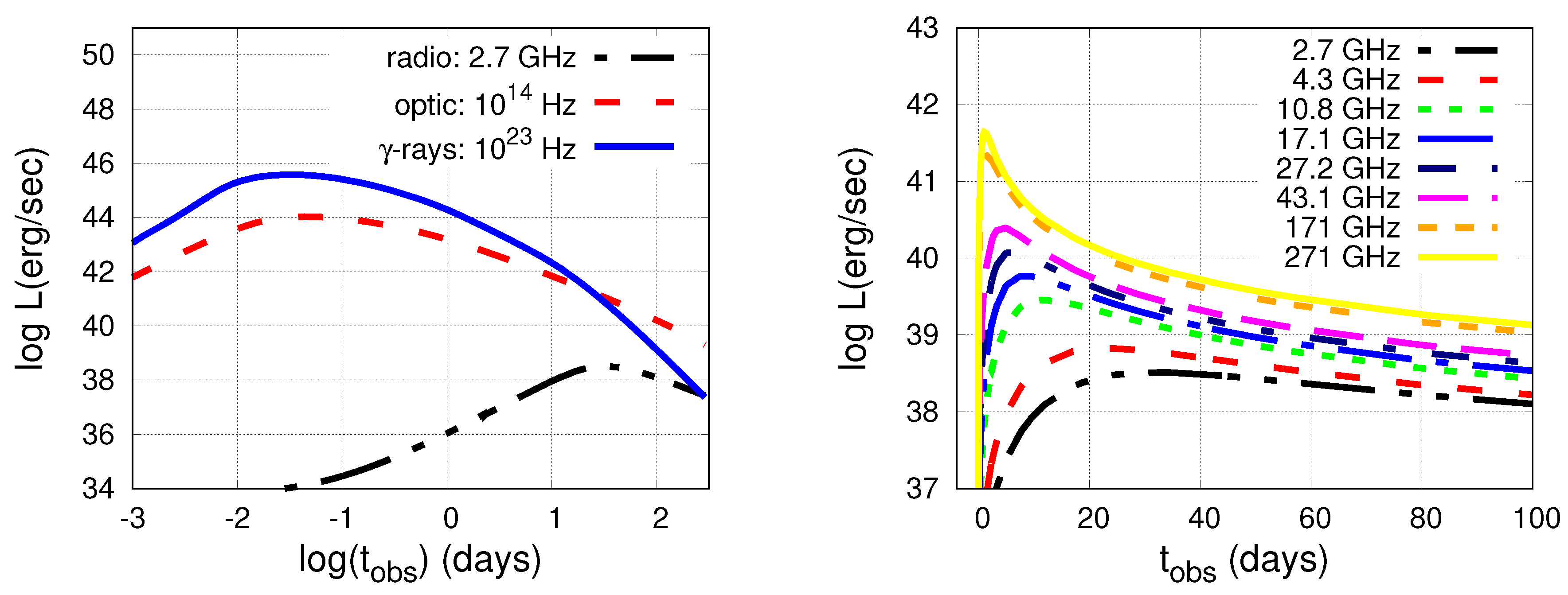
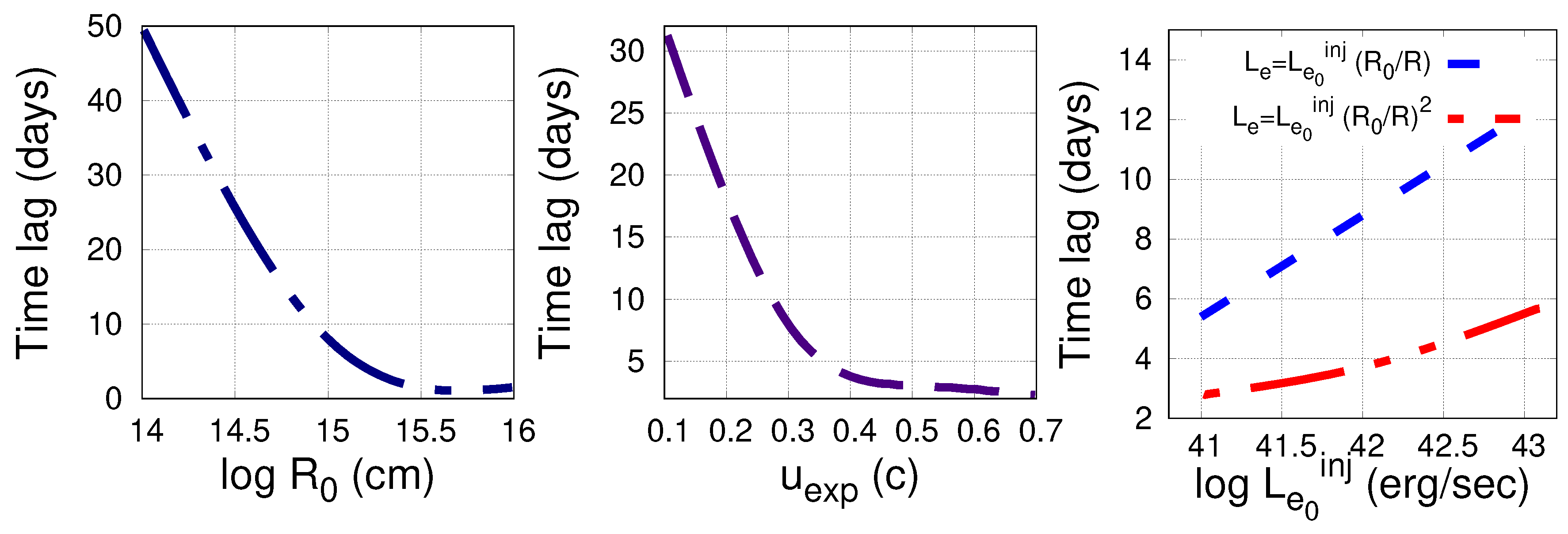
3. Results
4. Summary—Discussion
Funding
Acknowledgments
Conflicts of Interest
References
- Pavlidou, V.; Angelakis, E.; Myserlis, I.; Blinov, D.; King, O.G.; Papadakis, I.; Tassis, K.; Hovatta, T.; Pazderska, B.; Paleologou, E.; et al. The RoboPol optical polarization survey of gamma-ray-loud blazars. Mon. Not. R. Astron. Soc. 2014, 442, 1693–1705. [Google Scholar] [CrossRef]
- Hovatta, T.; Petropoulou, M.; Richards, J.L.; Giannios, D.; Wiik, K.; Baloković, M.; Lähteenmäki, A.; Lott, B.; Max-Moerbeck, W.; Ramakrishnan, V.; et al. A combined radio and GeV γ-ray view of the 2012 and 2013 flares of Mrk 421. Mon. Not. R. Astron. Soc. 2015, 448, 3121–3131. [Google Scholar] [CrossRef]
- Tavani, M.; Cavaliere, A.; Munar-Adrover, P.; Argan, A. The Blazar PG 1553+113 as a Binary System of Supermassive Black Holes. Astrophys. J. 2018, 854, 11. [Google Scholar] [CrossRef]
- Ackermann, M.; Ajello, M.; Atwood, W.B.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Becerra Gonzalez, J.; Bellazzini, R.; Bissaldi, E.; et al. The Third Catalog of Active Galactic Nuclei Detected by the Fermi Large Area Telescope. Astrophys. J. 2015, 810, 14. [Google Scholar] [CrossRef]
- Atwood, W.B.; Abdo, A.A.; Ackermann, M.; Althouse, W.; Anderson, B.; Axelsson, M.; Baldini, L.; Ballet, J.; Band, D.L.; Barbiellini, G.; et al. The Large Area Telescope on the Fermi Gamma-Ray Space Telescope Mission. Astrophys. J. 2009, 697, 1071–1102. [Google Scholar] [CrossRef]
- Abeysekara, A.U.; Alfaro, R.; Alvarez, C.; Álvarez, J.D.; Arceo, R.; Arteaga-Velázquez, J.C.; Rojas, D.A.; Solares, H.A.A.; Barber, A.S.; Bautista-Elivar, N.; et al. The HAWC Real-time Flare Monitor for Rapid Detection of Transient Events. Astrophys. J. 2017, 843, 116. [Google Scholar] [CrossRef]
- Blinov, D.; Pavlidou, V.; Papadakis, I.; Kiehlmann, S.; Liodakis, I.; Panopoulou, G.; Angelakis, E.; Balokovic, M.; Hovatta, T.; King, O.; et al. RoboPol: Connection between optical polarization plane rotations and gamma-ray flares in blazars. Mon. Not. R. Astron. Soc. 2018, 474, 1296–1306. [Google Scholar] [CrossRef]
- Jorstad, S.G.; Marscher, A.P.; Morozova, D.A.; Troitsky, I.S.; Agudo, I.; Casadio, C.; Foord, A.; Gómez, J.L.; MacDonald, N.R.; Molina, S.N.; et al. Kinematics of Parsec-scale Jets of Gamma-Ray Blazars at 43 GHz within the VLBA-BU-BLAZAR Program. Astrophys. J. 2017, 846, 98. [Google Scholar] [CrossRef]
- Fuhrmann, L.; Angelakis, E.; Zensus, J.A.; Nestoras, I.; Marchili, N.; Pavlidou, V.; Karamanavis, V.; Ungerechts, H.; Krichbaum, T.P.; Larsson, S.; et al. The F-GAMMA programme: Multi-frequency study of active galactic nuclei in the Fermi era. Programme description and the first 2.5 years of monitoring. Astron. Astrophys. 2016, 596, A45. [Google Scholar] [CrossRef]
- Lister, M.L.; Aller, M.F.; Aller, H.D.; Hodge, M.A.; Homan, D.C.; Kovalev, Y.Y.; Pushkarev, A.B.; Savolainen, T. MOJAVE. XV. VLBA 15 GHz Total Intensity and Polarization Maps of 437 Parsec-scale AGN Jets from 1996 to 2017. Astrophys. J. Suppl. 2018, 234, 12. [Google Scholar] [CrossRef]
- Hodge, M.A.; Lister, M.L.; Aller, M.F.; Aller, H.D.; Kovalev, Y.Y.; Pushkarev, A.B.; Savolainen, T. MOJAVE XVI: Multiepoch Linear Polarization Properties of Parsec-scale AGN Jet Cores. Astrophys. J. 2018, 862, 151. [Google Scholar] [CrossRef]
- Liodakis, I.; Hovatta, T.; Huppenkothen, D.; Kiehlmann, S.; Max-Moerbeck, W.; Readhead, A.C.S. Constraining the Limiting Brightness Temperature and Doppler Factors for the Largest Sample of Radio-bright Blazars. Astrophys. J. 2018, 866, 137. [Google Scholar] [CrossRef]
- Max-Moerbeck, W.; Richards, J.L.; Hovatta, T.; Pavlidou, V.; Pearson, T.J.; Readhead, A.C.S. A method for the estimation of the significance of cross-correlations in unevenly sampled red-noise time series. Mon. Not. R. Astron. Soc. 2014, 445, 437–459. [Google Scholar] [CrossRef]
- Max-Moerbeck, W.; Hovatta, T.; Richards, J.L.; King, O.G.; Pearson, T.J.; Readhead, A.C.S.; Reeves, R.; Shepherd, M.C.; Stevenson, M.A.; Angelakis, E.; et al. Time correlation between the radio and gamma-ray activity in blazars and the production site of the gamma-ray emission. Mon. Not. R. Astron. Soc. 2014, 445, 428–436. [Google Scholar] [CrossRef]
- Aharonian, F.; Akhperjanian, A.G.; Bazer-Bachi, A.R.; Behera, B.; Beilicke, M.; Benbow, W.; Berge, D.; Bernlöhr, K.; Boisson, C.; Bolz, O.; et al. An Exceptional Very High Energy Gamma-Ray Flare of PKS 2155-304. Astrophys. J. Lett. 2007, 664, L71–L74. [Google Scholar] [CrossRef]
- Aleksić, J.; Antonelli, L.A.; Antoranz, P.; Backes, M.; Barrio, J.A.; Bastieri, D.; Becerra González, J.; Bednarek, W.; Berdyugin, A.; Berger, K.; et al. MAGIC Discovery of Very High Energy Emission from the FSRQ PKS 1222+21. Astrophys. J. Lett. 2011, 730, L8. [Google Scholar] [CrossRef]
- Rybicki, G.B.; Lightman, A.P. Radiative Processes in Astrophysics; Wiley-VCH: Weinheim, Germany, 1979. [Google Scholar]
- Ghisellini, G.; Righi, C.; Costamante, L.; Tavecchio, F. The Fermi blazar sequence. Mon. Not. R. Astron. Soc. 2017, 469, 255–266. [Google Scholar] [CrossRef]
- Marscher, A.P.; Gear, W.K. Models for high-frequency radio outbursts in extragalactic sources, with application to the early 1983 millimeter-to-infrared flare of 3C 273. Astrophys. J. 1985, 298, 114–127. [Google Scholar] [CrossRef]
- Ghisellini, G.; Maraschi, L.; Treves, A. Inhomogeneous synchrotron-self-Compton models and the problem of relativistic beaming of BL Lac objects. Astron. Astrophys. 1985, 146, 204–212. [Google Scholar]
- Potter, W.J.; Cotter, G. Synchrotron and inverse-Compton emission from blazar jets—I. A uniform conical jet model. Mon. Not. R. Astron. Soc. 2012, 423, 756–765. [Google Scholar] [CrossRef]
- Marscher, A.P. Relativistic jets and the continuum emission in QSOs. Astrophys. J. 1980, 235, 386–391. [Google Scholar] [CrossRef]
- Marscher, A.P. Turbulent, Extreme Multi-zone Model for Simulating Flux and Polarization Variability in Blazars. Astrophys. J. 2014, 780, 87. [Google Scholar] [CrossRef]
- Hartman, R.C.; Böttcher, M.; Aldering, G.; Aller, H.; Aller, M.; Backman, D.E.; Balonek, T.J.; Bertsch, D.L.; Bloom, S.D.; Bock, H.; et al. Multiepoch Multiwavelength Spectra and Models for Blazar 3C 279. Astrophys. J. 2001, 553, 683–694. [Google Scholar] [CrossRef]
- Kharb, P.; Lister, M.L.; Cooper, N.J. Extended Radio Emission in MOJAVE Blazars: Challenges to Unification. Astrophys. J. 2010, 710, 764–782. [Google Scholar] [CrossRef]
- Ghirlanda, G.; Ghisellini, G.; Tavecchio, F.; Foschini, L.; Bonnoli, G. The radio-γ-ray connection in Fermi blazars. Mon. Not. R. Astron. Soc. 2011, 413, 852–862. [Google Scholar] [CrossRef]
- Arshakian, T.G.; León-Tavares, J.; Böttcher, M.; Torrealba, J.; Chavushyan, V.H.; Lister, M.L.; Ros, E.; Zensus, J.A. Radio-optical-gamma-ray properties of MOJAVE AGN detected by Fermi/LAT. A&A 2012, 537, A32. [Google Scholar] [CrossRef]
- Blandford, R.D.; Königl, A. Relativistic jets as compact radio sources. Astrophys. J. 1979, 232, 34–48. [Google Scholar] [CrossRef]
- Georganopoulos, M.; Marscher, A.P. Modeling the Variability of the BL Lacertae Object PKS 2155-304. Astrophys. J. 1998, 506, L11–L14. [Google Scholar] [CrossRef]
- Georganopoulos, M.; Marscher, A.P. A Viewing Angle-Kinetic Luminosity Unification Scheme for BL Lacertae Objects. Astrophys. J. 1998, 506, 621–636. [Google Scholar] [CrossRef]
- Katarzyński, K.; Sol, H.; Kus, A. The multifrequency variability of Mrk 421. Astron. Astrophys. 2003, 410, 101–115. [Google Scholar] [CrossRef]
- Hervet, O.; Boisson, C.; Sol, H. Linking radio and gamma-ray emission in Ap Librae. Astron. Astrophys. 2015, 578, A69. [Google Scholar] [CrossRef]
- Richter, S.; Spanier, F. A Numerical Model of Parsec-scale SSC Morphologies and Their Radio Emission. Astrophys. J. 2016, 829, 56. [Google Scholar] [CrossRef]
- Mastichiadis, A.; Kirk, J.G. Self-consistent particle acceleration in active galactic nuclei. Astron. Astrophys. 1995, 295, 613. [Google Scholar]
- Zacharias, M.; Wagner, S.J. The extended jet of AP Librae: Origin of the very high-energy γ-ray emission? Astron. Astrophys. 2016, 588, A110. [Google Scholar] [CrossRef]
- Petropoulou, M.; Mastichiadis, A. On the multiwavelength emission from gamma ray burst afterglows. Astron. Astrophys. 2009, 507, 599–610. [Google Scholar] [CrossRef]
- Shklovsky, J. Possible Secular Variation of the Flux and Spectrum of Radio Emissions of Source 1934–63. Nature 1965, 206, 176–177. [Google Scholar] [CrossRef]
- Van der Laan, H. A Model for Variable Extragalactic Radio Sources. Nature 1966, 211, 1131–1133. [Google Scholar] [CrossRef]
- Kardashev, N.S. Nonstationarity of Spectra of Young Sources of Nonthermal Radio Emission. Sov. Astron. 1962, 6, 317. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boula, S.; Petropoulou, M.; Mastichiadis, A. On the Connection of Radio and γ-Ray Emission in Blazars. Galaxies 2019, 7, 3. https://doi.org/10.3390/galaxies7010003
Boula S, Petropoulou M, Mastichiadis A. On the Connection of Radio and γ-Ray Emission in Blazars. Galaxies. 2019; 7(1):3. https://doi.org/10.3390/galaxies7010003
Chicago/Turabian StyleBoula, Stella, Maria Petropoulou, and Apostolos Mastichiadis. 2019. "On the Connection of Radio and γ-Ray Emission in Blazars" Galaxies 7, no. 1: 3. https://doi.org/10.3390/galaxies7010003
APA StyleBoula, S., Petropoulou, M., & Mastichiadis, A. (2019). On the Connection of Radio and γ-Ray Emission in Blazars. Galaxies, 7(1), 3. https://doi.org/10.3390/galaxies7010003




