Theoretical Discourse on Producing High Temporal Yields of Nuclear Excitations in Cosmogenic 26Al with a PW Laser System: The Pathway to an Astrophysical Earthbound Laboratory
Abstract
1. Introduction
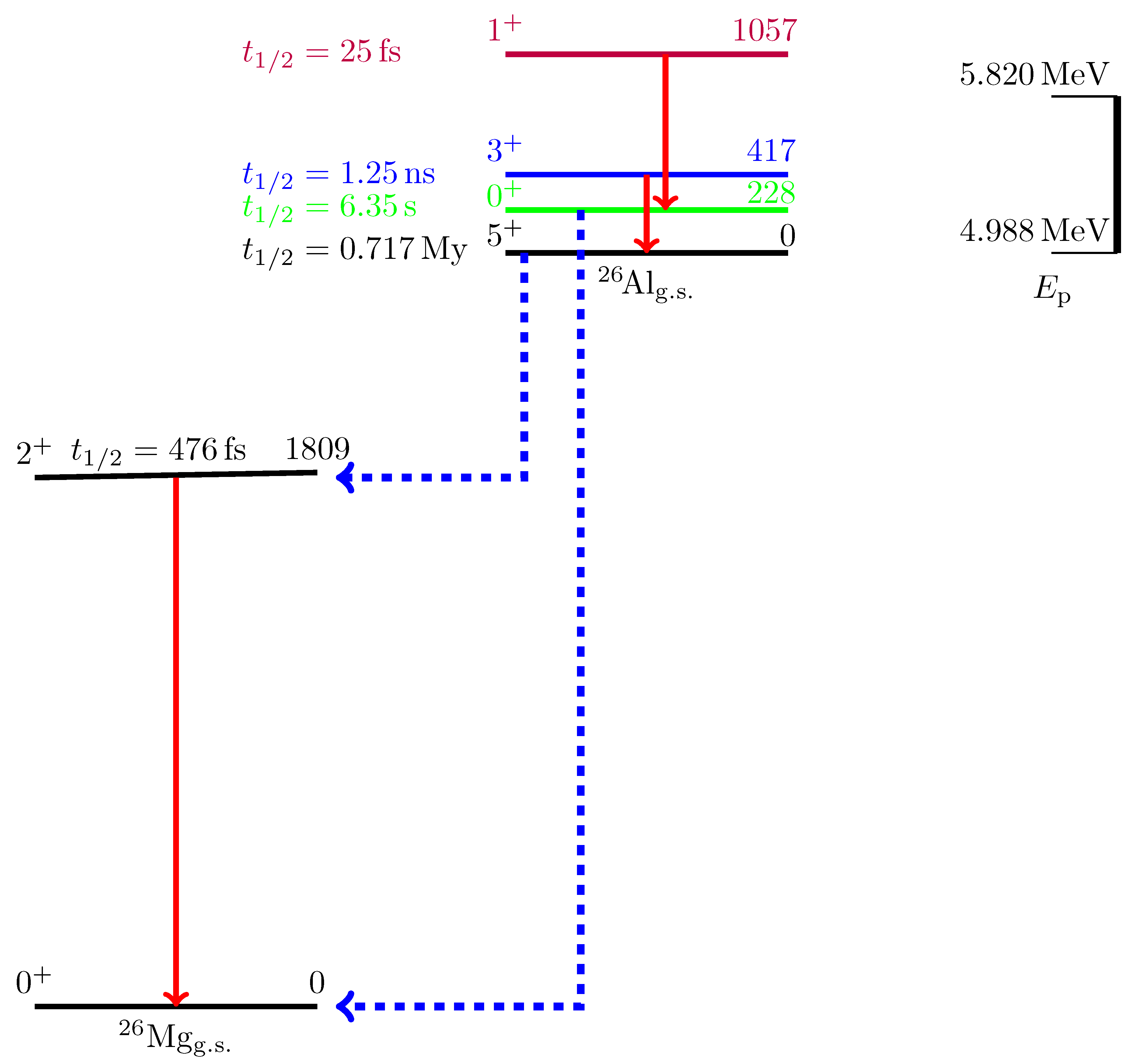
2. Production and Decay of Cosmogenic 26Al
2.1. Spontaneous Yields
2.2. Yield Distributions of Excited States and Temperature Equivalents
2.3. The Importance of 26Al for Astrophysics
2.4. Cross-Section of 26Al and Its Production in Laser Plasma Experiments
3. Theoretical Evaluation of Achievable Population Distributions for the First Three Excited States in 26Al in Laser Induced Plasma Experiments
3.1. General Considerations
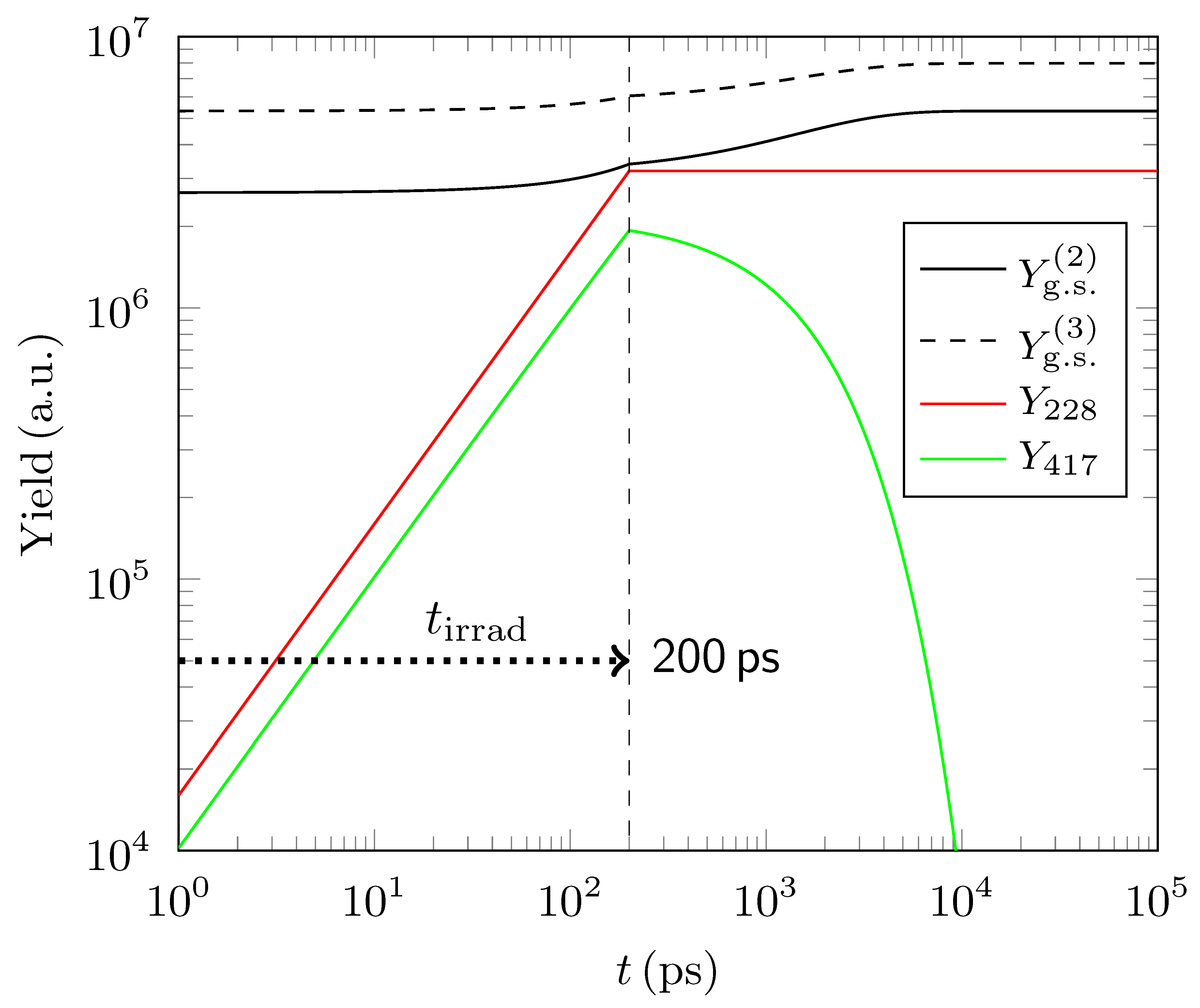
3.2. Simulations of Population Yields for 26Al Obtained by a Short Pulsed Laser Proton Beam of High Intensity
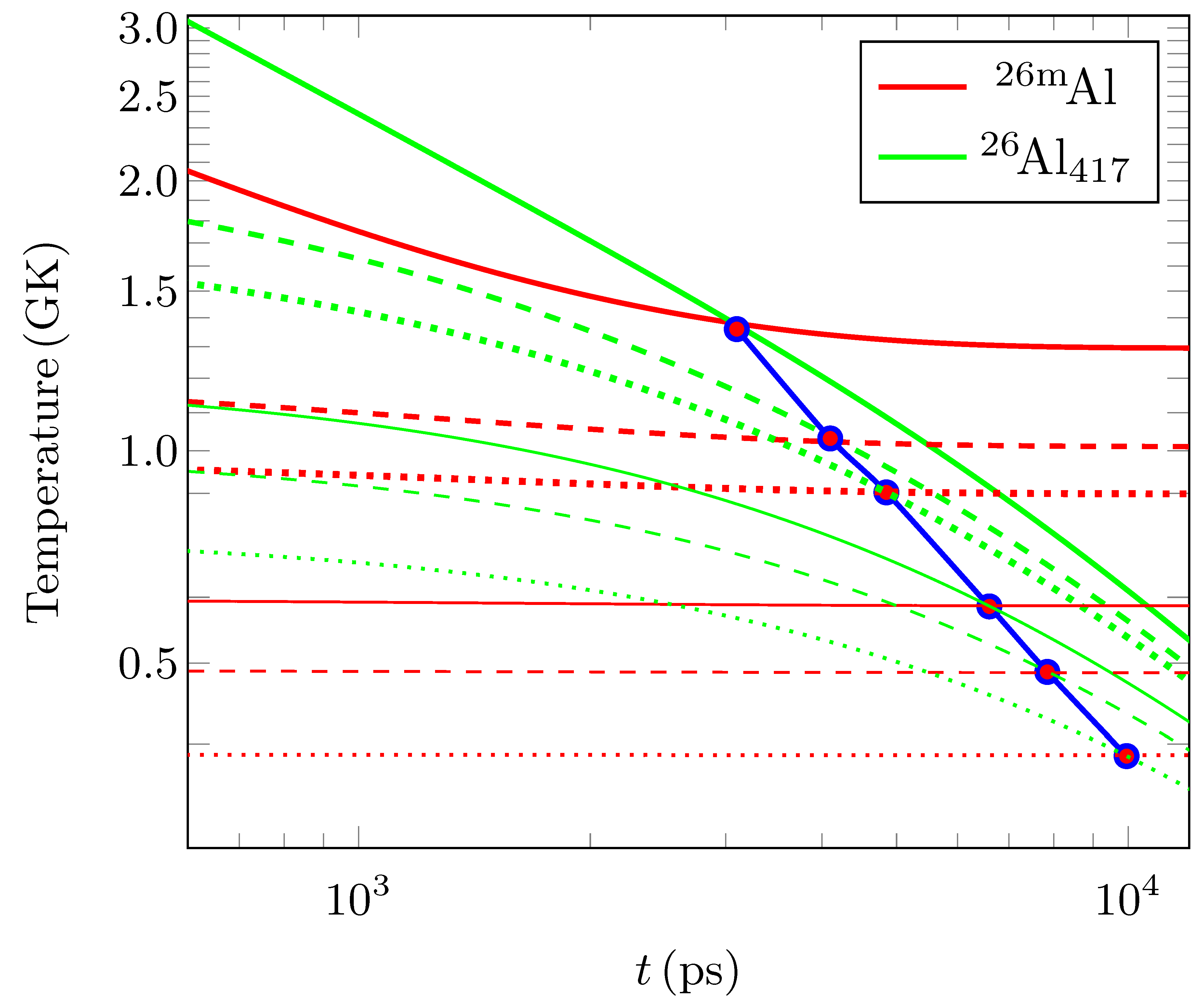
3.3. Thermodynamic Temperature Equivalents from the Distribution of the First Three Excited States in 26Al in Laser Plasma Experiments
3.4. Considerations about Measurability at HPLSs
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| CPA | Chirped pulse amplification |
| ELI-NP | Extreme Light Infrastructure-Nuclear Physics |
| EMP | Electromagnetic pulse |
| GCNDS | Graphite-cube neutron-detection system |
| HPLS | High-power laser system |
| RAL | Rutherford Appleton Laboratory |
| TNSA | Target normal sheath acceleration |
| TOF | Time-of-flight |
| WDM | Warm dense matter |
References
- Hauser, W.; Feshbach, H. The Inelastic Scattering of Neutrons. Phys. Rev. 1952, 87, 366–373. [Google Scholar] [CrossRef]
- Strickland, D.; Mourou, G. Compression of amplified chirped optical pulses. Opt. Commun. 1985, 56, 219–221. [Google Scholar] [CrossRef]
- Bateman, H. The solution of a system of differential equations occurring in the theory of radioactive transformations. Proc. Camb. Philos. Soc. 1910, 15, 423–427. [Google Scholar]
- Morrissey, D.J.; Bloch, C.; Benenson, W.; Kashy, E.; Blue, R.A.; Ronningen, R.M.; Aryaeinejad, R. Thermal population of nuclear excited states. Phys. Rev. C 1986, 34, 761–763. [Google Scholar] [CrossRef]
- Denis-Petit, D.; Ledingham, K.W.D.; McKenna, P.; Mascali, D.; Tudisco, S.; Spohr, K.M.; Tarisien, M. Nuclear Reactions in a Laser-Driven Plasma Environment. In Applications of Laser-Driven Particle Acceleration; Bolton, P., Parodi, K., Schreiber, J., Eds.; CRC-Press, Taylor & Francis Group: Boca Raton, FL, USA, 2018; Chapter 22; pp. 339–352. [Google Scholar]
- Spohr, K.M.; Ledingham, K.W.D.; Clarke, R.; Carroll, D.C.; Doria, D.; Gray, R.J.; Hassan, M.; Labiche, M.; McCanny, T.; McKenna, P.; et al. Unpublished work. 2019.
- Patel, P.K.; Mackinnon, A.J.; Key, M.H.; Cowan, T.E.; Foord, M.E.; Allen, M.; Price, D.F.; Ruhl, H.; Springer, P.T.; Stephens, R. Isochoric Heating of Solid-Density Matter with an Ultrafast Proton Beam. Phys. Rev. Lett. 2003, 91, 125004. [Google Scholar] [CrossRef] [PubMed]
- Ping, Y.; Correa, A.; Ogitsu, T.; Draeger, E.; Schwegler, E.; Ao, T.; Widmann, K.; Price, D.; Lee, E.; Tam, H.; et al. Warm dense matter created by isochoric laser heating. High Energy Density Phys. 2010, 6, 246–257. [Google Scholar] [CrossRef]
- Thirolf, P.G.; Habs, D.; Gross, M.; Allinger, K.; Bin, J.; Henig, A.; Kiefer, D.; Ma, W.; Schreiber, J. Fission-Fusion: A new reaction mechanism for nuclear astrophysics based on laser-ion acceleration. AIP Conf. Proc. 2011, 1377, 88–95. [Google Scholar]
- Oginni, B.; Iliadis, C.; Champagne, A. Theoretical evaluation of the reaction rates for 26Al(n, p)26Mg and 26Al(n, α)23Na. Phys. Rev. C 2011, 83, 025802. [Google Scholar] [CrossRef]
- Mahoney, W.A.; Ling, J.C.; Wheaton, W.A.; Jacobson, A.S. HEAO3 discovery of 26Al in the interstellar medium. Astrophys. J. 1984, 286, 578–585. [Google Scholar] [CrossRef]
- Arnould, M.; Norgaard, H.; Thielemann, F.K.; Hillebrandt, W. Synthesis of 26Al in explosive hydrogen burning. Astrophys. J. 1980, 237, 931–950. [Google Scholar] [CrossRef]
- Arnett, W.D. Explosive Nucleosynthesis in Stars. Astrophys. J. 1969, 157, 1369. [Google Scholar] [CrossRef]
- Diehl, R.; Halloin, H.; Kretschmer, K.; Lichti, G.; Schönfelder, V.; Strong, A.; von Kienlin, A.; Wang, W.; Jean, P.; Knödlseder, J.; et al. Radioactive 26Al from massive stars in the Galaxy. Nature 2006, 439, 45–47. [Google Scholar] [CrossRef] [PubMed]
- Lee, T.; Papanastassiou, D.; Wasserburg, G. Demonstration of 26Mg excess in Allende and evidence for 26Al. Geophys. Res. Lett. 1976, 3, 41–44. [Google Scholar] [CrossRef]
- Villeneuve, J.; Chaussidon, M.; Libourel, G. Homogeneous Distribution of 26Al in the Solar System from the Mg Isotopic Composition of Chondrules. Science 2009, 325, 985–988. [Google Scholar] [CrossRef] [PubMed]
- Kita, N.T.; Yin, Q.Z.; MacPherson, G.J.; Ushikubo, T.; Jacobsen, B.; Nagashima, K.; Kurahashi, E.; Krot, A.N.; Jacobsen, S.B. 26Al-26Mg isotope systematics of the first solids in the early solar system. Meteorit. Planet. Sci. 2013, 48, 1383–1400. [Google Scholar] [CrossRef]
- Skelton, R.; Kavanagh, R.; Sargood, D. 26Mg(p, n)26Al and 23Na(α, n)26Al Reactions. Phys. Rev. C 1987, 35, 45–54. [Google Scholar] [CrossRef]
- Ward, R.A.; Fowler, W.A. Thermalization of long-lived nuclear isomeric states under stellar conditions. Astrophys. J. 1980, 238, 266–286. [Google Scholar] [CrossRef]
- Coc, A.; Porquet, M.G.; Nowacki, F. Lifetimes of 26Al and 34Cl in an astrophysical plasma. Phys. Rev. C 1999, 61, 015801. [Google Scholar] [CrossRef]
- Gupta, S.; Meyer, B. Internal equilibration of a nucleus with metastable states: 26Al as an example. Phys. Rev. C 2001, 64, 025805. [Google Scholar] [CrossRef]
- Dunford, C.; Burrows, T. Online Nuclear Data Service; Report IAEA-NDS-150; NNDC Informal Report NNDC/ONL-95/10; BNL National Nuclear Data Center: Brookhaven, NY, USA, 1996; p. 015801.
- Äystö, J.; Eronen, T.; Jokinen, A.; Kankainen, A.; Moore, I.; Penttilä, H. An IGISOL portrait. Hyperfine Interact. 2013, 223, 1–3. [Google Scholar] [CrossRef]
- Wilks, S.C.; Langdon, A.B.; Cowan, T.E.; Roth, M.; Singh, M.; Hatchett, S.; Key, M.H.; Pennington, D.; MacKinnon, A.; Snavely, R.A. Energetic proton generation in ultra-intense laser–solid interactions. Phys. Plasmas 2001, 8, 542–549. [Google Scholar] [CrossRef]
- Higginson, A.; Gray, R.J.; King, M.; Dance, R.J.; Williamson, S.D.R.; Butler, N.M.H.; Wilson, R.; Capdessus, R.; Armstrong, C.; Green, J.S.; et al. Near-100 MeV protons via a laser-driven transparency-enhanced hybrid acceleration scheme. Nat. Commun. 2018, 9, 724. [Google Scholar] [CrossRef] [PubMed]
- Ziegler, J.F.; Ziegler, M.D.; Biersack, J.P. SRIM—The stopping and range of ions in matter. Nucl. Instrum. Methods Phys. Res. B 2010, 268, 1818–1823. [Google Scholar] [CrossRef]
- Negoita, F.; Roth, M.; Thirolf, P.G.; Tudisco, S.; Hannachi, F.; Moustaizis, S.; Pomerantz, I.; McKenna, P.; Fuchs, J.; Spohr, K.M.; et al. Laser Driven Nuclear Physics at ELI-NP. Rom. Rep. Phys. 2016, 68, S37–S144. [Google Scholar]
| State | /MeVmb | Method Used in [18] |
|---|---|---|
| 54.9(9) | Total neutron yield from the 26Mg(p, ntot)26Al reaction measured by the GCNDS. Note, due to the very long half-life of 26Alg.s., no delayed 511 keV annihilation radiation yield will be measurable emerging from the associated ground state decay. | |
| 30.2(3) | Delayed 511 keV annihilation radiation yield from the 26Mg(p, n228)26mAl reaction measured by two NaI(Tl) detectors in coincidence. An irradiation-count cycle with = 6 s and = 3 s was applied. | |
| 19.3(9) | Prompt 417 keV -ray yield from the 26Mg(p, n417)26Al using an ultrathin target with a thickness of 8.5 μgcm−2. The prompt radiation was measured by a 60 cm3 Ge(Li) detector. |
| 10 | 250 | 25 | 0.017 | >200 | kA-MA | |
| 1 | 25 | 25 | 1 | ∼100 | A-kA | |
| 0.1 | 2.5 | 25 | 10 | ∼30 | mA-A |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Spohr, K.M.; Doria, D.; Meyer, B.S. Theoretical Discourse on Producing High Temporal Yields of Nuclear Excitations in Cosmogenic 26Al with a PW Laser System: The Pathway to an Astrophysical Earthbound Laboratory. Galaxies 2019, 7, 4. https://doi.org/10.3390/galaxies7010004
Spohr KM, Doria D, Meyer BS. Theoretical Discourse on Producing High Temporal Yields of Nuclear Excitations in Cosmogenic 26Al with a PW Laser System: The Pathway to an Astrophysical Earthbound Laboratory. Galaxies. 2019; 7(1):4. https://doi.org/10.3390/galaxies7010004
Chicago/Turabian StyleSpohr, Klaus Michael, Domenico Doria, and Bradley Stewart Meyer. 2019. "Theoretical Discourse on Producing High Temporal Yields of Nuclear Excitations in Cosmogenic 26Al with a PW Laser System: The Pathway to an Astrophysical Earthbound Laboratory" Galaxies 7, no. 1: 4. https://doi.org/10.3390/galaxies7010004
APA StyleSpohr, K. M., Doria, D., & Meyer, B. S. (2019). Theoretical Discourse on Producing High Temporal Yields of Nuclear Excitations in Cosmogenic 26Al with a PW Laser System: The Pathway to an Astrophysical Earthbound Laboratory. Galaxies, 7(1), 4. https://doi.org/10.3390/galaxies7010004






