Abstract
The last few years have seen gamma-ray astronomy maturing and advancing in the field of time-domain astronomy, utilizing source variability on timescales over many orders of magnitudes, from a decade down to a few minutes and shorter, depending on the source. This review focuses on some of the key science issues and conceptual developments concerning the timing characteristics of active galactic nuclei (AGN) at gamma-ray energies. It highlights the relevance of adequate statistical tools and illustrates that the developments in the gamma-ray domain bear the potential to fundamentally deepen our understanding of the nature of the emitting source and the link between accretion dynamics, black hole physics, and jet ejection.
1. Introduction
The last decade has seen tremendous experimental progress in gamma-ray astronomy much beyond simple source detection (e.g., see [1,2,3] for a review). In many cases, detailed spectral and timing characterization have become possible allowing one to probe deeply into the nature and physics of these sources. In particular, gamma-ray astronomy has by now matured and progressed further in the field of time-domain astronomy, utilizing source variability on timescales over many orders of magnitudes, from a decade down to a few minutes and shorter. Instruments such as the Fermi Large Area Telescope (Fermi-LAT), the High-Altitude Water Cherenkov Gamma-Ray Observatory (HAWC) or the First G-APD Cherenkov Telescope (FACT), for example, have opened up the possibility for unbiased long-term (timescales up to several years) studies of bright astrophysical objects in the high energy (HE; >100 MeV) and the very high energy (VHE; >100 GeV) domain, respectively (e.g., [4,5,6]), while modern Imaging Atmospheric Cherenkov Telescopes (IACTs) have demonstrated their excellent capabilities to characterize VHE flaring states down to below sub-hour timescales.
This paper focuses on some of the key issues and conceptual developments concerning the timing characteristics of AGN (including rapid variability, log-normal flux distributions, power-law noise, and quasi-periodic oscillations) at gamma-ray energies.
2. Timing Characteristics
2.1. Rapid Variability at VHE Energies
Radio-loud AGN can be highly variable gamma-ray emitters. This not only applies to the strongly-Doppler-boosted blazar sources, but also to misaligned jet sources such as radio galaxies. VHE doubling timescales down to a few minutes ( 2–3 min) are known for the VHE blazars Mkn 501 [7] and PKS 2155-304 [8] and at HE for the flat spectrum radio quasar (FSRQ) blazar 3C279 [9]. Interestingly, rapid VHE activity has been seen in radio galaxies as well, i.e., from day-scale for M87 [10,11], see Figure 1, to intra-day ( h) for NGC 1275 [12], down to minute-scale for IC 310 [13]; see [14]. Rapid variability is usually taken to indicate extreme jet conditions. Causality arguments, for example, imply that the emission would need to arise in a very compact region of comoving size cm (where is the Doppler factor), possibly close to the black hole at distances d cm (where is the jet bulk Lorentz factor) only, i.e., typically less than a few hundred Schwarzschild radii away. Despite its compactness, the emitting region often needs to be highly luminous to account for the observed gamma-ray output, and this can impose a severe constraint on possible models (see below). In some cases such as for PKS 2155-304, the VHE light curve during the high state is sufficiently resolved to suggest the presence of multiple (possibly interacting) emitting zones. The discriminating potential will strongly increase with the upcoming Cherenkov Telescope Array (CTA). Figure 2 shows a simulation based on the strong VHE flare in 2006, demonstrating the capability to probe sub-minute timescales.
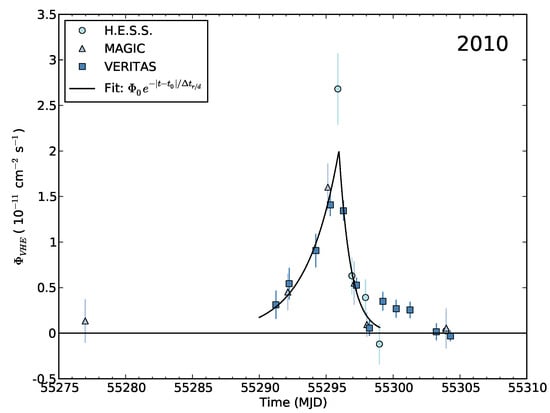
Figure 1.
The very high energy (VHE) flare of the radio galaxy M87 in April 2010 as observed by H.E.S.S., MAGIC and VERITAS. Significant day-scale activity is evident. Since the jet in M87 is believed to be misaligned (suggestive of modest Doppler beaming only) and its black hole light-crossing scale large ( days), this VHE activity is extremely fast. The curve represents a fit by an exponential function, indicating doubling times of days and days during rise and decay, respectively. From [11].
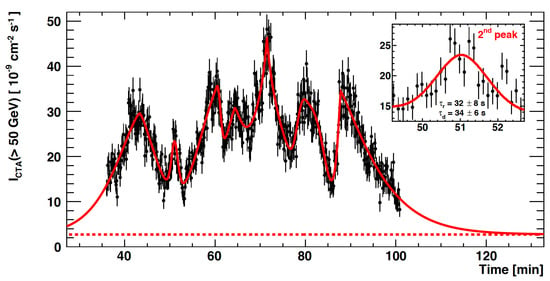
Figure 2.
Simulated CTA light curve based on an extrapolation of the power spectrum for the strong 2006 VHE flare of the blazar PKS 2155-304. CTA will allow probing sub-minute timescales (see inlay) and thereby help to discriminate between different physical models. From [15].
In the extragalactic jetted-source context, rapid variability comes along with a general challenge. In the conventional picture of an emission region embedded in a uni-directional jet flow, the observed variability imposes a constraint on the size of the central engine that is independent of Doppler boosting (e.g., [16,17]). To see this, note that the observed timescale is related to the comoving (flow) timescale by , where is the Doppler factor, and that by causality . Length scales in the rest frame of the central engine and the comoving (flow) frame, on the other hand, are related by (length contraction). Noting that the characteristic length scale in the rest frame of the central engine driving the jet is , one finds for the generic variability timescale:
using that in the head-on () approximation. The -min VHE variability observed in PKS 2155-304 () would then imply a black hole mass of only, much smaller than what is inferred from the host-galaxy luminosity relation (e.g., [18]). Faster variability could only be achieved if the jet collided with a small obstacle (size ). Yet, in this case, the jet power that could be tapped for producing radiation is much smaller, roughly by a factor , so that typically, very high jet powers would be needed to account for the observed VHE emission.
In principle, however, the dynamics and the geometry of the emission region(s) could be much more complex. Salvati et al. [19], for example, have argued that if the emission is due to a series of conical shocks, fast blazar variability does not necessarily require extreme jet parameters. In addition the observational findings have triggered new conceptual developments in which rapid variability is related to, e.g., moving subregions or turbulence within the jet, black hole magnetospheric processes, or the propagation of non-linear electromagnetic waves (e.g., [20,21,22,23,24,25]). Major reference scenarios currently include black hole horizon gaps, jets-in-jet, or jet interaction models (e.g., [26,27,28]); see Figure 3 for an illustration. Each of these has its own challenge from, e.g., limited power extraction in the case of magnetospheric gaps and unusual magnetizations in the case of reconnection-induced mini-jets to the requirement of maximal jet powers in the case of jet interaction models (see [14] for a recent discussion). At the current stage, the most promising way to gain further insights into the physical origin of variability seems to be to go beyond classical minimum variability considerations and homogeneous one-zone approaches and to take into account the full timing characteristics of the emission, as outlined below. Methodologically, this draws on the general concept that the variability in AGN can be fairly well understood as a stochastic process. An observed time series (i.e., a light curve) is then seen as a realization of the underlying stochastic process that is sampled by the observation.1
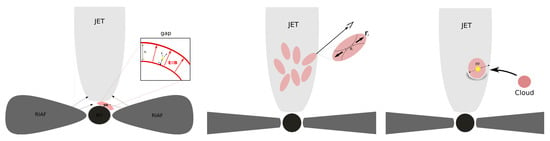
Figure 3.
Possible scenarios for the origin of rapidly-variable VHE emission in AGN. Left: Particle acceleration in unscreened (“gap”) electric fields close to the black hole horizon triggers an electron-positron pair cascade, which is accompanied by inverse Compton up-scattering of the ambient disk photon to the VHE regime. VHE variability then becomes a possible signature of jet formation [26]. Middle: Jets-in-jet model [27], where a variety of “mini-jet” features (“plasmoids”) is produced by magnetic reconnection events within the main jet flow. This could lead to an additional velocity component relative to the main flow () and allow for a favorable orientation (i.e., increased Doppler boosting and time scale reduction) with respect to the observer. Right: Illustration of a hadronic model, where interactions of the jet with a small, massive obstacle (star or cloud) facilitate shock-acceleration and introduce a sufficient target density to allow for efficient -collisions [28].
2.2. PDF Shape and Log-Normality
Important insights can be obtained by characterizing the underlying process driving the variability by its observed probability density function (PDF). The PDF can in principle be estimated by fitting a model function to the histogrammed data. As a simple comparison, one can study the distribution of VHE fluxes (e.g., the number of runs as a function of the measured photon flux or the logarithm thereof) and evaluate the appropriateness of a fit by a Gaussian distribution as representative of a normal random process. Figure 4 and Figure 5 provide examples in the case of PKS 21455-304 and Mkn 501, where a clear preference for the logarithm of the flux to be Gaussian (normal) distributed, i.e., for log-normality, has been found [36,37].2 Similar results are obtained by studying the relationship between the mean flux and the absolute (root mean square) variability (e.g., [38,39]),3 where a linear relationship is known to provide evidence for a log-normal distribution of the fluxes [40,41].
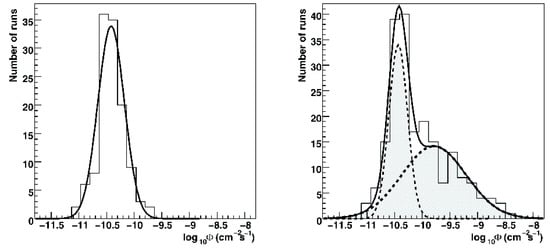
Figure 4.
Distributions of the logarithms of integral VHE fluxes above for PKS 2155-304. Left: From 2005–2007, without the strong flare period in July 2006. Right: All data, from 2005–2007; the solid line represents the fit by the sum of two Gaussians. The findings provide evidence that the source switches from a quiescent VHE state with rather minimal activity to a flaring state, with the flux distribution in each state following a lognormal distribution (see also [39]). From [36].
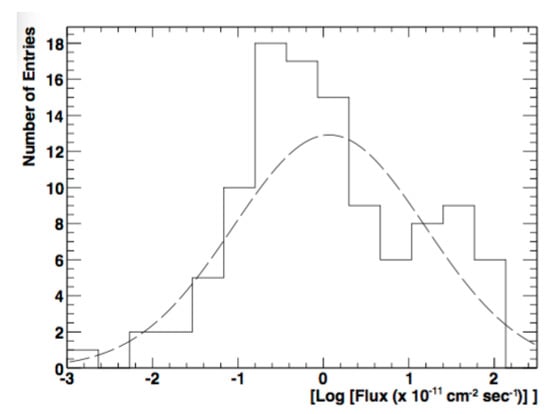
Figure 5.
Distributions of VHE fluxes (≥2 TeV) for the flare of Mkn 501 during 19–24 June 2014 based on a four-minute time binning. Furthermore, in this case, a log-normal distribution (dashed curve) is preferred over a Gaussian. The difference is not as significant, though (see also [42]), and one could also speculate whether the sum of two Gaussians might provide a better characterization of the log(flux)-distribution. From [37].
Where statistics permits, current evidence suggests that the gamma-ray fluxes in blazars are preferentially log-normally distributed (cf. also [43] in the case of Mkn 421 and [44] for the case of bright Fermi blazars). Lognormal flux variability is not unusual, but in fact is well-known for accreting galactic sources such as X-ray binaries [40], where it has been linked to the underlying accretion process. The current findings are of interest since in a lognormal process, the fluctuations of the flux are on average proportional, or at least correlated, to the flux itself. This rules out additive processes for the origin of the observed variability and instead favors multiplicative ones.4 If this is true, then additive models (e.g., shot-noise or a simple superposition of many “mini-jets”) are no longer adequate to describe the observed variability behavior, and multiplicative, cascade-like scenarios need to be invoked.
In principle, several scenarios for the origin of log-normal flux distributions could be envisaged:
(i) Similar as for X-binaries, the inferred log-normality at gamma-ray energies in blazars could mark the influence of the accretion disk on the jet (e.g., [46,47]). Independent density fluctuations in the accretion disk on local viscous timescale, i.e., in the case of a standard disk (where , h is the disk height, and the viscosity parameter), provide one possible realization. Provided damping is negligible, these fluctuations can propagate inward and couple together to produce a multiplicative (power-law noise) behavior in the innermost disk part [48,49,50]. If this behavior is efficiently transmitted to the jet (particle injection rate), the gamma-ray emission could be modulated accordingly [18]; see Figure 6. This requires, amongst others, that the timescale for particle acceleration and radiative losses within the jet be correspondingly small [18]. Log-normality at different wavelengths and over long timescales might then well be feasible (i.e., up to timescales where is the characteristic disk radius). Short timescales (on horizon light-crossing times), however, could only be achieved in the case of a thick (inner) disk (where ); see also below.
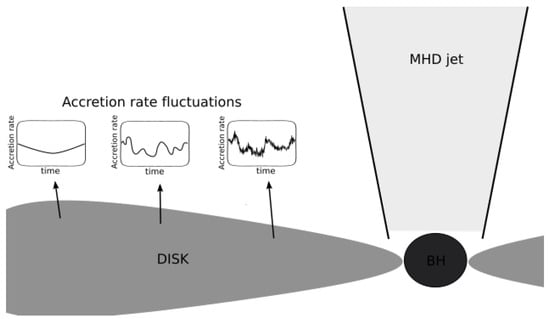
Figure 6.
A possible accretion-disk origin for log-normality. Density fluctuations in the disk, arising on local viscous timescales, can propagate inwards and couple together so as to produce a multiplicative behavior in the accretion rate. If this is transmitted to the jet and picked up by the acceleration mechanism, the resultant VHE emission might share in the underlying log-normal characteristics.
(ii) Cascade-related emission processes (e.g., proton-induced synchrotron cascades, cf. [51], or magnetospheric inverse-Compton pair production cascades, cf. [26]) might possibly lead to some log-normal flux distributions. Relevant constraints in these cases arise, however, from the energy bands in which log-normality has been seen (e.g., in the optical, X-ray, and gamma-ray range for PKS 2155-304 [38]) and the timescales over which log-normality has been found (i.e., from sub-hour to yearly timescales at gamma-ray energies). The latter are expected to be limited by the gap travel time for magnetospheric processes and the dynamical or escape time for hadronic cascades.
(iii) Alternatively, log-normality could be associated with the acceleration process itself, e.g., with random fluctuations in the particle acceleration rate [52]. In the case of diffusive shock acceleration, for example, the accelerated particle distribution contains powers in , i.e., , where denotes the acceleration and the escape timescale, respectively [53], is the injection Lorentz factor, is the shock speed, and is the maximum Lorentz factor determined by radiative losses. If diffusion is characterized by Gaussian perturbations such that , then the fractional variability becomes a linear combination of Gaussian and -terms [52]. Depending on the energy scale, the accelerated particle number density could thus resemble a lognormal distribution. Figure 7 provides an illustration of this effect. Log-normality in the radiating particle distribution could then well result in a log-normal flux distribution in the case of synchrotron or external inverse Compton. Log-normality in this case, however, would be energy-dependent, with its significance becoming weaker towards lower energies and disappearing for energies close to a threshold ().
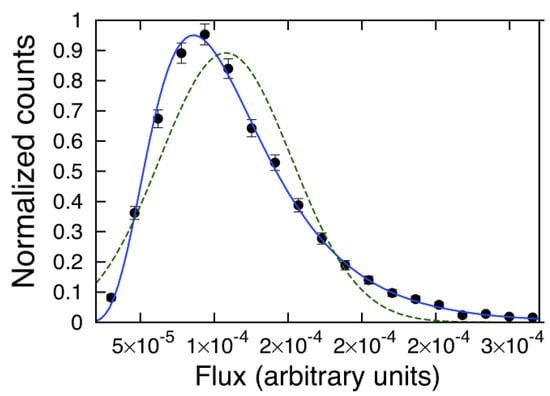
Figure 7.
Log-normality in the accelerated particle number density arising from random fluctuations in the particle acceleration rate at a shock front. The figure shows the histogram of the particle number density at based on simulations in which Gaussian perturbations are introduced into . The dashed green line represents the best-fitting Gaussian and the solid blue line the best-fitting log-normal PDF. Particle injection with has been assumed. From [52].
PDF studies at different frequencies (cf. [54] for PKS 2155-304) could be of help to distinguish between the noted scenarios. In principle, the above does not preclude the possibility that log-normality in different states (long term, low level, and short term, flare) arises due to different processes.
2.3. PSD and Power-Law Noise
In time series analysis, the power spectral density (PSD) represents an important tool for characterizing variability. The PSD provides a measure for the contribution of different timescales to the variability power, i.e., it quantifies the amount of variability power as a function of (temporal) frequency (). Methodologically, this implies a move from a signal description in the time domain to one in the frequency domain by means of Fourier transformation. In practice, we can only get an estimate of the PSD, and the simplest method is to estimate the PSD by the periodogram (i.e., the squared modulus of the discrete Fourier Transform, properly normalized). Accordingly, a periodicity at a given timescale would lead to a peak in the PSD at the corresponding frequency, while a continuum power spectrum would correspond to non-periodic signals. The latter are typically parameterized as power-law noise with a PSD of the form:
where is the power index (e.g., for white noise, for pink or flicker noise, and for red or Brownian noise). A broken power-law PSD would then be indicative of a characteristic timescale () at the corresponding break frequency ().
PSD analysis has by now been performed for a variety of gamma-ray-emitting AGN, particularly in the high-energy Fermi-LAT domain [31,55,56,57,58]. In the VHE domain, a particularly interesting result relates to PKS 2155-304, where an extended PSD analysis revealed a flicker noise behavior for its long-term low-level VHE activity over frequencies corresponding to timescales d (and with a power index similar to the one seen at HE on timescales d), cf. Figure 8, while the 2006 VHE flaring state showed a red-noise behavior (on frequencies corresponding to timescales h) [36,39].
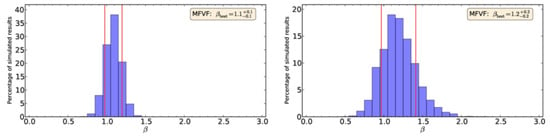
Figure 8.
Best-fit parameters and uncertainties for the power-law noise index for the long-term gamma-ray activity in PKS 2155-304 estimated from simulated light curves. Left: For VHE (H.E.S.S.) data. Right: For HE (Fermi-LAT) data. The vertical red bars indicate the 1 uncertainties on the best fit. Both the VHE and the HE variability are compatible with flicker noise . From [39].
In the simplest interpretation, the PSD slope is considered to be stationary and to follow a power-law with a transition from to at around , where d; see Figure 9. This would then be comparable to the X-ray PSDs of Seyfert AGNs, which reveal a similar steepening by at their break frequencies [59]. Interestingly, at X-ray energies, a break time of d has been suggested earlier for PKS 2155-304 [60].
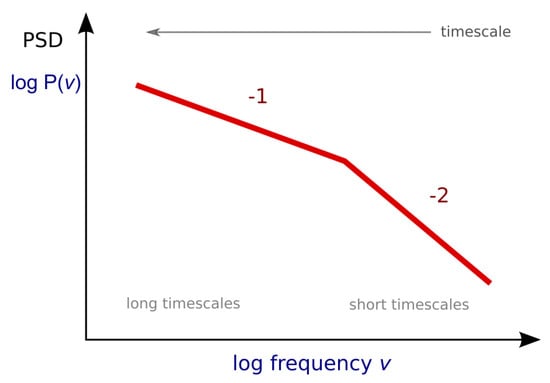
Figure 9.
The PSD behavior of the VHE emission from PKS 2155-304 is suggestive of a break from flicker () to Brownian () power-law noise at a break frequency corresponding to a break time of d.
In principle, accretion-disk fluctuations (see above) could also account for a power-law noise behavior [48]. In the case of the radio-quiet Seyfert AGNs, McHardy et al. [59] have reported a simple quantitative relationship between the break time —then associated with the characteristic timescale at the inner edge of the accretion disk—the observed (bolometric) luminosity , and the black hole mass of the source. Although PKS 2155-304 is not a radio-quiet object, one could speculate that a similar relation applies if the timing properties originate in the accretion flow [39]. For a standard disk (with the accretion rate as a proxy for ), this scaling relation becomes , where the accretion rate has been expressed in units of the Eddington rate. Hence, if this relation also applies to the supposed VHE break time of PKS 2155-304 ( d), accretion rates close to Eddington would be implied even for the quiescent VHE state. It seems thus more likely that the break time in PKS 2155-304 is related to a change in accretion flow conditions such as a transition from an inner advection-dominated to an outer standard disk configuration [39].
Obviously, Fourier analysis of non-thermal emission models could allow one to gain further insights into the origin of the gamma-ray variability in blazars. This particularly includes recent explorations as to the possible modifications of an underlying (injected) PSD shape by radiation [61,62]. This can be done by starting from the appropriate time-dependent particle transport equation (including the relevant acceleration and radiative loss terms) for , the number of electrons between and at time t. One can then look for solutions of the Fourier-transformed equation assuming injection of power-law noise with . This can be used to, e.g., evaluate the impact on the expected synchrotron, external Compton (EC), or synchrotron self-Compton (SSC) flux (with as the Fourier transform of the respective flux). Estimating the PSD from the periodogram, one, e.g., finds that at sufficiently low frequencies for SSC and in the case of EC [61]. Since the gamma-ray emission in flat spectrum radio quasars (FSRQs) and BL Lacs is thought to be dominated by different radiation processes (EC versus SSC), one might expect differences in the PSD slopes for these sources if the injection () would be similar. In particular, if the above relation is applied to the BL Lac object PKS 2155-304, believed to be dominated by SSC, this would suggest injection with (for the flare) and (for the long-term, low-level activity), respectively. The former could possibly be related to the flicker-noise behavior induced by accretion disk fluctuations, while the latter would require some radial dependencies [48]. At optical (R-band) frequencies, the emission of PKS 2155-304 has been reported to obey a PSD with slope ∼ (1.8–2.4) on timescales larger than several days [55] (but see also [54]). In the above approach, the PSD for synchrotron emission roughly follows and steepens towards higher frequencies (f) if escape is included [61]. Given current uncertainties in PSD slope determination, it seems thus possible to relate the different slopes at optical and HE/VHE to synchrotron and SSC radiation processes, respectively (cf. also [54]). More advanced modeling in this regard, however, seems desirable.
From a formal point of view (and also relevant to the below), it seems important to keep in mind that parameter estimation based on light curve simulations need to be consistent in as much as they account for both the details of the PDF (e.g., log-normality) and the PSD.5
2.4. Quasi-Periodic Variability
With the availability of continuously-sampled gamma-ray light curves, periodicity analysis has gained new momentum as a possible tool to probe deeper into the astrophysical nature of the sources. In particular, the (unbiased) Fermi-LAT light curves of blazars have been used to search for quasi-periodic oscillations (QPOs) on yearly timescales. A prominent example is provided by the BL Lac objects PG 1553+113 (at a redshift of ), where a periodicity of y in HE gamma-rays (and similarly, also in the optical) over y has been reported [63,64,65]; see Figure 10 for an illustration.
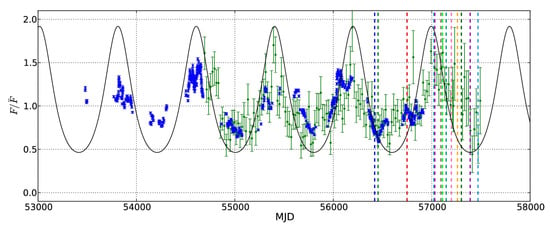
Figure 10.
The y-long light curve of PG 1553+113 in HE gamma-rays (20-d bins; green points) and in the optical (blue points) band. The black line shows the periodicity model, and the vertical line corresponds to some spectrum calculations. From [64].
Possible year-type HE periodicities (though at different significance levels) have now been reported for a variety of blazars including PKS 2155-304 ( y), Mkn 501 ( y), BL Lac ( y), PG 1553+113 ( y), PKS 0426-380 ( y), PKS 0537-441 ( y during the high state), and PKS 0310-243 ( y), see e.g., [63,66,67,68,69,70,71].
Multi-year quasi-periodic variability in AGN light curves has often been interpreted in the context of supermassive binary black holes (SBBHs), such as the optical -y periodicity in the BL Lac object OJ 287 () (e.g., [72]) or the apparent optical -y periodicity in the quasar PG 1302-102 () [73]. In general, SBBHs are a natural stage of hierarchical galaxy formation in which elliptical galaxies (e.g., the host galaxies of radio-loud AGN) are formed by galaxy mergers [74]. Depending on their evolutionary path, close SBBHs (with separation less than a few parsecs) could potentially still reside in the center of (some) radio-loud AGN (e.g., [75,76,77]). This is in fact supported by recent morphological evidence for SBBH-driven geodetic precession (– y) in the radio maps of powerful AGN [78]. Close, accreting SBBH systems are likely to be accompanied by a circumbinary disk surrounding the binary, with circumbinary gas streams feeding mini-disks around each black hole and affecting their evolution (e.g., [79,80]).
The HE findings noted above have led to the emergence of new SBBH interpretations. From a statistical point of view, however, some caution needs to be exercised concerning the significance of the inferred periods, as in most cases (perhaps apart from Mkn 501), only a few cycles are present over the available data. As shown by Vaughan et al. [81], clear phantom periodicities over ∼(2–3) cycles can be well found in pure noise data. Moreover, there are indications that the QPO results may be more dependent on the analysis method employed than initially thought [82]. In terms of a global significance (assuming the absence of other physical reasoning) (cf., e.g., [83]), year-type QPOs are often no longer significant [84]. Increasing the number of possible cycles by continuous (well-sampled) monitoring will be important to better assess the current evidence and qualify its impact. In addition, multi-wavelength comparison (as partly done for some of the sources) could improve the robustness of possible detections, though (physically) periods may not necessarily have to be coinciding for very different wavebands. The HE Fermi-LAT -ray observations could in principle be complemented by observations in the VHE domain, though gaps and uneven sampling may represent a more serious issue. Combining different VHE instruments such as FACT and HAWC (e.g., see [85] for the case of Mkn 501) could however improve the situation.
While speculative, one could still try to evaluate possible physical mechanisms for periodicity in AGN. While SBBHs are expected, they may often not provide the best explanation for the noted QPOs: QPOs with physical periods y would imply very close binary systems and thus a significant amount of gravitational wave emission. This would result in a very short gravitational lifetime of the system, – y, making it unlikely that we should be able to detect many of such systems. Similarly, Pulsar Timing Array observations impose upper limits on the (nano-hertz) gravitational stochastic background. If the binary hypothesis is tested for the HE blazar population, assuming year-like QPOs and using the respective luminosity functions, only a very minor fraction (0.01–0.1%) of BL Lacs and FSRQs could harbor SBBHs [86]. In fact, pervious results are rather suggestive of orbital periods of the order of y [76]. It seems thus more promising to relate year-type QPOs to other origins such as the helical motion of a component inside a rotating jet, where differential Doppler boosting accounts for a periodic lighthouse effects [87]; or some quasi-periodic modulation in the accretion flow (e.g., induced by modulations of the transition from an ADAF to a standard disk) feeding the jet (e.g., [88]). Constraints on the jet radius suggest possible periods y for the former scenario (cf., [89]), while the latter would suggest transition radii . At the current stage, it seems important to evaluate the adequacy of such explanations in more detail.
We note that a very interesting, month-type ( d) HE QPO over six cycles has been recently reported for the BL Lac object PKS 2247-131 () [90]. The QPO behavior follows an outburst of the source in October 2016 and is thought to be associated with a helical jet structure induced by the orbital motion in an SBBH. The observed month-type HE QPO could in principle results from a shortening of the real physical period due to relativistic travel-time effects (e.g., [89]), in which case it would be suggestive of a (physical) orbital period of y [90]. Interestingly, a similar month-type ( d) behavior (over 4–5 cycles) at VHE energies has been reported for Mkn 501 during a large flare in 1997 [91,92] and has also been interpreted in an SBBH framework [93].
3. A Possible Example: PKS 2155-304
Given the above-noted VHE timing characteristics of PKS 2155-304 (log-normality and power-law noise behavior) and the properties of disk fluctuations, one could hypothesize that the VHE variability is driven by density fluctuations in the accretion-disk. If these are efficiently transmitted to the jet, it could lead to a respective, power-law noise spectrum in injection for Fermi-type particle acceleration. One would only be able, however, to observe rapid VHE variations (occurring on timescales as short as s) with the corresponding disk characteristics if these signatures do not get obscured by other processes occurring on longer timescale within the source. As the flux changes seen by an observer will appear to be convolved and thus dominated by the longest timescale, this would require that the (observed) timescales for photons traveling across the radial width of the source and for the relevant radiative loss processes still remain smaller than . As shown in [18], this seems feasible in the case of PKS 2155-304. To account for the observed minimum variability, however, the black hole mass would need to be limited to (assuming a thick inner disk); see Equation (1). In particular, the scenario would require a black hole mass that is seemingly smaller than the total central black hole mass inferred from the relation. A straightforward way to account for this is to consider a binary black hole system where the jet dominating VHE emission is emitted from the secondary (less massive) black hole [18]; see Figure 11. As noted above, viewing elliptical galaxies as a merger product of spiral galaxies, an SBBH stage is expected to occur at some time. Once the secondary becomes embedded in the outer disk around the primary (more massive) black hole, it will start clearing up an annular gap. Mass supply from the circumbinary disk to the central binary, however, can still continue through tidal, time-dependent (periodically-modulated) gas streams, which penetrate the gap and preferentially feed the secondary (disk) (e.g., [79,94,95]). Numerical simulations in particular reveal that a reversal of mass accretion rates can occur (i.e., despite ), acting towards equal-mass binaries and suggesting that the secondary and its jet can become more luminous than the primary. In such a scenario, a high VHE luminosity, as inferred for PKS 2155-304, could be accounted for, despite the smaller (secondary) black hole mass.
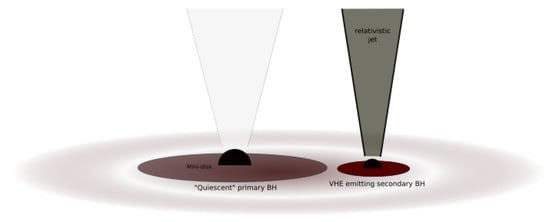
Figure 11.
A possible binary black hole model for PKS 2155-304, with the binary (black holes plus mini-disks) being surrounded by a circumbinary disk. The tidal gas stream from this disk preferentially feeds the less massive, secondary black hole, whose jet emission dominates the observed VHE radiation spectrum. Both the short VHE variability and the high (apparent) luminosity can thus be accommodated, cf. [18].
When put in context, these considerations suggest that care needs to be exercised in the interpretation of VHE variability constraints to avoid a spurious identification of the emitting (possibly secondary) black hole mass with the total (possibly primary + secondary) central black hole mass of the system. In the case of PKS 2155-305, there are additional pieces of circumstantial evidence, such as a (comparable) small black hole mass inferred from its X-ray variability (PSD) properties (e.g., [96]), indications for optical long-term ( y) periodicity [97], and jet bending on pc-scales (e.g., [98]), which may in fact be more easily integrated within a binary framework.
4. Conclusions
Time variability provides key information about the physics of astrophysical objects beyond that given solely in their energy spectra. As indicated in this paper, this information is vital to properly understand the phenomena and processes involved. Given the progress in gamma-ray astronomy, statistical tools can now be applied to study the timing properties of AGN and to characterize their variability in terms of, e.g., flux distributions (PDF) and (temporal) frequency dependence (PSD), along with characteristic timescales and possible QPOs. This positive development is set to strengthen with upcoming instrumental developments and will make it possible to deepen our understanding of the link between accretion dynamics, black hole physics, and jet ejection.
Funding
Funding by a DFG Heisenberg Fellowship RI 1187/6-1 is gratefully acknowledged.
Acknowledgments
Support and hospitality of the Max-Planck-Institut für Kernphysik (MPIK), Heidelberg, is gratefully acknowledged. I would like to thank Daniela Dorner and Thomas Bretz for organizing an inspiring conference, and Nachiketa Chakraborty for helpful comments on the manuscript.
Conflicts of Interest
The author declares no conflict of interest.
References
- Rieger, F.M.; de Oña-Wilhelmi, E.; Aharonian, F.A. TeV astronomy. Front. Phys. 2013, 8, 714–747. [Google Scholar] [CrossRef]
- Funk, S. Ground- and Space-Based Gamma-Ray Astronomy. Annu. Rev. Nucl. Part. Sci. 2015, 65, 245–277. [Google Scholar] [CrossRef]
- Madejski, G.; Sikora, M. Gamma-Ray Observations of Active Galactic Nuclei. Annu. Rev. Astron. Astrophys. 2016, 54, 725–760. [Google Scholar] [CrossRef]
- Thompson, D. Fermi: Monitoring the Gamma-Ray Universe. Galaxies 2018, 6, 117. [Google Scholar] [CrossRef]
- Abeysekara, A.U.; Albert, A.; Alfaro, R.; Alvarez, C.; Álvarez, J.D.; Arceo, R.; Arteaga-Velázquez, J.C.; Avila Rojas, D.; Ayala Solares, H.A.; Barber, A.S.; et al. Daily Monitoring of TeV Gamma-Ray Emission from Mrk 421, Mrk 501, and the Crab Nebula with HAWC. Astrophys. J. 2017, 841, 100. [Google Scholar] [CrossRef]
- Temme, F.; Adam, J.; Ahnen, M.; Baack, D.; Balbo, M.; Bergmann, M.; Biland, A.; Blank, M.; Bretz, T.; Brügge, K.; et al. Long-Term Monitoring of Bright Blazars in the Multi-GeV to TeV Range with FACT. Galaxies 2017, 5, 18. [Google Scholar] [CrossRef]
- Albert, J.; Aliu, E.; Anderhub, H.; Antoranz, P.; Armada, A.; Baixeras, C.; Barrio, J.A.; Bartko, H.; Bastieri, D.; Becker, J.K.; et al. Variable Very High Energy γ-Ray Emission from Markarian 501. Astrophys. J. 2007, 669, 862–883. [Google Scholar] [CrossRef]
- Aharonian, F.; Akhperjanian, A.G.; Bazer-Bachi, A.R.; Behera, B.; Beilicke, M.; Benbow, W.; Berge, D.; Bernlöhr, K.; Boisson, C.; Bolz, O.; et al. An Exceptional Very High Energy Gamma-Ray Flare of PKS 2155-304. Astrophys. J. 2007, 664, L71–L74. [Google Scholar] [CrossRef]
- Ackermann, M.; Anantua, R.; Asano, K.; Baldini, L.; Barbiellini, G.; Bastieri, D.; Becerra Gonzalez, J.; Bellazzini, R.; Bissaldi, E.; Blandford, R.D.; et al. Minute-timescale >100 MeV γ-Ray Variability during the Giant Outburst of Quasar 3C 279 Observed by Fermi-LAT in 2015 June. Astrophys. J. 2016, 824, L20. [Google Scholar] [CrossRef]
- Aharonian, F.; Akhperjanian, A.G.; Bazer-Bachi, A.R.; Beilicke, M.; Benbow, W.; Berge, D.; Bernlöhr, K.; Boisson, C.; Bolz, O.; Borrel, V.; et al. Fast Variability of Tera-Electron Volt γ Rays from the Radio Galaxy M87. Science 2006, 314, 1424–1427. [Google Scholar] [CrossRef]
- Abramowski, A.; Acero, F.; Aharonian, F.; Akhperjanian, A.G.; Anton, G.; Balzer, A.; Barnacka, A.; Barres de Almeida, U.; Becherini, Y.; Becker, J.; et al. The 2010 Very High Energy γ-Ray Flare and 10 Years of Multi-wavelength Observations of M 87. Astrophys. J. 2012, 746, 151. [Google Scholar] [CrossRef]
- MAGIC Collaboration; Ansoldi, S.; Antonelli, L.A.; Arcaro, C.; Baack, D.; Babić, A.; Banerjee, B.; Bangale, P.; Barres de Almeida, U.; Barrio, J.A.; et al. Gamma-ray flaring activity of NGC1275 in 2016–2017 measured by MAGIC. Astron. Astrophys. 2018, 617, A91. [Google Scholar] [CrossRef]
- Aleksić, J.; Ansoldi, S.; Antonelli, L.A.; Antoranz, P.; Babic, A.; Bangale, P.; Barrio, J.A.; González, J.B.; Bednarek, W.; Bernardini, E.; et al. Black hole lightning due to particle acceleration at subhorizon scales. Science 2014, 346, 1080–1084. [Google Scholar] [CrossRef]
- Rieger, F.; Levinson, A. Radio Galaxies at VHE Energies. Galaxies 2018, 6, 116. [Google Scholar] [CrossRef]
- Cherenkov Telescope Array Consortium; Acharya, B.S.; Agudo, I.; Samarai, I.A.; Alfaro, R.; Alfaro, J.; Alispach, C.; Alves Batista, R.; Amans, J.P.; Amato, E.; et al. Science with the Cherenkov Telescope Array. arXiv, 2017; arXiv:1709.07997v2. [Google Scholar]
- Levinson, A. Relativistic Flows in TeV Blazars. Proceedings of Science. 2008. Available online: http://pos.sissa.it/063/002/pdf (accessed on 28 January 2019).
- Dermer, C.D.; Finke, J.D.; Menon, G. Black-Hole Engine Kinematics, Flares from PKS 2155-304, and Multiwavelength Blazar Analysis. Proc. Sci. 2008, arXiv:0810.1055v1. [Google Scholar]
- Rieger, F.M.; Volpe, F. Short-term VHE variability in blazars: PKS 2155-304. Astron. Astrophys. 2010, 520, A23. [Google Scholar] [CrossRef]
- Salvati, M.; Spada, M.; Pacini, F. Rapid Variability of Gamma-Ray Blazars: A Model for Markarian 421. Astrophys. J. 1998, 495, L19–L21. [Google Scholar] [CrossRef]
- Begelman, M.C.; Fabian, A.C.; Rees, M.J. Implications of very rapid TeV variability in blazars. Mon. Not. R. Astron. Soc. 2008, 384, L19–L23. [Google Scholar] [CrossRef]
- Ghisellini, G.; Tavecchio, F.; Bodo, G.; Celotti, A. TeV variability in blazars: how fast can it be? Mon. Not. R. Astron. Soc. 2009, 393, L16–L20. [Google Scholar] [CrossRef]
- Kirk, J.G.; Mochol, I. Charge-starved, Relativistic Jets and Blazar Variability. Astrophys. J. 2011, 729, 104. [Google Scholar] [CrossRef]
- Narayan, R.; Piran, T. Variability in blazars: Clues from PKS 2155-304. Mon. Not. R. Astron. Soc. 2012, 420, 604–612. [Google Scholar] [CrossRef]
- Hirotani, K.; Pu, H.Y. Energetic Gamma Radiation from Rapidly Rotating Black Holes. Astrophys. J. 2016, 818, 50. [Google Scholar] [CrossRef]
- Aharonian, F.A.; Barkov, M.V.; Khangulyan, D. Scenarios for Ultrafast Gamma-Ray Variability in AGN. Astrophys. J. 2017, 841, 61. [Google Scholar] [CrossRef]
- Levinson, A.; Rieger, F. Variable TeV Emission as a Manifestation of Jet Formation in M87? Astrophys. J. 2011, 730, 123. [Google Scholar] [CrossRef]
- Giannios, D.; Uzdensky, D.A.; Begelman, M.C. Fast TeV variability in blazars: Jets in a jet. Mon. Not. R. Astron. Soc. 2009, 395, L29–L33. [Google Scholar] [CrossRef]
- Barkov, M.V.; Aharonian, F.A.; Bogovalov, S.V.; Kelner, S.R.; Khangulyan, D. Rapid TeV Variability in Blazars as a Result of Jet-Star Interaction. Astrophys. J. 2012, 749, 119. [Google Scholar] [CrossRef]
- Timmer, J.; Koenig, M. On generating power law noise. Astron. Astrophys. 1995, 300, 707. [Google Scholar]
- Emmanoulopoulos, D.; McHardy, I.M.; Papadakis, I.E. Generating artificial light curves: revisited and updated. Mon. Not. R. Astron. Soc. 2013, 433, 907–927. [Google Scholar] [CrossRef]
- Sobolewska, M.A.; Siemiginowska, A.; Kelly, B.C.; Nalewajko, K. Stochastic Modeling of the Fermi/LAT γ-Ray Blazar Variability. Astrophys. J. 2014, 786, 143. [Google Scholar] [CrossRef]
- Kelly, B.C.; Becker, A.C.; Sobolewska, M.; Siemiginowska, A.; Uttley, P. Flexible and Scalable Methods for Quantifying Stochastic Variability in the Era of Massive Time-domain Astronomical Data Sets. Astrophys. J. 2014, 788, 33. [Google Scholar] [CrossRef]
- Feigelson, E.D.; Babu, G.J.; Caceres, G.A. Autoregressive Times Series Methods for Time Domain Astronomy. Front. Phys. 2018, 6, 80. [Google Scholar] [CrossRef]
- Moreno, J.; Vogeley, M.S.; Richards, G.T. AGN Variability Analysis Handbook. arXiv, 2018; arXiv:1811.00154. [Google Scholar]
- Vio, R.; Kristensen, N.R.; Madsen, H.; Wamsteker, W. Time series analysis in astronomy: Limits and potentialities. Astron. Astrophys. 2005, 435, 773–780. [Google Scholar] [CrossRef]
- H.E.S.S. Collaboration; Abramowski, A.; Acero, F.; Aharonian, F.; Akhperjanian, A.G.; Anton, G.; Barres de Almeida, U.; Bazer-Bachi, A.R.; Becherini, Y.; Behera, B.; et al. VHE γ-ray emission of PKS 2155-304: spectral and temporal variability. Astron. Astrophys. 2010, 520, A83. [Google Scholar] [CrossRef]
- Chakraborty, N.; Cologna, G.; Kastendieck, M.A.; Rieger, F.; Romoli, C.; Wagner, S.J.; Jacholkowska, A.; Taylor, A.; H.E.S.S. Collaboration. Rapid variability at very high energies in Mrk 501. In Proceedings of the 34th International Cosmic Ray Conference (ICRC2015), The Hague, The Netherlands, 30 July–6 August 2015; Volume 34, p. 872. [Google Scholar]
- Chevalier, J.; Kastendieck, M.A.; Rieger, F.M.; Maurin, G.; Lenain, J.P.; Lamanna, G. Long term variability of the blazar PKS 2155-304. In Proceedings of the 34th International Cosmic Ray Conference (ICRC2015), The Hague, The Netherlands, 30 July–6 August 2015; Volume 34, p. 829. [Google Scholar]
- H.E.S.S. Collaboration; Abdalla, H.; Abramowski, A.; Aharonian, F.; Ait Benkhali, F.; Akhperjanian, A.G.; Andersson, T.; Angüner, E.O.; Arrieta, M.; Aubert, P.; et al. Characterizing the γ-ray long-term variability of PKS 2155-304 with H.E.S.S. and Fermi-LAT. Astron. Astrophys. 2017, 598, A39. [Google Scholar] [CrossRef]
- Uttley, P.; McHardy, I.M. The flux-dependent amplitude of broadband noise variability in X-ray binaries and active galaxies. Mon. Not. R. Astron. Soc. 2001, 323, L26–L30. [Google Scholar] [CrossRef]
- Uttley, P.; McHardy, I.M.; Vaughan, S. Non-linear X-ray variability in X-ray binaries and active galaxies. Mon. Not. R. Astron. Soc. 2005, 359, 345–362. [Google Scholar] [CrossRef]
- Romoli, C.; Chakraborty, N.; Dorner, D.; Taylor, A.; Blank, M. Flux Distribution of Gamma-Ray Emission in Blazars: The Example of Mrk 501. Galaxies 2018, 6, 135. [Google Scholar] [CrossRef]
- Sinha, A.; Shukla, A.; Saha, L.; Acharya, B.S.; Anupama, G.C.; Bhattacharjee, P.; Britto, R.J.; Chitnis, V.R.; Prabhu, T.P.; Singh, B.B.; et al. Long-term study of Mkn 421 with the HAGAR Array of Telescopes. Astron. Astrophys. 2016, 591, A83. [Google Scholar] [CrossRef]
- Shah, Z.; Mankuzhiyil, N.; Sinha, A.; Misra, R.; Sahayanathan, S.; Iqbal, N. Log-normal flux distribution of bright Fermi blazars. Res. Astron. Astrophys. 2018, 18, 141. [Google Scholar] [CrossRef]
- Ioka, K.; Nakamura, T. A Possible Origin of Lognormal Distributions in Gamma-Ray Bursts. Astrophys. J. 2002, 570, L21–L24. [Google Scholar] [CrossRef]
- Giebels, B.; Degrange, B. Lognormal variability in BL Lacertae. Astron. Astrophys. 2009, 503, 797–799. [Google Scholar] [CrossRef]
- McHardy, I. X-Ray Variability of AGN and Relationship to Galactic Black Hole Binary Systems; Belloni, T., Ed.; Lecture Notes in Physics; Springer Verlag: Berlin, Germnay, 2010; Volume 794, p. 203. [Google Scholar] [CrossRef]
- Lyubarskii, Y.E. Flicker noise in accretion discs. Mon. Not. R. Astron. Soc. 1997, 292, 679. [Google Scholar] [CrossRef]
- King, A.R.; Pringle, J.E.; West, R.G.; Livio, M. Variability in black hole accretion discs. Mon. Not. R. Astron. Soc. 2004, 348, 111–122. [Google Scholar] [CrossRef]
- Arévalo, P.; Uttley, P. Investigating a fluctuating-accretion model for the spectral-timing properties of accreting black hole systems. Mon. Not. R. Astron. Soc. 2006, 367, 801–814. [Google Scholar] [CrossRef]
- Mannheim, K. The proton blazar. Astron. Astrophys. 1993, 269, 67–76. [Google Scholar]
- Sinha, A.; Khatoon, R.; Misra, R.; Sahayanathan, S.; Mandal, S.; Gogoi, R.; Bhatt, N. The flux distribution of individual blazars as a key to understand the dynamics of particle acceleration. Mon. Not. R. Astron. Soc. 2018, 480, L116–L120. [Google Scholar] [CrossRef]
- Kirk, J.G.; Rieger, F.M.; Mastichiadis, A. Particle acceleration and synchrotron emission in blazar jets. Astron. Astrophys. 1998, 333, 452–458. [Google Scholar]
- Chevalier, J.; Sanchez, D.A.; Serpico, P.D.; Lenain, J.P.; Maurin, G. Variability studies and modeling of the blazar PKS 2155-304 in the light of a decade of multi-wavelength observations. Mon. Not. R. Astron. Soc. 2019, 484, 749–759. [Google Scholar] [CrossRef]
- Chatterjee, R.; Bailyn, C.D.; Bonning, E.W.; Buxton, M.; Coppi, P.; Fossati, G.; Isler, J.; Maraschi, L.; Urry, C.M. Similarity of the Optical-Infrared and γ-Ray Time Variability of Fermi Blazars. Astrophys. J. 2012, 749, 191. [Google Scholar] [CrossRef]
- Nakagawa, K.; Mori, M. Time Series Analysis of Gamma-Ray Blazars and Implications for the Central Black-hole Mass. Astrophys. J. 2013, 773, 177. [Google Scholar] [CrossRef]
- Kushwaha, P.; Sinha, A.; Misra, R.; Singh, K.P.; de Gouveia Dal Pino, E.M. Gamma-Ray Flux Distribution and Nonlinear Behavior of Four LAT Bright AGNs. Astrophys. J. 2017, 849, 138. [Google Scholar] [CrossRef]
- Goyal, A.; Stawarz, Ł.; Zola, S.; Marchenko, V.; Soida, M.; Nilsson, K.; Ciprini, S.; Baran, A.; Ostrowski, M.; Wiita, P.J.; et al. Stochastic Modeling of Multiwavelength Variability of the Classical BL Lac Object OJ 287 on Timescales Ranging from Decades to Hours. Astrophys. J. 2018, 863, 175. [Google Scholar] [CrossRef]
- McHardy, I.M.; Koerding, E.; Knigge, C.; Uttley, P.; Fender, R.P. Active galactic nuclei as scaled-up Galactic black holes. Nature 2006, 444, 730–732. [Google Scholar] [CrossRef] [PubMed]
- Kataoka, J.; Takahashi, T.; Wagner, S.J.; Iyomoto, N.; Edwards, P.G.; Hayashida, K.; Inoue, S.; Madejski, G.M.; Takahara, F.; Tanihata, C.; et al. Characteristic X-Ray Variability of TeV Blazars: Probing the Link between the Jet and the Central Engine. Astrophys. J. 2001, 560, 659–674. [Google Scholar] [CrossRef]
- Finke, J.D.; Becker, P.A. Fourier Analysis of Blazar Variability. Astrophys. J. 2014, 791, 21. [Google Scholar] [CrossRef]
- Finke, J.D.; Becker, P.A. Fourier Analysis of Blazar Variability: Klein-Nishina Effects and the Jet Scattering Environment. Astrophys. J. 2015, 809, 85. [Google Scholar] [CrossRef]
- Ackermann, M.; Ajello, M.; Albert, A.; Atwood, W.B.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Becerra Gonzalez, J.; Bellazzini, R.; et al. Multiwavelength Evidence for Quasi-periodic Modulation in the Gamma-Ray Blazar PG 1553+113. Astrophys. J. 2015, 813, L41. [Google Scholar] [CrossRef]
- Sobacchi, E.; Sormani, M.C.; Stamerra, A. A model for periodic blazars. Mon. Not. R. Astron. Soc. 2017, 465, 161–172. [Google Scholar] [CrossRef]
- Tavani, M.; Cavaliere, A.; Munar-Adrover, P.; Argan, A. The Blazar PG 1553+113 as a Binary System of Supermassive Black Holes. Astrophys. J. 2018, 854, 11. [Google Scholar] [CrossRef]
- Sandrinelli, A.; Covino, S.; Dotti, M.; Treves, A. Quasi-periodicities at Year-like Timescales in Blazars. Astron. J. 2016, 151, 54. [Google Scholar] [CrossRef]
- Sandrinelli, A.; Covino, S.; Treves, A.; Lindfors, E.; Raiteri, C.M.; Nilsson, K.; Takalo, L.O.; Reinthal, R.; Berdyugin, A.; Fallah Ramazani, V.; et al. Gamma-ray and optical oscillations of 0716+714, MRK 421, and BL Lacertae. Astron. Astrophys. 2017, 600, A132. [Google Scholar] [CrossRef]
- Prokhorov, D.A.; Moraghan, A. A search for cyclical sources of γ-ray emission on the period range from days to years in the Fermi-LAT sky. Mon. Not. R. Astron. Soc. 2017, 471, 3036–3042. [Google Scholar] [CrossRef]
- Zhang, P.F.; Yan, D.H.; Liao, N.H.; Wang, J.C. Revisiting Quasi-periodic Modulation in γ-Ray Blazar PKS 2155-304 with Fermi Pass 8 Data. Astrophys. J. 2017, 835, 260. [Google Scholar] [CrossRef]
- Zhang, P.F.; Yan, D.H.; Zhou, J.N.; Fan, Y.Z.; Wang, J.C.; Zhang, L. A γ-ray Quasi-periodic Modulation in the Blazar PKS 0301-243? Astrophys. J. 2017, 845, 82. [Google Scholar] [CrossRef]
- Bhatta, G. Blazar Mrk 501 shows rhythmic oscillations in its γ-ray emission. arXiv, 2018; arXiv:1808.06067. [Google Scholar]
- Valtonen, M.J.; Zola, S.; Ciprini, S.; Gopakumar, A.; Matsumoto, K.; Sadakane, K.; Kidger, M.; Gazeas, K.; Nilsson, K.; Berdyugin, A.; et al. Primary Black Hole Spin in OJ 287 as Determined by the General Relativity Centenary Flare. Astrophys. J. 2016, 819, L37. [Google Scholar] [CrossRef]
- Graham, M.J.; Djorgovski, S.G.; Stern, D.; Glikman, E.; Drake, A.J.; Mahabal, A.A.; Donalek, C.; Larson, S.; Christensen, E. A possible close supermassive black-hole binary in a quasar with optical periodicity. Nature 2015, 518, 74–76. [Google Scholar] [CrossRef]
- Begelman, M.C.; Blandford, R.D.; Rees, M.J. Massive black hole binaries in active galactic nuclei. Nature 1980, 287, 307–309. [Google Scholar] [CrossRef]
- Komossa, S. Observational evidence for binary black holes and active double nuclei. Mem. Soc. Astron. Ital. 2006, 77, 733. [Google Scholar]
- Rieger, F.M. Supermassive binary black holes among cosmic gamma-ray sources. Astrophys. Space Sci. 2007, 309, 271–275. [Google Scholar] [CrossRef]
- Merritt, D. Dynamics and Evolution of Galactic Nuclei; Princeton University Press: Princeton, NJ, USA, 2013. [Google Scholar]
- Krause, M.G.H.; Shabala, S.S.; Hardcastle, M.J.; Bicknell, G.V.; Böhringer, H.; Chon, G.; Nawaz, M.A.; Sarzi, M.; Wagner, A.Y. How frequent are close supermassive binary black holes in powerful jet sources? Mon. Not. R. Astron. Soc. 2019, 482, 240–261. [Google Scholar] [CrossRef]
- Farris, B.D.; Duffell, P.; MacFadyen, A.I.; Haiman, Z. Binary Black Hole Accretion from a Circumbinary Disk: Gas Dynamics inside the Central Cavity. Astrophys. J. 2014, 783, 134. [Google Scholar] [CrossRef]
- Bowen, D.B.; Campanelli, M.; Krolik, J.H.; Mewes, V.; Noble, S.C. Relativistic Dynamics and Mass Exchange in Binary Black Hole Mini-disks. Astrophys. J. 2017, 838, 42. [Google Scholar] [CrossRef]
- Vaughan, S.; Uttley, P.; Markowitz, A.G.; Huppenkothen, D.; Middleton, M.J.; Alston, W.N.; Scargle, J.D.; Farr, W.M. False periodicities in quasar time-domain surveys. Mon. Not. R. Astron. Soc. 2016, 461, 3145–3152. [Google Scholar] [CrossRef]
- Covino, S.; Sandrinelli, A.; Treves, A. Gamma-ray quasi-periodicities of blazars. A cautious approach. Mon. Not. R. Astron. Soc. 2019, 482, 1270–1274. [Google Scholar] [CrossRef]
- Benlloch, S.; Wilms, J.; Edelson, R.; Yaqoob, T.; Staubert, R. Quasi-periodic Oscillation in Seyfert Galaxies: Significance Levels. The Case of Markarian 766. Astrophys. J. 2001, 562, L121–L124. [Google Scholar] [CrossRef]
- Ait Benkhali, F.; Hofmann, W.; Rieger, F.M.; Chakraborty, N. Evaluating Quasi-Periodic Variations in the γ-ray Lightcurves of Fermi-LAT Blazars. Astron. Astrophys. 2019. submitted. [Google Scholar]
- Dorner, D.; Lauer, R.J.; FACT Collaboration; Adam, J.; Ahnen, M.; Baack, D.; Balbo, M.; Bergmann, M.; Biland, A.; Blank, M.; et al. First study of combined blazar light curves with FACT and HAWC. In Proceedings of the 6th International Symposium on High Energy Gamma-Ray Astronomy, Heidelberg, Germany, 11–15 July 2016; Volume 1792, p. 050020. [Google Scholar] [CrossRef]
- Holgado, A.M.; Sesana, A.; Sandrinelli, A.; Covino, S.; Treves, A.; Liu, X.; Ricker, P. Pulsar timing constraints on the Fermi massive black hole binary blazar population. Mon. Not. R. Astron. Soc. 2018, 481, L74–L78. [Google Scholar] [CrossRef]
- Camenzind, M.; Krockenberger, M. The lighthouse effect of relativistic jets in blazars - A geometric origin of intraday variability. Astron. Astrophys. 1992, 255, 59–62. [Google Scholar]
- Gracia, J.; Peitz, J.; Keller, C.; Camenzind, M. Evolution of bimodal accretion flows. Mon. Not. R. Astron. Soc. 2003, 344, 468–472. [Google Scholar] [CrossRef]
- Rieger, F.M. On the Geometrical Origin of Periodicity in Blazar-type Sources. Astrophys. J. 2004, 615, L5–L8. [Google Scholar] [CrossRef]
- Zhou, J.; Wang, Z.; Chen, L.; Wiita, P.J.; Vadakkumthani, J.; Morrell, N.; Zhang, P.; Zhang, J. A 34.5 day quasi-periodic oscillation in γ-ray emission from the blazar PKS 2247-131. Nat. Commun. 2018, 9, 4599. [Google Scholar] [CrossRef]
- Hayashida, N.; Hirasawa, H.; Ishikawa, F.; Lafoux, H.; Nagano, M.; Nishikawa, D.; Ouchi, T.; Ohoka, H.; Ohnishi, M.; Sakaki, N.; et al. Observations of TeV Gamma Ray Flares from Markarian 501 with the Telescope Array Prototype. Astrophys. J. 1998, 504, L71–L74. [Google Scholar] [CrossRef]
- Osone, S. Study of 23 day periodicity of Blazar Mkn501 in 1997. Astropart. Phys. 2006, 26, 209–218. [Google Scholar] [CrossRef]
- Rieger, F.M.; Mannheim, K. Implications of a possible 23 day periodicity for binary black hole models in Mkn 501. Astron. Astrophys. 2000, 359, 948–952. [Google Scholar]
- Artymowicz, P.; Lubow, S.H. Mass Flow through Gaps in Circumbinary Disks. Astrophys. J. 1996, 467, L77. [Google Scholar] [CrossRef]
- Hayasaki, K.; Mineshige, S.; Sudou, H. Binary Black Hole Accretion Flows in Merged Galactic Nuclei. Publ. Astron. Soc. Jpn. 2007, 59, 427–441. [Google Scholar] [CrossRef]
- Czerny, B.; Nikołajuk, M.; Piasecki, M.; Kuraszkiewicz, J. Black hole masses from power density spectra: Determinations and consequences. Mon. Not. R. Astron. Soc. 2001, 325, 865–874. [Google Scholar] [CrossRef]
- Fan, J.H.; Lin, R.G. The variability analysis of PKS 2155-304. Astron. Astrophys. 2000, 355, 880–884. [Google Scholar]
- Piner, B.G.; Pant, N.; Edwards, P.G. The Jets of TeV Blazars at Higher Resolution: 43 GHz and Polarimetric VLBA Observations from 2005 to 2009. Astrophys. J. 2010, 723, 1150–1167. [Google Scholar] [CrossRef]
| 1 | There are two common approaches to deal with irregular sampling in stochastic light curves, i.e., by means of extensive Monte Carlo simulations of artificial light curves [29,30] or by means of likelihood-based approaches using special parameterized stochastic models in the time domain such as, e.g., the first-order continuous-time autoregressive (Ornstein–Uhlenbeck) process (e.g., [31,32]). The latter offer an efficient means to extract information from large time-domain datasets, in particular the power spectral density (PSD). While autoregressive models are becoming increasingly popular (cf. [33,34]), general caveats concern the limitations of linear (e.g., ARMA, CARMA) models to extract physical information from (very probably) non-linear systems (e.g., [35]); see also Section 2.2. |
| 2 | A random variable X is log-normally distributed if obeys a normal (Gaussian) distribution. The PDF of such a random variable is of the form , where is the mean and the standard deviation. |
| 3 | Defined as the square-root of the light curve variance and related to the square-root of the integral of the PSD, see below, over the observable frequency range, i.e., . |
| 4 | For a stationary stochastic process X that results from a multiplication of N random subprocesses , , the logarithm of X is equivalent to the sum of the logarithm of the individual , i.e., . By the central limit theorem, this sum must approach a normal (Gaussian) distribution for . Astrophysically, N does not have to be large to achieve a good log-normal distribution [45]. |
| 5 | The widely employed Timmer and König algorithm [29] to simulate light curves assumes a normal (Gaussian) stochastic process, and thus potentially introduces errors in parameter estimation for log-normal processes [30]. It remains to be studied how this affects the results given the quality of available gamma-ray data. |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).