Modeling the Rising Tails of Galaxy Rotation Curves
Abstract
1. Introduction
2. Effective Weyl Matter Phenomenology
2.1. Overview
2.2. A Galactic Effective Weyl Matter Solution
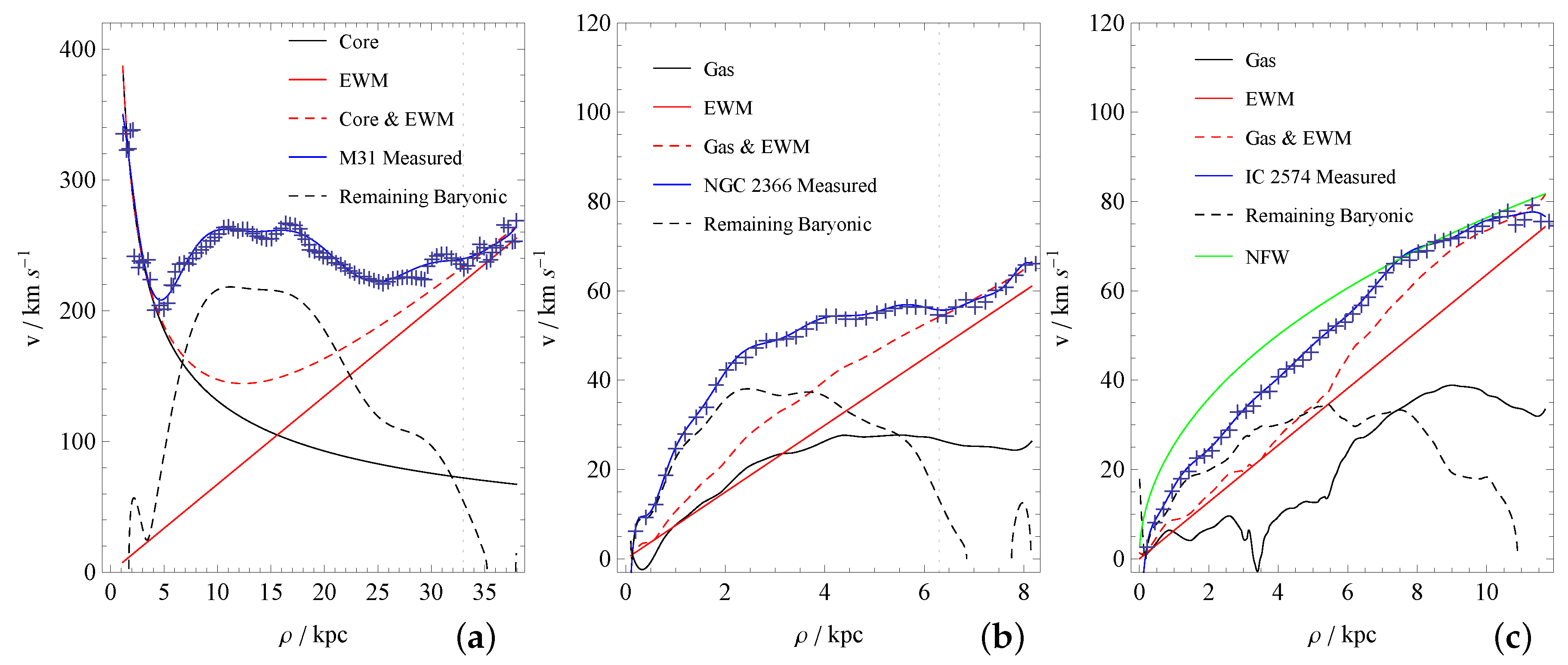
2.3. Anatomy of Rotation Curves
- Because M31 exhibits a strong bulge influence, it becomes possible to infer a bulge mass by fitting to the very inner part ( kpc) of the rotation curve. This is done because as discussed in the last paragraph, any reduction in the uncertainty about baryonic contributions will further reduce the errors when we fit to the tail section. The bulge contribution is modeled as a mass monopole , and by inspection, we obtain . See Figure 1a for the fitting results.
- We then turn to the tail section (beyond the dotted vertical line in Figure 1a at around 33 kpc). We begin by taking off the monopolar bulge contribution, so that the remainder contains the contribution from the EWM (dominate) and the other non-bulge baryonic components (subdominant).
- A fit for is then carried out. Equation (5) predicts an EWM contribution to the tail of the rotation curve at (where the speed of light c is in units of km/s), and we fit this functional form to the monopole-removed tail section of the rotation curve. The fitting is done using the standard computation package Mathematica, yielding the best fit . For comparison with a full linear fit, it is more convenient to present the result in terms of the overall slope , whose best fit value is , with standard error .
- The highly rigid nature of the EWM profile (containing only one free parameter) as compared to CDM profiles (containing many tunable parameters) allows us to carry out a test on whether its rigid functional form matches data. Namely, as discussed previously, we can carry out a full linear fit to the tail with and see whether a is close to the fit for we obtained during the last step, as well as whether b is close to zero. Recall though that the tail still contains non-bulge baryonic contributions, and they would contribute to b; nevertheless, since they are subdominant in the tail section, b should not be large. Our fitting yields the best fit slope at , with standard error , which matches rather well with the obtained earlier (well within one standard error). The parameter b has a best fit value of and a standard error of , which is also consistent with a nearly-vanishing intercept.
- Finally, a few words regarding the mid-section of the rotation curve are in order. The remaining miscellaneous contributions, from the stars, dust, and gas residing outside of the central core, are collected into the “remaining baryonic” in Figure 1a. We caution that the study by Bournaud et al. [49] on recycled dwarf galaxies suggests the presence of large amounts of difficult-to-see cold molecular gas in the discs of their parent spiral galaxies (see also, e.g., Li et al. [50] for more direct observational evidences); thus, there is likely still an invisible matter component in the aDM (but of a mundane variety; being ordinary matter, their amounts and distributions could also differ substantially between galaxies of different types and ages, just as stellar matter would) that contributes to the inner to intermediate regions of the rotation curves.Note further that all these aforementioned components are spread out on a disc, and not distributed in a spherically-symmetric manner, so the “remaining baryonic” curve is not bounded from below by a Keplerian profile. Instead, a rapid ∼ decline near a high matter density strip, being the distance to the sharp edge of the strip, provides a better approximation (and a slower decline in the orbiting speed is to be expected if the drop-off in density is more gradual), and is consistent with Figure 1a.
- The rotation curve does not contain a clear bulge-dominated inner segment, so we cannot infer a bulge monopole size, but this also means the bulge should not be significant (recall that we are dealing with a dwarf galaxy). Instead, the carefully-analyzed gas contribution derived from the integrated Hi map is available for this galaxy, so we explicitly account for this contribution.
- Turning to the tail section, we once again remove the contribution from the known baryonic component, gas this time, so as to scrub down the tail maximally to a cleaner EWM domination. We then fit for with the same procedure as was done with M31, yielding best fit at . Note that despite the drastically different nature of the galaxies (massive spiral versus dwarf) and different rotation speeds (hundreds of km/s versus dozens), the values are remarkably similar between NGC 2366 and M31, differing by only rather than orders of magnitude.
- The value translates into a slope at , with standard error . The full linear fit, on the other hand, yields a slope of with standard error , as well as an intercept with standard error . Once again, the EWM’s rigid form is consistent with the morphology of the tail section of the rotation curve (a and agree within one standard error, and b is consistent with being nearly zero).
- The uncertain stellar contributions for this faint dwarf galaxy are collected into the “remaining baryonic” contribution.
- Once again, the gas contribution from the integrated Hi map is available. However, this time, the gas contribution rises very rapidly on the outer regions, so we end up with a large and varying gas contribution in the tail. This unfortunately obscures the linear EWM tail there (the curve bends downwards following the trend in the gas contribution). Nevertheless, the gas contribution declines at the extreme large end, while EWM keeps rising to greater dominance there, so we can adopt a simpler procedure by letting the EWM match the last point in the rotation curve. This yields , differing from the value for M31 by only around , despite the very different galaxy types and rotation curve morphology.
- The very different (as compared to Figure 1a for massive spiral galaxies), continuously-rising rotation curve morphology (also more or less shared by NGC 2366) seen for the dwarfs is because for these aDM-dominated dwarf galaxies, the EWM contribution is significant throughout the entire curve, even on the inside. The almost linearly-rising curves thus provide a rather direct support for the rigid linear EWM profile. In contrast, they pose a serious challenge to common theoretical CDM profiles that flatten off at large , as they cannot provide sufficient speed on the outside without overshooting the inside. Since it is difficult to produce outward acceleration, overshooting is a more troublesome problem. In Figure 1c, we provide a demonstration of this difficulty by making a Navarro–Frenk–White [41] profile fit as a green curve. The fitting is done by inspection of the tail of the curve beyond kpc, yielding parameter values km/s, , and kpc, feeding into:where . Note that even though we have tried to suppress the overshooting by reducing to a perhaps unrealistically small value (it is around 10–15 for the Milky Way) and by making very large (beyond this value, the CDM profile turns downwards), the inner regions of the CDM predicted curve still rest significantly above the observed rotation curve.
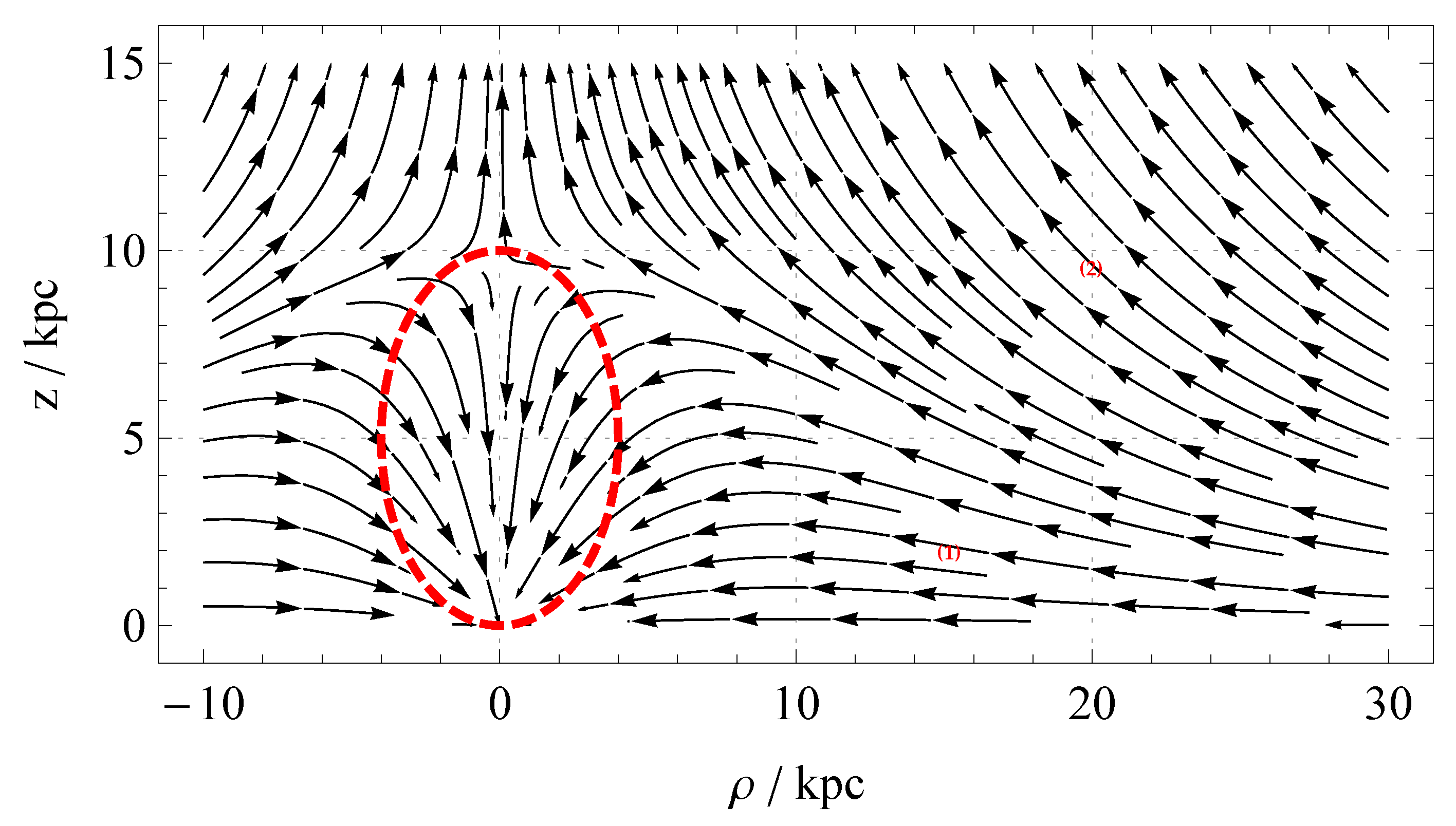
2.4. Off the Galactic Plane
3. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Akerib, D.S.; Alsum, S.; Araújo, H.M.; Bai, X.; Bailey, A.J.; Balajthy, J.; Beltrame, P.; Bernard, E.P.; Bernstein, A.; Biesiadzinski, T.P.; et al. Results from a Search for Dark Matter in the Complete LUX Exposure. Phys. Rev. Lett. 2017, 118, 021303. [Google Scholar] [CrossRef] [PubMed]
- Aprile, E.; Aalbers, J.; Agostini, F.; Alfonsi, M.; Amaro, F.D.; Anthony, M.; Arneodo, F.; Barrow, P.; Baudis, L.; Bauermeister, B.; et al. First Dark Matter Search Results from the XENON1T Experiment. Phys. Rev. Lett. 2017, 119, 181301. [Google Scholar] [CrossRef] [PubMed]
- Cui, X.; Abdukerim, A.; Chen, W.; Chen, X.; Chen, Y.; Dong, B.; Fang, D.; Fu, C.; Giboni, K.; Giuliani, F.; et al. Dark Matter Results From 54-Ton-Day Exposure of PandaX-II Experiment. arXiv, 2017; arXiv:1708.06917. [Google Scholar]
- Ackermann, M.; Ajello, M.; Albert, A.; Atwood, W.B.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Bellazzini, R.; Bissaldi, E.; et al. The Fermi Galactic Center GeV Excess and Implications for Dark Matter. Astrophys. J. 2017, 840, 43. [Google Scholar] [CrossRef]
- Dicus, D.A.; Kolb, E.W.; Teplitz, V.L.; Wagoner, R.V. Astrophysical bounds on the masses of axions and Higgs particles. Phys. Rev. D 1978, 18, 1829–1834. [Google Scholar] [CrossRef]
- Dicus, D.A.; Kolb, E.W.; Teplitz, V.L.; Wagoner, R.V. Astrophysical bounds on very-low-mass axions. Phys. Rev. D 1980, 22, 839–845. [Google Scholar] [CrossRef]
- Asztalos, S.J.; Carosi, G.; Hagmann, C.; Kinion, D.; van Bibber, K.; Hotz, M.; Rosenberg, L.J.; Rybka, G.; Hoskins, J.; Hwang, J.; et al. SQUID-Based Microwave Cavity Search for Dark-Matter Axions. Phys. Rev. Lett. 2010, 104, 041301. [Google Scholar] [CrossRef] [PubMed]
- Du, N.; Force, N.; Khatiwada, R.; Lentz, E.; Ottens, R.; Rosenberg, L.J.; Rybka, G.; Carosi, G.; Woollett, N.; Bowring, D.; et al. Search for Invisible Axion Dark Matter with the Axion Dark Matter Experiment. Phys. Rev. Lett. 2018, 120, 151301. [Google Scholar] [CrossRef]
- Navarro, J.F.; Benz, W. Dynamics of cooling gas in galactic dark halos. Astrophys. J. 1991, 380, 320–329. [Google Scholar] [CrossRef]
- MacCrann, N.; Zuntz, J.; Bridle, S.; Jain, B.; Becker, M.R. Cosmic discordance: Are Planck CMB and CFHTLenS weak lensing measurements out of tune? Mon. Not. R. Astron. Soc. 2015, 451, 2877–2888. [Google Scholar] [CrossRef]
- Klypin, A.; Kravtsov, A.V.; Valenzuela, O.; Prada, F. Where Are the Missing Galactic Satellites? Astrophys. J. 1999, 522, 82–92. [Google Scholar] [CrossRef]
- Shannon, R.M.; Ravi, V.; Coles, W.A.; Hobbs, G.; Keith, M.J.; Manchester, R.N.; Wyithe, J.S.B.; Bailes, M.; Bhat, N.D.R.; Burke-Spolaor, S.; et al. Gravitational-wave limits from pulsar timing constrain supermassive black hole evolution. Science 2013, 342, 334–337. [Google Scholar] [CrossRef] [PubMed]
- Wald, R. It is Not Easy to Fool Mother Nature With a Modified Theory of Gravity; Workshop on Tests of Gravity and Gravitational Physics: Cleveland, OH, USA, 2009. [Google Scholar]
- Yunes, N.; Siemens, X. Gravitational-Wave Tests of General Relativity with Ground-Based Detectors and Pulsar-Timing Arrays. Living Rev. Relativ. 2013, 16, 9. [Google Scholar] [CrossRef] [PubMed]
- Seifert, M.D. Stability of spherically symmetric solutions in modified theories of gravity. Phys. Rev. D 2007, 76, 064002. [Google Scholar] [CrossRef]
- Famaey, B.; McGaugh, S. Modified Newtonian Dynamics (MOND): Observational Phenomenology and Relativistic Extensions. Living Rev. Relativ. 2012, 15, 10. [Google Scholar] [CrossRef] [PubMed]
- de Sitter, W. On Einstein’s theory of gravitation and its astronomical consequences. Second paper. Mon. Not. R. Astron. Soc. 1916, 77, 155–184. [Google Scholar] [CrossRef]
- Gödel, K. An Example of a New Type of Cosmological Solutions of Einstein’s Field Equations of Gravitation. Rev. Mod. Phys. 1949, 21, 447–450. [Google Scholar] [CrossRef]
- Brill, D.R.; Hartle, J.B. Method of the Self-Consistent Field in General Relativity and its Application to the Gravitational Geon. Phys. Rev. 1964, 135, 271–278. [Google Scholar] [CrossRef]
- Misner, C.W.; Taub, A.H. A Singularity-free Empty Universe. Sov. J. Exp. Theor. Phys. 1969, 28, 122. [Google Scholar]
- Calabi, E. The space of Kähler metrics. Proc. Internat. Congr. Math. Amst. 1954, 2, 206–207. [Google Scholar] [CrossRef]
- Yau, S.T. On the Ricci curvature of a compact Kähler manifold and the complex Monge-Ampere equation. I. Commun. Pure Appl. Math. 1978, 31, 339–411. [Google Scholar] [CrossRef]
- Zhang, F.; Brink, J.; Szilágyi, B.; Lovelace, G. Geometrically motivated coordinate system for exploring spacetime dynamics in numerical-relativity simulations using a quasi-Kinnersley tetrad. Phys. Rev. D 2012, 86, 084020. [Google Scholar] [CrossRef]
- Hall, G.S.; MacNay, L. Sectional curvature and the energy momentum tensor. Class. Quantum Gravity 2005, 22, 1493–1502. [Google Scholar] [CrossRef]
- Lindblom, L.; Scheel, M.A.; Kidder, L.E.; Pfeiffer, H.P.; Shoemaker, D.; Teukolsky, S.A. Controlling the growth of constraints in hyperbolic evolution systems. Phys. Rev. D 2004, 69, 124025. [Google Scholar] [CrossRef]
- Clowe, D.; Bradač, M.; Gonzalez, A.H.; Markevitch, M.; Randall, S.W.; Jones, C.; Zaritsky, D. A Direct Empirical Proof of the Existence of Dark Matter. Astrophys. J. Lett. 2006, 648, L109–L113. [Google Scholar] [CrossRef]
- Jee, M.J.; Hoekstra, H.; Mahdavi, A.; Babul, A. Hubble Space Telescope/Advanced Camera for Surveys Confirmation of the Dark Substructure in A520. Astrophys. J. 2014, 783, 78. [Google Scholar] [CrossRef]
- Milosavljević, M.; Koda, J.; Nagai, D.; Nakar, E.; Shapiro, P.R. The Cluster-Merger Shock in 1E 0657-56: Faster than a Speeding Bullet? Astrophys. J. Lett. 2007, 661, L131–L134. [Google Scholar] [CrossRef]
- Dawson, W.A.; Wittman, D.; Jee, M.J.; Gee, P.; Hughes, J.P.; Tyson, J.A.; Schmidt, S.; Thorman, P.; Bradač, M.; Miyazaki, S.; et al. Discovery of a Dissociative Galaxy Cluster Merger with Large Physical Separation. Astrophys. J. Lett. 2012, 747, L42. [Google Scholar] [CrossRef]
- Alexander, S.; Yunes, N. Chern-Simons Modified General Relativity. Phys. Rept. 2009, 480, 1–55. [Google Scholar] [CrossRef]
- Obukhov, Y.N.; Hehl, F.W. On the relation between quadratic and linear curvature Lagrangians in Poincare gauge gravity. Acta Phys. Polon. 1996, B27, 2685–2694. [Google Scholar]
- Cherubini, C.; Bini, D.; Capozziello, S.; Ruffini, R. Second order scalar invariants of the Riemann tensor: Applications to black hole space-times. Int. J. Mod. Phys. 2002, D11, 827–841. [Google Scholar] [CrossRef]
- Penrose, R.; Rindler, W. Spinors and Space-Time, Volume 2; Cambridge University Press: Cambridge, UK, 1986. [Google Scholar]
- van Dokkum, P.; Danieli, S.; Cohen, Y.; Merritt, A.; Romanowsky, A.J.; Abraham, R.; Brodie, J.; Conroy, C.; Lokhorst, D.; Mowla, L.; et al. A galaxy lacking dark matter. Nature 2018, 555, 629–632. [Google Scholar] [CrossRef]
- Massey, R.; Kitching, T.; Richard, J. The dark matter of gravitational lensing. Rep. Progr. Phys. 2010, 73, 086901. [Google Scholar] [CrossRef]
- Trujillo, I.; Carretero, C.; Patiri, S.G. Detection of the Effect of Cosmological Large-Scale Structure on the Orientation of Galaxies. Astrophys. J. Lett. 2006, 640, L111–L114. [Google Scholar] [CrossRef]
- Karachentsev, I.D. Missing dark matter in the local universe. Astrophys. Bull. 2012, 67, 123–134. [Google Scholar] [CrossRef]
- de Blok, W.J.G. The Core-Cusp Problem. Adv. Astron. 2010, 2010, 789293. [Google Scholar] [CrossRef]
- Kent, S.M. Dark matter in spiral galaxies. II—Galaxies with H I rotation curves. Astron. J. 1987, 93, 816–832. [Google Scholar] [CrossRef]
- Corbelli, E.; Lorenzoni, S.; Walterbos, R.; Braun, R.; Thilker, D. A wide-field H I mosaic of Messier 31. II. The disk warp, rotation, and the dark matter halo. Astron. Astrophys. 2010, 511, A89. [Google Scholar] [CrossRef]
- Navarro, J.F.; Frenk, C.S.; White, S.D.M. The Structure of Cold Dark Matter Halos. Astrophys. J. 1996, 462, 563. [Google Scholar] [CrossRef]
- Navarro, J.F.; Frenk, C.S.; White, S.D.M. A Universal Density Profile from Hierarchical Clustering. Astrophys. J. 1997, 490, 493–508. [Google Scholar] [CrossRef]
- Ruiz-Granados, B.; Rubino-Martin, J.A.; Florido, E.; Battaner, E. Magnetic fields and the outer rotation curve of M31. Astrophys. J. 2010, 723, L44. [Google Scholar] [CrossRef]
- Milgrom, M. A modification of the Newtonian dynamics as a possible alternative to the hidden mass hypothesis. Astrophys. J. 1983, 270, 365–370. [Google Scholar] [CrossRef]
- Chemin, L.; Carignan, C.; Foster, T. H I Kinematics and Dynamics of Messier 31. Astrophys. J. 2009, 705, 1395–1415. [Google Scholar] [CrossRef]
- de Blok, W.J.G.; Walter, F.; Brinks, E.; Trachternach, C.; Oh, S.H.; Kennicutt, R.C., Jr. High-Resolution Rotation Curves and Galaxy Mass Models from THINGS. Astron. J. 2008, 136, 2648–2719. [Google Scholar] [CrossRef]
- Wojnar, A.; Sporea, C.; Borowiec, A. A Simple Model for Explaining Galaxy Rotation Curves. Galaxies 2018, 6, 70. [Google Scholar] [CrossRef]
- Oh, S.H.; de Blok, W.J.G.; Walter, F.; Brinks, E.; Kennicutt, R.C., Jr. High-Resolution Dark Matter Density Profiles of THINGS Dwarf Galaxies: Correcting for Noncircular Motions. Astron. J. 2008, 136, 2761–2781. [Google Scholar] [CrossRef]
- Bournaud, F.; Duc, P.A.; Brinks, E.; Boquien, M.; Amram, P.; Lisenfeld, U.; Koribalski, B.S.; Walter, F.; Charmandaris, V. Missing Mass in Collisional Debris from Galaxies. Science 2007, 316, 1166. [Google Scholar] [CrossRef]
- Li, D.; Tang, N.; Nguyen, H.; Dawson, J.R.; Heiles, C.; Xu, D.; Pan, Z.; Goldsmith, P.F.; Gibson, S.J.; Murray, C.E.; et al. Where is OH and Does It Trace the Dark Molecular Gas (DMG)? Astrophys. J. Suppl. 2018, 235, 1. [Google Scholar] [CrossRef]
- Pawlowski, M.S.; Kroupa, P.; Jerjen, H. Dwarf galaxy planes: The discovery of symmetric structures in the Local Group. Mon. Not. R. Astron. Soc. 2013, 435, 1928–1957. [Google Scholar] [CrossRef]
- Meurer, G.R.; Obreschkow, D.; Wong, O.I.; Zheng, Z.; Audcent-Ross, F.M.; Hanish, D.J. Cosmic clocks: A Tight Radius—Velocity Relationship for HI-Selected Galaxies. arXiv, 2018; arXiv:1803.04716. [Google Scholar]
- Li, P.; Lelli, F.; McGaugh, S.S.; Starkman, N.; Schombert, J.M. A constant characteristic volume density of dark matter haloes from SPARC rotation curve fits. arXiv, 2018; arXiv:1811.00553. [Google Scholar]
- Fall, S.M.; Romanowsky, A.J. Angular Momentum and Galaxy Formation Revisited: Effects of Variable Mass-to-light Ratios. Astrophys. J. Lett. 2013, 769, L26. [Google Scholar] [CrossRef]
- Saracco, P.; Gargiulo, A.; Longhetti, M. On the central stellar mass density and the inside-out growth of early-type galaxies. Mon. Not. R. Astron. Soc. 2012, 422, 3107–3117. [Google Scholar] [CrossRef]
- McGaugh, S.S.; Schombert, J.M.; Bothun, G.D.; de Blok, W.J.G. The Baryonic Tully-Fisher Relation. Astrophys. J. Lett. 2000, 533, L99–L102. [Google Scholar] [CrossRef]
- Gurovich, S.; Freeman, K.; Jerjen, H.; Staveley-Smith, L.; Puerari, I. The Slope of the Baryonic Tully-Fisher Relation. Astron. J. 2010, 140, 663–676. [Google Scholar] [CrossRef]
- Ponomareva, A.A.; Verheijen, M.A.W.; Papastergis, E.; Bosma, A.; Peletier, R.F. From light to baryonic mass: the effect of the stellar mass-to-light ratio on the Baryonic Tully-Fisher relation. Mon. Not. R. Astron. Soc. 2018, 474, 4366–4384. [Google Scholar] [CrossRef]
- McGaugh, S.S. The Baryonic Tully-Fisher Relation of Gas-rich Galaxies as a Test of ΛCDM and MOND. Astron. J. 2012, 143, 40. [Google Scholar] [CrossRef]
- Kormendy, J.; Drory, N.; Bender, R.; Cornell, M.E. Bulgeless Giant Galaxies Challenge Our Picture of Galaxy Formation by Hierarchical Clustering. Astrophys. J. 2010, 723, 54–80. [Google Scholar] [CrossRef]
- Tumlinson, J.; Thom, C.; Werk, J.K.; Prochaska, J.X.; Tripp, T.M.; Weinberg, D.H.; Peeples, M.S.; O’Meara, J.M.; Oppenheimer, B.D.; Meiring, J.D.; et al. The Large, Oxygen-Rich Halos of Star-Forming Galaxies Are a Major Reservoir of Galactic Metals. Science 2011, 334, 948. [Google Scholar] [CrossRef] [PubMed]
- Bergemann, M.; Sesar, B.; Cohen, J.G.; Serenelli, A.M.; Sheffield, A.; Li, T.S.; Casagrande, L.; Johnston, K.V.; Laporte, C.F.P.; Price-Whelan, A.M.; et al. Two chemically similar stellar overdensities on opposite sides of the plane of the Galactic disk. Nature 2018, 555, 334–337. [Google Scholar] [CrossRef]
- Carollo, D.; Beers, T.C.; Lee, Y.S.; Chiba, M.; Norris, J.E.; Wilhelm, R.; Sivarani, T.; Marsteller, B.; Munn, J.A.; Bailer-Jones, C.A.L.; et al. Two stellar components in the halo of the Milky Way. Nature 2007, 450, 1020–1025. [Google Scholar] [CrossRef]
- Hartwick, F.D.A. The Structure of the Galactic Halo; Gilmore, G., Carswell, B., Eds.; NATO Advanced Science Institutes (ASI) Series C; Springer: Berlin, Germany, 1987; Volume 207, pp. 281–290. [Google Scholar]
- Wu, X.B.; Wang, F.; Fan, X.; Yi, W.; Zuo, W.; Bian, F.; Jiang, L.; McGreer, I.D.; Wang, R.; Yang, J.; et al. An ultraluminous quasar with a twelve-billion-solar-mass black hole at redshift 6.30. Nature 2015, 518, 512–515. [Google Scholar] [CrossRef]
- Su, M.; Slatyer, T.R.; Finkbeiner, D.P. Giant Gamma-ray Bubbles from Fermi-LAT: Active Galactic Nucleus Activity or Bipolar Galactic Wind? Astrophys. J. 2010, 724, 1044–1082. [Google Scholar] [CrossRef]
- Dobler, G.; Finkbeiner, D.P.; Cholis, I.; Slatyer, T.; Weiner, N. The Fermi Haze: A Gamma-ray Counterpart to the Microwave Haze. Astrophys. J. 2010, 717, 825–842. [Google Scholar] [CrossRef]
- Finkbeiner, D.P. Microwave Interstellar Medium Emission Observed by the Wilkinson Microwave Anisotropy Probe. Astrophys. J. 2004, 614, 186–193. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Atrio-Barandela, F.; Aumont, J.; Baccigalupi, C.; Balbi, A.; Banday, A.J.; et al.; Planck Collaboration Planck intermediate results. IX. Detection of the Galactic haze with Planck. Astron. Astrophys. 2013, 554, A139. [Google Scholar] [CrossRef]
- Carretti, E.; Crocker, R.M.; Staveley-Smith, L.; Haverkorn, M.; Purcell, C.; Gaensler, B.M.; Bernardi, G.; Kesteven, M.J.; Poppi, S. Giant magnetized outflows from the centre of the Milky Way. Nature 2013, 493, 66–69. [Google Scholar] [CrossRef] [PubMed]
- Snowden, S.L.; Egger, R.; Freyberg, M.J.; McCammon, D.; Plucinsky, P.P.; Sanders, W.T.; Schmitt, J.H.M.M.; Trümper, J.; Voges, W. ROSAT Survey Diffuse X-Ray Background Maps. II. Astrophys. J. 1997, 485, 125–135. [Google Scholar] [CrossRef]
- Ackermann, M.; Albert, A.; Atwood, W.B.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Bellazzini, R.; Bissaldi, E.; Blandford, R.D.; et al. The Spectrum and Morphology of the Fermi Bubbles. Astrophys. J. 2014, 793, 64. [Google Scholar] [CrossRef]
- Bordoloi, R.; Fox, A.J.; Lockman, F.J.; Wakker, B.P.; Jenkins, E.B.; Savage, B.D.; Hernandez, S.; Tumlinson, J.; Bland-Hawthorn, J.; Kim, T.S. Mapping the Nuclear Outflow of the Milky Way: Studying the Kinematics and Spatial Extent of the Northern Fermi Bubble. Astrophys. J. 2017, 834, 191. [Google Scholar] [CrossRef]
- Purcell, C.W.; Bullock, J.S.; Tollerud, E.J.; Rocha, M.; Chakrabarti, S. The Sagittarius impact as an architect of spirality and outer rings in the Milky Way. Nature 2011, 477, 301–303. [Google Scholar] [CrossRef]
- Goobar, A.; Amanullah, R.; Kulkarni, S.R.; Nugent, P.E.; Johansson, J.; Steidel, C.; Law, D.; Mörtsell, E.; Quimby, R.; Blagorodnova, N.; et al. iPTF16geu: A multiply imaged, gravitationally lensed type Ia supernova. Science 2017, 356, 291–295. [Google Scholar] [CrossRef]
- Xu, D.; Sluse, D.; Gao, L.; Wang, J.; Frenk, C.; Mao, S.; Schneider, P.; Springel, V. How well can cold dark matter substructures account for the observed radio flux-ratio anomalies. Mon. Not. R. Astron. Soc. 2015, 447, 3189–3206. [Google Scholar] [CrossRef]
- Hsueh, J.W.; Fassnacht, C.D.; Vegetti, S.; McKean, J.P.; Spingola, C.; Auger, M.W.; Koopmans, L.V.E.; Lagattuta, D.J. SHARP–II. Mass structure in strong lenses is not necessarily dark matter substructure: A flux ratio anomaly from an edge-on disc in B1555+375. Mon. Not. R. Astron. Soc. 2016, 463, L51–L55. [Google Scholar] [CrossRef]
- Hsueh, J.W.; Oldham, L.; Spingola, C.; Vegetti, S.; Fassnacht, C.D.; Auger, M.W.; Koopmans, L.V.E.; McKean, J.P.; Lagattuta, D.J. SHARP–IV. An apparent flux-ratio anomaly resolved by the edge-on disc in B0712+472. Mon. Not. R. Astron. Soc. 2017, 469, 3713–3721. [Google Scholar] [CrossRef]
- Hsueh, J.W.; Despali, G.; Vegetti, S.; Xu, D.; Fassnacht, C.D.; Metcalf, R.B. Flux-ratio anomalies from discs and other baryonic structures in the Illustris simulation. Mon. Not. R. Astron. Soc. 2018, 475, 2438–2451. [Google Scholar] [CrossRef]
- Owen, R.; Brink, J.; Chen, Y.; Kaplan, J.D.; Lovelace, G.; Matthews, K.D.; Nichols, D.A.; Scheel, M.A.; Zhang, F.; Zimmerman, A.; et al. Frame-Dragging Vortexes and Tidal Tendexes Attached to Colliding Black Holes: Visualizing the Curvature of Spacetime. Phys. Rev. Lett. 2011, 106, 151101. [Google Scholar] [CrossRef] [PubMed]
- Zimmerman, A.; Nichols, D.A.; Zhang, F. Classifying the isolated zeros of asymptotic gravitational radiation by tendex and vortex lines. Phys. Rev. D 2011, 84, 044037. [Google Scholar] [CrossRef]
| 1. | Ordinary matter can also generate this type of curvature, so not all of it is autonomous, but all autonomous gravity is Weyl, because the Ricci tensor equates directly to the matter (incl.cosmological constant) stress-energy tensor. |
| 2. | The Gaussian curvature of the various 2D geodetic surfaces developed out of 2D planes in the tangent space of the spacetime at any location. |
| 3. | We work under a geometrized unit system where , with kiloparsecs being the fundamental length unit. |
| 4. | Note that for simplicity, we had not included the matter contribution from the extended disc. Including it will not change the basic picture apart from pushing the separatrix streamline further up, enhancing the size of Regime (1). The plot also does not include the centrifugal forces arising from any circular motion, which would be particle specific. |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, F. Modeling the Rising Tails of Galaxy Rotation Curves. Galaxies 2019, 7, 27. https://doi.org/10.3390/galaxies7010027
Zhang F. Modeling the Rising Tails of Galaxy Rotation Curves. Galaxies. 2019; 7(1):27. https://doi.org/10.3390/galaxies7010027
Chicago/Turabian StyleZhang, Fan. 2019. "Modeling the Rising Tails of Galaxy Rotation Curves" Galaxies 7, no. 1: 27. https://doi.org/10.3390/galaxies7010027
APA StyleZhang, F. (2019). Modeling the Rising Tails of Galaxy Rotation Curves. Galaxies, 7(1), 27. https://doi.org/10.3390/galaxies7010027




