Physics of “Cold” Disk Accretion onto Black Holes Driven by Magnetized Winds
Abstract
1. Introduction
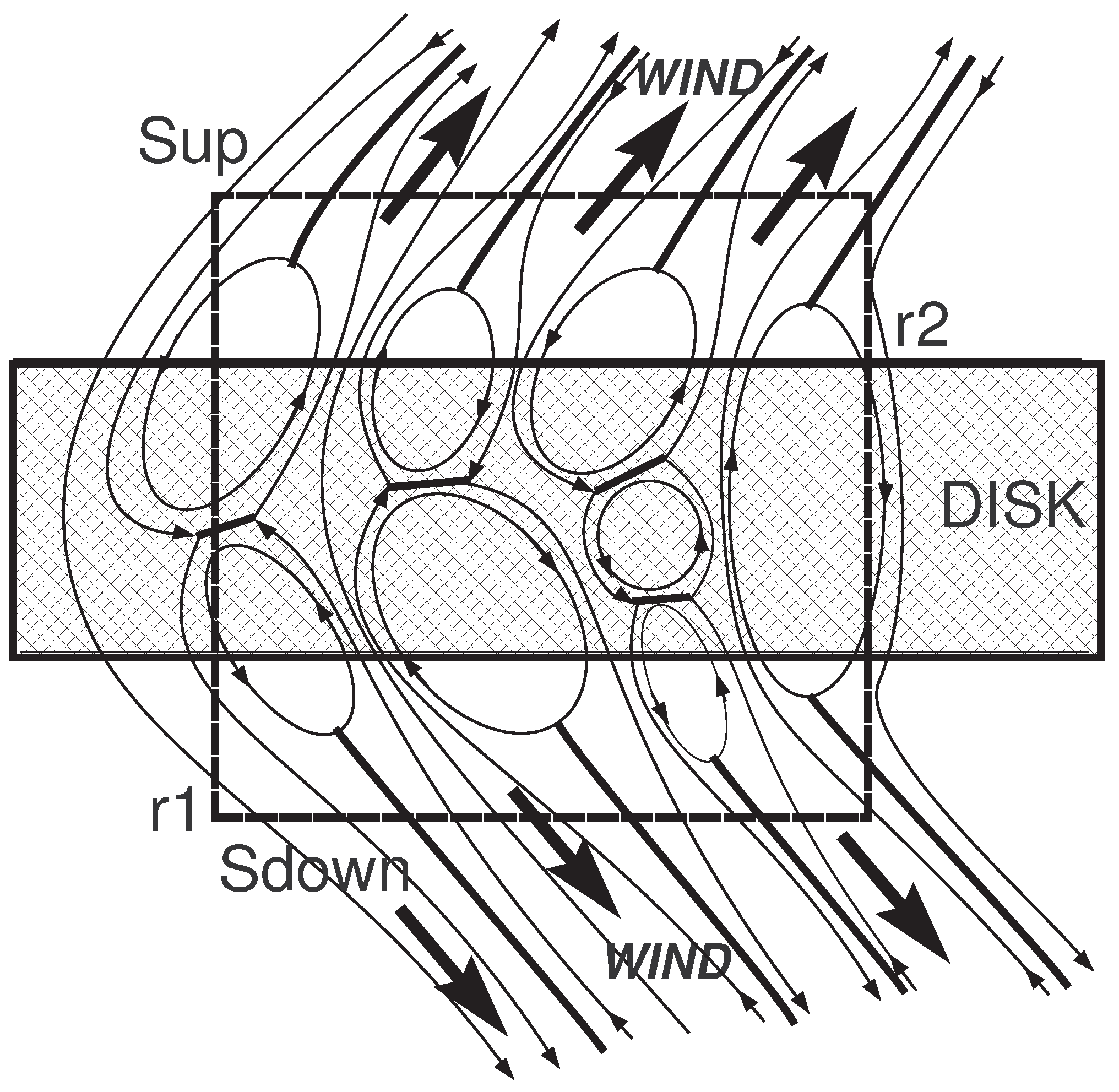
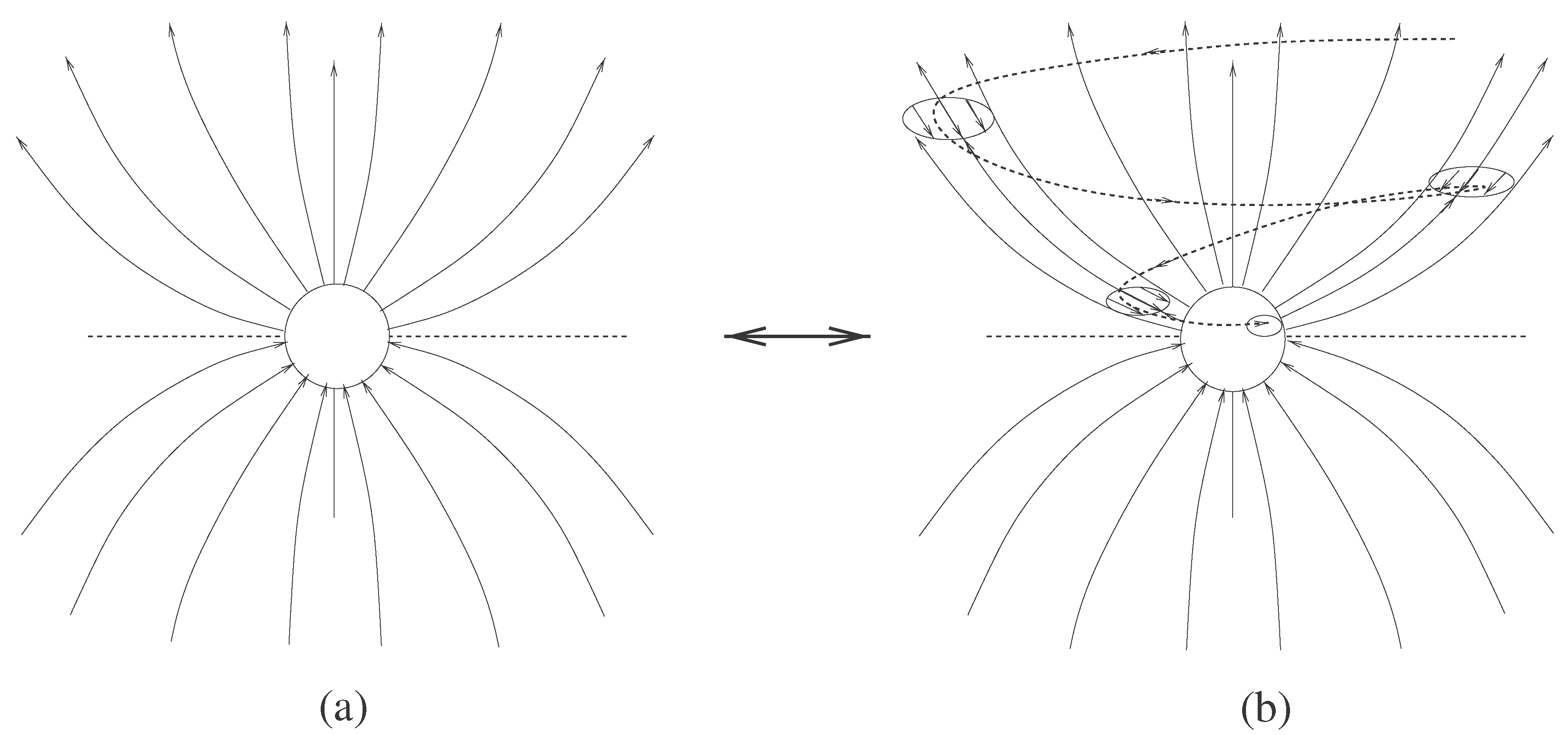
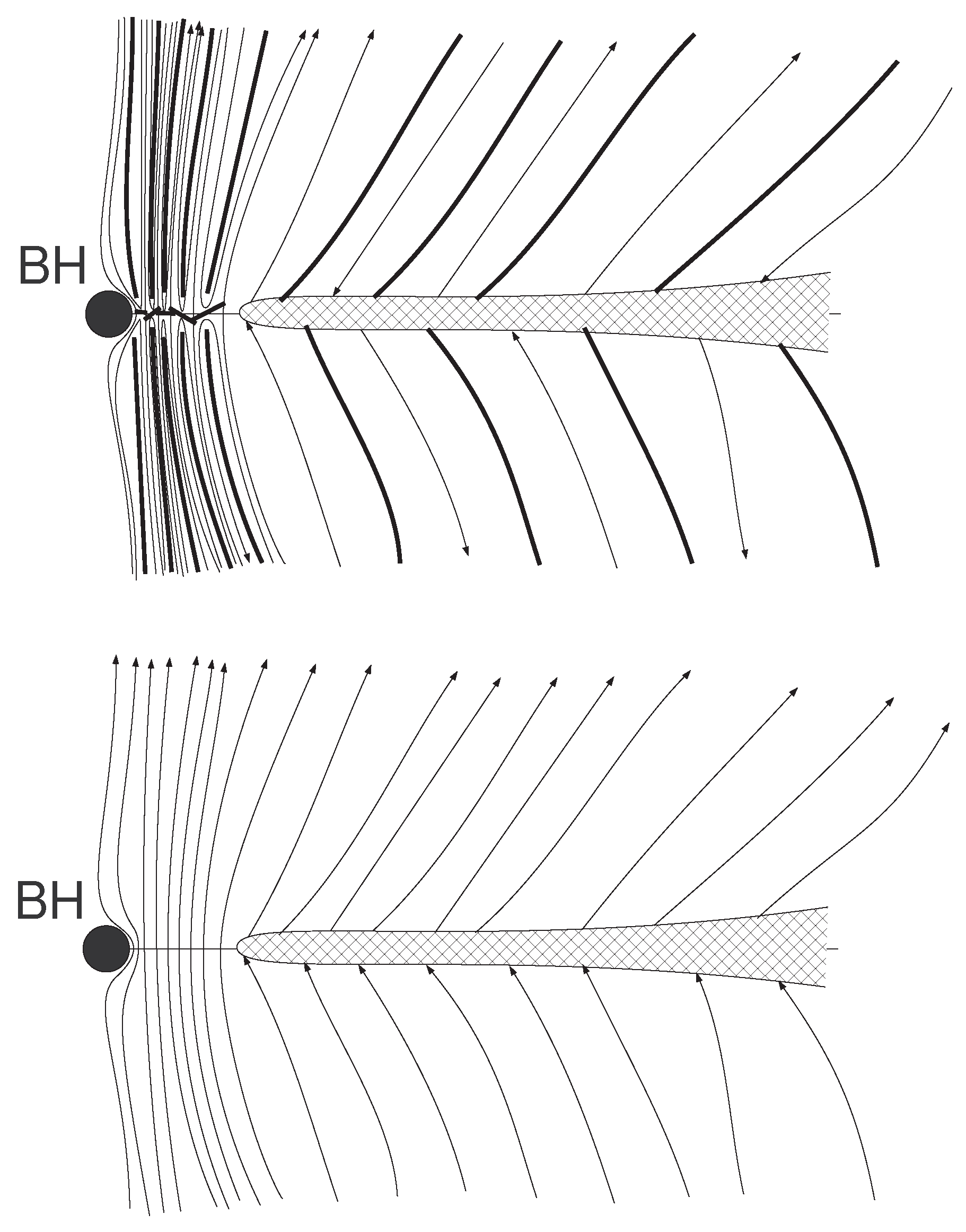
2. Magnetic Field of the Disk and Wind
Assumed Structure of the Magnetic Field in the Disk
3. Basic Equations of the Accretion and Outflow
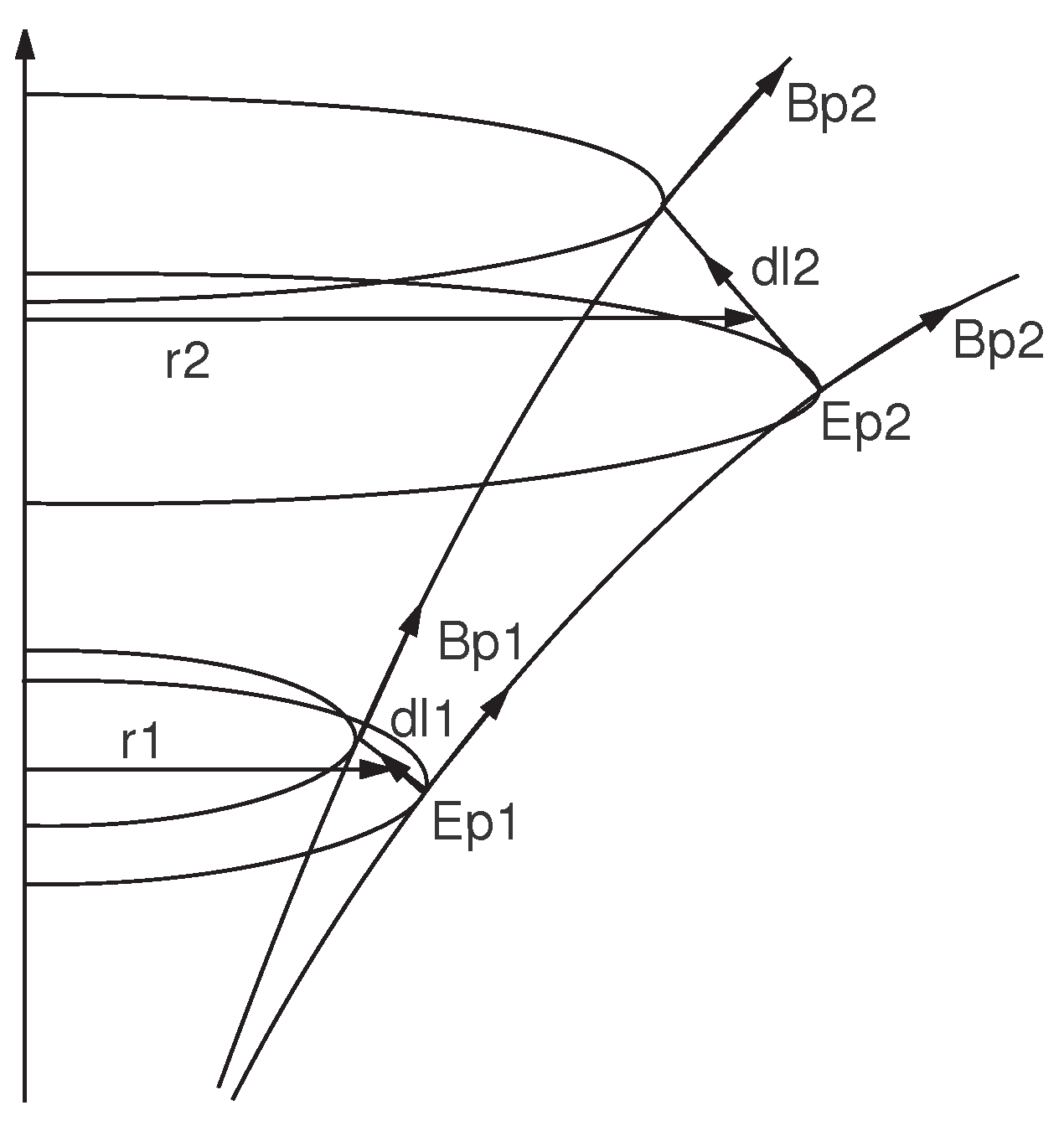
4. Conservation Laws for the Disk
5. The Problem of the Wind Outflow
5.1. Invariance Principle
5.2. The Role of the Azimuthal Electric Field in the Wind
5.3. Along Field Line MHD Equations of the Wind
6. Disk-Wind Connection at the “Cold” Accretion
Basic Properties of the “Cold” Accretion
7. Self-Consistent Solution of the Problem
7.1. Basic Properties of Self Similar Solutions
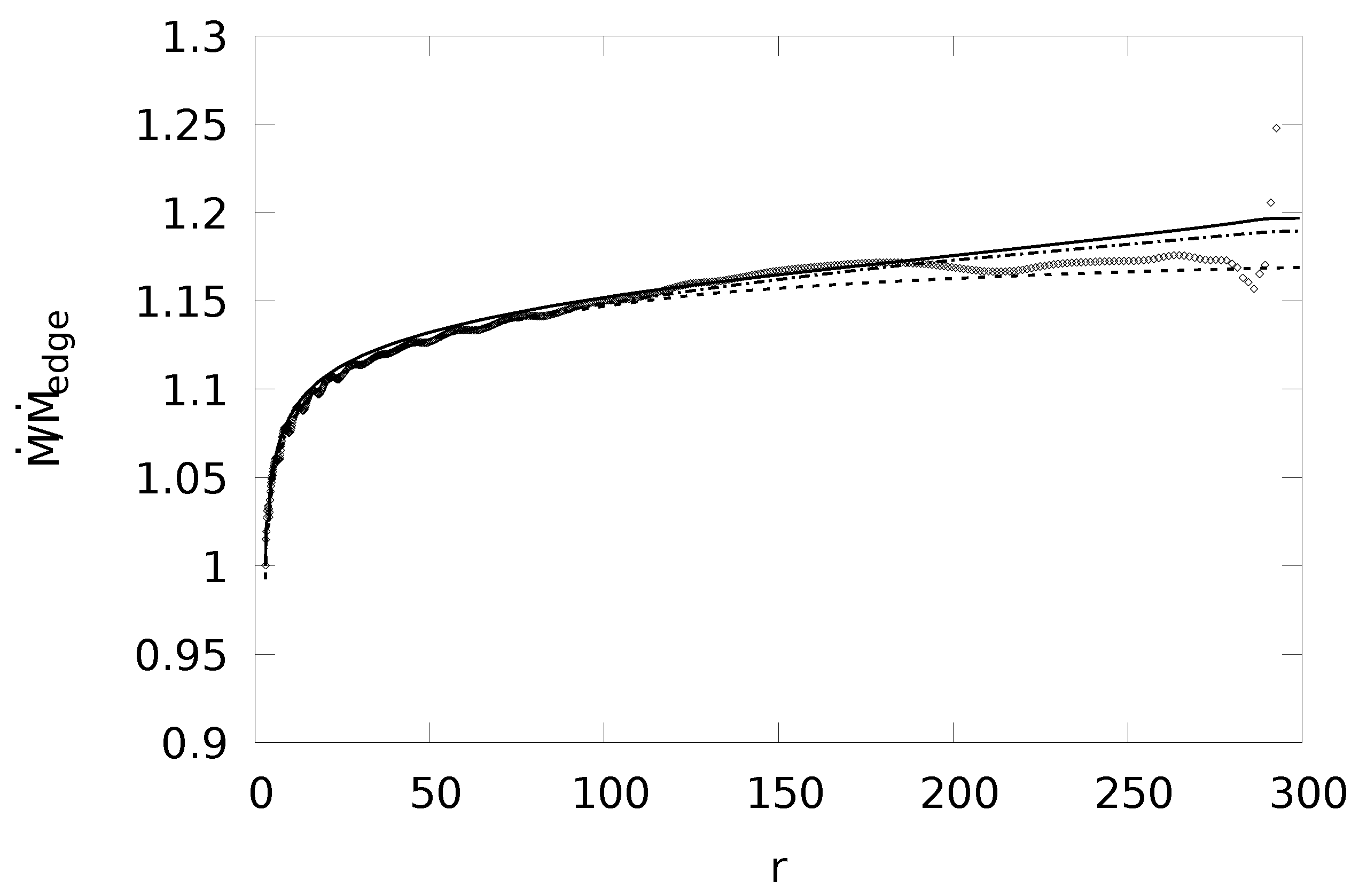
7.2. Numerical Solution of the Self-Consistent Problem
- The mass flux at the inner edge of the disk is specified and kept constant during the modeling;
- The initial distribution of the mass flux as a function of r is assumed. This is the iteration number . The most simple assumption at is . Thus, is constant.
- The initial distribution of the mass flux from the disk is specified. At , the distribution of is not connected with the accretion rate and the solution of the problem of the wind outflow is not self-consistent with the process of accretion.
- Internal iterations are performed. The objective of the internal iteration is to define the distribution of j which fulfills the angular momentum Equation (52).They are indexed by an additional index k. Therefore, the mass flux from the disk depends on two indexes and takes the form . At every step k, the problem of the wind outflow is solved in all of the computational domains. The steady state solution is obtained and thus we obtain new value of at the disk surface. Of course, this value does not satisfy Equation (52) for the specified . Here, we make the next step of the internal iterations according to the following procedure. Let us introduce functionspecified at the disk surface exploring the steady state solution in the computational domain. The equation for the angular momentum conservation (52) is reduced toThe new mass flux is defined by the equationwhere is the parameter of relaxation. This step means that, if the , then the mass flux from the point of the disk with radius r increases and decreases if the opposite inequality takes place. Finally, we find the distribution of the mass flux which satisfies Equation (52). However, it still does not satisfy the conservation of the mass in the disk—Equation (30).
- In this step, Equation (30) is solved taking the obtained mass distribution and boundary condition at . We obtain a new distribution of the accretion rate . This is the external iteration. After that, the entire procedure is repeated.
8. Ratio of Kinetic to Bolometric Luminosity of the Disk
8.1. Thermal Radiation from the Disk during “Cold” Accretion
8.2. Scattering Dominating over Free–Free Absorption
8.3. Free–Free Absorption Dominating over Scattering
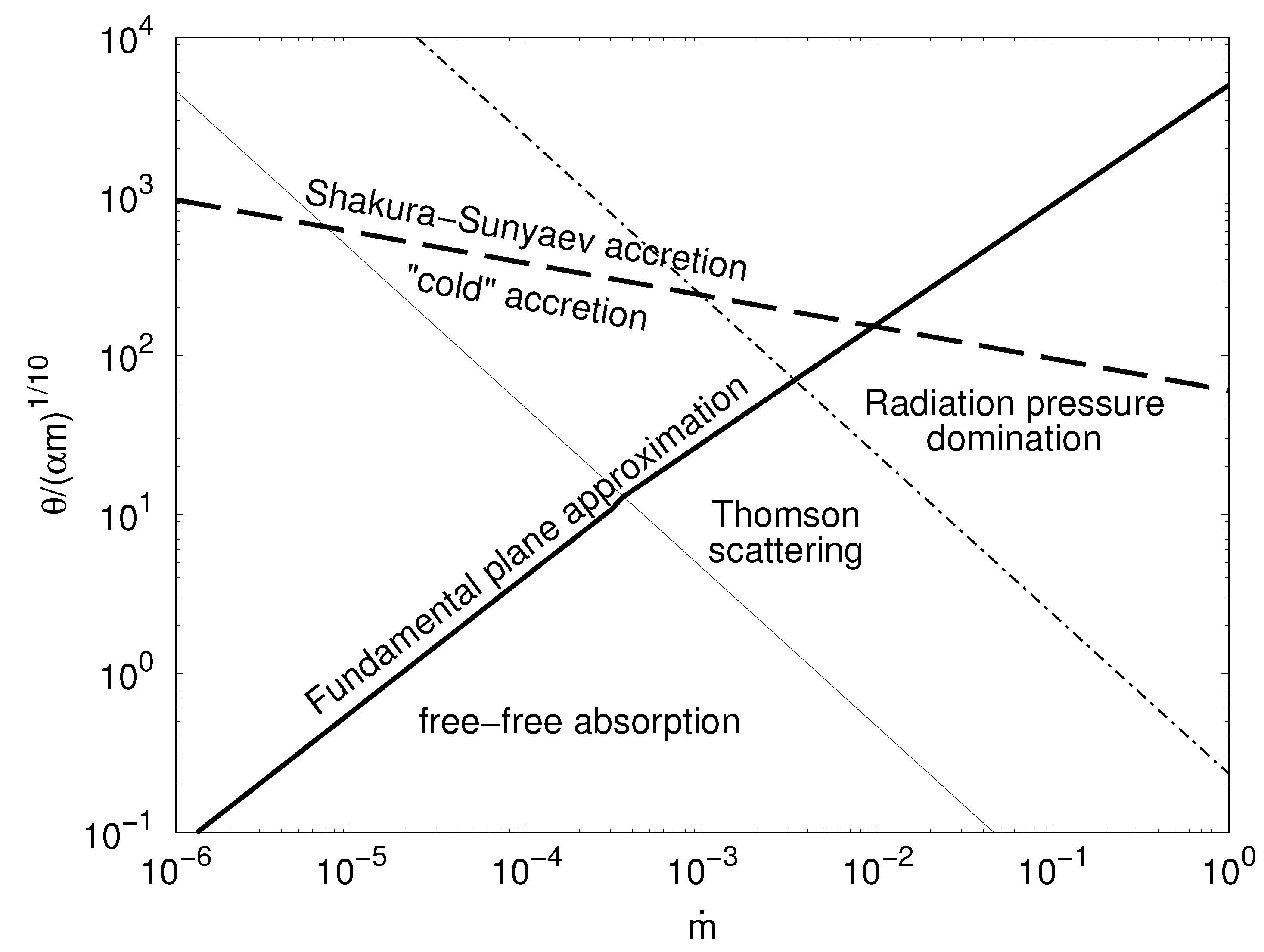
9. Comparison with the Fundamental Plane of Black Holes
10. Comparison with Specific Sources
10.1. M 87
10.2. Sgr A*
11. Conclusions
Funding
Conflicts of Interest
References
- Shakura, N.I. Disk Model of Gas Accretion on a Relativistic Star in a Close Binary System. Sov. Astron. 1972, 49, 921. [Google Scholar]
- Pringle, J.E.; Rees, M.J. Accretion Disc Models for Compact X-Ray Sources. Astron. Astrophys. 1972, 21, 1. [Google Scholar]
- Shakura, N.I.; Sunyaev, R.A. Black holes in binary systems. Observational appearance. Astron. Astrophys. 1973, 24, 337–355. [Google Scholar]
- Baganoff, F.K.; Maeda, Y.; Morris, M.; Bautz, M.W.; Brandt, W.N.; Cui, W.; Doty, J.P.; Feigelson, E.D.; Garmire, G.P.; Pravdo, S.H.; et al. Chandra X-Ray Spectroscopic Imaging of Sagittarius A* and the Central Parsec of the Galaxy. Astrophys. J. 2003, 591, 891–915. [Google Scholar] [CrossRef]
- Narayan, R.; Yi, I. Advection-dominated Accretion: Underfed Black Holes and Neutron Stars. Astrophys. J. 1995, 452, 710. [Google Scholar] [CrossRef]
- Bisnovatyi-Kogan, G.S.; Lovelace, R.V.E. Influence of Ohmic Heating on Advection-dominated Accretion Flows. Astrophys. J. 1997, 486, 43–46. [Google Scholar] [CrossRef]
- Quataert, E.; Gruzinov, A. Convection-dominated Accretion Flows. Astrophys. J. 2000, 539, 809–814. [Google Scholar] [CrossRef]
- Narayan, R.; Quataert, E.; Igumenshchev, I.V.; Abramowicz, M.A. The Magnetohydrodynamics of Convection-dominated Accretion Flows. Astrophys. J. 2002, 577, 295–301. [Google Scholar] [CrossRef]
- Blandford, R.D.; Begelman, M.C. On the fate of gas accreting at a low rate on to a black hole. Mon. Not. R. Astron. Soc. 1999, 303, 1–5. [Google Scholar] [CrossRef]
- Stone, J.M.; Pringle, J.E.; Begelman, M.C. Hydrodynamical non-radiative accretion flows in two dimensions. Mon. Not. R. Astron. Soc. 1999, 310, 1002–1016. [Google Scholar] [CrossRef]
- Blandford, R.D.; Begelman, M.C. Two-dimensional adiabatic flows on to a black hole—I. Fluid accretion. Mon. Not. R. Astron. Soc. 2004, 349, 68–86. [Google Scholar] [CrossRef]
- Falcke, H.; Markoff, S. The jet model for Sgr A*: Radio and X-ray spectrum. Astron. Astrophys. 2000, 362, 113–118. [Google Scholar]
- Yuan, F.; Markoff, S.; Falcke, H. A Jet-ADAF model for Sgr A*. Astron. Astrophys. 2002, 383, 854–863. [Google Scholar] [CrossRef]
- Bicknell, G.V.; Begelman, M.C. Understanding the Kiloparsec-Scale Structure of M87. Astrophys. J. 1996, 467, 597. [Google Scholar] [CrossRef]
- Reynolds, C.S.; Di Matteo, T.; Fabian, A.C.; Hwang, U.; Canizares, C.R. The ‘quiescent’ black hole in M87. Mon. Not. R. Astron. Soc. 1996, 283, 111–116. [Google Scholar] [CrossRef]
- Biretta, J.A.; Stern, C.P.; Harris, D.E. The radio to X-ray spectrum of the M87 jet and nucleus. Astron. J. 1991, 101, 1632–1646. [Google Scholar] [CrossRef]
- Rawlings, S.; Saunders, R. Evidence for a common central-engine mechanism in all extragalactic radio sources. Nature 1991, 349, 138–140. [Google Scholar] [CrossRef]
- Heinz, S.; Sunyaev, R.A. The non-linear dependence of flux on black hole mass and accretion rate in core-dominated jets. Mon. Not. R. Astron. Soc. 2003, 343, 59–64. [Google Scholar] [CrossRef]
- Merloni, A.; Heinz, S.; di Matteo, T. A Fundamental Plane of black hole activity. Mon. Not. R. Astron. Soc. 2003, 345, 1057–1076. [Google Scholar] [CrossRef]
- Falcke, H.; Körding, E.; Markoff, S. A scheme to unify low-power accreting black holes. Jet-dominated accretion flows and the radio/X-ray correlation. Astron. Astrophys. 2004, 414, 895–903. [Google Scholar] [CrossRef]
- Körding, E.G.; Fender, R.P.; Migliari, S. Jet-dominated advective systems: Radio and X-ray luminosity dependence on the accretion rate. Mon. Not. R. Astron. Soc. 2006, 369, 1451–1458. [Google Scholar] [CrossRef]
- Merloni, A.; Heinz, S. Measuring the kinetic power of active galactic nuclei in the radio mode. Mon. Not. R. Astron. Soc. 2007, 381, 589–601. [Google Scholar] [CrossRef]
- De Gasperin, F.; Merloni, A.; Sell, P.; Best, P.; Heinz, S.; Kauffmann, G. Testing black hole jet scaling relations in low-luminosity active galactic nuclei. Mon. Not. R. Astron. Soc. 2011, 415, 2910–2919. [Google Scholar] [CrossRef]
- Saikia, P.; Körding, E.; Falcke, H. The Fundamental Plane of black hole activity in the optical band. Mon. Not. R. Astron. Soc. 2015, 450, 2317–2326. [Google Scholar] [CrossRef]
- Körding, E.G.; Jester, S.; Fender, R. Measuring the accretion rate and kinetic luminosity functions of supermassive black holes. Mon. Not. R. Astron. Soc. 2008, 383, 277–288. [Google Scholar] [CrossRef]
- Ma, M.L.; Cao, X.W.; Jiang, D.R.; Gu, M.F. A New Approach for Estimating Kinetic Luminosity of Jet in AGNs. Chin. J. Astron. Astrophys. 2008, 8, 39–49. [Google Scholar] [CrossRef]
- López-Corredoira, M.; Perucho, M. Kinetic power of quasars and statistical excess of MOJAVE superluminal motions. Astron. Astrophys. 2012, 544, A56. [Google Scholar] [CrossRef]
- Daly, R.A. Spin properties of supermassive black holes with powerful outflows. Mon. Not. R. Astron. Soc. 2016, 458, 24–28. [Google Scholar] [CrossRef]
- Daly, R.A.; Stout, D.A.; Mysliwiec, J.N. The Fundamental Plane of Black Hole Activity Represented in Terms of Dimensionless Beam Power and Bolometric Luminosity. arXiv, 2016; arXiv:1606.01399. [Google Scholar]
- Fernandes, C.A.C.; Jarvis, M.J.; Rawlings, S.; Martínez-Sansigre, A.; Hatziminaoglou, E.; Lacy, M.; Page, M.J.; Stevens, J.A.; Vardoulaki, E. Evidence for a maximum jet efficiency for the most powerful radio galaxies. Mon. Not. R. Astron. Soc. 2011, 411, 1909–1916. [Google Scholar] [CrossRef]
- Punsly, B. High Jet Efficiency and Simulations of Black Hole Magnetospheres. Astrophys. J. 2011, 728, 17. [Google Scholar] [CrossRef]
- Ghisellini, G.; Tavecchio, F.; Maraschi, L.; Celotti, A.; Sbarrato, T. The power of relativistic jets is larger than the luminosity of their accretion disks. Nature 2014, 515, 376–378. [Google Scholar] [CrossRef]
- Abramowski, A.; Aharonian, F.; Benkhali, F.A.; Akhperjanian, A.G.; Angüner, E.O.; Backes, M.; Balzer, A.; Becherini, Y.; Tjus, J.B.; Berge, D.; et al. Acceleration of petaelectronvolt protons in the Galactic Centre. Nature 2016, 531, 476–479. [Google Scholar] [CrossRef]
- Genzel, R.; Eisenhauer, F.; Gillessen, S. The Galactic Center massive black hole and nuclear star cluster. Rev. Mod. Phys. 2010, 82, 3121–3195. [Google Scholar] [CrossRef]
- Striani, E.; Vercellone, S.; Tavani, M.; Vittorini, V.; D’Ammando, F.; Donnarumma, I.; Pacciani, L.; Pucella, G.; Bulgarelli, A.; Trifoglio, M.; et al. The Extraordinary Gamma-ray Flare of the Blazar 3C 454.3. Astrophys. J. 2010, 718, 455–459. [Google Scholar] [CrossRef]
- Ackermann, M.; Ajello, M.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Bechtol, K.; Bellazzini, R.; Berenji, B.; Blandford, R.D.; et al. Fermi Gamma-ray Space Telescope Observations of Gamma-ray Outbursts from 3C 454.3 in 2009 December and 2010 April. Astrophys. J. 2010, 721, 1383–1396. [Google Scholar] [CrossRef]
- Vercellone, S.; Striani, E.; Vittorini, V.; Donnarumma, I.; Pacciani, L.; Pucella, G.; Tavani, M.; Raiteri, C.M.; Villata, M.; Romano, P.; et al. The Brightest Gamma-Ray Flaring Blazar in the Sky: AGILE and Multi-wavelength Observations of 3C 454.3 During 2010 November. Astrophys. J. 2011, 736, L38. [Google Scholar] [CrossRef]
- Abdo, A.A.; Ackermann, M.; Ajello, M.; Allafort, A.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Bellazzini, R.; Berenji, B.; et al. Fermi Gamma-ray Space Telescope Observations of the Gamma-ray Outburst from 3C454.3 in November 2010. Astrophys. J. 2011, 733, 26. [Google Scholar] [CrossRef]
- Khangulyan, D.V.; Barkov, M.V.; Bosch-Ramon, V.; Aharonian, F.A.; Dorodnitsyn, A.V. Star-Jet Interactions and Gamma-Ray Outbursts from 3C454.3. Astrophys. J. 2013, 774, 113. [Google Scholar] [CrossRef]
- Pjanka, P.; Zdziarski, A.A.; Sikora, M. The power and production efficiency of blazar jets. Mon. Not. R. Astron. Soc. 2017, 465, 3506–3514. [Google Scholar] [CrossRef]
- Churazov, E.; Sazonov, S.; Sunyaev, R.; Forman, W.; Jones, C.; Böhringer, H. Supermassive black holes in elliptical galaxies: Switching from very bright to very dim. Mon. Not. R. Astron. Soc. 2005, 363, L91–L95. [Google Scholar] [CrossRef]
- Blandford, R.D.; Znajek, R.L. Electromagnetic extraction of energy from Kerr black holes. Mon. Not. R. Astron. Soc. 1977, 179, 433–456. [Google Scholar] [CrossRef]
- Narayan, R.; Igumenshchev, I.V.; Abramowicz, M.A. Magnetically Arrested Disk: An Energetically Efficient Accretion Flow. Publ. Astron. Soc. Jpn. 2003, 55, L69–L72. [Google Scholar] [CrossRef]
- Bisnovatyi-Kogan, G.S.; Ruzmaikin, A.A. The accretion of matter by a collapsing star in the presence of a magnetic field. II—self-consistent stationary picture. Astrophys. Space Sci. 1976, 42, 401–424. [Google Scholar] [CrossRef]
- McKinney, J.C.; Tchekhovskoy, A.; Blandford, R.D. General relativistic magnetohydrodynamic simulations of magnetically choked accretion flows around black holes. Mon. Not. R. Astron. Soc. 2012, 423, 3083–3117. [Google Scholar] [CrossRef]
- Parker, E.N. Dynamics of the Interplanetary Gas and Magnetic Fields. Astrophys. J. 1958, 128, 664. [Google Scholar] [CrossRef]
- Schatzman, E. A theory of the role of magnetic activity during star formation. Ann. d’Astrophys. 1962, 25, 18. [Google Scholar]
- Mestel, L. Magnetic braking by a stellar wind—I. Mon. Not. R. Astron. Soc. 1968, 138, 359. [Google Scholar] [CrossRef]
- Mestel, L. Magnetic braking by a stellar wind—II. Mon. Not. R. Astron. Soc. 1968, 140, 177. [Google Scholar] [CrossRef]
- Blandford, R.D.; Payne, D.G. Hydromagnetic flows from accretion discs and the production of radio jets. Mon. Not. R. Astron. Soc. 1982, 199, 883–903. [Google Scholar] [CrossRef]
- Pelletier, G.; Pudritz, R.E. Hydromagnetic disk winds in young stellar objects and active galactic nuclei. Astrophys. J. 1992, 394, 117–138. [Google Scholar] [CrossRef]
- Ferreira, J.; Pelletier, G. Magnetized accretion-ejection structures. 1. General statements. Astron. Astrophys. 1993, 276, 625. [Google Scholar]
- Ferreira, J.; Pelletier, G. Magnetized accretion-ejection structures. III. Stellar and extragalactic jets as weakly dissipative disk outflows. Astron. Astrophys. 1995, 295, 807. [Google Scholar]
- Ferreira, J. Magnetically-driven jets from Keplerian accretion discs. Astron. Astrophys. 1997, 319, 340–359. [Google Scholar]
- Ferreira, J.; Petrucci, P.O.; Henri, G.; Saugé, L.; Pelletier, G. A unified accretion-ejection paradigm for black hole X-ray binaries. I. The dynamical constituents. Astron. Astrophys. 2006, 447, 813–825. [Google Scholar] [CrossRef]
- Lubow, S.H.; Papaloizou, J.C.B.; Pringle, J.E. On the Stability of Magnetic Wind-Driven Accretion Discs. Mon. Not. R. Astron. Soc. 1994, 268, 1010. [Google Scholar] [CrossRef]
- Livio, M.; Pringle, J.E.; King, A.R. The Disk-Jet Connection in Microquasars and Active Galactic Nuclei. Astrophys. J. 2003, 593, 184–188. [Google Scholar] [CrossRef]
- Cao, X.; Spruit, H.C. The Large-scale Magnetic Fields of Thin Accretion Disks. Astrophys. J. 2013, 765, 149. [Google Scholar] [CrossRef]
- Li, S.L.; Begelman, M.C. Thermal Stability of a Thin Disk with Magnetically Driven Winds. Astrophys. J. 2014, 786, 6. [Google Scholar] [CrossRef]
- Li, S.L. The High-efficiency Jets Magnetically Accelerated from a Thin Disk in Powerful Lobe-dominated FRII Radio Galaxies. Astrophys. J. 2014, 788, 71. [Google Scholar] [CrossRef]
- Marcel, G.; Ferreira, J.; Petrucci, P.; Henri, G.; Belmont, R.; Clavel, M.; Malzac, J.; Coriat, M.; Corbel, S.; Rodriguez, J.; et al. A unified accretion-ejection paradigm for black hole X-ray binaries. II. Observational signatures of jet-emitting disks. arXiv, 2018; arXiv:1803.04335. [Google Scholar]
- Marcel, G.; Ferreira, J.; Petrucci, P.; Belmont, R.; Malzac, J.; Clavel, M.; Henri, G.; Coriat, M.; Corbel, S.; Rodriguez, J.; et al. A unified accretion-ejection paradigm for black hole X-ray binaries. III. Spectral signatures of hybrid disk configurations. Astron. Astrophys. 2018, 617, A46. [Google Scholar] [CrossRef]
- Bogovalov, S.V.; Kelner, S.R. Accretion and Plasma Outflow from Dissipationless Discs. Int. J. Mod. Phys. D 2010, 19, 339–365. [Google Scholar] [CrossRef]
- Bisnovatyi-Kogan, G.S.; Ruzmaikin, A.A. The Accretion of Matter by a Collapsing Star in the Presence of a Magnetic Field. Astrophys. Space Sci. 1974, 28, 45–59. [Google Scholar] [CrossRef]
- Van Ballegooijen, A.A. Magnetic fields in the accretion disks of cataclysmic variables. In Accretion Disks and Magnetic Fields in Astrophysics; Belvedere, G., Ed.; Springer: Dordrecht, The Netherlands, 1989; pp. 99–106. [Google Scholar]
- Lubow, S.H.; Papaloizou, J.C.B.; Pringle, J.E. Magnetic field dragging in accretion discs. Mon. Not. R. Astron. Soc. 1994, 267, 235–240. [Google Scholar] [CrossRef]
- Bisnovatyi-Kogan, G.S.; Lovelace, R.V.E. Large-Scale B-Field in Stationary Accretion Disks. Astrophys. J. 2007, 667, L167–L169. [Google Scholar] [CrossRef]
- Bisnovatyi-Kogan, G.S.; Lovelace, R.V.E. Vertical Structure of Stationary Accretion Disks with a Large-scale Magnetic Field. Astrophys. J. 2012, 750, 109. [Google Scholar] [CrossRef]
- Galeev, A.A.; Rosner, R.; Vaiana, G.S. Structured coronae of accretion disks. Astrophys. J. 1979, 229, 318–326. [Google Scholar] [CrossRef]
- Begelman, M.C.; Armitage, P.J. A Mechanism for Hysteresis in Black Hole Binary State Transitions. Astrophys. J. 2014, 782, L18. [Google Scholar] [CrossRef]
- Begelman, M.C.; Armitage, P.J.; Reynolds, C.S. Accretion Disk Dynamo as the Trigger for X-Ray Binary State Transitions. Astrophys. J. 2015, 809, 118. [Google Scholar] [CrossRef]
- Salvesen, G.; Simon, J.B.; Armitage, P.J.; Begelman, M.C. Accretion disc dynamo activity in local simulations spanning weak-to-strong net vertical magnetic flux regimes. Mon. Not. R. Astron. Soc. 2016, 457, 857–874. [Google Scholar] [CrossRef]
- Riols, A.; Rincon, F.; Cossu, C.; Lesur, G.; Ogilvie, G.I.; Longaretti, P.Y. Magnetorotational dynamo chimeras. The missing link to turbulent accretion disk dynamo models? Astron. Astrophys. 2017, 598, A87. [Google Scholar] [CrossRef]
- Contopoulos, I.; Kazanas, D. A Cosmic Battery. Astrophys. J. 1998, 508, 859–863. [Google Scholar] [CrossRef]
- Contopoulos, I.; Nathanail, A.; Katsanikas, M. The Cosmic Battery in Astrophysical Accretion Disks. Astrophys. J. 2015, 805, 105. [Google Scholar] [CrossRef]
- Bisnovatyi-Kogan, G.S.; Lovelace, R.V.E.; Belinski, V.A. A Cosmic Battery Reconsidered. Astrophys. J. 2002, 580, 380–388. [Google Scholar] [CrossRef]
- Romanova, M.M.; Ustyugova, G.V.; Koldoba, A.V.; Chechetkin, V.M.; Lovelace, R.V.E. Dynamics of Magnetic Loops in the Coronae of Accretion Disks. Astrophys. J. 1998, 500, 703–713. [Google Scholar] [CrossRef]
- Parfrey, K.; Giannios, D.; Beloborodov, A.M. Black hole jets without large-scale net magnetic flux. Mon. Not. R. Astron. Soc. 2015, 446, L61–L65. [Google Scholar] [CrossRef]
- Crooker, N.U.; Burton, M.E.; Siscoe, G.L.; Kahler, S.W.; Gosling, J.T.; Smith, E.J. Solar wind streamer belt structure. J. Geophys. Res. 1996, 101, 24331–24342. [Google Scholar] [CrossRef]
- Kahler, S.; Crooker, N.U.; Gosling, J.T. Properties of interplanetary magnetic sector boundaries based on electron heat-flux flow directions. J. Geophys. Res. 1998, 103, 20603–20612. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Electrodynamics of Continuous Media; Elsevier: Amsterdam, The Netherlands, 1960. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. The Classical Theory of Fields; Elsevier: Amsterdam, The Netherlands, 1975. [Google Scholar]
- Bogovalov, S.V. Boundary conditions and critical surfaces in astrophysical MHD winds. Astron. Astrophys. 1997, 323, 634–643. [Google Scholar]
- Contopoulos, J. General Axisymmetric Magnetohydrodynamic Flows: Theory and Solutions. Astrophys. J. 1996, 460, 185. [Google Scholar] [CrossRef]
- Bogovalov, S.V. On the Theory of Magnetohydrodynamic Winds from a Magnetosphere of Axisymmetric Rotators. Mon. Not. R. Astron. Soc. 1994, 270, 721. [Google Scholar] [CrossRef]
- Fukumura, K.; Kazanas, D.; Shrader, C.; Behar, E.; Tombesi, F.; Contopoulos, I. Magnetized Disk Winds in NGC 3783. Astrophys. J. 2018, 853, 40. [Google Scholar] [CrossRef]
- Bogovalov, S.V.; Tronin, I.V. Numerical simulations of dissipationless disk accretion. Astron. Lett. 2017, 43, 595–601. [Google Scholar] [CrossRef]
- Bogovalov, S.V.; Tronin, I.V. Toward the self-consistent model of cold disk accretion. Int. J. Mod. Phys. D 2018, 27, 1844005. [Google Scholar] [CrossRef]
- Walsh, J.L.; Barth, A.J.; Ho, L.C.; Sarzi, M. The M87 Black Hole Mass from Gas-dynamical Models of Space Telescope Imaging Spectrograph Observations. Astrophys. J. 2013, 770, 86. [Google Scholar] [CrossRef]
- Di Matteo, T.; Quataert, E.; Allen, S.W.; Narayan, R.; Fabian, A.C. Low-radiative-efficiency accretion in the nuclei of elliptical galaxies. Mon. Not. R. Astron. Soc. 2000, 311, 507–521. [Google Scholar] [CrossRef]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bogovalov, S. Physics of “Cold” Disk Accretion onto Black Holes Driven by Magnetized Winds. Galaxies 2019, 7, 18. https://doi.org/10.3390/galaxies7010018
Bogovalov S. Physics of “Cold” Disk Accretion onto Black Holes Driven by Magnetized Winds. Galaxies. 2019; 7(1):18. https://doi.org/10.3390/galaxies7010018
Chicago/Turabian StyleBogovalov, Sergey. 2019. "Physics of “Cold” Disk Accretion onto Black Holes Driven by Magnetized Winds" Galaxies 7, no. 1: 18. https://doi.org/10.3390/galaxies7010018
APA StyleBogovalov, S. (2019). Physics of “Cold” Disk Accretion onto Black Holes Driven by Magnetized Winds. Galaxies, 7(1), 18. https://doi.org/10.3390/galaxies7010018




