Minimum Length Uncertainty Relations in the Presence of Dark Energy
Abstract
1. Introduction
2. Károlyházy’s MLUR—New Perspectives
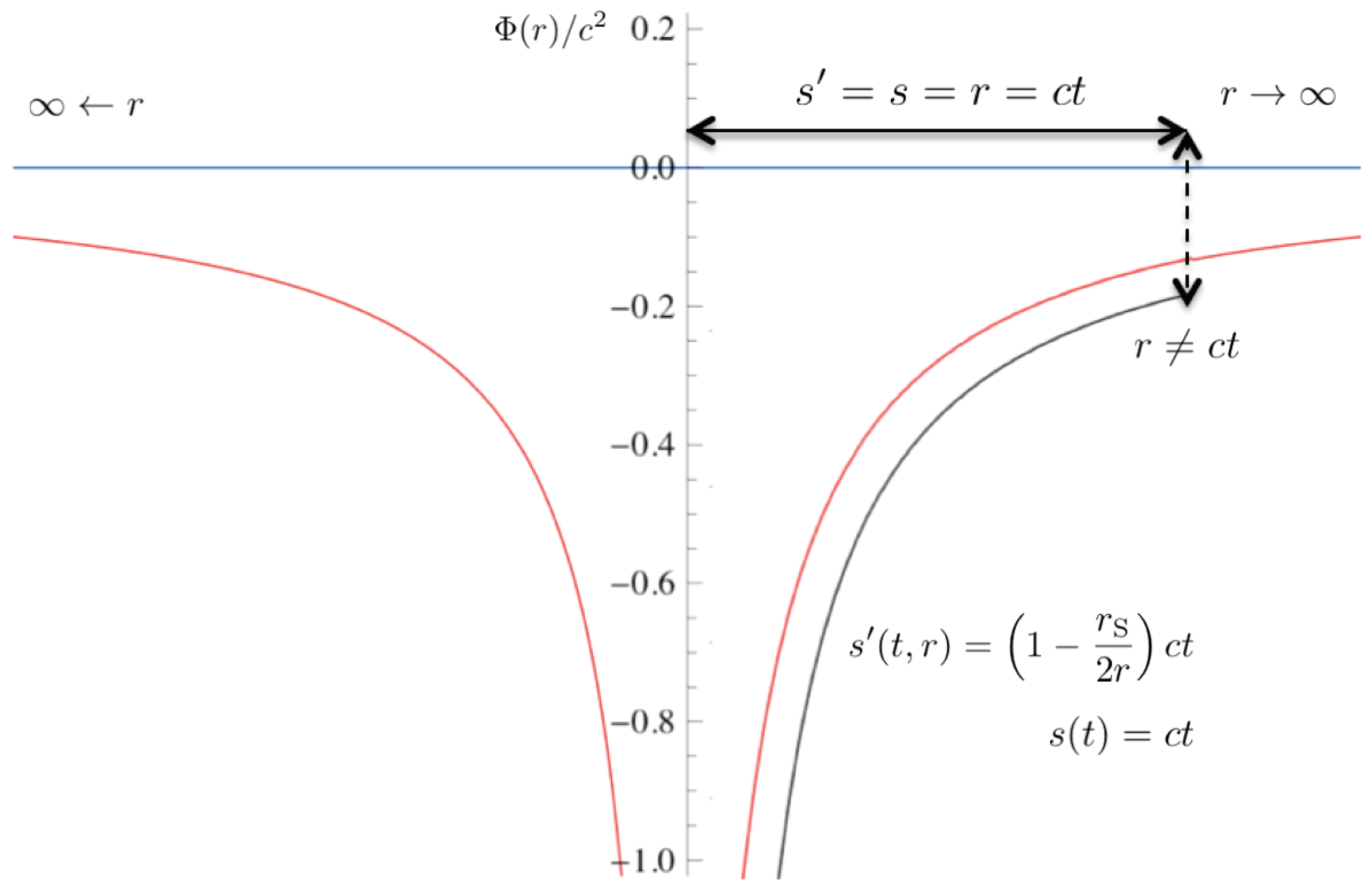
2.1. Classical Intervals in Perturbed and Unperturbed Backgrounds: and s
2.2. Classical Equivalence of Károlyházy’s Measurement Scheme and the Perturbative Result: Reinterpreting and s
2.2.1. Asymptotically Flat Space ()
2.2.2. Finite-Horizon Effects ()
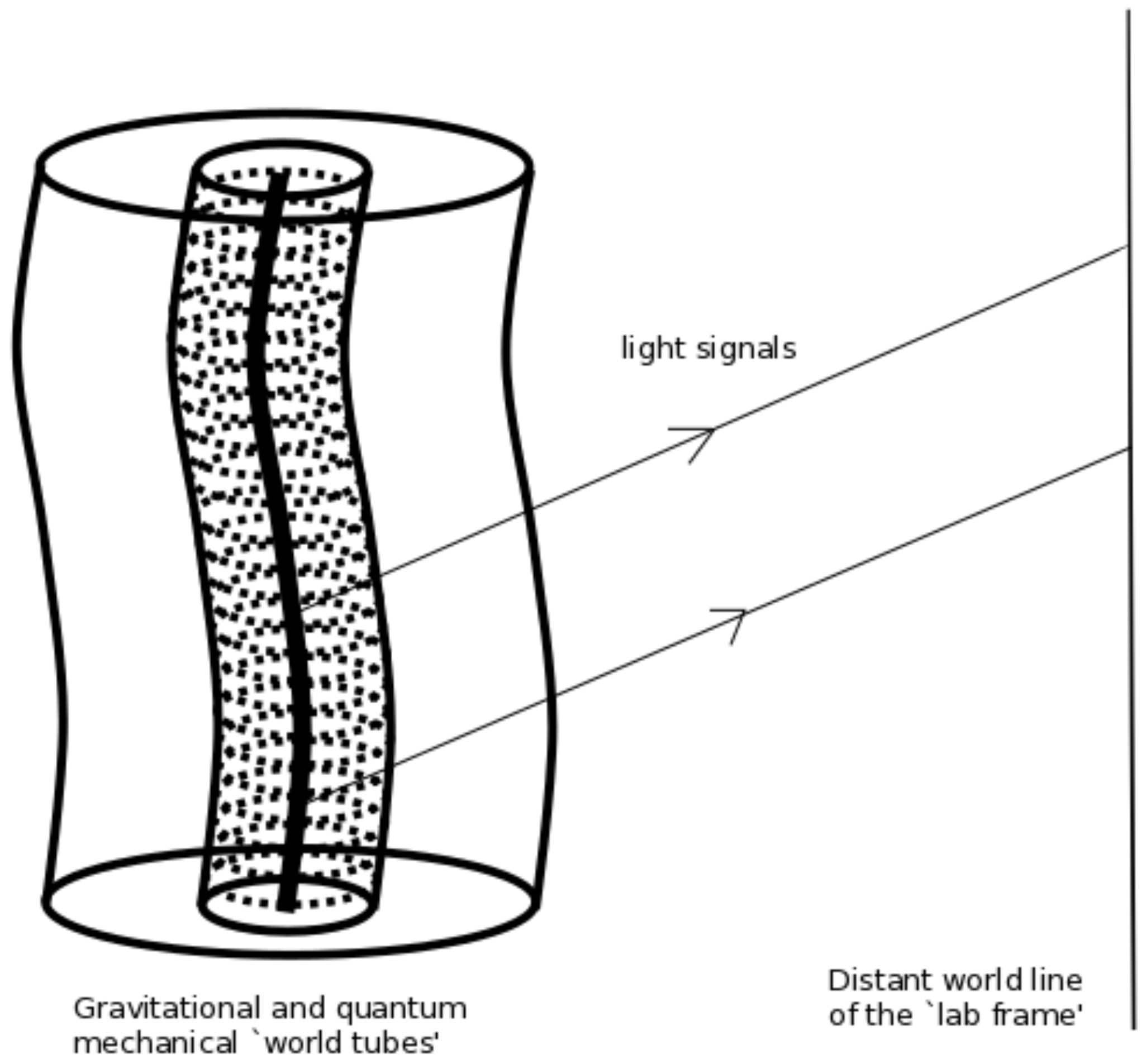
2.3. Probing Space-Time Intervals with Quantum Particles
2.3.1. Károlyházy’s MLUR (1968)
2.3.2. Ng and Van Dam’s Derivation (1994)
2.4. Motivations for the DE-UP
3. Dark Energy-Induced Modifications of the MLUR—The DE-UP
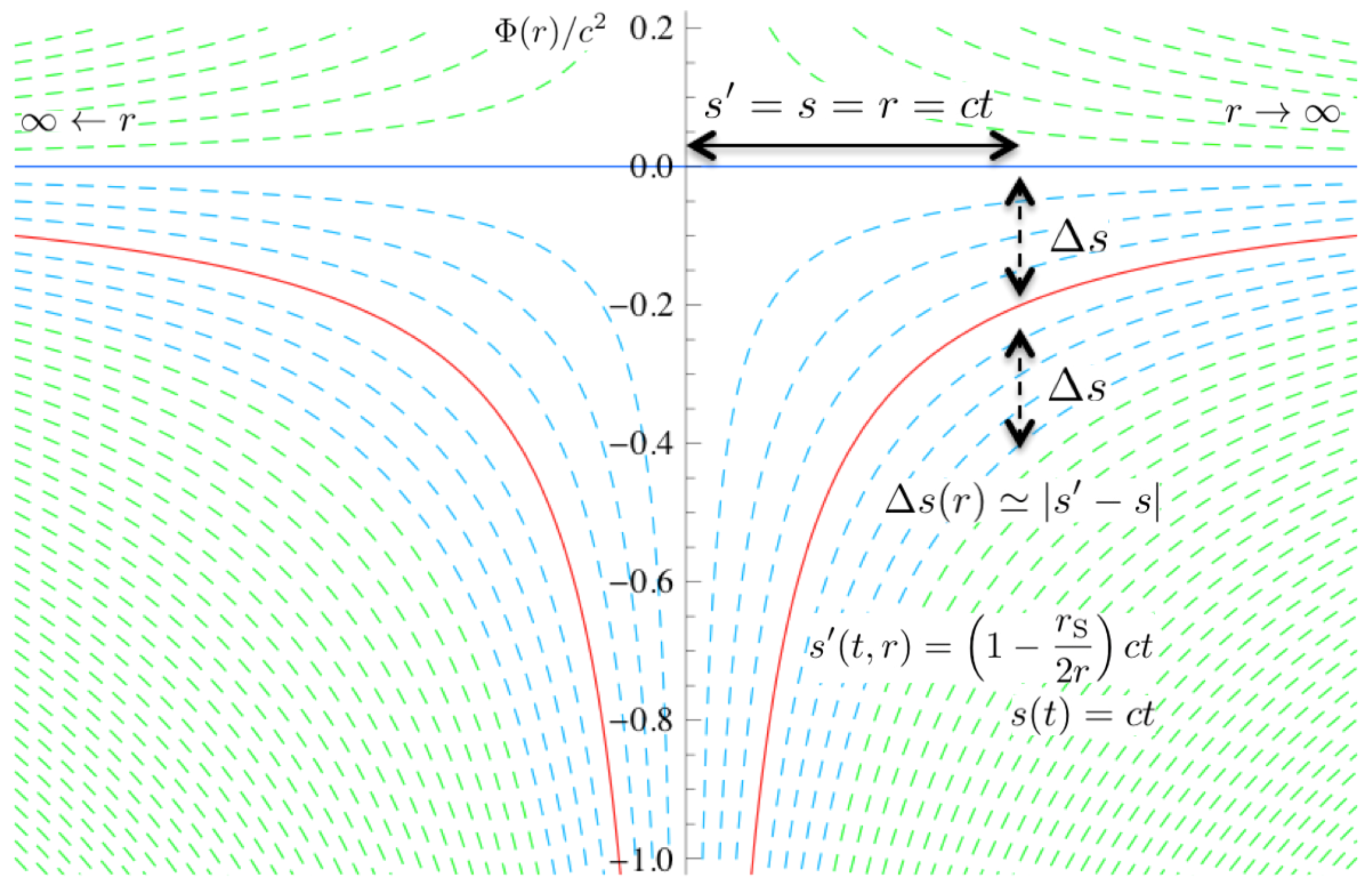
3.1. Space-Time Uncertainty and Classical Perturbations—A Connection?
3.2. Derivation of the DE-UP
3.3. Basic Properties of the DE-UP
3.3.1. Application to Neutral Particles
3.3.2. Application to Charged Particles
4. Cosmological Consequences of the DE-UP
4.1. Holography
4.2. Dark Energy Particles?
4.3. Time-Variation of “Fundamental” Constants?
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Conceptual Issues—Is r < (Δxtotal)min Physical?
References
- Davies, P.C.W. The Forces of Nature; Cambridge University Press: Cambridge, UK, 1986. [Google Scholar]
- Kiefer, C. Quantum gravity: A short overview. In Quantum Gravity; Fauser, B., Tolksdorf, J., Zeidle, E., Eds.; Springer Nature: Basel, Switzerland; pp. 1–13.
- Ellis, J.R.; Mavromatos, N.E.; Nanopoulos, D.V. Search for quantum gravity. Gen. Relativ. Gravit. 1999, 31, 1257–1262. [Google Scholar] [CrossRef]
- Károlyházy, F. Gravitation and quantum mechanics of macroscopic objects. Nuovo Cimento A 1966, 42, 390. [Google Scholar] [CrossRef]
- Károlyházy, F.; Frenkel, A.; Lukács, B. On the possible role of gravity in the reduction of the wave function. In Proceedings of the 3rd Symposium on Quantum Gravity, Oxford, UK, 21–23 March 1984. [Google Scholar]
- Diosi, L. Models For Universal Reduction Of Macroscopic Quantum Fluctuations. Phys. Rev. A 1989, 40, 1165. [Google Scholar] [CrossRef]
- Penrose, R. On gravity’s role in quantum state reduction. Gen. Relativ. Gravit. 1996, 28, 581. [Google Scholar] [CrossRef]
- Singh, T.P. Possible role of gravity in collapse of the wave-function: A brief survey of some ideas. J. Phys. Conf. Ser. 2015, 1, 012009. [Google Scholar] [CrossRef]
- Tawfik, A.N.; Diab, A.M. A Review of the Generalized Uncertainty Principle. Rep. Prog. Phys. 2015, 78, 126001. [Google Scholar] [CrossRef] [PubMed]
- Tawfik, A.N.; Diab, A.M. Generalized Uncertainty Principle: Approaches and Applications. Int. J. Mod. Phys. D 2014, 12, 1430025. [Google Scholar] [CrossRef]
- Hossenfelder, S. Minimal Length Scale Scenarios for Quantum Gravity. Living Rev. Relativ. 2013, 16, 2. [Google Scholar] [CrossRef]
- Garay, L.J. Quantum gravity and minimum length. Int. J. Mod. Phys. A 1995, 10, 145. [Google Scholar] [CrossRef]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astron. J. 1998, 116, 1009. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 high-redshift supernovae. Astrophys. J. 1999, 517, 565. [Google Scholar] [CrossRef]
- Ostriker, J.P.; Steinhardt, P.J. Cosmic concordance. arXiv, 1995; arXiv:astro-ph/9505066. [Google Scholar]
- Betoule, M.; Kessler, R.; Guy, J.; Mosher, J.; Hardin, D.; Biswas, R.; Astier, P.; El-Hage, P.; Konig, M.; Kuhlmann, S.; et al. Improved cosmological constraints from a joint analysis of the SDSS-II and SNLS supernova samples. Astron. Astrophys. 2014, 568, A22. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, N.; Alves, M.I.; Armitage-Caplan, C.; Arnaud, M.; Ashdown, M.; Atrio-Barandela, F.; Aumont, J.; Aussel, H.; Baccigalupi, C.; et al. Planck 2013 results. I. Overview of products and scientific results. arXiv, 2013; arXiv:1303.5062. [Google Scholar]
- Ade, P.A.R.; Aghanim, N.; Armitage-Caplan, C. Planck 2013 results. XVI. Cosmological parameters. Astron. Astrophys. 2014, 571, A16. [Google Scholar]
- Ade, P.A.R.; Alves, M.I.R.; Aniano, G.; Armitage-Caplan, C.; Arnaud, M.F.; Atrio-Barandela, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; et al. Planck intermediate results. XXII. Frequency dependence of thermal emission from Galactic dust in intensity and polarization. arXiv, 2014; arXiv:1405.0874. [Google Scholar]
- Ade, P.A.R.; Aghanim, N.; Alves, M.I.R.; Aniano, G.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; et al. Planck intermediate results. XXIX. All-sky dust modelling with Planck, IRAS, and WISE observations. arXiv, 2014; arXiv:1409.2495. [Google Scholar]
- Amendola, L.; Tsujikawa, S. Dark Energy: Theory and Observations; Cambridge University Press: Cambridge, UK, 2010; ISBN 9780521516006. [Google Scholar]
- Li, M.; Li, X.D.; Wang, S.; Wang, Y. Dark Energy: A Brief Review. Front. Phys. 2013, 8, 828. [Google Scholar] [CrossRef]
- Ng, Y.J.; Van Dam, H. Limit to space-time measurement. Mod. Phys. Lett. A 1994, 9, 335. [Google Scholar]
- Ng, Y.J.; Van Dam, H. Limitation to quantum measurements of space-time distances. Ann. N. Y. Acad. Sci. 1995, 755, 579. [Google Scholar] [CrossRef]
- Islam, J.N. An Introduction to Mathematical Cosmology; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Cai, Y.F.; Piao, Y.S. Probing noncommutativity with inflationary gravitational waves. Phys. Lett. B 2007, 657, 1–9. [Google Scholar] [CrossRef]
- Cai, Y.F.; Wang, Y. Testing quantum gravity effects with latest CMB observations. Phys. Lett. B 2014, 735, 108. [Google Scholar] [CrossRef]
- Christopherson, A.J. Applications of Cosmological Perturbation Theory. arXiv, 2011; arXiv:1106.0446. [Google Scholar]
- Lake, M.; Suyama, T. Evolution of FLRW spacetime after the birth of a cosmic string. Phys. Rev. D 2012, 85, 083521. [Google Scholar] [CrossRef]
- Hobson, M.P.; Efstathiou, G.P.; Lasenby, A.N. General Relativity: An Introduction for Physicists; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Bhattacharya, S.; Dialektopoulos, K.F.; Romano, A.E.; Skordis, C.; Tomaras, T.N. The maximum sizes of large scale structures in alternative theories of gravity. arXiv, 2016; arXiv:1611.05055. [Google Scholar] [CrossRef]
- Calmet, X.; Graesser, M.; Hsu, S.D.H. Minimum length from quantum mechanics and general relativity. Phys. Rev. Lett. 2004, 93, 211101. [Google Scholar] [CrossRef]
- Calmet, X.; Graesser, M.; Hsu, S.D.H. Minimum length from first principles. Int. J. Mod. Phys. D 2005, 14, 2195. [Google Scholar] [CrossRef]
- Rae, A.I.M. Quantum Mechanics, 4th ed.; Institute of Physics Publishing: Bristol, UK, 2000. [Google Scholar]
- Isham, C.J. Lectures on Quantum Theory: Mathematical and Structural Foundations; Imperial College Press: London, UK, 1995. [Google Scholar]
- Salecker, H.; Wigner, E.P. Quantum limitations of the measurement of space-time distances. Phys. Rev. 1958, 109, 571. [Google Scholar] [CrossRef]
- Peskin, M.E.; Schroeder, D.V. An Introduction to Quantum Field Theory; Addison-Wesley: Reading, PA, USA, 1995; p. 842. [Google Scholar]
- Spradlin, M.; Strominger, A.; Volovich, A. Les Houches lectures on de Sitter space. arXiv, 2001; arXiv:hep-th/0110007. [Google Scholar]
- Burikham, P.; Dhanawittayapol, R.; Wuthicharn, T. A new mass scale, implications on black hole evaporation and holography. Int. J. Mod. Phys. 2016, 31, 1650089. [Google Scholar] [CrossRef]
- Buchdahl, H.A. General Relativistic Fluid Spheres. Phys. Rev. 1959, 116, 1027. [Google Scholar] [CrossRef]
- Mak, M.K.; Dobson, P.N., Jr.; Harko, T. Maximum mass radius ratio for compact general relativistic objects in Schwarzschild-de Sitter geometry. Mod. Phys. Lett. A 2000, 15, 2153. [Google Scholar] [CrossRef]
- Boehmer, C.G.; Harko, T. Does the cosmological constant imply the existence of a minimum mass? Phys. Lett. B 2005, 630, 73. [Google Scholar] [CrossRef]
- Boehmer, C.G.; Harko, T. Physics of dark energy particles. Found. Phys. 2008, 38, 216. [Google Scholar] [CrossRef]
- Burikham, P.; Cheamsawat, K.; Harko, T.; Lake, M.J. The minimum mass of a spherically symmetric object in D-dimensions, and its implications for the mass hierarchy problem. Eur. Phys. J. C 2015, 75, 442. [Google Scholar] [CrossRef]
- Burikham, P.; Cheamsawat, K.; Harko, T.; Lake, M.J. The minimum mass of a charged spherically symmetric object in D dimensions, its implications for fundamental particles, and holography. Eur. Phys. J. C 2016, 76, 106. [Google Scholar] [CrossRef]
- Boehmer, C.G.; Harko, T. Minimum mass-radius ratio for charged gravitational objects. Gen. Relativ. Gravit. 2007, 39, 757–775. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Hydrostatic Equilibrium and Gravitational Collapse of Relativistic Charged Fluid Balls. Phys. Rev. D 1971, 4, 2185. [Google Scholar] [CrossRef]
- Dirac, P.A.M. An Extensible model of the electron. Proc. R. Soc. Lond. A 1962, 268, 57. [Google Scholar] [CrossRef]
- Dirac, P.A.M. The cosmological constants. Nature 1937, 139, 323. [Google Scholar] [CrossRef]
- Dirac, P.A.M. The Large Numbers Hypothesis and the Einstein Theory of Gravitation. Proc. R. Soc. Lond. A 1979, 365, 19–30. [Google Scholar] [CrossRef]
- Burikham, P.; Harko, T.; Lake, M.J. The QCD mass gap and quark deconfinement scales as mass bounds in strong gravity. arXiv, 2017; arXiv:1705.11174. [Google Scholar] [CrossRef]
- Perivolaropoulos, L. Sub-millimeter Spatial Oscillations of Newton’s Constant: Theoretical Models and Laboratory Tests. arXiv, 2016; arXiv:1611.07293. [Google Scholar]
- Antoniou, I.; Perivolaropoulos, L. Constraints on spatially oscillating sub-mm forces from the Stanford Optically Levitated Microsphere Experiment data. Phys. Rev. D 2017, 10, 104002. [Google Scholar] [CrossRef]
- Ng, Y.J. Quantum Foam, Gravitational Thermodynamics, and the Dark Sector. arXiv, 2016; arXiv:1701.00017. [Google Scholar] [CrossRef]
- Cai, R.G. A Dark Energy Model Characterized by the Age of the Universe. Phys. Lett. B 2007, 657, 228. [Google Scholar] [CrossRef]
- Wei, H.; Cai, R.G. A New Model of Agegraphic Dark Energy. Phys. Lett. B 2008, 660, 113. [Google Scholar] [CrossRef]
- Wei, H.; Zhang, S.N. Age Problem in the Holographic Dark Energy Model. Phys. Rev. D 2007, 76, 063003. [Google Scholar] [CrossRef]
- Nottale, L. Machs Principle, Diracs Large Numbers, and the Cosmological Constant Problem. Preprint 1993. Available online: https://pdfs.semanticscholar.org/d4c1/b2d158d09aa2f2f8c47274aac630e64e492d.pdf (accessed on 7 January 2019).
- Zel’dovich, Y.B.; Krasinski, A.; Zeldovich, Y.B. The Cosmological constant and the theory of elementary particles. Phys. Uspekhi 1968, 11, 381–393. [Google Scholar] [CrossRef]
- Lake, M.J. Is it there a connection between “dark” and “light” physics? J. Phys. Conf. Ser. 2017, 883, 012001. [Google Scholar] [CrossRef]
- Cai, Y.F.; Saridakis, E.N.; Setare, M.R.; Xia, J.Q. Quintom Cosmology: Theoretical implications and observations. Phys. Rep. 2010, 493, 1. [Google Scholar] [CrossRef]
- De Felice, A.; Tsujikawa, S. F(R) theories. Living Rev. Relativ. 2010, 13, 3. [Google Scholar] [CrossRef]
- Padmanabhan, T.; Kothawala, D. Lanczos-Lovelock models of gravity. Phys. Rep. 2013, 531, 115. [Google Scholar] [CrossRef]
- Bellini, E.; Cuesta, A.J.; Jimenez, R.; Verde, L. Constraints on deviations from? CDM within Horndeski gravity. JCAP 2016, 1602, 053, Erratum in 2016, 1606, E01. [Google Scholar] [CrossRef]
- Barreira, A.; Li, B.; Baugh, C.; Pascoli, S. The observational status of Galileon gravity after Planck. JCAP 2014, 1408, 059. [Google Scholar] [CrossRef]
- Burrage, C.; Sakstein, J. Tests of Chameleon Gravity. Living Rev. Relativ. 2018, 21, 1. [Google Scholar] [CrossRef] [PubMed]
- Trautman, A. Einstein-Cartan theory. arXiv, 2006; arXiv:gr-qc/0606062. [Google Scholar]
- Cai, Y.F.; Capozziello, S.; De Laurentis, M.; Saridakis, E.N. f(T) teleparallel gravity and cosmology. Rep. Prog. Phys. 2016, 79, 106901. [Google Scholar] [CrossRef] [PubMed]
- De Felice, A. The theory of Minimal Massive Gravity. J. Phys. Conf. Ser. 2017, 883, 012009. [Google Scholar] [CrossRef]
- Maartens, R.; Koyama, K. Brane-World Gravity. Living Rev. Relativ. 2010, 13, 5. [Google Scholar] [CrossRef]
- Fritzsch, H.; Solà, J.; Nunes, R.C. Running vacuum in the Universe and the time variation of the fundamental constants of Nature. Eur. Phys. J. C 2017, 77, 193. [Google Scholar] [CrossRef]
- Clifton, T.; Ferreira, P.G.; Padilla, A.; Skordis, C. Modified Gravity and Cosmology. Phys. Rep. 2012, 513, 1. [Google Scholar] [CrossRef]
- Giulini, D. Does cosmological expansion affect local physics? Stud. Hist. Philos. Sci. B 2014, 46, 24. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M.; Sykes, B.J.; Bell, J.S. Mechanics; Elsevier: Oxford, UK, 1976. [Google Scholar]
- Berestetsky, V.B.; Lifshitz, E.M.; Pitaevsky, L.P. Quantum Electrodynamics. In Course on Theoretical Physics; Pergamon: Oxford, UK, 1982. [Google Scholar]
| No. | r | Δp | Order |
|---|---|---|---|
| 1 | |||
| 2 | |||
| 3 | |||
| 4 | |||
| 5 | |||
| 6 | |||
| 7 | |||
| 8 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lake, M.J. Minimum Length Uncertainty Relations in the Presence of Dark Energy. Galaxies 2019, 7, 11. https://doi.org/10.3390/galaxies7010011
Lake MJ. Minimum Length Uncertainty Relations in the Presence of Dark Energy. Galaxies. 2019; 7(1):11. https://doi.org/10.3390/galaxies7010011
Chicago/Turabian StyleLake, Matthew J. 2019. "Minimum Length Uncertainty Relations in the Presence of Dark Energy" Galaxies 7, no. 1: 11. https://doi.org/10.3390/galaxies7010011
APA StyleLake, M. J. (2019). Minimum Length Uncertainty Relations in the Presence of Dark Energy. Galaxies, 7(1), 11. https://doi.org/10.3390/galaxies7010011





