Unitary Issues in Some Higher Derivative Field Theories

Abstract

We analyze the unitarity properties of higher derivative quantum field theories which are free of ghosts and ultraviolet singularities. We point out that in spite of the absence of ghosts most of these theories are not unitary. This result confirms the difficulties of finding a consistent quantum field theory of quantum gravity.

1. Introduction

Higher derivative interaction terms arise in the effective theories of most of local quantum field theories. However, from a fundamental viewpoint, they are usually avoided because of their undesirable behaviour concerning causality and unitarity principles. Fortunately, the Standard Model is a renormalizable theory with only first and second order derivative terms in the action, which is consistent with locality, causality and unitarity requirements. On the other hand, the quantum theory of Einstein’s general relativity is non-renormalizable. A quantum theory of gravitation requires incorporating terms with a higher number of derivatives. Dealing with renormalizable or even UV-finite theories of quantum gravity requires, thus, to address the possible implications of higher derivative couplings on fundamental properties of the theory like unitarity and causality. Local field theory models of quantum gravity involving higher order derivatives have been classified as generalizations of Horndeski models [1]. It is remarkable that the early model of inflation introduced by Starobinsky [2] is embedded in those families. The $R^2$ term, together with the cosmological constant term $\Lambda$, and the Einstein term R seem to account for the effective behaviour of gravitation at all scales, from the microworld to cosmology. The fact that all these terms are local seems to point out a general principle of the nature of fundamental interactions.

The earliest attempt to introduce a renormalizable theory of gravity was carried out by Stelle in the seventies [3]. Super-renormalizable theories of quantum gravity with higher derivatives were first analyzed two decades later [4,5].

However, the appearance of higher derivatives in local field theories raises several consistency problems. First, their energy density is not bounded from below at least for non-degenerate theories because of Ostrogradski theorem [6]. In the quantum theory, negative energy states can be traded by negative norm states (or ghosts) leading to non-unitary theories [7,8].

The standard Pauli-Villars regularization can be formulated as a higher derivative theory that obviously contains ghosts, which spoil unitarity and causality properties of the theory. It has been also shown that any theory with higher order polynomial terms of D’Alambertian operator with real roots always contains ghosts by topological reasons [4].

But there are other attempts to overcome the ghost problem by tricks that remove the negative effects of the ghosts in particular theories. For instance, Lee-Wick theories skip the appearance of unphysical ghosts by using polynomials with complex conjugate poles [9,10] to provide a unitary S-matrix of gravitational excitations [11].

Another way of avoiding the ghost problem is to consider non-local theories with an infinite number of terms with an arbitrary number of derivatives, which sum up to form an entire function of the D’Alambertian operator. Since these functions have no poles on the whole complex plane, the problem is apparently solved [5].

One has to remember that a consistent field theory should match a set of basic principles, including relativistic invariance, causality, and unitarity. These principles impose strong conditions on physical Green functions, which guarantee that the analytic continuation in complex time of Wightman functions gives rise to Schwinger functions in Euclidean time. Thus, a consistent field theory must define not only regular Wightman functions but also regular Schwinger functions. Moreover, the Schwinger functions must satisfy the reflection positivity requirement. In particular the 2-point function must admit a Källén-Lehmann representation [12,13].

In this paper, we analyze the consistency issue for a large family of higher derivative theories which are super-renormalizable and ghost-free. We show that, in spite of their better ultraviolet behaviour [5,14] the higher derivative theories of this class fail to match the complete set of basic requirements and therefore may lead to pathological quantum field theories. So, even if the non-local ghost-free theories have interesting quantum and cosmological applications (see e.g., [15] and references therein) they cannot be considered as candidates for consistent fundamental theories of quantum gravity.

2. Non-Local Finite Scalar Theories

Let us consider the simple case of a scalar field theory

$$\begin{array}{ccc}\hfill S\left(\varphi \right)& =& \frac{1}{2}\int \left({\left({\partial }^{\mu }\varphi \right)}^{†}\left({\partial }_{\mu }\varphi \right)-m^2{\left|\varphi \right|}^2-\frac{\lambda }{12}{\left|\varphi \right|}^4\right).\hfill \end{array}$$

(1)

Although it is unclear the renormalizability of the theory from a non-perturbative viewpoint, in four-dimensional spacetime the theory is perturbatively renormalizable. In perturbation theory the renormalization prescription requires a regularization of quadratically and logarithmically divergent Green functions. One way of regularizing the theory is by introducing an ultraviolet (UV) regulator. A particular choice is

$$\begin{array}{ccc}\hfill S\left(\varphi \right)& =& \frac{1}{2}\int \left({\varphi }^{†}{e}^{{(\square /{\Lambda }^2)}^s}\left(-\square -m^2\right)\varphi -\frac{\lambda }{12}{\left|\varphi \right|}^4\right),\hfill \end{array}$$

(2)

where $\square ={\partial }^{\mu }{\partial }_{\mu }$ is the D’Alambertian operator, $\Lambda$ is an UV-regulator and the exponent s is a positive number. The theory is finite in the Euclidean sector because the propagator

$$\begin{array}{c}\hfill \Delta \left(p\right)=\frac{e^{-p^{2s}/{\Lambda }^{2s}}}{p^2+m^2}\end{array}$$

(3)

is strongly suppressed in the UV.

However, not all theories with higher derivatives can be considered as fundamental theories. The first reason is due to the classical instability of non-degenerate higher derivative theories [8], pointed out by the Ostrogradski theorem [6]. However, in the non-interacting case $\lambda =0$, due to the quadratic dependence on the fields and the exponential nature of the higher derivative operators the energy density is always positive when evaluated on solutions of the classical equation of motion, rendering the free classical theory stable. This property can also be understood by the fact that one can re-absorb the exponential regulating factors in a field redefinition

$$\varphi \to {\varphi }^{\prime }=e^{{(\square /{\Lambda }^2)}^{s/2}}\varphi ,$$

giving rise to a standard free field theory without any instability.

From a quantum field theory viewpoint there are some basic principles that theories must satisfy. In particular [16,17,18]:

(i)

Analyticity: The n-point Wightman functions $W_n(x_1,x_2,\cdots ,x_n)=\langle 0|\varphi \left(x_1\right)\varphi \left(x_2\right)\cdots \varphi \left(x_n\right)|0\rangle$ should define regular distributions and must admit an analytic continuation to regular n-point Schwinger functions $S_n(x_1,x_2,\cdots ,x_n)=W_n({\tilde{x}}_1,{\tilde{x}}_2,\cdots ,{\tilde{x}}_n)$ in the Euclidean spacetime coordinates ${\tilde{x}}_j=(i{x}_j^0,{\mathbf{x}}_j)$.

(ii)

Reflection Positivity: The Schwinger functions $S_n$ should satisfy Osterwalder-Schrader reflection positivity property [19,20]. In the case of the Euclidean 2-point function this property implies that

$$\int \theta f\left(x\right)S_2(x,y)f\left(y\right)⩾0$$

(4)

for any function $f\in C_0\left({\mathbb{R}}_{+}^4\right)$, where $\theta$ is the time-reversal transform defined by $\theta f(x^0,\mathbf{x})=f^{\ast }(-x^0,\mathbf{x})$. The functions f in $C_0\left({\mathbb{R}}_{+}^4\right)$ are continuous functions with compact support in the positive time half-space $(x^0>0)$ of ${\mathbb{R}}^4$.

(iii)

Källén-Lehmann representation: The Fourier transform of the 2-point Schwinger function should admit a Källén-Lehmann representation [13]

$${\widehat{S}}_2\left(p\right)={\int }_0^{\infty }d\mu \frac{\rho \left(\mu \right)}{p^2+{\mu }^2}$$

with a non-negative spectral density $\rho \left(\mu \right)⩾0$.

The fundamental principles of the quantum theory (i)–(iii) together with some other technical requirements allow to reconstruct the quantum Hilbert space of the field theory from space-time multi-functionals $f(x_1,x_2,\dots ,x_n)$ with support on positive times $t_i>0,i=1,2,\cdots n$ (References [16,17]). The norm of the quantum states is defined by contraction of their indices with those of Schwinger functions (Refereces [16,17]). If the two-point function is not reflection positive Equation (4) the induced norm would be negative for states of the form $\varphi \left(f\right)|0\rangle =\int dx\varphi (x\left)f\right(x\left)\right|0\rangle$ and the construction of the quantum theory from the Euclidean Schwinger functions would fail. In this sense, the failure of reflection positivity implies a failure of unitarity in the quantum field theory.

In the simplest case $s=1$, the tree-level two-point Schwinger function

$$S_2(x,y)=\int \frac{d^{4}p}{{\left(2\pi \right)}^4}\Delta \left(p\right)e^{ip(y-x)}=\int \frac{d^{4}p}{{\left(2\pi \right)}^4}\frac{e^{-p^2/{\Lambda }^2}}{p^2+m^2}{e}^{ip(y-x)}$$

is finite. However, there is no analytic continuation to the real-time Minkowski space, as it is the case in the standard theory. The obstruction is due to the fact that the analytic continuation by Wick rotation requires the vanishing of the contribution of the contour integrals of the first and third quadrants at infinite distance, which is not satisfied in this case due to the existence of essential singularities at the infinity of the complex energy plane.

The only divergence of the theory arises in the vacuum energy density

$$\Delta {\mathcal{E}}_0=-\int \frac{d^{4}p}{{\left(2\pi \right)}^4}\frac{{\left(p^0\right)}^2}{{\Lambda }^2}.$$

(5)

However, the consistency of the quantum theory requires satisfying the reflection positivity property Equation (4). This means that in particular

$$S_2(\theta x,x)=S_2(-\tau ,\mathbf{x};\tau ,\mathbf{x})⩾0,$$

(6)

which is satisfied by the theory in the case $s=1$, where

$$S_2(\theta x,x)=\int \frac{d^{4}p}{{\left(2\pi \right)}^4}\frac{e^{-p^2/{\Lambda }^2}}{p^2+m^2}{e}^{2i{p}^0\tau }⩾0.$$

(7)

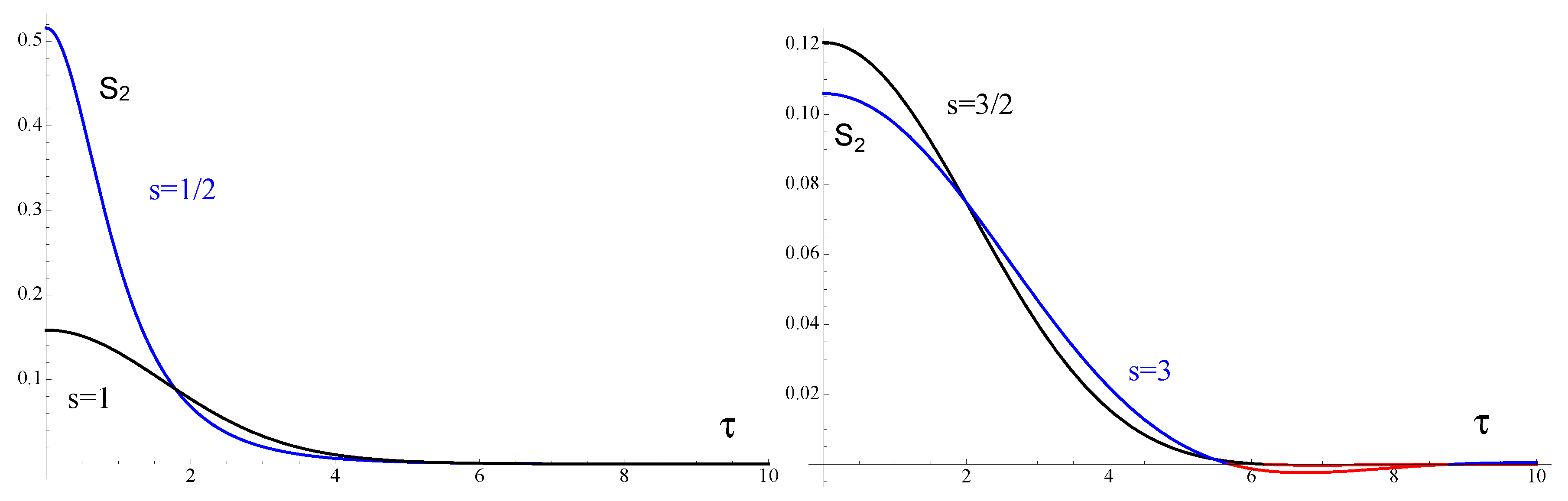
However, for theories with higher power exponents $s>1$, this test of reflection positivity is not matched and the corresponding theories are not consistent. The breaking of this test of reflection positivity can be explicitly shown by numerical analysis (see Figure 1) and rigorously proved by analytic arguments [21,22]. When $0<s⩽1$ the exponential term $e^{-p^{2s}/{\Lambda }^{2s}}$ can be expanded as a non-negative convex combination of Gaussian terms

$$e^{-p^{2s}/{\Lambda }^{2s}}={\int }_0^{\infty }{e}^{-x{p}^2/{\Lambda }^2}\rho \left(x\right)dx.$$

(8)

with $\rho \left(x\right)⩾0$ for $x>0$ due to Bernstein theorem [21]. Thus, the positivity of $S_2(\theta x,x)$ follows from that of the Gaussian with $s=1$ Equation (7). However, for $s>1$ the exponential term does not admit such a representation and the reflection positivity condition Equation (6) fails (see e.g., Reference [22]).

Thus, even if the theory has no ghosts, it does not mean that it is unitary, as we have shown for $s>1$.

Moreover, even in the case $s=1$ the fact that the 2-point Schwinger function is strictly positive $S_2(\theta x,x)⩾0$ does not imply that the corresponding operator $S_2$ is positive definite. It simply means that the diagonal elements of the corresponding matrix are positive. But the matrix itself might be not positive definite. In other terms, it simply signifies that the two-point function is positive for the set of functions f which are highly localized in points of spacetime. In fact, it can be shown that the operator $S_2$ is generally not a positive definite. It is enough to check that for some $f\in C_0\left({\mathbb{R}}_{+}^4\right)$

$$\int \theta f\left(x\right)S_2(x,y)f\left(y\right)<0.$$

(9)

This negative result can be derived from the fact that the 2-point Schwinger function $S_2(x,y)$ does not admit a Källén-Lehmann representation for any value of s. This fact is a consequence of a mathematical theorem [23] proved by Widder [24] (see also [25,26]).

3. Non-Local Gravitational Theories

The analogous super-renormalizable gravitational theories are described by the action

$$\begin{array}{cc}\hfill S\left(g\right)& =\lambda \kappa \int \sqrt{g}+\kappa \int \sqrt{g}R+\alpha \kappa \int \sqrt{g}{R}_{\mu \nu \alpha \beta }{e}^{{(\square /{\Lambda }^2)}^s}{R}^{\mu \nu \alpha \beta }\hfill \\ & +\beta \kappa \int \sqrt{g}{R}_{\mu \nu }{e}^{{(\square /{\Lambda }^2)}^s}{R}^{\mu \nu }+\gamma \kappa \int \sqrt{g}R{e}^{{(\square /{\Lambda }^2)}^s}R.\hfill \end{array}$$

(10)

Classical Ostrogradski instabilities also arise in these theories [8]. In perturbation theory, $S\left(g\right)$ describes a theory of two self-interacting massless particles with helicities 2 and 0. The absence of ghosts can be shown from the absence of unphysical poles in the 2-point Schwinger function of the perturbation of the gravitational field:

$$\begin{array}{cc}\hfill S_{\mu \nu \rho \sigma }^{\left(2\right)}\left(p^2\right)& =\frac{{\mathcal{P}}_{\mu \nu \rho \sigma }^{\left(2\right)}\left(p^2\right)}{p^2-\beta /2e^{p^{2s}/{\Lambda }^{2s}}{p}^4-2\gamma e^{p^{2s}/{\Lambda }^{2s}}{p}^4}\hfill \\ & -\frac{{\mathcal{P}}_{\mu \nu \rho \sigma }^{\left(0\right)}\left(p^2\right)}{p^2+(\beta /2+6\alpha )e^{p^{2s}/{\Lambda }^{2s}}{p}^4+8\gamma e^{p^{2s}/{\Lambda }^{2s}}{p}^4},\hfill \end{array}$$

(11)

where

$$\begin{array}{cc}\hfill {\mathcal{P}}_{\mu \nu \rho \sigma }^{\left(2\right)}\left(p^2\right)& =\frac{1}{2}\left({\delta }_{\mu \rho }{\delta }_{\nu \sigma }+{\delta }_{\nu \rho }{\delta }_{\mu \sigma }\right)-\frac{1}{3}{\delta }_{\mu \nu }{\delta }_{\rho \sigma }\hfill \\ & -\frac{p_{\mu }{p}_{\rho }}{p^2}{\delta }_{\nu \sigma }-\frac{p_{\nu }{p}_{\sigma }}{p^2}{\delta }_{\mu \rho }+\frac{1}{3}\frac{p_{\mu }{p}_{\nu }}{p^2}{\delta }_{\sigma \rho }\hfill \\ & -\frac{p_{\mu }{p}_{\sigma }}{p^2}{\delta }_{\nu \rho }-\frac{p_{\nu }{p}_{\rho }}{p^2}{\delta }_{\mu \sigma }+\frac{1}{3}\frac{p_{\sigma }{p}_{\rho }}{p^2}{\delta }_{\mu \nu }\hfill \\ & +\frac{2}{3}\frac{p_{\sigma }{p}_{\rho }{p}_{\mu }{p}_{\nu }}{p^4},\hfill \end{array}$$

(12)

and

$${\mathcal{P}}_{\mu \nu \rho \sigma }^{\left(0\right)}\left(p^2\right)=\frac{1}{3}\left({\delta }_{\mu \nu }{\delta }_{\rho \sigma }-\frac{p_{\mu }{p}_{\nu }}{p^2}{\delta }_{\sigma \rho }-\frac{p_{\sigma }{p}_{\rho }}{p^2}{\delta }_{\mu \nu }+\frac{p_{\sigma }{p}_{\rho }{p}_{\mu }{p}_{\nu }}{p^4}\right)$$

(13)

are the projectors onto the spin-2 and spin-0 (stress scalar) components of the 2-point function.

What happens in the higher derivative theory is that the 2-point Schwinger function Equation (11) does not satisfy the reflection positivity

$$\theta S_{\mu \nu \sigma \rho }^{\left(2\right)}⩾0.$$

As we have shown in the scalar case it is enough to prove that

$$S_{ijij}^{\left(2\right)}(\theta x,x)$$

(14)

is not positive for some values of $x\in {\mathbb{R}}^4$ and $i\ne j$. Indeed,

$$\begin{array}{cc}\hfill S_{ijij}^{\left(2\right)}(\theta x,x)& =\frac{2}{3}\int \frac{d^{4}p}{{\left(2\pi \right)}^4}\frac{(1+p_i^2{p}_j^2)e^{2i{p}^0\tau }}{p^2-\beta /2e^{p^{2s}/{\Lambda }^{2s}}{p}^4-2\gamma e^{p^{2s}/{\Lambda }^{2s}}{p}^4}\hfill \\ & -\frac{1}{3}\int \frac{d^{4}p}{{\left(2\pi \right)}^4}\frac{(1+p_i^2{p}_j^2)e^{2i{p}^0\tau }}{p^2+(\beta /2+6\alpha )e^{p^{2s}/{\Lambda }^{2s}}{p}^4+8\gamma e^{p^{2s}/{\Lambda }^{2s}}{p}^4}\hfill \end{array}$$

(15)

is not always positive definite for the same reasons that Equation (7) was not positive in the case of scalar fields. Thus, the absence of ghosts does not guarantee the unitarity of a theory.

The higher derivatives theories Equation(10) are relativistically covariant. If, instead of the exponential form-factor $e^{{(\square /{\Lambda }^2)}^s}$, we consider a form-factor $e^{{(\Delta /{\Lambda }^2)}^s}$ with only high spatial derivatives and only two time derivatives the field theory will be UV-finite and will satisfy the reflection positivity condition [27]. However, these theories are not relativistically invariant. Thus, it is the combination of Lorentz covariance with higher time derivatives which generates the unitarity issue.

4. Conclusions

The search for a consistent theory of quantum gravity in field theory framework is still a very challenging open problem. The promising approach based on higher derivative theories has been always very attractive because of its nice ultraviolet behaviour and cosmological applications, including Starobinsky model of inflation. From a classical field theory viewpoint, many of these models were discarded by the presence of Ostrogradski instabilities. Quantization imposes even more constraints because of the appearance of ghost modes, which introduce violations of unitarity and/or causality. One way of overcoming these problems is by introducing form-factors with an analytic dependence on the propagating momenta. This approach is non-local but has the advantage that enables one to avoid ghosts with the hope that this will preserve all fundamental properties of a quantum field theory.

We have shown that for all non-local theories involving an exponentially decreasing form-factors unitarity is not preserved. From the Euclidean approach to the quantum theory, we have demonstrated the existence of states with a negative norm. In summary, the family of non-local theories of this type cannot be considered as a consistent approach to quantum gravity. The analysis can be extended to other higher derivative models of gravity, which is left for a future work.

There are alternatives to the models discussed here. The Lee-Wick theories are very special cases, which require a more detailed analysis. A family of models which pass our unitarity check is the Hořava-Lifshitz family. However, in that case the recovery of general covariance and Lorentz symmetry in the infrared regime is not guaranteed.

In any case, the problem is very challenging and the restrictions which our results impose on viable models of quantum gravity constrain very much the search for a consistent theory. This is not a bad news. It only means that if there is a quantum theory of gravity based on standard field theory it would be very special. The search of such a special theory requires a good understanding of restrictions imposed by the quantum theory principles.