Galactic Structures from Gravitational Radii

Abstract

We demonstrate that the existence of a Noether symmetry in $f\left(R\right)$ theories of gravity gives rise to an additional gravitational radius, besides the standard Schwarzschild one, determining the dynamics at galactic scales. By this feature, it is possible to explain the baryonic Tully-Fisher relation and the rotation curve of gas-rich galaxies without the dark matter hypothesis. Furthermore, under the same standard, the Fundamental Plane of elliptical galaxies can be addressed.

1. Introduction

Our main motivation for this paper is to explain the observed galactic and extragalactic dynamics using gravitational potentials derived from Extended Gravity without dark matter (DM). There are two approaches for addressing extreme (weak field) gravity regime at galactic scales:

(i)

using DM hypothesis in addition to Newtonian gravity (standard approach);

(ii)

modifying fundamental laws of dynamics or gravity (alternative approach).

Regarding the latter approach, it was shown that MOND is able to successfully explain the dynamics of galaxies outside of galaxy clusters and a recently discovered tight relation between the radial acceleration inferred from their observed rotation curves and the acceleration due to the baryonic components of their disks (McGaugh et al. [1]). Some other theories of modified gravity which give the weak field point particle gravitational potential with Yukawa correction term are also able to explain flat rotation curves (see e.g., Brownstein & Moffat [2]). Recently, Israel & Moffat [3] showed that generalized Scalar-Tensor-Vector-Gravity (STVG) theory can also explain dynamics of the merging galaxy clusters, such as Abell 520 and the Bullet Cluster, without dark matter. This approach, however, requires modification of General Relativity (GR) and derivation of alternative field equations, as well as their cosmological reformulation for Friedmann-Lema$\widehat{\mathrm{i}}$tre-Robertson-Walker metric and perfect fluid-the Friedmann equations.

Here we will try to explain the possible new fundamental gravitational radii which play analogue role in the case of weak gravitational field at galactic scales, as the Schwarzschild radius for strong gravitational field in the vicinity of some massive object (we have IR and UV gravitational radii).

New gravitational radii come from the extra degrees of freedom of Extended Gravity.

In Section 2 we explain the fundamental plane (FP) of elliptical galaxies, and in Section 3 we explain extragalactic phenomena, such as the baryonic Tully-Fisher relation (BTFR) of gas-rich galaxies, all without the DM hypothesis.

2. Fundamental Plane of Elliptical Galaxies and $\mathit{f}\left(\mathit{R}\right)$ Gravity

2.1. Fundamental Plane of Ellipticals

It is well known that besides the spiral galaxies, elliptical galaxies could also have so called missing mass problem, where an extra mass is required to explain the observed differences between their dynamical masses and luminosities. The two possibilities explaining this missing mass problem would be dark matter (DM), or theories of modified gravity. As here we adopt the second approach, we study whether the $f\left(R\right)$ gravity could solve the missing mass problem in elliptical galaxies without dark matter hypothesis. We adopt such an approach because in the galaxies we can deal with the extreme gravity regimes, and higher order curvature corrections in gravity action can emerge. That is why instead of GR we will use its simplest extension: $f\left(R\right)$ gravity model.

Many characteristics of normal elliptical galaxies are correlated, which has been empirically shown. For example, a galaxy with a higher luminosity has a larger effective radius. Besides, more luminous elliptical galaxies have larger central velocity dispersions. A set of correlations connecting the global properties of elliptical galaxies is called fundamental plane (FP), and it is an empirical relation [4]:

$$log\left(r_e\right)=a\times log\left(v_c\right)+b\times log\left(I_e\right)+c,$$

(1)

with: $r_e$—effective or half-light radius (encloses half of the total luminosity emitted by a galaxy), $v_c$—central velocity dispersion, $I_e$—mean surface brightness within the effective radius. We illustrate this region of parameter space in Figure 1, Figure 2, Figure 3 and Figure 4. In this sense, some object can be represented as a point in the parameter space $r_e,v_c,I_e$.

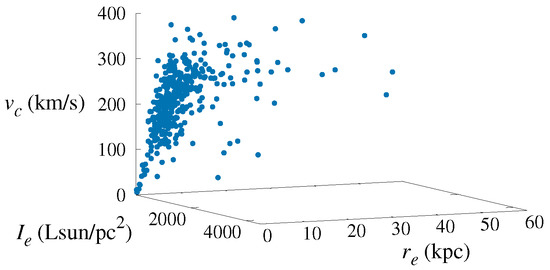
Figure 1. The three parameters of the fundamental plane (FP): surface brightness $I_e$, effective radius $r_e$ and circular velocity $v_c$, for a sample of elliptical galaxies listed in Table 1 from [5]. Note: in paper [5] it is printed the first page only, and we used the whole sample of 401 ellipticals, available among the source files of its arxiv version.

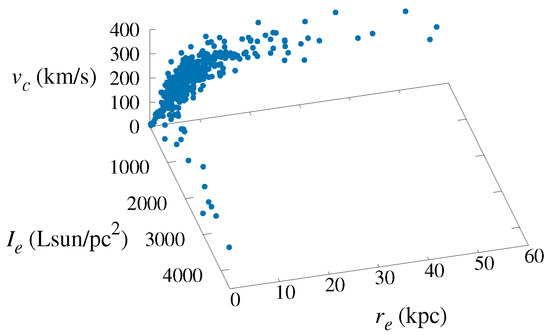
Figure 2. The same as Figure 1, but from different view.

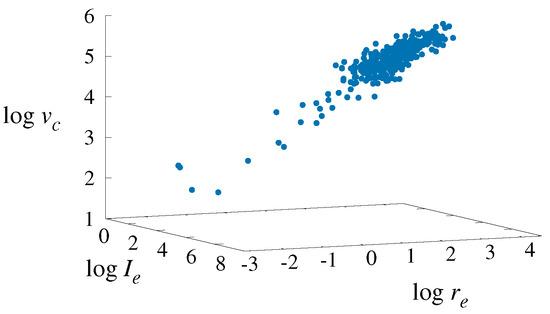
Figure 3. The FP parameter space from Figure 1, presented by logarithms of parameter values: $log{I}_e$, $log{r}_e$ and $log{v}_c$.

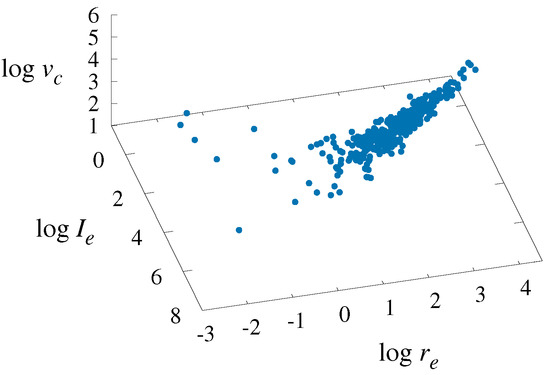
Figure 4. The same as Figure 3, but from different view.

2.2. $f\left(R\right)$ Gravity and Dynamics of Stellar Systems

We adopt $f\left(R\right)$ gravity which is the straightforward generalization of Einstein’s General Relativity as soon as the function is $f\left(R\right)\ne$ R, that is, it is not linear in the Ricci scalar R as in the Hilbert-Einstein action. $R^n$ gravity is the power-law version of $f\left(R\right)$ modified gravity. In the weak field limit, its potential (generated by a pointlike mass m at the distance r) is [6]:

$$\mathrm{\Phi }\left(r\right)=-\frac{Gm}{2r}\left[1+{\left(\frac{r}{r_c}\right)}^{\beta }\right],$$

(2)

where $r_c$ is scalelength depending on the gravitating system properties and $\beta$ is universal constant which depends on power n:

$$\beta =\frac{12n^2-7n-1-\sqrt{36n^4+12n^3-83n^2+50n+1}}{6n^2-4n+2}.$$

(3)

Regarding the consideration of the power-law fourth-order theories of gravity, and determining the space parameters of $f\left(R\right)$ gravity, see [6,7,8,9,10,11].

We want to show the connection of the fundamental plane of elliptical galaxies with $R^n$ gravity potential, by showing the correlation between the corresponding parameters. In paper [12] the empirical result for coefficients a and b is obtained: $a=1.4$, $b=-0.85$. The test for our method is to recover these coefficients, starting from the gravitational potential derived from $f\left(R\right)$ gravity. Recovering FP using $f\left(R\right)$ gravity, which means finding connection between the parameters of FP equation and parameters of the potential in Equation (2), we have done in the following way:

• addend with $r_e$: correlation between $r_e$ and $r_c$ ($r_c$—from $R^n$ potential)
• addend with ${\sigma }_0$: correlation between ${\sigma }_0$ and $v_{vir}$ ($v_{vir}$—virial velocity in $R^n$)
• addend with $I_e$: correlation between $I_e$ and $r_e$ (through the $r_c/r_e$ ratio).

In this sense, we showed that the three addends of FP have to be connected to $f\left(R\right)$ parameters (see [11] for more details).

We use the data given in Table 1 of [5], which represents the result of the collected efforts of many astronomers over the years (available in ASCI format among the source files of its arxiv version: https://arxiv.org/format/astro-ph/9707037, see ’metaplanetab1’). From that table we used values from the following columns: column (5) $log{v}_c$ (we get $v_c$ in km/s), column (6) $log{\sigma }_0$ (km/s), column (7) $log{r}_e$ (kpc) and column (8) $log{I}_e$ (L${}_{sun}$/pc${}^2$). For elliptical galaxies, the circular velocity inside effective radius is $v_c\left(r_e\right)={\sigma }_0$, while for other stellar systems it is $v_c\ne {\sigma }_0$.

The theoretical circular velocity we calculated for extended spherically symmetric systems, using Equation (25) from [6], given as a sum of Newtonian contribution ($v_{c,N}^2\left(r\right)$—Newtonian rotation curve) and the correction term from $f\left(R\right)$:

$$v_c^2\left(r\right)={\displaystyle \frac{v_{c,N}^2\left(r\right)}{2}}+{\displaystyle \frac{r}{2}}{\displaystyle \frac{\partial {\mathrm{\Phi }}_c}{\partial r}},$$

(4)

and taking into account the so called Hernquist profile for density distribution [13]:

$$\rho \left(r\right)={\displaystyle \frac{a_{H}M}{2\pi r{(r+a_H)}^3}},a_H={\displaystyle \frac{r_e}{1+\sqrt{2}}}.$$

(5)

We fitted FP coefficients a, b, c to the observed values $r_e$, $I_e$ and our calculated value $v_c^{theor}$, for different values of $r_c/r_e$ and $\beta$. One example of this fit we give in Figure 5 (with linear scale for $r_e$) and Figure 6 (with log scale for $r_e$). The coefficient a is exactly like in [12], while b has similar but not exactly the same value. However, we only calculated $v_c^{theor}$, while for $I_e$ we considered observed values, but in any case the agreement with data is very good.

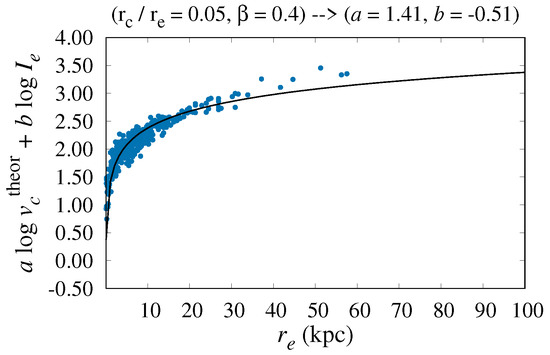
Figure 5. Fundamental plane (linear scale for x-axes) of elliptical galaxies with calculated circular velocity $v_c^{theor}$, and observed effective radius $r_e$ and mean surface brightness (within the effective radius) $I_e$, for $r_c/r_e$ = 0.05 and $\beta$ = 0.4. Black solid line is result of 3D fit of FP (calculated FP coefficients are a = 1.41 and b = $-0.51$).

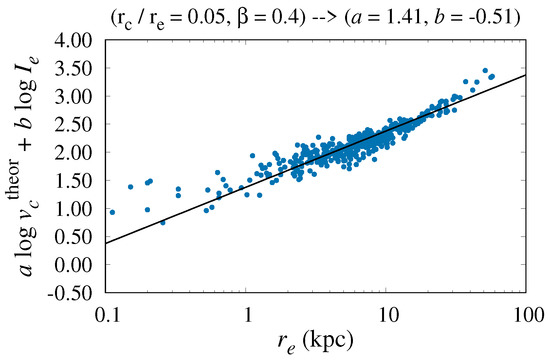
Figure 6. The same as Figure 5, but with log scale for x-axes.

We obtained that the characteristic radius $r_c$ of $R^n$ gravity is proportional to the effective radius $r_e$ (more precise, $r_c\approx 0.05r_e$ gives the best fit with data). This fact points out that the gravitational corrections induced by $R^n$ can lead photometry and dynamics of the system.

3. Explaining the Baryonic Tully-Fisher Relation with New Gravitational Radius

Some indications that $R^n$ gravity can explain the rotation curves of spiral galaxies, i.e., that the rotation curve of spiral galaxies could be fitted using the luminous components only, thus eliminating the need for dark matter, are argued in [6]. The authors investigated the possibility that the observed flatness of the rotation curves of spiral galaxies is not evidence for the existence of dark matter haloes, but rather a signal of the breakdown of General Relativity. In [14] it is found a reasonable agreement between the observed rotation curves of spiral galaxies and the circular velocity model in the framework of $R^n$ gravity, without the need for dark matter also. Due to the relevance of their sample, which contains objects in a large range of luminosities and with very accurate and proper kinematics, these results encouraged further investigations from both observational and theoretical points of view.

3.1. New Fundamental Gravitational Radius

Circular velocity of a point mass, in the $R^n$ gravity potential, can be found in the standard way, that is $v_c^2\left(r\right)=r{\displaystyle \frac{d\mathrm{\Phi }}{dr}}$, which gives (for a detailed explanation see [6]):

$$v_c^2\left(r\right)=\frac{GM}{2r}\left[1+(1-\beta ){\left(\frac{r}{r_c}\right)}^{\beta }\right].$$

(6)

Characteristic length $r_c$ of $R^n$ gravity can be related to the MOND acceleration constant $a_0$ (for details see [15]):

$$r_c=\sqrt{{\displaystyle \frac{GM}{a_0}}}.$$

(7)

Therefore, $r_c$ represents a new fundamental gravitational radius in the case of weak gravitational field.

3.2. Tully-Fisher Relation in MOND and f(R) Gravity

Baryonic Tully-Fisher relation is empirical relation between galaxy mass and rotation velocity:

$$M_b\sim v_c^4,$$

(8)

where $M_b$—baryonic mass: $M_b=M_{\ast }+M_g$ (star masses + gas mass), and $v_c$—circular velocity (after some radius $r_f$, we can assume that it becomes constant $v_c\approx v_f$).

The observational data for Figure 2 from [16], which shows BTFR, are given at the internet address http://astroweb.case.edu/ssm/data/gasrichdatatable.txt. These are collected data from references: [17,18,19]. In order to compare the BTF relations in MOND, $R^n$ and $\mathrm{\Lambda }$CDM, we used these observational data, and we draw these lines at the same $M_b\left(v_f\right)$ graph:

(i)

MOND: $M_b={\displaystyle \frac{v_f^4}{Ga}}$;

(ii)

$R^n$: $M_b={\displaystyle \frac{4a{v}_f^4}{G{a}_f^2{\left(1+(1-\beta ){\left({\displaystyle \frac{a}{a_f}}\right)}^{\beta }\right)}^2}}$;

We calculated BTFR for four cases of n: ${\displaystyle \frac{5}{4}},{\displaystyle \frac{3}{2}},2,{\displaystyle \frac{7}{2}}$, which correspond to $\beta =0.358,0.518,0.667,0.817$, respectively. $a_0$—MOND acceleration constant for point source in infinity; a —constant for spiral systems. In the case of spiral galaxies, we have a instead of $a_0$ (empirical calibration is $a_0$ = 0.8a, as reported in [20]).

(iii)

$\mathrm{\Lambda }$CDM: $M_b=0.17M_{vir},v_f=v_{vir}$.

Formula for $\mathrm{\Lambda }$CDM is taken from the paper [21], Equation (13): $M_{vir}=(4.6\times {10}^5{M}_{sun}{\mathrm{km}}^{-3}{\mathrm{s}}^3)v_{vir}^3$.

We show comparison between the observed and best fit baryonic Tully-Fisher relations of gas-rich galaxies in MOND, $R^n$ gravity (for four values of $\beta$) and $\mathrm{\Lambda }$CDM, in Figure 7 and Figure 8.

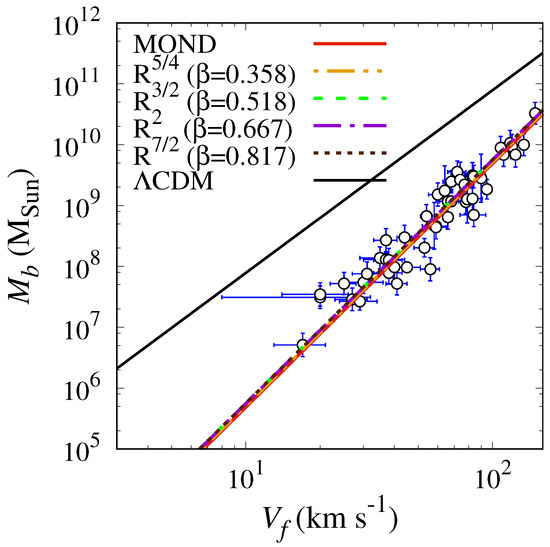
Figure 7. Comparison between best fit baryonic Tully-Fisher (BTF) relations of gas-rich galaxies (for a sample of galaxies used in [16]), in MOND, $R^n$ gravity for values of n = 1.25, 1.5, 2 and 3.5 (corresponding $\beta$ are 0.358, 0.518, 0.667 and 0.817, respectively) and $\mathrm{\Lambda }$CDM. Note: all values were calculated by us, except for open circles which are observed data from [16].

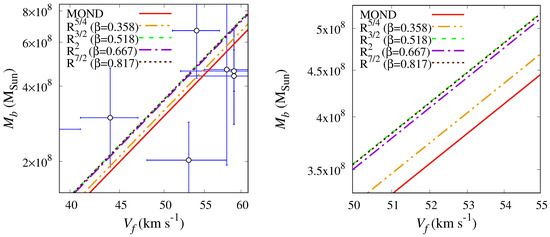
Figure 8. Left: one zoomed part of the Figure 7, showing BTF relations, in MOND and $R^n$ gravity. Right: a zoomed part of the figure, for even smaller range of $V_f$ and $M_b$.

Using the fact that the weak field limit of $f\left(R\right)$ power-law gravity gives MOND as a particular case, and as it can be seen from the equations in this subsection, the following form of BTF relation in $R^n$ gravity can be recovered: $M_b=A\left(\beta \right)v_f^4$. The only difference in respect to MOND ($M_b=A{v}_f^4$) is that normalization factor A depends on universal constant $\beta$ of $R^n$ gravity.

4. Discussion and Conclusions

We showed that it is possible to explain the baryonic Tully-Fisher relation, the rotation curve of gas-rich galaxies, and the features of fundamental plane of ellipticals without the dark matter hypothesis.

We can summarize our conclusions like this:

• We used power-law $f\left(R\right)$ gravity to demonstrate the existence of a new fundamental gravitational radius.
• This radius plays an analog role, in the case of weak gravitational field at galactic scales (IR scales) as the Schwarzschild radius in the case of strong gravitational field in the vicinity of compact massive objects (UV scales).
• The radius emerges as a conserved quantity from Noether’s symmetries that exist for any power-law $f\left(R\right)$ function.
• Using this new gravitational radius, $f\left(R\right)$ gravity is able to explain the baryonic Tully-Fisher relation of gas-rich galaxies without DM hypothesis.
• MOND is a particular case of $f\left(R\right)$ gravity in the weak field limit.
• The same radius is useful to address the FP of elliptical galaxies.
• The range $0.5\le \beta \le 0.8$ (corresponding to $1.5\le n\le 3.5$) is in a good agreement with observations. These values agree with observational constraints on $\beta$ obtained by fitting FP and MOND. We do not need DM to explain baryonic Tully-Fisher relation, and even more, $\mathrm{\Lambda }$CDM is not in satisfactory agreement with observations.
• For elliptical galaxies $r_c$ is proportional to $r_e$.
• Considering the definition of $r_e$, we can say that the effective radius (defined photometrically as the radius containing half of the luminosity of a galaxy) is led by gravity.
• In perspective, the whole galactic dynamics can be addressed by Extended Gravity.
• Work in progress for Faber-Jackson relation, galactic potentials, Boltzmann-Vlasov relation, and Virial Theorem.