The Third Quantization: To Tunnel or Not to Tunnel?
Abstract
1. Introduction
2. The Model
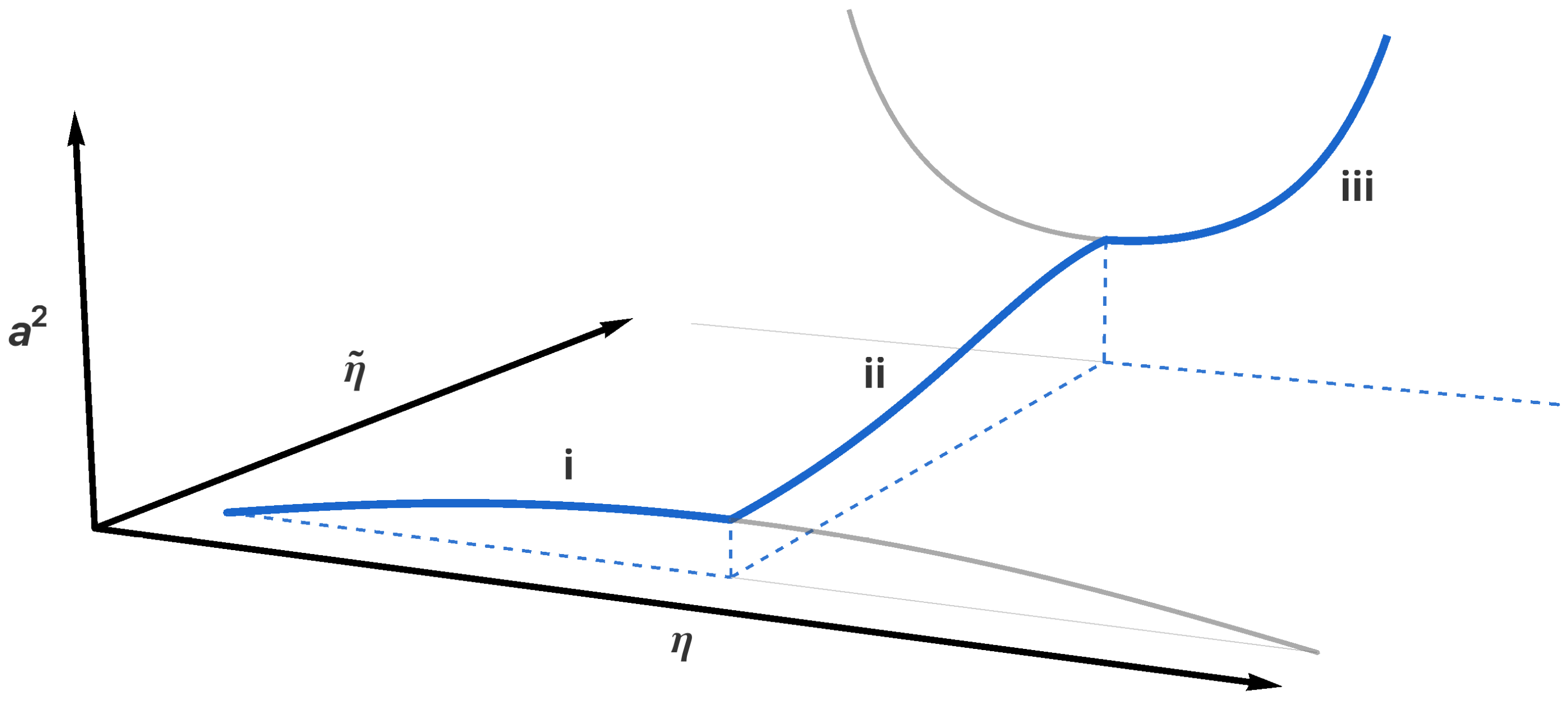
- (i)
- For , we find a baby universe that expands from until the maximum value at which point, classically, it starts to collapse. During the expanding phase, the analytical solution , where is the conformal time defined by , was obtained for the first time in [22] and readsHere, is the Jacobi elliptic function [28], we have introduced the constants and and is the value of the conformal time when .
- (ii)
- (iii)
- For , we observe a Euclidean region with . While this region is classically forbidden, from a quantum-mechanical point of view it can be interpreted as a Euclidean wormhole that connects the regions of and . The evolution inside the wormhole, which can be obtained by applying a Wick rotation to the Euclidean conformal time , was derived in [22]:Here, is the value of the Euclidean conformal time when .
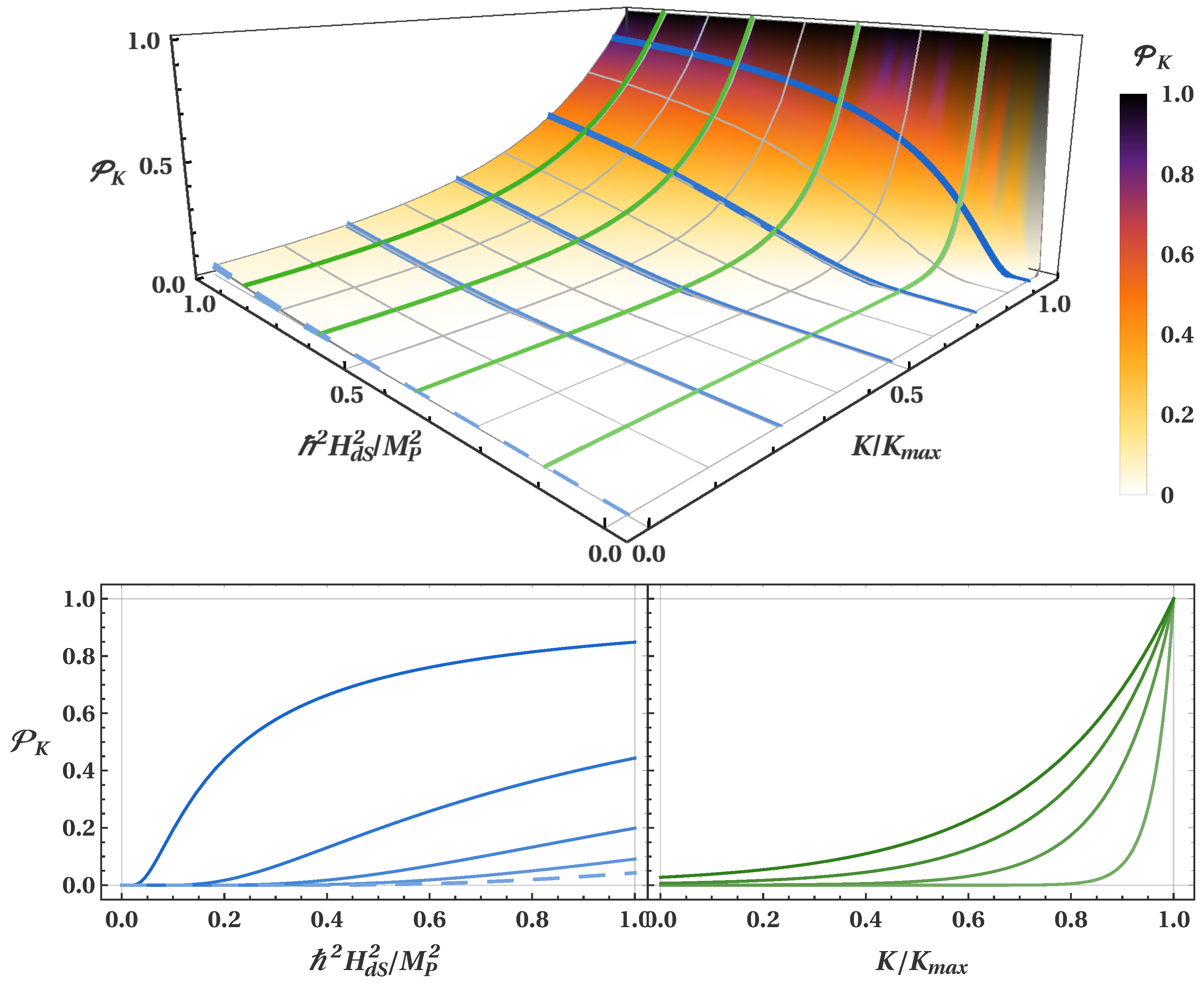
3. Tunnelling
4. Summary and Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| WDW | Wheeler–DeWitt |
References
- Everett, H. “Relative State” Formulation of Quantum Mechanics. Rev. Mod. Phys. 1957, 29, 454. [Google Scholar] [CrossRef]
- Linde, A.D. Chaotic Inflation. Phys. Lett. B 1983, 129, 177–181. [Google Scholar] [CrossRef]
- Linde, A.D. Eternally existing self-reproducing chaotic inflanationary universe. Phys. Lett. B 1986, 175, 395–400. [Google Scholar] [CrossRef]
- Susskind, L. The anthropic landscape of string theory. In Universe or Multiverse? Carr, B., Ed.; Cambridge University Press: Cambridge, UK, 2007; pp. 247–266. [Google Scholar]
- Khoury, J.; Ovrut, B.A.; Steinhardt, P.J.; Turok, N. The Ekpyrotic Universe: Colliding Branes and the Origin of the Hot Big Bang. Phys. Rev. D 2001, 64, 123522. [Google Scholar] [CrossRef]
- Steinhard, P.J.; Turok, N. Cosmic evolution in a cyclic universe. Phys. Rev. D 2002, 65, 126003. [Google Scholar] [CrossRef]
- Carr, B.J. Universe or Multiverse? Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Smolin, L. The Life of the Cosmos; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Tegmark, M. Parallel Universes. Sci. Am. 2003, 288, 40–51. [Google Scholar] [CrossRef] [PubMed]
- Freivogel, B.; Susskind, L. Framework for the string theory landscape. Phys. Rev. D 2004, 70, 126007. [Google Scholar] [CrossRef]
- Mersini-Houghton, L. Thoughts on Defining the Multiverse. arXiv, 2008; arXiv:0804.4280. [Google Scholar]
- Mersini-Houghton, L. Birth of the Universe from the Multiverse. arXiv, 2008; arXiv:0809.3623. [Google Scholar]
- Bouhmadi-López, M.; Vargas Moniz, P. Quantization of parameters and the string landscape problem. J. Cosmol. Astropart. Phys. 2007, 705, 5. [Google Scholar] [CrossRef]
- Robles-Pérez, S.; Martín-Moruno, P.; Rozas-Fernández, A.; González-Díaz, P.F. A dark energy multiverse. Class. Quantum Gravity 2007, 24, F41–F45. [Google Scholar] [CrossRef]
- Alonso-Serrano, A.; Bastos, C.; Bertolami, O.; Robles-Pérez, S. Interacting universes and the cosmological constant. Phys. Lett. B 2013, 719, 200–205. [Google Scholar] [CrossRef]
- Kiefer, C. Quantum Gravity, 3rd ed.; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Caderni, N.; Martellini, M. Third quantization formalism for Hamiltonian cosmologies. Int. J. Theor. Phys. 1984, 23, 233–249. [Google Scholar] [CrossRef]
- McGuigan, M. Third quantization and the Wheeler-DeWitt equation. Phys. Rev. D 1988, 38, 3031. [Google Scholar] [CrossRef]
- Strominger, A. Baby universes. In Quantum Cosmology and Baby Universes, Proceedings of the 7th Jerusalem Winter School for Theoretical Physics, Jerusalem, Israel, 27 December 1989–4 January 1990; Coleman, S., Hartle, J., Piran, T., Weinberg, S., River Edge, N.J., Eds.; World Scientific: Singapore, 1991. [Google Scholar]
- Robles-Pérez, S.; González-Díaz, P.F. Quantum state of the multiverse. Phys. Rev. D 2010, 81, 083529. [Google Scholar] [CrossRef]
- Coleman, S.R.; De Luccia, F. Gravitational effects on and of vacuum decay. Phys. Rev. D 1980, 21, 3305. [Google Scholar] [CrossRef]
- Bouhmadi-López, M.; Krämer, M.; Morais, J.; Robles-Pérez, S. What if? Exploring the multiverse through Euclidean wormholes. Eur. Phys. J. C 2017, 77, 718. [Google Scholar] [PubMed]
- Robles-Pérez, S.; González-Díaz, P.F. Quantum entanglement in the multiverse. J. Exp. Theor. Phys. 2014, 118, 34–53. [Google Scholar] [CrossRef]
- Vilenkin, A. Quantum Creation of Universes. Phys. Rev. D 1984, 30, 509. [Google Scholar] [CrossRef]
- Vilenkin, A. The quantum cosmology debate. AIP Conf. Proc. 1999, 478, 23. [Google Scholar]
- Linde, A.D. Particle physics and inflationary cosmology. arXiv, 2005; arXiv:hep-th/0503203v1. [Google Scholar]
- Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Arroja, F.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; et al. Planck 2015 results. XX. Constraints on inflation. Astron. Astrophys. 2016, 594, A20. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions, 9th ed.; National Bureau of Standards: Gaithersburg, MD, USA, 1970.
- Giddings, S.B.; Strominger, A. Axion Induced Topology Change in Quantum Gravity and String Theory. Nucl. Phys. B 1988, 306, 890–907. [Google Scholar] [CrossRef]
- Bartolo, N.; Caprini, C.; Domcke, V.; Figueroa, D.G.; Garcia-Bellido, J.; Guzzetti, M.C.; Liguori, M.; Matarrese, S.; Peloso, M.; Petiteau, A.; et al. Science with the space-based interferometer LISA. IV: Probing inflation with gravitational waves. J. Cosmol. Astropart. Phys. 2016, 1612, 26. [Google Scholar] [CrossRef]
- Bouhmadi-López, M.; Krämer, M.; Morais, J.; Robles-Pérez, S. Pre-inflation from the multiverse: Can it solve the quadrupole problem in the cosmic microwave background? arXiv, 2017; arXiv:1711.05138. [Google Scholar]
- Bouhmadi-López, M.; Chen, P.; Huang, Y.; Lin, Y. Slow-roll inflation preceded by a topological defect phase à la Chaplygin gas. Phys. Rev. D 2013, 87, 103513. [Google Scholar] [CrossRef]
| 1. | In the case of a massless scalar field with a cosmological constant, this decoupling is exact. In addition, the Starobinsky type of potentials, which have gained special attention since the results of the Planck mission [27], present a near constant plateau on which inflation can occur. In that case, as long as the field is far from the origin, we can consider, as a first approximation, that the value of the potential remains constant as the universe expands. |
| 2. | The third quantization is based in drawing parallels with quantum field theory. Therefore, the operators and in Equation (2) can be regarded as the annihilation and creation operators, respectively, of sub-universes with a give value of K. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bouhmadi-López, M.; Krämer, M.; Morais, J.; Robles-Pérez, S. The Third Quantization: To Tunnel or Not to Tunnel? Galaxies 2018, 6, 19. https://doi.org/10.3390/galaxies6010019
Bouhmadi-López M, Krämer M, Morais J, Robles-Pérez S. The Third Quantization: To Tunnel or Not to Tunnel? Galaxies. 2018; 6(1):19. https://doi.org/10.3390/galaxies6010019
Chicago/Turabian StyleBouhmadi-López, Mariam, Manuel Krämer, João Morais, and Salvador Robles-Pérez. 2018. "The Third Quantization: To Tunnel or Not to Tunnel?" Galaxies 6, no. 1: 19. https://doi.org/10.3390/galaxies6010019
APA StyleBouhmadi-López, M., Krämer, M., Morais, J., & Robles-Pérez, S. (2018). The Third Quantization: To Tunnel or Not to Tunnel? Galaxies, 6(1), 19. https://doi.org/10.3390/galaxies6010019




