Abstract
Within the framework of the third quantization, we consider the possibility that an initially recollapsing baby universe can enter a stage of near de Sitter inflation by tunnelling through a Euclidean wormhole that connects the recollapsing and inflationary geometries. We present the solutions for the evolution of the scale factor in the Lorentzian and Euclidean regions as well as the probability that the baby universe indeed crosses the wormhole when it reaches its maximum size.
1. Introduction
The idea that our Universe is not unique but instead resides in a collection of universes, dubbed the multiverse, has appeared several times in cosmology and within vastly different contexts, e.g., in Everett’s many worlds interpretation [1], in chaotic inflation [2,3], in the string theory landscape [4], in the ekpyrotic scenario [5,6], and many others [7,8,9,10,11,12,13,14,15]. While there is no unique precise interpretation of the term “multiverse” [9], a transversal idea is the possibility that different universes interact with each other via quantum effects. Such effects are of increased relevance in the context of the very early universe, when the energy density and curvature of the universe are expected to approach the Planck scale. Therefore, they could prove important in solving the question of the initial conditions of the universe and avoiding a Big-Bang-type of singularity [16].
As one of the many current proposals that attempt to provide a framework to study the dynamics of the multiverse, the third quantization scheme draws parallelisms with quantum field theory [17,18,19,20]. By quantizing the wave function of the spacetime and matter fields, which satisfies a possibly non-linear Wheeler–DeWitt equation, and defining creation and annihilation operators of individual universes with a particular spacetime–matter configuration, the third quantization treats the multiverse as a quantum system of particles (universes) with interactions (topology changes) [19,20]. At the semiclassical level, these interactions are often associated to the existence of Euclidean wormholes or instantons, which where first considered in the decay process of a false vacuum [21] (for further works on Euclidean wormholes and instantons in various contexts, please check the references cited in [22]). Although classically forbidden due to their Euclidean geometry, such solutions can nevertheless be traversed by means of quantum tunnelling effects and therefore connect remote patches of the universe, or in this case the multiverse.
In this work, we review how such a Euclidean wormhole appears in the third quantization treatment of a toy model of the multiverse filled by a minimally coupled massive scalar field and where homogeneity and isotropy is assumed for each sub-universe [20,22,23]. This wormhole solution connects two different Lorentzian regions, one corresponding to a small recollapsing baby universe and the other corresponding to a larger asymptotically de Sitter universe. Thus, the possibility arises for a baby universe to quantum tunnel through the wormhole and emerge as an inflating universe. We summarize the results of our recent paper [22], presenting the explicit solutions for the evolution of the scale factor in the two Lorentzian and the Euclidean regions as well as showing how the tunnelling probability varies with the inflationary scale and the momentum of the scalar field. To compute the tunnelling probability, we considered the tunnelling boundary conditions introduced by Vilenkin [24,25].
2. The Model
Let us consider a spatially closed Friedmann–Lemaître-Robertson–Walker universe containing a minimally coupled scalar field with a potential . For such a universe the Wheeler–DeWitt (WDW) equation reads [26]
where is the wave function of the spacetime and matter fields, a is the scale factor, , with G being the gravitational constant, and . Notice that the scalar field is made dimensionless by the rescaling . By identifying the scale factor a as an intrinsic time variable, which can be motivated from a semiclassical approximation, the WDW equation (1) can be regarded as an analogue to the Klein-Gordon wave equation in the minisuperspace [16] and in this picture the wave function assumes the role of the quantum field of spinless “particles”.
In the third quantization scheme, this analogy is taken one step further as the wave function of the spacetime and matter fields is elevated to an operator , which can be Fourier expanded as
where K is related to the momentum of the scalar field . By quantizing the wave function of the spacetime and matter fields as in (2), the third quantization draws parallels with the formalism of a quantum field theory (cf. Figure 1 of [20]) and the operators and can be interpreted as operators for the annihilation and creation, respectively, of universes (“particles”) with a definite value of K and amplitude . As such, the third quantization leads to a natural interpretation of the wave function of the spacetime and matter fields in terms of one-universe and multi-universe states which can be constructed by successive application of the operators and on the void [20]. Of course, in general the wave function does not have a definite value of the momentum of the scalar field since the multiverse is composed of a distribution of sub-universes with different values of K which in addition are coupled to each other. However, in the approximation that is constant, the different K modes decouple1 and each amplitude can be associated to a semiclassical solution of the WDW equation. For such a sub-universe, we can obtain an effective Friedmann equation at the semiclassical level by inserting the expansion (2) into the WDW equation (1), leading to:
Here, a dot indicates a derivative with respect to the classical cosmic time t and we assume that assumes a constant value throughout the evolution of the model. On the right hand side of Equation (3), the first term inside the brackets leads to an asymptotically de Sitter inflation for large a, the second term arises from the presence of spatial curvature and the third term is related to the momentum of the scalar field . As will become apparent below, the value of the ratio , which modulates the amplitude of this last term, will be critical in the evolution of the individual sub-universes for small values of the scale factor.
In order to obtain the time evolution of each sub-universe, we can rewrite the effective Friedmann Equation (3) as , where the values , and can be defined for as [23]
and satisfy . The dependency of the critical values , and on K is encoded in the phase . Based on the presence of two real and positive roots, and , for which , we can divide the spacetime described by the effective Friedmann Equation (3) into three separate regions:
- (i)
- For , we find a baby universe that expands from until the maximum value at which point, classically, it starts to collapse. During the expanding phase, the analytical solution , where is the conformal time defined by , was obtained for the first time in [22] and readsHere, is the Jacobi elliptic function [28], we have introduced the constants and and is the value of the conformal time when .
- (ii)
- For , we obtain an asymptotically de Sitter universe with a minimum allowed value for the scale factor. As in the previous case, a solution for was obtained in [22] in terms of Jacobi elliptic functions and [28]:where is the value of the conformal time when .
- (iii)
- For , we observe a Euclidean region with . While this region is classically forbidden, from a quantum-mechanical point of view it can be interpreted as a Euclidean wormhole that connects the regions of and . The evolution inside the wormhole, which can be obtained by applying a Wick rotation to the Euclidean conformal time , was derived in [22]:Here, is the value of the Euclidean conformal time when .
In Figure 1, we present the evolution of the scale factor in terms of and , as obtained in (7)–(9). The thick blue line indicates the evolution of a baby universe that traverses the wormhole instead of collapsing and then emerges as an inflating universe. The thin grey lines show the classical continuation of the evolution of the baby universe (into the future) and of the asymptotically de Sitter universe (into the past).
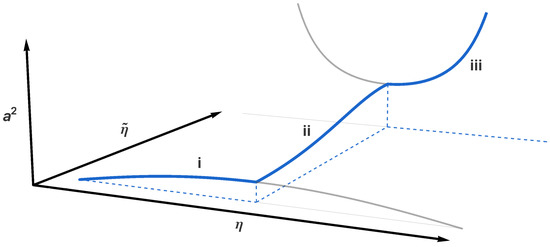
Figure 1.
The blue thick line represents the evolution of the squared scale factor for a baby universe (i) that once it reaches its maximum size traverses the Euclidean wormhole (ii) and emerges as an expanding universe (iii) that starts to inflate. The classical continuation of the evolution in the baby and inflating universes is shown as a thin grey line.
The solutions presented in (7) and (8) show how fundamentally different types of sub-universes such as small recollapsing baby universes and larger expanding inflationary universes can exist in the multiverse within the aforementioned framework of the third quantization. In addition, the existence of a Euclidean wormhole solution, described by (9), that connects these two types of universes leads to the possibility that a baby universe created in the multiverse with a momentum K avoids the collapsing phase altogether by quantum-mechanically traversing the wormhole and emerging as an expanding universe that evolves towards de Sitter inflation. This is similar to the tunnelling effect observed in the models of creation from nothing by Vilenkin [24] and of an axion-induced Giddings–Strominger instanton [29]. In fact, the effective Friedmann equation (3) and its solutions (7)–(9) can be seen as a generalization of the results obtained in those works.
3. Tunnelling
Once a baby universe reaches its maximum size , it can continue its classical evolution and start to collapse or it can enter the wormhole and eventually become an inflating universe, a process which is quantum-mechanical in nature. Following Vilenkin’s tunnelling conditions, the probability of this process to occur can be calculated as [24,25]:
This integral was solved in Ref. [22] and the results show that the tunnelling probability can be expressed as a linear combination of the complete elliptic integrals of the first, second and third kind [28], , , , respectively:
where the linear coefficients , and are defined as
and we have, and . Notice that the presence of the factor in the exponent means that the tunnelling probability is highly suppressed for realistic values of the scale of inflation, , which lie in the range [30]. However, we find that this suppression can be counterbalanced in the cases of baby universes with large values of K, as approaches unity when . This can be understood as a consequence of the narrowing of the Euclidean region as we consider values of K closer to the maximum allowed value , thus making it easier for the wormhole to be traversed. These effects are clearly visible in Figure 2, where we present a 3-dimensional plot of the tunnelling probability as a function of and , as well as different curves of obtained by fixing one of these variables. In a blue dashed line we present the tunnelling probability in the case of creation from nothing [24], which corresponds to the first line in Equation (11).
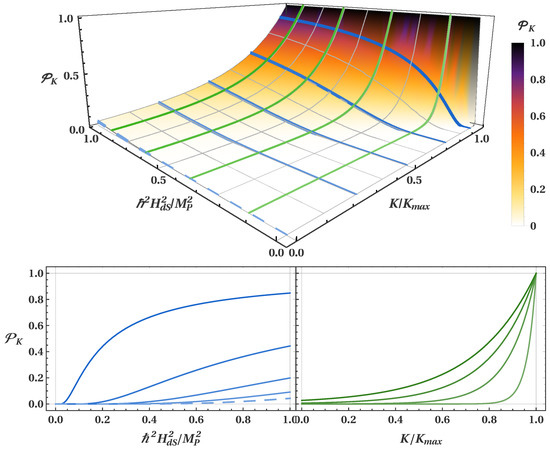
Figure 2.
The tunnelling probability plotted as a function of the ratio and the inflationary scale . In the two bottom panels we plot the tunnelling probability when (left panel, from bottom/darker to top/lighter) fixing ; and when (right panel, from bottom/darker to top/lighter) fixing . The tunnelling probability for the case of the creation of an expanding universe from nothing () is indicated by a dashed blue line.
4. Summary and Discussion
In this proceedings contribution, we presented our recent results regarding the existence of Euclidean wormholes in a multiverse scenario which can connect baby and inflating universes [22]. Using the third quantization scheme, a key feature in our framework2, we were able to describe the evolution of such a multiverse in terms of the creation and annihilation of individual universes, each of them identified by the number K related to the kinetic energy of the scalar field in that particular universe. By solving the effective Friedmann equation for each value of K we were able to find two classically disconnected solutions that correspond to small recollapsing baby universes and to larger expanding universes that evolve towards a de Sitter expansion and that are joined by an intermediate Euclidean wormhole solution. The existence of this wormhole allows for a baby universe to be transformed into a new expanding universe, leading to inflation in a new region of the multiverse. The solutions found can be seen as generalizations of the previous works by Vilenkin [24] and Giddings–Strominger [29]. In the former work only a (positive) cosmological constant is considered and therefore an inflating universe is created from nothing through tunnelling effects. In the latter, the existence of a wormhole solution that connects regions of spacetime with different topologies is supported by the presence of an axion which plays a similar role to the scalar field in the model analysed in this work.
The probability that a baby universe tunnels through the wormhole when it reaches its maximum size can be computed by using the Vilenkin tunnelling conditions [24,25]. In our model, this probability is in general highly suppressed due to the fact that the scale of inflation is several orders of magnitude below the Planck scale. Nevertheless, in universes where the scalar field has sufficient initial kinetic energy, the Euclidean region may become narrow enough for the tunnelling probability to be of order of unity. This is seen in Figure 2 where the tunnelling probability is extremely peaked around the maximum allowed value of . As a consequence, unless the creation of baby universes with large values of K is highly suppressed, the patches of the multiverse that undergo an inflationary phase should correspond to cases of .
Finally, we note that the presence of a term in the Friedmann equation with a -dependency suggests that these models could lead to a suppression of the primordial power spectrum on large scales by limiting the total number of e-folds of inflation. This possibility and its implications for the quadropole problem of the cosmic microwave background has been considered in our recent paper [31] (see also [32]). Of course, if the value of K is too high, the near-scale-invariance of the primordial power spectrum around the Planck pivot scale [27] is not recovered. Likewise, if the value of K is too small the effect of this pre-inflationary era would be washed away. Therefore, a comparison with available observational constraints on the primordial power spectrum could in principle be used to set upper limits on K.
Acknowledgments
This article is based upon work from COST Action CA15117 “Cosmology and Astrophysics Network for Theoretical Advances and Training Actions (CANTATA)”, supported by COST (European Cooperation in Science and Technology). The work of M.B.-L. is supported by the Basque Foundation of Science Ikerbasque. She and J.M. also wish to acknowledge the partial support from the Basque government Grant No. IT956-16 (Spain) and FONDOS FEDER under grant FIS2014-57956-P (Spanish government). The research of M.K. was financed by the Polish National Science Center Grant DEC-2012/06/A/ST2/00395 and by a grant for the Short Term Scientific Mission (STSM) “Multiverse impact onto the cosmic microwave background and its relation to modified gravity” (COST-STSM-CA15117-36137) awarded by the above-mentioned COST Action. M.K. and J.M. would like to thank the Centro de Matemática e Aplicações of the Universidade da Beira Interior in Covilhã, Portugal for kind hospitality while part of this work was done. M.K. also thanks M.P. Dąbrowski for fruitful discussions. J.M. is thankful to UPV/EHU for a PhD fellowship.
Author Contributions
All the authors contributed equally to this work.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| MDPI | Multidisciplinary Digital Publishing Institute |
| WDW | Wheeler–DeWitt |
References
- Everett, H. “Relative State” Formulation of Quantum Mechanics. Rev. Mod. Phys. 1957, 29, 454. [Google Scholar] [CrossRef]
- Linde, A.D. Chaotic Inflation. Phys. Lett. B 1983, 129, 177–181. [Google Scholar] [CrossRef]
- Linde, A.D. Eternally existing self-reproducing chaotic inflanationary universe. Phys. Lett. B 1986, 175, 395–400. [Google Scholar] [CrossRef]
- Susskind, L. The anthropic landscape of string theory. In Universe or Multiverse? Carr, B., Ed.; Cambridge University Press: Cambridge, UK, 2007; pp. 247–266. [Google Scholar]
- Khoury, J.; Ovrut, B.A.; Steinhardt, P.J.; Turok, N. The Ekpyrotic Universe: Colliding Branes and the Origin of the Hot Big Bang. Phys. Rev. D 2001, 64, 123522. [Google Scholar] [CrossRef]
- Steinhard, P.J.; Turok, N. Cosmic evolution in a cyclic universe. Phys. Rev. D 2002, 65, 126003. [Google Scholar] [CrossRef]
- Carr, B.J. Universe or Multiverse? Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Smolin, L. The Life of the Cosmos; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Tegmark, M. Parallel Universes. Sci. Am. 2003, 288, 40–51. [Google Scholar] [CrossRef] [PubMed]
- Freivogel, B.; Susskind, L. Framework for the string theory landscape. Phys. Rev. D 2004, 70, 126007. [Google Scholar] [CrossRef]
- Mersini-Houghton, L. Thoughts on Defining the Multiverse. arXiv, 2008; arXiv:0804.4280. [Google Scholar]
- Mersini-Houghton, L. Birth of the Universe from the Multiverse. arXiv, 2008; arXiv:0809.3623. [Google Scholar]
- Bouhmadi-López, M.; Vargas Moniz, P. Quantization of parameters and the string landscape problem. J. Cosmol. Astropart. Phys. 2007, 705, 5. [Google Scholar] [CrossRef]
- Robles-Pérez, S.; Martín-Moruno, P.; Rozas-Fernández, A.; González-Díaz, P.F. A dark energy multiverse. Class. Quantum Gravity 2007, 24, F41–F45. [Google Scholar] [CrossRef]
- Alonso-Serrano, A.; Bastos, C.; Bertolami, O.; Robles-Pérez, S. Interacting universes and the cosmological constant. Phys. Lett. B 2013, 719, 200–205. [Google Scholar] [CrossRef]
- Kiefer, C. Quantum Gravity, 3rd ed.; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Caderni, N.; Martellini, M. Third quantization formalism for Hamiltonian cosmologies. Int. J. Theor. Phys. 1984, 23, 233–249. [Google Scholar] [CrossRef]
- McGuigan, M. Third quantization and the Wheeler-DeWitt equation. Phys. Rev. D 1988, 38, 3031. [Google Scholar] [CrossRef]
- Strominger, A. Baby universes. In Quantum Cosmology and Baby Universes, Proceedings of the 7th Jerusalem Winter School for Theoretical Physics, Jerusalem, Israel, 27 December 1989–4 January 1990; Coleman, S., Hartle, J., Piran, T., Weinberg, S., River Edge, N.J., Eds.; World Scientific: Singapore, 1991. [Google Scholar]
- Robles-Pérez, S.; González-Díaz, P.F. Quantum state of the multiverse. Phys. Rev. D 2010, 81, 083529. [Google Scholar] [CrossRef]
- Coleman, S.R.; De Luccia, F. Gravitational effects on and of vacuum decay. Phys. Rev. D 1980, 21, 3305. [Google Scholar] [CrossRef]
- Bouhmadi-López, M.; Krämer, M.; Morais, J.; Robles-Pérez, S. What if? Exploring the multiverse through Euclidean wormholes. Eur. Phys. J. C 2017, 77, 718. [Google Scholar] [PubMed]
- Robles-Pérez, S.; González-Díaz, P.F. Quantum entanglement in the multiverse. J. Exp. Theor. Phys. 2014, 118, 34–53. [Google Scholar] [CrossRef]
- Vilenkin, A. Quantum Creation of Universes. Phys. Rev. D 1984, 30, 509. [Google Scholar] [CrossRef]
- Vilenkin, A. The quantum cosmology debate. AIP Conf. Proc. 1999, 478, 23. [Google Scholar]
- Linde, A.D. Particle physics and inflationary cosmology. arXiv, 2005; arXiv:hep-th/0503203v1. [Google Scholar]
- Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Arroja, F.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; et al. Planck 2015 results. XX. Constraints on inflation. Astron. Astrophys. 2016, 594, A20. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions, 9th ed.; National Bureau of Standards: Gaithersburg, MD, USA, 1970.
- Giddings, S.B.; Strominger, A. Axion Induced Topology Change in Quantum Gravity and String Theory. Nucl. Phys. B 1988, 306, 890–907. [Google Scholar] [CrossRef]
- Bartolo, N.; Caprini, C.; Domcke, V.; Figueroa, D.G.; Garcia-Bellido, J.; Guzzetti, M.C.; Liguori, M.; Matarrese, S.; Peloso, M.; Petiteau, A.; et al. Science with the space-based interferometer LISA. IV: Probing inflation with gravitational waves. J. Cosmol. Astropart. Phys. 2016, 1612, 26. [Google Scholar] [CrossRef]
- Bouhmadi-López, M.; Krämer, M.; Morais, J.; Robles-Pérez, S. Pre-inflation from the multiverse: Can it solve the quadrupole problem in the cosmic microwave background? arXiv, 2017; arXiv:1711.05138. [Google Scholar]
- Bouhmadi-López, M.; Chen, P.; Huang, Y.; Lin, Y. Slow-roll inflation preceded by a topological defect phase à la Chaplygin gas. Phys. Rev. D 2013, 87, 103513. [Google Scholar] [CrossRef]
| 1. | In the case of a massless scalar field with a cosmological constant, this decoupling is exact. In addition, the Starobinsky type of potentials, which have gained special attention since the results of the Planck mission [27], present a near constant plateau on which inflation can occur. In that case, as long as the field is far from the origin, we can consider, as a first approximation, that the value of the potential remains constant as the universe expands. |
| 2. | The third quantization is based in drawing parallels with quantum field theory. Therefore, the operators and in Equation (2) can be regarded as the annihilation and creation operators, respectively, of sub-universes with a give value of K. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).