Large Scale Cosmological Anomalies and Inhomogeneous Dark Energy
Abstract
:1. Introduction
- The Cosmic Microwave Background (CMB) Spectrum: The angular power spectrum of CMB primordial perturbations [2] is in good agreement with the predictions of ΛCDM. However, a few issues related to the orientation and magnitude of low multipole moments (CMB anomalies) constitute remaining puzzles for the standard model [3,4,5,6,7,8,9,10,11].
- Accelerating expansion: Cosmological observations using standard candles [Type Ia Supernovae (SnIa)] [14] and standard rulers (Baryon Acoustic Oscillations) [15] to map the recent accelerating expansion rate of the universe are consistent with the existence of a cosmological constant. No need has appeared for more complicated models based on dynamical dark energy or modified gravity, despite of the continuously improved data. The likelihood of the cosmological constant vs. more complicated homogeneous models has been continuously increasing during the past decade [16].
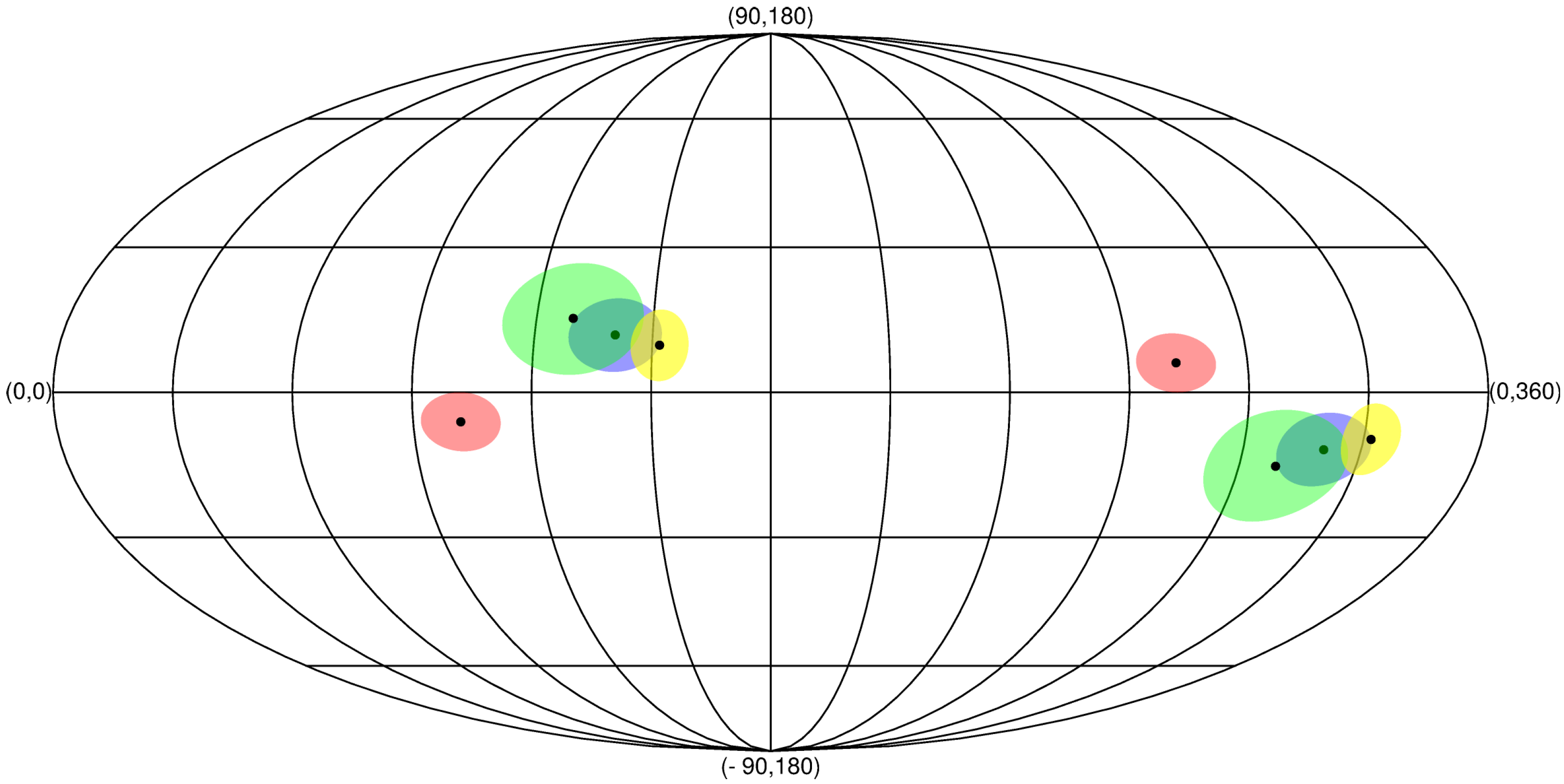
- Power Asymmetry of CMB perturbation maps: A hemispherical power asymmetry in the cosmic microwave background (CMB) on various different angular scales (multipole ranges) has been detected [22,23,24,25]. The power in all multipole ranges is consistently found to be significantly higher in the approximate direction towards Galactic longitude and latitude () than in the opposite direction. A more recent study of the WMAP9 data has found a hemispherical directional dependence of ΛCDM cosmological parameters which is maximized at the direction () at the multipole range 2–600 and is statistically significant at the σ level [26]. A related asymmetry, is the Maximum Temperature Asymmetry (MTA) defined as the maximized temperature difference between opposite pixels in the sky which shows significant alignment with other apparently unrelated asymmetries [27].
- Large Scale Velocity Flows: Recent studies have indicated the existence of dipole velocity flows on scales of 100 h Mpc [28,29] with magnitude about 400 km/s using a combination of peculiar velocity surveys, with direction towards , . Other studies [30] using the kinematic S-Z effect have found bulk flows on much larger scales (O(1 Gpc)) with magnitude 600–1000 km/s towards a similar direction. These results are inconsistent with the predictions of ΛCDM at a level of . These studies however have been challenged by other authors which do not confirm these results but find peculiar velocities on these scales consistent with ΛCDM [31]. Even though these studies agree with the direction of the observed flow they disagree on the magnitude and errorbar of the measured velocities.
- Alignment of low multipoles in the CMB angular power spectrum: The normals to the octopole and quadrupole planes are aligned with the direction of the cosmological dipole at a level inconsistent with Gaussian random, statistically isotropic skies at 99.7% [4]. This inconsistency has been reduced by the recent Planck results to a level of about 98% [22] (the exact level varies slightly depending on the foreground filtering method).
- Anisotropy in Accelerating Expansion Rate: Recent studies of the accelerating cosmic expansion rate using SnIa as standard candles have indicated that an anisotropic expansion rate fit by a dipole provides a better fit to the data than an isotropic expansion rate at the 2σ level [35] Interestingly, this dark energy dipole is abnormally aligned [35] with the fine structure constant dipole discussed below.
- Spatial dependence of the value of the fine structure constant α: A spatial cosmic variation of the fine structure constant has been recently identified on redshifts up to by analyzing the absorption spectra of quasars. This anisotropy analysis of the fine structure constant α [36,37] is based on a large sample of quasar absorption-line spectra (295 spectra) obtained using UVES (the Ultraviolet and Visual Echelle Spectrograph) on the VLT (Very Large Telescope) in Chile and also previous observations at the Keck Observatory in Hawaii. An apparent variation of α across the sky was found. It was shown to be well fit by an angular dipole model where θ is the angle with respect to a preferred axis and are the dipole magnitude and an isotropic monopole term. The dipole axis was found to point in the direction and the dipole amplitude A was found to be . The statistical significance over an isotropic model was found to be at the σ level.
- Large Quasar Group: An elongated structure of quasars with long dimension about 1240 Mpc and mean redshift has recently been discovered [38]. This structure is a factor of about three larger than the previously known largest structure (Sloan Great Wall ( and comoving size 450 Mpc [39]) and appears to be inconsistent with the cosmological principle in the context of the standard ΛCDM model in the sense that it is much larger than the scale of homogeneity in the context of ΛCDM (260–370 Mpc [40]).
- Dark matter perturbations on a few Gpc scale [51,52]. For example an off center observer in a 1 Gpc void would experience the existence of a preferred cosmological axis through the Lemaître-Tolman-Bondi metric [53,54,55,56,57]. Within this framework, an additional dark energy component is not needed to secure consistency with the cosmological data that indicate accelerating expansion. The basic idea is that the increased expansion rate occurs locally in space rather than at recent cosmological times, a fact that can be achieved by assuming a locally-reduced matter energy density [58,59]. Thus, the observer is placed close to the center of a giant void with dimensions of a few Gpc [60]. Even though this approach is free of dark energy, it is by no means free of fine tuning. Apart from the unnatural assumption of giant-size Gpc voids, which are very unlikely to be produced in any cosmology, these models require the observer to be placed within a very small volume at the center of the void (about of the total volume of the void). A slightly off-center observer, however, will naturally experience a preferred cosmological direction (towards the center of the void), which may help to resolve some of the observational puzzles of ΛCDM discussed above.Such matter perturbations could be induced by statistically anisotropic or non-gaussian primordial perturbations [61,62,63,64]. For example, inflationary perturbations induced by vector fields [65,66,67,68]. Note however that inflationary models with vector fields usually suffer from instabilities due to the existence of ghosts [69,70,71].
- Dark energy perturbations on scales comparable to the horizon. Even though the sound speed for dark energy is close to unity implying that it can not cluster on scales much smaller than the horizon, it can still produce observable effects due to clustering on horizon scales [77,78]. In addition the possible recent formation of topological defects with Hubble scale core (topological quintessence) could also behave as inhomogeneous dark energy [79].
- There is no simple physical mechanism to generate such large voids [84].
- The fit for the expansion rate as a function of redshift is worse than ΛCDM requires significant fine tuning of the void profile to obtain a comparable fit with ΛCDM [86].
- These models predict significant peculiar velocities for distant galaxies within the void. Such velocities could have been detected in CMB maps through the kinematic S-Z effects. The fact that such large radial velocities are not observed imposes the most severe class of constraints in this class of models [82].
- It is a new generic generalization of ΛCDM including ΛCDM as a special case.
- It naturally violates the cosmological principle on large cosmic scales and predicts a preferred axis for off center observers. Thus it has the potential to address at least some of the above discussed cosmic anomalies.
- There is a well defined physical mechanism that can give rise to this type on dark energy inhomogeneities. This mechanism will be discussed in some detail in Section 3. It is based on applying the principles of topological inflation [87] to the case of late-time acceleration. According to the idea of topological inflation, the false vacuum energy of the core of a topological defect can give rise to accelerating expansion if the core size reaches the Hubble scale when gravity starts dominating the dynamics. Thus, for example, a recently formed global monopole with appropriate scale of symmetry breaking and coupling could naturally produce a Hubble-scale, spherically symmetric, isocurvature dark energy overdensity. By analogy with topological inflation, this mechanism may be called topological quintessence.
2. A Review of Cosmic Anomalies
2.1. Power Asymmetry of CMB Perturbation Maps
- A large part (if not all) of the asymmetry appears to be due to the ISW effect which occurs at late times and is not related to the primordial nature of the CMB perturbations [94].
- The power spectrum of large scale structure does not show evidence for such an dipole asymmetry on smaller scales. This also hints towards a possible late time origin of the asymmetry.
2.2. Alignment of Low Multipoles in the CMB Angular Power Spectrum
2.3. Large Scale Velocity Flows
2.4. Large Scale Alignment in the QSO Optical Polarization Data
2.5. Anisotropy in Accelerating Expansion Rate (Dark Energy Dipole)
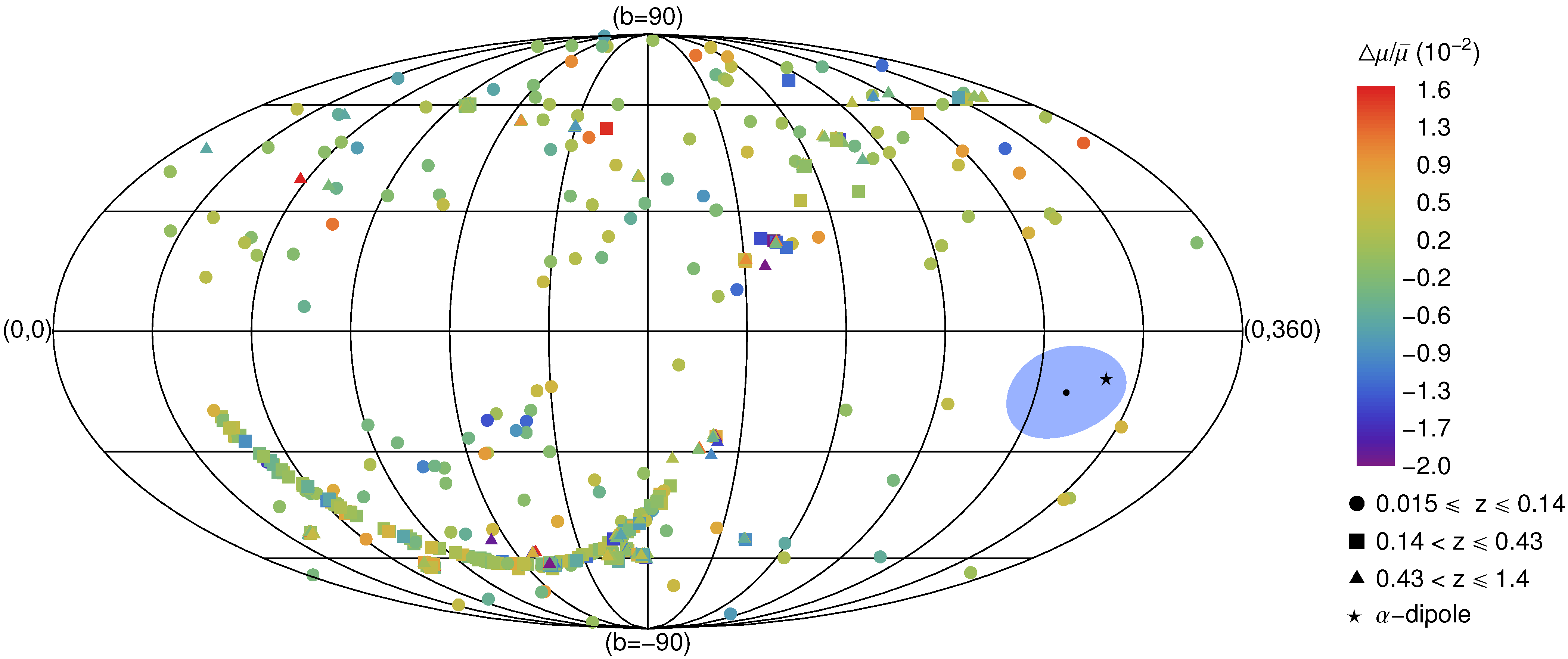
2.6. Anisotropy in the Values of the Fine Structure Constant α (α Dipole)
2.7. Large Quasar Groups
3. Anisotropic/Inhomogeneous Dark Energy Models
- Deviate from ΛCDM mainly on large cosmological scales.
- Reduce to ΛCDM for certain values of its parameters.
3.1. Anisotropic Dark Energy Models
3.2. Inhomogeneous Dark Energy Models
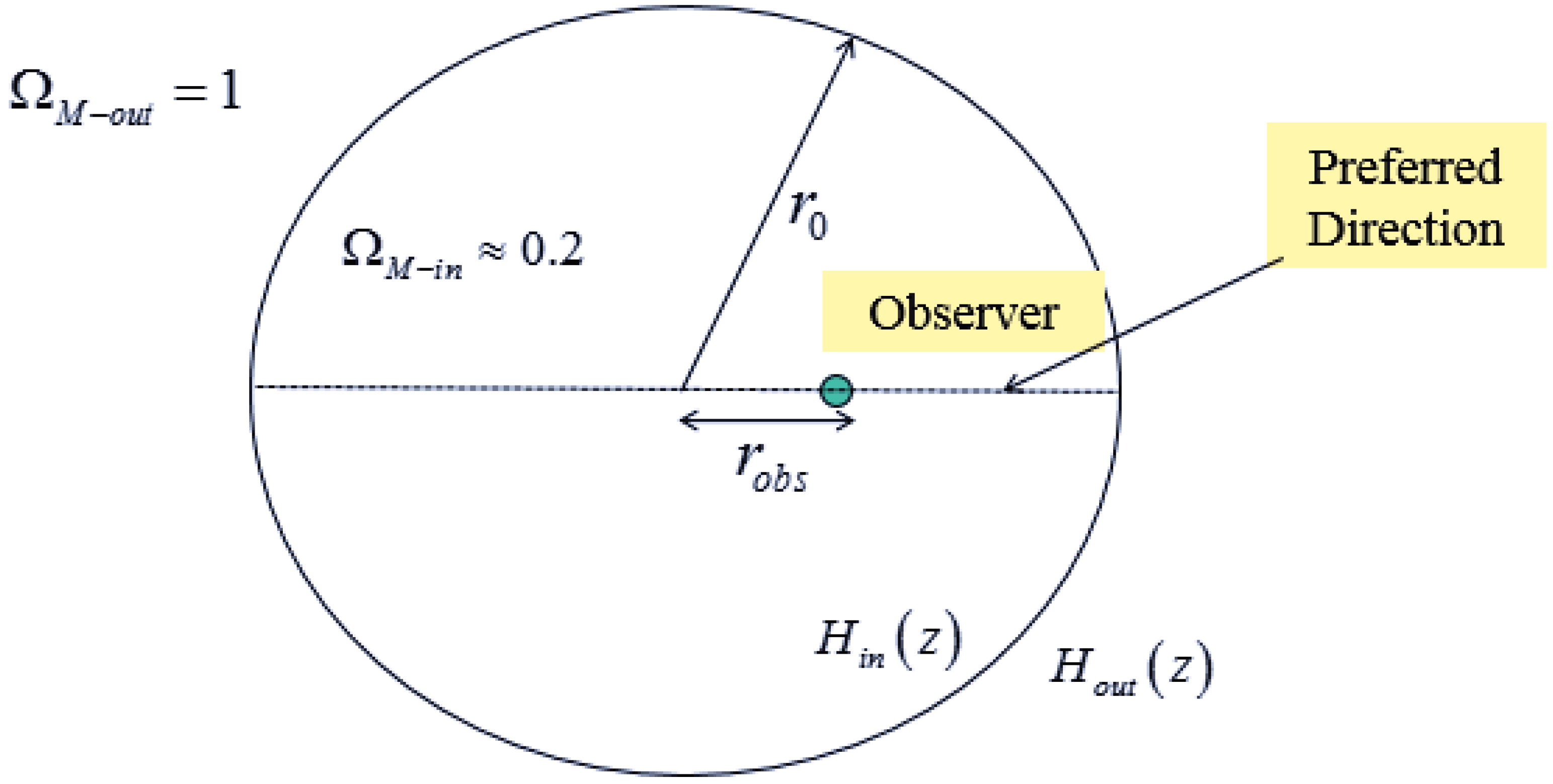
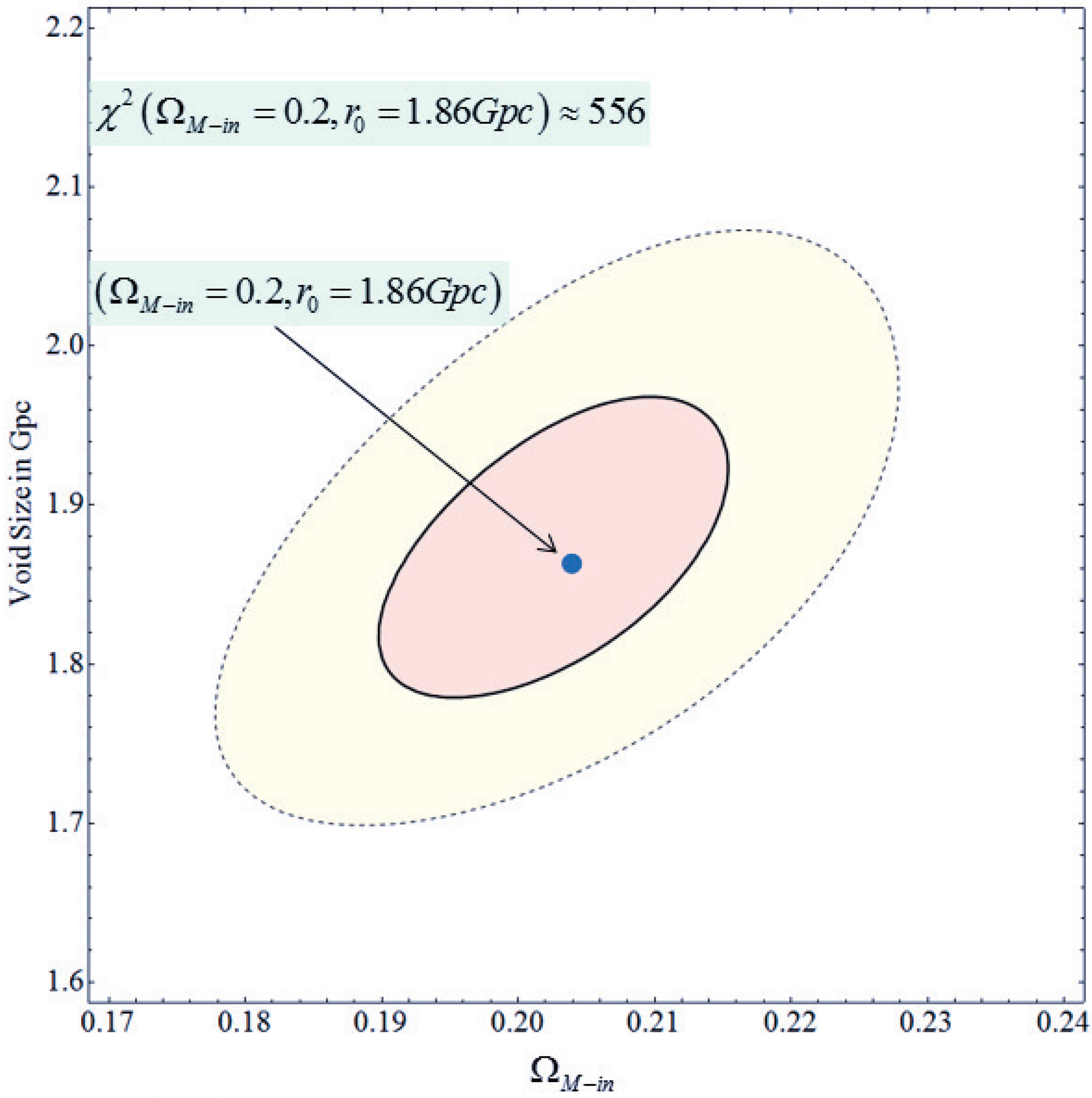
- They can naturally provide a preferred axis by utilizing a slight displacement of the observer from the center of the spherical void.
- The coincidence problem is not present since a void can naturally develop at late times along with other structures.
- In the context of standard cosmology there is no simple mechanism to create Gpc matter voids without conflicting other cosmological data (e.g., CMB fluctuations).
- There is no simple matter density profile that will provide an equal or better quality of fit compared to ΛCDM [86].
- This class of models generically predicts large peculiar velocities of free electrons and clusters with respect to the CMB. These velocities could have been detected via inverse Compton scattering of CMB photons onto moving free electrons (kinematic Synyaev-Zeldovich effect). The existing bounds on such velocities effectively rules out this class of models [82,83].
- The standard cosmological model ΛCDM assumes the existence of homogeneous matter on large scales, the validity of general relativity and the existence of homogeneous dark energy with constant in time energy density (cosmological constant). The generalization of most of these assumptions has been extensively studied in the literature. The main motivation for such generalizations originates at the coincidence problem expressed as a “Why now?” problem: “Why was the energy scale of the cosmological constant tuned to such low values so that it starts dominating at the present time?”. For example general relativity has been generalized to various models of modified gravity, dark energy was allowed to evolve in time as a scalar field (quintessence), matter was allowed to be inhomogeneous on Gpc scales (void models). The least studied generalization is the one based on allowing dark energy to become inhomogeneous on Gpc scales. Such a generalization could in principle address the coincidence problem if the later is expressed as a “Why here?” problem: “Why is the dark energy density in our horizon such that the universe has recently started its accelerating expansion?”. In the same manner that the answer to the “Why now?” question could be time dependence, the answer to the “Why here?” question could be spatial dependence of dark energy density. Therefore, the consideration of inhomogeneous dark energy constitutes a generic generalization of the standard ΛCDM models which reduces back to ΛCDM for a inhomogeneity scale that exceeds the current horizon scale. It is therefore interesting to use cosmological observations to impose constraints on the two basic parameters of this class of models: the scale of the inhomogeneity and the magnitude of the dark energy density inhomogeneity.
- As in the case of the dark matter void, an off-center observer in a spherically symmetric dark energy inhomogeneity will naturally experience an anisotropy in the accelerating expansion rate. In the case of inhomogeneous dark energy the scale of the inhomogeneity is allowed to be as large as the horizon scale (ΛCDM limit). For large enough inhomogeneity scale, the observer is allowed to be displaced significantly from the center without experiencing a large CMB dipole. Thus, inhomogeneous dark energy models are less subject to fine tuning with respect to the location of the observer [86].
- Due to negative pressure and speed of sound close to unity, dark energy inhomogeneities are not easy to sustain. However, there is a well defined physical mechanism (topological quintessence [79]) that can lead to sustainable large scale dark energy inhomogeneities, supported by topological considerations. This mechanism can be viewed as a generalization of topological inflation [87] in which early time accelerating expansion (inflation) takes place in the core of a topological defect due to the topologically trapped vacuum energy.
3.3. Topological Quintessence
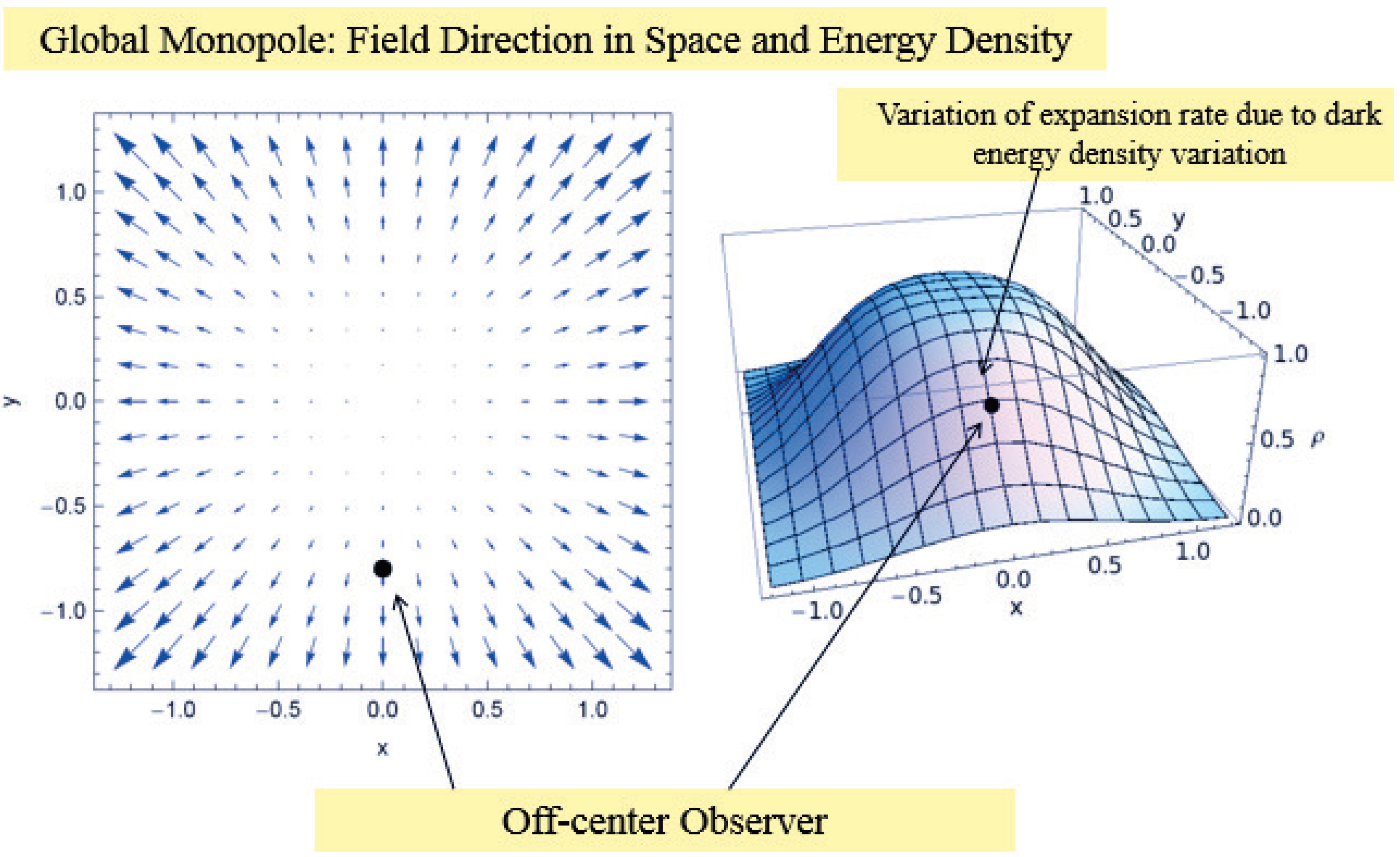
- Does the monopole energy density eventually dominate over matter in the monopole core?
- Does the possible monopole domination eventually lead to accelerating expansion in the monopole core?
- Can this cosmological expansion in the core fit the cosmological data?


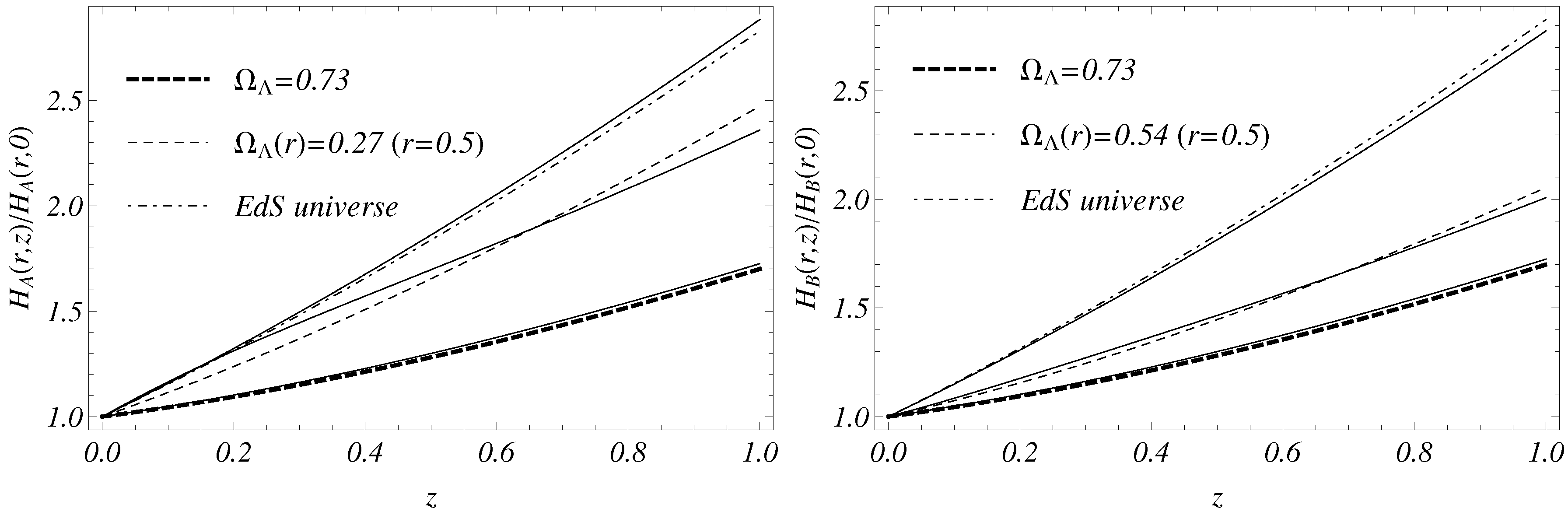
3.4. Spherical Dark Energy Overdensity



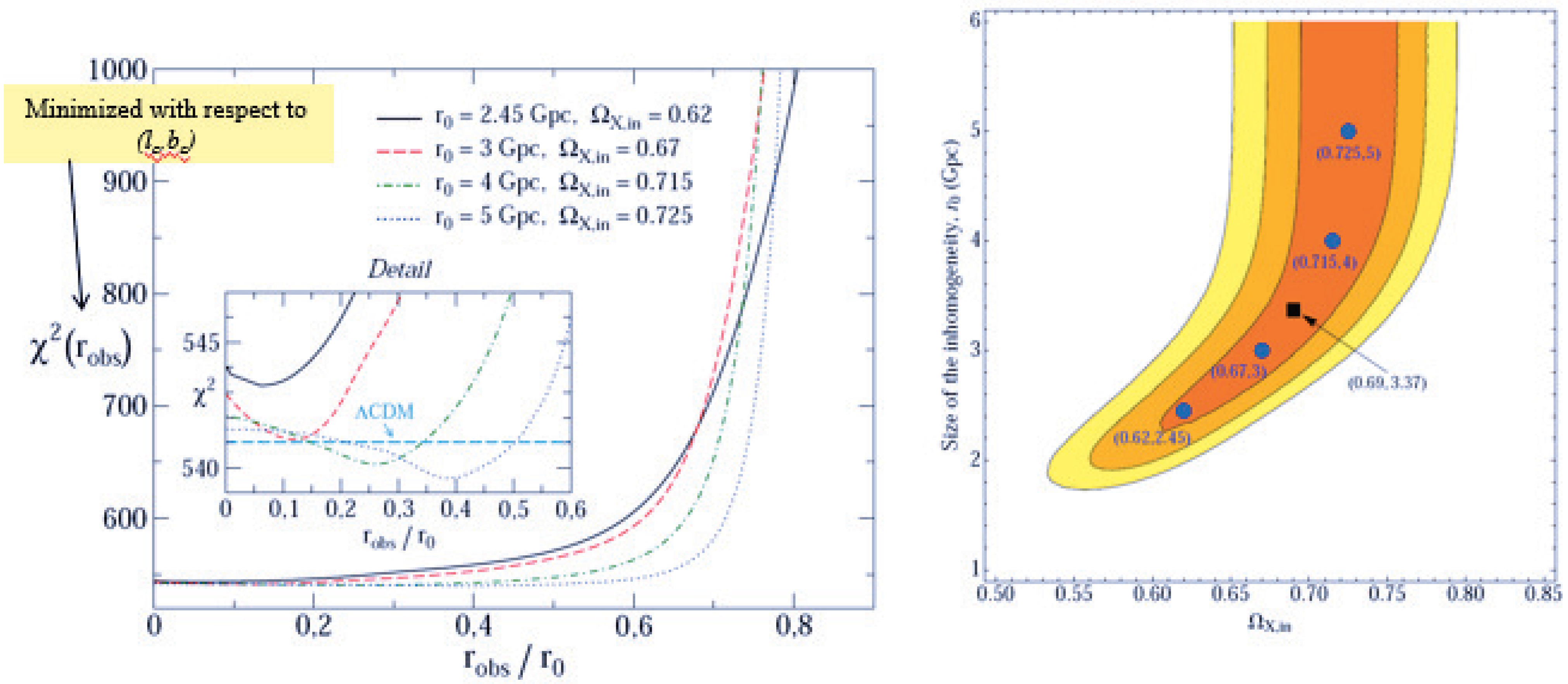
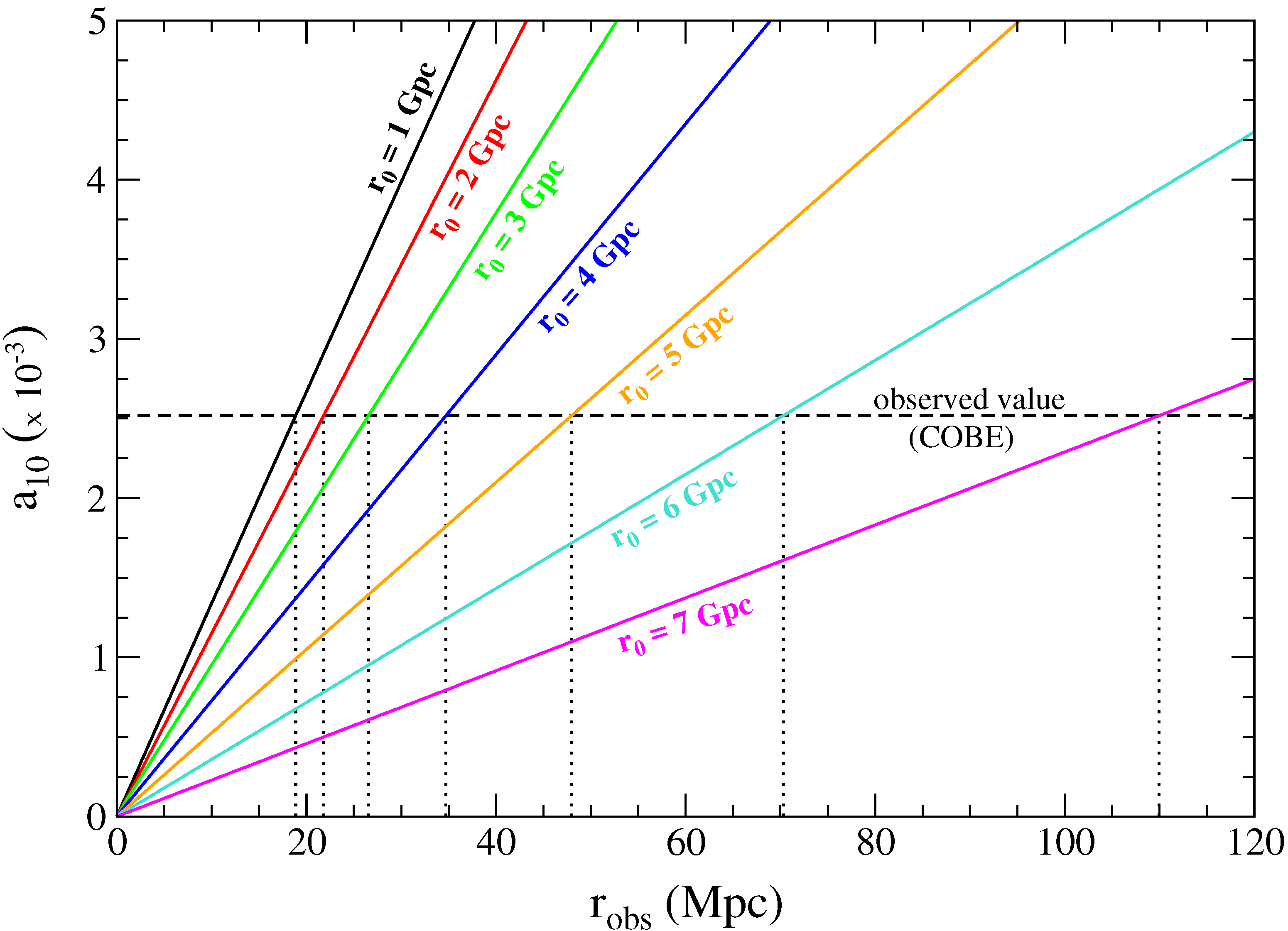
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Hamilton, J.-C. What have we learned from observational cosmology? ArXiv E-Prints 2013. arXiv:1304.4446. [Google Scholar]
- Komatsu, E.; Smith, K.M.; Dunkley, J.; Bennett, C.L.; Gold, B.; Hinshaw, G.; Jarosik, N.; Larson, D.; Nolta, M.R.; Page, L.; et al. Seven-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: Cosmological interpretation. Astrophys. J. 2011, 192. [Google Scholar] [CrossRef]
- Tegmark, M.; de Oliveira-Costa, A.; Hamilton, A. A high resolution foreground cleaned CMB map from WMAP. Phys. Rev. D 2003, 68, 123523. [Google Scholar] [CrossRef]
- Copi, C.J.; Huterer, D.; Schwarz, D.J.; Starkman, G.D. Large angle anomalies in the CMB. Adv. Astron. 2010, 2010, 847541. [Google Scholar] [CrossRef]
- Bennett, C.L.; Hill, R.S.; Hinshaw, G.; Larson, D.; Smith, K.M.; Dunkley, J.; Gold, B.; Halpern, M.; Jarosik, N.; Kogut, A.; et al. Seven-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: Are there cosmic microwave background anomalies? Astrophys. J. 2011, 192. [Google Scholar] [CrossRef]
- Schwarz, D.J.; Starkman, G.D.; Huterer, D.; Copi, C.J. Is the low-l microwave background cosmic? Phys. Rev. Lett. 2004, 93, 221301. [Google Scholar] [CrossRef] [PubMed]
- Land, K.; Magueijo, J. The axis of evil. Phys. Rev. Lett. 2005, 95, 071301. [Google Scholar] [CrossRef] [PubMed]
- Gruppuso, A.; Gorski, K.M. Large scale directional anomalies in the WMAP 5yr ILC map. J. Cosmol. Astropart. Phys. 2010, 2010, 019. [Google Scholar] [CrossRef]
- Sarkar, D.; Huterer, D.; Copi, C.J.; Starkman, G.D.; Schwarz, D.J. Missing power vs. low-l alignments in the cosmic microwave background: No correlation in the standard cosmological model. ArXiv E-Prints 2010. arXiv:1004.3784. [Google Scholar]
- Hanson, D.; Lewis, A. Estimators for CMB statistical anisotropy. Phys. Rev. D. 2009, 80, 063004. [Google Scholar] [CrossRef]
- Copi, C.J.; Huterer, D.; Schwarz, D.J.; Starkman, G.D. The uncorrelated universe: Statistical anisotropy and the vanishing angular correlation function in WMAP years 1–3. Phys. Rev. D 2007, 75, 023507. [Google Scholar] [CrossRef]
- Smith, K.M.; Senatore, L.; Zaldarriaga, M. Optimal limits on from WMAP 5-year data. J. Cosmol. Astropart. Phys. 2009, 2009, 006. [Google Scholar] [CrossRef] [PubMed]
- Ade, P.A.R.; Aghanim, N.; Armitage-Caplan, C.; Arnaud, M.; Ashdown, M.; Atrio-Barandela, F.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; et al. Planck 2013 results. I. Overview of products and scientific results. ArXiv E-Prints 2013. arXiv:1303.5062. [Google Scholar]
- Amanullah, R.; Lidman, C.; Rubin, D.; Aldering, G.; Astier, P.; Barbary, K.; Burns, M.S.; Conley, A.; Dawson, K.S.; Deustua, S.E.; et al. Spectra and light curves of six type Ia supernovae at 0.511 < z < 1.12 and the Union2 compilation. Astrophys. J. 2010, 716, 712. [Google Scholar] [CrossRef]
- Percival, W.J.; Cole, S.; Eisenstein, D.J.; Nichol, R.C.; Peacock, J.A.; Pope, A.C.; Szalay, A.S. Measuring the Baryon Acoustic Oscillation scale using the SDSS and 2dFGRS. Mon. Not. R. Astron. Soc. 2007, 381, 1053–1066. [Google Scholar] [CrossRef]
- Bueno Sanchez, J.C.; Nesseris, S.; Perivolaropoulos, L. Comparison of recent SnIa datasets. J. Cosmol. Astropart. Phys. 2009, 2009, 029. [Google Scholar] [CrossRef]
- Nesseris, S.; Perivolaropoulos, L. Testing ΛCDM with the growth function δ(a): Current constraints. Phys. Rev. D 2008, 77, 023504. [Google Scholar] [CrossRef]
- Trujillo-Gomez, S.; Klypin, A.; Primack, J.; Romanowsky, A.J. LCDM correctly predicts basic statistics of galaxies: Luminosity-velocity relation, baryonic mass-velocity relation, and velocity function. ArXiv E-Prints 2011. arXiv:1005.1289. [Google Scholar]
- Reid, B.A.; Percival, W.J.; Eisenstein, D.J.; Verde, L.; Spergel, D.N.; Skibba, R.A.; Bahcall, N.A.; Budavari, T.; Fukugita, M.; Richard Gott, J.; et al. Cosmological constraints from the clustering of the sloan digital sky survey DR7 luminous red galaxies. Mon. Not. R. Astron. Soc. 2010, 404, 60–85. [Google Scholar] [CrossRef]
- Perivolaropoulos, L. Six puzzles for LCDM cosmology. ArXiv E-Prints 2008. arXiv:0811.4684. [Google Scholar]
- Yang, R.-J.; Zhang, S.N. The age problem in ΛCDM model. Mon. Not. R. Astron. Soc. 2010, 407, 1835–1841. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, N.; Armitage-Caplan, C.; Arnaud, M.; Ashdown, M.; Atrio-Barandela, F.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; et al. Planck 2013 results. XXIII. Isotropy and Statistics of the CMB. ArXiv E-Prints 2013. arXiv:1303.5083. [Google Scholar]
- Eriksen, H.K.; Banday, A.J.; Gorski, K.M.; Hansen, F.K.; Lilje, P.B. Hemispherical power asymmetry in the third-year Wilkinson Microwave Anisotropy Probe sky maps. Astrophys. J. 2007, 660, L81. [Google Scholar] [CrossRef]
- Paci, F.; Gruppuso, A.; Finelli, F.; Cabella, P.; de Rosa, A.; Mandolesi, N.; Natoli, P. Power asymmetries in the cosmic microwave background temperature and polarization patterns. Mon. Not. R. Astron. Soc. 2010, 407, 399–404. [Google Scholar] [CrossRef]
- Hoftuft, J.; Eriksen, H.K.; Banday, A.J.; Gorski, K.M.; Hansen, F.K.; Lilje, P.B. Increasing evidence for hemispherical power asymmetry in the five-year WMAP data. Astrophys. J. 2009, 699, 985. [Google Scholar] [CrossRef]
- Axelsson, M.; Fantaye, Y.; Hansen, F.K.; Banday, A.J.; Eriksen, H.K.; Gorski, K.M. Directional dependence of ΛCDM cosmological parameters. Astrophys. J. 2013, 773, L3. [Google Scholar] [CrossRef]
- Mariano, A.; Perivolaropoulos, L. CMB maximum temperature asymmetry axis: Alignment with other cosmic asymmetries. Phys. Rev. D 2013, 87, 043511. [Google Scholar] [CrossRef]
- Watkins, R.; Feldman, H.A.; Hudson, M.J. Consistently large cosmic flows on scales of 100 Mpc/h: A challenge for the standard LCDM cosmology. Mon. Not. R. Astron. Soc. 2009, 392, 743–756. [Google Scholar] [CrossRef]
- Feldman, H.A.; Watkins, R.; Hudson, M.J. Cosmic flows on 100 Mpc/h scales: Standardized minimum variance bulk flow, shear and octupole moments. Mon. Not. R. Astron. Soc. 2010, 407, 2328–2338. [Google Scholar] [CrossRef]
- Kashlinsky, A.; Atrio-Barandela, F.; Kocevski, D.; Ebeling, H. A measurement of large-scale peculiar velocities of clusters of galaxies: Results and cosmological implications. Astrophys. J. 2008, 686, L49. [Google Scholar] [CrossRef]
- Lavaux, G.; Tully, R.B.; Mohayaee, R.; Colombi, S. Cosmic flow from 2MASS redshift survey: The origin of CMB dipole and implications for LCDM cosmology. Astrophys. J. 2010, 709, 483. [Google Scholar] [CrossRef]
- Hutsemekers, D.; Lamy, H. The polarization properties of broad absorption line QSOs: Observational results. ArXiv E-Prints 2001. arXiv:astro-ph/0109528. [Google Scholar]
- Hutsemekers, D.; Cabanac, R.; Lamy, H.; Sluse, D. Mapping extreme-scale alignments of quasar polarization vectors. Astron. Astrophys. 2005, 441, 915. [Google Scholar] [CrossRef]
- Hutsemekers, D.; Payez, A.; Cabanac, R.; Lamy, H.; Sluse, D.; Borguet, B.; Cudell, J.R. Large-scale alignments of quasar polarization vectors: Evidence at cosmological scales for very light pseudoscalar particles mixing with photons? ArXiv E-Prints 2008. arXiv:0809.3088. [Google Scholar]
- Mariano, A.; Perivolaropoulos, L. Is there correlation between fine structure and dark energy cosmic dipoles? Phys. Rev. D 2012, 86, 083517. [Google Scholar] [CrossRef]
- Webb, J.K.; King, J.A.; Murphy, M.T.; Flambaum, V.V.; Carswell, R.F.; Bainbridge, M.B. Indications of a spatial variation of the fine structure constant. Phys. Rev. Lett. 2011, 107, 191101. [Google Scholar] [CrossRef] [PubMed]
- King, J.A.; Webb, J.K.; Murphy, M.T.; Flambaum, V.V.; Carswell, R.F.; Bainbridge, M.B.; Wilczynska, M.R.; Koch, F.E. Spatial variation in the fine-structure constant—New results from VLT/UVES. Mon. Not. R. Astron. Soc. 2012, 422, 3370–3414. [Google Scholar] [CrossRef]
- Clowes, R.G.; Harris, K.A.; Raghunathan, S.; Campusano, L.E.; Soechting, I.K.; Graham, M.J. A structure in the early universe at z ∼ 1.3 that exceeds the homogeneity scale of the R-W concordance cosmology. ArXiv E-Prints 2012. arXiv:1211.6256. [Google Scholar]
- Gott, J.R., III; Juric, M.; Schlegel, D.; Hoyle, F.; Vogeley, M.; Tegmark, M.; Bahcall, N.; Brinkmann, J. A map of the universe. Astrophys. J. 2005, 624, 463. [Google Scholar] [CrossRef]
- Yadav, J.K.; Bagla, J.S.; Khandai, N. Fractal dimension as a measure of the scale of homogeneity. Mon. Not. R. Astron. Soc. 2010, 405, 2009–2015. [Google Scholar] [CrossRef]
- Luminet, J.-P. The shape and topology of the universe. ArXiv E-Prints 2008. arXiv:0802.2236. [Google Scholar]
- Bielewicz, P.; Riazuelo, A. The study of topology of the universe using multipole vectors. ArXiv E-Prints 2009. arXiv:0804.2437. [Google Scholar]
- Carneiro, S.; Mena Marugan, G.A. Anisotropic cosmologies containing isotropic background radiation. Phys. Rev. D 2001, 64, 083502. [Google Scholar] [CrossRef]
- Akofor, E.; Balachandran, A.P.; Jo, S.G.; Joseph, A.; Qureshi, B.A. Direction-dependent CMB power spectrum and statistical anisotropy from noncommutative geometry. J. High Energy Phys. 2008, 2008, 092. [Google Scholar] [CrossRef]
- Koivisto, T.S.; Mota, D.F.; Quartin, M.; Zlosnik, T.G. On the possibility of anisotropic curvature in cosmology. Phys. Rev. D 2011, 83, 023509. [Google Scholar] [CrossRef]
- Zumalacarregui, M.; Koivisto, T.S.; Mota, D.F.; Ruiz-Lapuente, P. Disformalscalar fields and the dark sector of the universe. J. Cosmol. Astropart. Phys. 2010, 2010, 038. [Google Scholar] [CrossRef]
- Koivisto, T.; Mota, D.F. Dark energy anisotropic stress and large scale structure formation. Phys. Rev. D 2006, 73, 083502. [Google Scholar] [CrossRef]
- Battye, R.; Moss, A. Anisotropic dark energy and CMB anomalies. Phys. Rev. D 2009, 80, 023531. [Google Scholar] [CrossRef]
- Armendariz-Picon, C. Could dark energy be vector-like? J. Cosmol. Astropart. Phys. 2004, 2004, 007. [Google Scholar] [CrossRef]
- Esposito-Farese, G.; Pitrou, C.; Uzan, J.-P. Vector theories in cosmology. Phys. Rev. D 2010, 81, 063519. [Google Scholar] [CrossRef]
- Rodrigues, D.C. Anisotropic cosmological constant and the CMB quadrupole anomaly. Phys. Rev. D 2008, 77, 023534. [Google Scholar] [CrossRef]
- Jimenez, J.B.; Maroto, A.L. Large-scale cosmic flows and moving dark energy model for anisotropization. J. Cosmol. Astropart. Phys. 2009, 2009, 015. [Google Scholar] [CrossRef]
- Alexander, S.; Biswas, T.; Notari, A.; Vaid, D. Local void vs. dark energy: Confrontation with wmap and type Ia supernovae. J. Cosmol. Astropart. Phys. 2009, 2009, 025. [Google Scholar] [CrossRef]
- Garcia-Bellido, J.; Haugboelle, T. Confronting Lemaître-Tolman-Bondi models with observational cosmology. J. Cosmol. Astropart. Phys. 2008, 2008, 003. [Google Scholar] [CrossRef]
- Biswas, T.; Notari, A.; Valkenburg, W. Testing the void against cosmological data: Fitting CMB, BAO, SN and H0. J. Cosmol. Astropart. Phys. 2010, 2010, 030. [Google Scholar] [CrossRef]
- Dunsby, P.; Goheer, N.; Osano, B.; Uzan, J.P. How close can an inhomogeneous universe mimic the concordance model? J. Cosmol. Astropart. Phys. 2010, 2010, 017. [Google Scholar] [CrossRef]
- Garfinkle, D. The motion of galaxy clusters in inhomogeneous cosmologies. Class. Quantum Gravity 2010, 27, 065002. [Google Scholar] [CrossRef]
- Krasinski, A. Inhomogeneous Cosmological Models; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Bolejko, K.; Celerier, M.-N.; Krasinski, A. Inhomogeneous cosmological models: Exact solutions and their applications. Class. Quantum Gravity 2011, 28, 164002. [Google Scholar] [CrossRef]
- Alnes, H.; Amarzguioui, M.; Gron, O. An inhomogeneous alternative to dark energy? Phys. Rev. D 2006, 73, 083519. [Google Scholar] [CrossRef]
- Armendariz-Picon, C. Creating statistically anisotropic and inhomogeneous perturbations. J. Cosmol. Astropart. Phys. 2007, 2007, 014. [Google Scholar] [CrossRef]
- Pullen, A.R.; Kamionkowski, M. Cosmic microwave background statistics for a direction-dependent primordial power spectrum. Phys. Rev. D 2007, 76, 103529. [Google Scholar] [CrossRef]
- Ackerman, L.; Carroll, S.M.; Wise, M.B. Imprints of aprimordial preferred direction on the microwave background. Phys. Rev. D 2007, 75, 083502. [Google Scholar] [CrossRef]
- Valenzuela-Toledo, C.A. Non-gaussianity and statistical anisotropy in cosmological inflationary models. ArXiv E-Prints 2010. arXiv:1004.5363. [Google Scholar]
- Dimopoulos, K.; Karciauskas, M.; Lyth, D.H.; Rodriguez, Y. Statistical anisotropy of the curvature perturbation from vector field perturbations. J. Cosmol. Astropart. Phys. 2009, 2009, 013. [Google Scholar] [CrossRef]
- Yokoyama, S.; Soda, J. Primordial statistical anisotropy generated at the end of inflation. J. Cosmol. Astropart. Phys. 2008, 2008, 005. [Google Scholar] [CrossRef]
- Golovnev, A.; Vanchurin, V. Cosmological perturbations from vector inflation. Phys. Rev. D 2009, 79, 103524. [Google Scholar] [CrossRef]
- Bartolo, N.; Dimastrogiovanni, E.; Matarrese, S.; Riotto, A. Anisotropic bispectrum of curvature perturbations from primordial non-Abelian vector fields. J. Cosmol. Astropart. Phys. 2009, 2009, 015. [Google Scholar] [CrossRef]
- Himmetoglu, B.; Contaldi, C.R.; Peloso, M. Instability of anisotropic cosmological solutions supported by vector fields. Phys. Rev. Lett. 2009, 102, 111301. [Google Scholar] [CrossRef] [PubMed]
- Himmetoglu, B.; Contaldi, C.R.; Peloso, M. Instability of the ACW model, and problems with massive vectors during inflation. Phys. Rev. D 2009, 79, 063517. [Google Scholar] [CrossRef]
- Himmetoglu, B.; Contaldi, C.R.; Peloso, M. Ghost instabilities of cosmological models with vector fields nonminimally coupled to the curvature. Phys. Rev. D 2009, 80, 123530. [Google Scholar] [CrossRef]
- Thorsrud, M.; Mota, D.F.; Hervik, S. Cosmology of a scalar field coupled to matter and an isotropy-violating Maxwell field. J. High Energy Phys. 2012, 2012, 066. [Google Scholar] [CrossRef]
- Kahniashvili, T.; Lavrelashvili, G.; Ratra, B. CMB temperature anisotropy from broken spatial isotropy due to an homogeneous cosmological magnetic field. Phys. Rev. D 2008, 78, 063012. [Google Scholar] [CrossRef]
- Barrow, J.D.; Ferreira, P.G.; Silk, J. Constraints on a primordial magnetic field. Phys. Rev. Lett. 1997, 78, 3610–3613. [Google Scholar] [CrossRef]
- Campanelli, L. A model of universe anisotropization. Phys. Rev. D 2009, 80, 063006. [Google Scholar] [CrossRef]
- Kim, J.; Naselsky, P. Cosmological Alfvén waves in the recent CMB data, and the observational bound on the primordial vector perturbation. J. Cosmol. Astropart. Phys. 2009, 2009, 041. [Google Scholar] [CrossRef]
- Bueno Sanchez, J.C.; Perivolaropoulos, L. Dark energy and matter perturbations in scalar-tensor theories of gravity. J. Phys. Conf. Ser. 2011, 283, 012006. [Google Scholar] [CrossRef]
- Bean, R.; Dore, O. Probing dark energy perturbations: The dark energy equation of state and speed of sound as measured by WMAP. Phys. Rev. D 2004, 69, 083503. [Google Scholar] [CrossRef]
- Bueno Sanchez, J.C.; Perivolaropoulos, L. Topological quintessence. Phys. Rev. D 2011, 84, 123516. [Google Scholar] [CrossRef]
- Marra, V.; Notari, A. Observational constraints on inhomogeneous cosmological models without dark energy. Class. Quantum Gravity 2011, 28, 164004. [Google Scholar] [CrossRef]
- Zumalacarregui, M.; Garcia-Bellido, J.; Ruiz-Lapuente, P. Tension in the void: Cosmic rulers strain inhomogeneous cosmologies. J. Cosmol. Astropart. Phys. 2012, 2012, 009. [Google Scholar] [CrossRef] [PubMed]
- Caldwell, R.R.; Stebbins, A. A test of the copernican principle. Phys. Rev. Lett. 2008, 100, 191302. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Bellido, J.; Haugboelle, T. Looking the void in the eyes—The kinematic Sunyaev–Zeldovich effect in Lemaître-Tolman-Bondi models. J. Cosmol. Astropart. Phys. 2008, 2008, 016. [Google Scholar] [CrossRef]
- Ricciardelli, E.; Quilis, V.; Planelles, S. The structure of cosmic voids in a LCDM Universe. ArXiv E-Prints 2013. arXiv:1306.2955. [Google Scholar]
- Alnes, H.; Amarzguioui, M. CMB anisotropies seen by an off-center observer in a spherically symmetric inhomogeneous Universe. Phys. Rev. D 2006, 74, 103520. [Google Scholar] [CrossRef]
- Grande, J.; Perivolaropoulos, L. Generalized Lemaître-Tolman-Bondi model with inhomogeneous isotropic dark energy: Observational constraints. Phys. Rev. D 2011, 84, 023514. [Google Scholar] [CrossRef]
- Vilenkin, A. Topological inflation. Phys. Rev. Lett. 1994, 72, 3137–3140. [Google Scholar] [CrossRef] [PubMed]
- Hansen, F.K.; Banday, A.J.; Gorski, K.M.; Eriksen, H.K.; Lilje, P.B. Power asymmetry in cosmic microwave background fluctuations from full sky to sub-degree scales: Is the universe isotropic? Astrophys. J. 2009, 704, 1448. [Google Scholar] [CrossRef]
- Eriksen, H.K.; Hansen, F.K.; Banday, A.J.; Gorski, K.M.; Lilje, P.B. Asymmetries in the cosmic microwave background anisotropy field. Astrophys. J. 2004, 605, 14. [Google Scholar] [CrossRef]
- Park, C.-G. Non-Gaussian signatures in the temperature fluctuation observed by the Wilkinson Microwave Anisotropy Probe. Mon. Not. R. Astron. Soc. 2004, 349, 313–320. [Google Scholar] [CrossRef]
- Hirata, C.M. Constraints on cosmic hemispherical power anomalies from quasars. J. Cosmol. Astropart. Phys. 2009, 2009, 011. [Google Scholar] [CrossRef]
- Dai, L.; Jeong, D.; Kamionkowski, M.; Chluba, J. The pesky power asymmetry. Phys. Rev. D 2013, 87, 123005. [Google Scholar] [CrossRef]
- Chang, Z.; Wang, S. Inflation and primordial power spectra at anisotropic spacetime inspired by Planck’s constraints on isotropy of CMB. Eur. Phys. J. C 2013, 73, 2516. [Google Scholar] [CrossRef]
- Rassat, A.; Starck, J.-L. On Preferred Axes in WMAP cosmic microwave background data after subtraction of the integrated sachs-wolfe effect. ArXiv E-Prints 2013. arXiv:1303.5051. [Google Scholar]
- Bielewicz, P.; Gorski, K.M.; Banday, A.J. Low-order multipole maps of CMB anisotropy derived from WMAP. Mon. Not. R. Astron. Soc. 2004, 355, 1283–1302. [Google Scholar] [CrossRef]
- Frommert, M.; Ensslin, T.A. The axis of evil—A polarization perspective. Mon. Not. R. Astron. Soc. 2010, 403, 1739–1748. [Google Scholar] [CrossRef]
- Land, K.; Magueijo, J. Is the Universe odd? Phys. Rev. D 2005, 72, 101302. [Google Scholar] [CrossRef]
- Land, K.; Magueijo, J. Cubic anomalies in WMAP. Mon. Not. R. Astron. Soc. 2005, 357, 994. [Google Scholar] [CrossRef]
- Park, C.-G.; Park, C.; Gott, J.R., III. Cleaned 3 year Wilkinson Microwave Anistropy Probe Cosmic Microwave Background map: Magnitude of the quadrupole and alignment of large-scale modes. Astrophys. J. 2007, 660, 959. [Google Scholar] [CrossRef]
- De Oliveira-Costa, A.; Tegmark, M. CMB multipole measurements in the presence of foregrounds. Phys. Rev. D 2006, 74, 023005. [Google Scholar] [CrossRef]
- Naselsky, P.D.; Verkhodanov, O.V.; Chiang, L.-Y.; Novikov, I.D. Phase analysis of the 1-year WMAP data and its application for the CMB foreground separation. ArXiv E-Prints 2003. arXiv:astro-ph/0310235. [Google Scholar]
- Lineweaver, C.H.; Tenorio, L.; Smoot, G.F.; Keegstra, P.; Banday, A.J.; Lubin, P. The dipole observed in the COBE DMR 4 year data. Astrophys. J. 1996, 470, 38. [Google Scholar] [CrossRef]
- Kashlinsky, A.; Atrio-Barandela, F. Measuring cosmological bulk flows via the kinematic Sunyaev-Zeldovich effect in the upcoming cosmic microwave background maps. Astrophys. J. 2000, 536, L67. [Google Scholar] [CrossRef] [PubMed]
- Kashlinsky, A.; Atrio-Barandela, F.; Ebeling, H.; Edge, A.; Kocevski, D. A new measurement of the bulk flow of X-ray luminous clusters of galaxies. Astrophys. J. 2010, 712, L81. [Google Scholar] [CrossRef]
- Atrio-Barandela, F.; Kashlinsky, A.; Ebeling, H.; Kocevski, D. Cosmic Microwave Background filters and the Dark-Flow measurement. ArXiv E-Prints 2013. arXiv:1211.4345. [Google Scholar]
- Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Balbi, A.; Banday, A.J.; Barreiro, R.B.; Battaner, E.; et al. Planck intermediate results. XIII. Constraints on peculiar velocities. ArXiv E-Prints 2013. arXiv:1303.5090. [Google Scholar]
- Hand, N.; Addison, G.E.; Aubourg, E.; Battaglia, N.; Battistelli, E.S.; Bizyaev, D.; Bond, J.R.; Brewington, H.; Brinkmann, J.; Brown, B.R.; et al. Evidence of galaxy cluster motions with the kinematic Sunyaev-Zel’dovich effect. Phys. Rev. Lett. 2012, 109, 041101. [Google Scholar] [CrossRef] [PubMed]
- Keisler, R. The statistical significance of the “dark flow”. Astrophys. J. 2009, 707, L42. [Google Scholar] [CrossRef]
- Osborne, S.J.; Mak, D.S.Y.; Church, S.E.; Pierpaoli, E. Measuring the galaxy cluster bulk flow from WMAP data. Astrophys. J. 2011, 737, 98. [Google Scholar] [CrossRef]
- Mody, K.; Hajian, A. One thousand and one clusters: Measuring the bulk flow with the planck ESZ and X-ray selected galaxy cluster catalogs. Astrophys. J. 2012, 758, 4. [Google Scholar] [CrossRef]
- Atrio-Barandela, F. On the statistical significance of the bulk flow measured by the PLANCK satellite. ArXiv E-Prints 2013. arXiv:1303.6614. [Google Scholar]
- Turnbull, S.J.; Hudson, M.J.; Feldman, H.A.; Hicken, M.; Kirshner, R.P.; Watkins, R. Cosmic flows in the nearby universe from Type Ia supernovae. Mon. Not. R. Astron. Soc. 2012, 420, 447–454. [Google Scholar] [CrossRef]
- Dai, D.-C.; Kinney, W.H.; Stojkovic, D. Measuring the cosmological bulk flow using the peculiar velocities of supernovae. J. Cosmol. Astropart. Phys. 2011, 2011, 015. [Google Scholar] [CrossRef]
- Payez, A.; Cudell, J.R.; Hutsemekers, D. Axions and polarisation of quasars. AIP Conf. Proc. 2008, 1038, 211. [Google Scholar] [CrossRef]
- Tiwari, P.; Jain, P. Polarization Alignment in JVAS/CLASS flat spectrum radio surveys. Int. J. Mod. Phys. D 2013, 22, 1350089. [Google Scholar] [CrossRef]
- Payez, A. Cornering the axionlike particle explanation of quasar polarisations. Phys. Rev. D 2012, 85, 087701. [Google Scholar] [CrossRef]
- Payez, A.; Cudell, J.R.; Hutsemekers, D. Can axionlike particles explain the alignments of the polarisations of light from quasars? Phys. Rev. D 2011, 84, 085029. [Google Scholar] [CrossRef]
- Kalus, B.; Schwarz, D.J.; Seikel, M.; Wiegand, A. Constraints on anisotropic cosmic expansion from supernovae. Astron. Astrophys. 2013, 553, A56. [Google Scholar] [CrossRef]
- Colin, J.; Mohayaee, R.; Sarkar, S.; Shafieloo, A. Probing the anisotropic local universe and beyond with SNe Ia data. Mon. Not. R. Astron. Soc. 2011, 414, 264–271. [Google Scholar] [CrossRef]
- Schwarz, D.J.; Weinhorst, B. (An)isotropy of the Hubble diagram: Comparing hemispheres. Astron. Astrophys. 2007, 474, 717–729. [Google Scholar]
- Cai, R.-G.; Tuo, Z.-L. Direction dependence of the deceleration parameter. J. Cosmol. Astropart. Phys. 2012, 2012, 004. [Google Scholar] [CrossRef] [PubMed]
- Campanelli, L.; Cea, P.; Fogli, G.L.; Marrone, A. Testing the isotropy of the Universe with type Ia supernovae. Phys. Rev. D 2011, 83, 103503. [Google Scholar] [CrossRef]
- Antoniou, I.; Perivolaropoulos, L. Searching for a cosmological preferred axis: Union2 data analysis and comparison with other probes. J. Cosmol. Astropart. Phys. 2010, 2010, 012. [Google Scholar] [CrossRef]
- Zhao, W.; Wu, P.X.; Zhang, Y. Anisotropy of cosmic acceleration. Int. J. Mod. Phys. D 2013, 22, 1350060. [Google Scholar] [CrossRef]
- Cai, R.-G.; Ma, Y.-Z.; Tang, B.; Tuo, Z.-L. Constraining the anisotropic expansion of the Universe. Phys. Rev. D 2013, 87, 123522. [Google Scholar] [CrossRef]
- Blomqvist, M.; Mortsell, E.; Nobili, S. Probing dark energy inhomogeneities with supernovae. J. Cosmol. Astropart. Phys. 2008, 2008, 027. [Google Scholar] [CrossRef]
- Blomqvist, M.; Enander, J.; Mortsell, E. Constraining dark energy fluctuations with supernova correlations. J. Cosmol. Astropart. Phys. 2010, 2010, 018. [Google Scholar] [CrossRef]
- Cooke, R.; Lynden-Bell, D. Does the Universe accelerate equally in all directions? Mon. Not. R. Astron. Soc. 2010, 401, 1409–1414. [Google Scholar] [CrossRef]
- Gupta, S.; Saini, T.D. Direction dependence in supernova data: Constraining isotropy. Mon. Not. R. Astron. Soc. 2010, 407, 651–657. [Google Scholar] [CrossRef]
- Cameron, E.; Pettitt, T. On the evidence for cosmic variation of the fine structure constant (I): A Parametric Bayesian model selection analysis of the quasar dataset. ArXiv E-Prints 2013. arXiv:1207.6223. [Google Scholar]
- Kanekar, N.; Langston, G.I.; Stocke, J.T.; Carilli, C.L.; Menten, K.L. Constraining fundamental constant evolution with HI and OH lines. Astrophys. J. 2012, 746, L16. [Google Scholar] [CrossRef]
- Levshakov, S.A.; Combes, F.; Boone, F.; Agafonova, I.I.; Reimers, D.; Kozlov, M.G. An upper limit to the variation in the fundamental constants at redshift z = 5.2. Astron. Astrophys. 2012, 540, L9. [Google Scholar] [CrossRef]
- Marinoni, C.; Bel, J.; Buzzi, A. The scale of cosmic isotropy. J. Cosmol. Astropart. Phys. 2012, 2012, 036. [Google Scholar] [CrossRef]
- Schneider, D.P.; Richards, G.T.; Hall, P.B.; Strauss, M.A.; Anderson, S.F.; Boroson, T.A.; Ross, N.P.; Shen, Y.; Brandt, W.N.; Fan, X.; et al. The sloan digital sky survey quasar catalog. V. seventh data release. Astron. J. 2010, 139, 2360. [Google Scholar] [CrossRef]
- Nadathur, S. Seeing patterns in noise: Gigaparsec-scale “structures” that do not violate homogeneity. Mon. Not. R. Astron. Soc. 2013, 434, 398–406. [Google Scholar] [CrossRef]
- Pilipenko, S.; Malinovsky, A. Testing statistical significance of large quasar groups with sheets model of large scale structure. ArXiv E-Prints 2013. arXiv:1306.3970. [Google Scholar]
- Koivisto, T.; Mota, D.F. Accelerating cosmologies with an anisotropic equation of state. Astrophys. J. 2008, 679, 1. [Google Scholar] [CrossRef]
- Mota, D.F.; Kristiansen, J.R.; Koivisto, T.; Groeneboom, N.E. Constraining dark energy anisotropic stress. Mon. Not. R. Astron. Soc. 2007, 382, 793–800. [Google Scholar] [CrossRef]
- Koivisto, T.; Mota, D.F. Anisotropic dark energy: Dynamics of background and perturbations. J. Cosmol. Astropart. Phys. 2008, 2008, 018. [Google Scholar] [CrossRef]
- Lemaître, A.G. The expanding universe. Gen. Relativ. Gravit. 1997, 29, 641–680. [Google Scholar] [CrossRef]
- Tolman, R.C. Effect of imhomogeneity on cosmological models. Proc. Natl. Acad. Sci. USA 1934, 20, 169–176. [Google Scholar] [CrossRef] [PubMed]
- Bondi, H. Spherically symmetrical models in general relativity. Mon. Not. R. Astron. Soc. 1947, 107, 410–425. [Google Scholar] [CrossRef]
- Enqvist, K.; Mattsson, T. The effect of inhomogeneous expansion on the supernova observations. J. Cosmol. Astropart. Phys. 2007, 2007, 019. [Google Scholar] [CrossRef]
- Alnes, H.; Amarzguioui, M. The supernova Hubble diagram for off-center observers in a spherically symmetric inhomogeneous Universe. Phys. Rev. D 2007, 75, 023506. [Google Scholar] [CrossRef]
- Szekeres, P. Quasispherical Gravitational Collapse. Phys. Rev. D 1975, 12, 2941–2948. [Google Scholar] [CrossRef]
- Szekeres, P. A class of inhomogeneous cosmological models. Commun. Math. Phys. 1975, 41, 55–64. [Google Scholar] [CrossRef]
- Goode, S.W.; Wainwright, J. Singularities and evolution of the Szekeres cosmological models. Phys. Rev. D 1982, 26, 3315–3326. [Google Scholar] [CrossRef]
- Bonnor, W.B. Non-radiative solutions of Einstein’s equations for dust. Commun. Math. Phys. 1976, 51, 191–199. [Google Scholar] [CrossRef]
- Cho, I.; Vilenkin, A. Spacetime structure of an inflating global monopole. Phys. Rev. D 1997, 56, 7621–7626. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Fine-structure constant: Is it really a constant? Phys. Rev. D 1982, 25, 1527–1539. [Google Scholar] [CrossRef]
- Sandvik, H.B.; Barrow, J.D.; Magueijo, J. A simple cosmology with a varying fine structure constant. Phys. Rev. Lett. 2002, 88, 031302. [Google Scholar] [CrossRef] [PubMed]
- Avgoustidis, A.; Martins, C.J.A.P.; Monteiro, A.M.R.V.L.; Vielzeuf, P.E.; Luzzi, G. Cosmological effects of scalar-photon couplings: Dark energy and varying-α models. ArXiv E-Prints 2013. arXiv:1305.7031. [Google Scholar]
- Sakai, N.; Shinkai, H.-A.; Tachizawa, T.; Maeda, K.-I. Dynamics of topological defects and inflation. Phys. Rev. D 1996, 53, 655–661. [Google Scholar] [CrossRef]
- Barriola, M.; Vilenkin, A. Gravitational field of a global monopole. Phys. Rev. Lett. 1989, 63, 341–343. [Google Scholar] [CrossRef] [PubMed]
- Balcerzak, A.; Dabrowski, M.P.; Denkiewicz, T. Off-center observers versus supernovae in inhomogeneous pressure universes. ArXiv E-Prints 2013. arXiv:1312.1567. [Google Scholar]
- Lineweaver, C.H. The CMB dipole: The most recent measurement and some history. ArXiv E-Prints 1996. arXiv:astro-ph/9609034. [Google Scholar]
© 2014 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Perivolaropoulos, L. Large Scale Cosmological Anomalies and Inhomogeneous Dark Energy. Galaxies 2014, 2, 22-61. https://doi.org/10.3390/galaxies2010022
Perivolaropoulos L. Large Scale Cosmological Anomalies and Inhomogeneous Dark Energy. Galaxies. 2014; 2(1):22-61. https://doi.org/10.3390/galaxies2010022
Chicago/Turabian StylePerivolaropoulos, Leandros. 2014. "Large Scale Cosmological Anomalies and Inhomogeneous Dark Energy" Galaxies 2, no. 1: 22-61. https://doi.org/10.3390/galaxies2010022
APA StylePerivolaropoulos, L. (2014). Large Scale Cosmological Anomalies and Inhomogeneous Dark Energy. Galaxies, 2(1), 22-61. https://doi.org/10.3390/galaxies2010022



