The Physical and Mathematical Meaning of Temperature and Its Implications for Astronomy

Abstract

Temperatures reported for astronomical objects are commonly extreme, and all are ascertained indirectly, using spectroscopy. However, narrow spectral peaks record microscopic behavior (transitions), whereas temperature is a macroscopic (bulk) feature of an object. Using macroscopic theories of heat, light, and their transport, we show that temperature is best defined in terms of the radiant flux of an object (Stefan–Boltzmann law)—including that from large gas bodies—because this flux defines which objects are hotter or colder, and because relevance to mathematical order is the essential attribute of any measurable quantity. Laboratory examples further show that spectroscopic determinations of temperature require the following: (1) use of a large spectral range relevant to that temperature; (2) observation of the unique peak shape characteristic of thermal emissions; (3) accounting for reflections at surfaces; and, most importantly, (4) that conditions are optically thick, a condition fostered by large object size and high temperatures. Temperature of monatomic gas is accurately described by classical kinetic theory because molecular translations are unaffected by electron dynamics. Inelastic molecular collisions provide continuous thermal emissions under optically thick conditions attained in immense astronomical environments. We show how thermal and non-thermal spectroscopic features can be distinguished. Our findings are applied to star-forming regions, intergalactic media, lightning, the Sun’s surface and the corona. Our results resolve long-standing problems regarding heat sources.

1. Introduction

Temperature is generally understood in the familiar, everyday context of a reading on an ordinary thermometer. However, the important distinctions between heat, measured temperature, and temperature that is calculated in various and sometimes inconsistent ways are blurred by semantic ambiguities. When we say an object is “hot”, are we referring to its temperature, to its content of thermal energy (i.e., heat), or to both? And just what is temperature?

These questions are relevant to current research in galactic astronomy because distant bodies are probed remotely, using light, not thermometers, and independent experimental validation is extremely limited. Furthermore, the immense values commonly calculated for temperature (T) that reach millions of degrees K for dense stellar interiors, rarefied stellar atmospheres, and some highly rarefied media in space are far beyond human experience or laboratory capabilities. The immense length and mass scales encountered in astronomy may lend credence to extreme values for T, yet the former are confirmable and the latter are not. Several questions arise, outlined below.

Can the proposed high temperatures of 10⁵ to 10⁷ K actually exist in a rarified gas? Since the source of coronal heating remains a long-standing mystery in astrophysics [1,2], could solar coronal temperatures be greatly overestimated? Do narrow emission or absorption peaks, or the presence of highly charged ions, provide reliable estimates of temperature? What is a reliable measure? Answering these questions pertains to diverse astrophysical entities and processes.

1.1. Purpose and Goals of This Paper

A close look at the meaning of temperature, and the data and methodology used to remotely determine T for astronomical objects, is warranted. One possible source of error in remote determinations of T is that non-thermal emissions accompany thermal emissions in many astronomical environments. For example,

• Fusion deep inside stars generates energetic particles as well as light of various wavelengths, including γ-rays;
• Solar cosmic rays (protons) stimulate the visible emissions of Earth’s aurorae [3];
• Electron beams are considered to stimulate redshifted emissions of hydrogen (Hα) during solar flares [4];
• Non-thermal radiation from radio to γ-ray wavelengths is emitted from star-forming galaxies [5].

• Reliably determining temperature requires distinguishing thermal from non-thermal signatures in spectra.

Isolating thermal behavior is possible because temperature, heat, and flux are macroscopic attributes, whereas narrow spectral peaks probe microscopic behavior, i.e., transitions between states. Consequently, principles of classical thermodynamics, heat transfer, and spectroscopic analysis all pertain to inferring T remotely in astrophysical environments. Because these theories are historic, the literature presumably provides all information needed for this important task; such is not the case:

• Fundamental concepts concerning temperature are derived from thermodynamics, although—as pointed out by Norton and Munoz [6]—there is nothing “dynamic” about comparing energy states; time never appears in any of the classical, master equations of this field. Yet, temperatures of real objects evolve with time, unless steady-state heat transfer applies. Moreover, not even steady state conforms to the equilibrium conditions that underlie the equations of classical thermodynamics. The proper name for the classical field is “thermostatics” [6].
• Fourier’s model for heat transfer, despite predating “thermostatics,” was not considered during that model’s development [7]. This known deficiency has been addressed for solids [8,9] but not for gases, which abound in astronomical environments.
• Similarly, the Stefan–Boltzmann law is not a part of “thermostatics.”

This combination of factors has led to misunderstandings of what temperature means. Astronomical research is particularly impacted because measurements of temperature are indirect and radiative transfer is involved, which is difficult to understand.

Our goal is to provide an improved exposé on the relevant macroscopic theories, and to clarify conditions under which spectroscopic measurements indicate macroscopic behavior, temperature in particular. Through this effort we identify methods to reliably establish the temperature of remote objects.

1.2. Organization of This Paper and Key Findings

This paper is organized as follows: Section 2 covers macroscopic theories connected with temperature and heat. We begin with static, classical thermodynamics, and illustrate some paradoxes and inconsistencies. Section 2.4 then discusses temperature in view of the macroscopic constructs for heat transfer (Fourier’s laws and the Stefan–Boltzmann law), in order to explore the dynamic thermal behavior found in astronomical environments. Section 3 discusses spectral analysis and radiative transfer using laboratory examples relevant to astronomy. Section 4 unites these macroscopic approaches, emphasizing that optically thick conditions are needed to link spectra to temperature and heat transfer. Section 5 applies our findings to planetary and astronomical objects. Section 6 provides additional discussion. Section 7 concludes.

This paper demonstrates that there is truly only one “type” of temperature, but that the word “temperature” has evolved to represent many different methods, situations, and phenomena, and not all such usages are mutually consistent. Through distinguishing between radiative transport under optically thin and optically thick conditions, and by illustrating those differences with examples, we show that only the latter is relevant to temperature. We show that the blackbody temperature is the thermodynamic temperature. By considering the effect of rudimentary atomic structure on gas dynamics, alongside basic spectroscopic principles, we show that electronic transitions do not indicate temperature. Our findings are then applied to important situations in galactic astronomy.

2. The Macroscopic Theory of Temperature, Heat, and Flux

2.1. Basic Properties of Temperature

Temperature is a measurable, macroscopic property of a medium. Because T is measurable, temperatures can be compared and placed in mathematical order. Because T is macroscopic, no special assumptions concerning the nature of matter are required to define or use it. Even so, temperature is central to many testable theories and laws that describe the behaviors of other measurable quantities, e.g., [6,10].

• Details of microscopic behavior are irrelevant to macroscopic theory but collective behaviors of populations of particles are germane;
• The fundamental Kelvin scale describes temperature as a unique, positive number that is a key characteristic of a macroscopic system.

Temperature is an “intensive variable”, and so it is not additive as it varies independently of the size or mass of the object of interest. If two identical objects with the same temperature are combined, the temperature is not doubled but instead remains constant. In contrast, stored heat (Q_stored) depends on the size of the object, and when combined, two identical objects will contain twice as much heat as each one. Thus, Q_stored is an “extensive” quantity.

2.2. Types of Temperature

“Temperature” currently refers to a quantity derived from many different methods and phenomena. Next we define these different uses and applications.

2.2.1. Direct Measurements of Temperature

Historically, measured temperature refers to a reading on a mercury thermometer using a scale that was based on the freezing and boiling points of water at 1 atm, and the fact that Hg expands as T rises. More recently, T is based on readings of various electronic devices, each calibrated against the defined historical scale, which employ some surrogate attribute such as electrical resistivity. Calibrated spectral measurements have also been made using devices such as optical pyrometers. All such measurements probe conditions possible in the laboratory. Although several different temperature scales exist, all are related to the fundamental Kelvin scale by simple algebraic manipulations.

2.2.2. Temperatures Calculated from Models

Different theories, assumptions, approximations, and/or phase relationships are commonly used to calculate the temperatures of regions that are inaccessible to direct measurement. Using Wien’s law to calculate T from electronic spectra is examined below. However, models and calculations are fundamentally different than measurements as the former require measurements for verification and validation, but the converse is not true. A reliable measurement stands on its own.

2.3. Properties of Temperature as Defined by Classical Thermodynamics

Many properties of temperature, and its theoretical conceptualization, stem from the fundamental laws of classical thermodynamics [6,11,12], as follows:

2.3.1. Zeroth Law

The zeroth law of thermodynamics states that, if each of two bodies is in thermal equilibrium with a third, then the two bodies are in thermal equilibrium with each other, and all three have the same temperature. The underlying mathematical basis can be applied to any characteristic or property that can be represented by a number because numbers represent an ordered sequence that progresses from smaller to larger [13]. Mathematically, if X = Z and Y = Z, then X = Y.

2.3.2. Second Law

The second law of thermodynamics has been stated and “explained” in several ways. Even so, inconsistencies remain.

• Arguably, the most fundamental and universal statement of the second law concerns entropy (S), classically defined in terms of adding an infinitesimal amount of externally applied heat: δS = δQ_ext/T. However, of the primary thermodynamic variables used in the Maxwell relations (pressure P, volume V, T, and S; see [14]), entropy is the only one that cannot be directly measured, diminishing its utility as a meaningful physical variable.
• An oft-repeated version of the second law is that “heat always flows from a hotter to a colder body,” and never in the reverse direction, unless external work is performed. If “hotter” and “colder” refer to temperature, and “flow” actually represents the net flow, this latter statement is consistent with the concept of flux. However, flux is defined by the Stefan–Boltzmann law and Fourier’s laws (provided below), which involve T and time but not S.
• Another common restatement of the second law is that “heat flows downhill.” If “heat” represents the enthalpy, this statement is not always true. For example, if substance A has a much lower heat capacity than substance B, heat can spontaneously flow “uphill” from A to B even if A has a lower enthalpy, provided that A has a higher temperature than B. This example proves that it is temperature, not the heat content, that quantifies which objects are hotter and which are colder, and defines the direction of heat flow.
• Eddington famously stated that entropy is “time’s arrow.” As mentioned above, no equations for entropy involve the key variables of dynamics, which are position x and time t. It follows that a more general and fundamental statement is that energy dissipation is time’s arrow. In most systems, T and flux define the direction of spontaneous change.

2.3.3. Third Law

Like the second law, the third law of thermodynamics is typically stated in terms of entropy. However, Nernst focused on temperature, stating: “It is impossible to start from a state of positive temperature, and reach a state with zero temperature by any finite number of steps.” The third law is, thus, underpinned by temperature being a positive, measurable quantity bounded by the unattainable value of 0 K. Consequently, a unique (average) temperature can be assigned to any object at any particular instant.

2.3.4. Temperature Portrayed by the Classical Kinetic Theory of Gases (KTG)

According to KTG, the average translational kinetic energy and the heat content of an ideal gas are directly proportional to its temperature. Collisions are presumably elastic, brief, and unimportant to the energetics, so temperature is independent of time. This assumption is consistent with the basic precepts of classical thermodynamics, which center on comparing theoretical equilibrium states [6]. The successes of KTG in describing gases pertain to whether T can be established from electron behavior, as follows.

Atoms differ from the rigid spheres envisioned. Electron clouds surround tiny nuclei. Largely due to mass disparity, dynamics of the electrons are distinct from dynamics of nuclei. This principle is known as the adiabatic approximation or the independent electron approximation in solid state physics [15,16], and as the Born–Oppenheimer approximation in molecular dynamics [17].

Independence of electron and nuclear motions underlies the Bohr theory of electron orbitals, which reasonably describes laboratory observations of hydrogen-like atoms. This independence is evident in astronomical observations: (1) Balmer line positions are the same in cold laboratory experiments as in the atmospheres of hot stars; (2) redshift determinations are based on the constancy of electronic lines of hydrogen, even when speeds are relativistic.

Consequences are as follows:

• KTG provides temperature of the gas while assuming particles are indivisible (whole atoms or molecules). This model agrees with the observed heat capacity of monatomic gas.
• Changes in vibrational states of molecules pertain to temperature because nuclei move during vibrations. When this additional heat reservoir is accounted for, KTG results agree with measurements of molecular gases (e.g., in [18], Table 5.1).
• The orbital transitions of electrons are irrelevant to temperature because temperature is defined by motions of nuclei.

Simply put, moving nuclei drag their whirling electronic clouds along, unperturbed.

However, electron clouds are not rigid and surround nuclei, so collisions of the atoms are inelastic. Modern models assume a few % of the collisions are inelastic [19]. Inelastic collisions cause a gas without a steady heat source to spontaneously cool. Thus, classical KTG actually describes a gas with a heat source in steady-state conditions, where inelastic losses (emissions) are offset by provision of heat from the surroundings. Neglecting inelastic losses affects computed gas transport properties [18] (Chapter 5 therein), for which a dynamical model is required, as discussed next.

2.4. The Dynamic Nature of Temperature

Time being omitted in “thermostatics” is a key flaw that conceals the most essential characteristic of temperature itself, as follows.

2.4.1. Fourier’s Laws

For simplicity, Fourier’s laws are presented in one dimension:

$$\Im =-K{\displaystyle \frac{\partial T}{\partial x}} =-\rho c_{P}D{\displaystyle \frac{\partial T}{\partial x}} \mathrm{and} {\displaystyle \frac{\partial T}{\partial t}}=D{\displaystyle \frac{{\partial }^{2}T}{\partial x^2}},$$

(1)

Fourier directly linked both temperature and flux (ℑ, in units of watts m⁻²) to the key variables of dynamics, which are distance (x) and time (t). Fourier quantified the associated transport of heat in the properties of thermal conductivity (K), thermal diffusivity (D), density ρ, and specific heat at constant pressure (c_P, which is on a per-mass basis here).

• Equation (1) proves that temperature is inherently dynamic. Classical thermodynamics does not.
• Because Fourier’s model describes gradients in temperature, solving these equations is required to calculate T. Cases where heat is internally generated require an additional term.

Steady-state conditions, where temperature varies spatially but not with time, are highly relevant to the meaning of temperature. During steady-state heat flow along some Cartesian direction, thin isothermal slices describe the two perpendicular directions. In low-temperature gradients, the effective thickness of these slices can be quite large.

Steady state is achievable, and since time is not involved, this condition reasonably approximates the thermodynamic ideal of equilibrium. However, heat still flows and not even local equilibrium exists, e.g., [20]. Flow exists because occupation of space by energy is independent of that by matter. Implications of the behavior of heat being decoupled from the behavior of matter on thermodynamic relations are covered in our earlier papers [8,9,21], with experimental verification.

Importantly, steady state is a limiting case of Fourier’s laws. Fourier’s laws are macroscopic and, thus, are independent of the mechanism by which heat flows. Hence, the meaning of temperature does not depend on equilibrium or any other condition.

2.4.2. Temperature from Blackbody Flux and Radiant Power

A perfect absorber of all wavelengths cannot reflect light due to energy conservation. This object emits light called blackbody radiation at any finite T.

According to the Stefan–Boltzmann law, the flux emitted by a perfect blackbody is:

$$\Im =\sigma T^4,$$

(2)

where T is temperature in Kelvins; and σ is the Stefan–Boltzmann constant (5.67037 × 10⁻⁸ Wm⁻²-K⁻⁴).

Equation (2) describes the thermal power emitted by a blackbody per unit surface area, as required by Fourier’s definition of flux. Hence, the power of a source is provided by integrating its flux over its surface, or if that flux is constant, by simply multiplying the flux by the surface area. The radiant power of a spherical blackbody with surface radius R is, thus:

$$\wp =4\mathsf{\pi }{R}^2\sigma T^4.$$

(3)

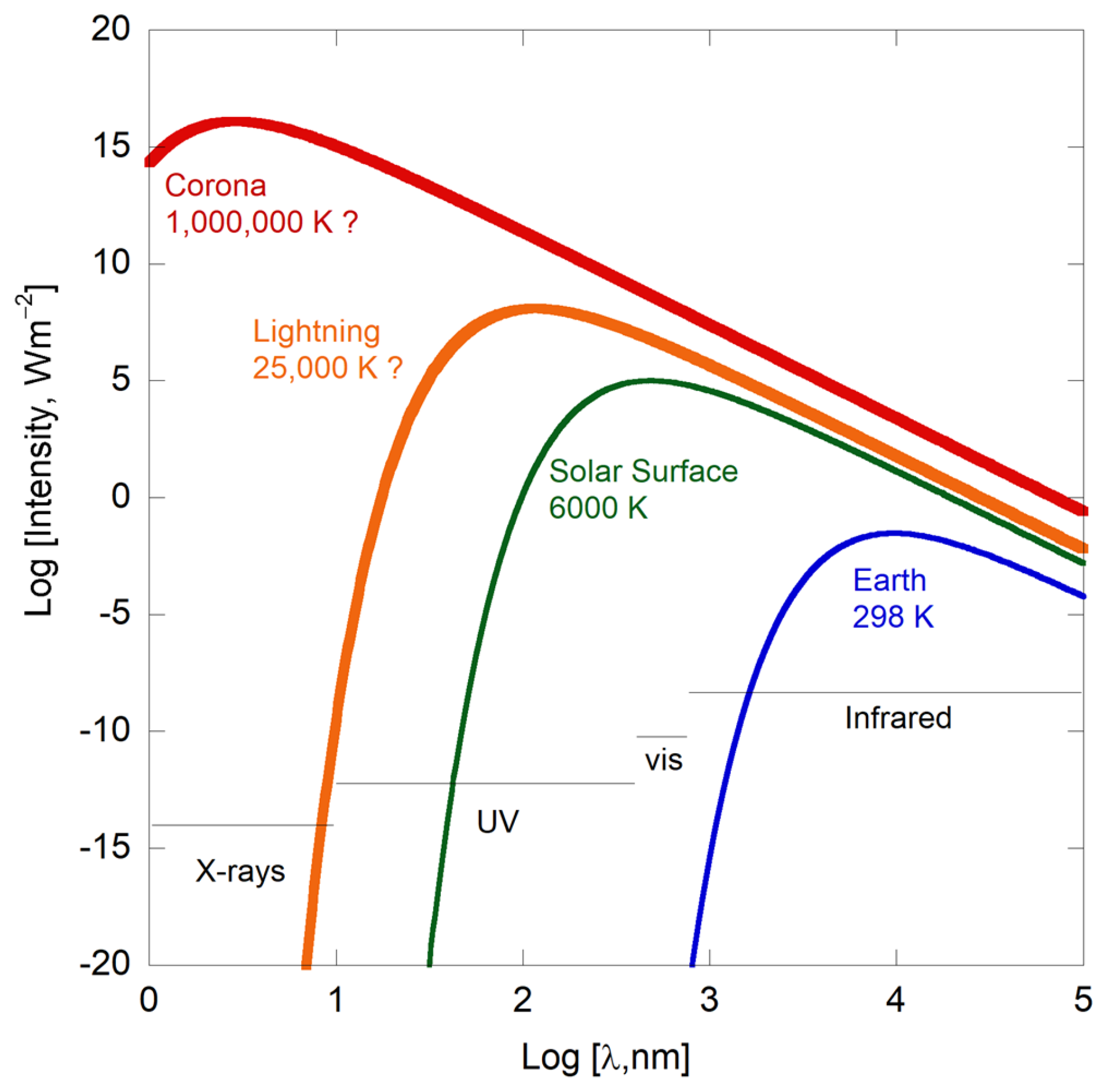
It is evident that integrating the continuous blackbody spectrum of a body at temperature T over all wavelengths will provide much larger power than integrating over a finite number of discrete, narrow spectral lines of electronic transitions in a rarefied gas at the same temperature T. This dichotomy underscores the gross incompatibility of blackbody temperatures with “temperatures” calculated from discrete spectral transitions.

2.4.3. Blackbody Spectra Characteristics

The variation of blackbody emissions with wavelength (λ) or frequency (ν) is denoted as the blackbody curve, or Planck function, as Planck provided the mathematical description for the historic Lummer and Pringsheim [22] experiments on solids. To provide an example highly relevant to astronomy, Figure 1 compares three ideal blackbody curves (defined in Section 2.4.4) to solar emissions [23,24], which are clearly not ideal (Section 5). Nonetheless, key attributes stand out: the blackbody curve is broad and continuous, and has a distinct shape (discussed next) and a prominent peak. Peak wavelength, λ_BB, is described by Wien’s displacement law. In units of nm:

$${\lambda }_{\mathrm{BB}}={\displaystyle \raisebox{1ex}{$2897800$}\!\left/ \!\raisebox{-1ex}{$T$}\right.}.$$

(4)

2.4.4. Mathematical Properties of Blackbodies

Planck’s famous curve takes on different mathematical forms, depending on whether it is expressed in terms of wavelength or frequency, and whether the interest is energy as perceived by the receiver or that emitted from the surface of the body. The need here is for a formula representing intensity at the body’s surface.

Sproul [25] provides intensity (I_λ) of blackbody radiation at the emitting body’s surface having temperature T as a function of wavelength λ:

$$I_{\lambda }(T) ={\displaystyle \frac{2\pi c^{2}h}{{\lambda }^5}}{\displaystyle \frac{1}{\exp \left(\raisebox{1ex}{$hc$}\!\left/ \!\raisebox{-1ex}{$\lambda k_{B}T$}\right.\right)-1}},$$

(5)

where I_λdλ = (dW/dλ)dλ; W is total power per area; c is the speed of light; h is Planck’s constant; and k_B is Boltzmann’s constant. Intensity I_λ has the standard units of watts per m² per unit wavelength range. Sproul’s [25] result is validated by simply integrating and differentiating Equation (5) with respect to λ, which directly and unambiguously provides, respectively, Stefan–Boltzmann and Wien’s laws, as follows:

Figure 1. Observed spectrum of the Sun. SSI = blue line; from Coddington et al. [23,24] as measured at Earth’s distance compared to the BB curves of an ideal, 5775 K source (black curve)—which is the effective temperature [26]—an ideal 6000 K blackbody (red dashed curve) whose maximum height agrees with that of the SSI, and an ideal 6275 K blackbody (dotted curve) that matches SSI intensity above 1500 nm. The calculated BB intensity (Equation (5)) has been reduced by a geometrical factor of 46, 240, or (146.7/0.695700)² to account for the fact that the observed spectrum was collected near Earth, rather than on the solar surface. (a) Full view, with superimposed absorption lines of the Balmer (squares; [27]) and Paschen neutral hydrogen series (diamonds, e.g., [28]). (b) Expanded view of the SSI in the UV, on a log scale. Assignments of emission bands in black type are from [29], confirmed with the persistent lines listed in the NIST database [30] for neutral or singly charged cations; Si IV position from Siems et al. [31]; CIII and CIV positions from Katai et al. [32]. Pink labels indicate tentative assignments based on the NIST database [30].

Figure 1. Observed spectrum of the Sun. SSI = blue line; from Coddington et al. [23,24] as measured at Earth’s distance compared to the BB curves of an ideal, 5775 K source (black curve)—which is the effective temperature [26]—an ideal 6000 K blackbody (red dashed curve) whose maximum height agrees with that of the SSI, and an ideal 6275 K blackbody (dotted curve) that matches SSI intensity above 1500 nm. The calculated BB intensity (Equation (5)) has been reduced by a geometrical factor of 46, 240, or (146.7/0.695700)² to account for the fact that the observed spectrum was collected near Earth, rather than on the solar surface. (a) Full view, with superimposed absorption lines of the Balmer (squares; [27]) and Paschen neutral hydrogen series (diamonds, e.g., [28]). (b) Expanded view of the SSI in the UV, on a log scale. Assignments of emission bands in black type are from [29], confirmed with the persistent lines listed in the NIST database [30] for neutral or singly charged cations; Si IV position from Siems et al. [31]; CIII and CIV positions from Katai et al. [32]. Pink labels indicate tentative assignments based on the NIST database [30].

The Stefan–Boltzmann law (Equation (2)) provides the flux (W per m²) on the surface of the blackbody, which is consistent with Fourier’s definitions (Equation (1)). Integrating Equation (5) using an integral derived in the late 1940s (Gradshteyn and Ryzhik [33] on p. 235 cite Fikhtengol’ts [34]) provides the following result:

$$\Im ={\displaystyle {\int }_0^{\infty }{I}_{\lambda }d\lambda =}\left\{{\displaystyle \frac{2{\pi }^5{k}_B^4}{15c^2{h}^3}}\right\}{T}^4,$$

(6)

The value of σ exactly equals the parameter ratio in curly brackets.

Differentiating Equation (5) with respect to λ, setting the result to zero, and solving similarly provides Wien’s law and its constants, which specify the wavelength at peak intensity:

$${\lambda }_{\max }={\displaystyle \frac{ch}{5k_{B}T}}\left\{{\displaystyle \frac{\exp \left(\raisebox{1ex}{$hc$}\!\left/ \!\raisebox{-1ex}{$\lambda k_{B}T$}\right.\right)}{\exp \left(\raisebox{1ex}{$hc$}\!\left/ \!\raisebox{-1ex}{$\lambda k_{B}T$}\right.\right)-1}}\right\}\cong {\displaystyle \frac{ch}{5k_{B}T}},$$

(7)

The ratio on the far right reasonably approximates Wien’s law (Equation (4)). Iteratively solving the above transcendental equation provides 4.9651 instead of 5 on the far-right side, and a precise match with Wien’s law [35,36].

The analogous equation for blackbody intensity (I_BB) in terms of frequency ν in hertz at the body surface is:

$$I_{\nu }(T) ={\displaystyle \frac{2\pi h{\nu }^3}{c^2}}{\displaystyle \frac{1}{\exp \left(\raisebox{1ex}{$h\nu $}\!\left/ \!\raisebox{-1ex}{$k_{B}T$}\right.\right)-1}},$$

(8)

Blackbody curves in this report (e.g., Figure 1) are calculated from Equation (5) or Equation (8).

Not only do blackbody spectra have a unique maximum, but moreover, this curve has a specific, characteristic, broad shape, with an intensity that strongly depends on T. Figure 1 and Figure 2 emphasize all three hallmark properties.

• Importantly, use of Wien’s law, Equation (4), presumes that the measured emissions have the broad, unique shape of the blackbody curve.
• Blackbodies are unachievable idealizations: thermal emissions from a hot object differ from I_BB depending on the spectral properties of the material (Section 3.4).
• Blackbody flux from hot objects dwarfs that from cooler objects (Figure 2), rendering the latter effectively invisible when both are present.

2.5. Summary

This section focused on macroscopic descriptions of heat and temperature. Neither entity can be compressed. Any amount of energy can exist in a given volume. Moreover, energy can flow through a volume, with or without interacting with the mass enclosed. Fourier’s laws describe diffusive flow of heat energy in terms of temperature changes and flux. The Stefan–Boltzmann law ties T directly to ℑ. Flux is measured at the surface of the body, where, in many situations relevant to astronomy, this heat-energy radiates to the surroundings. Clearly, temperature and heat are tied to light. This connection is discussed next.

3. Circumstances Under Which Spectroscopic Data Reveal Temperature

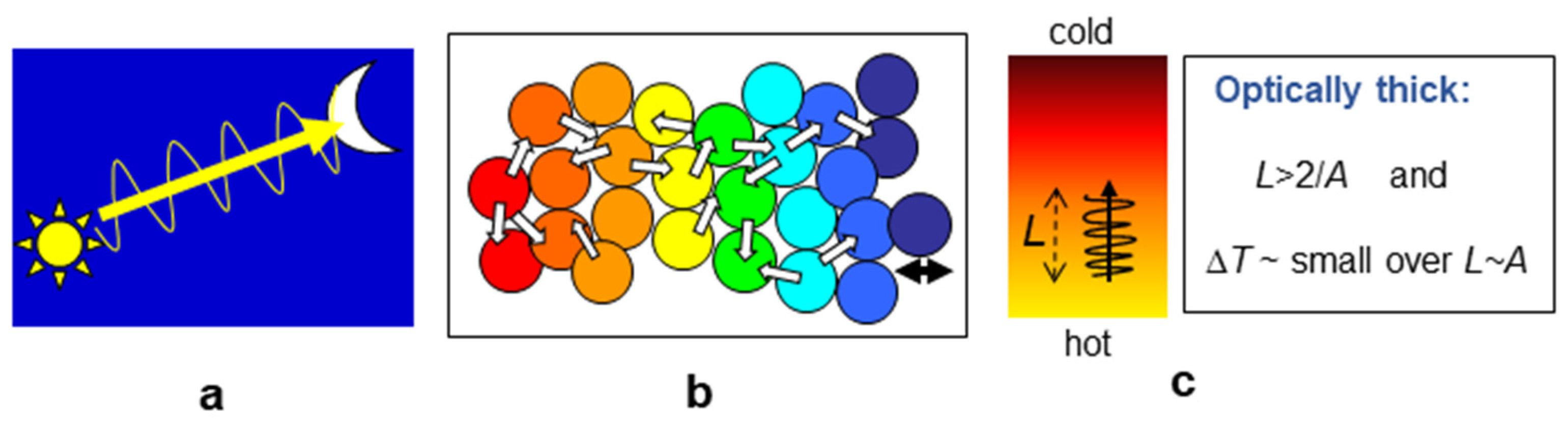
Laboratory measurements are used to clarify the difference between spectra measured under optically thin vs. optically thick conditions. We show that only the latter probes macroscopic behavior, i.e., temperature. How radiative transfer differs under these two conditions is also relevant to temperature.

3.1. Absorption Spectroscopy: A Non-Thermal Probe of Matter Under Optically Thin Conditions

Laboratory spectra record transitions in the sample that are stimulated when the applied energy from the instrument matches the transition energy. Thus, spectra probe differences between states but not the states themselves.

In Figure 3 (blue curve), absorption peaks point up because in the laboratory, absorption is extracted from measurements of transmission relative to a reference (details are in Appendix A). In transmission spectra, source intensity is reduced at the transitions so transmission peaks point down. Whether narrow transition peaks point up or down depends on the circumstance probed, what is being graphed, and the technique used, discussed further below.

Because the light source can have any dependence on wavelength, e.g., lasers are sometimes used, absorption spectra are non-thermal signatures. Absorption spectra are important indicators of chemical composition and phases. Only if peak parameters depend on T and the response is independently known can absorption spectra provide sample temperature. Electronic transition spectra of gas atoms are not amenable to ascertaining T because their peak parameters are little perturbed by temperature.

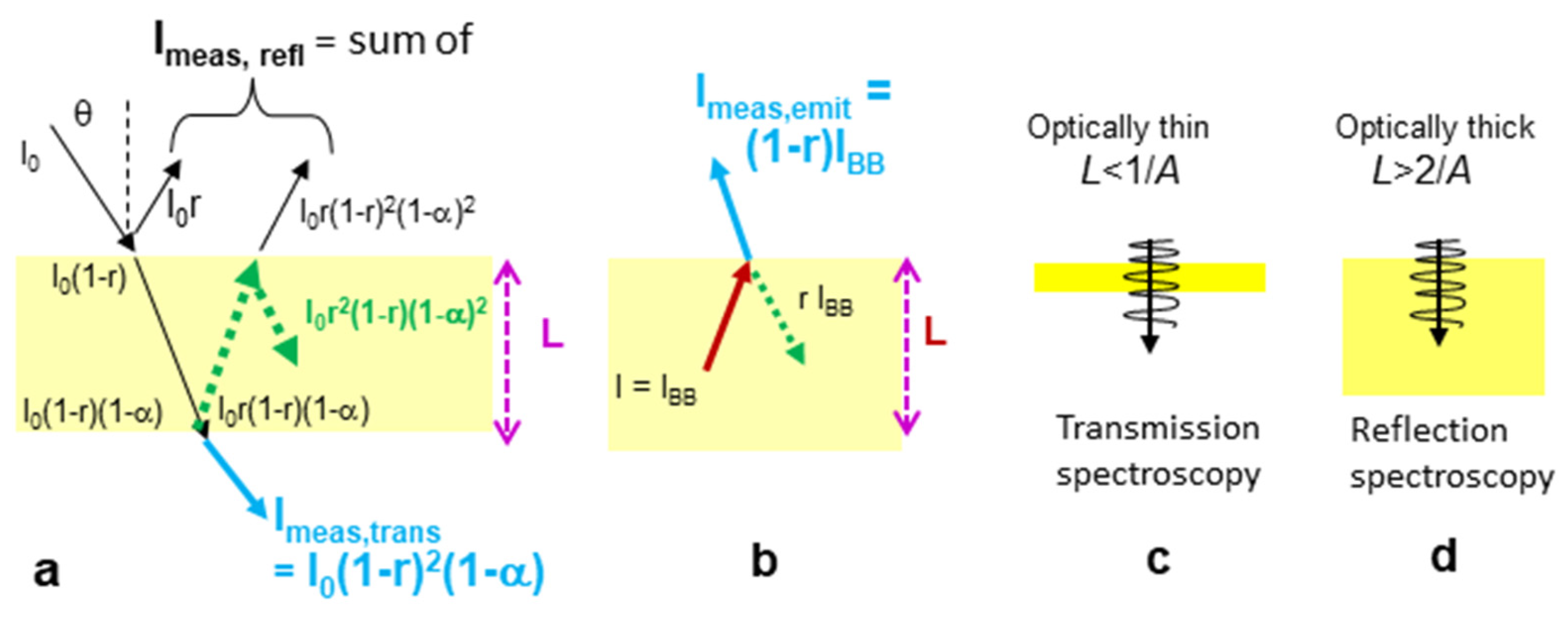
Figure 4 summarizes conditions in laboratory experiments. See Appendix A and references [39,40] for further discussion. To obtain absorption spectra requires optically thin conditions because a non-negligible fraction of the incident light must exit the sample at each wavelength. If the fraction is between the limiting values in Figure 4 (e.g., 1/A < L < 2/A), then peaks are distorted as detectors have finite sensitivity.

Remotely acquired absorption spectra indicate that the observed environment is optically thin. For this case, most light passes through without interacting with the medium.

3.2. Non-Thermal Emission Spectra

3.2.1. Electronically Stimulated Electrons and Ions in Gases

Many excited materials emit a spectrum consisting of discrete peaks. Lyman discovered the 1s ⟶ 2p electronic transition of H atoms by electrical stimulation. Importantly, absorption spectra record energy uptake during a perturbation, whereas emission lines record the release of energy during re-equilibration after a perturbation. The perturbation need not be thermal.

The red glow of a neon wavelength calibration lamp (Figure 5a) is electronically stimulated. The lamp is merely warm to the touch since little electrical energy was supplied. The spectrum (e.g., [43]) consists of many sharp, discrete lines of electronic transitions so the total flux is low, consistent with energy conservation. Likewise, the display of a plasma globe (Figure 5b) negligibly heats the surface of this toy. Yet, ions are created during this electrical discharge.

• Because ions can be created non-thermally, either by particle collisions (e.g., [4]) or by electrical discharge (Figure 5b), whether atoms are neutral or charged is irrelevant to temperature.
• Similarly, the presence of electronic transitions need not indicate T.

3.2.2. Laser-Stimulated Electrons Inside Metals

In ultrafast (femtosecond) optical spectroscopic experiments, electrons in thin metal films (e.g., [46]) and on surfaces of bulk metals (e.g., [47]) are first excited using high-intensity, monochromatic light, usually at some visible wavelength. Afterwards, the time-dependent reduction in intensity of the narrow emission peaks is monitored [48,49,50,51].

Inappropriate application of Wien’s law suggests that the electrons are 500 K hotter than the metal, yet neither the films nor the surface are detectably heated. Re-equilibration is rapid, such that the emission peaks disappear within ~10 ps (e.g., [46,52]). Rapid re-equilibration rates result from the high density of metals, which provides frequent collisions among its electrons and atoms.

Based on this example,

• The temperature of the medium is not indicated by the electrons, even for dense metals in which medium the electrons collide and interact due to high density;
• Gases behave likewise, although re-equilibration is slow due to infrequent collisions.

3.3. Radiative Transfer and Its Spectroscopic Foundation

Because matter reacts differently to applied light under optically thin vs. thick conditions (Figure 4), radiative transfer exists as two end-member types (Figure 6). These are described by different equations, as follows:

3.3.1. Ballistic Radiative Transfer Requires Optically Thin Conditions

Ballistic (or boundary-to-boundary) radiative transfer occurs under optically thin conditions where the light minimally interacts with the medium (space in Figure 6a), and so does not heat it. Hence, ballistic transfer is irrelevant to the medium’s temperature. Instead, weak interactions that may exist permit probing microscopic behavior of the medium. This process is analogous to absorption experiments and is non-thermal.

The equations for ballistic radiative transfer are identical to those used in spectroscopic analysis (Appendix A) since the optically thin conditions of Figure 4c apply.

3.3.2. Diffusive Transfer Requires Optically Thick Conditions and a Thermal Gradient in an Object or Medium

Under optically thick conditions, the medium is heated as radiation diffuses (Figure 5b) in accordance with Fourier’s laws (Section 2.4.1). Because the entire medium participates, this transfer mode is relevant to temperature.

For heat energy to diffuse, a thermal gradient must exist. Because distance and temperature are related through the gradient, the familiar definition for optically thick conditions of Figure 4d needs amending (Figure 6c):

• Optically thick conditions require that the attenuation distance (2/A) is smaller than the distance over which the temperature changes substantially [18,40,41].

“Substantially” can be gauged from the laser flash method for measuring thermal transport properties, where <4K is the guideline for temperature differences [53].

Importantly, blackbody radiation is the entity diffusing (e.g., [40,41,54]). On a microscopic scale, this process consists of sequential absorption and re-emission events. Diffusion can proceed grain-by-grain (Figure 4b) or atom-by-atom.

Lastly, thermal conductivity is the material property governing diffusion of heat (Fourier’s laws). This quantity is computed from the absorption coefficient A:

$$K(T)={\displaystyle {\int }_{\upsilon \mathrm{lower}}^{\nu \mathrm{upper}}\frac{1}{A(\nu ,T)}\frac{\partial I_{BB}(\nu ,T)}{\partial T}d\nu }$$

(9)

For details see [9,18,21]. Only A is germane to heat transfer because this material property describes the uptake of energy. The integral in Equation (9) is only valid over frequencies (wavelengths) where diffusion occurs.

3.4. Thermal Emission Spectra and Emissivity

3.4.1. Theory

As in absorption/transmission studies, optically thin conditions provide information on (microscopic) material properties. The material property of interest is emissivity (ε), which is dimensionless and varies from 0 to 1, as do the related properties of reflectivity (r), absorptivity (α), and transmissivity (τ). See Appendix A for basic equations and definitions, and Figure 4a,b for a schematic.

Optically thick conditions permit diffusion and so are relevant to heat flow and temperature of the (macroscopic) body. Under optically thick conditions, blackbody radiation (I_BB) is produced internally (e.g., [40,41,55]). For a solid or fluid, but not a gas, internal reflections can occur (Figure 4b) so different equations apply, as summarized in

Table 1. Effect of experimental conditions on emission spectra (E_emit).

	Gas	Equation	Condensed Matter	Equation
Optically Thick	$E_{\mathrm{emit}}=I_{\mathrm{BB}}$	(10)	$E_{\mathrm{emit}}=\left(1-r\right)I_{BB}$	(11)
Optically Thin	$E_{\mathrm{emit}}=\epsilon I_{\mathrm{BB}}$	(12)	$E_{\mathrm{emit}}=\epsilon \left(1-r\right)I_{BB}$	(13)

.

For gas, r = 0 and Kirchhoff’s experimentally determined law on Na vapor applies:

$$\alpha (\lambda ,T) = \mathsf{\epsilon }(\lambda ,T) \left(\mathrm{for\; gas}\right).$$

(14)

Because solids reflect light at their surfaces, Kirchhoff’s law is not strictly true. Thermodynamic considerations were used to extend Kirchhoff’s law [56,57]. Bates [58] derived an exact result by considering forwards and backwards radiation at an interface, giving $\epsilon +r+\tau =1+\epsilon r\tau +r\tau$. Recasting provides:

$$\epsilon ={\displaystyle \frac{1-r-\tau +r\tau }{1+r\tau }}=1-{\displaystyle \frac{r+\tau }{1+r\tau }}=1-{\displaystyle \frac{1-\alpha }{1+r(1-\alpha -r)}},$$

(15)

where the right-hand side utilized 1 = α + τ + r, which describes energy conservation in transmission measurements. If r is nearly 0, Equation (15) reduces to Equation (14).

3.4.2. Gas Behavior in Emission Experiments

In the laboratory, attaining the immense length scales required for a gas to be optically thick is impossible. Laboratory experiments probe emissions of gases under optically thin conditions, and this had led to the incorrect view that the thermal emissions of gas are “spikey”, as in Figure 1b. Kirchhoff’s experiments, being performed under optically thin conditions, went unrecognized. Consequently, Equation (14) has been considered as general and to hold for solids, which is untrue (Section 3.4.1). Importantly, “spikey” spectra are created non-thermally under optically thin conditions, as in neon lamps (Section 3.2), and thus provide emissivity of the gas, not its temperature.

Because a gas body has a temperature, the blackbody curve applies. Although the curve for a gas cannot be measured in the laboratory, the formulae of KTG, Planck, and Stefan–Boltzmann still hold.

3.4.3. Solid Behavior Under Optically Thick Conditions

The ideal spectrum of a blackbody is closely approached by laboratory experiments on solids because optically thick conditions for solids are easy to obtain. Classical experiments held wires at a constant temperature [22,59]. Graphite coatings minimized back (internal) reflections at the surface (Figure 4b). Spectra of graphite and metals, both depending weakly on wavelength over the relevant spectral range, are essential to represent a blackbody.

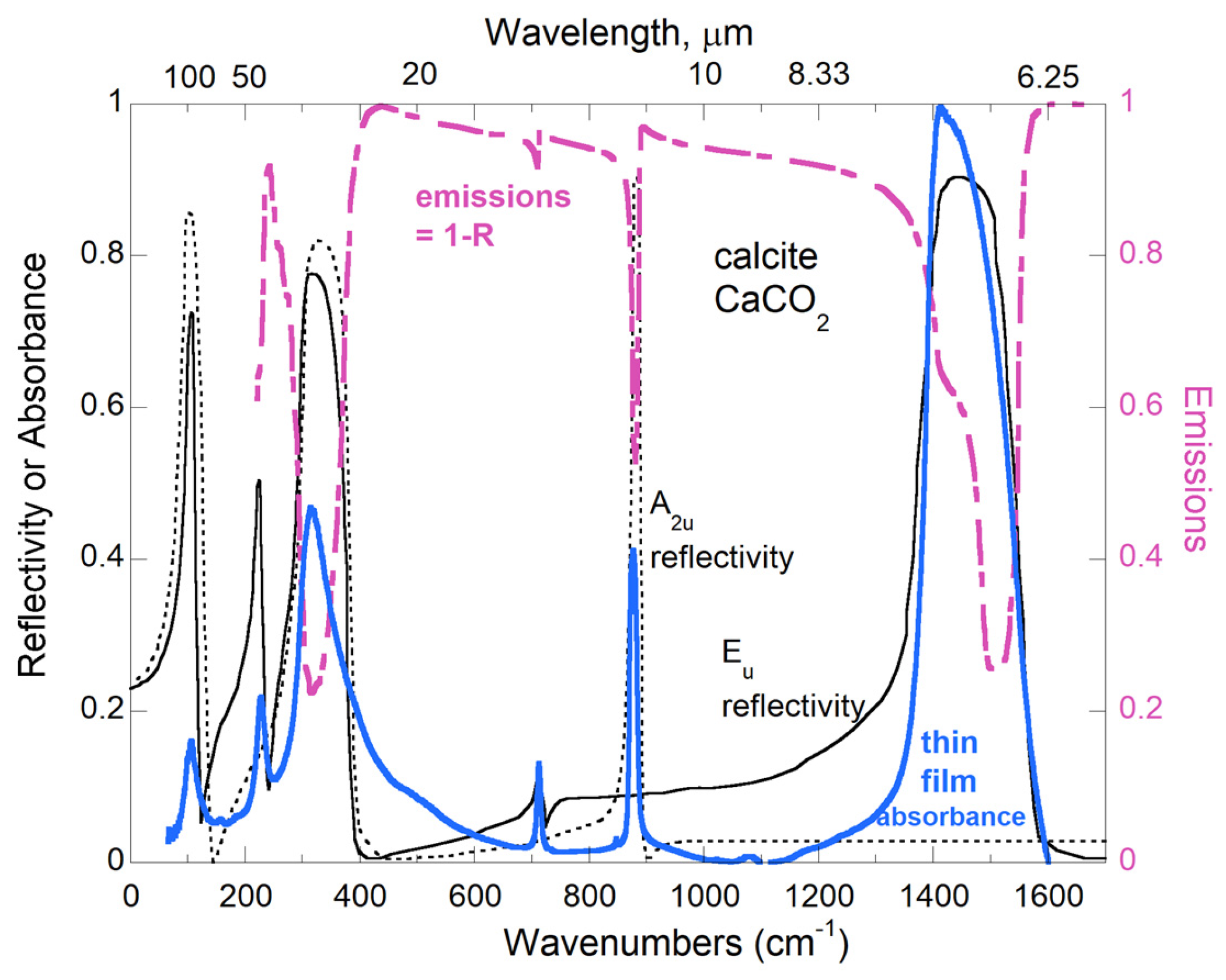
Confirmation of the (1 − r) factor in Equations (11) and (13) comes from data on insulators. For example, Christensen et al. [38] explored grain sizes of ~100 μm, which are much larger than the maximum thickness of ~1 μm needed for optically thin conditions. Thus, optically thick conditions prevail in this database [38]. Subtraction of the blackbody curve from raw emission data (Figure 3) provides a signal with reflection peaks pointing downwards, in accordance with Equations (11) and (13).

Misinterpretation has been fueled by the resemblance of downward-pointing peaks in emission spectra to absorption spectra. Similarities exist because absorption is high where reflection is strong but the profiles are clearly those of unpolarized, internal reflections (Figure 3). Confusion was furthered because Equation (12) for optically thin gases was thought to be generally true, as was Kirchhoff’s law. Equation (14) was derived for solids by chemists and spectroscopists [56,57,58] but has been ignored in many modern studies—Hofmeister [40] discusses misinterpretations of asteroid observations.

Misinterpretation has a further consequence:

• Integrating the product of ε(λ)I_BB(λ) does not produce the Stefan–Boltzmann law multiplied by an average ε because the shape of I_BB(λ) affects the average and differs from the shape of ε(λ);
• Consequently, Equation (2) is correct without ε. Correcting for reflectivity (Equation (11) in Table 1) depends on the surface gradient and layer thickness.

3.4.4. Solid Behavior Under Optically Thin Conditions

Measuring emissivity of a material requires optically thin conditions. At room temperature, great care must be taken to avoid heat transfer between instrument components [60,61]. These experiments on thin solids (tiny grains) at room temperature (Figure 7a) have peaks pointing up, as expected and as observed in gas experiments. However, E for the Si-O stretching bands near 10 μm is lower than E for the bending modes near 20 μm, which is the opposite of intensities in absorption spectra of similar minerals, e.g., [62]. Sample thickness in Figure 7a is likely larger than L near 1 μm for optically thin conditions for silicates established from films in diamond anvil cells [62]. Plus, reflections exist. Because absorption and reflection correlate, Si-O bands would be more reduced by the 1 − r factor than the weaker bending modes.

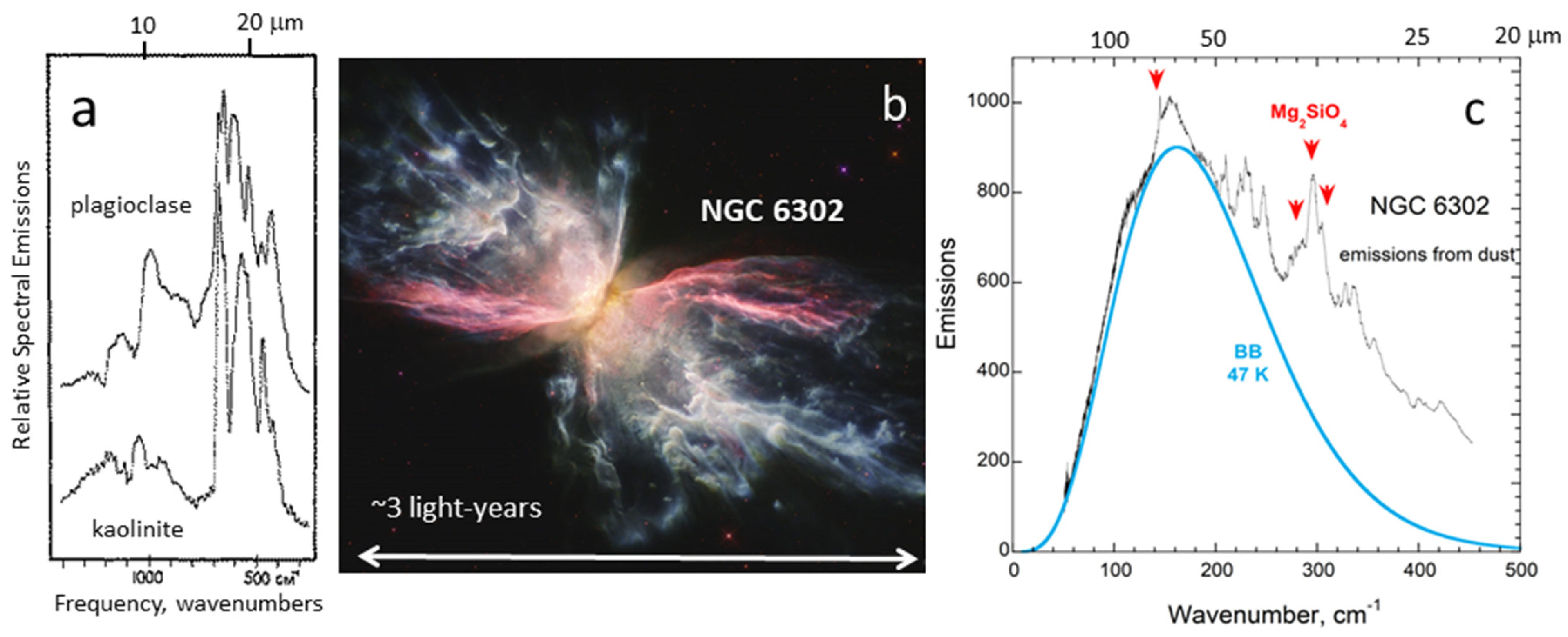
Spectra from dust in space (Figure 7c) are complicated due to multiple phases, with various grain sizes and a temperature gradient, but nonetheless qualitatively follow Kirchhoff’s law. Far-IR spectral emission features of silicate dust [63] are superimposed on a blackbody spectrum, probably from iron or large silicate particles (Figure 7c). As noted in the caption, the features suggest which dust phases are present in the explosion. For tiny silicates, reflectivity is low because peaks in the far-IR are generally weak, see data in [62,63,64,65].

4. Circumstances Needed to Establish Temperature Remotely from Spectra

Because T is a bulk, macroscopic characteristic of the whole medium, it must be determined by measurements made under optically thick conditions. The dichotomy between optically thin and thick conditions, emphasized in the macroscopic theories of Section 2 and Section 3, is summarized in

Table 2. The dichotomy relevant to temperature determinations.

Optically Thick	Optically Thin
Macroscopic Conditions	Microscopic Conditions
Stimulated Thermally by a Heat Source	Stimulated Non-Thermally, e.g., by Particles
Thermodynamic Distribution	Perturbations and Excited States *
Emission (or Reflection) Spectra	Transmission Spectra
Integrated Spectrum or Flux Indicates T	Peak Parameters Indicate Composition, Phase
Temperature Gradient	Transient Elevation of T †
Fourier’s and the Stefan–Boltzmann Laws	Spectral Analysis Equations
Slow Diffusive Radiative Transfer	Fast Ballistic Radiative Transfer

* May be limited to individual particles or to a subset of the collection. † Local equilibrium may alternatively exist.

. Several additional remarks are warranted before discussing astronomical environments.

4.1. Optically Thin Conditions

An absorption peak shows that net energy is assimilated at that particular λ, whereas the same peak in emission shows net release of energy. Both processes can be non-thermal. Uptake or release over some narrow wavelength range are properties of the collective medium but depict local behavior of a select few constituents of that medium. Moreover, peak parameters describe a transition between states, not the individual states. Findings relevant to astronomy include the following:

• Temperature of the object containing the perturbed electrons (or other entity) cannot be deduced either by applying Equation (4) to peak positions or by analyzing peak widths in electronic emission spectra.
• Excited states are not in equilibrium with their surroundings and, thus, do not represent the temperature of the medium or object.
• Hence, electronic transitions are non-thermal, transient, and local processes.
• Spectra of electronic transitions probe microscopic behavior, which permits identifying chemical species in astronomical entities, and is of great utility.
• Spectra record the energy of transitioning between two states, not the energy of either state. Peak breadths likewise embody differences between the two states.

4.2. Optically Thick Conditions

Use of Wien’s law to deduce temperature implicitly requires that the observed spectrum has the broad, lop-side shape of the Planck curve. This curve may be modified by internal reflections at the emitting surface (Section 3.4).

Blackbody radiation by an object involves diffusion and is detected only under optically thick conditions. Confusion has arisen because this condition cannot be realized for a gas in the lab. Findings relevant to astronomy include the following:

• A gas always has a temperature but thermal emissions from this collection can only be observed from a sufficiently large volume.
• Because the hallmark of a blackbody is the strong increase in intensity with T (the Stefan–Boltzmann law), thermal emissions can be observed from a much smaller volume of gas with a high T, than from a gas with a low T.
• Dynamics of electrons, particularly their transitions, are not part of temperature per the Born–Oppenheimer approximation and because KTG, which provides T by describing atoms as indivisible particles, has been experimentally validated. The best agreement is with monatomic gases.
• Because gas temperatures are derived through kinetic motions and inelastic collisions of entire atoms, the statistical representation of gas temperature (i.e., thermal emissions) is a continuous curve.
• Because temperature is macroscopic, for ionization to arise thermally, the entire region must be affected to the same degree.

4.3. Composite Media

Real objects are commonly composed of multiple layers. All of the different layers can contribute to the overall spectrum. The specific manifestation depends on whether individual layers are optically thick or optically thin. The examples provided below illustrate different situations encountered in astronomical environments.

5. Evaluation of Temperatures in Astronomical Environments

The Universe contains gargantuan expanses of gas. For a gas, reflectivity r = 0. Consequently, broad-band emissions exist and are those of a blackbody. The examples below progress up in length scale. The Sun is included, which necessitates addressing reflections at its condensed matter surface and considering its layered atmosphere.

5.1. Lightning, a Hot Gas with Layers

Behavior of a real, hot gas is documented by the atmospheric phenomenon of lightning. For this case, spectroscopic and other observations constrain the temperature. Lightning is observed on Earth, Jupiter, and Saturn, and is expected to occur elsewhere in the Universe.

5.1.1. Characteristics and Visible Spectra of Lightning Strikes on Earth

Lightning [66] is a transient path in the atmosphere heated by an immense electrostatic discharge of millions of volts. The path in a cloud-to-ground strike can be many kilometers long.

The hot central region has a diameter of generally a few cm, as gauged by fulgurites, which are fused soil tubes created during a strike [67]. When lightning strikes sand, fulgurites containing silica glass can be produced, which requires temperatures in the melt zone to exceed 1986 K during the strike. Petrographic and experimental studies of fulgurites support temperatures of about 2000 K for the central core (e.g., [68]) and provide no evidence that the cores have temperatures near 25,000 K, as calculated using models, e.g., [69].

The core of a lightning bolt is surrounded by a cylindrical shell of glowing gas. Images and eyewitnesses close to a strike suggest that this shell has a diameter of a few meters [70]. The width of this glowing shell is much greater than that of fulgurites, which is consistent with shell temperatures being much lower than core temperatures.

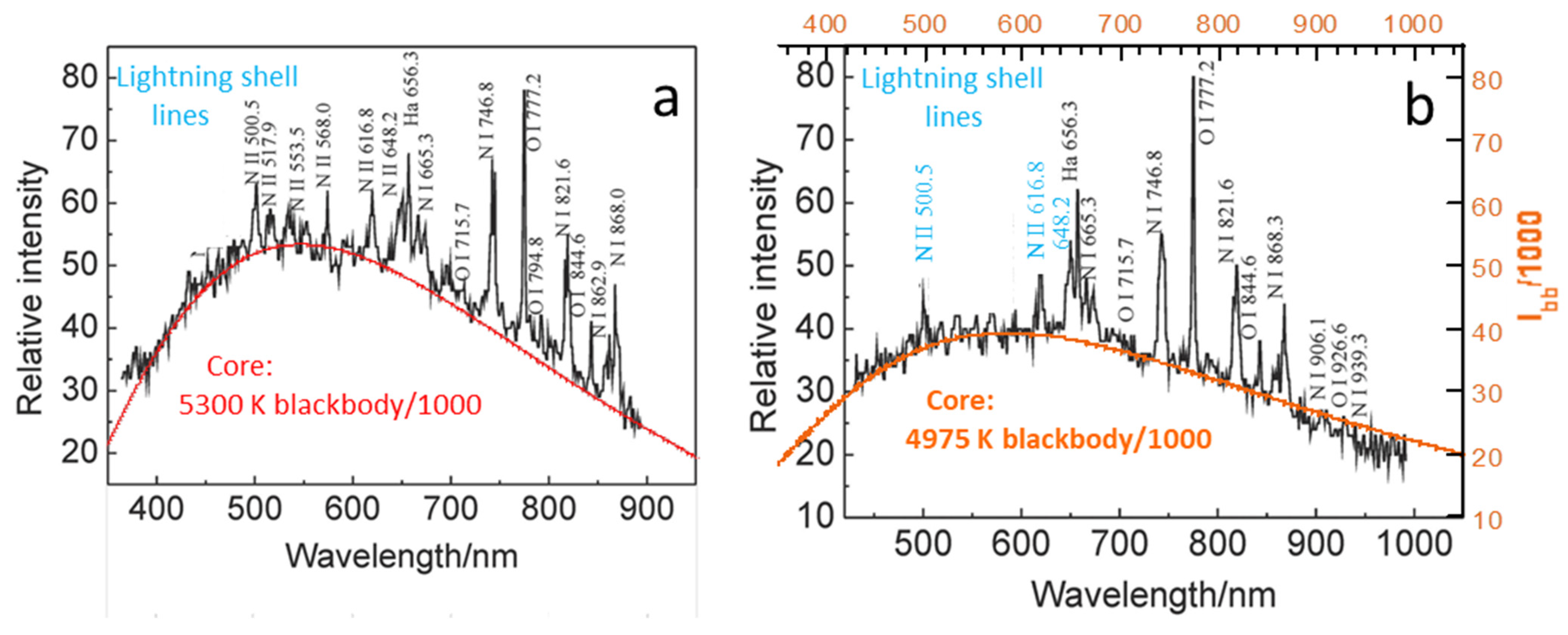
Figure 8a shows a spectrum of the return stroke from a cloud-to-ground strike [69]. The spectrum consists of a blackbody curve with a superimposed series of emission lines from both neutral atoms and ions. For convenience, the y-axes in Figure 8 were scaled to match the reported relative intensities to I_BB. Because the position of the detector was not changed, Figure 8b should quantify time-dependent changes in the bolt upon the 117 μs pause in data collection. Blackbody intensity is reduced but the relative intensities of the superimposed narrow peaks do not follow a consistent pattern. Over the briefer time interval of data collection, this rapid discharge appears isothermal. Cooling by ballistic radiative transfer to the surrounding gas is a rapid process, and could provide the ~300 K drop during the 117 μs pause (Figure 8a,b).

5.1.2. Implications

Light emissions from the two regions of the lightning bolt, the core and shell, add because the shell is peripheral and optically thin. The core, in contrast, must be optically thick to provide the observed blackbody spectrum. Due to the intensity of blackbody radiation near 5000 K, the core provides a blackbody curve, despite its tiny diameter. The inferred core temperature appears sufficient to create fulgurites a few centimeters in diameter but not to vaporize the ground.

The ~meter-diameter cylindrical shell observed by humans glows but is insufficiently hot to melt soil. Excitation of the electrons and production of ions in the shell are almost certainly non-thermal electrical processes, as in plasma globes (Figure 5b). Loss of lines from positive N ions with time (cf. Figure 7a,b) shows these states are dissipating. Diffusion of radiation is too slow compared to duration of the bolt to provide much heating, and moreover, any blackbody glow from the shell would be overwhelmed by the emissions from the much hotter core (e.g., Figure 2).

High-temperature estimates of ~25,000 K for lightning provided by models are inconsistent with the physical effects of the stroke (discussed above), and with the bolts consisting of a core and shell. These high estimates are largely based on the incorrect explicit assumption that the electrons are thermally excited and so their narrow emission lines indicate gas temperature; see, for example, Dong et al. [69]. Obviously, each line would suggest a different “temperature” that is connected with a particular transition of electrons around a cation, rather than with the collective behavior of the medium. Emission lines signify energy emitted as the non-thermally excited electrons re-equilibrate. Electrical discharge provides non-thermal stimulation, as in the neon lamp and plasma globe.

Our assignment of the bolt spectrum as distinct, summed contributions of its core and shell is compatible with the divisions summarized in Table 1. Due to its high T, the tiny core is an optically thick, nearly isothermal region that is created by electrical discharge. The large shell is an optically thin zone where the electrons are excited non-thermally. Due to the transient nature of lightning, emissions of electrons in the shell (cooling to the surroundings) are observed.

5.2. Solar Surface and Atmosphere Temperatures

Immense coronal temperatures of ~10⁶ K values are accepted in modern studies of solar and stellar physics. Yet, the source of the immense coronal heat remains a long-standing scientific enigma (e.g., [1,2]). The main focus of this section is to deduce average temperatures of the solar atmosphere by applying macroscopic physics (Section 2, Section 3 and Section 4) to the light emitted from the Sun. However, problems with spectroscopic assessments of ~10⁶ K values are worth mentioning, outlined as follows.

Corona temperatures have been based on ionization energies, peak assignments, and breaths of electronic peaks. First, spectra probe energy differences between states but not the states themselves. The breadths likewise describe differences between electron states, not velocities of the electrons in some specified state. Both reveal microscopic, not macroscopic, behavior. Second, the spectra do not probe an electron gas but rather describe changes in electronic configurations associated with various ions. Assignments of peaks to ions are instead relevant to chemical composition. Third, even if an electron gas existed, this still would not provide corona temperature, per femtosecond spectroscopy of metals (Section 3.2.2). The temperature of the corona is instead associated with translational motions of these ions. Fourth, ions can be produced by particle collisions.

Steady-state conditions, where heat transfer depends on space but not time, apply to our long-lived, main sequence star. We do not discuss short-term perturbations (e.g., solar flares), which are irrelevant to the time-averaged, long-term thermal structure at and above the Sun’s surface. Lightning, discussed above, exemplifies a transient perturbation.

5.2.1. Solar Emission Spectra

Solar emissions to space (Figure 1a) depart from an ideal blackbody spectrum. Understanding the implications requires considering many factors:

• Heat-energy flows down the thermal gradient (Equation (4)).
• Enormous internal heat sources reside in the Sun’s hot, deep interior, not in surficial or atmospheric layers.
• Images at all wavelengths ([71,72,73]; Figure 9) show the surface of the Sun, rather than an interface somewhere in its atmosphere. Thus, the solar atmosphere is optically thin at all wavelengths probed. This configuration of an optically thin shell around the optically thick solar body is similar to that of the shell and core of a lightning bolt (Section 5.1).
• Back reflections existing at the imaged solar surface (Figure 4) need accounting for.
• Absorption lines are produced when energy from the surface is taken up by the atmosphere under optically thin conditions so their presence does not constrain T (Section 3.1).
• Perturbed, excited states re-equilibrate to the temperatures of the surroundings by emitting light, such that energy is conserved within the collection but not at any given wavelength.

Figure 9. Images of the Sun at different wavelengths. (a) X-ray image of the solar corona taken by the Yohkoh satellite on 8 May 1992 [72]. Solar X-ray image courtesy of the Yohkoh Legacy data Archive at Montana State University. Reprinted with permission. (b,c) UV. (d) Visible. Images in panels (b–d) are open access and were all taken within a few minutes of each other on 20 January 2025 [73]; note the correspondence of the sunspots in panels (c,d) with the bright areas in panel (b), and the apparent limb darkening in panel (d).

Figure 9. Images of the Sun at different wavelengths. (a) X-ray image of the solar corona taken by the Yohkoh satellite on 8 May 1992 [72]. Solar X-ray image courtesy of the Yohkoh Legacy data Archive at Montana State University. Reprinted with permission. (b,c) UV. (d) Visible. Images in panels (b–d) are open access and were all taken within a few minutes of each other on 20 January 2025 [73]; note the correspondence of the sunspots in panels (c,d) with the bright areas in panel (b), and the apparent limb darkening in panel (d).

To address the many items above, a simplified solar structure (Figure 10) is considered. Specifically, the following applies:

“Solar surface” refers to the granulite layer, which, being condensed matter, provides a well-defined boundary upon which the Sun’s gaseous atmosphere rests. Imaging the granules [71] is possible because condensed matter reflects light. The granules are considered part of the photosphere from whence light comes, thought to be ~400 km thick [74]. Granules are small-scale (relative to the Sun) convection cells [71], which tend to be equant so the photosphere likely represents only the upper section of the ~1500-kilometer-diameter granules. Either thickness is negligible compared to the solar radius of 695,700 km, and so this thin zone composes the “solar surface.”

“Chromosphere” denotes the gassy region immediately above the solar surface, which is currently considered to be only ~1700 km thick [74]. The existence of a transition zone (~100 km thick) between the chromosphere and the corona is based on the presumed high T of the corona, and so it is discussed after our analysis is presented.

The “corona” is gaseous, optically thin, and grades into space. Temperatures of this region are the focus here.

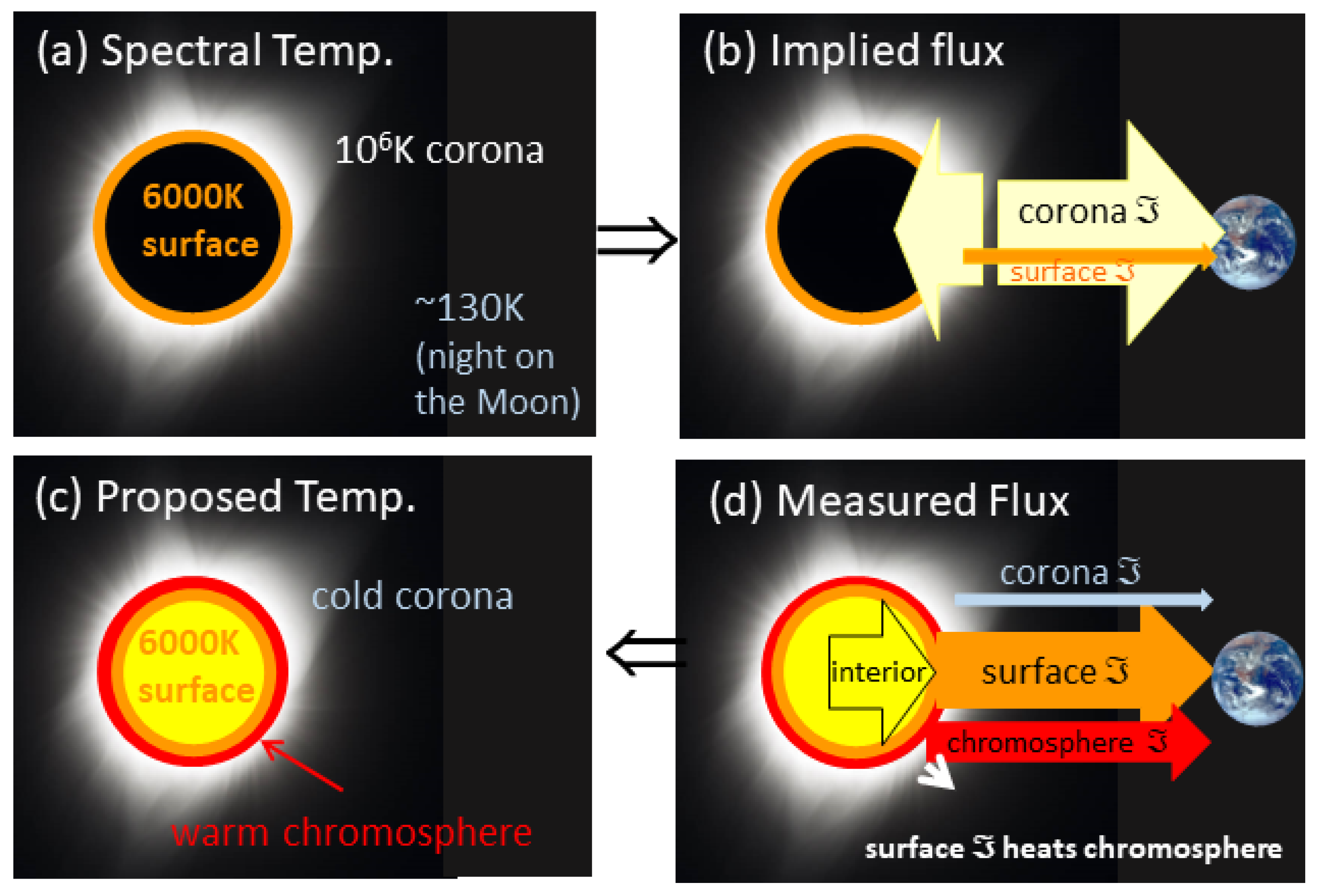
Figure 10. Temperatures of the outside layers of the Sun, superimposed on an image of the corona taken during a total solar eclipse on Monday, 21 August 2017 above Madras, Oregon. (a) Conventional view of the effective flux of the surface, the temperature of which is given in round numbers, and the proposed temperature of the corona based on spectral lines of ionized elements. For simplicity, the chromosphere is omitted. (b) Fluxes from the 2 hot layers shown in panel (a), required by the thermal gradient. The cold (~300 K) Earth receives fluxes from the surface (orange arrow) and corona (pale yellow arrow), while corona flux is also directed inwards. (c) Temperatures proposed in this work. (d) Measured fluxes, based on Figure 1, used to infer outer-layer relative temperatures. In all panels, the corona image is open-access information from NASA, which the governmental organization credits Aubrey Gemignani [75]. Earth’s image from NASA is likewise public domain [76].

Figure 10. Temperatures of the outside layers of the Sun, superimposed on an image of the corona taken during a total solar eclipse on Monday, 21 August 2017 above Madras, Oregon. (a) Conventional view of the effective flux of the surface, the temperature of which is given in round numbers, and the proposed temperature of the corona based on spectral lines of ionized elements. For simplicity, the chromosphere is omitted. (b) Fluxes from the 2 hot layers shown in panel (a), required by the thermal gradient. The cold (~300 K) Earth receives fluxes from the surface (orange arrow) and corona (pale yellow arrow), while corona flux is also directed inwards. (c) Temperatures proposed in this work. (d) Measured fluxes, based on Figure 1, used to infer outer-layer relative temperatures. In all panels, the corona image is open-access information from NASA, which the governmental organization credits Aubrey Gemignani [75]. Earth’s image from NASA is likewise public domain [76].

5.2.2. Immense Temperatures for the Corona Cannot Represent This Optically Thin Body

From theory and experiments on lightning (Section 5.1), a gas at a modest T of ~5000 K is optically thick over a tiny distance of centimeters. Thus, the immense corona, even if it were as “cool” as ~6000 K, would emit a blackbody spectrum with flux similar to that from the solar surface. Because light from this optically thin atmospheric layer is visible only when emissions from the hot solar surface are blocked, as during a total eclipse (Figure 9), the intensity of light emitted by the corona is much lower than the intensity of light emitted from the Sun’s surface.

• Should the corona’s T actually be ~10⁶ K, its flux would be gargantuan, as depicted in Figure 2, and the Sun’s surface would be invisible, particularly in the UV or X-ray regions, yet images of the surface at such wavelengths are available (Figure 10). Reflections cannot occur in the gaseous corona so none could reduce coronal emissions from I_BB (Section 3.4.1).
• Furthermore, the corona’s temperature cannot even approach that of the Sun’s surface, or the flux measured on Earth would dominantly come from this surrounding layer, and the Sun would not even appear to be round.
• Temperatures experienced by the Parker Solar Probe [77], which has passed several times through the outer zones of the corona, have never exceeded 1300 K, and are consistent with blackbody temperatures calculated for the probe’s distance from the Sun.

Likewise, the chromosphere cannot involve temperatures exceeding that of the solar surface it surrounds. Both the corona and chromosphere are optically thin over the vast wavelength range where data and images of the Sun’s surface are available. So, what temperatures for the various layers are consistent with the observed emissions and macroscopic theory?

5.2.3. Solar Surface Temperatures

Similarity of total flux from the Sun to that of a blackbody curve is the basis of effective temperature of the Sun and other stars [26]. However, experiments and theory show that the measured flux is reduced by surface reflections at each and every λ. From Equation (11), the frequency-dependent response of the solar surface spectrum is:

$$1-r={\displaystyle \frac{SSI}{I_{BB}}}\le 1$$

(16)

Consequently, at each wavelength, the surface emissions cannot exceed the blackbody spectra that represent this surface. From Figure 1, the minimum T of the solar surface is close to 6000 K. Assuming that the excess emissions at 1600 nm are due to reflection variations with λ, the surface may be at 6275 K. Figure 11 provides the spectral properties of the solar surface for these two possible temperatures.

The superimposed sharp peaks point down in the SSI (Figure 1) and in the extracted 1−r (Figure 11). These are well-known absorption features and, thus, describe uptake of the Sun’s surface emissions by its atmosphere. These absorption lines and the few emission lines present in the UV are further discussed below.

The overall pattern of the material properties is decreasing reflectivity from the UV to visible, and then roughly constant r at longer λ. Why reflectivity of solar material depends on wavelength is beyond the scope of this report. Irrespective of the microscopic, physical origin of reflections, the temperature of the solar surface is between 6000 and 6275 K.

5.2.4. Temperatures of the Chromosphere and Corona

Although the chromosphere must be emitting in accordance with its average macroscopic temperature, these emissions cannot be detected due to its optically thin character, and the much greater flux from the Sun’s surface. The latter finding was confirmed by attempts to fit the SSI (Figure 1) with two blackbody curves, one near 1800 K, as suggested by the “bump” near 1600 nm, and one near 6000 K, suggested by the maxima near 500 nm. Relative intensities fall rapidly with T, whereas large breadths are little affected by T, which cause the high T flux to obscure the low T flux.

The average temperature of the chromosphere must, thus, be <1800 K. Temperature decreasing outwards is required by the Stefan–Boltzmann law and Fourier’s laws, and the lack of a significant heat source inside the atmosphere. Thermal models of this situation are beyond the scope of this report, but as a first-order approximation, T varies from 6000 K at the surface to no more than 2400 K at about 2000 km elevation per the above fitting attempts. Temperature continues to decrease through the corona, ultimately becoming a few K at great distance.

5.2.5. Origin of Lines in Solar Emission Spectra and Implications

The solar atmosphere receives flux from the solar surface. However, being optically thin, the atmosphere can only uptake heat at discrete transitions. Down-pointing peaks indicate the wavelengths where net energy uptake occurs. Emission lines are limited to the UV region, where thermal emissions from the Sun are comparatively low (Figure 1).

The Ly_α line and other UV emission lines, all of which have very low intensity (Figure 1b and Figure 9) represent return of excited electrons in the atmosphere to their ground state. A steady-state energy balance exists over all wavelengths. Absorptions exist where the solar flux is substantial (λ > 175 nm) and, thus, can provide non-thermal stimulation. Emissions are observed below 175 nm if their intensity exceeds the solar emissions and spectral noise (Figure 1b). Excitation of neutral hydrogen’s electrons to the n = 2 state is likely by particles or possibly by strong magnetic fields acting on electrons, which are situated on atoms that move in accordance with gas temperature.

Particle fluxes also cause ionization, as in the lightning bolt and plasma globe examples. Prominent Fraunhofer lines are assigned to singly ionized Ca, Ti, and Sr [78]. These have fairly low single ionization potentials (<6.8 ev, e.g., [79]).

5.3. Temperatures in Nebulae and Intergalactic Media

5.3.1. Cold Molecular Clouds

These star-forming regions contain H₂ and CO molecules. Calculated temperatures of 8 to 20 K are typical [80], where rotational transitions of CO have been used to ascertain temperatures [81]. Gas kinetic temperature, which is modeled [82] provides similar temperatures. As discussed above, gas lines do not reveal temperature, and model temperatures rest on the assumptions made.

Another approach has involved measurements of flux and/or luminosity. By evaluating far-IR flux, Ryter and Pugett [83] infer T of 25 to 38 K for nine molecular clouds. These temperatures are reasonable because the high flux of the many young, large, and bright stars in these star-forming regions should provide T higher than the ~3 K estimated by Eddington [84] for which heating by “average” stars pertains. Subsequent studies similarly consider the flux and luminosity of molecular clouds [85], rather than a continuous curve. This approach to inferring T requires modeling dust properties [80].

To better constrain temperatures of star-forming regions, measurements of spectra over a wide wavelength range were called for in 2007 [80]. Such data should provide the required thermal emission curve. However, such results were not discussed in the 2015 review [81]. Rather, the focus recently has been on maps at certain long wavelengths (e.g., [86]).

Although the temperatures of molecular clouds are not yet definitive, these environments are clearly cold.

5.3.2. Is the Orion Nebula Hot or Cold?

The Orion Nebula (M42) is a visible, well-known collection of rarefied gas and newly formed stars in the Milky Way. Calculated temperatures of 10,000 K are estimated from electron transitions (e.g., [87] and many subsequent papers). Hundreds of emission lines exist [88], and each one would provide a different temperature. Many lines are connected with ions. The existence of a thin blister of ionized gas, which is considered to be hot, on the front of a giant molecular cloud in the Orion Nebula is viewed as a conundrum, i.e., how can the cold molecular cloud exist?

Like the corona, it is presumed that ionization occurs via heating and that the electron transition lines indicate the temperature. Neither is required. Instead, non-thermal stimulation is ample via UV and by the particles emitted from the many young, proximal stars. The glowing Orion Nebula may appear hot but it is very cold.

5.3.3. Temperatures in Intergalactic Media

Masses of gas in circumgalactic (CGM) and intergalactic (IGM) media, which have mostly been ascertained from forward fitting models [89], are underestimated, relative to models of the Big Bang [90]. One proposed explanation of this shortage is that temperatures in some low-density regions are sufficiently hot to ionize hydrogen, the dominant species, thereby rendering spectral signatures of the baryons indistinguishable from noise in most acquisitions (e.g., [91]).

The proposal of a warm–hot intergalactic media (WHIM) has not resolved the alleged mass shortfall, despite exploration of the WHIM hypothesis in two unrelated ways: via models of shock heating without collisions (e.g., [92]), as well as through measurements of absorptions (e.g., [93,94]). Furthermore, absorptions of Fe and O atoms have been attributed to cold outflows, rather than to WHIM itself [95], and so direct evidence for WHIM is lacking.

Several additional aspects of this proposal call its basis into question:

• Extreme temperatures of 10⁵ to 10⁷ K have been proposed for WHIM, which resemble the extreme temperatures calculated for the solar corona. Yet, spectral lines from the corona are well-resolved and have been amply studied, as reviewed in [96]. These lines are observed in both absorption and emission during an eclipse [97]. Should the corona actually be hot, then by previous reasoning, an extremely hot IGM could not obscure spectral evidence for baryons but would enhance their intensity.
• Should neutral H be ionized, where would the electrons reside? Coulombic forces are strong and charge is conserved.
• The observed absorption lines in IGM indicate that non-thermal excitation prevails. Absorption lines are produced under optically thin conditions and do not indicate T (Table 1). Optically thin conditions are indicated by images of galaxies throughout the IGM over a wide range of wavelengths.

Intergalactic media are cold.

The suggested shortage of baryons may not exist [98]. This shortage originates in forward fitting models [89] of galactic rotation curves (RC), which assume the existence of non-baryonic dark matter (NBDM). Inverse models by several authors explain RC without NBDM by accounting for galactic shape affecting gravitational attraction to these objects (reviewed by [99]).

6. Discussion

6.1. Temperature

Temperature is a key macroscopic attribute of an object, which is needed to quantify the transfer of energy between that object and all other matter in the universe. In many familiar situations, temperature can be directly measured using various conventional instruments and techniques, each calibrated against Kelvin’s historical scale. However, temperatures of remote astronomical objects must be estimated from their spectral signature, and as shown here, spectra typically contain contributions from both thermal and non-thermal processes. Attempts to use non-thermal spectroscopic features to estimate temperature have led to unrealistic assignments for diverse media and objects.

Light bulbs clarify the important difference between thermal and non-thermal spectral features. Among those in common use, only incandescent bulbs become dangerously hot, and these display a continuous spectrum of prismatic colors. In contrast, fluorescent tubes and LEDs are much cooler for the lumens generated, and these exhibit strong spectral lines, for example, see [100].

6.1.1. Temperature and the Independent Electron Approximation

Continuous spectra arise from blackbody radiation, which is a macroscopic characteristic of a material that originates from interactions that involve its entire population of particles. In contrast, discrete spectral lines are microscopic characteristics that involve a select few particles whose electrons have become excited into transient, non-equilibrium states. In the commonly explored visible range, the latter arise from electronic transitions, which change the shape and size of the electronic cloud around an atom. Yet, it is indisputable that heat is stored in the motions of whole atoms, which are governed by the motions of their massive nuclei, both locally (translations and for polyatomic additional vibrations) or globally (kinetic theory of gases).

The difference between electronic and atomic motions is most easily visualized for a gas as the electron clouds are simply carried along by their moving atomic nuclei. This difference is theoretically expressed as the “Born–Oppenheimer” [17] or “independent electron” [16] or “adiabatic” [14] approximation, where the latter connotes that heat lies in the nuclear motions. This difference is experimentally demonstrated by femtosecond spectroscopy of metals, as well as by line spectra of room-temperature neon lamps. In modern solid-state physics, the term “electron temperature” is used to describe excitation of the electron population and to distinguish this from the lattice temperature, which describes a condition common to the whole object.

6.1.2. Wien’s Law, Color, and Power

Use of Wien’s law to define temperature is valid if and only if the spectrum is that of a blackbody, owing to the mathematical properties of a blackbody. For example, rubies in jewelry have an attractive red color due to electronic transitions of their Cr ion impurities, yet the wearer is not burned by this red light. Transitions measured spectroscopically to not provide kinetic temperatures.

Spectra dominated by discrete peaks, e.g., the Ly_α and other UV emission lines in the SSI and previous studies [23,24,29] or the plethora of spikes in the spectrum of a neon lamp, are clearly different. This difference, and ambiguities in determining T from Wien’s law when more than one discrete peak exists, are recognized, yet the notion that line spectra indicate temperature persists (see the examples in Section 5).

The energy required to excite an electron or even a collection of electrons is tiny, as is evident in the small integrated area under any discrete spectral peak of interest. It is also evident in the specific heat of electrons being low, as is well-known for metals [15]. Electrons uptake and store little heat: see [101] for further discussion.

Total flux, not peak position or color, is a quantitative indicator of heat release, and thus of temperature, via the Stefan–Boltzmann law.

6.2. Heat Transfer and Spectroscopy

Qualifiers such as “electron temperature” and “gas, lattice, or body temperature” are needed to connect the spectroscopically assigned numerical value for T with microscopic physical processes of heat storage and heat transfer. Even more essential is differentiating “ballistic transfer” from “diffusive transfer.” In laboratory heat transfer measurements at ordinary temperatures, most techniques cannot differentiate between these two processes. A great advance was made in the 1990s when quantitative models were developed, which removed unwanted systematic ballistic radiation from laser-flash measurements [102]. This advance permitted quantifying the thermal conductivity of glasses, which are technologically important materials.

The present paper emphasizes how crucial the difference in transport modes is to understanding radiative heat transfer over small to gargantuan scales. Table 2 links ballistic radiative transfer to optically thin conditions and microscopic behavior, which portray the optical properties and chemical composition of materials. In great contrast, diffusive radiative transfer links to optically thick conditions and macroscopic behavior, which portray the temperature of an object. The dichotomy between modes of radiative transport and their spectroscopic and thermophysical underpinnings was not previously recognized in astronomy. This dichotomy underlies the fantastic temperatures of millions of degrees that have been proposed for rarified media of the solar corona, nebulae, and intergalactic media.

Additional repercussions exist. Not distinguishing ballistic from diffusive processes led to incorrectly interpreting laboratory emissions from gases as a modified blackbody curve, when optically thick conditions did not exist. Likewise, the same omission led to misinterpreting the emission spectra of solids as a simple consequence of emissivity, when optically thin conditions were not met. This omission has also led to confusing the reducing effect of surface back reflections on emission spectra (Figure 3) with emissivity. As discussed above, flux is also misinterpreted because emissivity cannot affect blackbody emissions. Because this ideal has r = 0 and ε = α = 1, any experiments approximating blackbody emissions must have material properties that approach these limits at all wavelengths. This misinterpretation of experimental conditions also rests on assuming that light always involves thermal stimulation. Instead, light stimulations of electron transitions are non-thermal events, consistent with the Born–Oppenheimer approximation. As a consequence, Kirchhoff’s law, which only applies to material properties of gases, is routinely applied to solids in the lab and in space, the usage of which cannot conserve energy (Equation (A2)).

In many astronomy applications, reflections are irrelevant since the bodies are gaseous. However, the Sun has a distinct surface, which is a phase transition between its gassy atmosphere and its condensed (or fluidized) surface, as evidenced by granules and images. It follows that back reflection at this interface modifies the emissions of deeply generated heat. We have bracketed the solar surface average temperature between 6000 and 6275 K. Below the granules, temperatures would be higher.

Due to reflectivity varying with wavelength, calculating an effective temperature for a star requires knowing its spectrum over a wide range. Data on the Sun show that UV light is largely back-reflected at its surface. Under steady state conditions, the Sun has evolved so that inward flux is “accounted for” in the total emissions. However, the total emissions as measured do not provide sub-surface temperatures. Conditions just below the solar surface are complicated as the granules are convection cells. Convection redistributes temperature when the thermal conductivity of the material cannot sustain the imposed thermal gradient [103]. Phase equilibria determine solar surface temperature but relevant conditions have not been achieved in the laboratory (e.g., [104]).

6.3. Non-Thermal Stimulation Excites Electrons and Produces Ions

Electrons are highly susceptible to many types of non-thermal excitation. With their tiny mass, little energy is needed to move these away (on average) from the central nucleus and even to separate electrons from nuclei, as in the plasma globe example. The close relationship of magnetic and electric fields shows that magnetic fields, which are immense in the Sun, would perturb its electrons without elevating their temperature. As is well-known, light is electro-magnetic radiation, and so this too will perturb electrons while negligibly heating the medium, as evidenced by experiments on metals [46,47,48,49,50,51,52].

This finding can also be framed in terms of the first law of thermodynamics (energy conservation). Moving low-mass electrons requires little work and so generates little heat.

6.4. Future Research Directions

6.4.1. Laboratory Studies

More experimental work is needed. Use of thin graphite coatings on solids scatter light, thus eliminating reflectivity, which was essential to successful measurements of blackbody flux by Stefan and the blackbody curve thereafter [22,59]. Emission spectra from bare metal wires at nearly 4000 K are available (e.g., tungsten filaments [105]) but reflections were neglected in the analysis of such data. Moreover, measurements stop in the visible. Yet, the tail into the UV is important to interpreting the SSI. In lieu of attaining solar pressures and temperatures in the laboratory, the behavior of other solids will provide the most relevant guidance. Carbon fibers may be worth exploring.

Gases have no reflectivity but their blackbody spectra have not been determined in the laboratory because the required optically thick conditions have not been achieved. However, lightning needs no container; measurements of its UV and far-IR spectra are needed.

Spectroscopic studies of materials simultaneously undergoing both thermal and non-thermal excitation would also be revealing. Such experiments would more closely reproduce the situation in real astronomical environments.

6.4.2. Astronomy Studies

A natural “laboratory” exists in space as stars have a wide range of colors and luminosity. Moreover, stars emit much UV light and are optically thick. Since their surface reflectivity is unknown, it is of great importance to measure spectra to ascertain flux, rather than to measure magnitudes using narrow-range filters. Especially needed are more spectral measurements of natural and astronomical objects that encompass large wavelength ranges.

Observation of neutral H transitions in corona spectra [96] provides confirmation of non-thermal excitation. The assignments of other lines in corona spectra to highly charged ions assume high temperatures. Collisions with protons (cosmic rays) are highly likely. Revisiting assignments is called for, particularly since temperatures directly measured by the Parker probe when it was located in the corona [77] are consistent with emissions from the ~6000 K solar surface at the reported distance.

7. Conclusions

Temperature is a key macroscopic attribute of a material object that is related to energy transfer. There is only one temperature. The fundamental Kelvin scale allows a temperature measurement to be expressed as a positive real number that is closely related to the ideal gas law, the kinetic theory of gas, and many macroscopic properties of materials. Most fundamental is the relation of temperature to the flux of blackbody energy emanated by an object, as quantified by Fourier’s laws and the Stefan–Boltzmann law. The omission of these dynamic laws from classical thermodynamics is a major theoretical flaw that impacts research in astronomy.

Spectra of real objects are a combination of thermal and non-thermal features, which may be associated with different layers in that object. Only thermal features are related to macroscopic temperature, via the continuous blackbody spectrum and the Stefan–Boltzmann law. In contrast, most discrete spectral lines are due to non-thermal excitation of electrons by not only light, but also by processes such as particle bombardment. Discrete spectral lines provide important data on the chemical composition and phase of the emitting objects. However, inappropriately using them to estimate the temperatures of remote objects has led to large overestimates of the actual macroscopic temperatures, resulting in thermal profiles that are physically impossible according to Fourier’s laws.

Blackbody spectra are prominent only for optically thick media. This condition is easily realized for solids but has not been achieved under laboratory conditions for gases. In contrast, line spectra are readily observed in optically thin media. Many objects, ranging from lightning bolts to stellar atmospheres, consist of an optically thick interior zone and an optically thin shell. The resultant spectra of such bodies are a continuous blackbody curve from the hot inner zone with superimposed, discrete spectral lines from the much cooler, optically thin shell. The manifestation (absorption or emission peaks) also depends on circumstances such as steady-state conditions or transient heating. Due to the complexity of layered media, additional observational and experimental work on means of distinguishing spectral features of thermal and non-thermal origin would greatly benefit astronomical research.