On the Probability of the Astrometric Resolution of Spectroscopic Binaries into Components
Abstract
1. Introduction
2. Methodology for Estimating the Resolution Probability Function of Spectroscopic Binary Stars
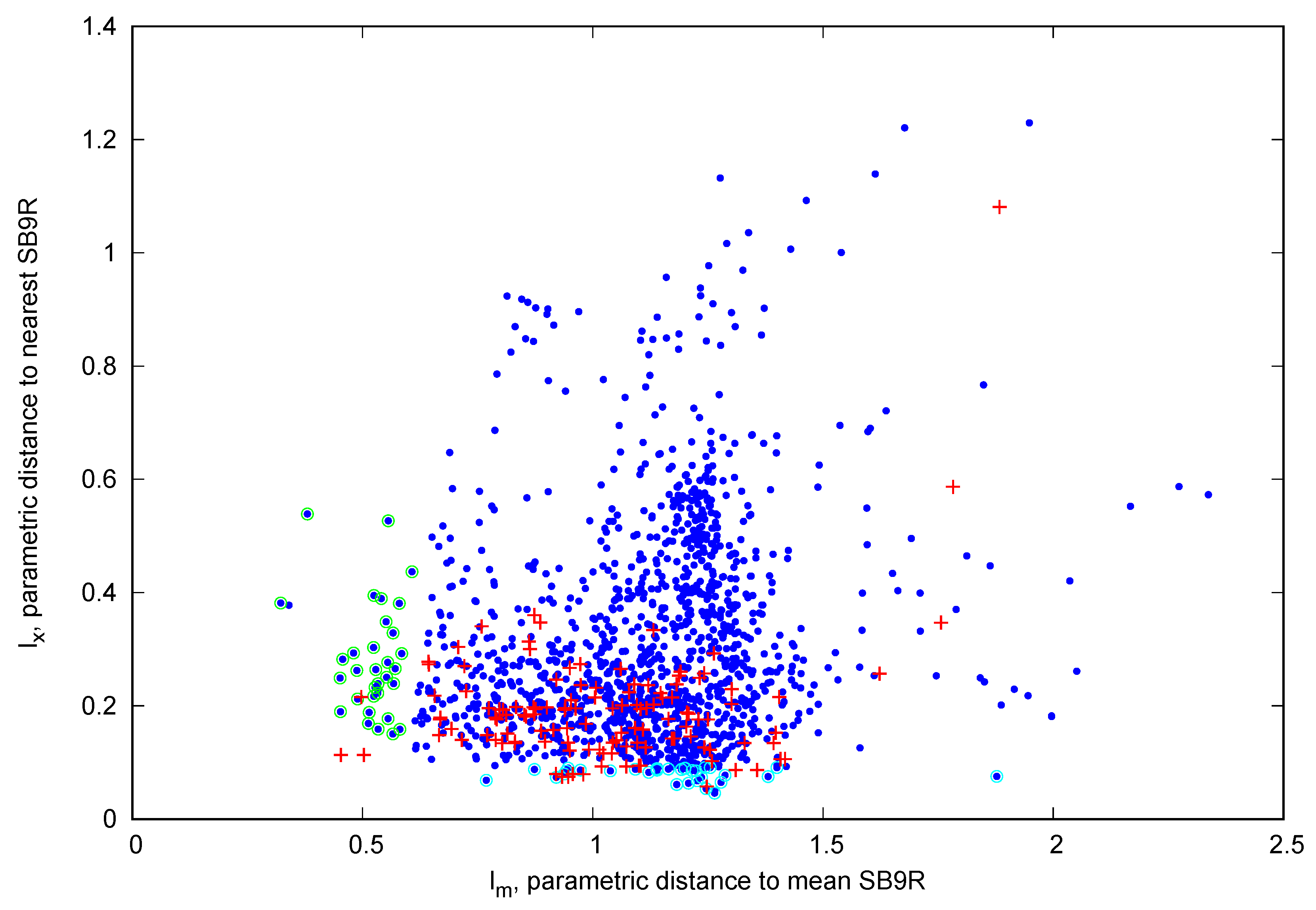
3. Results and Discussion
4. Conclusions
- The probability of the resolution of unresolved objects could be inferred from the similarity to resolved objects;
- Distances in the space of observational parameters could be used as a basic and straightforward measure of similarity;
- The highest similarity is achieved between individual objects, and it is loosely connected to the parameter space occupied by resolved objects.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Duchêne, G.; Kraus, A. Stellar Multiplicity. Annu. Rev. Astron. Astrophys. 2013, 51, 269–310. [Google Scholar] [CrossRef]
- Duquennoy, A.; Mayor, M. Multiplicity among Solar Type Stars in the Solar Neighbourhood—Part Two—Distribution of the Orbital Elements in an Unbiased Sample. Astron. Astrophys. 1991, 248, 485. [Google Scholar]
- Raghavan, D.; McAlister, H.A.; Henry, T.J.; Latham, D.W.; Marcy, G.W.; Mason, B.D.; Gies, D.R.; White, R.J.; ten Brummelaar, T.A. A Survey of Stellar Families: Multiplicity of Solar-type Stars. Astrophys. J. Suppl. Ser. 2010, 190, 1–42. [Google Scholar] [CrossRef]
- Sheikhi, N.; Hasheminia, M.; Khalaj, P.; Haghi, H.; Zonoozi, A.H.; Baumgardt, H. The binary fraction and mass segregation in Alpha Persei open cluster. Mon. Not. R. Astron. Soc. 2016, 457, 1028–1036. [Google Scholar] [CrossRef]
- Yuan, H.; Liu, X.; Xiang, M.; Huang, Y.; Chen, B.; Wu, Y.; Hou, Y.; Zhang, Y. Stellar Loci II. A Model-free Estimate of the Binary Fraction for Field FGK Stars. Astrophys. J. 2015, 799, 135. [Google Scholar] [CrossRef]
- Pourbaix, D. Resolved double-lined spectroscopic binaries: A neglected source of hypothesis-free parallaxes and stellar masses. Astron. Astrophys. Suppl. Ser. 2000, 145, 215–222. [Google Scholar] [CrossRef]
- Anguita-Aguero, J.; Mendez, R.A.; Claveria, R.M.; Costa, E. Orbital Elements and Individual Component Masses from Joint Spectroscopic and Astrometric Data of Double-line Spectroscopic Binaries. Astron. J. 2022, 163, 118. [Google Scholar] [CrossRef]
- Gallenne, A.; Mér, A.; Kervella, P.; Graczyk, D.; Pietrzyński, G.; Gieren, W.; Pilecki, B. The Araucaria project: High-precision orbital parallaxes and masses of binary stars. I. VLTI/GRAVITY observations of ten double-lined spectroscopic binaries. Astron. Astrophys. 2023, 672, A119. [Google Scholar] [CrossRef]
- Jancart, S.; Jorissen, A.; Babusiaux, C.; Pourbaix, D. Astrometric orbits of SB9 stars. Astron. Astrophys. 2005, 442, 365–380. [Google Scholar] [CrossRef]
- Piccotti, L.; Docobo, J.Á.; Carini, R.; Tamazian, V.S.; Brocato, E.; Andrade, M.; Campo, P.P. A study of the physical properties of SB2s with both the visual and spectroscopic orbits. Mon. Not. R. Astron. Soc. 2020, 2, 2709–2721. [Google Scholar] [CrossRef]
- Zeleke, D.B.; Sachkov, A.M.; Malkov, O.Y.; Negu, S.H.; Tessema, S.B.; Grinenko, A.D. Resolved spectroscopic binaries: Orbital elements and parallaxes. Astrophys. Space Sci. 2025, 370, 1. [Google Scholar] [CrossRef]
- Taylor, S.F.; Harvin, J.A.; McAlister, H.A. The CHARA Catalog of Orbital Elements of Spectroscopic Binary Stars. Publ. Astron. Soc. Pac. 2003, 115, 609–617. [Google Scholar] [CrossRef][Green Version]
- Pourbaix, D.; Tokovinin, A.A.; Batten, A.H.; Fekel, F.C.; Hartkopf, W.I.; Levato, H.; Morrell, N.I.; Torres, G.; Udry, S. The ninth catalogue of spectroscopic binary orbits. Astron. Astrophys. 2004, 424, 727–732. [Google Scholar] [CrossRef]
- Zeleke, D.B.; Pakhomova, P.V.; Tessema, S.B.; Negu, S.H.; Malkov, O.Y. The Catalog of Resolved Spectroscopic Binaries: Development and Description. Astron. Rep. 2023, 67, 576–580. [Google Scholar] [CrossRef]
- Luo, A.; Zhao, Y.; Zhao, G.; Deng, L.; Liu, X.; Jing, Y.; Wang, G.; Zhang, H.; Shi, J.; Cui, X.; et al. The first data release (DR1) of the LAMOST regular survey. Res. Astron. Astrophys. 2015, 15, 1095. [Google Scholar] [CrossRef]
- Luo, A.L.; Zhao, Y.H.; Zhao, G. VizieR Online Data Catalog: LAMOST DR5 catalogs (Luo+, 2019). Vizier Online Data Cat. 2019, 5165, V / 164. [Google Scholar]
- Guo, S.; Kovalev, M.; Li, J.; Lü, G.; Jia, S.; Li, Z.; Li, J.; Xiong, J.; Yang, M.; Han, Z.; et al. Orbital Parameters of 665 Double-lined Spectroscopic Binaries in the LAMOST Medium-Resolution Survey. arXiv 2025, arXiv:2504.11954. [Google Scholar] [CrossRef]
- Jing, Y.; Mao, T.X.; Wang, J.; Liu, C.; Chen, X. Half a Million Binary Stars Identified from the Low-resolution Spectra of LAMOST. Astrophys. J. Suppl. Ser. 2025, 277, 15. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, B.; Wu, J.; Ting, Y.S. Double-lined Spectroscopic Binaries from the LAMOST Low-resolution Survey. Astrophys. J. Suppl. Ser.s 2024, 275, 40. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, S.; Liu, J. Searching for Accreting Compact Binary Systems from Spectroscopy and Photometry: Application to LAMOST Spectra. Astrophys. J. 2025, 984, 9. [Google Scholar] [CrossRef]
| Parameter | Designation | Unit of Measurement | Availability in RSBcat | Availability in SB9 |
|---|---|---|---|---|
| Orbit semi-major axis | a | mas | ✓ | |
| Orbital inclination | i | deg | ✓ | |
| Orbital parallax | mas | ✓ | ||
| Longitude of node | deg | ✓ | ||
| Mass of primary | ✓ | |||
| Mass of secondary | ✓ | |||
| Coordinates | , | deg | ✓ | ✓ |
| Period | P | yr | ✓ | ✓ |
| Periastron time | JD | ✓ | ✓ | |
| Orbital eccentricity | e | – | ✓ | ✓ |
| Argument of periastron | deg | ✓ | ✓ | |
| Trigonometric parallax (*) | mas | ✓ | ✓ | |
| B-flux (*) | mag | ✓ | ✓ | |
| V-flux (*) | mag | ✓ | ✓ | |
| G-flux (*) | mag | ✓ | ✓ | |
| J-flux (*) | mag | ✓ | ✓ | |
| H-flux (*) | mag | ✓ | ✓ | |
| K-flux (*) | mag | ✓ | ✓ | |
| Velocity amplitude of primary | km/s | ✓ | ||
| Velocity amplitude of secondary | km/s | ✓ | ||
| Systematic velocity | km/s | ✓ | ||
| Magnitude of component 1 | mag | ✓ | ||
| Magnitude of component 2 | mag | ✓ |
| SB9U | SB9R | SB9U-SB9R | Normalised | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Min | Max | Mean | Stddev | Min | Max | Mean | Stddev | Mean Diff. | Mean Diff. | |
| −1.273 | 4.972 | 3.332 | 2.131 | −0.056 | 5.056 | 4.440 | 2.527 | −1.107 | −0.203 | |
| e | 0 | 0.972 | 0.423 | 0.315 | 0 | 0.975 | 0.739 | 0.457 | −0.316 | −0.376 |
| −134.3 | 360.0 | 248.1 | 171.5 | 0 | 357.1 | 331.1 | 198.7 | −83.04 | −0.268 | |
| 0.001 | 379.2 | 18.99 | 17.90 | 0.538 | 742.1 | 72.33 | 74.69 | −53.34 | −0.083 | |
| −1.460 | 23.40 | 18.10 | 9.485 | 0.720 | 13.26 | 13.10 | 6.882 | 5.004 | 0.233 | |
| −1.460 | 22.77 | 17.10 | 9.028 | 0.010 | 11.52 | 11.84 | 6.228 | 5.267 | 0.252 | |
| 2.089 | 20.94 | 17.32 | 9.204 | 1.714 | 9.934 | 12.08 | 6.223 | 5.237 | 0.316 | |
| −2.300 | 18.63 | 14.84 | 7.990 | −1.454 | 7.563 | 9.761 | 5.109 | 5.085 | 0.282 | |
| −3.220 | 17.68 | 14.19 | 7.696 | −1.886 | 7.209 | 9.218 | 4.848 | 4.979 | 0.276 | |
| −3.510 | 17.49 | 13.95 | 7.584 | −2.008 | 7.121 | 9.049 | 4.764 | 4.906 | 0.271 | |
| 0.000 | 593.0 | 87.09 | 69.15 | 1.870 | 135.6 | 61.16 | 39.01 | 25.92 | 0.051 | |
| 0.000 | 457.0 | 219.4 | 139.9 | 2.960 | 201.0 | 75.29 | 48.52 | 144.1 | 0.366 | |
| −460.0 | 617.0 | −6.448 | 47.30 | −88.27 | 55.67 | 1.435 | 24.51 | −7.883 | −0.001 | |
| −1.470 | 22.50 | 17.24 | 9.096 | −0.010 | 11.48 | 12.02 | 6.303 | 5.221 | 0.253 | |
| 2.260 | 19.70 | 19.82 | 10.34 | 1.330 | 9.832 | 15.03 | 7.845 | 4.794 | 0.303 | |
| SB9 ID | RSBcat HIP | V, mag | SpType | P. day | , mas | ||
|---|---|---|---|---|---|---|---|
| CD -49 11403 | 103055 | 10.849 | 1318.2 | 1.1176 ± 0.0197 | 0.322 | 0.381 | |
| G 9-27 | 83064 | 12.050 | 1018.53 | 3.71 ± 0.1113 | 0.380 | 0.538 | |
| HIP 109767 | 102545 | 10.100 | K0 | 650.19 | 11.0174 ± 0.1428 | 0.451 | 0.248 |
| HIP 64787 | 77725 | 9.190 | G0V | 3751.0 | 8.6413 ± 0.055 | 0.480 | 0.293 |
| HIP 70534 | 10952 | 8.610 | K0 | 26,000.0 | 2.2475 ± 0.0402 | 0.514 | 0.188 |
| BD +17 2603 | 77725 | 9.800 | G6V | 9278.0 | 7.6548 ± 0.0267 | 0.523 | 0.303 |
| HIP 77122 | 83064 | 8.950 | 4290.0 | 9.8175 ± 0.0579 | 0.552 | 0.348 | |
| BD +51 2091 | 102545 | 9.580 | G5 | 247.08 | 3.5091 ± 0.024 | 0.554 | 0.276 |
| HIP 13498 | 83064 | 7.730 | G1V? | 18,794.0 | 11.9650 ± 0.3677 | 0.555 | 0.177 |
| HIP 17102 | 77725 | 9.050 | K2 | 183.113 | 25.4343 ± 0.0319 | 0.565 | 0.310 |
| BD +22 2581 | 77725 | 9.590 | G0V | 15,000.0 | 6.9482 ± 0.4934 | 0.570 | 0.333 |
| GAIADR2 45574 | 102545 | 11.020 | F9 | 18.4359535 | 2.7714 ± 0.0135 | 0.579 | 0.380 |
| 02515188596224 | |||||||
| HIP 56229 | 77725 | 9.750 | M0 | 186.3 | 22.7378 ± 0.0511 | 0.580 | 0.278 |
| HIP 56622 | 100287 | 8.320 | G7V | 1690.15 | 21.1416 ± 0.0165 | 0.615 | 0.165 |
| HIP 11537 | 77725 | 9.450 | G5V | 1146.44 | 15.5178 ± 0.4379 | 0.616 | 0.129 |
| HIP 101472 | 77725 | 9.380 | G8V | 354.88 | 11.3768 ± 0.0977 | 0.621 | 0.224 |
| HIP 88639 | 102545 | 10.600 | K7V | 25.7631 | 24.694 ± 0.0225 | 0.625 | 0.236 |
| HIP 105879 | 98416 | 7.180 | F7V | 2935.6 | 12.4373 ± 0.2139 | 0.626 | 0.203 |
| Gl 220 | 117415 | 9.918G | M1.5V | 721.0 | 47.7313 ± 0.5115 | 0.641 | 0.399 |
| HIP 117666 | 77725 | 8.730 | G5V | 10,984.0 | 13.3973 ± 1.2719 | 0.643 | 0.231 |
| 2E 3709 | 102545 | 12.230 | K7 | 35.95 | 5.9041 ± 0.3012 | 0.651 | 0.391 |
| HIP 107731 | 117415 | 8.640 | G1/G2V | 469.92 | 14.9306 ± 0.2675 | 0.652 | 0.224 |
| HIP 2563 | 19508 | 8.720 | 2127.82 | 17.315 ± 0.1009 | 0.660 | 0.245 | |
| BD +28 387 | 102545 | 11.000 | G0 | 41.2013 | 3.6606 ± 0.2174 | 0.669 | 0.359 |
| BD +29 2313 | 102545 | 10.140 | G8V | 17.778584 | 7.5141 ± 0.0185 | 0.669 | 0.325 |
| HIP 79979 | 98416 | 6.820 | F9V | 1083.16 | 25.5345 ± 0.232 | 0.671 | 0.165 |
| BD +29 2313 | 102545 | 10.140 | G8V | 17.7786 | 7.5141 ± 0.0185 | 0.673 | 0.325 |
| HIP 28432 | 4889 | 7.940 | Am | 60.6378 | 5.7711 ± 0.0371 | 0.674 | 0.338 |
| RX J0532.1-0732 | 102545 | 12.570 | K2-K3 | 46.85 | 2.7331 ± 0.0131 | 0.674 | 0.517 |
| HIP 91935 | 102545 | 8.310 | F5 | 34.8634 | 8.0971 ± 0.0169 | 0.675 | 0.151 |
| HIP 3428 | 102545 | 10.970 | K7V | 97.25 | 22.8103 ± 0.0695 | 0.677 | 0.303 |
| GAIADR2 30174 | 34603 | 11.130 | F9IV | 118.34 | 3.5561 ± 0.0279 | 0.690 | 0.568 |
| 02443157072768 | |||||||
| ADS 8861 | 77725 | 9.510 | dM1.5 | 200.26 | 72.9733 ± 0.3217 | 0.690 | 0.262 |
| GAIADR2 33168 | 77725 | 11.890 | 352.49 | 6.8078 ± 0.0557 | 0.690 | 0.515 | |
| 44608086144128 | |||||||
| HIP 105585 | 19508 | 8.100 | G8V | 87,658.0 | 30.24 ± 4.85 | 0.690 | 0.364 |
| Cl* Melotte | 102545 | 12.400 | K0III | 94.4384 | 3.4746 ± 0.0166 | 0.695 | 0.583 |
| 111 AV 390 | |||||||
| HIP 61732 | 77725 | 9.180 | G5 | 595.18 | 6.852 ± 0.3285 | 0.697 | 0.307 |
| HIP 84129 | 100287 | 7.140 | F5 | 556.213 | 14.3755 ± 0.0255 | 0.699 | 0.229 |
| SB9 ID | RSBcat HIP | V, mag | SpType | P. day | , mas | ||
|---|---|---|---|---|---|---|---|
| HIP 89925 | 99404 | 5.630 | A5m | 5.5146126 | 17.9191 ± 0.0489 | 1.264 | 0.050 |
| HIP 64478 | 20284 | 6.350 | G0V | 4.23345 | 23.1989 ± 0.0946 | 1.246 | 0.053 |
| HIP 105660 | 46704 | 6.160 | A2V | 6.9463 | 5.5323 ± 0.0768 | 1.207 | 0.063 |
| HIP 3572 | 52980 | 5.630 | A1V | 4.4672235 | 10.6528 ± 0.0511 | 1.278 | 0.065 |
| HIP 4572 | 52980 | 5.968 | A0III | 6.82054 | 9.1239 ± 0.0375 | 1.227 | 0.067 |
| HIP 61727 | 117186 | 7.590 | F5 | 54.87864 | 10.1467 ± 0.0382 | 1.033 | 0.073 |
| HIP 92117 | 52980 | 5.900 | A2Vm | 4.7653 | 10.8978 ± 0.0549 | 1.236 | 0.073 |
| HIP 66438 | 16042 | 5.630 | F6V | 8.0714 | 27.99 ± 0.58 | 1.380 | 0.074 |
| HIP 63143 | 52980 | 5.820 | A5m | 5.1259 | 11.54 ± 0.51 | 1.877 | 0.075 |
| HIP 95176 | 57565 | 4.610 | B8p+F2pe | 137.9343 | 2.0869 ± 0.1716 | 1.287 | 0.077 |
| HIP 42871 | 111170 | 6.543 | F7V | 700.3 | 13.3908 ± 0.0374 | 1.014 | 0.079 |
| HIP 31850 | 52980 | 6.360 | F8IV | 5.6983 | 27.6925 ± 0.0393 | 1.223 | 0.084 |
| HIP 107238 | 46704 | 6.220 | Am | 6.3702 | 8.9617 ± 0.0285 | 1.216 | 0.085 |
| HIP 759 | 18277 | 7.170 | G2V | 23.49785 | 19.3683 ± 0.0238 | 0.972 | 0.086 |
| HIP 68064 | 46704 | 6.790 | F2V | 4.9918 | 9.3946 ± 0.0234 | 1.192 | 0.087 |
| HIP 10961 | 46704 | 6.880 | F5 | 4.2220168 | 16.0685 ± 0.0202 | 1.200 | 0.089 |
| HIP 29746 | 20284 | 6.360 | F6V | 2.184952 | 13.6168 ± 0.8743 | 1.254 | 0.091 |
| HIP 48273 | 20284 | 6.230 | F6V | 3.05459836 | 21.1803 ± 0.1565 | 1.399 | 0.091 |
| HIP 43496 | 52980 | 5.540 | A4m | 2.8952 | 7.3105 ± 0.1725 | 1.420 | 0.092 |
| HIP 41564 | 52980 | 6.380 | A5m | 5.9771 | 13.41 ± 0.79 | 1.202 | 0.092 |
| HIP 10285 | 46704 | 7.170 | A7m | 4.1212 | 7.4227 ± 0.0192 | 1.176 | 0.093 |
| BD +45 172 | 111528 | 8.840 | G0 | 5556.0000 | 11.1479 ± 0.252 | 0.787 | 0.094 |
| HIP 113770 | 46704 | 7.390 | F8 | 5.21465 | 15.1122 ± 0.0242 | 1.164 | 0.095 |
| HIP 88581 | 46704 | 6.870 | O6.5V | 6.14 | 0.7893 ± 0.0297 | 1.135 | 0.095 |
| HIP 25776 | 22407 | 6.190 | A0V | 8.569 | 8.0907 ± 0.0381 | 1.482 | 0.095 |
| HIP 32067 | 46704 | 6.370 | O6e | 3.078098 | 0.7632 ± 0.0417 | 1.227 | 0.096 |
| HIP 48218 | 20284 | 6.090 | A8IV | 4.1467465 | 5.22 ± 0.63 | 1.242 | 0.096 |
| HIP 84586 | 20284 | 6.670 | G5IV | 1.6817 | 32.9511 ± 0.0184 | 1.264 | 0.097 |
| HIP 115500 | 22407 | 6.660 | F8 | 6.0499 | 15.0601 ± 0.0228 | 1.626 | 0.097 |
| HIP 2888 | 20284 | 6.780 | G3V | 3.7418 | 22.5227 ± 0.0179 | 1.212 | 0.098 |
| HIP 81305 | 99404 | 5.470 | O9Ia | 9.81475 | 0.7601 ± 0.0709 | 1.273 | 0.099 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeleke, D.B.; Sytov, A.Y.; Negu, S.H.; Sachkov, A.M.; Tessema, S.B.; Malkov, O.Y. On the Probability of the Astrometric Resolution of Spectroscopic Binaries into Components. Galaxies 2025, 13, 87. https://doi.org/10.3390/galaxies13040087
Zeleke DB, Sytov AY, Negu SH, Sachkov AM, Tessema SB, Malkov OY. On the Probability of the Astrometric Resolution of Spectroscopic Binaries into Components. Galaxies. 2025; 13(4):87. https://doi.org/10.3390/galaxies13040087
Chicago/Turabian StyleZeleke, Dugasa Belay, Alexey Yu. Sytov, Seblu Humne Negu, Arseniy M. Sachkov, Solomon Belay Tessema, and Oleg Yu. Malkov. 2025. "On the Probability of the Astrometric Resolution of Spectroscopic Binaries into Components" Galaxies 13, no. 4: 87. https://doi.org/10.3390/galaxies13040087
APA StyleZeleke, D. B., Sytov, A. Y., Negu, S. H., Sachkov, A. M., Tessema, S. B., & Malkov, O. Y. (2025). On the Probability of the Astrometric Resolution of Spectroscopic Binaries into Components. Galaxies, 13(4), 87. https://doi.org/10.3390/galaxies13040087









