The Galactic Pizza: Flat Rotation Curves in the Context of Cosmological Time-Energy Coupling
Abstract
1. Introduction
2. Newtonian Gravity with Variable Mass and Radius
2.1. Time-Dependent Gravitational Acceleration from Dimensional Analysis
2.2. Mass and Radius in Galaxy Formation Models
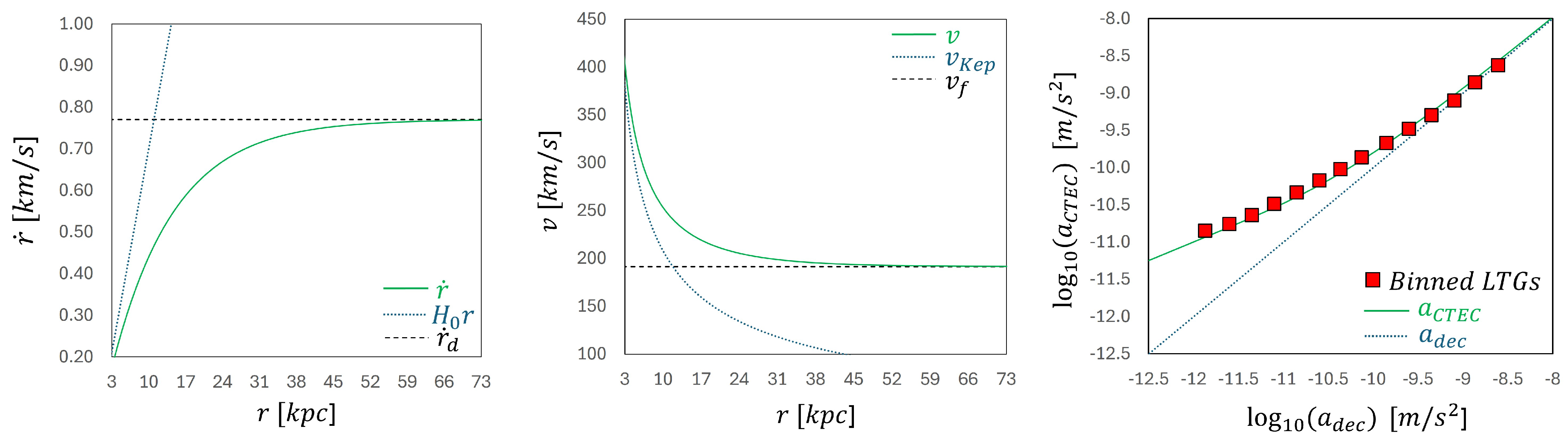
2.3. The Radial Acceleration Relation
2.4. The Baryonic Tully-Fisher Relation
3. The Galactic Pizza
4. Cosmological Time-Energy Coupling
5. The Cosmological Acceleration Scale
Notes on Total Energy Budget and Dark Energy
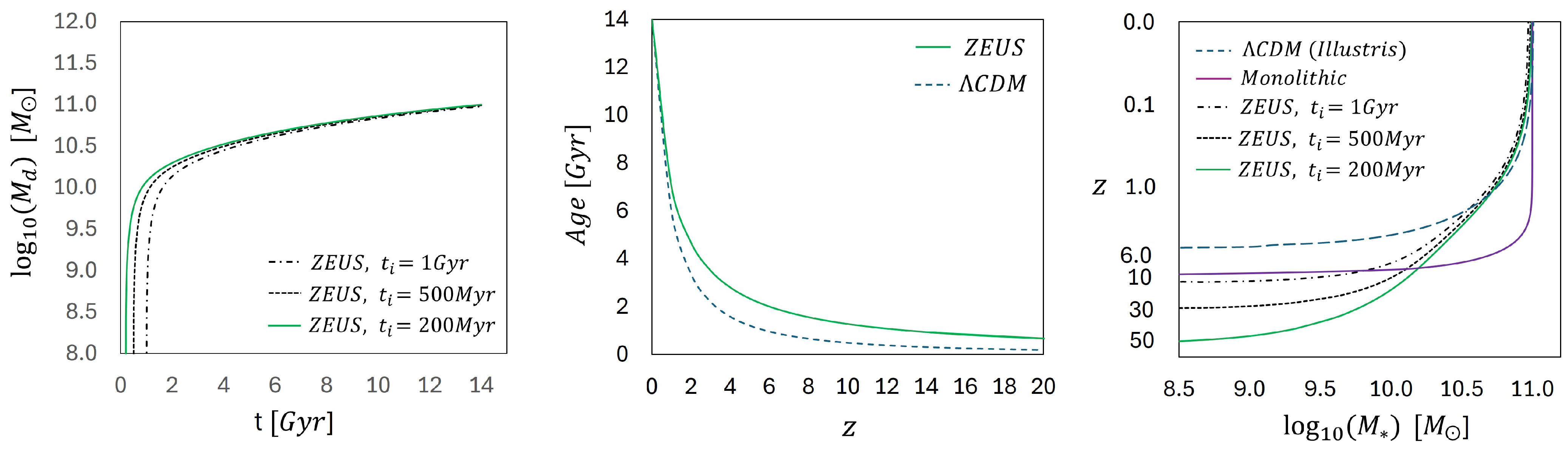
6. Early Galaxy Evolution
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rubin, V.; Ford, W.K.J. Rotation of the Andromeda Nebula from a Spectroscopic Survey of Emission Regions. Astrophys. J. 1970, 159, 379. [Google Scholar] [CrossRef]
- Rubin, V.; Ford, W.K.J.; Thonnard, N.; Burstein, D. Rotational properties of 23Sb galaxies. Astrophys. J. 1982, 261, 439–456. [Google Scholar] [CrossRef]
- Planck Collaboration; Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; et al. Planck 2018 results—VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar] [CrossRef]
- Paraficz, D.; Kneib, J.; Richard, J.; Morandi, A.; Limousin, M.; Jullo, E.; Martinez, J. The Bullet cluster at its best: Weighing stars, gas, and dark matter. Astron. Astrophys. 2016, 594, A121. [Google Scholar] [CrossRef]
- Cyburt, R.H.; Fields, B.D.; Olive, K.A.; Yeh, T.H. Big bang nucleosynthesis: Present status. Rev. Mod. Phys. 2016, 88, 015004. [Google Scholar] [CrossRef]
- Vogelsberger, M.; Genel, S.; Springel, V.; Torrey, P.; Sijacki, D.; Xu, D.; Snyder, G.; Nelson, D.; Hernquist, L. Introducing the Illustris Project: Simulating the coevolution of dark and visible matter in the Universe. Mon. Not. R. Astron. Soc. 2014, 444, 1518–1547. [Google Scholar] [CrossRef]
- de Martino, I.; Chakrabarty, S.S.; Cesare, V.; Gallo, A.; Ostorero, L.; Diaferio, A. Dark Matters on the Scale of Galaxies. Universe 2020, 6, 107. [Google Scholar] [CrossRef]
- Bergström, L. Dark matter evidence, particle physics candidates and detection methods. Ann. Phys. 2007, 524, 479–496. [Google Scholar] [CrossRef]
- Misiaszek, M.; Rossi, N. Direct Detection of Dark Matter: A Critical Review. Symmetry 2024, 16, 201. [Google Scholar] [CrossRef]
- Efstathiou, G.; Gratton, S. The evidence for a spatially flat Universe. Mon. Not. R. Astron. Soc. Lett. 2020, 496, L91–L95. [Google Scholar] [CrossRef]
- Kutschera, M.; Dyrda, M. Coincidence of Universe age in LCDM and Milne cosmologies. Phys. Pol. B 2007, 38, 215. [Google Scholar]
- Melia, F.; Shevchuk, A. The Rh=ct Universe. Mon. Not. R. Astron. Soc. 2012, 419, 2579–2586. [Google Scholar] [CrossRef]
- Novais, A.; Ribeiro, A.L.B. Lorentzian Correction for the evolution of the CMB Temperature. Astrophysics 2024, 67, 359–374. [Google Scholar] [CrossRef]
- Steinhardt, C.L.; Capak, P.; Masters, D.; Speagle, J.S. The Impossibly Early Galaxy Problem. Astrophys. J. 2016, 824, 21. [Google Scholar] [CrossRef]
- Melia, F. The premature formation of high-redshift galaxies. Astron. J. 2014, 147, 120. [Google Scholar] [CrossRef]
- Robertson, B. Identification and properties of intense star-forming galaxies at redshifts z greater than 10. Nat. Astron. 2023, 7, 611–621. [Google Scholar] [CrossRef]
- McGaugh, S.S.; Schombert, J.M.; Lelli, F.; Franck, J. Accelerated Structure Formation: The Early Emergence of Massive Galaxies and Clusters of Galaxies. Astrophys. J. 2024, 976, 13. [Google Scholar] [CrossRef]
- Maeder, A.; Gueorguiev, V.G. The Scale-Invariant Vacuum (SIV) Theory: A Possible Origin of Dark Matter and Dark Energy. Universe 2020, 6, 46. [Google Scholar] [CrossRef]
- Milgrom, M. A modification of the Newtonian dynamics as a possible alternative to the hidden mass hypothesis. Astrophys. J. 1983, 270, 365–370. [Google Scholar] [CrossRef]
- Roszkowski, L.; Sessolo, E.M.; Trojanowski, S. WIMP dark matter candidates and searches—Current status and future prospects. Rep. Prog. Phys. 2018, 81, 066201. [Google Scholar]
- Sanders, R.H.; McGaugh, S.S. Modified Newtonian Dynamics as an Alternative to Dark Matter. Annu. Rev. Astron. Astrophys. 2002, 40, 263–317. [Google Scholar] [CrossRef]
- Tully, R.; Fisher, J. A new method of determining distances to galaxies. Astron. Astrophys. 1977, 54, 661–673. [Google Scholar]
- Lelli, F.; McGaugh, S.S.; Schombert, J.M.; Pawlowski, M.S. One Law to Rule Them All: The Radial Acceleration Relation of Galaxies. Astrophys. J. 2017, 836, 152. [Google Scholar] [CrossRef]
- Mistele, T.; McGaugh, S.; Lelli, F.; Schombert, J.; Li, P. Indefinitely Flat Circular Velocities and the Baryonic Tully–Fisher Relation from Weak Lensing. Astrophys. J. Lett. 2024, 969, L3. [Google Scholar] [CrossRef]
- de Blok, W.J.G. The Core-Cusp Problem. Adv. Astron. 2010, 2010, 789293. [Google Scholar] [CrossRef]
- Kroupa, P. Galaxies as simple dynamical systems: Observational data disfavor dark matter and stochastic star formation. Can. J. Phys. 2015, 93, 169–202. [Google Scholar] [CrossRef]
- Boylan-Kolchin, M.; Bullock, J.S.; Kaplinghat, M. The Milky Way’s bright satellites as an apparent failure of LCDM. Mon. Not. R. Astron. Soc. 2012, 422, 1203–1218. [Google Scholar] [CrossRef]
- Kaplinghat, M.; Valli, M.; Yu, H.B. Too Big To Fail in Light of Gaia. Mon. Not. R. Astron. Soc. 2019, 490, 231–242. [Google Scholar] [CrossRef]
- Gentile, G.; Famaey, B.; de Blok, W.J.G. THINGS about MOND. Astron. Astrophys. 2011, 527, A76. [Google Scholar] [CrossRef]
- Banik, I.; Pittordis, C.; Sutherland, W.; Famaey, B.; Ibata, R.; Mieske, S.; Zhao, H. Strong constraints on the gravitational law from Gaia DR3 wide binaries. Mon. Not. R. Astron. Soc. 2023, 527, 4573–4615. [Google Scholar] [CrossRef]
- Milgrom, M. MOND theory. Can. J. Phys. 2015, 93, 107–118. [Google Scholar] [CrossRef]
- Sakr, Z.; Sapone, D. Can varying the gravitational constant alleviate the tensions? J. Cosmol. Astropart. Phys. 2022, 2022, 034. [Google Scholar] [CrossRef]
- van den Bosch, F.C. On the Origin and Evolution of Disk Galaxy Morphology. Mon. Not. R. Astron. Soc. 2002, 332, 456–464. [Google Scholar] [CrossRef][Green Version]
- Kassin, S.A.; Weiner, B.J.; Faber, S.M.; Gardner, J.P.; Willmer, C.N.A.; Coil, A.L.; Cooper, M.C.; Newman, J.A.; Charlot, S.; Conselice, C.J.; et al. The Assembly of Galaxy Disks at High Redshift. Astrophys. J. 2012, 758, 106. [Google Scholar] [CrossRef]
- Hopkins, P.F.; Quataert, E.; Murray, N. Stellar feedback in galaxies and the origin of galaxy-scale winds. Mon. Not. R. Astron. Soc. 2012, 421, 3522–3537. [Google Scholar] [CrossRef]
- Hester, J.A. Ram Pressure Stripping in Clusters and Groups. Astrophys. J. 2006, 647, 910. [Google Scholar] [CrossRef]
- Melia, F.; McClintock, T.M. Supermassive black holes in the early Universe. Proc. R. Soc. A 2015, 471, 20150449. [Google Scholar] [CrossRef]
- Navarro, J.F.; Frenk, C.S.; White, S.D. The Structure of Cold Dark Matter Halos. Astrophys. J. 1996, 462, 563. [Google Scholar] [CrossRef]
- Sancisi, R.; Fraternali, F.; Oosterloo, T.; van der Hulst, T. Cold gas accretion in galaxies. Astron. Astrophys. Rev. 2008, 15, 189–223. [Google Scholar] [CrossRef]
- Farrah, D.; Croker, K.S.; Zevin, M.; Tarlé, G.; Faraoni, V.; Petty, S.; Afonso, J.; Fernandez, N.; Nishimura, K.A.; Pearson, C.; et al. Observational Evidence for Cosmological Coupling of Black Holes and its Implications for an Astrophysical Source of Dark Energy. Astrophys. J. Lett. 2023, 944, L31. [Google Scholar] [CrossRef]
- Croker, K.S.; Tarlé, G.; Ahlen, S.P.; Cartwright, B.G.; Farrah, D.; Fernandez, N.; Windhorst, R.A. DESI dark energy time evolution is recovered by cosmologically coupled black holes. J. Cosmol. Astropart. Phys. 2024, 2024, 094. [Google Scholar] [CrossRef]
- Fahr, H.; Sokaliwska, M. The influence of gravitational binding energy on cosmic expansion dynamics: New perspectives for cosmology. Astrophys. Space Sci. 2012, 339, 379–387. [Google Scholar] [CrossRef]
- Maeder, A. MOND as a peculiar case of the SIV theory. Mon. Not. R. Astron. Soc. 2023, 520, 1447–1455. [Google Scholar] [CrossRef]
- Hunt, J.A.S.; Bovy, J.; Carlberg, R.G. Detection of a dearth of stars with zero angular momentum in the solar neighborhood. Astrophys. J. Lett. 2016, 832, L25. [Google Scholar] [CrossRef]
- Gueorguiev, V.G. Elucidating the z-dependence of the MOND acceleration (a0) within the scale invariant vacuum (SIV) paradigm. Mon. Not. R. Astron. Soc. Lett. 2024, 535, L13–L17. [Google Scholar] [CrossRef]
- Del Popolo, A.; Chan, M.H. Corrigendum to “On the time dependency of a0” [Phys. Dark Univ. (2024) DARK 101393]. Phys. Dark Universe 2024, 45, 101414. [Google Scholar] [CrossRef]
- Sancisi, R. The visible matter—Dark matter coupling. Symp. Int. Astron. Union 2004, 220, 233–240. [Google Scholar] [CrossRef]
- Criss, R.E.; Hofmeister, A.M. Density Profiles of 51 Galaxies from Parameter-Free Inverse Models of Their Measured Rotation Curves. Galaxies 2020, 8, 19. [Google Scholar] [CrossRef]
- McGaugh, S.S.; Schombert, J.M.; Bothun, G.D.; de Blok, W.J.G. The Baryonic Tully-Fisher Relation. Astrophys. J. 2000, 533, L99. [Google Scholar] [CrossRef]
- Valentino, E.D.; Mena, O.; Pan, S.; Visinelli, L.; Yang, W.; Melchiorri, A.; Mota, D.F.; Riess, A.G.; Silk, J. In the realm of the Hubble tension—A review of solutions*. Class. Quantum Gravity 2021, 38, 153001. [Google Scholar] [CrossRef]
- Carroll, S. The Cosmological Constant. Living Rev. Relativ. 2001, 4, 1. [Google Scholar] [CrossRef]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Omega and Lambda from 42 High-Redshift Supernovae. Astrophys. J. 1999, 517, 565. [Google Scholar] [CrossRef]
- Guth, A.H. Inflationary universe: A possible solution to the horizon and flatness problems. Phys. Rev. D 1981, 23, 347–356. [Google Scholar] [CrossRef]
- Hoyle, F. A New Model for the Expanding Universe. Mon. Not. R. Astron. Soc. 1948, 108, 372. [Google Scholar] [CrossRef]
- McVittie, G.C. The Mass-Particle in an Expanding Universe. Mon. Not. R. Astron. Soc. 1933, 93, 325–339. [Google Scholar] [CrossRef]
- Price, R.H.; Romano, J.D. In an expanding universe, what doesn’t expand? Am. J. Phys. 2012, 80, 376–381. [Google Scholar] [CrossRef]
- Faraoni, V.; Jacques, A. Cosmological expansion and local physics. Phys. Rev. D 2007, 76, 063510. [Google Scholar] [CrossRef]
- Giulini, D. Does cosmological expansion affect local physics? Stud. Hist. Philos. Sci. Part Stud. Hist. Philos. Mod. Phys. 2014, 46, 24–37. [Google Scholar] [CrossRef]
- Spengler, F.; Belenchia, A.; Rätzel, D.; Braun, D. Influence of cosmological expansion in local experiments. Class. Quantum Gravity 2022, 39, 055005. [Google Scholar] [CrossRef]
- Pathria, R.K. The Universe as a Black Hole. Nature 1972, 240, 298–299. [Google Scholar] [CrossRef]
- Smolin, L. Cosmological natural selection as the explanation for the complexity of the universe. Phys. Stat. Mech. Its Appl. 2004, 340, 705–713. [Google Scholar] [CrossRef]
- Gaztanaga, E. The Black Hole Universe, Part I. Symmetry 2022, 14, 1849. [Google Scholar] [CrossRef]
- Davis, T.M.; Lineweaver, C.H. Expanding Confusion: Common Misconceptions of Cosmological Horizons and the Superluminal Expansion of the Universe. Publ. Astron. Soc. Aust. 2004, 21, 97–109. [Google Scholar] [CrossRef]
- McGaugh, S.S. The Halo by Halo Missing Baryon Problem. Proc. Int. Astron. Union 2007, 3, 136–145. [Google Scholar] [CrossRef]
- Yang, K.B.; Wu, Q.; Wang, F.Y. Finding the Missing Baryons in the Intergalactic Medium with Localized Fast Radio Bursts. Astrophys. J. Lett. 2022, 940, L29. [Google Scholar] [CrossRef]
- Chodorowski, M. Cosmology Under Milne’s Shadow. Publ. Astron. Soc. Aust. 2005, 22, 287–291. [Google Scholar] [CrossRef]
- Melia, F. Cosmological test using the Hubble diagram of high-z quasars. Mon. Not. R. Astron. Soc. 2019, 489, 517–523. [Google Scholar] [CrossRef]
- Carniani, S.; Hainline, K.; D’Eugenio, F.; Eisenstein, D.J.; Jakobsen, P.; Witstok, J.; Johnson, B.D.; Chevallard, J.; Maiolino, R.; Helton, J.M.; et al. Spectroscopic confirmation of two luminous galaxies at a redshift of 14. Nature 2024, 633, 318–322. [Google Scholar] [CrossRef]
- Rodriguez-Gomez, V.; Pillepich, A.; Sales, L.V.; Genel, S.; Vogelsberger, M.; Zhu, Q.; Wellons, S.; Nelson, D.; Torrey, P.; Springel, V.; et al. The stellar mass assembly of galaxies in the Illustris simulation: Growth by mergers and the spatial distribution of accreted stars. Mon. Not. R. Astron. Soc. 2016, 458, 2371–2390. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Novais, A.; Ribeiro, A.L.B. The Galactic Pizza: Flat Rotation Curves in the Context of Cosmological Time-Energy Coupling. Galaxies 2025, 13, 51. https://doi.org/10.3390/galaxies13030051
Novais A, Ribeiro ALB. The Galactic Pizza: Flat Rotation Curves in the Context of Cosmological Time-Energy Coupling. Galaxies. 2025; 13(3):51. https://doi.org/10.3390/galaxies13030051
Chicago/Turabian StyleNovais, Artur, and André L. B. Ribeiro. 2025. "The Galactic Pizza: Flat Rotation Curves in the Context of Cosmological Time-Energy Coupling" Galaxies 13, no. 3: 51. https://doi.org/10.3390/galaxies13030051
APA StyleNovais, A., & Ribeiro, A. L. B. (2025). The Galactic Pizza: Flat Rotation Curves in the Context of Cosmological Time-Energy Coupling. Galaxies, 13(3), 51. https://doi.org/10.3390/galaxies13030051






